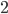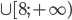ЕГЭ по математике — 2015. Досрочная волна, Запад.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Бегун пробежал 250 м за 36 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
Ответ:
2
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа за данный период впервые выпало ровно 1,5 миллиметра осадков.
Ответ:
3
Телефонная компания предоставляет на выбор три тарифных плана.
| Тарифный план | Абонентская плата
(в месяц) |
Плата за 1 минуту разговора |
|---|---|---|
| «Повременный» | Нет | 0,3 руб. |
| «Комбинированный» | 160 руб. за 420 мин. | 0,2 руб. (сверх 420 мин. в месяц) |
| «Безлимитный» | 255 руб. | Нет |
Абонент предполагает, что общая длительность разговоров составит 700 минут в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить абонент за месяц, если общая длительность разговоров действительно будет равна 700 минутам?
Ответ:
4
На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите синус этого угла.
Ответ:
5
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ:
6
Найдите корень уравнения
Ответ:
7
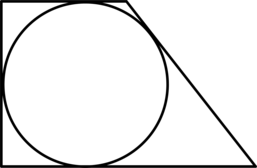
Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.
Ответ:
8
На рисунке изображён график функции y = f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?
Ответ:
9
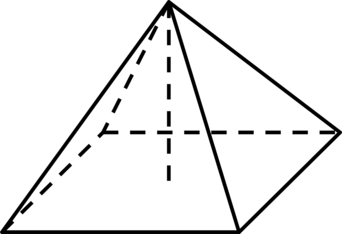
В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.
Ответ:
10
Найдите значение выражения
Ответ:
11
Водолазный колокол, содержащий υ = 2 моля воздуха при давлении p1 = 1,75 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением где
— постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
Ответ:
12
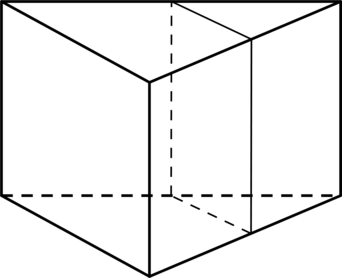
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 43. Найдите площадь боковой поверхности исходной призмы.
Ответ:
13
Смешав 24-процентный и 67-процентный растворы кислоты и добавив 10 кг чистой воды, получили 41-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси?
Ответ:
14
Найдите наибольшее значение функции на отрезке
Ответ:
15
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.
а) Докажите, что A1P: PB1 = 2:1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H , точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара.
За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
20
Найдите все значения a, при каждом из которых система уравнений
имеет ровно два различных решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
21
На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Реальные варианты ЕГЭ 2015
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Пёс Барбос пробежал (500 м) за (1,5 минуты). Найдите его среднюю скорость. Ответ дайте в километрах в час.
Так как средняя скорость есть отношение всего пути к затраченному на него времени, то средняя скорость пса Барбоса равна [dfrac{500}{1,5} dfrac{text{м}}{text{мин}} = dfrac{1000}{3}
dfrac{text{м}}{text{мин}} = dfrac{1}{3}
dfrac{text{км}}{text{мин}} = dfrac{20}{60}
dfrac{text{км}}{text{мин}} = 20 dfrac{text{км}}{text{ч}}]
Ответ: 20
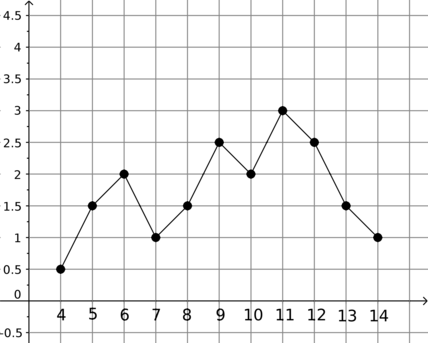
На рисунке жирными точками показано суточное количество осадков, выпавших в Кирове с (4) по (14) декабря (2000) года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день (в мм). Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа в Кирове впервые выпало (2,5 мм) осадков.
По рисунку видно, что в Кирове впервые выпало (2,5 мм) осадков (9) числа.
Ответ: 9
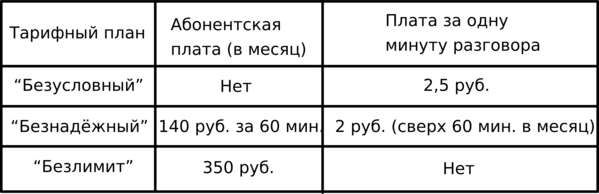
Телефонная компания предоставляет на выбор три тарифных плана.
Абонент надеется, что общая длительность разговоров составит (180
минут) в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить абонент за месяц, если общая длительность разговоров действительно будет равна (180
минутам)?
По тарифному плану “Безусловный” (180 минут) обойдутся в (2,5cdot 180 = 450 руб).
По тарифному плану “Безнадёжный” (180 минут) обойдутся в (140 + (180 — 60)cdot 2 = 380 руб).
По тарифному плану “Безлимит” (180 минут) обойдутся в (350 руб).
Наиболее выгодный план – “Безлимит”. Ответ: (350 руб).
Ответ: 350
На клетчатой бумаге с размером клетки (1times 1) изображён угол. Найдите косинус этого угла.
По рисунку видно, что данный угол является острым углом в прямоугольном треугольнике с катетами (3) и (4) единицы (катет, равный (3) единицам – прилежащий к рассматриваемому углу). По теореме Пифагора гипотенуза в таком треугольнике равна (sqrt{4^2 +
3^2} = 5), следовательно, косинус рассматриваемого угла равен (0,6).
Ответ: 0,6
Арья и Санса играют в шахматы. Играя белыми, Арья выигрывает с вероятностью (0,38). Играя чёрными, Арья выигрывает с вероятностью (0,4). Арья и Санса играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что Арья выиграет оба раза.
Так как Арья один раз играет белыми и один раз играет чёрными фигурами, то вероятность того, что она выиграет оба раза, равна (0,38cdot 0,4 = 0,152).
Ответ: 0,152
Найдите корень уравнения [121^{x + 2} = dfrac{1}{11}]
Исходное уравнение равносильно [11^{2x + 4} = 11^{-1}qquadLeftrightarrowqquad 2x + 4 = -1qquadLeftrightarrowqquad x = -2,5,.]
Ответ: -2,5
Периметр прямоугольной трапеции, в которую вписана окружность, равен (25), а одна из её боковых сторон равна (7). Найдите радиус вписанной окружности.
Суммы противоположных сторон описанного четырёхугольника равны, тогда сумма боковых сторон данной трапеции равна сумме оснований и равна (25 : 2 = 12,5).
Так как одна из боковых сторон равна (7), то другая боковая сторона равна (12,5 — 7 = 5,5). Кроме того, меньшая из боковых сторон равна диаметру вписанной окружности, следовательно, радиус данной вписанной окружности равен (0,5cdot 5,5 = 2,75).
Ответ: 2,75
На рисунке изображён график функции (y = f(x)). На оси абсцисс отмечены семь точек: (x_1), (x_2), (x_3), (x_4), (x_5), (x_6), (x_7). В скольких из этих точек производная функции (f(x)) отрицательна?
Производная отрицательна там, где функция убывает. В данном случае, (f'(x) < 0) в точках (x_4), (x_6), (x_7), то есть в трёх точках.
Ответ: 3
В правильной четырёхугольной пирамиде высота равна (3), а боковое ребро равно (3sqrt{3}). Найдите её объём.
Рассмотрим правильную четырёхугольную пирамиду как на рисунке
По теореме Пифагора [FD = sqrt{ED^2 — EF^2} = 3sqrt{2},,] тогда (BD = 6sqrt{2}), следовательно, по теореме Пифагора [AD^2 = BD^2 — AB^2qquadRightarrowqquad BD^2 = 2AD^2qquadRightarrowqquad AD = 6,.] [V_{text{пирамиды}} = dfrac{1}{3}cdot EFcdot S_{ABCD} =
dfrac{1}{3}cdot 3cdot 6^2 = 36,.]
Ответ: 36
Найдите значение выражения [dfrac{sqrt[4]{7}cdot 7cdotsqrt[8]{7^3}}{sqrt[8]{7}cdotsqrt{7}}]
Исходное выражение равносильно [dfrac{sqrt[4]{7}cdot 7cdotsqrt[8]{7^3}}{sqrt[8]{7}cdotsqrt{7}} =
7^{frac{1}{4} + 1 + frac{3}{8} — frac{1}{8} — frac{1}{2}} = 7^1 = 7,.]
Ответ: 7
Водолазный колокол, содержащий (nu = 1 моль) воздуха при давлении (p_1 = 1,5 атмосферы), медленно опускают на дно бака, заполненного водой. При этом происходит изотермическое сжатие воздуха до конечного давления (p_2). Работа, совершаемая водой при сжатии воздуха, определяется выражением (A = alphanu
Tlog_2dfrac{p_2}{p_1}), где (alpha = 13,3
dfrac{text{Дж}}{text{моль}cdot K}), (T = 290 К) – температура воздуха. Найдите давление (p_2) в атмосферах, которое должен иметь воздух в колоколе, чтобы при сжатии воздуха была совершена работа (7714 Дж).
По условию задачи требуется найти (p_2), такое что [7714 text{Дж} = 13,3cdot 1cdot 290cdot log_2dfrac{p_2}{1,5} text{Дж},,] откуда (2 = log_2 dfrac{p_2}{1,5}), следовательно, [log_2 4 = log_2 dfrac{p_2}{1,5}qquadRightarrowqquad 4 = dfrac{p_2}{1,5}qquadRightarrowqquad p_2 = 6,.]
Ответ: 6
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна (0,75). Найдите площадь боковой поверхности исходной призмы.
Рассмотрим призму как на рисунке
(QM) – средняя линия в параллелограмме (CC_1B_1B), тогда (S_{CC_1B_1B} = 2S_{QMBB_1}).
Аналогично (S_{AA_1B_1B} = 2S_{PNBB_1}).
(MNparallel AC), (QMparallel C_1C), следовательно, (angle ACC_1 =
angle NMQ), при этом (MN = dfrac{1}{2}AC), (QM = CC_1) ((QMCC_1) – параллелограмм по определению). Таким образом, (S_{AA_1C_1C} =
2S_{PQMN}), следовательно, площадь боковой поверхности исходной призмы в два раза больше, чем площадь боковой поверхности отсечённой призмы, и равна (1,5).
Ответ: 1,5
В лаборатории смешали (15)-процентный и (7)-процентный растворы кислоты, и добавив (4,9 кг) чистой воды, получили (10)-процентный раствор кислоты. Если бы вместо (4,9 кг) воды добавили (3 кг) (7)-процентного раствора той же кислоты, то получили бы (11)-процентный раствор кислоты. Сколько килограммов (15)-процентного раствора использовали для получения смеси?
Пусть (15)-процентного раствора было (x кг), а
(7)-процентного раствора было (y кг), тогда [0,15x + 0,07y = 0,1(x + y + 4,9),,] кроме того, по условию при добавлении (3 кг) (7)-процентного раствора той же кислоты вместо (4,9 кг) воды, получили бы (11)-процентный раствор кислоты [0,15x + 0,07y + 0,07cdot 3 = 0,11(x + y + 3),.] Вычитая первое уравнение из второго, получим [0,21 = 0,01(x + y) — 0,16,,] откуда (x + y = 37). Подставляя (y = 37 — x) в первое уравнение, находим [x = 20,.]
Ответ: 20
Найдите наибольшее значение функции [y = 71x + 65cos x + 21]
на отрезке ([-pi; 0]).
ОДЗ: (x) – произвольный. [y’ = 71 — 65sin x,.] [y’ = 0qquadLeftrightarrowqquad 71 — 65sin x = 0,.] Так как (|sin x|leqslant 1), то у уравнения (y’ = 0) решений нет. Тогда у данной функции (y) производная (y’) всюду принимает значения одного знака. Определить этот знак можно, подставив любое число в (y’), например, (x = 0): [y'(0) = 71 > 0,,] то есть (y’ > 0) при всех (x), значит, функция (y) возрастает на (mathbb{R}), откуда следует, что наибольшее на отрезке ([-pi; 0]) значение она принимает на конце отрезка, то есть в точке (x = 0): [y(0) = 71cdot 0 + 65cdot cos 0 + 21 = 86,.]
Ответ: 86
а) Решите уравнение [2sqrt{3}cos x + 2sin 2x = 3 + 2sqrt{3}sin x]
б) Найдите все корни этого уравнения, принадлежащие отрезку ([0;
pi]).
а) ОДЗ: (x) – произвольный.
По формуле синуса двойного угла:
[begin{aligned}
&2sqrt{3}cos x + 4sin xcdotcos x = 3 + 2sqrt{3}sin xqquadLeftrightarrow\
Leftrightarrowqquad & (2sqrt{3}cos x + 4sin xcdotcos x) — (3 + 2sqrt{3}sin x) = 0qquadLeftrightarrow\
Leftrightarrowqquad & 4cos xleft(dfrac{sqrt{3}}{2} + sin xright) — 2sqrt{3}left(dfrac{sqrt{3}}{2} + sin xright) = 0qquadLeftrightarrow\
Leftrightarrowqquad & (4cos x — 2sqrt{3})left(dfrac{sqrt{3}}{2} + sin xright) = 0qquadLeftrightarrow\
Leftrightarrowqquad & left(cos x —
dfrac{sqrt{3}}{2}right)left(dfrac{sqrt{3}}{2} + sin xright)
= 0,,
end{aligned}]
откуда (cos x = dfrac{sqrt{3}}{2}) или (sin x = -dfrac{sqrt{3}}{2}).
1) (cos x = dfrac{sqrt{3}}{2}), тогда (x = pmdfrac{pi}{6} + 2pi k), (kinmathbb{Z}).
2) (sin x = -dfrac{sqrt{3}}{2}), тогда (x = -dfrac{pi}{3} +
2pi n), (x = dfrac{4pi}{3} + 2pi m), (n,minmathbb{Z}).
б) (0 leqslant dfrac{pi}{6} + 2pi k_1 leqslant pi) равносильно (-dfrac{pi}{6} leqslant 2pi k_1 leqslant dfrac{5pi}{6}), что равносильно (-dfrac{1}{12} leqslant k_1 leqslant dfrac{5}{12}), но (k_1inmathbb{Z}), следовательно, среди этих решений подходит только решение при (k_1 = 0): (x = dfrac{pi}{6}).
(0 leqslant -dfrac{pi}{6} + 2pi k_2 leqslant pi) равносильно (dfrac{pi}{6} leqslant 2pi k_2 leqslant dfrac{7pi}{6}), что равносильно (dfrac{1}{12} leqslant k_2 leqslant dfrac{7}{12}), но (k_2inmathbb{Z}), следовательно, среди этих решений подходящих нет.
(0 leqslant -dfrac{pi}{3} + 2pi n leqslant pi) равносильно (dfrac{pi}{3} leqslant 2pi n leqslant dfrac{4pi}{3}), что равносильно (dfrac{1}{6} leqslant n leqslant dfrac{2}{3}), но (ninmathbb{Z}), следовательно, среди этих решений подходящих нет.
(0 leqslant dfrac{4pi}{3} + 2pi m leqslant pi) равносильно (-dfrac{4pi}{3} leqslant 2pi m leqslant -dfrac{pi}{3}), что равносильно (-dfrac{2}{3} leqslant m leqslant -dfrac{1}{6}), но (minmathbb{Z}), следовательно, среди этих решений подходящих нет.
Ответ:
а) (pmdfrac{pi}{6} + 2pi k, -dfrac{pi}{3} + 2pi n,
dfrac{4pi}{3} + 2pi m, k,n,minmathbb{Z})
б) (dfrac{pi}{6})
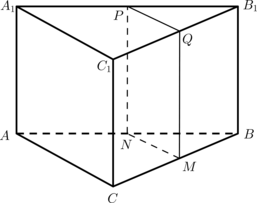
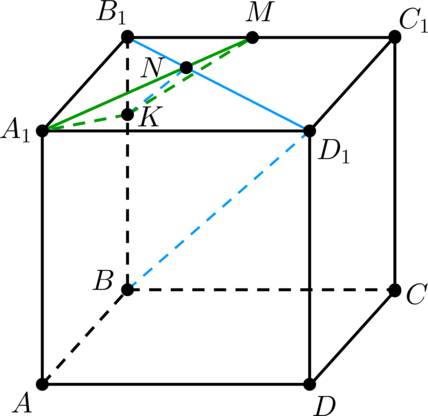
(ABCDA_1B_1C_1D_1) – куб. На ребре (BB_1) отмечена точка (K) так, что (KB : KB_1 = 3 : 1). Через точки (K) и (A_1) проведена плоскость (pi), параллельная прямой (BD_1).
а) Докажите, что (C_1M : MB_1 = 2 : 1), где (M) – точка пересечения плоскости (pi) с ребром (B_1C_1).
б) Найдите угол между плоскостями ((A_1B_1B)) и (pi).
а) Рассмотрим треугольник (BB_1D_1). Пусть (N) – точка на (B_1D_1) такая, что (KNparallel BD_1). Плоскость (pi) проходит через точку (N), так как (piparallel BD_1) и (pi) проходит через точку (K), а (KNparallel BD_1).
Тогда (M) – точка пересечения (A_1N) и (B_1C_1). Так как (KNparallel BD_1), то (angle B_1KN = angle B_1BD_1). Рассмотрим треугольники (B_1KN) и (B_1BD_1). Они подобны по двум углам, откуда [dfrac{B_1N}{B_1D_1} = dfrac{B_1K}{B_1B} = dfrac{B_1K}{B_1K +
KB} = dfrac{B_1K}{B_1K + 3B_1K} = dfrac{1}{4},,] следовательно, [dfrac{B_1N}{ND_1} = dfrac{B_1N}{B_1D_1 — B_1N} =
dfrac{B_1N}{4B_1N — B_1N} = dfrac{1}{3},.]
Рассмотрим треугольники (A_1ND_1) и (B_1NM). Так как (B_1Mparallel
A_1D_1), то (angle NB_1M = angle ND_1A_1), (angle NMB_1 = angle
NA_1D_1), следовательно, треугольники (A_1ND_1) и (B_1NM) подобны по двум углам, откуда [dfrac{B_1M}{A_1D_1} = dfrac{B_1N}{ND_1} =
dfrac{1}{3},,] следовательно, [B_1M = dfrac{1}{3}B_1C_1,,] откуда и получается доказываемое утверждение.
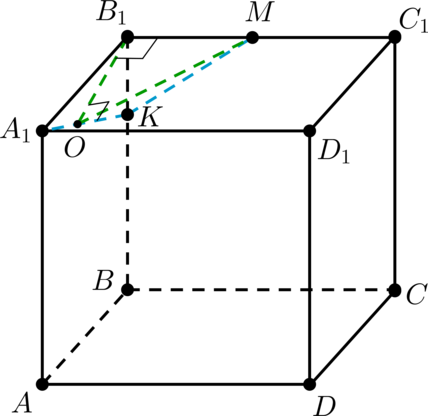
б) Опустим из точки (B_1) перпендикуляр (B_1O) на (A_1K). Так как (B_1Mperp (A_1B_1B)), то (B_1O) – проекция (MO) на плоскость ((A_1B_1B)) и (angle B_1OM) – искомый.
Треугольники (A_1B_1O) и (A_1B_1K) подобны, откуда [dfrac{B_1O}{B_1K} = dfrac{A_1B_1}{A_1K} =
dfrac{A_1B_1}{sqrt{{A_1B_1}^2 + B_1K^2}} =
dfrac{A_1B_1}{A_1B_1frac{sqrt{17}}{4}} =
dfrac{4}{sqrt{17}},,] следовательно, [mathrm{tg}, angle
B_1OM = dfrac{B_1M}{B_1O} =
dfrac{frac{1}{3}A_1B_1}{frac{1}{sqrt{17}}A_1B_1} =
dfrac{sqrt{17}}{3},,] следовательно, искомый угол равен (mathrm{arctg}, dfrac{sqrt{17}}{3}).
Ответ:
б) (mathrm{arctg}, dfrac{sqrt{17}}{3})
Решите неравенство [log_6^2 (36 — x^2) — 8log_6(36 — x^2) + 7 geqslant 0]
ОДЗ:
[begin{aligned}
36 — x^2 > 0qquadLeftrightarrowqquad xin(-6; 6)
end{aligned}]
Решим на ОДЗ. Сделаем замену (t = log_6(36 —
x^2)):
[begin{aligned}
t^2 — 8t + 7 geqslant 0qquadLeftrightarrowqquad (t — 7)(t —
1)geqslant 0
end{aligned}]
По методу интервалов:
откуда (t leqslant 1) или (tgeqslant 7).
1) (tleqslant 1), тогда на ОДЗ [log_6(36 — x^2)leqslant 1quadLeftrightarrowquad log_6(36 — x^2)leqslant log_6 6quadLeftrightarrowquad 36 — x^2leqslant 6quadLeftrightarrowquad x^2geqslant 30,,] откуда с учётом ОДЗ (xin (-6; -sqrt{30}]cup[sqrt{30}; 6)).
2) (tgeqslant 7), тогда на ОДЗ [log_6(36 — x^2)geqslant 7quadLeftrightarrowquad log_6(36 — x^2)geqslant log_6 6^7quadLeftrightarrowquad 36 — x^2geqslant 6^7,,] но тогда (x^2leqslant 6^2 — 6^7 < 0), чего быть не может.
В итоге ответ: [xin (-6; -sqrt{30}]cup[sqrt{30}; 6),.]
Ответ:
((-6; -sqrt{30}]cup[sqrt{30}; 6))
Окружность с центром (O) построена на боковой стороне (AB) равнобедренной трапеции (ABCD) как на диаметре. Эта окружность касается стороны (CD) и второй раз пересекает большее основание (AD) в точке (N). Точка (M) – середина (CD).
а) Докажите, что (OMDN) – параллелограмм.
б) Найдите (AD), если (angle BAD = 75^circ) и (BC = 4).
а) (ON = OA) – как радиусы. Так как трапеция (ABCD) равнобедренная, то (MD = OA = ON).
Так как (OA = ON), то (angle OAN = angle ONA), но (angle OAN =
angle MDA), следовательно, (angle ONA = angle MDA), тогда (ONparallel MD).
В итоге стороны (ON) и (MD) четырёхугольника (ONDM) параллельны и равны, следовательно, (ONDM) – параллелограмм.
б) [ND = OM = dfrac{AD + BC}{2} = dfrac{AD}{2} +
2quadRightarrowquad AN = dfrac{AD}{2} — 2,quad ND = AN + 4,.]
Пусть (B’) – проекция точки (B) на (AD), тогда [AB’ = dfrac{AD —
BC}{2} = dfrac{AD}{2} — 2 = AN,,] следовательно, точки (B’) и (N) совпадают и (BNperp AD).
Пусть радиус данной окружности равен (r), (BN = h), тогда из треугольника (ABN): [AN^2 = 4r^2 — h^2,qquad AN = dfrac{h}{mathrm{tg}, 75^circ}]
Пусть (P) – точка касания данной окружности и (CD), тогда (OPperp
CD). Так как внутренние накрест лежащие углы при параллельных прямых и секущей равны, то [angle PMO = angle MON = angle ONA = angle OAN = 75^circ,.]
Таким образом, прямоугольные треугольники (POM) и (ABN) подобны по острому углу, следовательно, [dfrac{OP}{BN} = dfrac{OM}{AB}qquadRightarrowqquad dfrac{r}{h} = dfrac{AN + 4}{2r},.]
Найдём (mathrm{tg}, 75^circ) при помощи формулы тангенса половинного угла: [mathrm{tg}, 75^circ = mathrm{tg}, dfrac{150^circ}{2} = dfrac{sin 150^circ}{1 + cos 150^circ} = dfrac{frac{1}{2}}{1 — frac{sqrt{3}}{2}} = dfrac{1}{2 — sqrt{3}},.]
Тогда [AN = (2 — sqrt{3})h,qquad (2 — sqrt{3})^2h^2 = 4r^2 —
h^2,qquad dfrac{r}{h} = dfrac{(2 — sqrt{3})h + 4}{2r},,] откуда (r = hsqrt{2 — sqrt{3}}), [2r^2 = (2 — sqrt{3})h^2 + 4hquadRightarrowquad (2 — sqrt{3})h^2 = 4hquadRightarrowquad h = dfrac{4}{2 — sqrt{3}},,] тогда (AN = 4), откуда (ND = 
Ответ:
б) (12)
Компании N принадлежат две шахты в разных городах. В шахтах добываются абсолютно одинаковые минералы, но в шахте, расположенной в первом городе, используется более современное оборудование. В результате, если рабочие первой шахты трудятся суммарно (t^2) часов в день, то за день они добывают (8t) единиц минералов, а рабочие второй шахты за те же (t^2) часов в день добывают (6t) единиц минералов. За каждый час работы компания (N) платит каждому своему рабочему по (100) рублей. Компания готова выделять (1, 000, 000) рублей в день на оплату труда рабочих. Какое наибольшее количество единиц минералов можно добыть за день на этих двух шахтах?
Компания N готова оплачивать (10000) часов в день.
Пусть (x^2) часов в день суммарно трудятся рабочие первой шахты,
Пусть (y^2) часов в день суммарно трудятся рабочие второй шахты, тогда [x^2 + y^2 = 10000,.]
Обозначим за (S) количество суммарно добытых за день единиц минералов, тогда [S = 8x + 6y]
Так как (y = sqrt{10000 — x^2}), то [S(x) = 8x + 6sqrt{10000 — x^2},.]
ОДЗ: (xin[-100; 100]). Необходимо найти наибольшее значение функции (S(x)) при (xin[0; 100]). [S'(x) = 8 — 6cdotdfrac{x}{sqrt{10000 — x^2}} = 0]
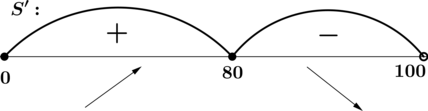
Критические точки функции (S(x)) – это внутренние точки её области определения, в которых её производная равна (0) или не определена. (S'(x) = 0) при (x = 80).
Найдём промежутки возрастания/убывания (S(x)) на ([0; 100]):
то есть (x = 80) точка локального максимума. Кроме того, (S'(x)) не определена при (x = pm 100). Легко убедиться, что среди этих (x), попадающих на отрезок ([0; 100]), наибольшее значение (S(x)) достигается при (x = 80). Более того, (S(80) > S(0)), следовательно, (S(80)) – наибольшее значение функции (S(x)) на отрезке ([0; 100]). [S(80) = 640 + 360 = 1000,.]
Ответ:
(1000)
Найдите все значения параметра (a), при каждом из которых система уравнений
[begin{aligned}
begin{cases}
dfrac{(y^2 — xy + x — y)sqrt{x + 4}}{sqrt{3 — x}} = 0\
a = x + y
end{cases}
end{aligned}]
имеет ровно два различных решения
ОДЗ:
[begin{aligned}
begin{cases}
3 — x > 0\
x + 4geqslant 0
end{cases}
qquadLeftrightarrowqquad -4leqslant x < 3
end{aligned}]
Заметим, что при любом (ainmathbb{R}) у системы имеется решение [x = -4,qquad y = a + 4,,] таким образом, с учётом того, что (y
= -x + a), задача может быть переформулирована так: найти значения параметра (a), при каждом из которых на множестве ((-4; 3)) уравнение
[begin{aligned}
(-x + a)^2 — x(-x + a) + x — (-x + a) = 0quadLeftrightarrowquad
2x^2 + (2 — 3a)x + a^2 — a = 0
end{aligned}]
имеет ровно одно решение.
Решения данного уравнения: [x = dfrac{3a — 2 pm(a — 2)}{4}qquadLeftrightarrowqquad
left[
begin{gathered}
x = a — 1\
x = 0,5a,,
end{gathered}
right.] следовательно, у данного уравнения одно решение только при (a = 2). При этом это решение (x = 1) – подходит по условию, следовательно, (a = 2) идёт в ответ.
При (aneq 2) у данного уравнения два различных решения. По условию необходимо и достаточно, чтобы среди этих решений ровно одно попало на интервал ((-4; 3)).
1) Пусть (-4 < a — 1 < 3), тогда (-3 < a < 4), следовательно, (-1,5 < 0,5a < 2), то есть тогда и второе решение попадает в этот интервал, что не подходит по условию.
2) Пусть (-4 < 0,5a < 3), тогда (-8 < a < 6), следовательно, (-9 < a
— 1 < 5), то есть второе решение не попадает в этот интервал только при условии [left[
begin{gathered}
-9 < a — 1 leqslant — 4\
3 leqslant a — 1 < 5
end{gathered}
right. qquadLeftrightarrowqquad left[
begin{gathered}
-8 < a leqslant — 3\
4 leqslant a < 6
end{gathered}
right.]
Таким образом, ответ [ain (-8; -3]cup{2}cup[4; 6),.]
Ответ:
((-8; -3]cup{2}cup[4; 6))
На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной (330). В каждом числе поменяли местами первую и вторую цифры (например, число (17) заменили на число (71)).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в (4) раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в (2) раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Пусть (i-)ое выписанное число имеет вид (10cdot a_i + b_i), где (a_i, b_i in {1, 2, …, 9}). Для суммы (b_i) по всем значениям индекса (i), таким, что слагаемое (b_i) есть этой в сумме, используем обозначение (underset{i}{Sigma} b_i). Тогда сумма всех исходных чисел имеет вид [underset{i}{Sigma} (10a_i + b_i) =
10cdotunderset{i}{Sigma} a_i + underset{i}{Sigma} b_i.] Обозначим (A = underset{i}{Sigma} a_i), (B = underset{i}{Sigma}
b_i), тогда (330 = 10cdot A + B).
После смены мест цифр (i-)ое полученное число имеет вид (10cdot b_i
+ a_i). Тогда сумма всех полученных чисел имеет вид [underset{i}{Sigma} (10b_i + a_i) = 10cdotunderset{i}{Sigma}
b_i + underset{i}{Sigma} a_i = 10cdot B + A.]
а) Увеличение суммы в (4) раза равносильно тому, что новая сумма равна (330cdot 4 = 1320), что равносильно (10cdot B + A = 1320). Рассмотрим систему
[begin{aligned}
begin{cases}
10cdot A + B = 330\
A + 10cdot B = 1320
end{cases}
end{aligned}]
вычитая из второго уравнения первое, находим, что (9cdot B — 9cdot
A = 990), откуда (B = 110 + A). Подставляя это в первое уравнение системы, находим (A = 20), тогда (B = 130).
Попробуем брать в качестве (b_i) (9), пока их сумма не превосходит (130) – так можно положить [b_1 = … = b_{14} = 9,quad b_{15} =
130 — 14cdot 9 = 4,] то есть в сумме (15) слагаемых. Тогда можно положить [a_1 = … = a_{14} = 1,quad a_{15} = 20 — 14cdot 1 =
6.]
б) Увеличение суммы в (2) раза равносильно тому, что новая сумма равна (330cdot 2 = 660), что равносильно (10cdot B + A = 660). Рассмотрим систему
[begin{aligned}
begin{cases}
10cdot A + B = 330\
A + 10cdot B = 660
end{cases}
end{aligned}]
вычитая из второго уравнения первое, находим, что (9cdot B — 9cdot
A = 330), но (330) не делится на (9), следовательно, такой случай не возможен.
в) Пусть сумма полученных чисел равна (S), что равносильно системе
[begin{aligned}
begin{cases}
10cdot A + B = 330\
A + 10cdot B = S
end{cases}
end{aligned}]
вычитая из второго уравнения первое, находим, что [9cdot B —
9cdot A = S — 330,] откуда [B = dfrac{S}{9} — dfrac{110}{3} +
A.] Подставляя это в первое уравнение системы, находим [A =
dfrac{100}{3} — dfrac{S}{99},] откуда в частности следует, что [dfrac{S}{99} = s + dfrac{1}{3},] то есть (S = 99s + 33) для некоторого целого неотрицательного (s), тогда (A = 33 — s), (B =
10s).
Покажем, что (B < 170):
в самом деле, если бы было (Bgeqslant 170), тогда число слагаемых в исходной сумме было бы не менее, чем (19) (так как (18cdot 9 <
170)), но тогда [10cdot A + B geqslant 190 + 170 > 330.]
Так как (B < 170), то (10s < 170), то есть (sleqslant 16).
При (s = 16) получим (A = 17), (B = 160), но даже (17cdot 9 = 153 < B), а количество чисел не может быть больше, чем (17 (= A)), следовательно, (sleqslant 15).
При (s = 15) получим (A = 18), (B = 150)
Аналогично примеру из пункта а) построим решение:
Попробуем брать в качестве (b_i) (9), пока их сумма не превосходит (150) – так можно положить [b_1 = … = b_{16} = 9,quad b_{17} =
150 — 16cdot 9 = 6,,] то есть в сумме (17) слагаемых. Тогда можно положить [a_1 = … = a_{16} = 1quad a_{17} = 18 — 16cdot 1 =
2,] итого, искомая сумма (16times 19 + 26), максимальная (S =
99cdot 15 + 33 = 1518).
Ответ:
а) (14times 19 + 64), где запись (14times 19) означает сумму из (14) слагаемых, каждое из которых равно (19)
б) Нет
в) (1518)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
13. а) Решите уравнение $2cos^3 x — cos^2 x + 2cos x — 1 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $left[ 2pi; dfrac{7pi}{2} right]$.
14. В кубе $ABCDA_1B_1C_1D_1$ все ребра равны 5. На его ребре $BB_1$ отмечена точка $K$ так, что $KB=3$. Через точки $K$ и $C_1$ проведена плоскость $alpha$, параллельная прямой $BD_1$.
а) Докажите, что $A_1P:PB_1=1:2$, где $P$ — точка пересечения плоскости $alpha$ с ребром $A_1B_1$.
б) Найдите объем большей из двух частей куба, на которые он делится плоскостью $alpha$.
15. Решите неравенство $$log_2^2(4+3x-x^2) + 7log_{0,5}(4+3x-x^2) + 10 > 0.$$
16. К окружности, вписанной в квадрат $ABCD$, проведена касательная, пересекающая стороны $AB$ и $AD$ в точках $M$ и $N$ соответственно.
а) Докажите, что периметр треугольника $AMN$ равен стороне квадрата.
б) Прямая $MN$ пересекает прямую CD в точке $P$. В каком отношении делит сторону $BC$ прямая, проходящая через точку $P$ и центр окружности, если $AM:MB=1:2$?
17. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно $t^2$ часов в неделю, то за эту неделю они производят $2t$ единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно $t^2$ часов в неделю, то за эту неделю они производят $5t$ единиц товара.
За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придется тратить еженедельно на оплату труда рабочих?
18. Найдите все значения параметра $a$, при каждом из которых система уравнений $$ begin{cases} dfrac{(y^2-xy-4y+2x+4)sqrt{x+4}}{sqrt{5-y}}=0,\ a = x + y end{cases} $$ имеет единственное решение.
19. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 2970. В каждом числе поменяли местами первую и вторую цифры (например, число 16 заменили на число 61).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 3 раза меньше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 5 раз меньше, чем сумма исходных чисел?
в) Найдите наименьшее возможное значение суммы получившихся чисел.

Единый государственный экзамен но МАТЕМАТИКЕ 2015. Профильный уровень
Инструкция по выполнению работы
Экзаменационная работа состоит из двух частей, включающих в себя 21 задание. Часть 1 содержит 9 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 5 заданий повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1-14 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1.
При выполнении заданий 15-21 требуется записать полное решение и ответ в бланке ответов № 2.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Условия КИМов досрочного ЕГЭ 2015 по математике (профильный уровень)
Решение заданий №1-9 досрочного ЕГЭ 2015 по математике (профильный уровень)
Решение заданий №10-14 досрочного ЕГЭ 2015 по математике (профильный уровень)
Решение заданий №15-18 досрочного ЕГЭ 2015 по математике (профильный уровень)
Решение заданий №19-21 досрочного ЕГЭ 2015 по математике (профильный уровень)
- 06.05.2015
Стали доступны варианты досрочного ЕГЭ в 2015 году.
К сожалению, каждый предмет представлен всего лишь одним вариантом.
Здесь опубликован вариант КИМа досрочного ЕГЭ 2015 по математике (профильный уровень), который проходил 26 марта в 2015 году.
Предлагаем вам его тщательно разобрать и решить.
Правильные ответы: 1 — 25; 2 — 9; 3 — 210; 4 — 0,6; 5 — 0,16; 6 — 4,5; 7 — 3,5; 8 — 4; 9 — 28; 10 — 5; 11 — 7; 12 — 86; 13 — 60; 14 — 29.
Досрочный ЕГЭ по математике (профильный уровень) стал доступен на сайте ФИПИ 5 мая 2015 года.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
ЕГЭ 2015 Досрочный вариант по математике 11 класс
Условия задач с ответами и решениями
- Бегун пробежал 180 метров за 20 секунд. Найдите среднюю скорость бегуна. Ответ дайте в километрах в час.
- На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа впервые выпало 5 миллиметров осадков.
- Телефонная компания предоставляет на выбор три тарифных плана. Абонент предполагает, что общая длительность разговоров составит 700 минут в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить абонент за месяц, если общая длительность разговоров действительно будет равна 700 минутам?
Тарифный план Абонентская плата (за месяц) Плата за 1 минуту разговора Повременный нет 0,3 руб Комбинированный 160 руб. за 420 мин 0,2 руб (сверх 420 мин) Безлимитный 255 руб нет - На клетчатой бумаге с размером клетки 1х1 изображен угол. Найдите синус этого угла.
- Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
- Найдите корень уравнения
- Периметр прямоугольной трапеции, описанной около окружности, равен 32, ее большая боковая сторона равна 9. Найдите радиус окружности.
- На рисунке изображён график функции и шесть точек на оси абсцисс:
. В скольких из этих точек производная функции отрицательна?
- В правильной четырехугольной пирамиде высота равна 3, боковое ребро равно 5. Найдите ее объем.
- Вычислите
- Водолазный колокол, содержащий
моля воздуха при давлении
атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления
. Работа, совершаемая водой при сжатии воздуха, определяется выражением
, где
Дж/(моль
К) — постоянная,
K — температура воздуха. Найдите, какое давление (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15960 Дж.
- Через среднюю линию основания треугольной призмы, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности призмы, если площадь боковой поверхности отсеченной треугольной призмы равна 37.
- Смешав 43‐процентный и 89‐процентный растворы кислоты и добавив 10 кг чистой воды, получили 69‐процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50‐процентного раствора той же кислоты, то получили бы 73‐процентный раствор кислоты. Сколько килограммов 43‐процентного раствора использовали для получения смеси?
- Найдите наибольшее значение функции
на отрезке
Решение
- а) Решите уравнение
; б) Укажите корни этого уравнения, принадлежащие отрезку
. Решение
- В кубе
все ребра равны 5. На отрезке
отмечена точка
так, что
равно 3. Через точки
и
проведена плоскость
, параллельная прямой
. а) Докажите, что
, где
— точка пересечения плоскости
с ребром
; б) Найдите объем большей из двух частей куба, на которые он делится плоскостью
. Решение
- Решите неравенство
Решение
- К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. а) Докажите, что периметр треугольника AMN равен стороне квадрата. б) Прямая MN пересекает прямую CD в точке P. Найдите отношение, в котором делится сторона BC прямой, проходящей через точку P и центр окружности, если известно, что AM : MB = 1 : 2. Решение
- Петя является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе первого города трудятся суммарно
часов в неделю, то за эту неделю они производят
единиц товара, а рабочие на заводе второго города, если суммарно трудятся
часов в неделю, то производят
единиц товара за эту неделю. На обоих заводах за каждый час работы Петя платит рабочему 500 руб. Какую наименьшую сумму придется тратить на оплату рабочим в неделю, чтобы производилось 580 единиц товара в неделю? Решение
- Найдите все значения параметра
, при каждом из которых система уравнений
имеет единственное решение. Решение
- На доске написано несколько двузначных натуральных чисел, не содержащих нулей. Сумма этих чисел равна 2970. В каждом числе поменяли местами первую и вторую цифры (например, 23 заменили на число 32). а) Приведите пример исходных чисел, для которых сумма получившихся после перестановки цифр чисел ровно в 3 раза меньше суммы исходных чисел; б) Могла ли сумма получившихся чисел быть ровно в 5 раз меньше суммы исходных чисел? в) Найдите наименьшее возможное значение суммы получившихся чисел. Решение
смотрите также Досрочный ЕГЭ по математике 2014
Ответы
- 32,4
- 11
- 210
- 4/5
- 0,15
- 9/2
- 7/2
- 2
- 32
- 3
- 7
- 74
- 35
- 29
- а)
б)
- 1:2
- 5800000
{
}
- а) один из вариантов ответа: 32 раза число 92 и число 26; б) нет; в) 693

Единый государственный экзамен но МАТЕМАТИКЕ 2015. Профильный уровень
Инструкция по выполнению работы
Экзаменационная работа состоит из двух частей, включающих в себя 21 задание. Часть 1 содержит 9 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 5 заданий повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1-14 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1.
При выполнении заданий 15-21 требуется записать полное решение и ответ в бланке ответов № 2.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Условия КИМов досрочного ЕГЭ 2015 по математике (профильный уровень)
Решение заданий №1-9 досрочного ЕГЭ 2015 по математике (профильный уровень)
Решение заданий №10-14 досрочного ЕГЭ 2015 по математике (профильный уровень)
Решение заданий №15-18 досрочного ЕГЭ 2015 по математике (профильный уровень)
Решение заданий №19-21 досрочного ЕГЭ 2015 по математике (профильный уровень)





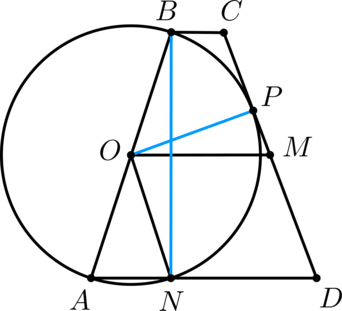



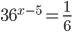
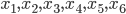

![displaystylefrac{sqrt[28]{3}cdot 3cdotsqrt[21]{3}}{sqrt[12]{3}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_7094c03471f8f8ec27ee6a8742f44286.gif)
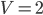
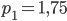
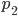
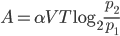
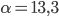

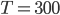
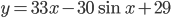
![displaystyle [-frac{pi}{2}; 0]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_9085c4924a7d200873662be3f4bc4f45.gif)
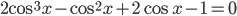
![[2pi; frac{7pi}{2}]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_36fcfd780e97f1754b7cb743e1a91b49.gif)
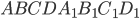
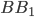
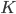
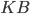
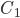

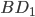
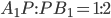
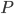
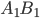
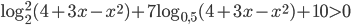
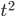
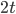
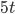

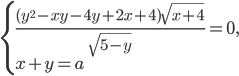
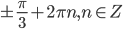
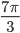
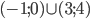
![(-infty; -6]cup](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_a9fb2f0915c2c559d22e8828bbdb5c0e.gif)