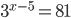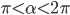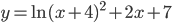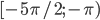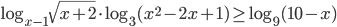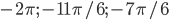Егэ 2015 математика профильный уровень 2015 - Помощь в подготовке к экзаменам и поступлению

Демонстрационная версия ЕГЭ—2015 по математике. Профильный уровень.

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?

Ответ:

На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали  — температура в градусах Цельсия. Для наглядности точки соединены линией. Определите по рисунку, сколько месяцев из данного периода средняя температура была больше 18 градусов Цельсия.

Ответ:

Строительный подрядчик планирует купить 20 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице.

Поставщик	Цена кирпича (руб.за 1 шт.)	Стоимость доставки (рублей)	Специальные условия
А	19	3000	Нет
Б	18	5000	Доставка бесплатная, если сумма заказа превышает 50 000 рублей
В	16	6500	При заказе товара на сумму свыше 50 000 рублей скидка на доставку 50%

Поставщик

Цена кирпича

(руб.за 1 шт.)

Стоимость

доставки (рублей)

Специальные условия

3000

Нет

5000

Доставка бесплатная, если сумма

заказа превышает 50 000 рублей

6500

При заказе товара на сумму свыше

50 000 рублей скидка на доставку 50%

Во сколько рублей обойдётся наиболее дешёвый вариант покупки с учётом доставки?

Ответ:

В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

Ответ:

Найдите корень уравнения 3^{x − 5} = 81.

Ответ:

Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32°.

Ответ:

На рисунке изображён график дифференцируемой функции y  =  f(x). На оси абсцисс отмечены девять точек: x₁, x₂, …, x₉. Среди этих точек найдите все точки, в которых производная функции y  =  f(x) отрицательна. В ответе укажите количество найденных точек.

Ответ:

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.

Ответ:

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен Найдите образующую конуса.

Ответ:

Весной катер идёт против течения реки в раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Ответ:

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие промежутку

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

В основании прямой призмы ABCDA₁B₁C₁D₁ лежит квадрат ABCD со стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD₁, причём BE  =  1.

а)  Постройте сечение призмы плоскостью A₁C₁E.

б)  Найдите угол между плоскостью сечения и плоскостью ABC.

Решите неравенство

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй  — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а)  Докажите, что прямые AD и BC параллельны.

б)  Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Найдите все значения параметра a, при каждом из которых наименьшее значение функции больше 1.

На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно −8.

а)  Сколько чисел написано на доске?

б)  Каких чисел написано больше: положительных или отрицательных?

в)  Какое наибольшее количество положительных чисел может быть среди них?

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

Подборка ссылок на страницы с контрольно-измерительными материалами и отдельными заданиями с реального ЕГЭ-2015.

1) Тексты с досрочного ЕГЭ 2015

(смотрите также в комментариях)

2) 2 варианта по математике:
→ https://4ege.ru/matematika/6549-1-variant-s-dosrochnogo-ege-po-matematike.html
→ https://4ege.ru/trening-matematika/6546-polnyy-variant-s-dosrochnogo-ege-po-matematike.html

3) По одному варианту с досрочного ЕГЭ-2015 по всем предметам

4) 1 вариант базового уровня по математике с основной волны.

5) 1 вариант профильного уровня по математике с основной волны.

По возможности ссылки на задания будут добавляться. Публикация только после прошедших экзаменов!

2014 год | 2013 год.

Источник

Досрочный ЕГЭ-2015 по математике (23.03.2015). Профильный уровень. Задания и решения ОНЛАЙН

Единый государственный экзамен но МАТЕМАТИКЕ 2015. Профильный уровень
Инструкция по выполнению работы
Экзаменационная работа состоит из двух частей, включающих в себя 21 задание. Часть 1 содержит 9 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 5 заданий повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1-14 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1.
При выполнении заданий 15-21 требуется записать полное решение и ответ в бланке ответов № 2.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Условия КИМов досрочного ЕГЭ 2015 по математике (профильный уровень)

Решение заданий №1-9 досрочного ЕГЭ 2015 по математике (профильный уровень)

Решение заданий №10-14 досрочного ЕГЭ 2015 по математике (профильный уровень)

Решение заданий №15-18 досрочного ЕГЭ 2015 по математике (профильный уровень)

Решение заданий №19-21 досрочного ЕГЭ 2015 по математике (профильный уровень)

Источник

2014-08-30
2018-08-30

2015

ЕГЭ 2015

Демоверсия ЕГЭ 2015

Демоверсия базового ЕГЭ по математике 2015

Демоверсия профильного ЕГЭ по математике 2015

Апробация КИМ ЕГЭ, базовый уровень (октябрь 2014)

1, 2, 3, 4, 5, 6, 7

Диагностическая работа по математике (январь 2015)

профильный уровень

базовый уровень

Диагностическая работа по математике (февраль 2015)

базовый уровень

Диагностическая работа по математике (5 марта 2015)

профильный уровень

Досрочный ЕГЭ по математике (26 марта 2015)

профильный уровень (с критериями)

Тренировочная работа по математике апрель 2015

профильный уровень

Досрочный ЕГЭ по математике (резервный день)

профильный уровень (задания 15-21)

Диагностическая работа по математике апрель 2015

профильный уровень, разбор на сайте 1-20, 15-21 (критерии)

базовый уровень

Реальный ЕГЭ по математике (4 июня 2015)

Образец варианта

ОГЭ 2015

Демонстрационный вариант ОГЭ 2015

Демо версия ОГЭ 2015

ОГЭ от 27 мая 2015 г.

ОГЭ по математике

Источник

ЕГЭ 2015 Демонстрационный вариант

ЕГЭ

Профильный уровень
Условия задач с ответами и решениями

Часть 1

1. Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?

2. На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией. Определите по рисунку, сколько месяцев из данного периода средняя температура была больше 18 градусов Цельсия.

3. Строительный подрядчик планирует купить 15 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант покупки с учётом доставки?

4. Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в см².

5. В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

6. Найдите корень уравнения $3^{x-5}=81$

7. Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32^o. Ответ дайте в градусах.

8. На рисунке изображен график дифференцируемой функции 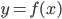y=f(x) . На оси абсцисс отмечены девять точек: . Среди этих точек найдите все точки, в которых производная функции y=f(x) отрицательна. В ответе укажите количество найденных точек.

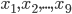
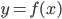
9. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого? Ответ выразите в см.

Часть 2

10. Найдите 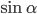, если и

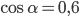
11. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением 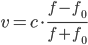$v=ccdotdisplaystylefrac{f-f_{0}}{f+f_{0}}$ ,где c = 1500 м/с — скорость звука в воде; f0— частота испускаемого сигнала (в МГц); f — частота отражённого сигнала (в МГц). Найдите частоту (в МГц) отражённого сигнала, если батискаф погружается со скоростью 2 м/с.

12. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром снования конуса. Радиус сферы равен 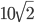. Найдите образующую конуса.

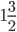
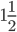
13. Весной катер идёт против течения реки в $1frac{3}{2}$ раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в $1frac{1}{2}$ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

14. Найдите точку максимума функции

15. а) Решите уравнение 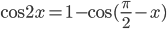$cos 2x=1-cos(frac{pi}{2}-x)$ ; б) Найдите все корни этого уравнения принадлежащие промежутку

16. В основании прямой призмы ABCDA₁B₁C₁D₁ лежит квадрат ABCD со стороной 2, а высота призмы равна 1. Точка Е лежит на диагонали BD₁, причем BE равно 1. a) Постройте сечение призмы плоскостью A₁C₁E. б) Найдите угол между плоскостью сечения и плоскостью АВС.

17. Решите неравенство $log_{x-1}sqrt{x+2}cdotlog_3(x^2-2x+1)gelog_9(10-x)$

18. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C. а) Докажите, что прямые AD и BC параллельны. б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

19. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

20. Найдите все значения a, при каждом из которых наименьшее значение функции 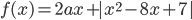больше 1.

21. На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно -3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно -8. а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных?в) Какое наибольшее количество положительных чисел может быть среди них?

смотрите еще Репетиционное ЕГЭ 2015 11 класс

Ответы

1. 8
2. 4
3. 54000
4. 12
5. 0,92
6. 9
7. 64
8. 3
9. 4
10. -0,8
11. 751
12. 20
13. 1.875 км/ч
14. -5
15. а)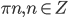; б)
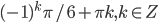
16. arctg sqrt{2}
17. (1;2), (2;10)
18. 3,2
19. 3 993 000 рублей
20.
21. а) 44; б) отрицательных; в) 17

Источник

Серия «ЕГЭ. ФИПИ — школе» подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена. В сборнике представлены: • 36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ 2015 года; • инструкция по выполнению экзаменационной работы; ответы ко всем заданиям; • решения и критерии оценивания заданий 15-21. Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки. Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.

скачать учебник ЕГЭ 2015. Математика. Типовые экзаменационные варианты: 36 вариантов. Под ред — Ященко И.В.

Источник