ЕГЭ Профиль №9. Прямая
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Прямая
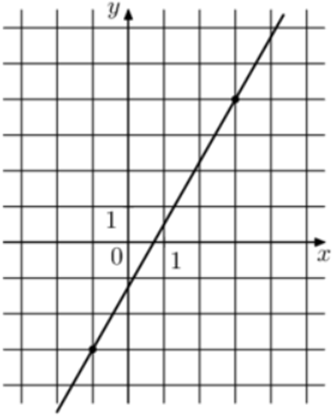
| Задача 1. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 5} right).)
Ответ
ОТВЕТ: — 10. |
 |
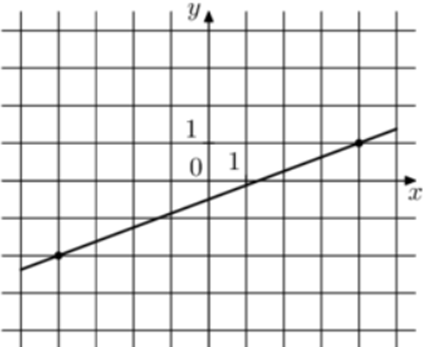
| Задача 2. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( {12} right).)
Ответ
ОТВЕТ: 4. |
 |
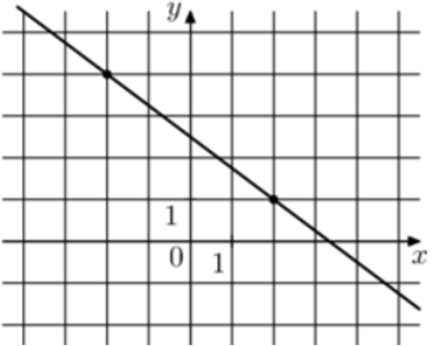
| Задача 3. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 16} right).)
Ответ
ОТВЕТ: 14,5. |
 |
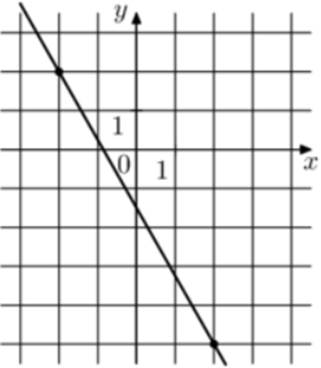
| Задача 4. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 16} right).)
Ответ
ОТВЕТ: 26,5. |
 |
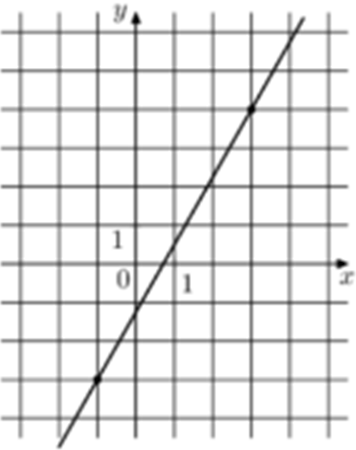
| Задача 5. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = — 13,5.)
Ответ
ОТВЕТ: — 7. |
 |
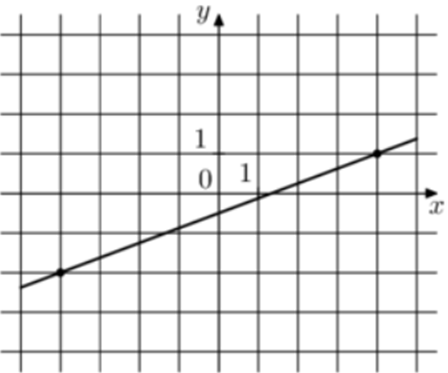
| Задача 6. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = 4,75.)
Ответ
ОТВЕТ: 14. |
 |
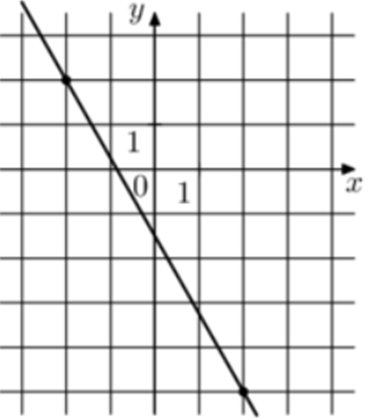
| Задача 7. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = 16.)
Ответ
ОТВЕТ: — 10. |
 |
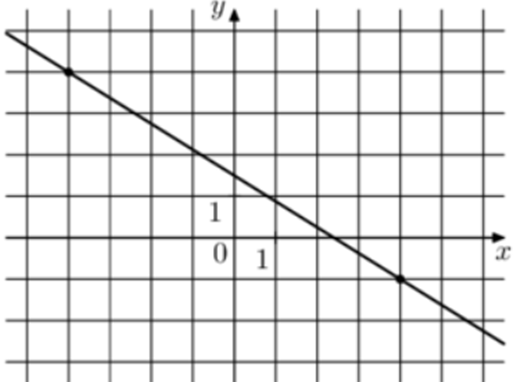
| Задача 8. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = — 7,25.)
Ответ
ОТВЕТ: 14. |
 |
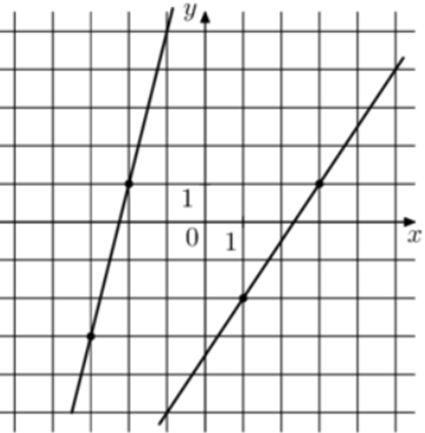
| Задача 9. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 5. |
 |
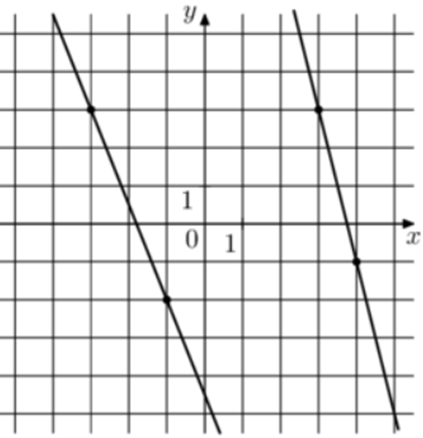
| Задача 10. На рисунке изображены графики функций вида (fleft( x right) = k,x + b.) которые пересекаются в точке А. Найдите абсциссу точки А.
Ответ
ОТВЕТ: 13. |
 |
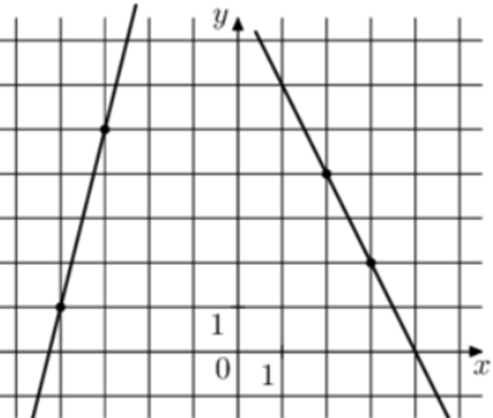
| Задача 11. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 11. |
 |
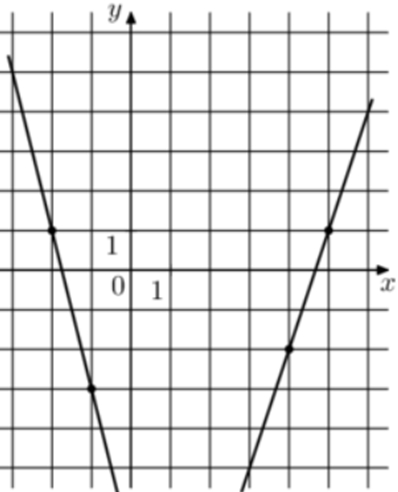
| Задача 12. На рисунке изображены графики функций вида (fleft( x right) = k,x + b.) которые пересекаются в точке А. Найдите ординату точки А.
Ответ
ОТВЕТ: — 11. |
 |
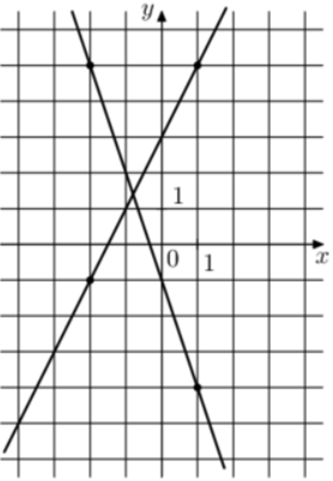
| Задача 13. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 0,8. |
 |
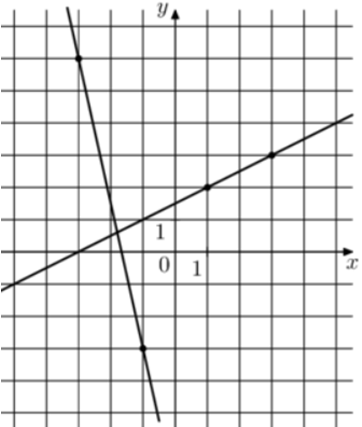
| Задача 14. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 1,8. |
 |
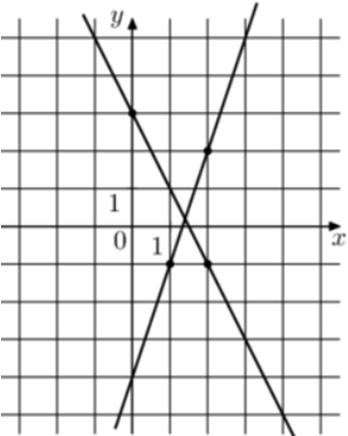
| Задача 15. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 0,2. |
 |
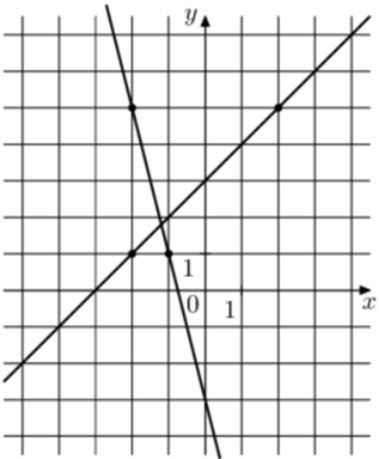
| Задача 16. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 1,8. |
 |
Нужна регистрация для бесплатного обучения
21.03.2017
И
Комментариев нет
63
Задание №9 (№ 26735 профильный уровень), задача №1, №2 и №5 (базовый уровень) ЕГЭ 2016 по математике. Урок 1. Найдите значение выражения. Дистанционные занятия для школьников и студентов здесь: http://sin2x.ru/ или здесь: http://асимптота.рф
Последние сообщения
- Книги
- ЕГЭ по математике
- С. А. Шестаков
📚 ЕГЭ 2016. Математика. Значения выражений. Задача 9 (профильный уровень). Задачи 2 и 5 (базовый уровень). Рабочая тетрадь
Эта и ещё 2 книги за 399 ₽
По абонементу вы каждый месяц можете взять из каталога одну книгу до 700 ₽ и две книги из персональной подборки. Узнать больше
Оплачивая абонемент, я принимаю условия оплаты и её автоматического продления, указанные в оферте
Описание книги
Рабочая тетрадь по математике серии «ЕГЭ 2016. Математика» ориентирована на подготовку учащихся старшей школы к успешной сдаче единого государственного экзамена по математике в 2016 году по базовому и профильному уровням. В рабочей тетради представлены задачи по одной позиции контрольных измерительных материалов ЕГЭ-2016.
На различных этапах обучения пособие поможет обеспечить уровневый подход к организации повторения, осуществить контроль и самоконтроль знаний по теме «Значения выражений». Рабочая тетрадь ориентирована на один учебный год, однако при необходимости позволит в кратчайшие сроки восполнить пробелы в знаниях выпускника.
Тетрадь предназначена для учащихся старшей школы, учителей математики, родителей.
Издание соответствует Федеральному государственному образовательному стандарту (ФГОС).
Подробная информация
- Возрастное ограничение:
- 12+
- Дата выхода на ЛитРес:
- 11 марта 2016
- Дата написания:
- 2016
- Объем:
- 66 стр.
- ISBN:
- 978-5-4439-2422-9
- Общий размер:
- 1 MB
- Общее кол-во страниц:
- 66
- Размер страницы:
- 165 x 210 мм
- Редактор:
- И. В. Ященко
- Правообладатель:
- МЦНМО
Книга С. А. Шестакова «ЕГЭ 2016. Математика. Значения выражений. Задача 9 (профильный уровень). Задачи 2 и 5 (базовый уровень). Рабочая тетрадь» — скачать в pdf или читать онлайн. Оставляйте комментарии и отзывы, голосуйте за понравившиеся.
Книга входит в серию
«ЕГЭ 2016. Математика»
Оставьте отзыв
Другие книги автора
Поделиться отзывом на книгу
С. А. Шестаков
ЕГЭ 2016. Математика. Значения выражений. Задача 9 (профильный уровень). Задачи 2 и 5 (базовый уровень). Рабочая тетрадьPDF
Мы используем куки-файлы, чтобы вы могли быстрее и удобнее пользоваться сайтом. Подробнее
Подробные решения контрольных измерительных материалов Единого государственного экзамена по МАТЕМАТИКЕ от 06.06.2016. Профильный уровень. Основная волна
Условия КИМов реального ЕГЭ 2016 по математике (тип 1)
Часть 1
1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 сентября составляли 103 куб, м воды, а 1 октября — 114 куб. м. Сколько нужно заплатить за холодную воду за сентябрь, если стоимость 1 куб, м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
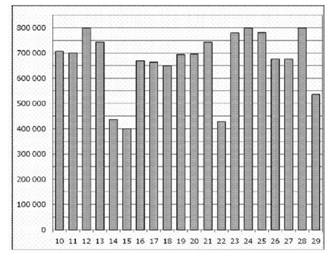
2. На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей больше, чем наименьшее количество посетителей за день.
3. Найдите площадь треугольника, изображенного на рисунке.
4. В соревнованиях по толканию ядра участвуют 8 спортсменов из Великобритании, 6 спортсменов из Франции, 5 спортсменов из Германии и 5 — из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции.
5. Наидите корень уравнения: .
6. В четырехугольник , периметр которого равен 48 вписана окружность,
. Найдите
.
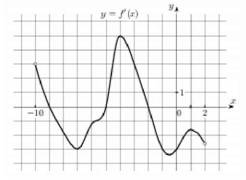
7. На рисунке изображён график производной функции
, определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции
параллельна прямой
или совпадает с ней.
8. Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
Часть 2
9. Найдите значение выражений .
10. Груз массой 0,8 кг колеблется на пружине. Его скорость меняется по закону
. где
— время с момента начала колебаний,
— период колебаний,
м/с. Кинетическая энергия
(в джоулях) груза вычисляется по формуле
, где
— масса груза в килограммах,
— скорость груза в м/с.
Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях
11. Шесть одинаковых рубашек дешевле куртки на 2%. На сколько процентов девять таких же рубашек дороже куртки?
12. Найдите точку минимума функции
Тип 1
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку .
14. В правильной треугольной призме сторона основания
равна 6, а боковое ребро
равно 3 . На ребре
отмечена точка
так, что
. Точки
и
— середины ребер
и
соответственно. Плоскость
параллельна прямой
и содержит точки
и
.
а) Докажите, что прямая перпендикулярна плоскости
;
б) Найдите объем пирамиды, вершина которой — точка , а основание — сечение данной призмы плоскостью
.
15. Решите неравенство:
16. В трапеции боковая сторона
перпендикулярна основаниям. Из точки
на сторону
опустили перпендикуляр
. На стороне
отмечена точка
так, что прямые
и
перпендикулярны.
а) Докажите, что прямые и
параллельны.
б) Найдите отношение , если угол
.
17. 15-го января планируется взять кредит в банке на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наименьшее значение , при котором общая сумма выплат будет составлять более 1,25 млн рублей.
18. Найдите все значения параметра , при каждом из которых уравнение
имеет ровно три различных решения
19. На доске написаны числа 1, 2, 3, …,30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стёртых на предыдущих ходах.
а) Приведите пример последовательности 5 ходов, б (Можно ли сделать 10 ходов?
в) Какое наибольшее число ходов можно сделать?
Подробные решения КИМов ЕГЭ №№1-12 и №№13-19(тип 1)
Условия КИМов основного ЕГЭ 2016 по математике (тип 2)
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
14. В правильной четырехугольной пирамиде сторона основания
равна 16, а высота равна 4. На ребрах
и
отмечены точки
и
соответственно, причем
и
.
а) Докажите, что плоскости и
параллельны.
б) Найдите расстояние от точки до плоскости
.
15. Решите неравенство
16. В трапеции точка
— середина основания
, точка
— середина боковой стороны
. Отрезки
и
пересекаются в точке
.
а) Докажите, что площади четырехугольника и треугольника
равны
б) Найдите, какую часть от площади трапеции составляет площадь четырехугольника , если
17. В июле 2016 года планируется взять кредит в банке на млн рублей, где
— целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
Найдите наибольшее значение , чтобы общая сумма выплат была меньше 50 млн рублей?
18. Найдите все значения , при каждом из которых уравнение
имеет единственный корень.
19. На доске написаны числа 2 и 3. За один ход разрешено заменить написанные на доске числа и
числами
и
(например, из чисел 2 и 3 можно получить либо 3 и 5, либо 5 и 5).
а) Может ли после нескольких ходов на доска появиться число 19?
б) может ли через 100 ходов на доске быть написано число 200?
в) укажите наименьшую разность чисел через 1007 ходов.
Условия КИМов основного ЕГЭ 2016 по математике (тип 3)
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
14. В правильной треугольной призме сторона основания
равна 6, а боковое ребро
равно 3. На ребре
отмечена точка
так, что
. Точки
и
— середины ребер
и
соответственно. Плоскость у параллельна прямой
и содержит точки
и
.
а) Докажите, что прямая перпендикулярна плоскости
.
б) Найдите расстояние от точки до плоскости
.
15. Решите неравенство
16. В треугольнике проведены высоты
и
. На них из точек
и
опущены перпендикуляры
и
соответственно
а) Докажите, что прямые и
параллельны.
б) Найдите отношение , если угол
равен
.
17. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
-1-го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
Найдите наибольшее значение , при котором общая сумма выплат будет составлять менее 1,2 млн. рублей.
18. Найдите все значения , при каждом из которых уравнение
имеет ровно три различных решения.
Подробные решения КИМов ЕГЭ №№13-19(тип 2 и 3)
Условия КИМов основного ЕГЭ 2016 по математике (тип 4)
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
14. В правильной треугольной пирамиде сторона основания
равна 12, а высота равна 1. На ребрах
и
отмечены точки
и
соответственно, причем
и
а) Докажите, что плоскости и
параллельны.
б) Найдите расстояние от точки до плоскости
.
15. Решите неравенство .
16. Один из двух отрезков, соединяющих середины противоположных сторон четырехугольника, делит его площадь пополам, а другой в отношении 11:17
а) Докажите, что данный четырехугольник — трапеция
б) Найдите отношение оснований этой трапеции
17. В июле 2016 года планируется взять кредит в банке на млн рублей, где
— целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
Найдите наименьшее значение , чтобы общая сумма выплат была больше 10 млн рублей?
18. Найдите все значения , при каждом из которых уравнение
имеет единственный корень.
Подробные решения КИМов ЕГЭ №№13-19(тип 4)