ЕГЭ, Математика, Профильный уровень, Задание 18, Задачи с параметром, Садовничий Ю.В., 2017.
Данная книга посвящена задачам, аналогичным задаче 18 ЕГЭ по математике (задача с параметром). Рассматриваются различные методы решения таких задач, также большое внимание уделяется графическим иллюстрациям. Книга будет полезна учащимся старших классов, учителям математики, репетиторам. Приказом № 699 Министерства образования и науки Российской Федерации учебные пособия издательства «Экзамен» допущены к использованию в общеобразовательных организациях.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Из всех решений (х, у) уравнения х2у — х2 + 4ху + 6у — 2х = 3 найти те решения, для которых у принимает наименьшее значение.
Найти наибольшее из значений, которые принимает выражение х + 3у, если х и у удовлетворяют неравенству х2 + ху + 4у2 ≤ 3.
Определить, под каким углом видно из начала координат множество, заданное на координатной плоскости неравенством 14х2 + ху + у2 + 14х + 2у + 4 < 0.
Числа х, у, z таковы, что х2 + 3у2 + z2 = 2. Какое наибольшее значение может принять выражение 2х + у — z?
Найти все значения а, при каждом из которых существует единственная тройка чисел (х, у, z), удовлетворяющая равенствам: x + y + z — x2 + 4y2 и x + 2y + 3z = a.
Найти наибольшее и наименьшее значение выражения: х2 + 2у2, если х2 — ху + 2у2 = 1.
Найти все целочисленные решения уравнения:
х2 + 5у2 + 34z2 + 2ху — 10хz — 22уz = 0.
СОДЕРЖАНИЕ
Введение
§1. Линейные уравнения и системы линейных уравнений
Задачи для самостоятельного решения
§2. Исследование квадратного трехчлена с помощью дискриминанта
Задачи для самостоятельного решения
§3. Теорема Виета
Задачи для самостоятельного решения
§4. Расположение корней квадратного трехчлена
Задачи для самостоятельного решения
§5. Применение графических иллюстраций к исследованию квадратного трехчлена
Задачи для самостоятельного решения
§6. Ограниченность функции. Нахождение области значений
Задачи для самостоятельного решения
§7. Другие свойства функций
Задачи для самостоятельного решения
§8. Логические задачи с параметром
Задачи для самостоятельного решения
Иллюстрации на координатной плоскости
Задачи для самостоятельного решения
Метод «Оха»
Задачи для самостоятельного решения
Ответы.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ, Математика, Профильный уровень, Задание 18, Задачи с параметром, Садовничий Ю.В., 2017 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать
— pdf — Яндекс.Диск.
Дата публикации: 04.04.2017 09:38 UTC
Теги:
ЕГЭ по математике :: математика :: Садовничий
Следующие учебники и книги:
- ЕГЭ, 4000 задач с ответами по математике, Все задания закрытый сегмент, Базовый и профильный уровни, Ященко И.В., Высоцкий И.Р., Забелин А.В., 2017
- ЕГЭ 2017, Математика, Профильный уровень, 50 вариантов, Ященко И.В., Волчкевич М.А., Высоцкий И.Р.
- ЕГЭ 2017, Математика, Тематические тренировочные задания, Кочагин В.В., Кочагина М.Н., 2016
- Математика, Краткий справочник, Готовимся к ЕГЭ, Янборисова Р.Ш.
Предыдущие статьи:
- ЕГЭ, Математика, Профильный уровень, Задание 16, Планиметрия, Садовничий Ю.В., 2017
- ЕГЭ, Математика для нелюбителей, Базовый уровень, Высоцкий И.Р., Ященко И.В., 2017
- ЕГЭ, Математика, Базовый уровень, Высоцкий И.Р., Ященко И.В., 2017
- Математика, Новый полный справочник для подготовки ЕГЭ, Маслова Т.Н., Суходский А.М., 2017
ЕГЭ 2017. Математика. Задание 18. Задачи с параметром — Садовничий Ю.В.:
Данная книга посвящена задачам, аналогичным задаче 18 ЕГЭ по математике (задача с параметром). Рассматриваются различные методы решения таких задач, также большое внимание уделяется графическим иллюстрациям. Книга будет полезна учащимся старших классов, учителям математики, репетиторам.
- Рубрика: ЕГЭ / ЕГЭ по математике
- Автор: Садовничий Ю.В.
- Язык: Русский
- Год: 2017
- Класс: 11 класс
- Просмотров: 172
Поделиться с друзьями:
Скачать в pdf
Барашкова английский язык на каникулах н…
Узорова английский язык в схемах и табл…
Державина английский язык для начальной …
Барашкова английский язык на каникулах н…
Карачаева 100 тестов по лексике и грамма…
Мордкович учебник алгебра углубленный ур…
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с параметром из ЕГЭ прошлых лет
Задание
1
#6329
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых система [begin{cases} (x-2a-2)^2+(y-a)^2=1\
y^2=x^2end{cases}]
имеет ровно четыре решения.
(ЕГЭ 2018, основная волна)
Второе уравнение системы можно переписать в виде (y=pm x). Следовательно, рассмотрим два случая: когда (y=x) и когда (y=-x). Тогда количество решений системы будет равно сумме количества решений в первом и во втором случаях.
1) (y=x). Подставим в первое уравнение и получим: [2x^2-2(3a+2)x+(2a+2)^2+a^2-1=0quad(1)] (заметим, что в случае (y=-x) мы поступим так же и тоже получим квадратное уравнение)
Чтобы исходная система имела 4 различных решения, нужно, чтобы в каждом из двух случаев получилось по 2 решения.
Квадратное уравнение имеет два корня, когда его (D>0). Найдем дискриминант уравнения (1):
(D=-4(a^2+4a+2)).
Дискриминант больше нуля: (a^2+4a+2<0), откуда (ain (-2-sqrt2;
-2+sqrt2)).
2) (y=-x). Получаем квадратное уравнение: [2x^2-2(a+2)x+(2a+2)^2+a^2-1=0quad (2)] Дискриминант больше нуля: (D=-4(9a^2+12a+2)>0), откуда (ain
left(frac{-2-sqrt2}3; frac{-2+sqrt2}3right)).
Необходимо проверить, не совпадают ли решения в первом случае с решениями во втором случае.
Пусть (x_0) – общее решение уравнений (1) и (2), тогда [2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=2x_0^2-2(a+2)x_0+(2a+2)^2+a^2-1] Отсюда получаем, что либо (x_0=0), либо (a=0).
Если (a=0), то уравнения (1) и (2) получаются одинаковыми, следовательно, имеют одинаковые корни. Этот случай нам не подходит.
Если (x_0=0) – их общий корень, то тогда (2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=0), откуда ((2a+2)^2+a^2-1=0), откуда (a=-1) или (a=-0,6). Тогда вся исходная система будет иметь 3 различных решения, что нам не подходит.
Учитывая все это, в ответ пойдут:

-0,6right)cupleft(-0,6; -2+sqrt2right)]
Ответ:
(ainleft(frac{-2-sqrt2}3; -1right)cupleft(-1;
-0,6right)cupleft(-0,6; -2+sqrt2right))
Задание
2
#4032
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых система [begin{cases}
(a-1)x^2+2ax+a+4leqslant 0\
ax^2+2(a+1)x+a+1geqslant 0 end{cases}]
имеет единственное решение.
(ЕГЭ 2018, СтатГрад, 19 апреля 2018)
Перепишем систему в виде: [begin{cases}
ax^2+2ax+aleqslant x^2-4\
ax^2+2ax+ageqslant -2x-1
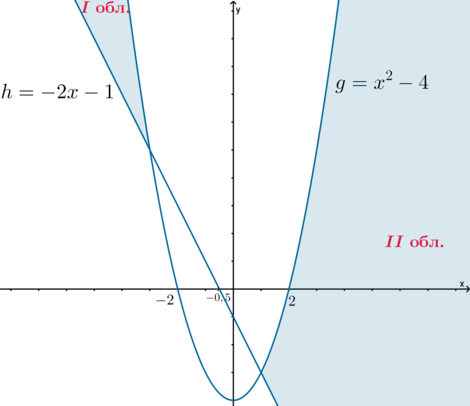
end{cases}] Рассмотрим три функции: (y=ax^2+2ax+a=a(x+1)^2), (g=x^2-4), (h=-2x-1). Из системы следует, что (yleqslant g), но (ygeqslant
h). Следовательно, чтобы система имела решения, график (y) должен находиться в области, которая задается условиями: “выше” графика (h), но “ниже” графика (g):
(будем называть “левую” область областью I, “правую” область – областью II)
Заметим, что при каждом фиксированном (ane 0) графиком (y) является парабола, вершина которой находится в точке ((-1;0)), а ветви обращены либо вверх, либо вниз. Если (a=0), то уравнение выглядит как (y=0) и графиком является прямая, совпадающая с осью абсцисс.
Заметим, что для того, чтобы исходная система имела единственное решение, нужно, чтобы график (y) имел ровно одну общую точку с областью I или с областью II (это значит, что график (y) должен иметь единственную общую точку с границей одной из этих областей).
Рассмотрим по отдельности несколько случаев.
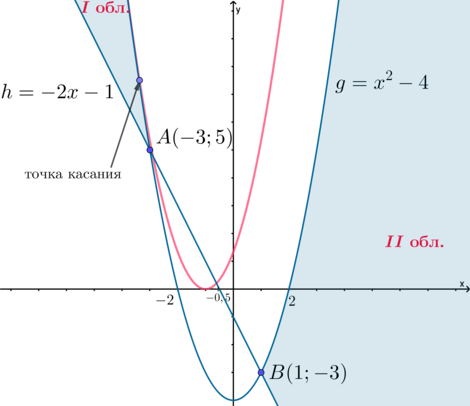
1) (a>0). Тогда ветви параболы (y) обращены вверх. Чтобы у исходной системы было единственное решение, нужно, чтобы парабола (y) касалась границы области I или границы области II, то есть касалась параболы (g), причем абсцисса точки касания должна быть (leqslant
-3) или (geqslant 2) (то есть парабола (y) должна коснуться границы одной из областей, которая находится выше оси абсцисс, раз парабола (y) лежит выше оси абсцисс).
(y’=2a(x+1)), (g’=2x). Условия касания графиков (y) и (g) в точке с абсциссой (x_0leqslant -3) или (x_0geqslant 2): [begin{cases}
2a(x_0+1)=2x_0\
a(x_0+1)^2=x_0^2-4 \
left[begin{gathered}begin{aligned} &x_0leqslant -3\
&x_0geqslant 2 end{aligned}end{gathered}right. end{cases}
quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} &x_0leqslant -3\
&x_0geqslant 2 end{aligned}end{gathered}right.\[1ex]
a=dfrac{x_0}{x_0+1}\[1ex]
x_0^2+5x_0+4=0 end{cases}] Из данной системы (x_0=-4), (a=frac43).
Получили первое значение параметра (a).
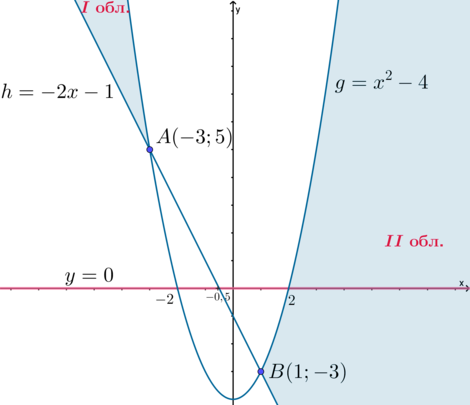
2) (a=0). Тогда (y=0) и видно, что прямая имеет бесконечное множество общих точек с областью II. Следовательно, это значение параметра нам не подходит.
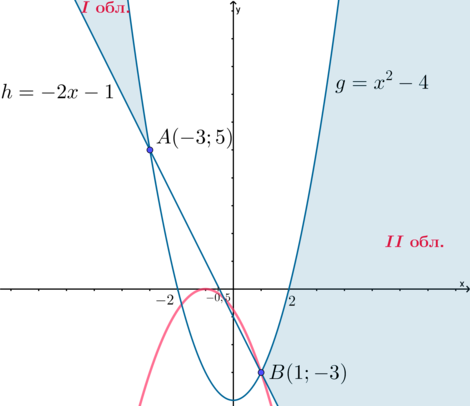
3) (a<0). Тогда ветви параболы (y) обращены вниз. Чтобы у исходной системы было единственное решение, нужно, чтобы парабола (y) имела одну общую точку с границей области II, лежащей ниже оси абсцисс. Следовательно, она должна проходить через точку (B), причем, если парабола (y) будет иметь еще одну общую точку с прямой (h), то эта общая точка должна быть “выше” точки (B) (то есть абсцисса второй точки должна быть (<1)).
Найдем (a), при которых парабола (y) проходит через точку (B): [-3=a(1+1)^2quadRightarrowquad a=-dfrac34] Убеждаемся, что при этом значении параметра вторая точка пересечения параболы (y=-frac34(x+1)^2) с прямой (h=-2x-1) – это точка с координатами (left(-frac13; -frac13right)).
Таким образом, получили еще одно значение параметра.
Так как мы рассмотрели все возможные случаи для (a), то итоговый ответ: [ain left{-dfrac34; dfrac43right}]
Ответ:
(left{-frac34; frac43right})
Задание
3
#4013
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых система уравнений [begin{cases}
2x^2+2y^2=5xy\
(x-a)^2+(y-a)^2=5a^4 end{cases}]
имеет ровно два решения.
(ЕГЭ 2018, СтатГрад, 26 января 2018)
1) Рассмотрим первое уравнение системы как квадратное относительно (x): [2x^2-(5y)x+2y^2=0] Дискриминант равен (D=9y^2), следовательно, [x_{1,2}=dfrac{5ypm 3y}4quadRightarrow quad x_1=2y, quad x_2=dfrac12y] Тогда уравнение можно переписать в виде [(x-2y)cdot (2x-y)=0] Следовательно, всю систему можно переписать в виде [begin{cases}
left[begin{gathered}begin{aligned} &y=2x\[1ex]
&y=0,5xend{aligned}end{gathered}right.\[1ex]
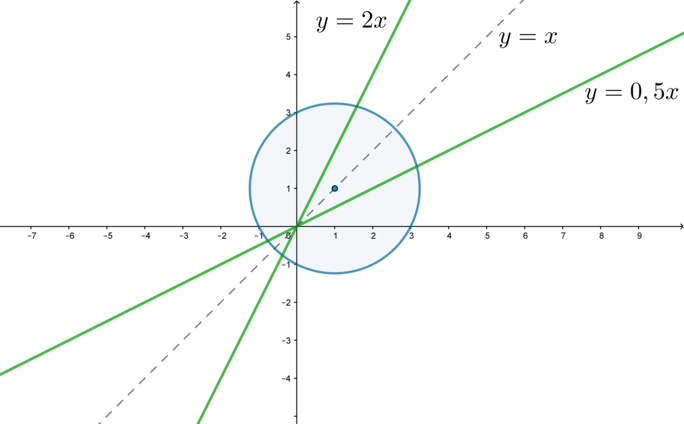
(x-a)^2+(y-a)^2=5a^4end{cases}] Совокупность задает две прямые, второе уравнение системы задает окружность с центром в ((a;a)) и радиусом (R=sqrt5a^2). Чтобы исходное уравнение имело два решения, нужно, чтобы окружность пересекала график совокупности ровно в двух точках. Вот чертеж, когда, например, (a=1):
Заметим, что так как координаты центра окружности равны, то центр окружности “бегает” по прямой (y=x).
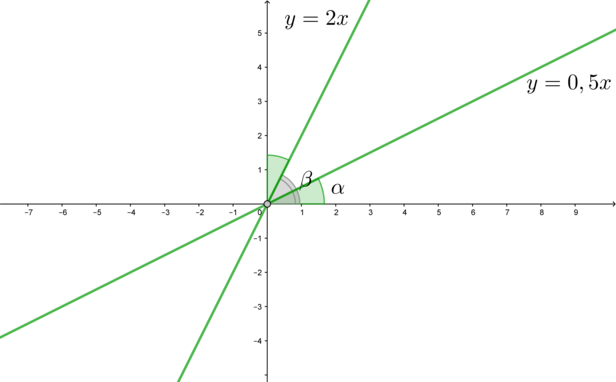
2) Так как у прямой (y=kx) тангенс угла наклона этой прямой к положительному направлению оси (Ox) равен (k), то тангенс угла наклона прямой (y=0,5x) равен (0,5) (назовем его (mathrm{tg},alpha)), прямой (y=2x) – равен (2) (назовем его (mathrm{tg},beta)). Заметим, что (mathrm{tg},alphacdot
mathrm{tg},beta=1), следовательно, (mathrm{tg},alpha=mathrm{ctg},beta=mathrm{tg},(90^circ-beta)). Следовательно, (alpha=90^circ-beta), откуда (alpha+beta=90^circ). Это значит, что угол между (y=2x) и положительным направлением (Oy) равен углу между (y=0,5x) и положительным направлением (Ox):
А так как прямая (y=x) является биссектрисой I координатного угла (то есть углы между ней и положительными направлениями (Ox) и (Oy) равны по (45^circ)), то углы между (y=x) и прямыми (y=2x) и (y=0,5x) равны.
Все это нам нужно было для того, чтобы сказать, что прямые (y=2x) и (y=0,5x) симметричны друг другу относительно (y=x), следовательно, если окружность касается одной из них, то она обязательно касается и второй прямой.
Заметим, что если (a=0), то окружность вырождается в точку ((0;0)) и имеет лишь одну точку пересечения с обеими прямыми. То есть этот случай нам не подходит.
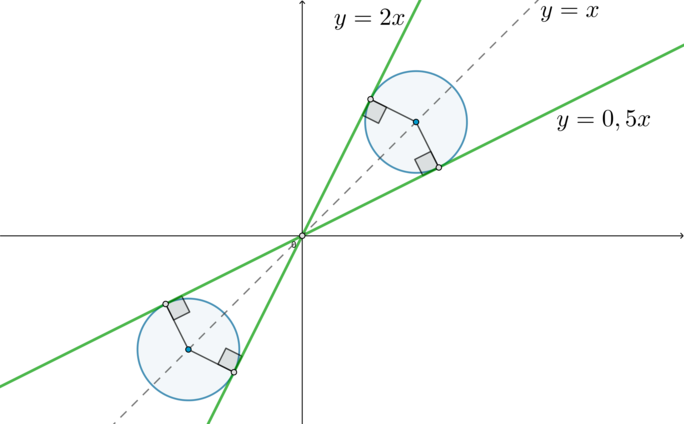
Таким образом, для того, чтобы окружность имела 2 точки пересечения с прямыми, нужно, чтобы она касалась этих прямых:
Видим, что случай, когда окружность располагается в третьей четверти, симметричен (относительно начала координат) случаю, когда она располагается в первой четверти. То есть в первой четверти (a>0), а в третьей (a<0) (но такие же по модулю).
Поэтому рассмотрим только первую четверть.
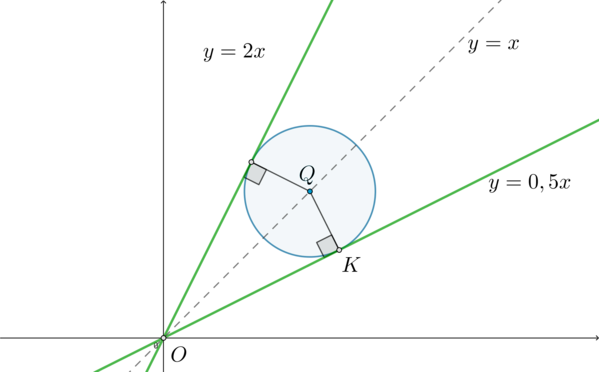
Заметим, что (OQ=sqrt{(a-0)^2+(a-0)^2}=sqrt2a), (QK=R=sqrt5a^2). Тогда [OK=sqrt{2a^2-5a^4}] Тогда [mathrm{tg},angle
QOK=dfrac{sqrt5a^2}{sqrt{2a^2-5a^4}}] Но, с другой стороны, [mathrm{tg},angle QOK=mathrm{tg},(45^circ-alpha)=dfrac{mathrm{tg},
45^circ-mathrm{tg},alpha}{1+mathrm{tg},45^circcdot
mathrm{tg},alpha}] следовательно, [dfrac{1-0,5}{1+1cdot 0,5}=dfrac{sqrt5a^2}{sqrt{2a^2-5a^4}}
quadLeftrightarrowquad a=pm dfrac15] Таким образом, мы уже сразу получили и положительное, и отрицательное значение для (a). Следовательно, ответ: [ain {-0,2;0,2}]
Ответ:
({-0,2;0,2})
Задание
4
#3278
Уровень задания: Равен ЕГЭ
Найдите все значения (a), для каждого из которых уравнение [25^x-(a+6)cdot 5^x=(5+3|a|)cdot 5^x-(a+6)(3|a|+5)]
имеет единственное решение.
(ЕГЭ 2017, официальный пробный 21.04.2017)
Сделаем замену (t=5^x, t>0) и перенесем все слагаемые в одну часть: [t^2-bigg((a+6)+(5+3|a|)bigg)cdot t+(a+6)(3|a|+5)=0] Получили квадратное уравнение, корнями которого по теореме Виета являются (t_1=a+6) и (t_2=5+3|a|). Для того, чтобы исходное уравнение имело один корень, достаточно, чтобы полученное уравнение с (t) тоже имело один (положительный!) корень.
Заметим сразу, что (t_2) при всех (a) будет положительным. Таким образом, получаем два случая:
1) (t_1=t_2): [a+6=5+3|a| quadLeftrightarrowquad 3|a|=a+1 quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} & 3a=a+1\
&3a=-a-1 end{aligned} end{gathered} right. \
a+1geqslant 0 end{cases}quadLeftrightarrowquad
left[begin{gathered}begin{aligned} & a=dfrac12\[2ex]
&a=-dfrac14 end{aligned} end{gathered} right.]
2) Так как (t_2) всегда положителен, то (t_1) должен быть (leqslant
0): [a+6leqslant 0 quadLeftrightarrowquad aleqslant -6.]
Ответ:
((-infty;-6]cupleft{-frac14;frac12right})
Задание
5
#3252
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [sqrt{x^2-a^2}=sqrt{3x^2-(3a+1)x+a}]
имеет ровно один корень на отрезке ([0;1]).
(ЕГЭ 2017, резервный день)
Уравнение можно переписать в виде: [sqrt{(x-a)(x+a)}=sqrt{(3x-1)(x-a)}] Таким образом, заметим, что (x=a) является корнем уравнения при любых (a), так как уравнение принимает вид (0=0). Для того, чтобы этот корень принадлежат отрезку ([0;1]), нужно, чтобы (0leqslant
aleqslant 1).
Второй корень уравнения находится из (x+a=3x-1), то есть (x=frac{a+1}2). Для того, чтобы это число было корнем уравнения, нужно, чтобы оно удовлетворяло ОДЗ уравнения, то есть: [left(dfrac{a+1}2-aright)cdot
left(dfrac{a+1}2+aright)geqslant 0quadRightarrowquad
-dfrac13leqslant aleqslant 1] Для того, чтобы этот корень принадлежал отрезку ([0;1]), нужно, чтобы [0leqslant dfrac{a+1}2leqslant 1
quadRightarrowquad -1leqslant aleqslant 1] Таким образом, чтобы корень (x=frac{a+1}2) существовал и принадлежал отрезку ([0;1]), нужно, чтобы (-frac13leqslant aleqslant 1).
Заметим, что тогда при (0leqslant aleqslant 1) оба корня (x=a) и (x=frac{a+1}2) принадлежат отрезку ([0;1]) (то есть уравнение имеет два корня на этом отрезке), кроме случая, когда они совпадают: [a=dfrac{a+1}2quadRightarrowquad a=1] Таким образом, нам подходят (ain left[-frac13; 0right)) и (a=1).
Ответ:
(ain left[-frac13;0right)cup{1})
Задание
6
#3238
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [xsqrt{x-a}=sqrt{6x^2-(6x+3a)x+3a}]
имеет единственный корень на отрезке ([0;1].)
(ЕГЭ 2017, резервный день)
Уравнение равносильно: [xsqrt{x-a}=sqrt{3a(1-x)}] ОДЗ уравнения: [begin{cases} xgeqslant 0\ x-ageqslant 0\3a(1-x)
geqslant 0end{cases}] На ОДЗ уравнение перепишется в виде: [x^3-a(x^2-3x+3)=0]
1) Пусть (a<0). Тогда ОДЗ уравнения: (xgeqslant 1). Следовательно, для того, чтобы уравнение имело единственный корень на отрезке ([0;1]), этот корень должен быть равен (1). Проверим: [1^3-a(1^2-3cdot 1+3)=0 quadRightarrowquad a=1.] Не подходит под (a<0). Следовательно, эти значения (a) не подходят.
2) Пусть (a=0). Тогда ОДЗ уравнения: (xgeqslant 0). Уравнение перепишется в виде: [x^3=0 quadRightarrowquad x=0] Полученный корень подходит под ОДЗ и входит в отрезок ([0;1]). Следовательно, (a=0) – подходит.
3) Пусть (a>0). Тогда ОДЗ: (xgeqslant a) и (xleqslant 1). Следовательно, если (a>1), то ОДЗ – пустое множество. Таким образом, (0<aleqslant 1) и при этих (a) ОДЗ: (aleqslant xleqslant
1). Следовательно, если корень подойдет по ОДЗ, то он попадет и в отрезок ([0;1]).
Рассмотрим функцию (y=x^3-a(x^2-3x+3)). Исследуем ее.
Производная равна (y’=3x^2-2ax+3a). Определим, какого знака может быть производная. Для этого найдем дискриминант уравнения (3x^2-2ax+3a=0): (D=4a(a-9)). Следовательно, при (ain (0;1]) дискриминант (D<0). Значит, выражение (3x^2-2ax+3a) положительно при всех (x). Следовательно, при (ain (0;1]) производная (y’>0). Следовательно, (y) возрастает. Таким образом, по свойству возрастающей функции уравнение (y(x)=0) может иметь не более одного корня.
Следовательно, для того, чтобы корень уравнения (точка пересечения графика (y) с осью абсцисс) находился на отрезке ([a;1]), нужно, чтобы [begin{cases} y(1)geqslant 0\
y(a)leqslant 0 end{cases}quadRightarrowquad ain [0;1]] Учитывая, что изначально в рассматриваемом случае (ain (0;1]), то ответ (ain (0;1]).
Итоговый ответ, полученный объединением ответов во всех трех случаях: [ain [0;1]]
Ответ:
([0;1])
Задание
7
#3267
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых уравнение [sqrt{1-4x}cdot ln(9x^2-a^2)=sqrt{1-4x}cdot ln (3x+a)]
имеет ровно один корень.
(ЕГЭ 2017, основная волна)
Данное уравнение можно переписать как [begin{cases}
sqrt{1-4x}cdot ln dfrac{(3x-a)(3x+a)}{3x+a}=0\[2ex]
3x+a>0end{cases} quadLeftrightarrowquad
begin{cases}
sqrt{1-4x}cdot ln (3x-a)=0\
3x+a>0end{cases}] Система имеет два корня:
1) (x_1=frac14), если он удовлетворяет (3x+a>0) и (3x-a>0): [begin{cases}
dfrac34+a>0\[1ex]
dfrac34-a>0end{cases} quadLeftrightarrowquad
-dfrac34<a<dfrac34]
2) (x_2=frac{a+1}3), если он удовлетворяет (3x+a>0) и (1-4xgeqslant 0): [begin{cases}
a+1+a>0\[1ex]
1-dfrac43a-dfrac43geqslant 0end{cases}quadLeftrightarrowquad
-dfrac12<aleqslant -dfrac14]
Рассмотрим случаи, когда данная система имеет ровно один корень. Пусть (x_1ne x_2), то есть (ane -frac14).
1. Пусть (x_1=frac14) – единственное решение системы.
(x_1) будет корнем, если (-frac34<a<frac34), (x_2) не будет корнем, если (ain
left(-infty;-frac12right]cupleft(-frac14;+inftyright)). Пересекая эти значения, а также учитывая, что (ane -frac14), получаем: [ain left(-dfrac34;-dfrac12right]cupleft(-dfrac14;dfrac34right)] 2. Пусть (x_2=frac{a+1}3) – единственное решение системы.
(x_1) не будет корнем, если (ain
left(-infty;-frac34right]cupleft[frac34;+inftyright)), (x_2) будет корнем, если (-frac12<aleqslant -frac14). Пересекая эти значения, а также учитывая, что (ane -frac14), получаем: [ain varnothing]
Пусть (x_1=x_2). Тогда (a=-frac14). Заметим, что при этом значении что (x_1), что (x_2) являются решением, следовательно, оно нам подходит.
Итоговый ответ: [ain left(-dfrac34;-dfrac12right]cupleft[-dfrac14;dfrac34right)]
Ответ:
(ain
left(-dfrac34;-dfrac12right]cupleft[-dfrac14;dfrac34right)
)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Home » ЕГЭ 2020. 100 баллов. Математика. Профильный уровень. Задачи с параметром [Юрий Викторович Садовничий] (pdf)
Юрий Викторович Садовничий
Математика Учебники и пособия: прочее
 |
Добавлена: 14.12.2022 Версия: 1.0. Дата создания файла: 2014-11-10 ISBN: 9785377150046 Издательство: Экзамен Город: Москва Поделиться: (ссылка для форума) Аннотация Данная книга посвящена задачам ЕГЭ по математике (задачи с параметром). Рассматриваются различные методы решения таких задач, также большое внимание уделяется графическим иллюстрациям. Книга необходима учащимся старших классов, учителям математики, репетиторам. Рекомендации:эту книгу рекомендовали 0 пользователей. Теги: ЕГЭ математика |