Егэ 2019 математика задачи по стереометрии задача 8 профильный уровень - Помощь в подготовке к экзаменам и поступлению

Задание 2 Профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объемов и площадей поверхности многогранников и тел вращения.

Ничего сложного здесь нет. Все эти задачи доступны даже десятикласснику. И даже гуманитарию.

Как решать задания по стереометрии из первой части Профильного ЕГЭ?

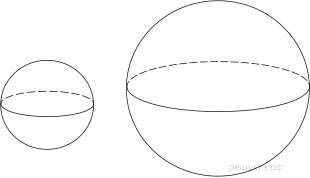
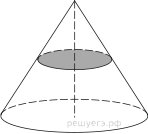
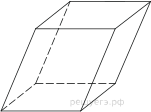
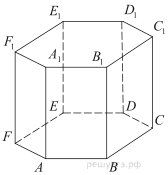
Повторим формулы для вычисления объемов и площадей поверхности многогранников (призмы, пирамиды… ) и тел вращения (цилиндра, конуса и шара)

Проверим себя – умеем ли мы рисовать чертежи?

Посмотрим, как решаются простые задачи по стереометрии и задачи с секретами.

Запоминаем один из главных лайфхаков решения задач по стереометрии:

Отношение объемов подобных тел равно кубу коэффициента подобия.

Если все линейные размеры объемного тела увеличить в k раз, то его площадь увеличится в k^2 раз, а объем в k^3 раз.

И решаем задачи. У нас все получится!

1. Во сколько раз увеличится площадь поверхности и объем куба, если его ребро увеличить в два раза?

Отношение площадей поверхности подобных тел равно квадрату коэффициента подобия, а отношение объемов – кубу коэффициента подобия. При увеличении ребра в 2 раза площадь поверхности увеличится в 4 раза, а объем – в 8 раз.

2. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 3 раза меньше, чем у большого. Поэтому площадь сечения в 9 раз меньше площади основания. Она равна 2.

3. Объем пирамиды равен 10. Через середину высоты параллельно основанию пирамиды проведено сечение, которое является основанием меньшей пирамиды с той же вершиной. Найдите объем меньшей пирамиды.

Меньшая пирамида подобна большой, коэффициент подобия $k=frac{1}{2}.$ Отношение объемов подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен $frac{10}{8}=1,25.$

4. Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.

Площадь основания пирамиды ЕАВС в 2 раза меньше, чем у пирамиды ABCDS. Высота пирамиды ЕАВС равна половине высоты пирамиды ABCDS. Значит, объем пирамиды ЕАВС в 4 раза меньше объема пирамиды ABCDS. Он равен $frac{116}{4}=29.$

5. В правильной четырехугольной пирамиде SABCD точка E – середина ребра AB, боковое ребро SC равно 4, длина отрезка SE равна Найти объем пирамиды SABCD .

Найдем сторону основания пирамиды. По теореме Пифагора, для треугольника SAE получаем, что Соответственно, сторона основания пирамиды равна Если обозначить центр основания за H, то высоту пирамиды найдем по теореме Пифагора, для треугольника SHE – она равна 2.

Применяя формулу для объема пирамиды $V=frac{1}{3}S_{ABCD}cdot h$ , получаем ответ: 16.

Многие задания №2 Профильного ЕГЭ по математике можно считать подготовительными – для того, чтобы научиться решать задачу 14 из второй части ЕГЭ.

Для решения некоторых из них стоит выучить основные определения и теоремы стереометрии. В общем, то, что входит в программу по стереометрии.

6. Стороны основания треугольной пирамиды равны 15, 16 и 17. Боковые ребра наклонены к плоскости основания под углами 45°. Найдите объем пирамиды.

Пусть точка О – проекция точки S на плоскость основания пирамиды. Прямоугольные треугольники АОS, ВОS, СОS равны (по общему катету ОS и острому углу). Значит, АО = ВО = СО. Точка О, равноудаленная от вершин основания, – это центр окружности, описанной вокруг треугольника АВС. Тогда АО = ВО = СО = OS = R, где R – радиус этой окружности.

Радиус описанной окружности найдем по формуле

$R=frac{abc}{4S}.$

Площадь найдем по формуле Герона:

$S_{triangle ABC}=sqrt{p(p-a)(p-b)(p-c)}$ , где $p=frac{15+16+17}{2}=24$ – полупериметр.

$S_{triangle ABC}= sqrt{24cdot 9cdot 8cdot 7}=sqrt{3cdot 8cdot 3cdot 3cdot 8cdot 7}=24sqrt{21};$

$R=frac{15cdot 16cdot 17}{4cdot 24sqrt{21}}=frac{5cdot 17}{2sqrt{21}};$

$V=frac{1}{3}S_{triangle ABC}cdot OS=frac{1}{3}cdot 24sqrt{21}cdot frac{5cdot 17}{2cdot sqrt{21}}=4cdot5cdot17=340.$

Заметим, что если боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то вершина проецируется в центр основания.

7. В правильной треугольной призме , все ребра которой равны 3, найдите угол между прямыми и . Ответ дайте в градусах.

Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Поскольку CC_1 и AA_1 параллельны, найдем угол между CC_1 и BC_1 . Он равен 45 градусов, так как грань – квадрат.

Ответ: 45.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Профильный ЕГЭ по математике. Задание №2. Стереометрия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

ЕГЭ 2019, Математика, Задачи по стереометрии, Задача 8, Профильный уровень, Задача 13 и 16, Базовый уровень, Рабочая тетрадь, Ященко И.В., Шестаков С.А.

Рабочая тетрадь по математике серии «ЕГЭ 2019. Математика» ориентирована на подготовку учащихся старшей школы к успешной сдаче Единого государственного экзамена по математике в 2019 году по базовому и профильному уровням.
Настоящее пособие предназначено для подготовки к решению стереометрических задач первой части ЕГЭ по математике. Оно состоит из трёх частей: «Многогранники. Призмы», «Многогранники. Пирамиды» и «Тела вращения», каждая из которых открывается начальной диагностической работой и включает в себя несколько тематических модулей, а также тренировочные работы к каждому из таких модулей. Помимо тренировочных работ в каждом модуле приводятся необходимые теоретические сведения и краткие методические рекомендации с разбором типовых примеров. Завершают пособие итоговые диагностические работы, в которые включены задачи по всем темам каждой из частей. Все тренировочные и диагностические работы даются в двух вариантах.
Тетрадь предназначена для учащихся средней школы, учителей математики, родителей.

Примеры.
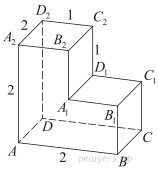
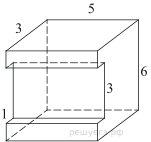
Найдите площадь поверхности многогранника, изображённого на рисунке, если все его двугранные углы прямые, а числа на рисунке означают длины соответствующих рёбер.

Дана наклонная призма АВСА1В1С1, основаниями которой являются правильные треугольники АВС и А1В1С1. Найдите синус угла наклона бокового ребра к плоскости основания, если высота призмы равна 3, а боковое ребро равно 10.

Тангенс угла между боковым ребром и плоскостью основания правильной треугольной пирамиды равен 5. Найдите тангенс угла между плоскостью боковой грани пирамиды и плоскостью её основания.

Расстояние от вершины основания правильной треугольной пирамиды до плоскости боковой грани, не содержащей эту вершину, равно 7. Высота основания пирамиды равна 10. Найдите синус угла между плоскостью боковой грани и плоскостью основания пирамиды.

Содержание.
От редактора серии.
Предисловие.
Часть I. Многогранники. Призмы
Диагностическая работа 1.
1. Призма, её элементы. Прямая призма. Правильная треугольная призма.
Тренировочная работа 1.
2. Параллелепипед, его элементы. Прямоугольный параллелепипед. Куб.
Тренировочная работа 2.
3. Площадь поверхности призмы.
Тренировочная работа 3.
4. Произвольные многогранники, площади их поверхностей.
Тренировочная работа 4.
5. Объём призмы.
Тренировочная работа 5.
Часть II. Многогранники. Пирамиды
Диагностическая работа 2.
6. Пирамида, её элементы. Правильная треугольная пирамида.
Тренировочная работа 6.
7. Правильная четырёхугольная пирамида. Правильная шестиугольная пирамида Тренировочная работа 7.
8. Площадь поверхности пирамиды.
Тренировочная работа 8.
9. Объём пирамиды.
Тренировочная работа 9.
Часть III. Тела вращения
Диагностическая работа 3.
10. Цилиндр, его элементы. Площадь поверхности цилиндра.
Тренировочная работа 10.
11. Конус, его элементы. Площадь поверхности конуса.
Тренировочная работа 11.
12. Объём цилиндра и объём конуса.
Тренировочная работа 12.
13. Сфера и шар, их элементы. Площадь сферы и объём шара.
Тренировочная работа 13.
14. Комбинации тел вращения и многогранников.
Тренировочная работа 14.
15. Изменение площади поверхности и объёма фигуры при изменении её линейных размеров.
Тренировочная работа 15.
Часть IV. Диагностические работы
Диагностическая работа 4.
Диагностическая работа 5.
Диагностическая работа 6.
Диагностическая работа 7.
Диагностическая работа 8.
Ответы.

Купить
.

По кнопкам выше и ниже «Купить бумажную книгу» и по ссылке «Купить» можно купить эту книгу с доставкой по всей России и похожие книги по самой лучшей цене в бумажном виде на сайтах официальных интернет магазинов Лабиринт, Озон, Буквоед, Читай-город, Литрес, My-shop, Book24, Books.ru.

По кнопке «Купить и скачать электронную книгу» можно купить эту книгу в электронном виде в официальном интернет магазине «ЛитРес», и потом ее скачать на сайте Литреса.

По кнопке «Найти похожие материалы на других сайтах» можно найти похожие материалы на других сайтах.

On the buttons above and below you can buy the book in official online stores Labirint, Ozon and others. Also you can search related and similar materials on other sites.

Дата публикации: 21.12.2018 16:58 UTC

Теги:

ЕГЭ по математике :: математика :: Ященко :: Шестаков

Следующие учебники и книги:

ЕГЭ, Математика, Профильный уровень, Задания с развернутым ответом, Садовничий Ю.В., 2019
Математика, Тематическая подготовка к ЕГЭ, Садовничий Ю.В., 2011
ЕГЭ 2019, Математика, Графики и диаграммы, Задача 2, Профильный уровень, Задача 11, Базовый уровень, Рабочая тетрадь, Трепалин А.С., Ященко И.В.
ЕГЭ 2019, Математика, Значения выражений, Задача 9, Профильный уровень, Задача 2 и 5, Базовый уровень, Рабочая тетрадь, Ященко И.В., Шестаков С.А.

Предыдущие статьи:

ЕГЭ 2019, Математика, Геометрический смысл производной, Задача 7, Профильный уровень, Задача 14, Базовый уровень, Рабочая тетрадь, Ященко И.В., Захаров П.И.
ЕГЭ 2019, Математика, Задачи по планиметрии, Задача 6, Профильный уровень, Задача 8 и 15, Базовый уровень, Рабочая тетрадь, Хачатурян А.В., Ященко И.В.
ЕГЭ 2019, Математика, Простейшие уравнения, Задача 5, Профильный уровень, Задача 4 и 7, Базовый уровень, Рабочая тетрадь, Шестаков С.А., Ященко И.В.
ЕГЭ 2019, Математика, Теория вероятностей, Задача 4, Профильный уровень, Задача 10, Базовый уровень, Рабочая тетрадь, Высоцкий И.H., Ященко И.В.

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

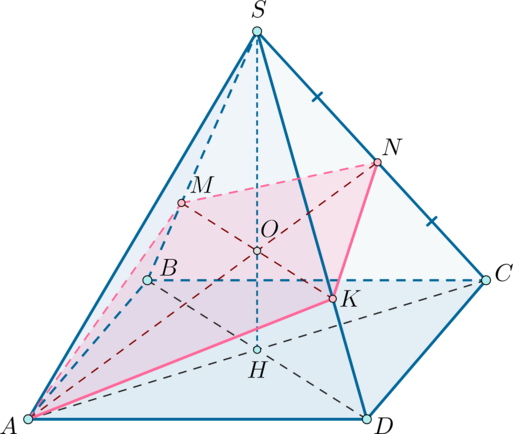
В правильной четырёхугольной пирамиде SABCD сторона AB основания равна а высота SH пирамиды равна 3. Точки M и N  — середины рёбер CD и AB, соответственно, а NT  — высота пирамиды NSCD с вершиной N и основанием SCD.

а)  Докажите, что точка T является серединой SM.

б)  Найдите расстояние между NT и SC.

Источник: Задания 14 (С2) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Вариант 512 (C часть).

Основанием прямой треугольной призмы ABCA₁B₁C₁ является прямоугольный треугольник ABC с прямым углом C. Грань ACC₁A₁ является квадратом.

а)  Докажите, что прямые CA₁ и AB₁ перпендикулярны.

б)  Найдите расстояние между прямыми CA₁ и AB₁, если AC  =  4, BC  =  7.

Источник: Задания 14 (C2) ЕГЭ 2017

В правильной четырёхугольной пирамиде PABCD сторона основания ABCD равна 12, боковое ребро PA ― Через вершину A проведена плоскость α, перпендикулярная прямой PC и пересекающая ребро PC в точке K.

а)  Докажите, что плоскость α делит высоту PH пирамиды PABCD в отношении 2 : 1, считая от вершины P.

б)  Найдите расстояние между прямыми PH и BK.

Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 04.03.2018. Вариант 1.

В кубе ABCDA₁B₁C₁D₁ все ребра равны 6.

а)  Докажите, что угол между прямыми AC и BC₁ равен 60°.

б)  Найдите расстояние между прямыми AC и BC₁.

Источник: ЕГЭ по математике 01.06.2018. Основная волна. Вариант 991 (C часть). Он же: вариант 751 (резервная волна 25.06.2018), Задания 14 (С2) ЕГЭ 2018

В кубе ABCDA₁B₁C₁D₁ рёбра равны 1. На продолжении отрезка A₁C₁ за точку C₁ отмечена точка M так, что A₁C₁  =  C₁M, а на продолжении отрезка B₁C за точку C отмечена точка N так, что B₁C  =  CN.

а)  Докажите, что MN  =  MB₁.

б)  Найдите расстояние между прямыми B₁C₁ и MN.

Источник: Резервная волна ЕГЭ по математике 24.06.2019. Вариант 992, Задания 14 (С2) ЕГЭ 2019

Пройти тестирование по этим заданиям

Источник

16 февраля 2021

В закладки

Обсудить

Жалоба

Задание 8 профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объёмов и площадей поверхности многогранников и тел вращения.

→ Конспект: 1.pdf
→ Формулы стереометрии: 2.pdf
→ Задачи открытого банка ФИПИ: 3.pdf

Автор: Алькаева Лариса Рахимовна.

Источник: vk.com/alkaevalr

Источник

Вариант 1 8. Стереометрия

1.Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

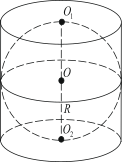
2. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

3. Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

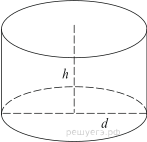
4. Площадь боковой поверхности цилиндра равна , а диаметр основания — 8. Найдите высоту цилиндра.

5. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.

6. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

8. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?

9. Радиусы двух шаров равны 32 и 60. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.

10. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Вариант 2 8. Стереометрия

1. Диаметр основания конуса равен 42, а длина образующей равна 75. Найдите высоту конуса.

2. Гранью параллелепипеда является ромб со стороной 4 и острым углом 30°. Одно из ребер параллелепипеда составляет с этой гранью угол в 30° и равно 6. Найдите объем параллелепипеда.

3. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁, C₁, D₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 9, а боковое ребро равно 10.

4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.

5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

6. В правильной четырехугольной пирамиде точка — центр основания, вершина, , Найдите длину отрезка

7. Гранью параллелепипеда является ромб со стороной 1 и острым углом 45°. Одно из ребер параллелепипеда составляет с этой гранью угол в 45° и равно 5. Найдите объем параллелепипеда.

8. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

9. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.

10.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.

Вариант 3 8. Стереометрия

1. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C₂C₃B₂.

2. Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

3. Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

6. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 0,5 и 16. Найдите ребро равновеликого ему куба.

7. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 24. Найдите объем пирамиды.

8. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.

9. Объем правильной четырехугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

10. В прямоугольном параллелепипеде известно, что Найдите длину ребра

Вариант 4 8. Стереометрия

1. Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

2. В прямоугольном параллелепипеде известно, что Найдите длину ребра

3. Площадь боковой поверхности цилиндра равна 18, а диаметр основания равен 9. Найдите высоту цилиндра.

4. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в три раза?

5. Найдите объём многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 9, а боковое ребро равно 8.

6. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 3. Объем призмы равен 18. Найдите ее боковое ребро.

7. Найдите объем многогранника, вершинами которого являются точки , , , , , , правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3.

8. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 13. Найдите его объем, деленный на π.

9. Диагональ куба равна 13. Найдите площадь его поверхности.

10. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 48 и высота равна 7.

Вариант 5 8. Стереометрия

1. Диагональ куба равна 1. Найдите площадь его поверхности.

2. Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.

3. В правильной треугольной призме ABCA₁B₁C₁ стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A₁B₁ и A₁C₁.

4. Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

5. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.

6. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см³.

7. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.

8. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

9. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы

10.Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Вариант 6 8. Стереометрия

1. В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.

2. Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

3. Во сколько раз увеличится объем куба, если его ребра увеличить в пятнадцать раз?

4. Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.

5. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁, C₁, D₁ правильной шестиугольной призмыABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 6, а боковое ребро равно 2.

6. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.

7. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.

8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

10. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.

Вариант 7 8. Стереометрия

1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

2. Найдите объем части конуса, изображенной на рисунке. В ответе укажите

3. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

4. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

5. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

6. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

7. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

8. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

9. Найдите объем части конуса, изображенной на рисунке. В ответе укажите

10. Найдите объем части конуса, изображенной на рисунке. В ответе укажите

Вариант 8 8. Стереометрия

1. Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

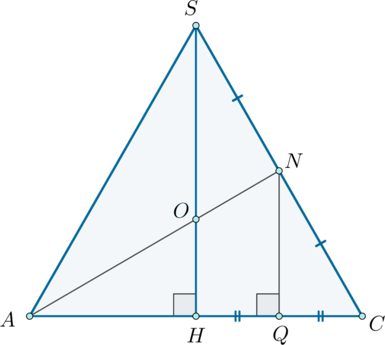
2. В правильной четырехугольной пирамиде точка — центр основания, вершина, , Найдите длину отрезка

3. В правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.

4. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.

5. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.

6. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.

7. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.

8. В правильной треугольной пирамиде медианы основания пересекаются в точке Объем пирамиды равен , Найдите площадь треугольника

9. В прямоугольном параллелепипеде известно, что , , Найдите длину ребра

10. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.

Вариант 9 8. Стереометрия

1. Найдите расстояние между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

2. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

3. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на

4. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

5. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

6. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

7. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.

8. Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

9. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

10. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.

Вариант 10 8. Стереометрия

1. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁, C₁, D₁ правильной шестиугольной призмыABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 6, а боковое ребро равно 2.

2.Высота конуса равна 12, образующая равна 15. Найдите его объем, деленный на

3. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.

4. В правильной четырехугольной пирамиде точка О — центр основания, вершина, , Найдите длину отрезка

5. В правильной четырехугольной пирамиде точка — центр основания, вершина, , Найдите длину отрезка

6. ЗВ правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.

7. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.

8. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.

9. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.

10. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.

8. Стереометрия

Вариант 1

12
166,5
60
2
28
75
96
27
68
1,25

Вариант 2

Вариант 3

3
60
45
4
152
2
2304
48
29
4

Вариант 4

29
5
2
27
24
6
4
19,5
338
4704

Вариант 5

Вариант 6

9
45
3375
8
6
1,5
22
110
94
36

Вариант 7

340
216
4
3,75
144
937,5
14
105
87,75
243

Вариант 8

Вариант 9

Вариант 10

Источник

Прототипы задания №8 ЕГЭ по математике профильного уровня — текстовые задачи. Практический материал для подготовки к экзамену в 11 классе.

Для успешного выполнения задания №8 необходимо уметь строить и исследовать простейшие математические модели.

Практика

Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2

Уровень сложности задания — повышенный.

Максимальный балл за выполнение задания — 1

Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 7

Примеры заданий:

Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.

Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.

Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?

Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?

Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.

Связанные страницы:

Источник

14. Задачи по стереометрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по стереометрии формата ЕГЭ

Задание
1

#3868

Уровень задания: Равен ЕГЭ

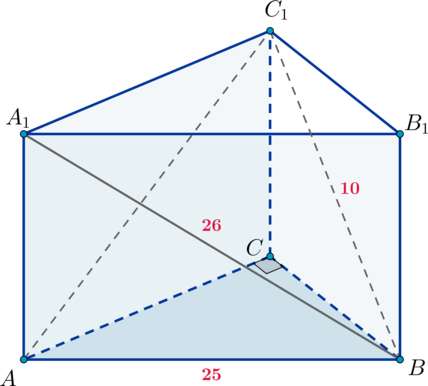
Основанием прямой треугольной призмы (ABCA_1B_1C_1) является прямоугольный треугольник (ABC), причем (angle C=90^circ). Диагонали боковых граней (AA_1B_1B) и (BB_1C_1C) равны соответственно (26) и (10), (AB=25).

а) Докажите, что (triangle BA_1C_1) – прямоугольный.

б) Найдите объем пирамиды (AA_1C_1B).

а) Так как (BB_1perp (A_1B_1C_1)), (B_1C_1perp A_1C_1), то по теореме о трех перпендикулярах (BC_1perp A_1C_1) (как наклонная). Следовательно, (triangle A_1C_1B) – прямоугольный.

б) Заметим, что (BCperp AC) и (BCperp CC_1), следовательно, по признаку (BCperp (AA_1C_1)). Следовательно, (BC) – высота пирамиды (BAA_1C_1) с основанием (AA_1C_1).
Так как (triangle AA_1C_1) прямоугольный, то [V_{BAA_1C_1}=dfrac{frac12cdot AA_1cdot A_1C_1cdot BC}3] По теореме Пифагора [begin{aligned}
&A_1C_1=sqrt{26^2-10^2}=sqrt{16cdot 36}=24\[1ex]
&AA_1=sqrt{26^2-25^2}=sqrt{1cdot 51}=sqrt{51}\[1ex]
&BC=sqrt{10^2-51}=sqrt{49}=7 end{aligned}] Тогда [V_{BAA_1C_1}=dfrac{frac12cdot 24cdot sqrt{51}cdot 7}3=28sqrt{51}]

Ответ:

б) (28sqrt{51})

Задание
2

#6924

Уровень задания: Равен ЕГЭ

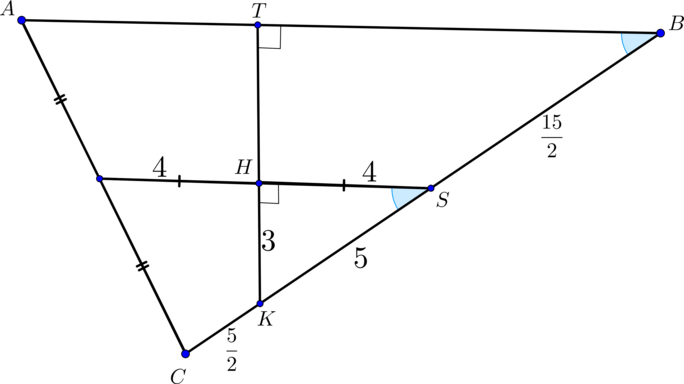
(ABCA_1B_1C_1) — прямая треугольная призма, (AB=16, BC=15,
AA_1=8), (cosangle ABC=0,8). (M, N) – середины ребер (AC) и (B_1C_1) соответственно. (K,P) – такие точки на ребрах (BC) и (B_1C_1) соответственно, что (CK=B_1P=dfrac{1}{6}BC).

а) Построить сечение призмы плоскостью (alpha), параллельной прямой (MN) и проходящей через точки (K) и (P).

б) Найти площадь сечения призмы плоскостью (alpha).

а)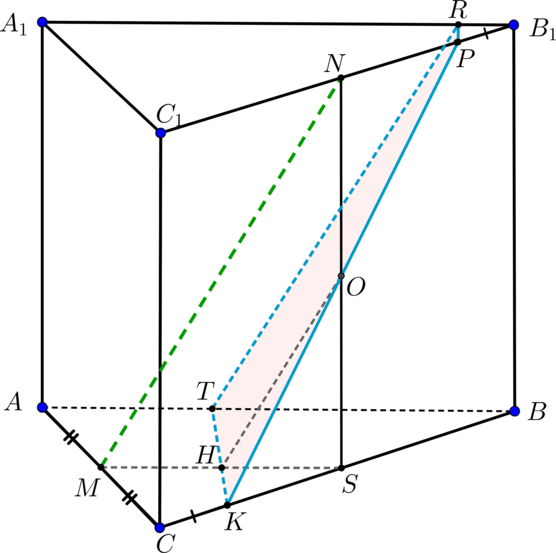

Если прямая (MNparallel alpha Rightarrow MN) параллельна некоторой прямой, лежащей в (alpha). Проведем (NSperp BC, NScap
KP=O). В плоскости (MNS) проведем (OHparallel MN Rightarrow
MH=HS). Тогда прямая (KHcap AB=T). Так как плоскости (ABC) и (A_1B_1C_1) параллельны, то (alpha) пересечет плоскость (A_1B_1C_1) по прямой, параллельной (KT). Следовательно, проведем (PRparallel
KT). Таким образом, (TRPK) – искомое сечение (трапеция).

б) Заметим, что (CK=dfrac{1}{6} cdot 15=dfrac{5}{2} Rightarrow
KS=5). Т.к. (MS) – средняя линия треугольника (ABC Rightarrow MS=8
Rightarrow HS=4). Так как (angle HSK=angle ABC), то по теореме косинусов (HK=sqrt{16+25-2cdot 4cdot 5cdot frac45}=3). Таким образом, по обратной теореме Пифагора треугольник (HKS) – прямоугольный, следовательно, (angle H =90^circ). Таким образом, по теореме о трех перпендикулярах, из того, что (NSperp (ABC),
HSperp KT Rightarrow
OHperp KT).

Проведем (PH_1 perp KT). Из подобия треугольников (HOK) и (H_1PK) следует, что (PH_1=2OH). Т.к. (OS=dfrac{1}{2}NS=4, HS=4 Rightarrow
OH=4sqrt2). Таким образом найдена высота трапеции (PH_1=8sqrt2).

Найдем основания трапеции (KT) и (PR).

(sin angle KSH = dfrac{3}{5}=sin angle B=dfrac{KT}{KB}
Rightarrow KT=dfrac{15}{2}).

(bigtriangleup PRB_1 sim bigtriangleup KTB Rightarrow
PR=dfrac{3}{2}).

Таким образом, (S_{TRPK} = dfrac{1}{2}cdot
left(dfrac{15}{2}+dfrac{3}{2}right)cdot 8sqrt2 = 36sqrt2)

Ответ:

б) (36sqrt2)

Задание
3

#2300

Уровень задания: Равен ЕГЭ

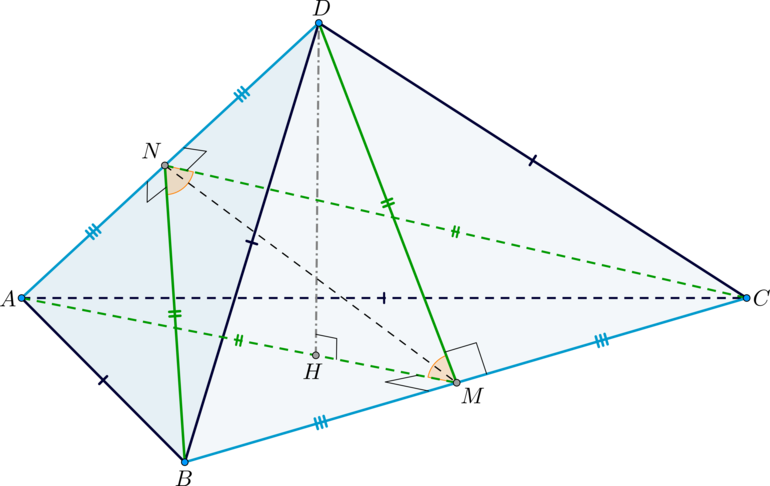
В треугольной пирамиде (DABC) двугранные углы при ребрах (AD) и (BC) равны. Известно также, что (AB=BD=DC=AC=sqrt{15}).

а) Докажите, что (AD=BC).

б) Найдите объем пирамиды, если двугранные углы при (AD) и (BC) равны по (60^circ).

а) Рассмотрим пирамиду (DABC), (AB=BD=DC=CA), (angle
(BAD,CAD)=angle (BAC,BDC)).

Т.к. (triangle ABD) и (triangle ACD) – равнобедренные, причем (AD) – общее основание, то высоты к основаниями попадут в одну точку – в середину стороны (AD), точку (N). То есть (BNperp AD), (CNperp AD). Таким образом, (angle BNC) – линейный угол двугранного угла (angle(BAD,CAD)).

Аналогичным образом строится угол (angle AMD) – линейный угол двугранного угла (angle (BAC,BDC)), где (M) – середина (BC). Таким образом, (angle BNC=angle AMD).

Т.к. (triangle ABD=triangle ACD) по трем сторонам, то (BN=CN). Аналогично (AM=DM). Значит, (triangle AMD) и (triangle BNC) – равнобедренные и подобные (по двум пропорциональным сторонам и углу между ними).

Заметим, что плоскости ((AMD)) и ((BNC)) имеют две общие точки – это точки (N) и (M). Следовательно, они пересекаются по прямой (MN). Отрезок (NM) – это высота в (triangle AMD) и (triangle BNC) к основаниям (AD) и (BC) соответственно. Следовательно, эти треугольники равны. Следовательно, (AD=BC), чтд.

б) Из пункта а) также следует, что (AM=DM=BN=CN). Т.к. двугранные углы равны (60^circ), то (triangle AMD) и (triangle BNC) – равносторонние.
Пусть (AM=DM=BN=CN=AD=BC=x).

Проведем высоту пирамиды (DH). Т.к. (DMperp BC), то по теореме о трех перпендикулярах (HMperp BC). Таким образом, точка (H) должна лежать на (AM), причем на середине, т.к. (triangle AMD) – равносторонний.

(DH=frac{sqrt3}2cdot AD=frac{sqrt3}2x). Найдем по теореме Пифагора (x) из (triangle ABM):

(AM=x), (BM=frac x2), (AB=sqrt{15}), следовательно, (x=2sqrt3).

Таким образом, [V_{DABC}=frac13cdot DHcdot S_{ABC}=dfrac13cdot
frac{sqrt3}2xcdot frac12x^2=6]

Ответ:

б) (6)

Задание
4

#1265

Уровень задания: Равен ЕГЭ

Дан правильный тетраэдр (SABC), (H) – такая точка на высоте (SO), что (OH:HS=1:3). Плоскость (alpha) проходит через точки (A) и (H) параллельно медиане (BM) треугольника (ABC) и пересекает ребро (CS) в точке (P).

а) Докажите, что (CP:PS=2:3).

б) Найдите угол между плоскостями (alpha) и (ABC).

а)

Правильный тетраэдр — это правильная треугольная пирамида, у которой все ребра равны. Пусть ребро пирамиды равно (a).
Т.к. пирамида правильная, то высота (SO) падает в точку пересечения медиан (bigtriangleup ABC). Рассмотрим плоскость (BSM), точка (H) лежит в этой плоскости. Т.к. плоскость (alpha) параллельна (BM), то она пересекает плоскость (BSM) по прямой, параллельной (BM).

Проведем (RTparallel BM, Hin RT). Тогда по теореме Фалеса (dfrac{SH}{HO}=dfrac{ST}{TM}=dfrac{3}{1}).

Прямая (AT) пересечет (CS) в точке (P). (bigtriangleup APR) – сечение пирамиды плоскостью (alpha).
Напишем теорему Менелая для (bigtriangleup CSM) и прямой (AP):
[dfrac{CP}{PS}cdot dfrac{ST}{TM}cdot dfrac{MA}{AC}=1] Из этого равенства находим, что (dfrac{CP}{PS}=dfrac{2}{3})

б) Докажем, что линия пересечения плоскостей (alpha) и (ABC) параллельна прямой (BM). Пусть это не так: пусть (l) – линия пересечения (alpha) и (ABC) и (lcap BM=Z). Тога прямая (BMcap
alpha=Z), следовательно, не может быть параллельна (alpha). Получили противоречие, следовательно, (lparallel BM). Заметим, что прямая (l) проходит через точку (A).

Построим линейный угол двугранного угла между (alpha) и (ABC). Т.к. (HOperp ABC), проведем (OKperp l), следовательно, по теореме о трех перпендикулярах (HKperp l). Таким образом, (angle HKO) – искомый угол.

1) Найдем (HO).
(BO=dfrac{2}{3}cdot BM=dfrac{2}{3}cdot
dfrac{sqrt3}{2}a=dfrac{a}{sqrt3})

Тогда (SO=sqrt{a^2 -dfrac{a^2}{3}}=sqrt{dfrac{2}{3}}a
Rightarrow HO=dfrac{1}{4}SO=dfrac{sqrt2a}{4sqrt3})

2) Найдем (OK).
(BMperp AC, BMparallel l Rightarrow ACperp l). Т.к. (OKperp l
Rightarrow OKparallel AC). Таким образом, (OMAK) – параллелограмм, следовательно, (OK=MA=dfrac{1}{2}a).
Треугольник (HOK) – прямоугольный, следовательно, (mathrm{ctg},angle
HKO=dfrac{OK}{HO}=sqrt6)
Тогда (angle HKO= mathrm{arcctg},sqrt6).

Ответ:

б) (mathrm{arcctg},sqrt6)

Задание
5

#3059

Уровень задания: Равен ЕГЭ

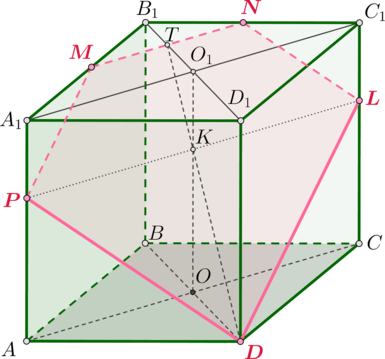
Дана правильная четырехугольная призма (ABCDA_1B_1C_1D_1), стороны основания которой равна (4), а боковые ребра равны (5).

а) Постройте сечение призмы плоскостью (DMN), где (M) и (N) – середины отрезков (A_1B_1) и (B_1C_1).

б) Найдите угол между данным сечением и плоскостью (ABC).

(Задача от подписчиков)

а) Из условия следует, что призма прямая и основаниями являются квадраты.
(MN) – средняя линия в (triangle A_1B_1C_1), следовательно, (MNparallel A_1C_1). Тогда плоскость (DMN) пересечет плоскость (A_1C_1CA) по прямой (l), параллельной (A_1C_1) (в противном случае (l) пересечет (A_1C_1) в некоторой точке (K), которая будет лежать и на (A_1C_1), и в плоскости (DMN), следовательно, должна будет лежать и на (MN), что невозможно, так как (MN) не пересекает (A_1C_1)).
Таким образом, найдем точку, в которой плоскость (DMN) пересекает плоскость (A_1C_1CA).

Пусть плоскость (B_1D_1DB) пересекает (MN) в точке (T). Тогда (DTin
(DMN)). Если (O) и (O_1) – точки пересечения диагоналей оснований, то прямые (DT) и (OO_1) лежат в плоскости (B_1D_1DB). Пусть точка их пересечения – точка (K). Тогда (K) – искомая точка пересечения плоскости (DMN) и плоскости (A_1C_1CA).
Проведем через точку (K) прямую (l) параллельно (A_1C_1). Пусть она пересекла (AA_1) в точке (P), (CC_1) в точке (L). Таким образом, получили сечение (DPMNL) призмы плоскостью (DMN).

б) Заметим, что (KOperp (ABC)), следовательно, так как (ODperp
AC), то и (KDperp AC) по теореме о трех перпендикулярах. Значит, (angle KDO) равен углу между плоскостями (DMN) и (ABC).
По теореме Фалеса [dfrac{A_1M}{MB_1}=dfrac11=dfrac{O_1T}{TB_1}
quadRightarrowquad O_1T=TB_1.] (triangle TO_1Ksim triangle DOK), следовательно, [dfrac{O_1T}{OD}=dfrac12=dfrac{O_1K}{OK}] Следовательно, (OK=frac23OO_1=frac23AA_1=frac23cdot
5=frac{10}3).

(OD=frac12 BD=frac12cdot sqrt2AB=2sqrt2.)

Тогда [mathrm{tg},angle KDO=dfrac{OK}{OD}=dfrac56sqrt2
quadRightarrowquad
angle KDO=mathrm{arctg},dfrac56sqrt2.]

Ответ:

б) (mathrm{arctg},dfrac56sqrt2)

Задание
6

#3064

Уровень задания: Равен ЕГЭ

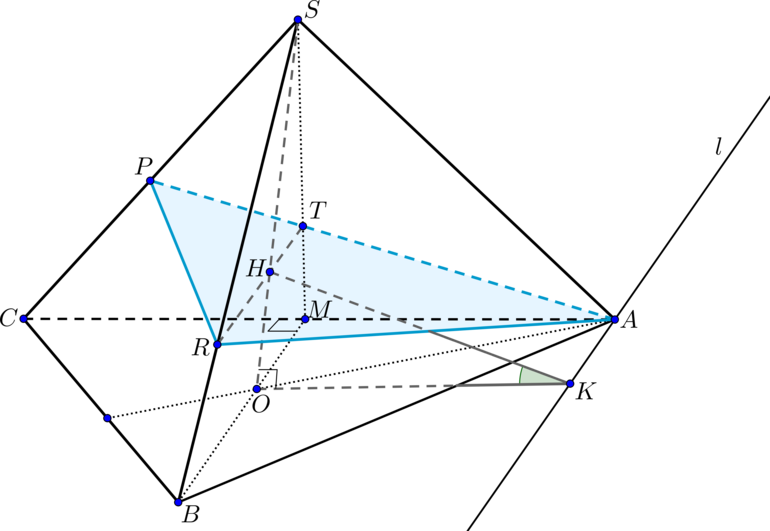
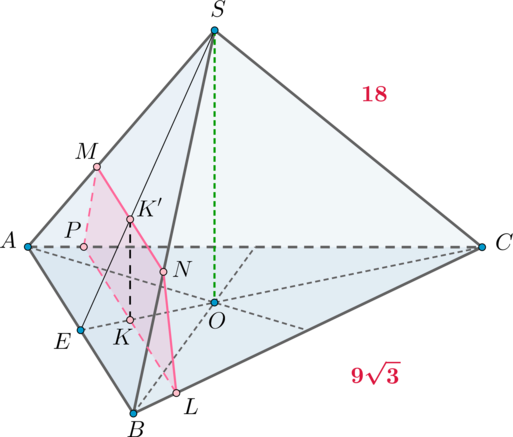
В правильной треугольной пирамиде (SABC) с основанием (ABC) на медиане основания (CE) взята точка (K) так, что (CK:KE=8:1). Через точку (K) проведена плоскость (alpha), которая перпендикулярна прямой (CE) и пересекает боковые ребра (SA) и (SB) в точках (M) и (N) соответственно.

а) Докажите, что (MN:AB=2:3).

б) Найдите объем пирамиды, вершиной которой является точка (C), а основанием – сечение пирамиды (SABC) плоскостью (alpha), если известно, что (AB=9sqrt3), (SA=18).

(Задача от подписчиков)

а) Пусть (SO) – высота пирамиды, (O) – точка пересечения медиан. Следовательно, [dfrac{CO}{OE}=dfrac21] Так как по условию (CK:KE=8:1), то можно обозначить (CK=8x), (KE=x). Тогда (CE=9x). Следовательно, (CO=frac23CE=6x), (OE=3x), (OK=2x).
Так как (CE) перпендикулярна плоскости (alpha), то нужно построить две пересекающиеся прямые в плоскости (alpha), которым (CE) будет перпендикулярна.
Первая прямая: так как (CEperp AB), то проведем через точку (K) прямую (PLparallel AB). Тогда (CEperp PL) ((Pin AC, Lin BC)).
Вторая прямая: так как (SOperp (ABC)), то (SOperp CE). Следовательно, проведем (KK’parallel SO), тогда (KK’perp CE) ((K’in SE)).
Следовательно, (alpha) проходит через точки (P, L, K’).

Заметим, что (alpha) пересечет плоскость (ASB) по прямой, параллельной (AB) (в противном случае (alpha) будет иметь общую точку с (AB), что невозможно, так как (ABparallel PL
quadRightarrowquad ABparallel alpha)).
Следовательно, (MNparallel AB) и проходит через (K’).
Из подобия (triangle K’EKsim triangle SEO): [dfrac{SE}{K’E}=dfrac{OE}{KE}=dfrac31 quadRightarrowquad K’E=
dfrac13SE
quadRightarrowquad SK’=dfrac23SE.] Из подобия (triangle
MSNsim triangle ASB): [dfrac{MN}{AB}=dfrac{SK’}{SE}=dfrac23.]

б) Рассмотрим пирамиду (CPMNL). (CK) – высота этой пирамиды, (PMNL) – трапеция ((MNparallel ABparallel PL)).
Следовательно, [V=dfrac13cdot CKcdot dfrac{MN+PL}2cdot KK’] Так как (BC=9sqrt3), то (CE=sqrt{BC^2-EB^2}=frac{27}2). Следовательно, [CK=dfrac89CE=12.] Из подобия (triangle PCLsim triangle ACB): [dfrac{PL}{AB}=dfrac{CK}{CE}=dfrac89quadRightarrowquad PL=
8sqrt3.] Из пункта а) [MN=dfrac23AB=6sqrt3.] Из подобия (triangle
EK’Ksim triangle ESO): [KK’=dfrac13SO=dfrac13sqrt{SC^2-CO^2}=dfrac13sqrt{18^2-9^2}=
3sqrt3.] Следовательно, [V=dfrac13cdot 12cdot dfrac{6sqrt3+8sqrt3}2cdot 3sqrt3=252.]

Ответ:

б) 252

Задание
7

#3063

Уровень задания: Равен ЕГЭ

Дана правильная четырехугольная пирамида (SABCD) с вершиной (S), стороны основания которой равны (6sqrt2), а боковые ребра равны (21).

а) Постройте сечение пирамиды плоскостью, проходящей через точку (A) и середину ребра (SC) параллельно прямой (BD).

б) Найдите площадь построенного сечения.

(Задача от подписчиков)

а) Пусть (N) – середина ребра (SC), (SH) – высота пирамиды (падает в точку пересечения диагоналей основания).
Необходимо построить прямую, лежащую в плоскости сечения и параллельную (BD). Рассмотрим плоскость (ASC). Прямая (AN) пересекает (SH) в точке (O). Теперь рассмотрим (BSD). Проведем в этой плоскости через точку (O) прямую, параллельную (BD). Пусть она пересечет ребра (SB) и (SD) в точках (M) и (K) соответственно. Таким образом, (AMNK) – искомое сечение.

б) Заметим, что по теореме о трех перпендикулярах (так как (OHperp
(ABC), AHperp BD)) (AOperp BD). Так как (BDparallel MK), то (AOperp MK), следовательно, (ANperp MK). Следовательно, у четырехугольника (AMNK) диагонали взаимно перпендикулярны. Значит, его площадь можно найти как [S=dfrac12 ANcdot MK.]

Заметим сразу, что (BD=AC=ABsqrt2=12).
Рассмотрим плоскость (ASC).

По теореме Менелая: [dfrac{SN}
{NC}cdot dfrac{CA}{AH}cdot dfrac{HO}{OS}=1 quadRightarrow
quad dfrac{HO}{OS}=dfrac12 quadRightarrowquad OS=2OH
quadRightarrowquad dfrac{SO}{SH}=dfrac23.] (это нам понадобится позже для поиска (MK))

Проведем (NQperp AC). Тогда из подобия (triangle SHC) и (triangle
NQC): [dfrac{SH}{NQ}=dfrac{SC}{NC}=2 quadRightarrowquad
NQ=dfrac12SH=dfrac12sqrt{SC^2-HC^2}=dfrac12sqrt{21^2-6^2}=
dfrac12sqrt{81cdot 5}] (Q) – середина (HC), следовательно, (AQ=frac34AC=frac34cdot 12=9). Тогда по теореме Пифагора [AN=sqrt{AQ^2+NQ^2}=sqrt{dfrac{81cdot 5}4+81}=dfrac{27}2.]
Рассмотрим (BSD). Так как (triangle MSKsim triangle BSD), то [dfrac{MK}{BD}=dfrac{SO}{SH}=dfrac23 quadRightarrowquad
MK=dfrac23BD=dfrac23cdot 12=8.] Следовательно, площадь сечения равна [S=dfrac12cdot 8cdot dfrac{27}2=54.]

Ответ:

б) 54

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник