Егэ 2021 математика 36 вариантов ященко профильный уровень 36 вариантов ответы - Помощь в подготовке к экзаменам и поступлению

Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».

Вариант 1

1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5
5,832
9) 2
10) -4
11) -2910

Вариант 2

1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1
0,216
9) 16
10) -8
11) 12,25

Вариант 3

1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2
51,2
9) 14
10) 32
11) 204

Вариант 4

1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8
281,25
9) 18
10) -56
11) -10,9

Вариант 5

1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19
60
9) 17
10) 16
11) -52

Вариант 6

1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4
30
9) 24
10) -1
11) -6

Вариант 7

1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9
0,6
9) 55
10) 6
11) 0,5

Вариант 8

1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7
1,8
9) 11
10) 0,25
11) 17

Вариант 9

1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1
756
9) 20
10) -3
11) 9

Вариант 10

1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18
220,5
9) 9
10) 253
11) -23,25

Вариант 11

1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1
50
9) 17,5
10) 78
11) 6,75

Вариант 12

1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4
40
9) 13,5
10) -23
11) 6,25

Вариант 13

1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4
33
9) 9
10) -0,5
11) 77

Вариант 14

1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39
23
9) 24
10) 0,4
11) 37

Вариант 15

1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2
0,32
9) 3
10) 2,5
11) 208

Вариант 16

1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4
1,16
9) 1
10) -15
11) 5

Вариант 17

1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2
175
9) 18
10) 16
11) -24

Вариант 18

1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28
43,75
9) 21
10) 2,25
11) -15

Вариант 19

1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2
115
9) 135
10) 2
11) -34

Вариант 20

1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25
220
9) 52
10) 27
11) 0

Вариант 21

1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2
6250
9) 14
10) 15
11) 7

Вариант 22

1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7
1,3
9) 5
10) 3,4
11) 1,2

Вариант 23

1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6
60
9) 75
10) 28
11) 18

Вариант 24

1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6
30
9) 10
10) -28
11) -2

Вариант 25

1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2
6
9) 1 35
10) -0,4
11) 14

Вариант 26

1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75
96
9) 28
10) -13
11) 1

Вариант 27

1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6
7
9) 77
10) 76
11) -3

Вариант 28

1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3
28
9) 6
10) -5
11) 38

Вариант 29

1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4
6,5
9) 6,4
10) 67
11) -21

Вариант 30

1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14
9,6
9) 22
10) 3
11) -8

Вариант 31

1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2
25
9) 54
10) -7
11) 8

Вариант 32

1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3
17
9) 12
10) 13
11) -9

Вариант 33

1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3
8
9) 48
10) -2,5
11) 26

Вариант 34

1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6
633
9) 64
10) -0,25
11) -1

Вариант 35

1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5
0,31
9) 20
10) 0,75
11) 9

Вариант 36

1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5
1,728
9) 756
10) -0,5
11) 30

Источник

Задание 1

Призёрами городской олимпиады по математике стали 20 учеников, что составило 10 % от числа участников. Сколько человек участвовало в олимпиаде?

Ответ: 200

Скрыть

Для определения исходного числа участников, нужно 20 разделить на коэффициент 10/100 , получим: 20:0,1 = 200 участников.

Задание 2

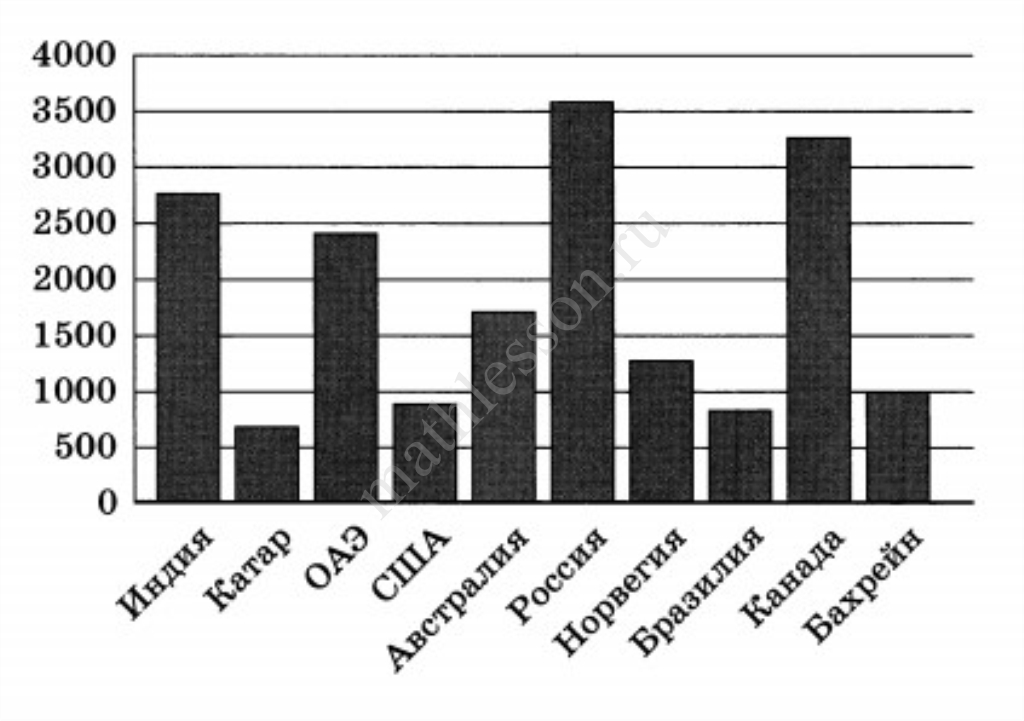
На диаграмме показано распределение выплавки алюминия в 10 странах мира (в тысячах тонн) за 2016 год. Среди представленных стран первое место по выплавке алюминия занимала Россия, десятое место занимал Катар. Какое место занимала Норвегия?

Ответ: 6

Скрыть

Больше у Индии, ОАЭ, Австралии, России и Канады. Следовательно, 6 место

Задание 3

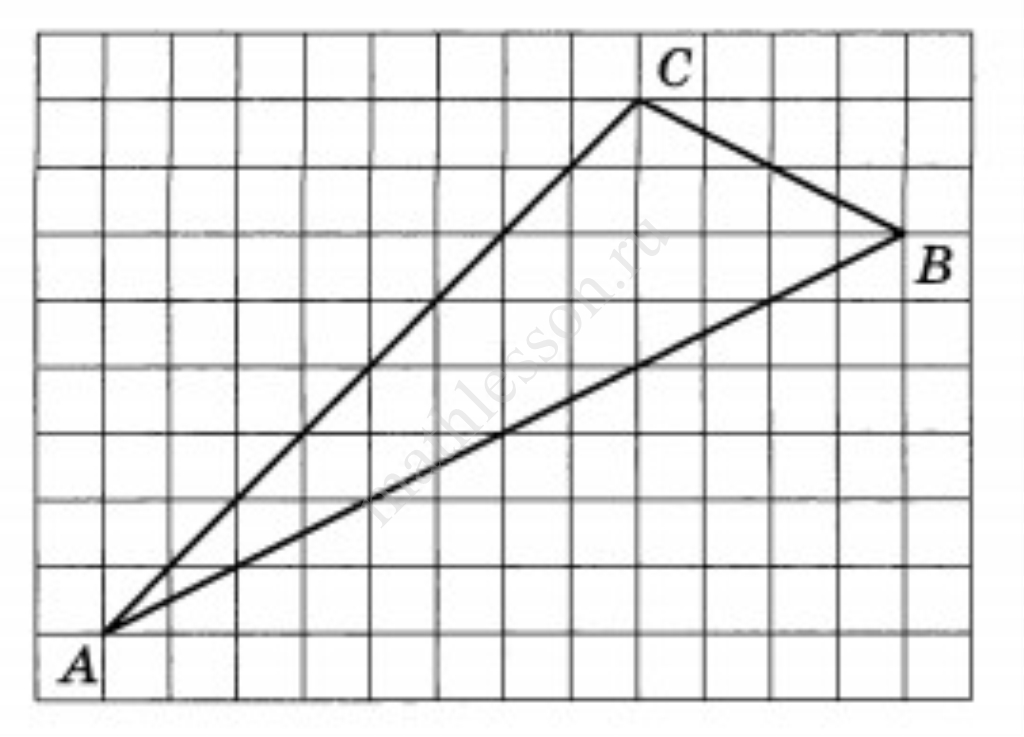
На клетчатой бумаге с размером клетки 1×1 изображён треугольник АВС. Найдите длину его биссектрисы, проведённой из вершины В.

Ответ: 6

Скрыть

Угол С — прямой, его биссектриса пойдет по сторонам клетки и составит по длине 4 клетки.

Задание 4

За круглый стол на 11 стульев в случайном порядке рассаживаются 9 мальчиков и 2 девочки. Найдите вероятность того, что девочки окажутся на соседних местах.

Ответ: 0,2

Скрыть

Допустим, первая девочка уже села на какое-то место. Вероятность этого события 1. Осталось 11-1=10 мест. Чтобы вторая девочка оказалась рядом с первой, она может сесть либо слева, либо справа от нее. Получаем число благоприятных исходов m=2. Учитывая, что всех возможных исходов n=10, получаем значение искомой вероятности:

$$P=frac{m}{n}=frac{2}{10}=0,2$$

Задание 5

Найдите корень уравнения $${left(x — 4right)}^3 = 729$$

Ответ: 13

Скрыть

$$(x-4)^{3}=729Leftrightarrow$$$$x-4=sqrt[3]{729}Leftrightarrow$$$$x=9+4=13$$

Задание 6

Четырёхугольник ABCD вписан в окружность. Угол ABD равен 72$${}^circ$$, угол CAD равен 58$${}^circ$$. Найдите угол АВС. Ответ дайте в градусах.

Ответ: 130

Скрыть

Угол ∠АВD = 72° – вписанный в окружность угол. Вписанный в окружность угол измеряется половиной дуги, на которую он опирается, следовательно, дуга АD = 144°.

Угол ∠CAD = 58° – вписанный в окружность угол, следовательно, дуга CD = 116°.

Дуга AC = AD + DC AC = AD + DC = 144° + 116° = 260°

Угол ∠ABC – вписанный в окружность угол, который опирается на дугу АС, следовательно, ∠AВС = 130°.

Задание 7

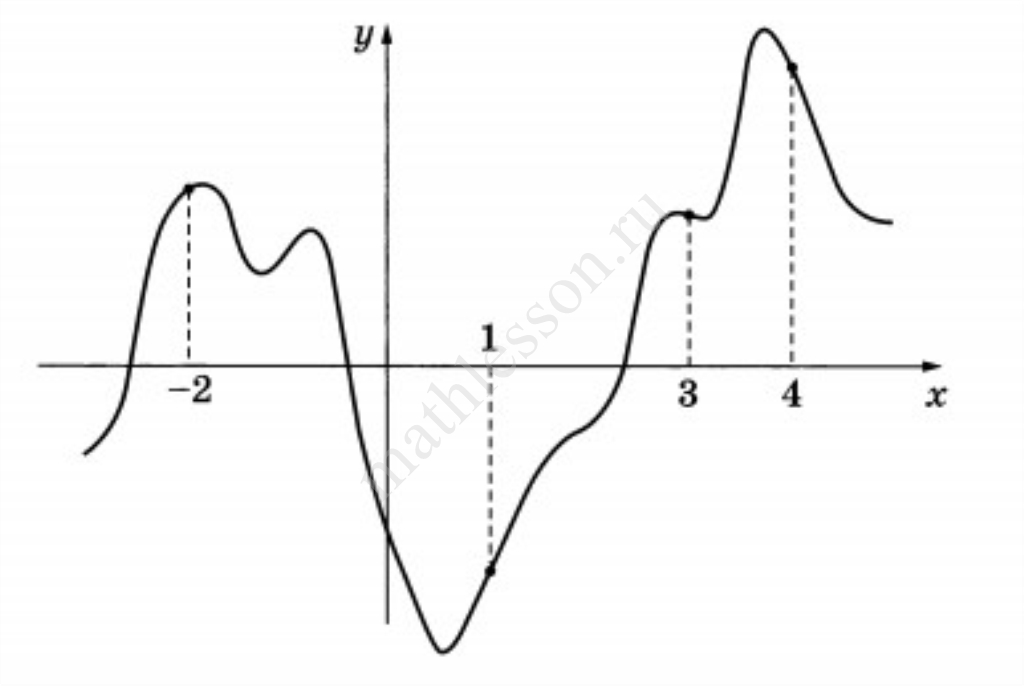
На рисунке изображён график функции $$y = f(x).$$ На оси абсцисс отмечены точки -2, 1, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Ответ: 1

Скрыть

1. Значение производной положительно в некоторой точке x, если в окрестности этой точки функция возрастает. Наоборот, если в окрестности точки x функция убывает, то производная в ней отрицательна. Причем значение производной тем больше, чем сильнее изменение функции в окрестности точки x.

2. Выберем точку на графике, в которой функция возрастает наибольшим образом. Это точка 1.

Задание 8

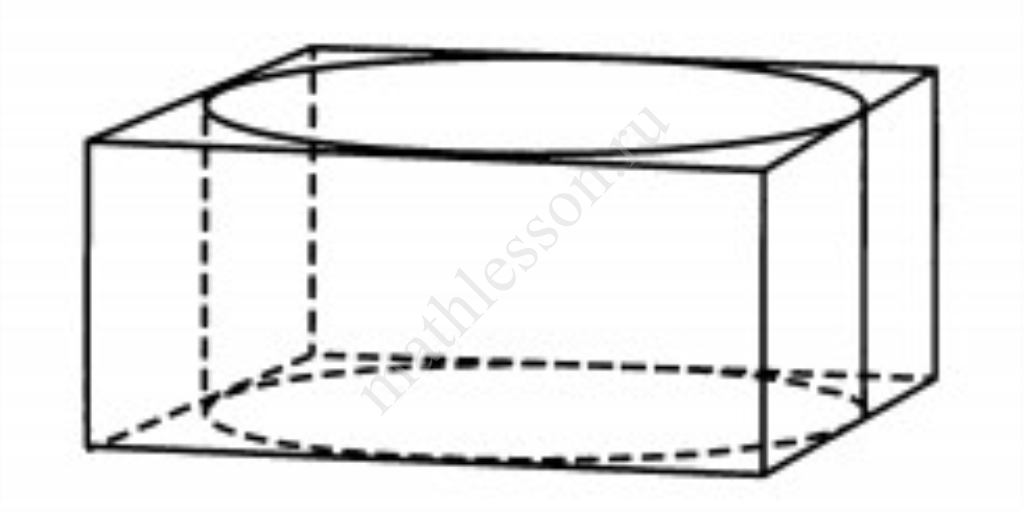
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 7. Найдите объём параллелепипеда.

Ответ: 1372

Скрыть

Объем прямоугольного параллелепипеда равен: V = a·b·c Так как прямоугольный параллелепипед описан около цилиндра, то

a = b = 2R = 2·7 = 14

c = h = 7

V = 14·14·7 = 1372

Задание 9

Найдите значение выражения $$2sqrt{3}{{cos }^{{rm 2}} frac{17pi }{12} }-2sqrt{3}{{sin }^{{rm 2}} frac{17pi }{12} }$$

Ответ: -3

Скрыть

$$2sqrt{3}{{cos }^{{rm 2}} frac{17pi }{12} }-2sqrt{3}{{sin }^{{rm 2}} frac{17pi }{12} }=$$$$2sqrt{3}(cos^{2}frac{17pi}{12}-sin^{2}frac{17pi}{12})=$$$$2sqrt{3}cos frac{17pi}{6}=$$$$2sqrt{3}cos frac{5pi}{6}=$$$$2sqrt{3}cdot (-frac{sqrt{3}}{2})=-3$$

Задание 10

В ходе распада радиоактивного изотопа его масса уменьшается по закону $$m=m_0cdot 2^{-frac{t}{T}}$$, где $$m_0$$ — начальная масса изотопа, t — время, прошедшее от начального момента, Т — период полураспада. В начальный момент времени масса изотопа 52 мг. Период его полураспада составляет 9 мин. Найдите, через сколько минут масса изотопа будет равна 13 мг.

Ответ: 18

Скрыть

Задача сводится к решению неравенства m(t) больше или равно 13 при заданных значениях параметров $$m_{0}=52$$ мг и T=9 мин:

$$52cdot 2^{-frac{t}{9}}geq 13Leftrightarrow$$$$2^{frac{t}{9}}geq frac{1}{4}Leftrightarrow$$$$-frac{t}{9}geq -2Leftrightarrow$$$$tleq 18$$

Таким образом, масса радиоактивного изотопа будет не меньше 13 мг в течение 18 минут.

Задание 11

Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 12 км/ч. Ответ дайте в км/ч.

Ответ: 1

Скрыть

Обозначим через x км/ч скорость течения. Тогда при движении ложки против течения, ее скорость была равна 12-x км/ч и на преодоления 143 км было потрачено $$frac{143}{12-x}$$ часов. При обратном движении лодка шла по течению, то есть ее скорость была равна 12+x км/ч и на преодоления 112 км было затрачено $$frac{143}{12+x}$$ часов. Известно, что на обратный путь было потрачено на 2 часов меньше. Имеем уравнение:

$$frac{143}{12-x}+frac{143}{12+x}=2$$

$$143(12+x)+143(12-x)=2(144-x^{2})$$

$$2x^{2}+286x-288=0$$

$$x^{2}+143x-144=0$$

Решаем квадратное уравнение получаем два корня:

$$x_{1}=1; x_{2}<0$$

Получаем один положительный корень x=3 км/ч.

Задание 12

Найдите точку минимума функции $$y = left(2x^2 — 26x + 26right)e^{x-17}.$$

Ответ: 11

Скрыть

1. Вычислим производную функции, получим: $$y’=(4x-26)e^{x-17}+(2x^{2}-26x+26)e^{x-17}=$$$$e^{x-17}(2x^{2}-22x)$$

2. Приравняем производную нулю и найдем точки экстремума функции: $$e^{x-17}(2x^{2}-22x)=0Leftrightarrow$$$$$$

так как $$e^{x-17}>0, xin R$$, то $$x_{1}=0, x_{2}=11$$

3. Точкой минимума будет являться та точка экстремума, в окрестности которой производная меняет свой знак с «-» на «+». Получаем точку $$x = 11$$.

Задание 13

а) Решите уравнение $$2sin^2x + cosx-1 = 0.$$

б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-5pi ; -4pi ]$$

Ответ: а) $$frac{2pi k}{3}, k in Z$$; б) $$-frac{14pi }{3}; -4pi $$

Задание 14

В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а $$AB = BC =AC = 10.$$

а) Докажите, что эта пирамида правильная.

б) На рёбрах DA и DC отмечены точки М и N соответственно, причём $$DM : MA = DN : NC = 3:2. $$Найдите площадь сечения MNB.

Ответ: $$3sqrt{59}$$

Задание 15

Решите неравенство $$frac{3}{{left(2^{2-x^2}-1right)}^2}-frac{4}{2^{2-x^2}-1}+1ge 0$$

Ответ: $$(-infty ; -sqrt{2}); (-sqrt{2}; -1]; 0; [1; sqrt{2}); (sqrt{2}; +infty )$$

Задание 16

Окружность с центром О, вписанная в треугольник АВС, касается его сторон АВ, АС и ВС в точках $$C_1,B_1,A_1$$ соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника $${AB}_1C_1$$

а) Докажите, что $$C_1Q$$ — биссектриса угла $$AC_1B_1$$

б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник $$AB_1C_1$$, если известно, что $$BC = 7, AB = 15, AC = 20.$$

Ответ: 2

Задание 17

В июле 2022 года планируется взять кредит в банке на сумму 427 000 рублей. Условия его возврата таковы:

— каждый январь долг увеличивается на 25 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года)?

Ответ: 656250

Задание 18

Найдите все значения а, при каждом из которых уравнение $$(9x-4){ln (x+a) } = (9x-4){ln (2x+a) }$$ имеет ровно один корень на отрезке [0; 1].

Ответ: $$-frac{4}{9}<aleq 0; a=frac{2}{9}; frac{1}{2}<a<frac{8}{9}$$

Задание 19

Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа — n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1131 фотографий больше, чем Маша, и что фотографировали они больше одного дня.

а) Могли ли они фотографировать в течение 13 дней?

б) Могли ли они фотографировать в течение 12 дней?

в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 35 фотографий?

Ответ: а) да; б) нет; в) 1711

Источник

Ященко И.В. (2021, 256с.) по Математике 11 класс.Пособие прошло научно-методическую оценку ФГБНУ «ФИПИ». Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.

Читать онлайн и скачать сборник в формате PDF: Скачать

* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы

Источник

Математика ЕГЭ
Математика ОГЭ
Биология ОГЭ
Биология ЕГЭ
Физика ОГЭ
Физика ЕГЭ
Химия ЕГЭ
Химия ОГЭ
Русский язык ОГЭ
Русский язык ЕГЭ
Английский язык ОГЭ
Английский язык ЕГЭ
Литература ЕГЭ
Литература ОГЭ
История ЕГЭ
История ОГЭ
Информатика ЕГЭ
Информатика ОГЭ
География ЕГЭ
География ОГЭ

Вы здесь: ✔️ Главная сайта ГДЗ Математика ЕГЭ Ященко ЕГЭ-2021 профильный уровень 36 вариантов математика

👀 Просмотров: 2242

Инфо

Автор: И.В. Ященко

Предмет (категория): 36 экзаменационных вариантов

Класс:

Читать онлайн: Да

Скачать бесплатно: Да

Формат книги: jpg

Размер книги/ГДЗ: 47.1 Мб

Год публикации (выпуска): 2021

Читать онлайн или скачать 36 тренировочных вариантов для подготовки к Единому государственному экзамену по математике под редакцией Ященко 2021 года:

Самые популярные статьи:

ЕГЭ 2015. Ященко Математика. 36 вариантов.
Лысенко, Калабухова ЕГЭ-2019 профильный уровень 40 тренировочных вариантов математика
Ященко ЕГЭ-2019 36 типовых экзаменационных вариантов профильный уровень математика
Подготовка к ЕГЭ-2016. Математика. 40 тренировочных вариантов по демоверсии на 2016 год. Профильный уровень. Лысенко Ф.Ф., Кулабухов С.Ю.
Ященко ЕГЭ-2019 50 вариантов заданий профильный уровень математика

Новые материалы для вашего класса:

Семенов ЕГЭ-2022 готовимся к итоговой аттестации базовый уровень математика
Математика ЕГЭ-2021 диагностические работы профильный уровень
Семенов, Высоцкий ЕГЭ-2021 базовый уровень готовимся к итоговой аттестации математика
Ященко ЕГЭ-2021 профильный уровень 10 вариантов типовые варианты математика

< НазадВперёд >

Вам это пригодится

Барашкова английский язык на каникулах н…

Узорова английский язык в схемах и табл…

Державина английский язык для начальной …

Барашкова английский язык на каникулах н…

Карачаева 100 тестов по лексике и грамма…

Мордкович учебник алгебра углубленный ур…

Источник

31.10.2020

Сборник ответов для пособия ЕГЭ 2021, 36 типовых вариантов по математике профильного уровня, под редакцией Ященко И.В.

Тренировочные варианты ЕГЭ 2021 по математике
Реальные варианты ЕГЭ 2020 по математике
Работы СтатГрад 2020-2021

Выбирайте вариант и смотрите ответы по PDF файлу. Вы можете скачать их совершенно бесплатно.

Видеоразбор варианта №7 из сборника Ященко

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Видеоразбор варианта №5, Ященко

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Источник

Главная » ЕГЭ » ЕГЭ 2021. Математика. Профильный уровень. 36 типовых экзаменационных вариантов — Под ред. Ященко И.В.

Пособие прошло научно-методическую оценку ФГБНУ «ФИПИ». Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена. В сборнике представлены: • 36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2021 года; • инструкция по выполнению экзаменационной работы; • ответы ко всем заданиям; • решения и критерии оценивания заданий 13-19. Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки. Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.

Рубрика: ЕГЭ / ЕГЭ по математике
Автор: Под ред. Ященко И.В.
Год: 2021
Для учеников: 11 класс
Язык учебника: Русский
Формат: PDF
Страниц: 256