Задание 14
Решите неравенство $$(5cdot0,2^{x+0,5}-0,2cdot5^{x+0,5})(0,5log^2_{0,2}(x+0,5)-2log_5 (х + 0,5))>0.$$
Ответ: $$(-0,5; 0,5); (0,5; 624,5)$$
Скрыть
$$(5cdot5^{-x-0,5}-5^{x-0,5})(0,5log^2_{0,2}(x+0,5)+2log_{0,2} (х + 0,5))>0$$
$$(5^{0,5-x}-5^{x-0,5})(log_{0,2}(x+0,5)(0,5log_{0,2} (х + 0,5)+2))>0$$
Метод рационализации.
На всей ОДЗ выражение $$a^{f_1(x)}-a^{f_2(x)}$$ совпадает по знаку с $$(a-1)(f_1(x)-f_2(x)),$$ выражение $$log_a b$$ совпадает по знаку с $$(a-1)(b-1),$$ выражение $$log_{y(x)}f_1(x)-log_{y(x)}f_2(x)$$ совпадает по знаку с $$(varphi(x)-1)(f_1(x)-f_2(x)).$$
В данном случае:
1) $$5^{0,5-x}-5^{x-0,5}$$ заменим $$(0,5-x-x+0,5)$$
2) $$log_{0,2}(x+0,5)$$ заменим $$(0,2-1)(x-0,5)$$
3) $$0,5log_{0,2}(x+0,5)+2$$ совпадает по знаку с $$(log_{0,2}(x+0,5)+4)=log_{0,2}(x+0,5)-log_{0,2}0,2^{-4},$$ последнее совпадает по знаку с выражением $$(0,2-1)(x+0,5-0,2^{-4})Rightarrow (-0,8)(x-624,5)$$
Данное неравенство примет вид:
$$(1-2x)(-0,8)(x-0,5)(-0,8)(x-624,5)>0$$
Осталось решить его при ОДЗ $$x>-0,5$$
$$left{begin{matrix} x>-0,5\ (1-2x)(x-0,5)(x-624,5)>0 end{matrix}right.$$
$$xin (-0,5; 0,5); (0,5; 624,5)$$
| 3226 | Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,4 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,9? Решение |
Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,9 ! 36 вариантов ФИПИ Ященко 2022 Вариант 16 Задание 10 |  |
| 3225 | Найдите наибольшее значение функции y=(x-6)e^(7-x) на отрезке [2; 15]Решение  График |
Найдите наибольшее значение функции y=(x-6) e 7-x ! 36 вариантов ФИПИ Ященко 2022 Вариант 16 Задание 11 | |
| 3224 | В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9, BC=8, AA1=6. Найдите объём многогранника, вершинами которого являются точки ABCB1Решение |
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9, BC=8, AA1=6 ! 36 вариантов ФИПИ Ященко 2022 Вариант 16 Задание 5 | |
| 3223 | а) Решите уравнение sin^2(x/4+pi/4)sin^2(x/4-pi/4). =0.375sin^2(-pi/4). б) Найдите все корни этого уравнения, принадлежащие отрезку [-3pi; pi].Решение График |
а) Решите уравнение sin2 (x/4+pi/4) sin2(x/4-pi/4) = 0,375 sin2(-pi/4) ! 36 вариантов ФИПИ Ященко 2022 Вариант 16 Задание 12 | |
| 3222 | Решите неравенство (5*0.2^(x+0.5)-0.2*5^(x+0.5)). *(0.5log_{0.2}^2(x+0.5)-2log_{5}(x+0.5)) > 0.Решение График |
Решите неравенство (5 0.2 x+0,5 -0,2 5 x+0.5) (0.5log2 0,2 (x+0,5) -2log 5 (x+0.5)) > 0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 16 Задание 14 🔥 | |
| 2559 | В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 22,5^@. Точка P лежит вне прямоугольника, а угол BPC равен 135^@. а) Докажите, что углы BCP и POB равны. б) Прямая PO пересекает сторону AB в точке F. Найдите DF, если BP=7 и CP=5sqrt2Решение |
В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 22,5 градуса ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 16 Задание 16 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 6 Задание 16 | |
|
Clear |
Решение и ответы заданий Варианта №16 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
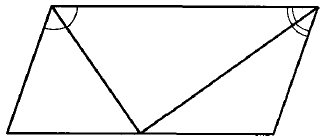
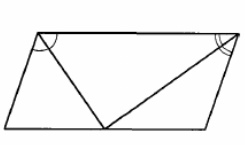
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 6. Найдите его большую сторону.
Задание 2.
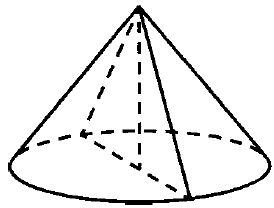
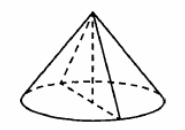
Диаметр основания конуса равен 32, а длина образующей равна 20. Найдите площадь осевого сечения этого конуса.
Задание 3.
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °C, равна 0,71. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °C или выше.
Задание 4.
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последние 2 раза промахнулся. Результат округлите до сотых.
Задание 5.
Найдите корень уравнения sqrt{72+x}=-x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{2^{log_{6}2}}{2^{log_{6}432}}.
Задание 7.
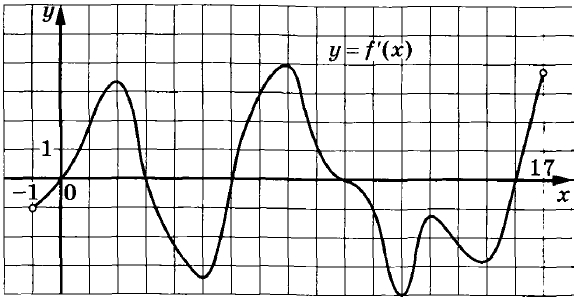
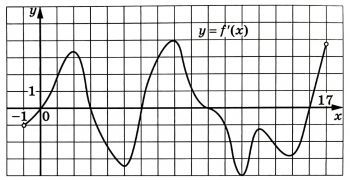
На рисунке изображён график у = f′(x) – производной функции f(x), определённой на интервале (–1; 17). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Задание 8.
Груз массой 0,58 кг колеблется на пружине. Его скорость v меняется по закону v=v_{0}cos frac{2pi t}{T}, где t – время с момента начала колебаний, Т = 2с – период колебаний, v0 = 2 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E=frac{mv^{2}}{2}, где m – масса груза в килограммах, v – скорость груза в м/с2. Найдите кинетическую энергию груза через 50 секунд после начала колебаний. Ответ дайте в джоулях.
Задание 9.
Лодка в 5:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв 2 часа в пункте В, лодка отправилась назад и вернулась в пункт А в 23:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость лодки равна 4 км/ч.
Задание 10.
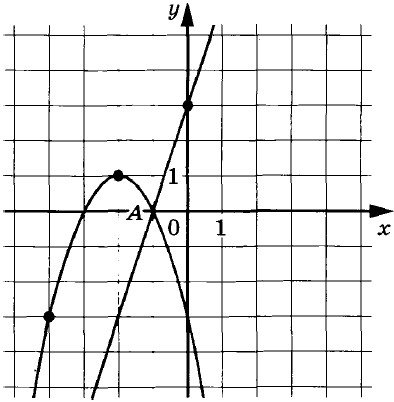
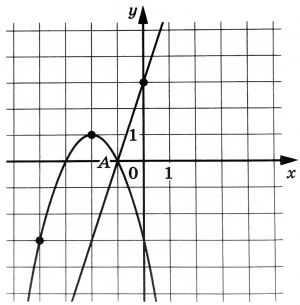
На рисунке изображены графики функций f(x) = 3x + 3 и g(x) = ax2 + bх + с, которые пересекаются в точках А(–1; 0) и В(х0; у0). Найдите у0.
Задание 11.
Найдите точку минимума функции у = х3 – 8,5x2 + 10х – 13.
Задание 12.
а) Решите уравнение cos2x + sin2x + 1 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; frac{9pi }{2}].
Задание 13.
В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно 2, а сторона основания равна √6. Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая l.
а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 2:1.
б) Найдите угол между прямыми l и СD1.
Задание 14.
Решите неравенство 5^{log_{frac{1}{5}}log_{3}(–2x)}< 3^{log_{frac{1}{3}}log_{5}(–2x)}.
Задание 15.
В июле 2023 года планируется взять кредит на 8 лет в размере 800 тыс. рублей. Условия возврата таковы:
– каждый январь с 2024 по 2027 год долг возрастает на r% по сравнению с концом предыдущего года;
– каждый январь с 2028 по 2031 год долг возрастает на 15 % по сравнению с концом предыдущего года;
– с февраля по июнь необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
– к июлю 2031 года кредит должен быть полностью погашен.
Найдите r, если общая сумма выплат по кредиту должна составить 1444 тыс. рублей.
Задание 16.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.
а) Докажите, что треугольник АОВ прямоугольный.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac{16}{81} площади трапеции ABCD.
Задание 17.
Найдите все такие значения а, при каждом из которых неравенство
–1 ≤ cosx(cos2x – a –1) ≤ 1
верно при всех действительных значениях х.
Задание 18.
Отношение трёхзначного натурального числа к сумме его цифр – целое число.
а) Может ли это отношение быть равным 11?
б) Может ли это отношение быть равным 5?
в) Какое наибольшее значение может принимать это отношение, если число не делится на 100 и его первая цифра равна 7?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Решение 16 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 6. Найдите его бòльшую сторону.
Диаметр основания конуса равен 32, а длина образующей равна 20. Найдите площадь осевого сечения этого конуса.
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °C, равна 0,71. Найдите вероятность того, что в случайный момент времени у здорового человека температуры окажется 36,8 °C или выше.
Биатлонист 5 раз стреляет по мишеням. Вероятность попадения в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последние 2 раза промахнулся. Результат округлите до сотых.
Решите уравнение ( sqrt{72+x}=-x ). Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Найдите значение выражения (dfrac{2^{log{_6}{2}}}{2^{log{_6}{432}}}).
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-1;17). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Груз массой 0,58 кг колеблется на пружине. Его скорость (v) меняется по закону (v = v_0 cosdfrac{2pi t}{T}), где (t) – время с момента начала колебаний, (T= 2) с – период колебаний, (v_0= 2) м/с. Кинетическая энергия (E) (в джоулях) груза вычисляется по формуле (E = dfrac{mv^2}{2}), где (m) – масса груза в килограммах, (v) – скорость груза в м/с. Найдите кинетическую энергию груза через 50 секунд после начала колебаний. Ответ дайте в джоулях.
Лодка в 5:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв 2 часа в пункте В, лодка отправилась назад и вернулась в пункт А в 23:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость лодки равна 4 км/ч.
На рисунке изображены графики функций (f(x)=3x+3) и (g(x)=ax^2+bx+c), которые пересекаются в точках (A(-1;0)) и (B(x_0;y_0)). Найдите (y_0).
Найдите точку минимума функции (y=x^3-8{,}5x^2+10x-13).
а) Решите уравнение (cos{2x}+sin{2x}+1=0).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[ 3pi; dfrac{9pi}{2}right]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π | 18. 19π/6 | 19. 13π/4 | 20. 10π/3 |
| 21. 7π/2 | 22. 11π/3 | 23. 15π/4 | 24. 23π/6 |
| 25. 4π | 26. 25π/6 | 27. 17π/4 | 28. 13π/3 |
| 29. 9π/2 |
В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно 2, а сторона основания равна (sqrt{6}). Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая (l).
а) Докажите, что прямая (l) пересекает отрезок АС и делит его в отношении 2:1.
б) Найдите угол между прямыми (l) и СD1.
Решите неравенство (5^{log_{frac{1}{5}}{log_{3}{left(-2xright)}}}< 3^{log_{frac{1}{3}}{log_{5}{left(-2xright)}}})
В июле 2023 года планируется взять кредит на 8 лет в размере 800 тыс. рублей. Условия его возврата таковы:
— каждый январь с 2024 по 2027 год долг возрастает на r% по сравнению с концом предыдущего года;
— каждый январь с 2028 по 2031 год долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
— к июлю 2031 года кредит должен быть полностью погашен.
Найдите r, если общая сумма выплат по кредиту должна составить 1444 тыс. рублей.
Около окружности с центром O описана трапеция ABCD с основаниями AD и BC.
а) Докажите, что треугольник AOB прямоугольный.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что AB=CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет 16/81 площади трапеции ABCD.
Найдите все значения (a), при каждом из которых неравенство ( -1leqslant cos{xleft(cos{2x-a-1}right)}leqslant1) верно при всех действительных значениях (x).
Отношение трёхзначного натурального числа к сумме его цифр — целое число.
а) Может ли это отношение быть равным 11?
б) Может ли это отношение быть равным 5?
в) Какое наибольшее значение может принимать это отношение, если число не делится на 100 и его первая цифра равна 7?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
- Математика ЕГЭ
- Математика ОГЭ
- Биология ОГЭ
- Биология ЕГЭ
- Физика ОГЭ
- Физика ЕГЭ
- Химия ЕГЭ
- Химия ОГЭ
- Русский язык ОГЭ
- Русский язык ЕГЭ
- Английский язык ОГЭ
- Английский язык ЕГЭ
- Литература ЕГЭ
- Литература ОГЭ
- История ЕГЭ
- История ОГЭ
- Информатика ЕГЭ
- Информатика ОГЭ
- География ЕГЭ
- География ОГЭ
Вы здесь: ✔️ Главная сайта ГДЗ 
Математика ЕГЭ Ященко ЕГЭ-2022 36 вариантов профильный уровень математика
👀 Просмотров: 5787
Инфо
Автор: И.В. Ященко
Предмет (категория): Профильный уровень. 36 вариантов заданий
Класс:
Читать онлайн: Да
Скачать бесплатно: Да
Формат книги: jpg / pdf
Размер книги/ГДЗ: 25,8 Мб
Год публикации (выпуска): 2022
Читать онлайн или скачать 36 вариантов для подготовки к Единому государственному экзамену по математике под редакцией Ященко 2022 года:
Самые популярные статьи:
- ЕГЭ 2015. Ященко Математика. 36 вариантов.
- Лысенко, Калабухова ЕГЭ-2019 профильный уровень 40 тренировочных вариантов математика
- Ященко ЕГЭ-2019 36 типовых экзаменационных вариантов профильный уровень математика
- Подготовка к ЕГЭ-2016. Математика. 40 тренировочных вариантов по демоверсии на 2016 год. Профильный уровень. Лысенко Ф.Ф., Кулабухов С.Ю.
- Ященко ЕГЭ-2019 50 вариантов заданий профильный уровень математика
Вперёд >
Вам это пригодится
Барашкова английский язык на каникулах н…
Узорова английский язык в схемах и табл…
Державина английский язык для начальной …
Барашкова английский язык на каникулах н…
Карачаева 100 тестов по лексике и грамма…
Мордкович учебник алгебра углубленный ур…
Перейти к содержимому
И.В. Ященко, И.Р. Высоцкий, Е. А. Коновалов ЕГЭ-2022. Сборник тренировочных вариантов. Книга предназначена для подготовки учащихся к ЕГЭ по математике. В сборнике представлены: 36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ 2022 года; ответы ко всем заданиям и критерии оценивания.
Читать онлайн и скачать сборник в формате PDF: Скачать
* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы
Поделиться:
Варианты Ященко (ЕГЭ профиль): разбор в видеоформате
На данной странице представлены ссылки на видеоразборы всех 36 вариантов из сборника Ященко 2019 года.
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
31
32
33
34
35
36