- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.
А. Ларин. Тренировочный вариант № 314. (Часть C)
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Основание ABCD призмы — трапеция с основаниями AB = 2CD.
а) Докажите проходит через середину бокового ребра
б) Найдите угол между боковым ребром и этой плоскостью, если призма прямая, трапеция ABCD прямоугольная с прямым углом при вершине B, а BC = CD и
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Точка I — центр окружности, вписанной в треугольник ABC. Луч BI пересекает описанную около треугольника ABC окружность в точке N . Известно, что угол ABC равен 60°.
а) Докажите, что N — центр окружности, описанной около треугольника AIC.
б) Найдите радиус окружности, описанной около треугольника ABC, если известно, что IN = 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Клиент положил в банк некоторую сумму денег. Через год, после начисления процентов, он добавил на свой счет сумму, составляющую 0,9 исходной, в результате чего остаток на счете стал равен 3,4 млн рублей. А еще через год, после начисления процентов, остаток на его счете увеличился в 2,2 раза по сравнению с исходной суммой. Какую сумму клиент положил в банк первоначально, если в конце каждого года банк
начислял один и тот же процент годовых?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра такие, что неравенство
не имеет решений.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
На доске выписаны все натуральные числа от 1 до 2014 без пропусков и повторений: 1, 2, 3, …, 2013, 2014. С выписанными на доске числами проделывают следующие операции: выбирают какие‐либо два числа и записывают на доске модуль их разности, увеличенный на 1, а сами выбранные числа стирают. Так продолжают до тех пор, пока на доске не останется только одно число.
а) Какое наименьшее число может остаться на доске?
б) Какое наибольшее число может остаться на доске?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Задание 1
Поезд Иркутск‐Казань отправляется в 01:07 15 декабря (время иркутское), а прибывает в 15:52 17 декабря (время казанское). Сколько часов поезд находится в пути, учитывая, что смещение времени в Иркутске относительно Казани составляет +5 часов?
Ответ: 67,75
Задание 2
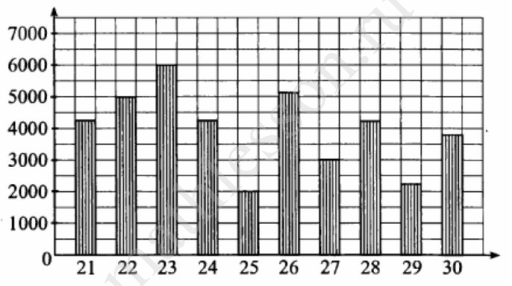
На диаграмме показано количество посетителей сайта любителей кошек во все дни с 21 по 30 мая 2009 года. По горизонтали указываются дни месяца, по вертикали – количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей превышает наименьшее количество посетителей за день (в указанный период)
Ответ: 3
Задание 3
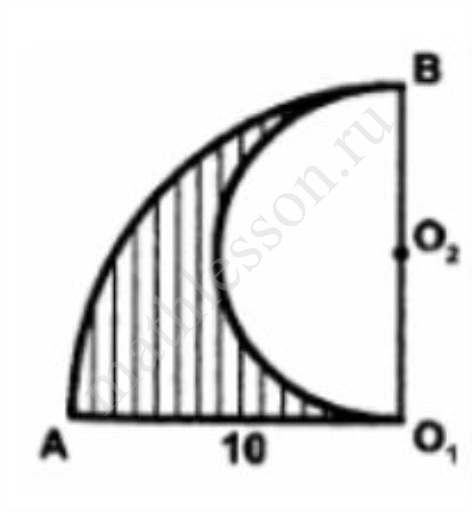
Найдите площадь S заштрихованной фигуры, изображенной на рисунке, если АО1=10. В ответе укажите $$frac{S}{pi}$$.
Ответ: 12,5
Задание 4
Магазин покупает сливочное масло у двух молокозаводов. 40% масла первого и 20% масла второго молокозавода имеет жирность 80%. Всего жирность 80% имеет 35% закупленного масла. Найдите вероятность того, что масло, купленное в магазине, произведено первым молокозаводом.
Ответ: 0,75
Задание 5
Решите уравнение $$ln(frac{pi^{x}}{e^{x}}+2x-10)=x(ln pi-1)$$. Если корней больше одного, то в ответе запишите их сумму.
Ответ: 5
Задание 6
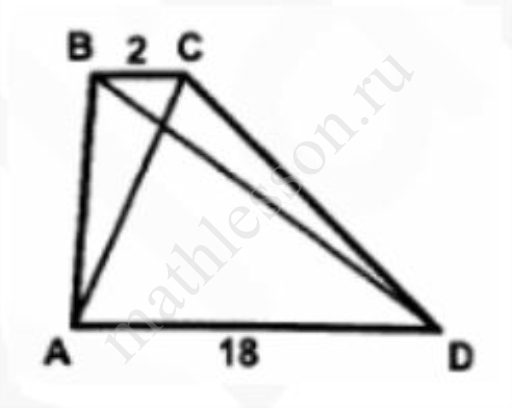
Найдите площадь трапеции, изображенной на рисунке, если АС=7, BD=15
Ответ: 42
Задание 7
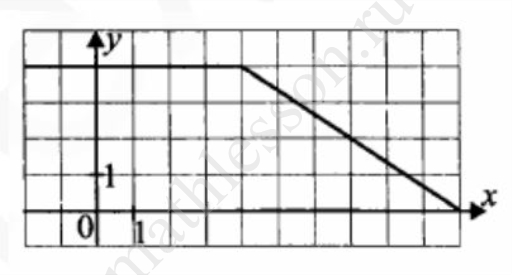
На рисунке изображен график функции $$y=f(x)$$. Пользуясь графиком, вычислите $$F(10)-F(2)$$, где $$F(x)$$ ‐ одна из первообразных функции $$y=f(x)$$.
Ответ: 20
Задание 8
В правильной треугольной пирамиде SABC сторона основания $$AB=8sqrt{3}$$ , а боковое ребро $$SA=sqrt{73}$$. Найдите расстояние от точки В до плоскости SAC.
Ответ: 7,2
Задание 9
Найдите значение выражения $$frac{log^{2}_{2}6+log_{2}6cdotlog_{2}3-2log^{2}_{2}3}{log_{2}6+2log_{2}3}$$
Ответ: 1
Задание 10
Опорные «башмаки» шагающего экскаватора, имеющего массу m=2520 т, представляют собой две пустотелые балки длиной $$l=36$$ м и S шириной метров каждая. Давление P, в кПа, оказываемое экскаватором на почву, определяется формулой $$P=frac{mg}{2lS}$$, где m‐масса экскаватора (в тоннах), $$l$$ — длина балок (в метрах), g = 10 м/с2‐ ускорение свободного падения. Определите наименьшую возможную ширину опорных балок, если известно, что давление P должно не превышать 280 кПа. Ответ выразите в метрах.
Ответ: 1,25
Задание 11
Отрезок арифметической прогрессии содержит 16 членов с номерами от 1 до 16. Сумма членов с четными номерами равна 42, а сумма членов с нечетными номерами равна 18. Найдите разность прогрессии.
Ответ: 3
Задание 12
Найдите наибольшее значение функции $$y=(1+x)log_{5}x$$ на отрезке [1;5]
Ответ: 6
Задание 13
а) Решите уравнение $$sqrt{ctg x}(sin^{2}x-frac{1}{4})=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{3pi}{2};0]$$
Ответ: А)$$frac{pi}{6}+pi n, frac{pi}{2}+pi n, nin Z$$ Б)$$-frac{3pi}{2};-frac{5pi}{6};-frac{pi}{2}$$
Задание 14
Основание ABCD призмы ABCDA1B1C1D1 – трапеция с основаниями $$AB=2cdot CD$$
а) Докажите, что плоскость BA1D1 проходит через середину бокового ребра CC1
б) Найдите угол между боковым ребром AA1 и этой плоскостью, если призма прямая, трапеция ABCD прямоугольная с прямым углом при вершине B , а BC=CD и $$AA_{1}=sqrt{6}CD$$
Ответ: $$30^{circ}$$
Задание 15
Решите неравенство $$frac{(4x-|x-6|)(log_{frac{1}{3}}(x+4)+1)}{2^{x^{2}}-2^{|x|}}geq 0$$
Ответ: $$(1;frac{6}{5}]$$
Задание 16
Точка I ‐ центр окружности, вписанной в треугольник ABC . Луч BI пересекает описанную около треугольника ABC окружность в точке N . Известно, что $$angle ABC=60^{circ}$$
а) Докажите, что N ‐ центр окружности, описанной около треугольника ABC N AIC
б) Найдите радиус окружности, описанной около треугольника , если известно, что IN=1.
Ответ: 1
Задание 17
Клиент положил в банк некоторую сумму денег. Через год, после начисления процентов, он добавил на свой счет сумму, составляющую 0,9 исходной, в результате чего остаток на счете стал равен 3,4 млн. рублей. А еще через год, после начисления процентов, остаток на его счете увеличился в 2,2 раза по сравнению с исходной суммой. Какую сумму клиент положил в банк первоначально, если в конце каждого года банк начислял один и тот же процент годовых?
Ответ: 1,7 млн. руб.
Задание 18
Найдите все значения параметра
$$aneq 0$$, такие что неравенство $$log^{2}_{2}(x^{2}+2ax+a^{2}-a+1)-log_{2}frac{a^{2}}{6}cdot log_{2}(x^{2}+2ax+a^{2}-a+1)leq 0$$
не имеет решений.
Ответ: $$(-3-sqrt{15};0)$$
Задание 19
На доске выписаны все натуральные числа от 1 до 2014 без пропусков и повторений: 1, 2, 3, …, 2013, 2014. С выписанными на доске числами проделывают следующие операции: выбирают какие‐либо два числа и записывают на доске модуль их разности, увеличенный на 1, а сами выбранные числа стирают. Так продолжают до тех пор, пока на доске не останется только одно число.
а) Какое наименьшее число может остаться на доске?
б) Какое наибольшее число может остаться на доске?
Ответ: А)2 Б)2014
Пробные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Пробные варианты ЕГЭ 2023 по математике (профиль)
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| time4math.ru | |
| вариант 1-2 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2022-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2022-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2022-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2022-yagubov-prof-var36 |
| math100.ru (с ответами) | |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| alexlarin.net | |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий.
Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности.
Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Связанные страницы:
Пробные варианты ЕГЭ 2022 по математике (профильный уровень)
Сборник задач по стереометрии для 10-11 классов
Задание 10 по профильной математике — новые задачи по теории вероятностей в ЕГЭ-2022
Тест по теме «Производная» 11 класс алгебра с ответами
Основные тригонометрические тождества и формулы
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Пробники ЕГЭ ↓
Математика,
Физика,
Информатика,
Химия,
Русский,
Обществознание,
Литература,
История,
Иностранные языки,
География,
Биология
1 ноября 2022
В закладки
Обсудить
Жалоба
Пять пробных вариантов ЕГЭ по профильной математике + видеоразбор + конспект.
Разбор пробного варианта ЕГЭ по профильной математике №1
Файл с вариантом: probnyi-variant-1.pdf
Разбор пробного варианта ЕГЭ по профильной математике №2
Файл с вариантом: probnik-2.pdf
Конспект с разбором: konspekt-variant-2.pdf
Разбор пробного варианта ЕГЭ по профильной математике №3
Файл с вариантом: probnik-3.pdf
Конспект с разбором: konspekt-variant-3.pdf
Разбор пробного варианта ЕГЭ по профильной математике №4
Файл с вариантом: probnik-4.pdf
Конспект с разбором: konspekt-razbora-4.pdf
Разбор пробного варианта ЕГЭ по профильной математике №5
Файл с вариантом: probnik_5.pdf
Конспект с разбором: 5_konspekt-s-razborom.pdf
Автор: Марсель Нуртдинов.
Источник: vk.com/marsel_tutor