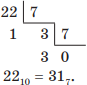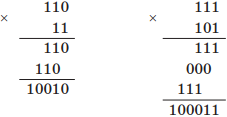Егэ алфавитный подход к измерению информации

Информация и ее кодирование

Различные подходы к определению понятия «информация». Виды информационных
процессов. Информационный аспект в деятельности человека

Информация (лат. informatio — разъяснение, изложение, набор сведений) — базовое понятие в информатике, которому нельзя дать строгого определения, а можно только пояснить:

• информация — это новые факты, новые знания;
• информация — это сведения об объектах и явлениях окружающей среды, которые повышают уровень осведомленности человека;
• информация — это сведения об объектах и явлениях окружающей среды, которые уменьшают степень неопределенности знаний об этих объектах или явлениях при принятии определенных решений.

Понятие «информация» является общенаучным, т. е. используется в различных науках: физике, биологии, кибернетике, информатике и др. При этом в каждой науке данное понятие связано с различными системами понятий. Так, в физике информация рассматривается как антиэнтропия (мера упорядоченности и сложности системы). В биологии понятие «информация» связывается с целесообразным поведением живых организмов, а также с исследованиями механизмов наследственности. В кибернетике понятие «информация» связано с процессами управления в сложных системах.

Основными социально значимыми свойствами информации являются:

• полезность;
• доступность (понятность);
• актуальность;
• полнота;
• достоверность;
• адекватность.

В человеческом обществе непрерывно протекают информационные процессы: люди воспринимают информацию из окружающего мира с помощью органов чувств, осмысливают ее и принимают определенные решения, которые, воплощаясь в реальные действия, воздействуют на окружающий мир.

Информационный процесс — это процесс сбора (приема), передачи (обмена), хранения, обработки (преобразования) информации.

Сбор информации — это процесс поиска и отбора необходимых сообщений из разных источников (работа со специальной литературой, справочниками; проведение экспериментов; наблюдения; опрос, анкетирование; поиск в информационно-справочных сетях и системах и т. д.).

Передача информации — это процесс перемещения сообщений от источника к приемнику по каналу передачи. Информация передается в форме сигналов — звуковых, световых, ультразвуковых, электрических, текстовых, графических и др. Каналами передачи могут быть воздушное пространство, электрические и оптоволоконные кабели, отдельные люди, нервные клетки человека и т. д.

Хранение информации — это процесс фиксирования сообщений на материальном носителе. Сейчас для хранения информации используются бумага, деревянные, тканевые, металлические и другие поверхности, кино- и фотопленки, магнитные ленты, магнитные и лазерные диски, флэш-карты и др.

Обработка информации — это процесс получения новых сообщений из имеющихся. Обработка информации является одним из основных способов увеличения ее количества. В результате обработки из сообщения одного вида можно получить сообщения других видов.

Защита информации — это процесс создания условий, которые не допускают случайной потери, повреждения, изменения информации или несанкционированного доступа к ней. Способами защиты информации являются создание ее резервных копий, хранение в защищенном помещении, предоставление пользователям соответствующих прав доступа к информации, шифрование сообщений и др.

Язык как способ представления и передачи информации

Для того чтобы сохранить информацию и передать ее, с давних времен использовались знаки.

В зависимости от способа восприятия знаки делятся на:

• зрительные (буквы и цифры, математические знаки, музыкальные ноты, дорожные знаки и др.);
• слуховые (устная речь, звонки, сирены, гудки и др.);
• осязательные (азбука Брайля для слепых, жесты-касания и др.);
• обонятельные;
• вкусовые.

Для долговременного хранения знаки записывают на носители информации.

Для передачи информации используются знаки в виде сигналов (световые сигналы светофора, звуковой сигнал школьного звонка и т. д.).

По способу связи между формой и значением знаки делятся на:

• иконические — их форма похожа на отображаемый объект (например, значок папки «Мой компьютер» на «Рабочем столе» компьютера);
• символы — связь между их формой и значением устанавливается по общепринятому соглашению (например, буквы, математические символы ∫, ≤, ⊆, ∞; символы химических элементов).

Для представления информации используются знаковые системы, которые называются языками. Основу любого языка составляет алфавит — набор символов, из которых формируется сообщение, и набор правил выполнения операций над символами.

Языки делятся на:

• естественные (разговорные) — русский, английский, немецкий и др.;
• формальные — встречающиеся в специальных областях человеческой деятельности (например, язык алгебры, языки программирования, электрических схем и др.)

Системы счисления также можно рассматривать как формальные языки. Так, десятичная система счисления — это язык, алфавит которого состоит из десяти цифр 0..9, двоичная система счисления — язык, алфавит которого состоит из двух цифр — 0 и 1.

Методы измерения количества информации: вероятностный и алфавитный

Единицей измерения количества информации является бит. 1 бит — это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.

Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли:

N = 2^I.

Например, пусть шарик находится в одной из четырех коробок. Таким образом, имеется четыре равновероятных события (N = 4). Тогда по формуле Хартли 4 = 2^I. Отсюда I = 2. То есть сообщение о том, в какой именно коробке находится шарик, содержит 2 бита информации.

Алфавитный подход

При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:

I = log₂ N.

Например, в русском языке 32 буквы (буква ё обычно не используется), т. е. количество событий будет равно 32. Тогда информационный объем одного символа будет равен:

I = log₂ 32 = 5 битов.

Если N не является целой степенью 2, то число log₂N не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как log₂N’, где N′ — ближайшая к N степень двойки — такая, что N′ > N.

Например, в английском языке 26 букв. Информационный объем одного символа можно найти так:

N = 26; N’ = 32; I = log₂N’ = log₂(2⁵) = 5 битов.

Если количество символов алфавита равно N, а количество символов в записи сообщения равно М, то информационный объем данного сообщения вычисляется по формуле:

I = M · log₂N.

Примеры решения задач

Пример 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

Решение. С помощью n лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2ⁿ сигналов. 2⁵ < 50 < 2⁶, поэтому пяти лампочек недостаточно, а шести хватит.

Ответ: 6.

Пример 2. Метеорологическая станция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

Решение. В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения I = log₂101. Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128 = 27. Принимаем для одного измерения I = log₂128 = 7 битов. Для 80 измерений общий информационный объем равен:

80 · 7 = 560 битов = 70 байтов.

Ответ: 70 байтов.

Вероятностный подход

Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:

$I=-∑↙{i=1}↖{N}p_ilog_2p_i$,

где $I$ — количество информации;

$N$ — количество возможных событий;

$p_i$ — вероятность $i$-го события.

Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:

$p_1={1}/{2}, p_2={1}/{4}, p_3={1}/{8}, p_4={1}/{8}$.

Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:

$I=-({1}/{2}·log_2{1}/{2}+{1}/{4}·log_2{1}/{4}+{1}/{8}·log_2{1}/{8}+{1}/{8}·log_2{1}/{8})={14}/{8}$ битов $= 1.75 $бита.

Единицы измерения количества информации

Наименьшей единицей информации является бит (англ. binary digit (bit) — двоичная единица информации).

Бит — это количество информации, необходимое для однозначного определения одного из двух равновероятных событий. Например, один бит информации получает человек, когда он узнает, опаздывает с прибытием нужный ему поезд или нет, был ночью мороз или нет, присутствует на лекции студент Иванов или нет и т. д.

В информатике принято рассматривать последовательности длиной 8 битов. Такая последовательность называется байтом.

Производные единицы измерения количества информации:

1 байт = 8 битов

1 килобайт (Кб) = 1024 байта = 2¹⁰ байтов

1 мегабайт (Мб) = 1024 килобайта = 2²⁰ байтов

1 гигабайт (Гб) = 1024 мегабайта = 2³⁰ байтов

1 терабайт (Тб) = 1024 гигабайта = 2⁴⁰ байтов

Процесс передачи информации. Виды и свойства источников и приемников информации. Сигнал, кодирование и декодирование, причины искажения информации при передаче

Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними.

В качестве источника информации может выступать живое существо или техническое устройство. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал.

Сигнал — это материально-энергетическая форма представления информации. Другими словами, сигнал — это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение. Сигналы могут быть аналоговыми (непрерывными) или дискретными (импульсными).

Сигнал посылается по каналу связи. В результате в приемнике появляется принимаемый сигнал, который декодируется и становится принимаемым сообщением.

Передача информации по каналам связи часто сопровождается воздействием помех, вызывающих искажение и потерю информации.

Примеры решения задач

Пример 1. Для кодирования букв А, З, Р, О используются двухразрядные двоичные числа 00, 01, 10, 11 соответственно. Этим способом закодировали слово РОЗА и результат записали шестнадцатеричным кодом. Указать полученное число.

Решение. Запишем последовательность кодов для каждого символа слова РОЗА: 10 11 01 00. Если рассматривать полученную последовательность как двоичное число, то в шестнадцатеричном коде оно будет равно: 1011 0100₂ = В4₁₆.

Ответ: В4₁₆.

Скорость передачи информации и пропускная способность канала связи

Прием/передача информации может происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации, или скорость информационного потока.

Скорость выражается в битах в секунду (бит/с) и кратных им Кбит/с и Мбит/с, а также в байтах в секунду (байт/с) и кратных им Кбайт/с и Мбайт/с.

Максимальная скорость передачи информации по каналу связи называется пропускной способностью канала.

Примеры решения задач

Пример 1. Скорость передачи данных через ADSL-соединение равна 256000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.

Решение. Размер файла можно вычислить, если умножить скорость передачи информации на время передачи. Выразим время в секундах: 3 мин = 3 ⋅ 60 = 180 с. Выразим скорость в килобайтах в секунду: 256000 бит/с = 256000 : 8 : 1024 Кбайт/с. При вычислении размера файла для упрощения расчетов выделим степени двойки:

Размер файла = (256000 : 8 : 1024) ⋅ (3 ⋅ 60) = (2⁸ ⋅ 10³ : 2³ : 2¹⁰) ⋅ (3 ⋅ 15 ⋅ 2²) = (2⁸ ⋅ 125 ⋅ 2³ : 2³ : 2¹⁰) ⋅ (3 ⋅ 15 ⋅ 2²) = 125 ⋅ 45 = 5625 Кбайт.

Ответ: 5625 Кбайт.

Представление числовой информации. Сложение и умножение в разных системах счисления

Представление числовой информации с помощью систем счисления

Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.

Система счисления — это система записи чисел с помощью определенного набора цифр.

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.

Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.

Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.

Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.

Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.

Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.

Например: 8527 = 8 ⋅ 10³ + 5 ⋅ 10² + 2 ⋅ 10¹ + 7 ⋅ 10⁰.

Развернутая форма записи чисел произвольной системы счисления имеет вид

$∑↙{i=n-1}↖{-m}a_iq^i$,

где $X$ — число;

$a$ — цифры численной записи, соответствующие разрядам;

$i$ — индекс;

$m$ — количество разрядов числа дробной части;

$n$ — количество разрядов числа целой части;

$q$ — основание системы счисления.

Например, запишем развернутую форму десятичного числа $327.46$:

$n=3, m=2, q=10.$

$X=∑↙{i=2}↖{-2}a_iq^i=a_2·10^2+a_1·10^1+a_0·10^0+a_{-1}·10^{-1}+a_{-2}·10^{-2}=3·10^2+2·10^1+7·10^0+4·10^{-1}+6·10^{-2}$

Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.

Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В₁₂ можно расписать так:

7А,5В₁₂ = В ⋅ 12^-2 + 5 ⋅ 2^-1 + А ⋅ 12⁰ + 7 ⋅ 12¹.

В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.

Перевод чисел в позиционных системах счисления

Перевод чисел из произвольной системы счисления в десятичную

Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂ = 1 ⋅ 2³ + 1 ⋅ 2² + 0 ⋅ 2¹ + 1 ⋅ 2⁰ = 13₁₀;

17D,ECH = 12 ⋅ 16^–2 + 14 ⋅ 16^–1 + 13 ⋅ 160 + 7 ⋅ 16¹ + 1 ⋅ 16² = 381,921875.

Перевод чисел из десятичной системы счисления в заданную

Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

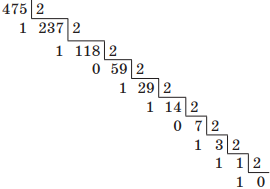
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:

Читая остатки от деления снизу вверх, получим 111011011.

Проверка:

1 ⋅ 2⁸ + 1 ⋅ 2⁷ + 1 ⋅ 2⁶ + 0 ⋅ 2⁵ + 1 ⋅ 2⁴ + 1 ⋅ 2³ + 0 ⋅ 2² + 1 ⋅ 2¹ + 1 ⋅ 2⁰ = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 475₁₀.

Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.

Например, переведем десятичную дробь 0,375₁₀ в двоичную систему счисления:

Полученный результат — 0,011₂.

Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно

Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2^І; І = 3).

Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.

Например:

1234,777₈ = 001 010 011 100,111 111 111₂ = 1 010 011 100,111 111 111₂;

1234567₈ = 001 010 011 100 101 110 111₂ = 1 010 011 100 101 110 111₂.

При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.

Например:

1100111₂ = 001 100 111₂ = 147₈;

11,1001₂ = 011,100 100₂ = 3,44₈;

110,0111₂ = 110,011 100₂ = 6,34₈.

Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2^І; І = 4).

Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.

Например:

1100111₂ = 0110 0111₂ = 67₁₆;

11,1001₂ = 0011,1001₂ = 3,9₁₆;

110,0111001₂ = 0110,0111 0010₂ = 65,72₁₆.

Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.

Например:

1234,AB77₁₆ = 0001 0010 0011 0100,1010 1011 0111 0111₂ = 1 0010 0011 0100,1010 1011 0111 0111₂;

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂.

При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.

Например, переведем троичное число 211₃ в семеричную систему счисления. Для этого сначала преобразуем число 211₃ в десятичное, записав его развернутую форму:

211₃ = 2 ⋅ 3² + 1 ⋅ 3¹ + 1 ⋅ 3⁰ = 18 + 3 + 1 = 22₁₀.

Затем переведем десятичное число 22₁₀ в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:

Итак, 211₃ = 31₇.

Примеры решения задач

Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.

Решение. Обозначим искомое основание п. По правилу записи чисел в позиционных системах счисления 12₁₀ = 110_n = 0 ·n⁰ + 1 · n¹ + 1 · n². Составим уравнение: n² + n = 12 . Найдем натуральный корень уравнения (отрицательный корень не подходит, т. к. основание системы счисления, по определению, натуральное число большее единицы): n = 3 . Проверим полученный ответ: 110₃ = 0· 3⁰ + 1 · 3¹ + 1 · 3² = 0 + 3 + 9 = 12 .

Ответ: 3.

Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.

Решение. Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. 22 — 4 = 18. Найдем делители числа 18. Это числа 2, 3, 6, 9, 18. Числа 2 и 3 не подходят, т. к. в системах счисления с основаниями 2 и 3 нет цифры 4. Значит, искомыми основаниями являются числа 6, 9 и 18. Проверим полученный результат, записав число 22 в указанных системах счисления: 22₁₀ = 34₆ = 24₉ = 14₁₈.

Ответ: 6, 9, 18.

Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.

Решение. Для удобства воспользуемся восьмеричной системой счисления. 101₂ = 5₈. Тогда число х можно представить как x = 5 · 8⁰ + a₁ · 8¹ + a₂ · 8² + a₃ · 8³ + … , где a₁, a₂, a₃, … — цифры восьмеричной системы. Искомые числа не должны превосходить 25, поэтому разложение нужно ограничить двумя первыми слагаемыми ( 8² > 25), т. е. такие числа должны иметь представление x = 5 + a₁ · 8. Поскольку x ≤ 25 , допустимыми значениями a₁ будут 0, 1, 2. Подставив эти значения в выражение для х, получим искомые числа:

a₁ = 0; x = 5 + 0 · 8 = 5;.

a₁=1; x = 5 + 1 · 8 = 13;.

a₁ = 2; x = 5 + 2 · 8 = 21;.

Выполним проверку:

5₁₀ = 101₂;

13₁₀ = 1101₂;

21₁₀ = 10101₂.

Ответ: 5, 13, 21.

Арифметические операции в позиционных системах счисления

Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.

Сложение	Вычитание	Умножение
0 + 0 = 0	0 – 0 = 0	0 ⋅ 0 = 0
0 + 1 = 1	1 – 0 = 1	0 ⋅ 1 = 0
1 + 0 = 1	1 – 1 = 0	1 ⋅ 0 = 0
1 + 1 = 10	10 – 1 = 1	1 ⋅ 1 = 1

Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.

Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:

Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:

Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:

Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.

Например, выполним сложение восьмеричных чисел 36₈ и 15₈, а также вычитание шестнадцатеричных чисел 9С₁₆ и 67₁₆:

При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.

Представление чисел в компьютере

Формат с фиксированной запятой

В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно

1 ⋅ 2⁷ + 1 ⋅ 2⁶ + 1 ⋅ 2⁵ + 1 ⋅ 2⁴ + 1 ⋅ 2³ + 1 ⋅ 2² + 1 ⋅ 2¹ + 1 ⋅ 2⁰ = 255₁₀.

Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.

Для п-разрядного представления диапазон будет составлять от 0 до 2ⁿ – 1.

Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.

Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2ⁿ − |А|.

Алгоритм получения дополнительного кода отрицательного числа:

1. Записать прямой код числа в п двоичных разрядах.

2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)

3. Прибавить единицу к полученному обратному коду.

Например, получим дополнительный код числа –2014₁₀ для шестнадцатиразрядного представления:

Прямой код	Двоичный код числа 201410 со знаковым разрядом	1000011111011110
Обратный код	Инвертирование (исключая знаковый разряд)	1111100000100001
	Прибавление единицы	1111100000100001 + 0000000000000001
Дополнительный код		1111100000100010

При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.

Например:

1) Найдем разность 13₁₀ – 12₁₀ для восьмибитного представления. Представим заданные числа в двоичной системе счисления:

13₁₀ = 1101₂ и 12₁₀ = 1100₂.

Запишем прямой, обратный и дополнительный коды для числа –12₁₀ и прямой код для числа 13₁₀ в восьми битах:

	1310	–1210
Прямой код	00001101	10001100
Обратный код	—	11110011
Дополнительный код	—	11110100

Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):

Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.

2) Найдем разность 8₁₀ – 13₁₀ для восьмибитного представления.

Запишем прямой, обратный и дополнительный коды для числа –13₁₀ и прямой код для числа 8₁₀ в восьми битах:

	810	–1310
Прямой код	00001000	10001101
Обратный код	—	11110010
Дополнительный код	—	11110011

Вычитание заменим сложением:

В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:

11111011 – 00000001 = 11111010.

Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –5₁₀.

Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2^n–1, а максимальное: |А| = 2^n–1 или А = –2^n–1 – 1.

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно

А = –2³¹ = –2147483648₁₀.

Максимальное положительное число равно

А = 2³¹ – 1 = 2147483647₁₀.

Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.

Формат с плавающей запятой

Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.

Число в экспоненциальном формате представляется в таком виде:

$A=m·q^n$,

где $m$ — мантисса числа (правильная отличная от нуля дробь);

$q$ — основание системы счисления;

$n$ — порядок числа.

Например, десятичное число 2674,381 в экспоненциальной форме запишется так:

2674,381 = 0,2674381 ⋅ 10⁴.

Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.

Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.

Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 1111111₂ = 127₁₀. Так как числа представляются в двоичной системе счисления, то

$q^n = 2^{127}≈ 1.7 · 10^{38}$.

Аналогично, максимальное значение мантиссы равно

$m = 2^{23} — 1 ≈ 2^{23} = 2^{(10 · 2.3)} ≈ 1000^{2.3} = 10^{(3 · 2.3)} ≈ 10^7$.

Таким образом, диапазон чисел обычной точности составляет $±1.7 · 10^{38}$.

Кодирование текстовой информации. Кодировка ASCII. Основные используемые кодировки кириллицы

Соответствие между набором символов и набором числовых значений называется кодировкой символа. При вводе в компьютер текстовой информации происходит ее двоичное кодирование. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа на экран производится обратная операция — декодирование, т. е. преобразование кода символа в его изображение.

Присвоенный каждому символу конкретный числовой код фиксируется в кодовых таблицах. Одному и тому же символу в разных кодовых таблицах могут соответствовать разные числовые коды. Необходимые перекодировки текста обычно выполняют специальные программы-конверторы, встроенные в большинство приложений.

Как правило, для хранения кода символа используется один байт (восемь битов), поэтому коды символов могут принимать значение от 0 до 255. Такие кодировки называют однобайтными. Они позволяют использовать 256 символов ( N = 2^I = 2⁸ = 256 ). Таблица однобайтных кодов символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией). Первая часть таблицы ASCII-кодов (от 0 до 127) одинакова для всех IBM-PC совместимых компьютеров и содержит:

• коды управляющих символов;
• коды цифр, арифметических операций, знаков препинания;
• некоторые специальные символы;
• коды больших и маленьких латинских букв.

Вторая часть таблицы (коды от 128 до 255) бывает различной в различных компьютерах. Она содержит коды букв национального алфавита, коды некоторых математических символов, коды символов псевдографики. Для русских букв в настоящее время используется пять различных кодовых таблиц: КОИ-8, СР1251, СР866, Мас, ISO.

В последнее время широкое распространение получил новый международный стандарт Unicode. В нем отводится по два байта (16 битов) для кодирования каждого символа, поэтому с его помощью можно закодировать 65536 различных символов ( N = 2¹⁶ = 65536 ). Коды символов могут принимать значение от 0 до 65535.

Примеры решения задач

Пример. С помощью кодировки Unicode закодирована следующая фраза:

Я хочу поступить в университет!

Оценить информационный объем этой фразы.

Решение. В данной фразе содержится 31 символ (включая пробелы и знак препинания). Поскольку в кодировке Unicode каждому символу отводится 2 байта памяти, для всей фразы понадобится 31 ⋅ 2 = 62 байта или 31 ⋅ 2 ⋅ 8 = 496 битов.

Ответ: 32 байта или 496 битов.

Измерение информации, алфавитный подход

Методика преподавания темы в 10-11 классах и подготовки к ЕГЭ

В данной методике рассматривается алфавитный подход к измерению информации.

При изучении данной темы обращаем особое внимание на таблицы степеней двойки и соответствия единиц измерения количества информации, а так же их взаимосвязь, что послужит изложенному выше принципу решения задач.

При этом знание таблиц является необходимым условием для максимально быстрого и точного решения, без потери времени и математических ошибок.

Ниже приведена таблица степеней двойки, где k – это степень, а 2k — результат возведения числа 2 в степень k. При алфавитном подходе эта таблица показывает, сколько вариантов всевозможных «слов» Q= 2^k можно закодировать с помощью k бит на символ.

n	0	1	2	3	4	5	6	7	8	9	10	11	12
2n	1	2	4	8	16	32	64	128	256	512	1024	2048	4096

Бит — наименьшая единица измерения количества информации, может принимать только два значения – 0 или 1.

Байт содержит 8 бит (23 бит). При этом байт является неделимой единицей и всегда отображается целым числом.

Во второй таблице даны укрупненные единицы информации и их соответствие.

В России правила образования укрупненных единиц в информатике подтверждены постановлением № 879 Правительства РФ от 31 октября 2009г. Это постановление гласит:

«Наименование и обозначение единицы количества информации «байт» применяются с двоичными приставками «Кило», «Мега», «Гига», которые соответствуют множителям 210, 220 и 230 (1 Килобайт = 1024 байт, 1 Мегабайт = 1024 Килобайт,

1 Гигабайт = 1024 Мегабайт). Эти приставки пишутся с большой буквы».

Таким образом, каждая следующая единица измерения количества информации в 1024 = 210 раза больше предыдущей, на основании чего и строится таблица их соответствия:

Наименование ед.изм.	В бит=	В бит / байт	Примечание
1 Кбит (один Килобит)	210 бит	1 024 бит	более 1 тыс.бит
бит (один Мегабит)	220 бит	1 048 576 бит	более 1 млн.бит
1 Гбит (один Гигабит)	230 бит	более 109 бит	более 1 млрд.бит
1 Кбайт (один Килобайт)	213 бит	210 байт = 1024 байт	более 1 тыс.байт
1 Мбайт (один Мегабайт)	223 бит	220 байт = 1 048 576 байт	более 1 млн.байт
1 Гбайт (один Гигабайт)	233 бит	230 байт = 109 байт	более 1 млрд.байт

Таблицы не нужно учить наизусть! Рекомендуется пользоваться ими при решении задач, но при этом заглядывать в них все реже и реже, пытаясь сначала вспомнить значения, приведенные в них. Тогда эти таблицы сами «улягутся» в Вашей голове, и очень поможет Вам на экзамене в этой и в других темах!

Отцом-основателем теории информации, нашедшей применение в современных высокотехнологических системах связи, является американский инженер, криптоаналитик и математик Клод Шеннон. Именно он в 1948 году предложил использовать слово «бит» для обозначения наименьшей единицы измерения информации (в статье «Математическая теория связи»). Кроме того, понятие энтропии было важной особенностью теории Шеннона. Он продемонстрировал, что введённая им энтропия эквивалентна мере неопределённости информации в передаваемом сообщении, что и лежит в основе содержательного подхода к измерению информации, который в данной разработке нами не рассматривается. Статьи Шеннона «Математическая теория связи» и «Теория связи в секретных системах» считаются основополагающими для теории информации и криптографии.

В начале 60-х гг. русский советский математик, один из крупнейших математиков XX века Андрей Николаевич Колмогоров начал искать пути построения теории информации и теории вероятностей на принципиально новой, алгоритмической основе. В свое первой статье по алгоритмической теории информации «Три подхода к определению понятия «количество информации», вышедшей в первом выпуске первого тома журнала «Проблемы передачи информации», в 1965г, А.Н.Колмогоров указал способ измерения сложности конечного объекта (слова), для чего он ввел понятие, называемое сейчас «колмогоровской сложностью». Свое новое понятие он применил для построения алгоритмического варианта теории информации, позволяющего измерять информацию в конечной строке знаков.

Согласно Колмогорову, количество информации, содержащейся в тексте, определяется минимально возможной длиной двоичного кода, необходимого для представления этого текста.

Общей формулой, применяемой в двух различных подходах к измерению информации является формула Хартли — логарифмическая мера информации, которая определяет количество информации, содержащееся в сообщении (объем сообщения):

I = N *log₂М

Здесь М — количество символов в используемом алфавите (мощность алфавита), N — длина сообщения (количество символов в сообщении), I — количество информации в сообщении в битах.

Формула была предложена Ральфом Хартли в 1928 году как один из научных подходов к оценке сообщений.

Для случая определения количества информации k в одном символе (бит на символ) алфавита мощности М, формула Хартли принимает вид:

k = log₂М

Соответственно, мощность алфавита равна:

M= 2^k

Из формулы Хартли следует, что алфавит, содержащий только 1 символ, не может быть использован для передачи информации, так как

log₂1 = 0.

Пусть, имеется алфавит, из M букв которого составляется сообщение.

Количество возможных вариантов Q всех возможных «слов» (символьных цепочек без учета смысла) длиной N равно

Q = М^k

где М — количество букв в алфавите, k — информационный вес символа (количество бит, необходимое для его кодирования, бит на символ).

Для простоты понимания и решения задач, за М мы будем принимать значения терминов, наиболее часто применяемых в условиях задач – виды, типы, состояния символов. Это упростит понимание и решение задач в алфавитном подходе.

Отметим, что формулы вычисления объема информации I = N * k и подсчета количества вариантов Q=M^k взаимодействуют друг с другом через величину k (бит на символ).

Алфавитный подход к измерению информации

Основные понятия и термины:

Алфавит – это набор символов, используемых в языке, на котором передается сообщение. При этом символом алфавита могут быть буквы, цифры и прочие символы, входящие в сообщение.

Мощность алфавита — это количество символов в алфавите.

Например, мощность русского алфавита равна 32 при Е =Ё и 33 – в противном случае. Мощность английского алфавита равно 26.0

Для упрощения понимания и легкости запоминания различий в рассматриваемых далее задачах, разобьем их на 5 типов и будем рассматривать решения соответственно этим типам.

Для быстрого и точного вычисления количества информации следует применять таблицу степеней двойки, которая показывает, сколько вариантов всевозможных «слов» Q можно закодировать с помощью k бит на символ.

Так же при решении задач следует обязательно привести единицы измерения количества информации к одному виду. При этом помним, что значение k – это бит на символ, другого измерения здесь быть не может!

Задача 1 типа.

В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена.

Каков информационный объем в битах сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов?

Рекомендации к решению.

Перед решением этой задачи следует проговорить ее условие, заменяя слова из него синонимами, которые можно найти в формулах.

Читаем условие очень внимательно, находим хотя бы один синоним – и задача практически решена, остается только подставить формулы и получить ответ!

Чтобы легче запомнить задачи 1 типа, будем называть их общим термином «велосипедисты».

Решение.

Есть 119 спортсменов с различными номерами, т.е. 119 вариантов различных номеров, тогда Q=119.

Так как Q = М^k, то для одного номера получаем Q = 119 ≤ 128=27, откуда k=7.

Тогда для N = 70 номеров получаем информационный объем сообщения

I = N * k = 70 * 7 = 490 бит.

Также для вычисления значения бита на символ можно использовать математическое решение формулы Хартли:

k= log₂N

В данном случае k= log₂8 = 3.

Ответ: 490

Задача 2 типа.

Объем сообщения, содержащего 4096 символов, равен 1/512 части Мбайт. Какова мощность алфавита, с помощью которого записано это сообщение?

Рекомендации к решению.

Задачи данного типа – чисто математические (так и запомним их определение), и здесь очень полезно использовать таблицы степеней двойки и соответствия единиц измерения количества информации.

Подставляем числовые значения в формулы, заменяем числа степенями числа 2 и упрощаем. При этом не забываем привести единицы измерения к одному виду и помнить, что k – это бит на символ!

Решение.

Воспользовавшись таблицей степеней двойки, имеем: N = 4096 = 212 символов, тогда I =1/512 Мбайта = 223/29=214 бит. Отсюда k = I/N = 214/212=22=4 бита на символ.

Тогда мощность алфавита (количество различных вариантов символов)

М=24 = 16 символов.

Ответ: 16

Задача 3 типа.

В некоторой стране автомобильный номер длиной 7 символов составляется из заглавных букв (всего используется 26 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт.

Определите объем памяти, необходимый для хранения 20 автомобильных номеров.

Рекомендации к решению.

Решая задачи данного типа, необходимо обратить внимание на слова «каждый символ» и «каждый номер», которые подразумевают разделение информации при решении. Поэтому при решении задач 3 типа следует сначала считать объем одного номера в битах, перевести его в байты (с округлением до целого числа в большую сторону!) и только потом искать общий объем на несколько номеров.

Округление в большую сторону при вычислении объема одного номера необходимо, чтобы не потерять ни одного символа кодируемой информации.

Запомним, что округление при вычислении объемов информации всегда будем выполнять в большую сторону!

Будем так и называть этот тип задач – «автомобильные номера», хотя здесь встречаются и задачи на нахождение паролей (решение задач от этого не зависит).

Решение.

Особенность решения данной задачи – решение в два шага, т.е. поиск двух видов объема:

I₁ — отдельно для каждого номера, I₂ – для всех номеров.

Шаг 1. Мощность используемого алфавита Q = 26 + 10 = 36 ≤26, откуда k=6 бит на символ. Тогда I1 = 7*6=42 бита = 6 байт на один номер.

Шаг 2.Следовательно, на 20 номеров требуется I2 = 20 * 6 = 120 байт.

Ответ: 120

Для проверки правильности рассуждений пересчитаем объем без учета рекомендаций, данных ранее, и сравним итоги.

Мощность используемого алфавита и значение k=6 бит на символ остаются. Тогда объем одного номера I₁ = 7*6=42 бита, а 20 номеров I₂ = 42 * 20 = 840 бит = 105 байт.

В итоге потеряны 15 байт информации, а это значит, что не все номера были бы закодированы.

Задача 4 типа.

В школьной базе данных хранятся записи, содержащие информацию об учениках:

• -16 символов: русские буквы (первая прописная, остальные строчные),

• -12 символов: русские буквы (первая прописная, остальные строчные),

• — 16 символов: русские буквы (первая прописная, остальные строчные),

• — числа от 1992 до 2003.

Каждое поле записывается с использованием минимально возможного количества бит. Определите минимальное количество байт, необходимое для кодирования одной записи, если буквы е и ё считаются совпадающими.

Рекомендации к решению.

Перед решением задач данного типа вспомним, что базы данных (далее – БД) состоят из записей, которые делятся на поля.

И преимущество БД перед другим способом хранения информации в том, что поля в одной записи могут иметь разные форматы данных(числовые, символьные, даты и др.), которые кодируются соответственно их форматам.

Поэтому для подсчета общего объема одной записи следует считать объем каждого поля отдельно, а затем сложить их.

При этом помним, что в таблице ASCII (так как таблица кодировки в условии задачи не указана, берем ее по умолчанию) каждый символ занимает один байт памяти. Число (до определенного значения) – тоже кодируется одним байтом памяти.

Запомним определение задач 4 типа как «базы данных».

Решение.

Определяем минимально возможные размеры в битах для каждого из полей (в данном случае – четырех) с учетом их типов отдельно.
Так как по условию задачи первые буквы имени, отчества и фамилии – всегда заглавные, то будем хранить их в виде строчных и делать заглавными только при выводе на экран.

Таким образом, для символьных полей достаточно использовать алфавит из 32 символов (русские строчные буквы, «е» и «ё» совпадают, пробелы не нужны).

Для кодирования каждого символа 32-символьного алфавита нужно 5 бит (32 = 25), то для хранения имени, отчества и фамилии нужно (16 + 12 + 16)•5=220 бит.

Для года рождения есть 12 вариантов чисел, поэтому для него нужно отвести 4 бита

(12 ≤ 16 = 24).

Таким образом, всего требуется 220+4 = 224 бита или 28 байт.

Ответ: 28

Задача 5 типа (1).

В зоопарке 32 обезьяны живут в двух вольерах, А и Б. Одна из обезьян заболела. Сообщение «Заболевшая обезьяна живет в вольере А» содержит 4 бита информации.

Сколько обезьян живут в вольере Б?

Рекомендации к решению.

Заметим, что условие этой задачи отличается от задачи 1 типа только тем, что там все номера считались как единая информация, а здесь требуется выбор мотка определенного цвета, т.е. вся информация разделена на части.

Поэтому в решении задач 5 типа делается один дополнительный шаг — определяется, какую часть от общего количества составляет выделенная информация.

Решение.

По условию, красные клубки составляют 1/8 часть от целого (от всех клубков).

Поэтому сообщение о том, что первый вынутый клубок шерсти – красный, соответствует выбору одного из 8 вариантов, и это будет: Q = 8 = 23, что дает нам k = 3 бит.

(Можно запомнить решение задач 5 типа без дробей и дополнительных объяснений: в дополнительном по отношению к задачам 1 типа шаге находим Q = 32/4 = 8 вариантов, а затем решаем, как и задачи 1 типа: Q = 8 = 23, что дает нам k = 3 бит).

Ответ: 3

Задача 5 типа (2).

В зоопарке 32 обезьяны живут в двух вольерах, А и Б. Одна из обезьян заболела. Сообщение «Заболевшая обезьяна живет в вольере А» содержит 4 бита информации.

Сколько обезьян живут в вольере Б?

Решение.

Почему эта задача относится к 5 типу? Потому что информация разделена на части – обезьяны здоровые и больные.

Решается она в порядке, обратном решению предыдущей задачи.

Итак, информация в 4 бита соответствует выбору одного из 16 вариантов, поэтому в вольере А живет 1/16 часть всех обезьян: 32/16 = 2 обезьяны

Тогда в вольере Б живут все оставшиеся 32 – 2 = 30 обезьян.

Описание задач 5 типа можно определить и запомнить как задачи «про шары и обезьян».

Ответ: 30

Задачи смешанных типов.

Усвоив решение каждого типа задач отдельно, можно рассмотреть задачи смешанных типов.

Для их успешного решения необходимо прежде всего внимательно рассмотреть условие задачи, чтобы не пропустить это смешивание, а потом уже решать с учетом всех тонкостей, описанных ранее.

Разберем две из таких задач.

Задача 1.

При регистрации в компьютерной системе каждому пользователю выдаётся идентификатор, состоящий из 8 символов, первый и последний из которых – одна из 18 букв, а остальные – цифры (допускается использование 10 десятичных цифр.

Каждый такой идентификатор в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование; все цифры кодируются одинаковым и минимально возможным количеством бит, все буквы также кодируются одинаковым и минимально возможным количеством бит).

Определите объём памяти в байтах, отводимый этой программой для записи 500 паролей.

Решение.

Рассмотрим условие и разделим его на части, относящиеся к разным типам задач.

В первом абзаце говорится, что идентификатор состоит из букв и цифр в определенном порядке, а они кодируются по-разному. Это подтверждается и во-втором абзаце, где способ кодировки для цифр и букв описывается отдельно. Следовательно, каждый идентификатор рассматривается как запись из БД, то есть эта часть задачи относится к типу 4.

Во втором абзаце условия так же сказано, что каждый идентификатор записывается минимально возможным и одинаковым целым количеством байт, а посимвольное (т.е. для каждого символа отдельно) кодирование выполняется минимальным количеством бит для каждого вида символов. Следовательно, эта часть задачи относится к типу 3.

Тогда решение будет следующим:

В идентификаторе шесть цифр из алфавита мощностью 10 символов.

Тогда k₁=4 и I1=6*k₁=24 бита.

Вторая часть идентификатора длиной 2 символа состоит из алфавита мощностью 18 символов. Тогда k₂=5 и I₂=2*k2=10 бит.
Значит, объем одного идентификатора равен I₁ + I₂ = 24 + 10 = 34 бита.

Далее решаем задачу соответственно решению, описанному в 3 типе задач:

34 бита = 5 байт,

Общий объем 500 идентификаторов равен I = 5*500=2500 байт.

Ответ: 2500

Задача 2.

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит.

Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт на одного пользователя.

Определите объём памяти (в байтах), необходимый для хранения сведений о 50 пользователях. В ответе запишите только целое число – количество байт.

Решение.

В условии сказано, что сведения о пользователях хранятся в БД, где запись состоит из двух полей – собственно идентификатора и дополнительных сведений (тип 4).

При этом идентификатор рассчитывается как в задачах 1 типа, а дополнительные сведения заданы конкретным значением и расчет их не нужен.

Тогда решение будет следующим:

Мощность используемого алфавита Q = 12 ≤24, откуда k=4 бита на символ. Тогда I₁ = 15*4 = 60 бит = 8 байт на один идентификатор.

Объем одной записи равен I₁+2 = 8 + 12 = 20 байт.

Следовательно, для 50 записей требуется I50 = 20 * 50 = 1000 байт.

Ответ: 1000

РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «КОЛИЧЕСТВО ИНФОРМАЦИИ»

Алфавитный подход к определению количества информации

РЕШЕНИЕ ЗАДАЧ

При хранении и передаче
информации с помощью технических устройств информацию следует рассматривать как
последовательность символов — знаков (букв, цифр, кодов цветов точек
изображения и т.д.).

Набор символов знаковой
системы (алфавит) можно рассматривать как различные возможные состояния
(события). 
Тогда, если считать, что
появление символов в сообщении равновероятно, количество возможных событийN можно
вычислить как N=2ⁱ 
Количество информации в
сообщении I можно подсчитать умножив количество символов K на
информационный вес одного символа i 
Итак, мы имеем формулы,
необходимые для определения количества информации в алфавитном подходе:

N=2i	i	Информационный вес символа, бит
	N	Мощность алфавита
I=K*i	K	Количество символов в тексте
	I	Информационный объем текста

Возможны следующие
сочетания известных (Дано) и искомых (Найти) величин:

Тип	Дано	Найти	Формула
1	i	N	N=2i
2	N	i
3	i,K	I	I=K*i
4	i,I	K
5	I, K	i
6	N, K	I	Обе формулы
7	N, I	K
8	I, K	N

Если к этим задачам
добавить задачи на соотношение величин, записанных в разных единицах измерения,
с использованием представления величин в виде степеней двойки мы получим 9
типов задач. 
Рассмотрим задачи на все
типы. Договоримся, что при переходе от одних единиц измерения информации к
другим будем строить цепочку значений. Тогда уменьшается вероятность
вычислительной ошибки.

Задача 1. Получено сообщение, информационный
объем которого равен 32 битам. чему равен этот объем в байтах? 

Решение: В одном байте 8
бит. 32:8=4 
Ответ: 4 байта.

Задача 2. Объем информацинного сообщения
12582912 битов выразить в килобайтах и мегабайтах. 

Решение: Поскольку
1Кбайт=1024 байт=1024*8 бит, то 12582912:(1024*8)=1536 Кбайт и 
поскольку 1Мбайт=1024
Кбайт, то 1536:1024=1,5 Мбайт 
Ответ:1536Кбайт и
1,5Мбайт.

Задача 3. Компьютер имеет оперативную
память 512 Мб. Количество соответствующих этой величине бит больше:

1) 10 000 000 000бит 2) 8
000 000 000бит 3) 6 000 000 000бит 4) 4 000 000 000бит Решение: 512*1024*1024*8
бит=4294967296 бит. 
Ответ: 4.

Задача 4. Определить количество битов в
двух мегабайтах, используя для чисел только степени 2. 
Решение: Поскольку
1байт=8битам=2³битам, а 1Мбайт=2¹⁰Кбайт=2²⁰байт=2²³бит.
Отсюда, 2Мбайт=2²⁴бит. 
Ответ: 2²⁴бит.

Задача 5. Сколько мегабайт информации
содержит сообщение объемом 2²³бит? 
Решение: Поскольку
1байт=8битам=2³битам, то 
2²³бит=2²³*2²³*2³бит=2¹⁰2¹⁰байт=2¹⁰Кбайт=1Мбайт. 
Ответ: 1Мбайт

Задача 6. Один символ алфавита
«весит» 4 бита. Сколько символов в этом алфавите? 
Решение: 
Дано:

i=4	По формуле N=2i находим N=24, N=16
Найти: N — ?

Ответ: 16

Задача 7. Каждый символ алфавита записан
с помощью 8 цифр двоичного кода. Сколько символов в этом алфавите? 
Решение: 
Дано:

i=8	По формуле N=2i находим N=28, N=256
Найти:N — ?

Ответ: 256

Задача 8. Алфавит русского языка иногда
оценивают в 32 буквы. Каков информационный вес одной буквы такого сокращенного
русского алфавита? 
Решение: 
Дано:

N=32	По формуле N=2i находим 32=2i, 25=2i,i=5
Найти: i— ?

Ответ: 5

Задача 9. Алфавит состоит из 100
символов. Какое количество информации несет один символ этого алфавита? 
Решение: 
Дано:

N=100	По формуле N=2i находим 32=2i, 25=2i,i=5
Найти: i— ?

Ответ: 5

Задача 10. У племени «чичевоков»
в алфавите 24 буквы и 8 цифр. Знаков препинания и арифметических знаков нет.
Какое минимальное количество двоичных разрядов им необходимо для кодирования
всех символов? Учтите, что слова надо отделять друг от друга! 
Решение: 
Дано:

N=24+8=32	По формуле N=2i находим 32=2i, 25=2i,i=5
Найти: i— ?

Ответ: 5

Задача 11. Книга, набранная с помощью компьютера,
содержит 150 страниц. На каждой странице — 40 строк, в каждой строке — 60
символов. Каков объем информации в книге? Ответ дайте в килобайтах и
мегабайтах 
Решение: 
Дано:

K=360000	Определим количество символов в книге 150*40*60=360000. Один символ занимает один байт. По формуле I=K*iнаходим I=360000байт 360000:1024=351Кбайт=0,4Мбайт
Найти: I— ?

Ответ: 351Кбайт или
0,4Мбайт

Задача 12. Информационный объем текста
книги, набранной на компьютере с использованием кодировки Unicode, — 128 килобайт.
Определить количество символов в тексте книги. 
Решение: 
Дано:

I=128Кбайт,i=2байт	В кодировке Unicode один символ занимает 2 байта. Из формулыI=K*iвыразимK=I/i,K=128*1024:2=65536
Найти: K— ?

Ответ: 65536

Задача 13.Информационное сообщение объемом 1,5
Кб содержит 3072 символа. Определить информационный вес одного символа
использованного алфавита 
Решение: 
Дано:

I=1,5Кбайт,K=3072	Из формулы I=K*iвыразимi=I/K,i=1,5*1024*8:3072=4
Найти: i— ?

Ответ: 4

Задача 14.Сообщение, записанное буквами из
64-символьного алфавита, содержит 20 символов. Какой объем информации оно
несет? 
Решение: 
Дано:

N=64, K=20	По формуле N=2i находим 64=2i, 26=2i,i=6. По формуле I=K*i I=20*6=120
Найти: I— ?

Ответ: 120бит

Задача 15. Сколько символов содержит
сообщение, записанное с помощью 16-символьного алфавита, если его объем
составил 1/16 часть мегабайта? 
Решение: 
Дано:

N=16, I=1/16 Мбайт	По формуле N=2i находим 16=2i, 24=2i,i=4. Из формулы I=K*i выразим K=I/i, K=(1/16)*1024*1024*8/4=131072
Найти: K— ?

Ответ: 131072

Задача 16. Объем сообщения, содержащего
2048 символов,составил 1/512 часть мегабайта. Каков размер алфавита, с помощью
которого записано сообщение? 
Решение: 
Дано:

K=2048,I=1/512 Мбайт	Из формулы I=K*i выразим i=I/K, i=(1/512)*1024*1024*8/2048=8. По формулеN=2iнаходим N=28=256
Найти: N— ?

Ответ: 256

Задачи для
самостоятельного решения:

1.     Каждый символ алфавита записывается с
помощью 4 цифр двоичного кода. Сколько символов в этом алфавите?

2.     Алфавит для записи сообщений состоит
из 32 символов, каков информационный вес одного символа? Не забудьте указать
единицу измерения.

3.     Информационный объем текста,
набранного на компьюте¬ре с использованием кодировки Unicode (каждый символ
кодируется 16 битами), — 4 Кб. Определить количество символов в тексте.

4.     Объем информационного сообщения
составляет 8192 бита. Выразить его в килобайтах.

5.     Сколько бит информации содержит
сообщение объемом 4 Мб? Ответ дать в степенях 2.

6.     Сообщение, записанное буквами из
256-символьного ал¬фавита, содержит 256 символов. Какой объем информации оно
несет в килобайтах?

7.     Сколько существует различных звуковых
сигналов, состоящих из последовательностей коротких и длинных звонков. Длина
каждого сигнала — 6 звонков.

8.     Метеорологическая станция ведет
наблюдение за влажностью воздуха. Результатом одного измерения является целое
число от 20 до 100%, которое записывается при помощи минимально возможного
количества бит. Станция сделала 80 измерений. Определите информационный объем
результатом наблюдений.

9.     Скорость передачи данных через
ADSL-соединение равна 512000 бит/с. Через данное соединение передают файл
размером 1500 Кб. Определите время передачи файла в секундах.

10.  Определите скорость работы модема, если за 256 с он может передать
растровое изображение размером 640х480 пикселей. На каждый пиксель приходится 3
байта. А если в палитре 16 миллионов цветов?

Тема определения
количества информации на основе алфавитного подхода используется в заданиях А1,
А2, А3, А13, В5 контрольно-измерительных материалов ЕГЭ.

В вычислительной технике используют 
алфавитный   подход к измерению
количества информации.

N=2^I , где  
N  —мощность
алфавита (полное количество символов)

 I –
количество информации,

Изучить теорию подробнее..

Алфавитный подход к измерению количества информации

Алфавитный  подход 
-это  измерение количества
информации в тексте (символьном сообщении), составленном из символов некоторого
алфавита.

К содержанию
текста такая мера информации отношения не имеет.

Число символов в
алфавите называется мощностью алфавита.

Чем меньше
знаков в используемом алфавите, тем длиннее сообщение.

Так, например, в
алфавите азбуки Морзе всего три знака (точка, тире, пауза), поэтому для
кодирования каждой русской или латинской буквы нужно использовать несколько
знаков, и текст, закодированный по Морзе, будет намного длиннее, чем при
обычной записи.

Количество
символов в алфавите (мощность алфавита) находится по формуле N=2^I,
где I – информационный вес одного символа (в битах).

Количество
символов в сообщении (тексте) определяется по формуле  Т = К·I, где К — количество символов в
сообщении (тексте), I – информационный вес одного символа (в битах)

Какова минимальная мощность алфавита, с помощью которого можно
кодировать информацию?

Сообщение любой
длины, использующее односимвольный алфавит, содержит нулевую информацию.

Интуитивно
понятно, что сообщить что-либо с помощью единственного символа невозможно.( Представьте себе
толстую книгу в 1000 страниц, на всех страницах которой написаны одни единицы
(единственный символ используемого алфавита).

— Сколько
информации в ней содержится?

Ответ:
Нисколько, ноль.

Минимальная
мощность алфавита, пригодного для передачи информации,
равна 2.

Такой алфавит
называется двоичным алфавитом.

Информационный
вес символа в двоичном алфавите легко определить.

Поскольку

2ⁱ = 2,

то i = 1 бит

Итак, один
символ двоичного алфавита несет 1 бит информации.

1 бит
– исходная единица измерения информации.

Мощность
русского алфавита

Каждая буква
русского алфавита

(если считать,
что е = ё)

несет информацию
5 бит

(32 = 2⁵).

Компьютерный
алфавит

Современный
компьютер может обрабатывать числовую, текстовую, графическую, звуковую и видео
информацию.

Все эти виды
информации в компьютере представлены в двоичном коде, т. е. используется
алфавит мощностью два (всего два символа 0 и 1).

Связано это с
тем, что удобно представлять информацию в виде последовательности электрических
импульсов: импульс отсутствует (0), импульс есть (1).

Такое кодирование
принято называть двоичным, а сами логические последовательности нулей и
единиц — машинным языком.

Алфавитный подход к измерению информации

Из школьных уроков вы знаете, что масса измеряется с помощью граммов, а единицей измерения для времени является секунда. Информацию также можно измерить, и для этого существует три подхода: алфавитный, содержательный и вероятностный. Рассмотрим первый из них.

Сущность алфавитного подхода

Алфавитный подход применяется в цифровых системах хранения и передачи информации, в которых используется двоичный способ кодирования информации, то есть с помощью 0 и 1. Для определения количества информации алфавитный подход учитывает только объем кода, а не содержание информации. Итак, с помощью i-разрядного двоичного кода можно закодировать алфавит, состоящий из N символов, при этом N является целой степенью двойки и называется мощность алфавита.

Из примеров видно, что величина i – это длина двоичного кода, с помощью которого кодируется один символ алфавита, она называется информационным весом символа и определяется из уравнения:

(2^{i} = N)

Единицы измерения информации

В двоичном коде цифра (0 или 1) несет одну наименьшую единицу информации, которая называется 1 бит.

Помимо битов существуют более крупные единицы измерения информации. Чтобы не запутаться при решении задач, следует запомнить таблицу переводов, представленную ниже:

1 байт	= 23 бит	= 8 бит
1 Кб (килобайт)	= 210 байтов	= 1024 байта
1 Мб (мегабайт)	= 210 Кб	= 1024 Кб
1 Гб (гигабайт)	= 210 Мб	= 1024 Мб
1 Тб (терабайт)	= 210 Гб	= 1024 Гб

Рассмотрев формулу информационного веса символа и единицы измерения информации, решим задачу.

Пример. Представим, что нам надо закодировать латинский алфавит, который содержит 26 символов. Сколько бит потребуется для кодирования каждого символа?

Давайте попробуем посчитать. Кодировка предполагает, что каждому символу алфавита мы ставим в соответствие уникальный набор битов, т.е. у всех символов эти наборы разные. Количество комбинаций N, которое можно составить из i битов (каждый их них может быть либо 0, либо 1), будет равно:

(N = 2^{i})

В нашем случае N = 26. Получаем

(26 = 2^{i})

26 не является степенью двойки, но это не страшно — нам надо найти такое минимальное i, чтобы 2ⁱ точно было больше 26:

• 2⁴ = 16 – не подходит (получается, что с помощью 4 бит мы можем закодировать только 16 символов);

• 2⁵ = 32 — подходит.

Нашли, что i = 5, т.е. вес одного символа — 5 бит.

Информационный объем

Теперь, когда мы умеем находить вес одного символа, рассмотрим, как находить информационный объем слова, предложения или текста. Для этого обозначим буквой K – количество символов в тексте, записанном с помощью алфавита, i – информационный вес одного символа, тогда информационный объем I текста в битах можно выразить с помощью формулы:

(I = K bullet i)

Пример. Используя данные с прошлого примера, а именно, что i = 5, найдем какой объем информации будет нужен для хранения слова из 10 закодированных нами букв?

Одна буква весит 5 бит, значит, 10 букв будут весить 5×10 = 50 бит.

КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ

Кодирование – это перевод информации в удобную для передачи, обработки или хранения форму с помощью некоторого кода. В компьютере символы, изображения, музыка – все кодируется двоичным кодом.

Двоичный код — это способ представления данных в виде кода, в котором каждый разряд принимает одно из двух возможных значений, обычно обозначаемых цифрами 0 и 1. 0 и 1 – это алфавит двоичной системы счисления. Основание двоичной системы счисления – q =2, т.к. в алфавит входят всего две цифры.

Для решения задач на двоичное кодирование необходимо:

1) уметь строить таблицу соответствия двоичных чисел десятичным, восьмеричным и шестнадцатеричным числам (знать алфавиты данных систем счисления и двоичную арифметику(8 класс))

2) уметь переводить из двоичной системы счисления в восьмеричную, шестнадцатеричную, десятичную и обратно (8 класс)

Примеры задач на кодирование:

1. Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.

Алгоритм решения:

1) строим таблицу из того, что дано по условию задачи:

O	В	Д	П	А
0	1	2	3	4

2) Вычисляем двоичное представление чисел 0, 1, 2, 3 и 4: для этого строим таблицу соответствия двоичной (с сохранением одного незначащего нуля в случае одноразрядного представления) и десятичной системы:

q=10	q=2
0	00
1	01
2	10
3	11
4	100
5	101
6	110
7	111

3) Записываем двоичные числа в таблицу:

O	В	Д	П	А
0	1	2	3	4
00	01	10	11	100

4) Записываем двоичную последовательность для указанного слова ВОДОПАД = 01 00 10 00 11 100 10

5) Переводим полученное число двоичной системы счисления в указанную систему (в данном случае в восьмеричную):

ВОДОПАД = 010010001110010

Для этого делим СПРАВА налево полученное число на ТРИАДЫ (если переводим в шестнадцатеричную систему, то разделяем на ТЕТРАДЫ (группы по 4)): получится 010 010 001 110 010 и каждое полученное трехразрядное число переводим в восьмеричную систему счисления по уже созданной таблице (она включает числа от 0 до 7 – что совпадает с алфавитом восьмеричной системы счисления):

010	010	001	110	010
2	2	1	6	2

Ответ: 22162

2. Для пе­ре­да­чи по ка­на­лу связи сообщения, со­сто­я­ще­го только из букв А, Б, В, Г, ре­ши­ли использовать не­рав­но­мер­ный по длине код: A=1, Б=01, В=001. Как нужно за­ко­ди­ро­вать букву Г, чтобы длина кода была ми­ни­маль­ной и до­пус­ка­лось однозначное раз­би­е­ние кодированного со­об­ще­ния на буквы?

1) 0001

2) 000

3) 11

4) 101

Алгоритм решения:

1) Находим среди вариантов двоичное число с наименьшим количеством разрядов, в данном случае это 11

2) Проверяем можно ли закодировать однозначно букву Г этим числом: А=1, поэтому, 11 можно принять как АА, таким образом это число не подходит

3) Находим следующее число после 11 с наименьшим количеством разрядов: 000 и 101.

4) Проверяем, можно ли закодировать букву Г данными числами: 101 можно принять как АБ, т.е. этот вариант не подходит. 000 – подходит.

Ответ: 2)000

ИЗМЕРЕНИЕ ИНФОРМАЦИИ.

ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИ

Основная единица измерения информации – бит.

Существует несколько подходов к измерению информации – алфавитный и содержательный. В алфавитном подходе речь идет об объеме информации. Количество символов в алфавите называется мощностью алфавита (N), а то, сколько «весит» один символ в битах – информационным весом символа (i). Чем больше символов в тексте, тем больше будет объем сообщения. Содержательный подход говорит не об объеме сообщения, а о количестве информации, которое человек может получить из него. В данном случае сообщение, уменьшающее неопределенность знания в два раза будет нести 1 бит информации. Если сообщение не несет нового знания и не убирает неопределенность, то оно несет в себе 0 бит, в независимости от того, сколько символов в данном сообщении.

Что нужно знать:

1) Единицы измерения информации и их перевод(8класс):

8 бит = 1 байт

1024 байта = 2¹⁰ байта = 1 Кбайт

1024 Кб = 2¹⁰ Кб = 1 Мб

1024 Мб = 2¹⁰ Мб = 1 Гб

1024 Гб = 2¹⁰ Гб = 1 Тб

2) Главную формулу информатики (7-9 класс):

N = 2ⁱ, где N – количество информации, i – количество бит на единицу информации.

3) Применение главной формулы информатики для алфавитного и содержательного подхода:

	Алфавитный подход	Содержательный подход
N	мощность алфавита (количество символов в алфавите)	количество равновероятных вариантов
i	информационный вес одного символа алфавита в битах	количество бит в одном сообщении

4)Целые степени двойки для вычисления i:

i	0	1	2	3	4	5	6	7	8	9	10
2i	1	2	4	8	16	32	64	128	256	512	1024

5) Формулу информационного объема сообщения:

I = K*i, где I – объем сообщения, K – количество символов в сообщении, i – количество бит на один символ сообщения.

Примеры задач:

1. B некоторой стране автомобильный номер длиной 6 символов составляют из заглавных букв (используются только 33 различных буквы) и десятичных цифр в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байтов (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов). Определите объём памяти, отводимый этой программой для записи 125 номеров. (Ответ дайте в байтах.)

Алгоритм решения:

1) находим N – в данном случае 33+10 = 43

2) находим i по формуле N = 2i: 25 (32)– мало, 26 (64) – достаточно, значит i = 6 бит (на один символ номера)

3) находим I номера (т.е. количество информации в одном номере): К = 6, i = 6, значит I = 36 бит (6 символов в номере – каждый по 6 бит)

4) Переводим в байты и округляем В БОЛЬШУЮ СТОРОНУ (ВСЕГДА!): 36/8 = 4,5 байта – не целое число, в большую сторону = 5 байт на 1 номер

5) Находим I для общего количества номеров: 125 номеров, каждый по 5 байт – 125*5 = 625 байт

Ответ: 625 байт

2. В скач­ках участвуют 20 лошадей. Спе­ци­аль­ное устройство регист­рирует про­хож­де­ние каждой ло­ша­дью финиша, за­пи­сы­вая ее номер с ис­поль­зо­ва­ни­ем минимально воз­мож­но­го количества бит, одина­кового для каж­дой лошади. Каков ин­фор­ма­ци­он­ный объем сообще­ния, за­пи­сан­но­го устройством, если до фи­ни­ша добрались толь­ко 15 из 20 участ­во­вав­ших в скач­ках лошадей? (Ответ дайте в битах.)

Это подобная задача, алгоритм почти тот же.

N = 20 (т.к. всего лошадей 20), i = 5 бит на одну лошадь, т.к. 24= 16 – мало, К = 15, т.к. из 20 только 15 добрались до финиша. I = 15*5 = 45 бит на 15 лошадей

Ответ: 45 бит

3. В корзине лежат 32 клубка шерсти, из них 4 красных. Сколько бит информации несет сообщение о том, что достали клубок красной шерсти?

Задача на содержательный подход. Алгоритм решения:

1) Находим какую часть от 32 составляет 4 клубка: 4 шара – 1/8 от 32

2) Если 1/8 часть – то частей всего – 8, т.е. количество вариантов – 8, иными словами N=8

3) N=8, значит i = 3 бита

Ответ: 3 бита

4. В корзине лежат 32 шаров. Сообщение о том, что из корзины достали красный шар содержит 3 бита. Сколько красных шаров?

Это обратная задача. Алгоритм:

1) i = 3 бита, значит N = 8, т.е. 1/8 от всех шаров

2) Всего шаров 32. 1/8 от 32 – 4 шара красных.

(находим сколько частей, находим какая это часть от всего количества, находим количество)

Ответ: 4 шара