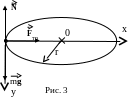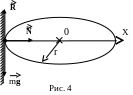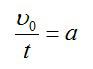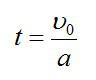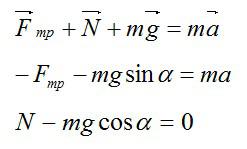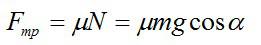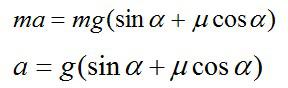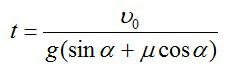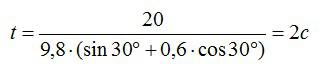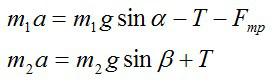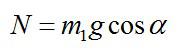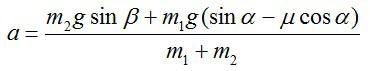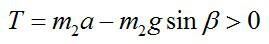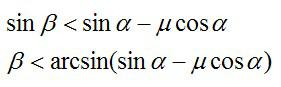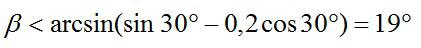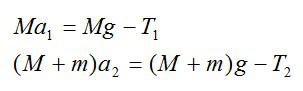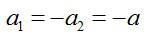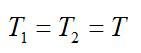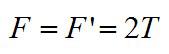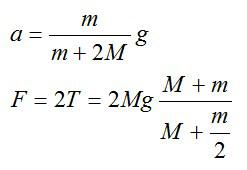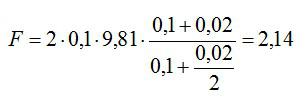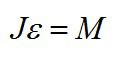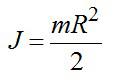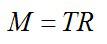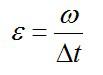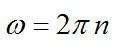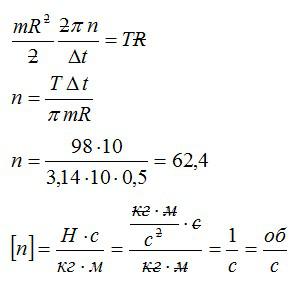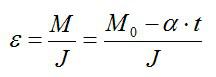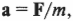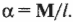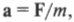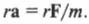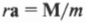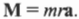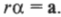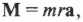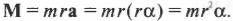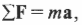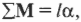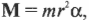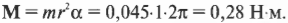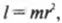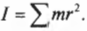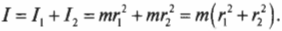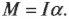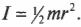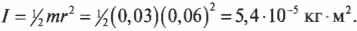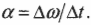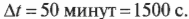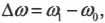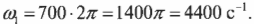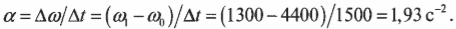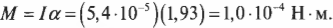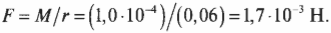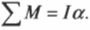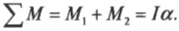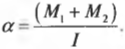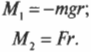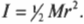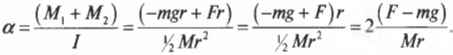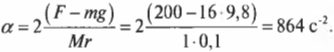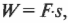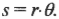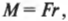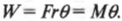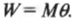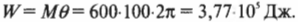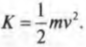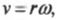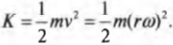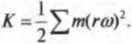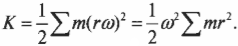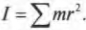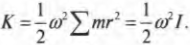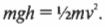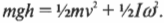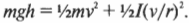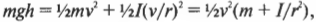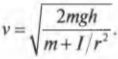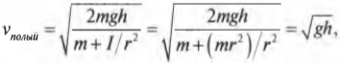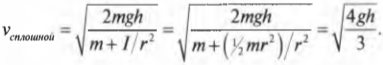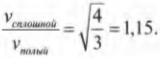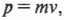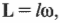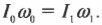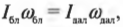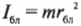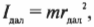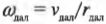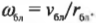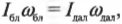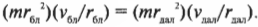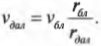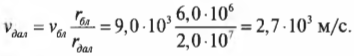Максимальный угол наклона к вертикали, под которым может стоять лестница массой m, прислонённая к вертикальной гладкой стене и опирающаяся на горизонтальный шероховатый пол, равен
Коэффициент трения между ножками лестницы и полом равен
Лестницу установили, наклонив её именно под углом
Из приведённого ниже списка выберите два правильных утверждения.
1) Модуль силы реакции со стороны стены равен модулю силы трения между ножками лестницы и полом.
2) Модуль силы трения между лестницей и полом равен произведению коэффициента трения μ на модуль суммы сил реакции пола и стены.
3) Модуль силы трения между лестницей и полом больше произведения коэффициента трения на модуль силы тяжести.
4) Модуль силы тяжести равен модулю силы реакции со стороны пола.
5) Момент силы трения относительно оси, проходящей через точку А, по модулю больше момента силы тяжести, относительно этой же оси.
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Основное уравнение динамики вращательного движения
Вспомним формулу, которая связывает линейную скорость v, угловую скорость ω и радиус кривизны окружности R, по которой перемещается некоторая точка абсолютно твёрдого тела:
v=ωR.
Очевидно, что каждая точка объекта имеет свою собственную скорость и ускорение. Единственное, что их объединяет – это угловая скорость. Она одинакова для всех точек абсолютно твёрдого тела.
Угловая скорость имеет направление, которое определяется правилом буравчика. Вспомним его: если направление вращения ручки буравчика совпадает с направлением вращением тела, то поступательное движение буравчика указывает направление вектора угловой скорости.
В жизни же крайне сложно найти примеры равномерного вращательного движения. Всё-таки все процессы, протекающие вокруг нас, характеризуются изменением скорости. Так и угловая скорость меняется особенно отчётливо в начале и в конце движения. Причина этого изменения таится в воздействии сил.
По аналогии с линейным ускорением угловое ускорение – это изменение скорости с течением времени.
В связи с тем, что тело в редких случаях движется с одинаковым ускорением, в кинематике говорят о среднем угловом ускорении. Оно равно отношению изменения угловой скорости к временному промежутку, за которое это изменение произошло: ε = Δω/Δt.
В случае равноускоренного движения угловое ускорение не меняется с течением времени и при неподвижности оси вращения характеризует изменение угловой скорости по модулю. Если увеличить угловую скорость вращения тела, то угловое ускорение сориентируется в том же направлении, что и угловая скорость (а). И, наоборот, в случае уменьшения – развернётся в обратную сторону (б).
Угловая скорость связана с линейной посредством соотношения: υ = ωR. Тогда изменение линейной скорости за некоторое количество времени Δt равно Δυ =ΔωR. Разделим обе части уравнения на временной промежуток Δt, то получим соотношение: Δv/Δt = RΔω/Δt.
Последнее выражение можно преобразовать в вид: а = εR, подразумевая под ε – касательное (линейное) ускорение, направленное по касательной к траектории движения. Теперь определим размерность этой величины. Мы знаем, что время измеряется в секундах, а угловая скорость – в радианах в секунду. Следовательно, угловое ускорение определяется радианами в секунду в квадрате.
Момент силы
Почему некоторые тела при воздействии на них сил вращаются, а другие – двигаются поступательно? Всё зависит не только от величины силы, но и от точки её приложения. Если, например, попытаться открыть окно, надавливая на противоположную сторону от ручки, то придется приложить немало усилий. Но, если открывать окно стандартным способом, потянув за ручку, то оно открывается при минимальном воздействии. Это связано с тем, что ручка располагается на значительном расстоянии от оси вращения. Поэтому вращательное движение заметно в случае, когда расстояние от оси вращения до точки воздействия достаточно велико.
Получается, что за вращение тела отвечают сразу две составляющие – плечо силы d, равное кратчайшему расстоянию от оси вращения до линии действия силы и величина этой самой силы F. Если перемножить d и F, то можно получить момент силы M: M = dF.
Теперь представим, что на тело действует сразу несколько сил. Чему тогда будет равен суммарный момент? По аналогии с принципом суперпозиций, суммарный момент равен алгебраической сумме моментов каждой из сил относительно рассматриваемой оси вращения.
На рисунке моменты сил, которые вызывают вращение тела против часовой стрелки считаются положительными (сила F2), а моменты сил, которые вызывают противоположное вращение (то есть по часовой стрелке) – отрицательными (F1 и F3).
Основное уравнение динамики вращательного движения
Угловое ускорение прямо пропорционально моменту силы: ε ∼ М.
Предположим, что на материальную точку, которая двигается по окружности, действует сила F.
Вспомним второй закон Ньютона, согласно которому в проекции на касательное направление выполняется соотношение: maк = Fк. Если умножить это уравнение с обеих сторон на r, то получим выражение:
maкr = Fкr, которое равно: mr2ε = М.
Под r в этом случае понимается кратчайшее расстояние от оси вращения до материальной точки, на которую действует сила.
Важно запомнить, что произведение массы материальной точки на квадрат расстояния до оси вращения – есть момент инерции материальной точки. Его обозначают буквой I.
Исходя из этого, уравнение для углового ускорения можно переписать в виде: ε = M/I, где I – момент инерции, M – суммарный момент сил. Собственно, так мы получили основное уравнение динамики вращательного движения. Оно выполняется в случае вращения твёрдого тела, которое обладает неподвижной осью вращения.
Рассмотрим систему, которая состоит из набора материальных точек. Обозначим ось вращения ОО’ и скажем, что момент инерции равен сумме моментов инерции каждой материальной точки относительно неё: I = m1r21 + m2r22 + … .
Встаёт очевидный вопрос: а как рассчитать момент инерции твёрдого тела? Для этого понадобится разделить его на маленькие части, которые в своем относительном рассмотрении смогут считаться материальными точками.
Очевидно, что момент инерции зависит от «разброса» материальных точек относительно оси вращения. Следовательно, момент инерции I характеризует распределение массы тела относительно ОО’. Чем больше момент инерции, тем сложнее тело заставить вращаться.
Величина момента инерции для некоторых абсолютно твёрдых тел – это табличная величина.
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
-
Динамика вращательного движения
2.1. По второму закону Ньютона, F
= ma,
ускорение появляется только
в том случае, если равнодействующая
всех сил, действующих на точку, отлична
от нуля.
Обратимся еще раз к понятию ускорения.
Модуль скорости изменяется только в
случае, если равнодействующая сила
направлена параллельно вектору скорости.
Иными словами, сила, параллельная
вектору скорости, сообщает телу
тангенциальное ускорение, F׀׀=
maτ.
Направление скорости может
изменить сила, перпендикулярная вектору
скорости. То есть,
сила,
перпендикулярная вектору скорости,
сообщает телу нормальное ускорение,
F=
man.
Поскольку при равномерном
движении по окружности а
= 0, значит, полное
ускорение тела а
есть ускорение нормальное аn.
Направлено оно к центру
вращения (окружности), поэтому при
равномерном движении точки по
окружности нормальное ускорение называют
еще центростремительным.
2.2. При неравномерном движении
по окружности вектор ускорения а
не направлен к центру
вращения и его удобно разложить на две
составляющие – нормальное и тангенциальное
ускорение. Модуль нормального ускорения
в любой момент времени можно найти по
формуле
,
где v
и ω
— линейная и угловая скорости в этот
момент. Из рисунка 2 видно, что при
неравномерном движении по окружности
проекция ускорения а
на ось X,
направленную вдоль
радиуса к центру вращения, всегда равна
аn.
На этом основано решение
многих задач на неравномерное движение
по окружности.
2.3. Очень большие трудности у учащихся
вызывают задачи, в которых рассматривается
движение тела под действием нескольких
сил, не всегда направленных вдоль одной
оси. В этом случае можно посоветовать
не отходить от принятой схемы расчета:
-
Выявление всех сил, действующих на
тело. -
Обязательное изображение всех этих
сил на рисунке. -
Выбор
удобной для расчета системы координат. -
Составление динамических уравнений
(вначале в векторном виде, а затем в
проекциях на выбранные координатные
оси).
5. Сила, параллельная вектору скорости,
сообщает телу тангенциальное ускорение.
Сила, перпендикулярная вектору
скорости, сообщает телу нормальное
ускорение: F׀׀=
maτ,
F=
man.
3. Примеры решения задач
Задача 1. При какой скорости автомобиль
«не занесет» на повороте горизонтальной
дороги радиусом r = 100 м,
если коэффициент трения между колесами
и дорогой равен =
0,1?
Решение
Н
а
автомобиль действует сила тяжести
mg;
сила реакции опоры N и сила трения
Fтр,
направленная перпендикулярно скорости
к центру окружности (рис.3).
Выберем систему координат так, чтобы
одна из осей (например, Х) была направлена
в плоскости движения к центру вращения.
Тогда вторая ось Y,
перпендикулярная оси Х, будет направлена
вертикально (вверх или вниз – значения
не имеет). Направим ось Y
вниз.
Запишем динамическое уравнение в
векторном виде
mg + N+
Fтр= ma
и в проекциях на координатные оси:
на ось Y: mg
— N = 0, так как вдоль оси Y
ускорение равно 0; отсюда N = mg
; Fтр= N
= mg;
на ось Х: Fтр = man,
действующая вдоль этой оси сила трения
перпендикулярна скорости Fтрv,
поэтому она сообщает автомобилю
нормальное (центростремительное)
ускорение an
= v2/r.
Получаем mg
= mv2/r,
откуда находим значение скорости v
=
=10
м/с = 36 км/ч. (ускорение свободного падения
принимаем равным 10 м/с2 ).
Ответ: скорость автомобиля не
должна превышать 10 м/с, что соответствует
36 км/ч.
Задача 2. При каком числе оборотов
в минуту тело, лежащее на горизонтальной
вращающейся платформе на расстоянии r
= 5 м от ее центра, не удержится на ней
при коэффициенте трения между телом и
платформой = 0,1?
Решение
На тело действует сила тяжести mg;
сила реакции опоры N
и сила трения Fтр,
направленная перпендикулярно скорости
к центру вращения платформы (рис.3).
Выберем систему двух взаимно
перпендикулярных координат Х и Y,
направив их по принципу, обусловленному
в предыдущей задаче. Динамическое
уравнение имеет вид: mg+N+Fтр
= ma.
Запишем его в проекциях на
координатные оси.
На ось Y: mg-N=0,
так как вдоль оси Y ускорение
равно 0; отсюда N= mg ;
Fтр= N
= mg.
На ось Х: Fтр = man,
так как действующая вдоль этой оси сила
трения перпендикулярна скорости, и,
значит, сообщает телу нормальное
ускорение an
= 2минr
. Здесь удобен именно этот вариант
формулы нормального ускорения, так как
искомая величина может быть выражена
через угловую скорость nмин=
/2
(заметьте, что значение частоты вращения
n получается в этом случае в оборотах
в секунду). Итак, mg
= m2минr,
g =
42n2
минr,
.
Подставляя данные величины, получаем
n ≥ 0,45 об/с = 4,2 об/ мин.
Ответ: тело не удержится на платформе
при частоте вращения большей, чем 4,2
об/мин.
З
адача
3. С какой угловой скоростью
должна вращаться горизонтальная
центрифуга, чтобы космонавт испытывал
8-кратную перегрузку, если радиус
центрифуги r = 5 м?
Решение
Перегрузкой называют число, равное
отношению реакции опоры, действующей
на тело (в данном случае, на космонавта),
к силе тяжести его. Значит, N
= 8 mg.
Рассмотрим силы, действующие на космонавта
в горизонтально-вертикальной системе
координат ХОУ. В вертикальном направлении
сила тяжести mg
уравновешивается силой реакции
горизонтальной опоры R
(рис.4), mg = R.
Сила реакции опоры N
(в данной задаче опорой является
вертикальная стенка центрифуги)
направлена горизонтально к центру
вращения. Значит, в направлении оси Х
единственная сила реакции опоры N,
перпендикулярная скорости движения,
сообщает космонавту нормальное ускорение:
N = man
= m2r.
8 mg = m 2r,
отсюда
=
;
=
4 с-1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
- Подробности
- Обновлено 09.08.2018 23:11
- Просмотров: 848
«Физика — 10 класс»
При решении задач на эту тему следует иметь в виду, что моменты силы, инерции и импульса зависят от выбора оси вращения. Кроме этого, нужно обращать внимание на то, что моменты импульса всех тел записываются относительно одной и той же системы отсчёта.
Задача 1.
На блок радиусом r и массой m1 намотана нить, к концу которой привязан груз массой m2 (рис. 6.12).
Груз отпускают, и он движется вниз, раскручивая нить. Определите ускорение груза. Массой нити можно пренебречь.
Р е ш е н и е.
Обозначим на рисунке силы, действующие на блок и груз.
На блок действуют сила тяжести m1


На груз действуют сила тяжести m2

Согласно второму закону Ньютона в проекции на ось Y для груза запишем:
m2a = m2g — T’. (1)
Согласно основному закону динамики вращательного движения для блока запишем:
Iε = Tr. (2)
Момент инерции блока 
Так как по условию задачи нить невесома, то Т = Т’.
Преобразуем уравнение (2): 

Подставив это выражение в уравнение (1), получим 
Окончательно 
Задача 2.
Скамья Жуковского радиусом 1 м со стоящим в центре человеком вращается, делая 2 об/с. Человек переходит на край скамьи. Определите изменение угловой скорости вращения скамьи. Масса человека 50 кг, момент инерции скамьи 30 кг • м2.
Р е ш е н и е.
Так как внешние силы — сила тяжести и сила реакции опоры, направленные параллельно оси вращения, не могут изменить момент импульса системы тел «скамья—человек», то согласно закону сохранения импульса
I1ω1 = I2ω2. (1)
Когда человек находится в центре скамьи, то момент инерции системы равен только моменту инерции скамьи: I1 = Iск.
После того как человек перешёл на край скамьи, момент инерции системы стал равен I2 = Iск + mr2.
Угловая скорость связана с числом оборотов в секунду соотношением ω1 = 2πn.
Подставив найденные выражения в уравнение (1), получим Iск2πn = (Iск + mr2)ω2. Тогда 
Изменение угловой скорости 
Задача 3.
На наклонную плоскость вкатывается колесо, двигавшееся по горизонтальной поверхности со скоростью 4 м/с. Вся масса колеса сосредоточена в ободе. Определите максимальную высоту, на которую поднимется колесо. Работой силы трения можно пренебречь.
Р е ш е н и е.
Выберем нулевой уровень отсчёта потенциальной энергии так, как показано на рисунке 6.13. Учтём, что момент инерции колеса-обруча I = mR2, а угловая скорость вращения ω = υ/R. Механическая энергия колеса на горизонтальной поверхности равна сумме кинетических энергий поступательного и вращательного движений колеса:
На максимальной высоте механическая энергия равна потенциальной энергии Е2 = mgh. Согласно закону сохранения механической энергии получим Е1 = Е2, или mυ2 = mgh, откуда h = υ2/g = 1,6 м.
Задача 4.
Сплошной цилиндр раскрутили до угловой скорости ω и положили на пол к стенке. Коэффициент трения между стенкой, полом и цилиндром μ, радиус цилиндра R. Определите, сколько оборотов сделает цилиндр до остановки.

Р е ш е н и е.
Решаем задачу, используя теорему об изменении кинетической энергии. При этом учтём, что ось вращения цилиндра неподвижна, момент инерции цилиндра относительно этой оси равен 

Изменение кинетической энергии равно алгебраической сумме работ сил, действующих на него:
На цилиндр (рис. 6.14) действуют силы тяжести m




Так как перемещается относительно стенок угла только точка приложения сил трения, то работу совершают только силы трения. В связи с этим справедливо уравнение
Работы сил трения равны Aтp1 = -Fтp12πRn; Aтp2 = -Fтp12πRn, где n — число полных оборотов цилиндра до остановки, а силы трения определяются силами реакции опоры стенок на цилиндр: Fтp1 = μN1; Fтp2 = μN2.
Найдём силы реакции опоры.
По условию задачи цилиндр только вращается, его центр тяжести не движется, следовательно, векторная сумма сил, действующих на него, равна нулю:
m




В проекциях на оси ОХ и OY имеем
Fтp1 — N2 = 0; (2)
N1 + Fтp2 — mg = 0. (3)
Подставив в уравнения (2) и (3) выражения для сил трения, получим
μN1 — N2 = 0; (4)
N1 + μN2 — mg = 0. (5)
Решая систему уравнений (4) и (5), найдём силы реакции опоры:
Тогда число оборотов до остановки цилиндра
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Импульс материальной точки —
Закон сохранения импульса —
Реактивное движение. Успехи в освоении космоса —
Примеры решения задач по теме «Закон сохранения импульса» —
Механическая работа и мощность силы —
Энергия. Кинетическая энергия —
Примеры решения задач по теме «Кинетическая энергия и её изменение» —
Работа силы тяжести. Консервативные силы —
Работа силы упругости. Консервативные силы —
Потенциальная энергия —
Закон сохранения энергии в механике —
Работа силы тяготения. Потенциальная энергия в поле тяготения —
Примеры решения задач по теме «Закон сохранения механической энергии» —
Основное уравнение динамики вращательного движения —
Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси —
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
Динамика вращательного движения

4.1
Средняя оценка: 4.1
Всего получено оценок: 118.
4.1
Средняя оценка: 4.1
Всего получено оценок: 118.
Динамика – это раздел механики, изучающий причины механических движений тел. Любое движение может быть представлено суммой прямолинейных и вращательных движений, поэтому законы динамики изучаются в первую очередь для них. Рассмотрим динамику вращательного движения твердого тела.
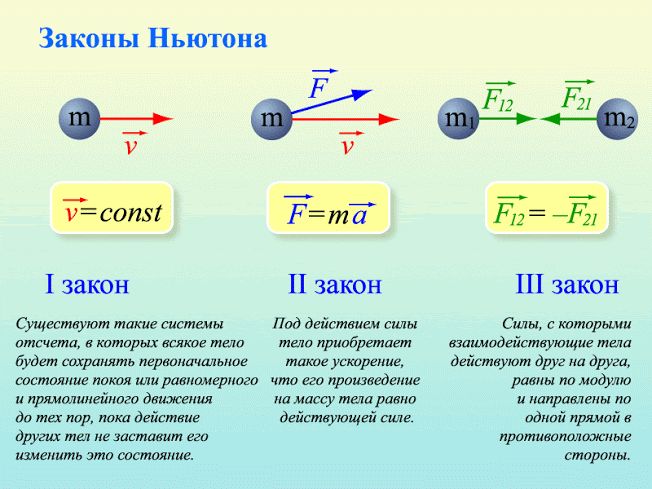
Три закона динамики
Законы динамики были четко сформулированы И. Ньютоном в труде «Математические начала натуральной философии» в 1687 г. В этом трактате были систематизированы и обобщены результаты исследований многих ученых, изучавших причины движений до Ньютона. Поэтому эти законы носят его имя.
Первый Закон Ньютона устанавливает неизменность и вечность движения. Согласно ему, тело сохраняет покой или движется равномерно и прямолинейно, пока на него не подействуют силы, со стороны других тел.
Второй Закон Ньютона связывает меру взаимодействия тел и меру инертности тела с результатом взаимодействия. Мерой взаимодействия является сила, мерой инертности – масса. Результат взаимодействия выражается в изменении скорости – ускорении. Ускорение, получаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально его массе.
Третий Закон Ньютона устанавливает невозможность одностороннего приложения силы. Фактически, это закон сохранения, утверждающий, что если на тело действует сила со стороны другого тела, то на другое тело действует точно такая же сила со стороны первого. Силы эти не компенсируют друг друга потому, что приложены к разным телам.
Совершая прыжок, вы сообщаете некоторую силу Земле. В результате чего Земля, согласно Третьему Закону Ньютона, также сообщает вам точно такую же силу. И вы, и Земля – приобретаете некоторые ускорения, и начинаете двигаться в разных направлениях. Поскольку масса Земли примерно в $10^{23}$ раз больше вашей массы, скорость приобретенная Землей в результате вашего прыжка, будет во столько же раз меньше.
Динамика вращения
Вращение тела заключается в том, что при движении траектории его точек являются окружностями с центрами, лежащими на одной прямой, называемой осью вращения.
То есть, путь, проходимый различными точками различен и пропорционален радиусу поворота. Поэтому динамические характеристики вращательного движения используют не величину пройденного пути, а величину угла поворота и радиус поворота. И мера взаимодействия, и мера инертности включает в себя этот радиус (расстояние от точки приложения до центра вращения).
Мера взаимодействия для вращения называется момент силы, и равна произведению величины силы на ее плечо (если сила направлена перпендикулярно радиусу, плечо равно радиусу):
$$M=F l_F$$
Мера инертности называется момент инерции, и для матеральной точки он равен произведению массы на квадрат радиуса вращения:
$$J=m R^2$$
Перемещение, скорость и сила для вращательного движения становятся угловыми – угол поворота $alpha$ радиан, угловая скорость $omega$ радиан в секунду, угловое ускорение $varepsilon$ радиан в секунду за секунду.
Таким образом, законы динамики вращения материальной точки выглядят следующим образом:
- Первый закон: $omega = const, при M=0$;
- Второй закон: $varepsilon = {M over J}$;
- Третий закон: $M_{12}=- M_{21}$
Все три закона имеют вид, аналогичный законам для поступательного движения.
Что мы узнали?
Все три закона динамики для вращательного движения имеют вид, аналогичный законам динамики для прямолинейного движения. Но, все динамические параметры для вращения являются угловыми и включают в себя радиус вращения.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.1
Средняя оценка: 4.1
Всего получено оценок: 118.
А какая ваша оценка?
Динамика – раздел механики, которому уделяется больше всего учебных часов. Уделите 5 минут на то, чтобы прочесть нашу статью и чуть больше разобраться в решении задач по динамике.
Наш телеграм – место, где мы скрупулезно отбираем, фильтруем и выкладываем все, что может быть полезно современному студенту. Под лежачий камень вода не течет, подписывайтесь!
Для начала, вопрос. Какой алгоритм решения задач по динамике? Собственно, алгоритм такой же, как и для любой задачи по физике. Мы уже писали об этом в памятке по решению задач. Не забываем держать под рукой полезные формулы, повторяем вопросы из теории, и можно приступать к практическим заданиям.
Вопросы по теме «Динамика»
Вопрос 1. Что изучает динамика?
Ответ. Динамика – раздел механики, который изучает взаимодействия между телами.
Вопрос 2. Каково основное уравнение динамики?
Ответ. Основное уравнение динамики устанавливает связь между приложенной к телу силой, его массой и ускорением тела.
Вопрос 3. Что такое вес тела и зависит ли он от местоположения тела на поверхности Земли?
Ответ. Вес – это сила, с которой тело действует на опору. Вес зависит от ускорения свободного падения, а значит и от географического местоположения на поверхности планеты. А вот масса тела всегда неизменна (за исключением движения со скоростью, близкой к скорости света).
Вопрос 4. В каких системах отсчета справедлив второй закон Ньютона?
Ответ. Второй закон Ньютона справедлив в инерциальных системах отсчета.
Вопрос 5. Сила тяжести на земле является отдельным проявлением одного из фундаментальных физических взаимодействий. Что это за взаимодействие.
Ответ. Конечно, это гравитационное взаимодействие. А сила тяжести – проявление силы всемирного тяготения.
Задачи по динамике поступательного движения с решениями
Задача №1. Определение времени движения
Условие
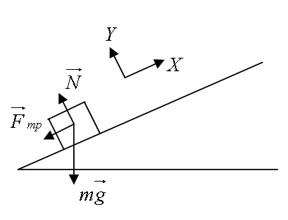
Тело находится у основания наклонной плоскости с углом при основании α = 30°. Коэффициент трения о поверхность равен µ = 0,6 и масса тела m = 2 кг. Сколько времени тело будет двигаться по наклонной плоскости, если его толкнуть вверх вдоль плоскости со скоростью υ0 = 20 м/с? (g = 9,8 м/с2).
Решение
Для начала, выполним рисунок:
Тело будет двигаться равнозамедленно с ускорением, равным –a в течение времени t, при этом
Откуда
Определим ускорение a. Запишем второй закон Ньютона в векторной форме и в проекциях на оси Х и Y соответственно:
Сила трения определяется выражением
Тогда,
Следовательно, время, в течение которого тело будет двигаться по наклонной плоскости:
Подставим числовые значения:
Ответ: 2 секунды.
Задача №2. Применение второго закона Ньютона
Условие
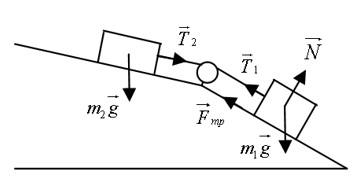
В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30, а верхний брусок – вдоль наклонной плоскости, составляющий с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и наклонной плоскостью равен µ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси, найдите, при каких значениях угла β нить будет растянута.
Решение
Так как тангенс угла α больше, чем коэффициент трения между бруском и поверхностью, нижний брусок будет скользить по наклонной плоскости даже при ненатянутой нити. Следовательно, в том случае, когда оба бруска движутся и нить натянута, модули ускорений брусков будут одинаковыми. Обозначим массу нижнего бруска как m1, массу верхнего бруска как m2, а силу натяжения соединяющей их нити как T. Тогда для каждого из брусков можно записать второй закон Ньютона в проекции на направление его движения:
где Fтр – действующая на нижний брусок сила трения скольжения, N – действующая на него сила нормальной реакции опоры.
Так как нижний брусок не движется в направлении, перпендикулярном плоскости, то из второго закона Ньютона следует:
Решая совместно полученные уравнения, найдем:
Для того, чтобы нить была натянута, должно выполняться неравенство:
С учетом полученного выражения для модуля ускорения a, это неравенство можно переписать в следующем виде:
Подставим числовые значения и найдем искомый угол:
Ответ: 19°.
Задача №3. Нахождение силы
Условие
Два одинаковых груза массой M = 100 г каждый подвешены на концах невесомой и нерастяжимой нити, перекинутой через невесомый блок с неподвижной осью. На один из них кладут перегрузок массой m = 20 г, после чего система приходит в движение. Найдите модуль силы F, действующей на ось блока во время движения грузов. Трением пренебречь.
Решение
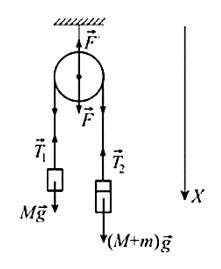
На основании второго закона Ньютона уравнение движение для обоих грузов с учетом перегрузки на одном из них в проекции на вертикальную ось, направленную вниз, выглядит следующим образом:
где a1 и a2 – проекции ускорений грузов M и (M+m) на вертикальную ось;
T1 и T2 – проекции сил натяжения нити на вертикальную ось. Так как нить не растяжима (по условию задачи), то
Из-за невесомости блока и нити и отсутствия трения, справедливо равенство:
В силу третьего закона Ньютона:
где F с индексом штрих – сила, действующая на блок со стороны его оси. Из первых двух уравнений получим:
Подставим числовые значения:
Ответ: 2,14 Ньютона.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задачи по динамике вращательного движения с решениями
Задача №4. Нахождение числа оборотов маховика
Условие
Маховик радиусом R=0,5 м и массой 10 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно Т=98 Н. Какое число оборотов в секунду будет делать маховик через Δt=10 с после начала движения. Маховик считать однородным диском.
Решение
Основное уравнение динамики вращательного движения:
где J — момент инерции маховика. Принимая маховик за однородный диск, можно записать:
Момент силы натяжения ремня:
Угловое ускорение маховика:
Угловая скорость маховика:
Решая уравнения, записанные выше, получим ответ:
Ответ: 62,4 оборота в секунду
Задача №5. Нахождение углового ускорения
Условие
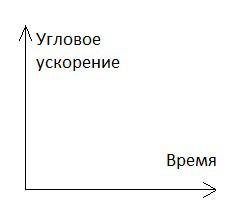
Момент силы, приложенный к вращающемуся телу изменяется по закону M=M0-αt. Момент остаётся постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке. Найти выражение для углового ускорения.
Решение
Согласно основному закону динамики вращательного движения:
Это уравнение прямой с отрицательным углом наклона, что соответствует рисунку.
Нужна помощь в решении задач по динамике, теоретической механике, деталям машин, химии, etc? Обращайтесь за ней в профессиональный студенческий сервис.
В этой главе…
- Переходим от динамики поступательного движения к динамике вращательного движения
- Вычисляем момент инерции
- Определяем работу вращательного движения
- Находим связь между работой и изменением кинетической энергии
- Изучаем закон сохранения момента импульса
Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.
Содержание
- Применяем второй закон Ньютона для вращательного движения
- Преобразуем тангенциальное ускорение в угловое
- Пример: вычисляем момент силы для обеспечения углового ускорения
- Вычисляем момент инерции протяженного объекта
- Пример: замедление вращения компакт-диска
- Еще один пример: поднимаем груз
- Вычисляем энергию и работу при вращательном движении
- Работа при вращательном движении
- Изучаем кинетическую энергию вращательного движения
- Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости
- Не можем остановиться: момент импульса
- Сохраняем момент импульса
- Пример закона сохранения момента импульса: вычисляем скорость спутника
Применяем второй закон Ньютона для вращательного движения
Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:
где ( mathbf{a} ) — это вектор ускорения, ( mathbf{F} ) — вектор силы, а ( m ) — масса объекта. Подробнее о векторах рассказывается в главе 4. Соблюдается ли этот закон для вращательного движения?
В главе 10 мы уже познакомились характеристиками вращательного движения, которые являются эквивалентами (аналогами) некоторых характеристик поступательного движения. А как будет выглядеть аналог у второго закона Ньютона? Похоже, что во вращательном движении роль ускорения ( mathbf{a} ) играет угловое ускорение ( alpha ), а роль силы ( mathbf{F} ) — момент силы ( mathbf{M} )? Не вдаваясь в подробности, скажем лишь, что это действительно так. А что же с массой? Оказывается, что для этого используется новое понятие — момент инерции ( l ). Известно, что второй закон Ньютона для вращательного движения принимает следующий вид:
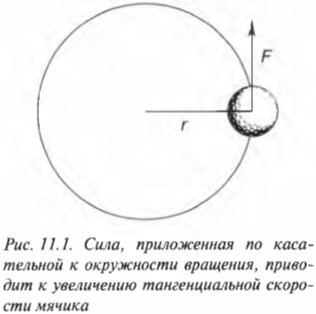
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)
Поскольку:
то, умножая обе части этой формулы на радиус окружности ( r ), получим:
Поскольку ( rmathbf{F}=mathbf{M} ) то
или
Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ( r ). Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)
Преобразуем тангенциальное ускорение в угловое
Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ( alpha ) и тангенциальным ускорением ( mathbf{a} ). Как нам уже известно из главы 10, они связаны следующим соотношением:
Подставляя это выражение в приведенную выше формулу
получим:
Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ( l=mr^2 ), называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.
Пример: вычисляем момент силы для обеспечения углового ускорения
Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:
где ( mathbf{sum!F} ) обозначает векторную сумму всех сил, действующих на объект.
Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:
где ( mathbf{sum! M} ) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м2.
Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула ( mathbf{sum! M}=lalpha ), т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.
Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ( 2pi с^{-2} )? Подставляя значения в уже известную нам формулу
получим:
Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.
Вычисляем момент инерции протяженного объекта
Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ( r ). В таком случае момент инерции имеет знакомый вид:
где ( r ) — это расстояние, на котором сосредоточена вся масса мячика ( m ).
Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:
Например, момент инерции ( l ) системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ( m ) на расстояниях ( r_1 ) и ( r_2 ) равен сумме их отдельных моментов инерции ( l_1=mr_1^2 ) и ( l_2=mr_2^2 ):
А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.
Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.
Пример: замедление вращения компакт-диска
Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:
Момент инерции диска с радиусом ( r ), вращающегося относительно своего центра в плоскости диска, выражается формулой:
Подставляя значения, получим:
Теперь нужно определить угловое ускорение, которое определяется следующей формулой:
Изменение угловой скорости ( Deltaomega ) произошло за промежуток времени:
В данном примере изменение угловой скорости:
где ( omega_1 ) — конечная, а ( omega_0 ) — начальная угловая скорость компакт-диска.
Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ( 2pi ) радиан:
Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит ( 2pi ) радиан:
Подставляя значения в формулу углового ускорения, получим:
Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:
Итак, средний момент равен 10-4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:
Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.
Еще один пример: поднимаем груз
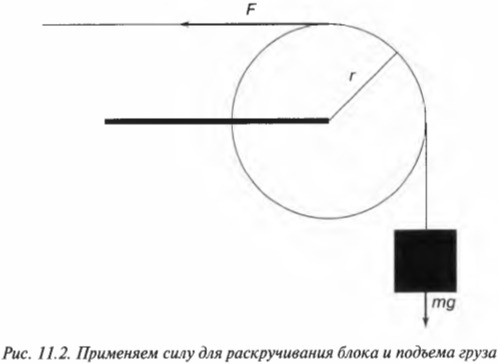
Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.
В данном примере нужно вычислить сумму всех моментов сил ( mathbf{sum! M} ), которые действуют на веревку:
В данном примере на веревку действует два момента сил: один ( M_1 ) со стороны груза весом ( mg ), а другой ( M_2 ) — со стороны горизонтальной силы ( F ):
Отсюда получаем формулу для углового ускорения:
Эти моменты ( M_1 ) и ( M_2 ) имеют одинаковое плечо, равное радиусу блока ( r ), поэтому:
Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:
Подставляя выражения для ( l ), ( M_1 ) и ( M_2 ) в формулу для углового ускорения, получим:
Подставляя значения, получим:
Вычисляем энергию и работу при вращательном движении
При изучении поступательного движения в главе 8 мы познакомились с понятием работа. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.
Работа при вращательном движении
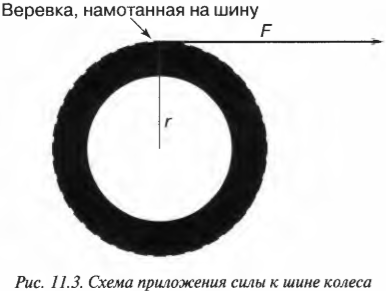
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.
Пусть шина имеет радиус ( r ) и для ее вращения используется сила ( F ), как показано на рис. 11.3.
Чему равна работа этой силы? Применим знакомую нам формулу:
где ( s ) — это перемещение веревки под действием этой силы. В данном примере перемещение ( s ) равно произведению радиуса ( r ) на угол поворота шины ( theta ):
Подставляя это выражение в формулу работы, получим:
Поскольку момент ( M ), создаваемой этой силой, равен:
то получаем для работы:
Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.
Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.
Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м. Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:
Полный оборот соответствует повороту на угол ( 2pi ). Подставляя значения в формулу, получим:
Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.
Изучаем кинетическую энергию вращательного движения
Из главы 8 нам уже известно, что объект массы ( m ), движущийся поступательно со скоростью ( v ), обладает кинетической энергией:
А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.
При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.
Как известно (см. главу 10), тангенциальная скорость ( v ) и угловая скорость ( omega ) связаны соотношением:
где ( r ) — это радиус окружности вращения.
Подставляя это соотношение в предыдущую формулу, получим:
Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:
Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:
Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:
Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:
Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду. Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.
Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости
Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.
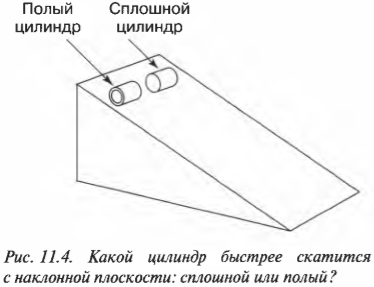
На рис. 11.4 показан случай, когда с наклонной плоскости высотой ( h ) скатываются сплошной и полый цилиндры с одинаковой массой ( m ). Какой цилиндр достигнет нижнего конца наклонной плоскости?
Иначе говоря: какой цилиндр будет обладать большей скоростью в конце наклонной плоскости? Поскольку действующие на цилиндры силы постоянны, то постоянны и их ускорения, а значит, большая скорость в конце пути означает меньшее время его прохождения. В случае только поступательного движения цилиндра и при отсутствии трения уменьшение потенциальной энергии ( mgh ) преобразуется в увеличение кинетической энергии только поступательного движения ( {}^1!/!_2mv^2 ), т.е.:
Однако в данном примере эта формула не годится, потому что цилиндры скатываются без проскальзывания. Это значит, что часть уменьшения потенциальной энергии будет преобразовываться в увеличение кинетической энергии поступательного движения ( {}^1!/!_2mv^2 ), а часть — в кинетическую энергию вращательного движения ( {}^1!/!_2Iomega ^2 ). Тогда предыдущее равенство принимает следующий вид:
Сделаем подстановку ( omega=v/r ) и получим:
Путем несложных алгебраических преобразований получим:
откуда легко получить выражение для скорости цилиндра:
Для обоих цилиндров все параметры одинаковы, кроме момента инерции ( I ). Как это повлияет на скорость цилиндров? Согласно данным из табл. 11.1, полый цилиндр имеет момент инерции ( mr^2 ), а сплошной — ( {}^1!/!_2mr^2 ).
Итак, для полого цилиндра получим:
а для сплошного цилиндра:
А их отношение равно:
Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.
Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.
Не можем остановиться: момент импульса
Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.
В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:
где ( m ) — это масса, a ( v ) — скорость материальной точки.
По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):
где ( l ) — это момент инерции, а ( omega ) — угловая скорость материальной точки.
Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.
Момент импульса в системе СИ измеряется в кг·м2·с-1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.
Сохраняем момент импульса
Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста ( omega_0 ) и его моменты инерции в позе с разведенными руками ( I_0 ) и в позе с сомкнутыми руками ( I_1 ), легко найти конечную угловую скорость ( omega_1 ) по формуле:
Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.
Пример закона сохранения момента импульса: вычисляем скорость спутника
Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·106 м от центра Плутона и имеет скорость 9·103 м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·107 м от центра Плутона?
Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.
Итак, рассмотрим формулу закона сохранения момента импульса:
где ( I_{бл} ) — это момент инерции спутника в самой близкой точке, ( I_{дал} ) — это момент инерции спутника в самой далекой точке, ( omega_{бл} ) — угловая скорость спутника в самой близкой точке, а ( omega_{дал} ) — угловая скорость спутника в самой далекой точке.
Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:
и
где ( r_{бл} ) — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а ( r_{дал} ) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.
Кроме того:
и
Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса
получим:
Отсюда путем несложных алгебраических преобразований, получим:
Подставляя значения, получим:
Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.
Глава 11. Раскручиваем объекты: момент инерции
3 (59.26%) 27 votes