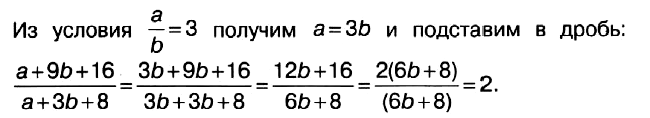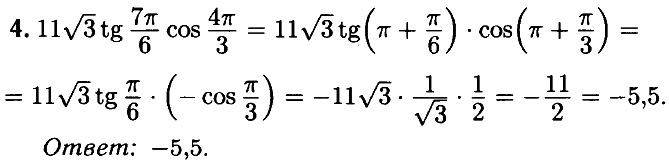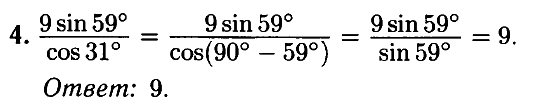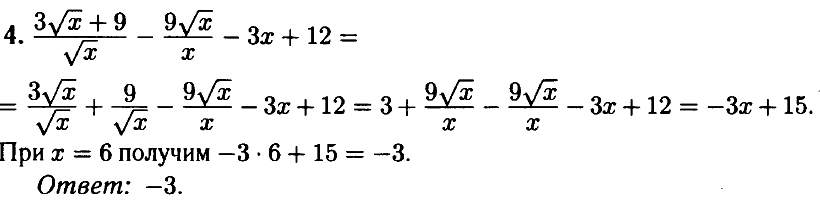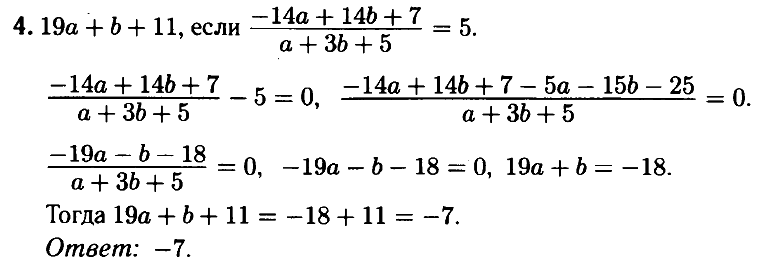Егэ дроби профиль - Помощь в подготовке к экзаменам и поступлению

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения $frac{2,88cdot 44,5}{0,288cdot 4,45}.$

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

$frac{2,88cdot 44,5}{0,288cdot 4,45}=frac{2,88cdot 44,5}{2,88cdot 0,445}=frac{44,5}{0,445}=100.$

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения $7frac{9}{13}:frac{5}{13}.$

$7frac{9}{13}:frac{5}{13}=frac{100}{13}cdot frac{13}{5}=20.$

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

$left ( sqrt{a} right )^{2}=a;;sqrt{a}geq 0;;ageq 0$ .

3. Вычислите .

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:

Упростим множители:

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7} right )^{2}+2sqrt{3}cdot sqrt{7}+left ( sqrt{3} right )^{2}}=$

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7}+sqrt{3}right )^{2}}=2left ( sqrt{7}-sqrt{3} right )left ( sqrt{7}+sqrt{3} right )=$

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

$a^{m}cdot a^{n}=a^{m+n}.$

$frac{a^{m}}{a^{n}}=a^{m-n}.$

$left ( a^{m} right )^{n}=left ( a^{n} right )^{m}=a^{mn}.$

$a^{n}b^{n}=left ( ab right )^{n}.$

$frac{a^{n}}{b^{n}}=left ( frac{a}{b} right )^{n}.$

5. Найдите значение выражения: $frac{a^{8,9}}{a^{4,9}}$ при a=4.

$frac{a^{8,9}}{a^{4,9}}=a^{8,9-4,9}=a^{4}=4^{4}=256.$

Применили формулу частного степеней $frac{a^{m}}{a^{n}}=a^{m-n}.$

Ответ: 256.

6. Вычислите $left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}.$

$left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}=left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{2^{frac{1}{12}}} right )^{2}=left ( 2^{frac{1}{3}+frac{1}{4}-frac{1}{12}} right )^{2}=left ( 2^{frac{4}{12}+frac{3}{12}-frac{1}{12}} right )^{2}=$

$=left (2^{frac{1}{2}} right )^{2}=2.$

Ответ: 2.

7. Вычислите $frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}$ , если .

Спокойно, не пугаемся. И конечно, не спешим подставлять значение m=3,7. Сначала упростим выражение.

$frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}=frac{5m^{30}+13m^{30}}{4m^{30}}=frac{18m^{30}}{4m^{30}}=4,5.$

Ответ: 4,5.

8. Вычислите $0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}.$

$0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}=left ( frac{3}{4} right )^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot left ( 3cdot 4 right )^{frac{7}{8}}=frac{3^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 3^{frac{7}{8}}cdot 4^{frac{7}{8}}}{4^{frac{1}{8}}}=3cdot 4=12.$

Применили формулу для произведения степеней: $a^{m}cdot a^{n}=a^{m+n}.$

Ответ: 12.

9. Вычислите $frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}.$

$frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}=frac{3^{frac{1}{28}}cdot 3cdot 3^{frac{1}{21}}}{3^{frac{1}{12}}}=3^{frac{1}{28}+1+frac{1}{21}-frac{1}{12}}=3^{frac{3}{84}+1+frac{4}{84}-frac{7}{84}}=3.$

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

$log _{a}b=cLeftrightarrow a^{c}=b$ .

При этом > 0, > 0, aneq 1.

Основные логарифмические формулы:

Основное логарифмическое тождество: $boldsymbol{log _{a}a^{c}=c, ; a^{log _{a}b}=b}.$

Логарифм произведения равен сумме логарифмов: $boldsymbol{log _{a}left ( bc right )=log _{a}b+log _{a}c}.$

Логарифм частного равен разности логарифмов: $boldsymbol{log _{a}left ( frac{b}{c} right )=log _{a}b-log _{a}c}.$

Формула для логарифма степени: $boldsymbol{log _{a}b^{m}=mlog_{a}b}.$

Формула перехода к новому основанию: $boldsymbol{log _{a}b=frac{1}{log _{b}a},; log _{a}b=frac{log _{c}b}{log _{c}a}}.$

10. Вычислите: $log _{5}7cdot log _{7}25$ .

$log _{5}7cdot log _{7}25=log _{5}7cdot log _{7}5^{2}=2log _{5}7cdot log _{7}5=2.$

Снова формула перехода к другому основанию.

$log _{a}b=frac{1}{log _{b}a}$ , поэтому
$log _{a}bcdot log _{b};a=1.$

11. Найдите $log _{a}frac{a^{6}}{b^{4}}$ , если $log _{a}b=-2$ .

$log _{a}frac{a^{6}}{b^{4}}=log _{a}a^{6}-log _{a}b^{6}=6-4log _{a}b=6-4cdot left ( -2 right )=6+8=14.$

12. Найдите значение выражения $frac{log _{2}80}{3+log _{2}10}$ .

$frac{log _{2}80}{3+log _{2}10}=frac{log _{2}left (8cdot 10 right )}{3+log _{2}10}=frac{log _{2}8+log _{2}10}{3+log _{2}10}=frac{3+log _{2}10}{3+log _{2}10}=1.$

13. Найдите значение выражения $frac{log _{9}sqrt[10]{8}}{log _{9}8}$ .

$frac{log _{9}sqrt[10]{8}}{log _{9}8}=frac{log _{9}8^{frac{1}{10}}}{log _{9}8}=frac{1}{10}=0,1$ .

14. Найдите значение выражения $left ( 1-log _{3}18 right )left ( log _{6}54 -1right )$ .

$left ( 1-log _{3}18 right )left ( log _{6}54 -1right )=-left ( log _{3}18-log _{3}3 right )cdot left ( log _{6}54-log _{6}6 right )=-log _{3}6cdot log _{6}9=-2log _{3}6cdot log _{6}3=-2.$

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите: $44sqrt{3}tgleft ( -480^{circ} right ).$

$44sqrt{3}tgleft ( -480^{circ} right )=44sqrt{3}cdot frac{sin left ( -480^{circ} right )}{cos left ( -480^{circ} right )}=-44sqrt{3}cdot frac{sin 480^{circ}}{cos 480^{circ}}=-44sqrt{3}cdot frac{sin 120^{circ}}{cos 120^{circ}}=-44sqrt{3}cdot frac{sqrt{3}}{2}:left ( -frac{1}{2} right )=132.$

16. Найдите , если $sin alpha =-frac{2sqrt{2}}{3}$ и $alpha in left ( frac{3pi }{2};;2pi right )$ .

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{2sqrt{2}}{3} right )^{2}=1-frac{8}{9}=frac{1}{9}.$

Т.к. $alpha in left ( frac{3pi }{2};;2pi right )$ , то $cos alpha =frac{1}{3}.$
$3cos alpha =3cdot frac{1}{3}=1.$

17. Найдите , если $sin alpha =-frac{1}{sqrt{5}}$ и

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{1}{sqrt{5}} right )^{2}=1-frac{1}{5}=frac{4}{5}.$

Т.к. , то
$cos alpha =frac{2}{sqrt{5}}.$

$tgalpha =frac{sin alpha }{cos alpha }=-frac{1}{sqrt{5}}:frac{2}{sqrt{5}}=-2.$

18. Найдите значение выражения: $frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}.$

$frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{13cdot 2sin 76^{circ}cdot cos 76^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{26sin 76^{circ}}{cos 14^{circ}}=frac{26sin left ( 90^{circ}-14^{circ} right )}{cos 14^{circ}}=$

$=frac{26cos 14^{circ}}{cos 14^{circ}}=26.$

Применили формулу приведения.

19. Упростите выражение: $frac{3cos(pi - beta)+sin(frac{pi}{2}+beta)}{cos(beta+3pi)}.$

$frac{3cos left ( pi -beta right )+sin left ( frac{pi }{2}+beta right )}{cos left ( beta +3pi right )}=frac{-3cos beta +cos beta }{-cos beta }=frac{-2cos beta }{-cos beta }=2.$

Применили формулу приведения.

20. Найдите , если .

$2cos 2alpha =2left ( 1-2sin ^{2}alpha right )=2-4sin ^{2}alpha =2-4cdot left ( -0,7 right )^{2}=0,04.$

21. Вычислите $frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }$ , если

$frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }=frac{1-cos ^{2}alpha +sin ^{2}alpha +2sin alpha cos alpha }{1+cos ^{2}alpha -sin ^{2}alpha +2sin alpha cos alpha }=$

$=frac{2sin ^{2}alpha +2sin alpha cos alpha }{2cos ^{2}alpha +2sin alpha cos alpha }=frac{sin alpha left ( sin alpha +cos alpha right )}{cos alpha left ( cos alpha +sin alpha right )}=frac{sin alpha }{cos alpha }=tgalpha =0,3.$

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти $sqrt{a^{2}}$ .

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}$ при .

Запомним: $sqrt{a^{2}}=left | a right |.$

$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}=left | a-2 right |+left | a-4 right |$ .

Если , то и .

При этом и .

При получаем: .

Ответ: 2.

23. Найдите значение выражения

$x+sqrt{x^{2}-24x+144}$ при xleq 12 .

При xleq 12 получим:

$x+sqrt{x^{2}-24x+144}=x+sqrt{left ( x-12 right )^{2}}=x+left | x-12 right |=x+12-x=12.$

Ответ: 12.

24. Найдите $frac{gleft ( 5-x right )}{gleft ( 5+x right )}$ , если , при .

Что такое ? Это функция, каждому числу ставящая в соответствие число . Например, ;

Тогда:

Заметим, что .

Значит, при
$frac{gleft ( 5-x right )}{gleft ( 5+x right )}=1$ .

25. Найдите $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ , если $pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ , при .

$pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ — функция, каждому числу b ставящая в соответствии число
$left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ .

Тогда при bneq 0.

$pleft ( frac{1}{b} right )=left ( frac{1}{b}-9b right )left ( -frac{9}{b} +bright )=left ( b-frac{9}{b} right )left (-9b +frac{1}{b} right )=pleft ( b right )$ , и значение выражения $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ равно 1.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Профильный уровень ЕГЭ по математике, в отличие от базового, более сложный и его должны сдавать выпускники, планирующие поступать в вузы на технические, инженерные, экономические специальности.

Задания в экзаменационной работе обычно выстроены от простого к сложному и первое задание это, как правило, самое легкое, как бы разминочное. Так и Задание 1 ЕГЭ по профильной математике – это задание базового уровня на знания элементарной математики, представляющее собой простейшую задачу на несложные арифметические действия.

• Вид задания — текстовая задача.

• Тип — с кратким ответом.

• Сложность — базовая.

• Максимальное количество получаемых баллов — 1.

• Период выполнения — 120 секунд.

Необходимые знания

1-е Задание по профильной математике — это текстовая задача базового уровня сложности. Ответ должен быть дан в краткой форме в виде целого числа или конечной десятичной дроби, оценивается в 1 балл.

Для выполнения задания необходимо знать:

арифметические действия;
простые и десятичные дроби и действия с ними;
проценты;
пропорции;
перевод одних единиц измерения в другие;
построение математической модели задачи;
интерпретация результата решения задачи;
учет реальных ограничений в интерпретации результата.

5 типов заданий

Наиболее часто встречаются задания пяти типов:

задачи, связанные с жизненными ситуациями (определение времени, веса, стоимости и т.д.);
на вычисление процентов;
на округление результата в большую или меньшую сторону;
на пропорции;
различные комбинации четырех предыдущих вариантов.

Опыт подготовки к ЕГЭ прошлых лет показал, что у учащихся часто возникают трудности с решением задач на перевод из одних единиц измерения в другие (часы в сек., км в см, кг в гр. и т. п.). Следует обратить внимание на то, что часы и минуты считаются не в десятичной системе, ведь в часе – 60 минут, а в минуте – 60 секунд. Наиболее эффективным способом подготовки к профильной математике являются курсы «Уникум» РУДН по математике. Здесь вы получите разбор всех типов заданий, теорию и практику, пробные варианты ЕГЭ на протяжении всей подготовки. Преподаватель курсов, в том числе, сделает разбор 1-го задания ЕГЭ по математике профильного уровня.

Примеры

Пример 1

Автомобиль проехал 80 миль, в 1 миле 1609,34 метров. Сколько километров проехал автомобиль? Ответ округлить до целого значения.

Решение:

Определяем сколько км в 1 миле: 1 миля=1609,34 м:1000 м=1,60934 км

Сколько км проехал автомобиль: 80 миль*1,60934 км=128,7472 км

Округляем до целого значения по правилам математического округления: 128,7472 км

Ответ: 129

Пример 2

В магазине по акции продаются шоколадки. Обычная цена 1 шоколадки 35 рублей. По акции 3 шоколадки продаются по цене 2-х. Какое максимальное количество шоколадок может по акции приобрести покупатель, если он готов потратить на них не более 300 рублей?

Решение:

Определяем стоимость 3 шоколадок по акции: 2 шок.*35 руб.+1 шок.*0 руб.=70 руб.

При продаже по акции 3 шоколадки являются одной товарной позицией. Определим, сколько таких товарных позиций можно купить на 300 руб.: 300 руб.:70 руб.=4,29

Округляем до целого, т.к. шоколадки продаются только по 3 шт.: 4*3 шок.= 12 шок.

Ответ: 12

Пример 3

Площадь стен в ванной составляет 23,8 м2. Сколько понадобится пластиковых панелей для отделки стен, если панель имеет размер 40 Х 120 см.

Решение:

Переведем размеры 1 панели из см в м: 40 см:100=0,4 м и 120 см:100=1,2 м

Площадь 1 панели в м2: 0,4м*1,2м=0,48 м2

В 23,8 м2 уложится: 23,8 м2:0,48 м2=49,58 шт.

Поскольку панели продаются целиком, для покрытия всей площади понадобится 50 панелей.

Ответ: 50

Пример 4

Средняя скорость полета самолета составляет 360 км/час. Определить его среднюю скорость в м/сек.

Решение:

Переводим км в метры: 360*1000 м=360 000 м

Часы в минуты: 1 час=60 мин, минуты в секунды: 60 мин=60*60сек= 3600 сек

Определяем скорость: 360 000 м:3600 сек=100 м/сек

Ответ: 100

Пример 5

Поезд отправился из Самары в Москву в 22 часа 10 минут (время московское) и прибыл в Москву в 10 часов 10 минут на следующие сутки. Сколько часов поезд находился в пути?

Решение:

В день отбытия из Самары поезд был в пути: 24 ч-22 ч 10 мин=23 ч 60 мин–22 ч 10 мин=1 ч 50 мин

В день прибытия поезд был в пути: 10 ч 10 мин

Общее время в пути: 1 ч 50 мин+10 ч 10 мин=11 ч 60 мин=12 ч

Ответ: 12

Пример 6

Олег живет в 9-этажном многоподъездном доме. На каждом этаже находится по 4 квартиры. Олег живёт в квартире №81. Укажите номер подъезда, в котором живёт Олег?

Решение:

Количество квартир в одном подъезде: 9 * 4=32

Значит квартиры распределяются по подъездам так:

1-й подъезд – с 1-й по 32-ю

2-й – с 33-й по 64-ю

3-й – с 65-й по 96-ю

Квартира №81 находится в 3-м подъезде

Ответ: 3

В Задании 1 профильной математики как правило встречаются задачи на действия с дробями в том или ином виде.

Действия с дробями

Для того, чтобы получить правильный ответ на 1 задание ЕГЭ по математике, теорию нужно знать в первую очередь. Сложности у сдающих ЕГЭ возникают с дробями и задачами, где представлены дроби. Дробью называется форма представления числа. Сама дробная черта означает деление. Делимое — это числитель дроби, знаменатель — делитель. С дробями можно делать все то, что и с обычными числами: делить, умножать, складывать, вычитать.

Сложение дробей

Сложение дробей с одинаковыми знаменателями.

Пример: сложить дроби

Числители 1-й и 2-й дроби складываются, знаменатель остается неизменным

Сложение дробей с различающимися знаменателями:

Пример: сложить дроби

Сначала дроби нужно привести к общему знаменателю, таким знаменателем является произведение знаменателей 1-й и 2-й дроби, а числитель 1-й дроби умножается на знаменатель 2-й, числитель 2-й дроби на знаменатель 1-й. Затем числители складываются:

Вычитание дробей проводится аналогично сложению. Просто числители не складываются, а вычитаются.

Умножение дробей

Пример: перемножить дроби:

Просто перемножаются числители и знаменатели

Деление дробей

Пример: разделить

Деление заменяем на умножение на дробь обратную дроби, на которую делим

Как видите, задачи из Задания 1 по профильной математике легкие, на знания математики из курса младших и средних классов, что, однако не отменяет необходимость освежить в памяти эти знания и еще раз порешать эти несложные задачи. Особенно полезно решать реальные варианты заданий прошлых лет под контролем опытных преподавателей. А такую возможность и дают подготовительные курсы «Уникум» РУДН по математике.

Источник

Вычисления с десятичными алгебраическими и обыкновенными дробями егэ математика профиль задание 9

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 4 № 26795

Найдите значение выражения

Задание 4 № 26797

Найдите значение выражения

Задание 4 № 26799

Найдите значение выражения

Задание 4 № 26802

Найдите значение выражения

В решении, в третьей скобке числительного перед второй тройкой разве не минус будет стоять? И ответ 0.

Задание 4 № 26803

Найдите если при

При p(1/b) в первой скобке не может быть 3b, ведь дробь по сути должна переворачиваться, и выходит 1/b+b/3. То же и со второй скобкой — 1/3b+b.

Задание 4 № 26795

Задание 4 № 26802

За пи сы вай тесь на бес плат ное за ня тие.

Ege. sdamgia. ru

14.03.2020 18:15:56

2020-03-14 18:15:56

Источники:

Https://ege. sdamgia. ru/test? theme=60

Задание 4 ЕГЭ по математике. Вычисления и преобразования » /> » /> .keyword { color: red; } Вычисления с десятичными алгебраическими и обыкновенными дробями егэ математика профиль задание 9

Задание 4 ЕГЭ по математике. Вычисления и преобразования

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых можно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №4 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

Дробно-рациональные выражения. Формулы сокращенного умножения

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

Первый множитель в знаменателе умножили на 10, а второй поделили на 10 – просто передвинув запятую.

2. Найдите значение выражения

Корни и степени. Иррациональные выражения

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен.

3. Вычислите .

Применили одну из формул сокращенного умножения.

Действия со степенями

5. Найдите значение выражения: при

Применили формулу частного степеней

6. Вычислите

7. Вычислите, если.

Спокойно, не пугаемся. И конечно, не спешим подставлять значение Сначала упростим выражение.

8. Вычислите

Применили формулу для произведения степеней:

9. Вычислите

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Логарифмические выражения

Темы для повторения:
Логарифмы

Основные логарифмические формулы:

Основное логарифмическое тождество:

Логарифм произведения равен сумме логарифмов:

Логарифм частного равен разности логарифмов:

Формула для логарифма степени:

Формула перехода к новому основанию:

10. Вычислите: .

Снова формула перехода к другому основанию.

11. Найдите, если.

12. Найдите значение выражения.

13. Найдите значение выражения.

14. Найдите значение выражения.

Тригонометрия. Формулы тригонометрии и формулы приведения

15. Вычислите:

16. Найдите, если и.

17. Найдите, если и

18. Найдите значение выражения:

Применили формулу приведения.

19. Упростите выражение:

Применили формулу приведения.

20. Найдите, если.

21. Вычислите, если

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 9 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти.

Другие типы заданий

22. Найдите значение выражения
При.

23. Найдите значение выражения

24. Найдите, если, при.

Что такое? Это функция, каждому числу ставящая в соответствие число. Например, ;

Оказывается, и это не всё.

Ege-study. ru

17.08.2020 11:13:16

2020-08-17 11:13:16

Источники:

Https://ege-study. ru/ru/ege/materialy/matematika/zadanie-9-vychisleniya-i-preobrazovaniya/

Задача 9 Вычисления и преобразования ЕГЭ 2021 Практика. | Университет СИНЕРГИЯ » /> » /> .keyword { color: red; } Вычисления с десятичными алгебраическими и обыкновенными дробями егэ математика профиль задание 9

Задание 9 Вычисления и преобразования ЕГЭ Профильный уровень

В задание 9 ЕГЭ математика профильный уровень нужно найти значения алгебраических выражений. Раздел содержит 15 заданий. Во всех нужно найти численные значения выражений. При решении задач нужно применять формулы приведения, разности квадратов, использовать свойства показательной и степенной функций Задания 1, 2, 12 — 15 содержат тригонометрические выражения, задания 9 — 11 — логарифмы. К заданиям приведены ответы и краткие указания по решению.

При решении задач нужно применять формулы приведения, разности квадратов, использовать свойства показательной и степенной функций Задания 1, 2, 12 15 содержат тригонометрические выражения, задания 9 11 логарифмы.

Synergy. ru

13.04.2020 17:13:24

2020-04-13 17:13:24

Источники:

Https://synergy. ru/edu/ege/ege_2021/matematika/prakticheskaya_chast/zadanie_9_vyichisleniya_i_preobrazovaniya_ege_profilnyij_uroven

Источник

9. Преобразование числовых и буквенных выражений

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на дробно рациональные выражения

Справедливы следующие формулы сокращенного умножения:

(blacktriangleright) Квадрат суммы и квадрат разности: [(a+b)^2=a^2+2ab+b^2] [(a-b)^2=a^2-2ab+b^2]

(blacktriangleright) Куб суммы и куб разности: [(a+b)^3=a^3+3a^2b+3ab^2+b^3=a^3+b^3+3ab(a+b)] [(a-b)^3=a^3-3a^2b+3ab^2-b^3=a^3-b^3-3ab(a-b)]

(blacktriangleright) Разность квадратов: [a^2-b^2=(a-b)(a+b)]

(blacktriangleright) Сумма кубов и разность кубов: [a^3+b^3=(a+b)(a^2-ab+b^2)] [a^3-b^3=(a-b)(a^2+ab+b^2)]

Заметим, что не существует формулы суммы квадратов (a^2+b^2).

Задание
1

#1812

Уровень задания: Легче ЕГЭ

Найдите значение выражения (dfrac{11cdot (2x — 1)^2}{x — 1}) при (x = 0).

При (x = 0): [dfrac{11cdot (2x — 1)^2}{x — 1} = dfrac{11cdot (2cdot 0 — 1)^2}{0 — 1} = dfrac{11cdot (-1)^2}{-1} = dfrac{11cdot 1}{-1} = -11.]

Ответ: -11

Задание
2

#479

Уровень задания: Легче ЕГЭ

Найдите значение выражения (dfrac{8cdot (x — 3)^4}{(x — 3)^3}) при (x = 0).

Так как при (x = 0) знаменатель отличен от 0, то: [dfrac{8cdot (x — 3)^4}{(x — 3)^3} = 8cdot(x — 3)^{4 — 3} = 8cdot(x — 3),] что при (x = 0) равно (8cdot (0 — 3) = -24).

Ответ: -24

Задание
3

#482

Уровень задания: Легче ЕГЭ

Найдите значение выражения (dfrac{3cdot(x^2 — 4)}{(x-2)(x+2)}) при тех значениях (x), при которых оно имеет смысл.

[dfrac{3cdot(x^2 — 4)}{(x-2)(x+2)} = dfrac{3cdot (x^2 — 4)}{x^2 — 4} = 3] – при тех значениях (x), при которых знаменатель исходной дроби отличен от 0, то есть, при тех (x), при которых исходное выражение имеет смысл.

Ответ: 3

Задание
4

#488

Уровень задания: Легче ЕГЭ

Найдите значение выражения (9x — dfrac{81x^2 — 49}{9x + 7}) при тех значениях (x), при которых оно имеет смысл.

Используя формулу для разности квадратов, получаем: [9x — dfrac{81x^2 — 49}{9x + 7} = 9x — dfrac{(9x — 7)(9x + 7)}{9x + 7}.] Выражение в правой части последнего равенства при всяком числе (x), для которого выполняется (9x + 7 neq 0), равно (9x — (9x — 7) = 7).

Ответ: 7

Задание
5

#483

Уровень задания: Равен ЕГЭ

Найдите значение выражения (dfrac{5cdot(3 — x^2)}{(x-sqrt{3})(x+sqrt{3})}) при тех значениях (x), при которых оно имеет смысл.

[dfrac{5cdot(3 — x^2)}{(x-sqrt{3})(x+sqrt{3})} = dfrac{5cdot(3 — x^2)}{x^2-(sqrt{3})^2} = dfrac{5cdot(3 — x^2)}{x^2-3} = dfrac{-5cdot(x^2 — 3)}{x^2-3} = -5] – при тех значениях (x), при которых знаменатель исходной дроби отличен от 0, то есть, при тех (x), при которых исходное выражение имеет смысл.

Ответ: -5

Задание
6

#484

Уровень задания: Равен ЕГЭ

Найдите значение выражения (dfrac{7cdot(7 — 2x^2)}{(x-sqrt{3,5})(x+sqrt{3,5})}) при тех значениях (x), при которых оно имеет смысл.

[dfrac{7cdot(7 — 2x^2)}{(x-sqrt{3,5})(x+sqrt{3,5})} = dfrac{7cdot(7 — 2x^2)}{x^2-(sqrt{3,5})^2} = dfrac{7cdot(7 — 2x^2)}{x^2-3,5} = dfrac{-14cdot(x^2 — 3,5)}{x^2-3,5} = -14] – при тех значениях (x), при которых знаменатель исходной дроби отличен от 0, то есть, при тех (x), при которых исходное выражение имеет смысл.

Ответ: -14

Задание
7

#485

Уровень задания: Равен ЕГЭ

Найдите значение выражения (dfrac{17^2x^3 — 17x^2}{x^2(17x — 1)}) при тех значениях (x), при которых оно имеет смысл.

[dfrac{17^2x^3 — 17x^2}{x^2(17x — 1)} = dfrac{17x^2(17x — 1)}{x^2(17x — 1)} = 17] – при тех значениях (x), при которых знаменатель исходной дроби отличен от 0, то есть, при тех (x), при которых исходное выражение имеет смысл.

Ответ: 17

Решение задач ЕГЭ на преобразование дробно-рациональных выражений — обязательная часть аттестационного испытания. Уметь справляться с ними должны выпускники, сдающие как базовый уровень экзамена, так и профильный. Зная, что такое дробно-рациональные выражения, и как осуществляется их упрощение, учащиеся смогут решить задачу с любым количеством действий и рассчитывать на конкурентные баллы по итогам сдачи ЕГЭ.

Важные нюансы

Упрощение дробных буквенных выражений осуществляется в соответствии с определенными правилами. Все знаменатели и числители необходимо раскладывать на множители, применяя формулы сокращенного умножения. Они помогут привести сложные буквенные дробные выражения к более простому виду. Рекомендуем освежить с памяти формулы квадрата суммы, квадрата разности, куба суммы и разности, разность квадратов, а также сумму и разность кубов. Повторить данный материал можно, посетив раздел «Теоретическая справка» на образовательном портале «Школково». Там вы найдете всю необходимую информацию, подобранную нашими специальными для выпускников средних школ.

Для лучшего усвоения теоретических данных и отработки навыков рекомендуем выполнить упражнения – примеры на преобразование дробно-рациональных выражений, подобные тем, что встречаются в ЕГЭ. Их можно найти в разделе «Каталог». Задания здесь регулярно обновляются и дополняются. Попрактиковаться в решении задач на преобразование целых и дробных рациональных выражений можно в режиме онлайн, находясь в Москве или любом другом городе России.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 4

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 4 проверяет умение производить вычисления и преобразования рациональных, иррациональных, степенных, логарифмических и тригонометрических выражений. Задание состоит из числового или алгебраического выражения, значение которого необходимо найти, применяя математические преобразования. Ответом является целое число или конечная десятичная дробь.

План выполнения:

Внимательно прочитайте условие задачи.
Выполните преобразования.
Найдите числовое значение выражения.
Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Вычисление значений рациональных выражений

Задачи этого типа заключаются в вычислении значений рациональных, то есть дробных выражений. При подготовке необходимо повторить правила действий с дробями, формулы сокращённого умножения.

Задача № 4 (1). Найдите значение выражения

Решение:

Ответ: 1.

Задача № 4 (2). Найдите (a + 9b + 16)/(a + 3b + 8), если a/b = 3.

Решение:

Ответ: 2.

Вычисление значений иррациональных выражений

Задачи этого типа заключаются в вычислении значений иррациональных (содержащих корни) выражений. При подготовке следует повторить правила вычисления корней, свойства корней.

Задача № 4 (3). Найдите значение выражения (³√5 • ⁶√5) : √5.

Решение:

Ответ: 1.

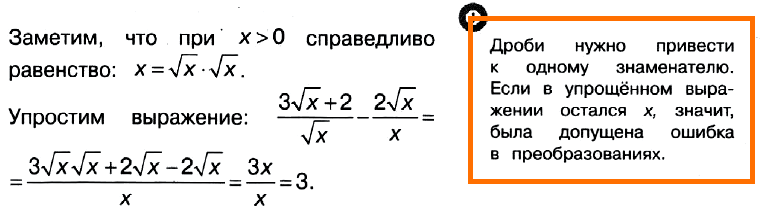
Задача № 4 (4). Найдите значение выражения (3√x + 2)/√x – 2√x/x при х > 0.

Решение:

Ответ: 3.

Вычисление значений степенных выражений

Задачи этого типа заключаются в вычислении значений степенных выражений. При подготовке нужно повторить правила действий со степенями, правило возведения числа в степень.

Задача № 4 (5). Найдите значение выражения 2^1,5 • 8^0,5.

Решение:

Ответ: 8.

Задача № 4 (6). Найдите значение выражения (3 – 14^0,25)(3 + 14^0,25) : (9 + (7^0,5 – 2^1/2)²).

Решение:

Ответ: 27.

Вычисление значений логарифмических выражений

Задачи этого типа заключаются в вычислении значений логарифмических выражений. При подготовке нужно повторить понятие логарифма, основные свойства логарифмов.

Задача № 4 (7). Вычислите log_1/2 ⁴√2.

Решение:

Ответ: –0,25.

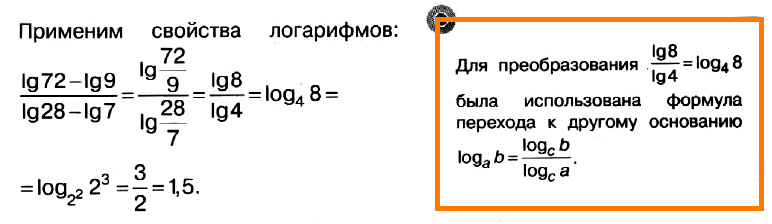
Задача № 4 (8). Найдите значение выражения (lg 72 – lg 9) : (lg 28 – lg 7).

Решение:

Ответ: 1,5.

Вычисление значений тригонометрических выражений

Задачи этого типа заключаются в вычислении значений тригонометрических выражений. При подготовке необходимо повторить основное тригонометрическое тождество, знаки синуса, косинуса, тангенса, формулы приведения, формулы синуса и косинуса двойного аргумента, понятие периодичности тригонометрических функций и табличные значения тригонометрических функций основных углов.

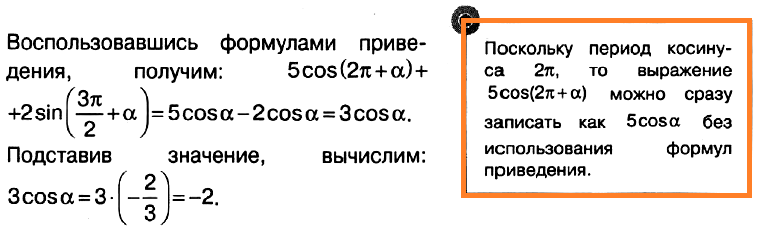
Задача № 4 (9). Найдите значение выражения 5 cos (2π + α) + 2 sin (3π/2 + α), если cos α = –2/3.

Решение:

Ответ: –2.

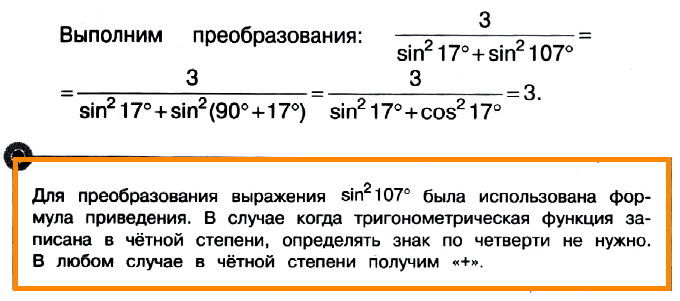
Задача № 4 (10). Найдите значение выражения 3/(sin² 17° + sin² 107°).

Решение:

Ответ: 3.

Тренировочные задания с самопроверкой

№ 4.1. Найдите значение выражения 11√3 • tg (7π/6) • cos (4π/3).

Открыть ОТВЕТ

№ 4.2. Найдите значение выражения (9 sin 59°) / (cos 31°).

Открыть ОТВЕТ

№ 4.3. Найдите значение выражения

Открыть ОТВЕТ

№ 4.4. Найдите значение выражения (3√x + 9)/√x – (9√x)/x – 3x + 12 при х = 6.

Открыть ОТВЕТ

№ 4.5. Найдите значение выражения 19а + b + 11, если (–14a + 14b + 7) : (a + 3b + 5) = 5.

Открыть ОТВЕТ

Вы смотрели: ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

Источник

Задание №12. Уравнения — профильный ЕГЭ по математике

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Упростим левую часть по формуле приведения.

Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок

Видим, что указанному отрезку принадлежат решения

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.

2. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

Степени равны, их основания равны. Значит, равны и показатели.

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку

Отметим на тригонометрическом круге отрезок и найденные серии решений.

Видим, что указанному отрезку принадлежат точки и из серии

Точки серии не входят в указанный отрезок.

А из серии в указанный отрезок входит точка

Ответ в пункте (б):

3. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Применим формулу косинуса двойного угла:

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а)

б) Отметим на тригонометрическом круге найденные серии решений и отрезок

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

5. а) Решите уравнение

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых

Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

Материал для подготовки к заданию номер 12 из ЕГЭ по профильной математике

Все уравнения можно разделить на несколько групп:

— Целые рациональные уравнения

Каждая группа уравнений имеет свои особенности. На первый взгляд может показаться, что это очень большой материал и на его изучение понадобится много времени, однако на самом деле для подготовки в экзамену и выполнению задания номер 12 можно подготовиться достаточно быстро, используя верно подобранные материалы и разбирая примеры заданий

Комбинируя все представленные в данных материалах способы и обладая базовыми знаниями математики, можно успешно решить большинство уравнений, которые могут встретиться учащимся во время обучения в средней и старшей школе а так же успешно решить задания на данную тему в контрольно-измерительных материалах

СОВЕТ: после прохождения какой-либо темы в моём пособии, необходимо прорешать похожие уравнения (этой же группы) на одном из подобранных мной сайтов (смотрите ниже)

Часть I. Способы решения уравнений. Метод “Замена переменной”

Уравнение вида af²(x)+bf (x)+c=0 Такие уравнения (их иногда называют трехчленными) являются одними из наиболее распространенных. Скорее всего, самый известный и яркий пример этого типа уравнений — биквадратное уравнение ax⁴ + bx2 + c = 0 (здесь f (x) = x 2 ). Заменой переменной t = f (x) трехчленное уравнение сводится к квадратному относительно переменной t уравнению at² + bt + c = 0

Решить уравнение (2x² – 3x + 1) = 22x² – 33x + 1.

Задание 12 ЕГЭ по математике профильный уровень — уравнения

Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.

Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.

Практика

Источник	Задания
math100.ru	Рациональные уравнения Уравнения смешанного типа, содержащие тригонометрические функции
vk.com/ekaterina_chekmareva	Скачать задания
semenova-klass.moy.su	Скачать уравнения

Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2

Уровень сложности задания — повышенный.

Максимальный балл за выполнение задания — 2

Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10

источники:

http://vc.ru/u/1019775-egor-borodin/330865-material-dlya-podgotovki-k-zadaniyu-nomer-12-iz-ege-po-profilnoy-matematike

http://vpr-ege.ru/ege/matematika/1709-zadanie-12-ege-po-matematike-profilnyj-uroven-uravneniya

Источник