Ниже приведена программа, записанная на пяти языках программирования.
| Бейсик | Python |
|---|---|
|
DIM s, t AS INTEGER INPUT s INPUT t IF s > 5 AND t > 5 THEN PRINT ‘YES’ ELSE PRINT ‘NO’ ENDIF |
s = int(input()) t = int(input()) if s > 5 and t > 5: print(«YES») else: print(«NO») |
| Паскаль | Алгоритмический язык |
|
var s, t: integer; begin readln(s); readln(t); if (s > 5) and (t > 5) then writeln(‘YES’) else writeln(‘NO’) end. |
алг нач цел s, t ввод s ввод t если s > 5 и t > 5 то вывод «YES» иначе вывод «NO» все кон |
| С++ | |
|
#include <iostream> using namespace std; int main() { int s, t; cin >> s; cin >> t; if (s > 5 && t > 5) cout << «YES»; else cout << «NO»; return 0; } |
Было проведено 9 запусков программы, при которых в качестве значений переменных s и t вводились следующие пары чисел:
(6, 8); (3, 5); (–7, 2); (7, 7); (9, 8); (–1, 3); (–4, 5); (6, 9); (2, –1).
Сколько было запусков, при которых программа напечатала «YES»?
Урок посвящен тому, как решать 5 задание ЕГЭ по информатике
Содержание:
- Объяснение 5 задания
- Исполнитель для возведения в квадрат, деления, умножения и сложения
- Проверка числовой последовательности на соответствие алгоритму
- Разбор 5 задания
- Решение задания про алгоритм, который строит число R
- Решение заданий для темы Проверка числовой последовательности (Автомат)
5-е задание: «Анализ алгоритмов и исполнители»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 4 минуты.
Проверяемые элементы содержания: Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд
До ЕГЭ 2021 года — это было задание № 6 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Как и в других заданиях базового уровня сложности, источником ошибок служит недостаточная внимательность и отсутствие или поверхностность самостоятельной проверки полученного ответа»
ФГБНУ «Федеральный институт педагогических измерений»
Проверка числовой последовательности на соответствие алгоритму
- для выполнения некоторых заданий необходимо повторить тему системы счисления;
- максимальное значение суммы цифр десятичного числа — это 18, так как 9 + 9 = 18;
- для проверки правильности переданного сообщения иногда вводится бит четности — дополнительный бит, которым дополняется двоичный код таким образом, чтобы в результате количество единиц стало четным: т.е. если в исходном сообщении количество единиц было четным, то добавляется 0, если нечетным — добавляется 1:
например: 310 = 112 после добавления бита четности: 110 ---- 410 = 1002 после добавления бита четности: 1001
например: 1112 - это 710 добавим 0 справа: 11102 - это 1410
Теперь будем рассматривать конкретные типовые экзаменационные варианты по информатике с объяснением их решения.
Разбор 5 задания
Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:
Решение задания про алгоритм, который строит число R
5_11:
На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:
- Строится двоичная запись числа 4N.
- К этой записи дописываются справа еще два разряда по следующему правилу:
- складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
- над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись является двоичной записью искомого числа R.
Укажите такое наименьшее число N, для которого результат работы алгоритма больше 129. В ответе это число запишите в десятичной системе счисления.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение аналитическим способом:
- Заметим, что после выполнения второго пункта задания, будут получаться только четные числа! Наименьшим возможным четным числом, превышающим 129, является число 130. С ним и будем работать.
- Переведем 130 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать
bin(130). Получим:
13010 = 100000102
в обратном порядке: было 1000001 -> стало 10000010 еще раз то же самое: было 100000 -> стало 1000001
int('100000',2).1000002 = 3210
✎ Решение с использованием программирования:
PascalAbc.Net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
uses school; begin var n_ := 1; while True do begin var n := 4*n_; var ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2 n := 2 * n + ost; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряру (+ost) ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2 n := 2 * n + ost; if n > 129 then begin println(n_); break end; n_ += 1; end; end. |
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
n_ = 1 while True: n = 4*n_ r = str(bin(n)) r = r[2:] for i in range(2): if r.count('1') % 2 == 0: r+='0' else: r+='1' n = int(r, base=2) if n > 129: print(n_) break n_+=1 |
Результат: 8
Для более детального разбора предлагаем посмотреть видео теоретического решения данного 5 задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
5_12: Демоверсия ЕГЭ 2018 информатика:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
- Строится двоичная запись числа N.
- К этой записи дописываются справа ещё два разряда по следующему правилу:
- складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
- над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
✍ Решение:
- Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
- Наименьшим возможным числом, превышающим 83, является число 84. С ним и будем работать.
- Переведем 84 в двоичную систему счисления. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать
bin(84). Получим:
84 = 1010100
86 = 1010110
Результат: 86
Подробное решение данного 5 (раньше №6) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Видеорешение с программированием (PascalAnc.Net):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Аналитическое видеорешение:
📹 Видеорешение на RuTube здесь -> аналитическое решение
5_18:
Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3. Шаг 2 повторяется ещё два раза.
4. Результат переводится в десятичную систему счисления.
При каком наименьшем исходном числе N > 65 в результате работы алгоритма получится число, кратное 4?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение с использованием программирования:
PascalAbc.Net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
uses school; begin var n_ := 1; while True do begin var n := n_; for var i := 1 to 3 do begin if bin(n).CountOf('1') = bin(n).CountOf('0') then // сравниваем if n mod 2 = 0 then // если четное, то в конце 0 n := 2 * n // добавляем разряд = 0 else n := 2 * n + 1 // иначе добавляем разряд = 1 else if bin(n).CountOf('1') > bin(n).CountOf('0') then n := 2 * n else n := 2 * n + 1 end; if (n_ > 65) and (n mod 4 = 0) then begin println(n_); break end; n_ += 1; end; end. |
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
n_ = 1 while True: n = n_ r = str(bin(n)) r = r[2:] for i in range(3): if r.count('1') == r.count('0'): r+=r[-1] elif r.count('1')>r.count('0'): r+='0' else: r+='1' n = int(r, base=2) if n_ > 65 and n % 4 == 0 : print(n_,n) break n_+=1 |
Ответ: 79
5_19:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Число N переводим в двоичную запись.
2) Инвертируем все биты числа кроме первого.
3) Переводим в десятичную запись.
4) Складываем результат с исходным числом N.
Полученное число является искомым числом R.
Укажите наименьшее нечетное число N, для которого результат работы данного алгоритма больше 99. В ответе это число запишите в десятичной системе счисления.
✍ Решение:
-
✎ Решение с использованием программирования:
PascalAbc.Net:
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
n_ = 1 while True: n = n_ r = str(bin(n)) r = r[2:] for i in range(1,len(r)): if r[i]== '0': r=r[:i]+'1'+r[i+1:] else: r=r[:i]+'0'+r[i+1:] n = int(r, base=2) n+=n_ if n > 99 and n_ % 2 != 0 : print(n_,n) break n_+=1 |
Ответ: 65
5_13:
На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа еще два разряда по следующему правилу:
— если N делится нацело на 4, в конец числа (справа) дописывается сначала ноль, а затем еще один ноль;
— если N при делении на 4 дает в остатке 1, то в конец числа (справа) дописывается сначала ноль, а затем единица;
— если N при делении на 4 дает в остатке 2, то в конец числа (справа) дописывается сначала один, а затем ноль;
— если N при делении на 4 дает в остатке 3, в конец числа (справа) дописывается сначала один, а затем еще одна единица.
Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.
Укажите максимальное число R, которое меньше 100 и может являться результатом работы данного алгоритма. В ответе это число запишите
в десятичной системе счисления
.
Типовые задания для тренировки
✍ Решение:
- Поскольку требуется найти наибольшее число, то возьмем наибольшее из возможных чисел, которые < 100 — это число 99. Переведем его в двоичную систему. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать
bin(99). Получим:
99 = 11000112
1100011 N
int('11000',2)11000 = 2410
98 = 11000102 : 10 в конце добавлено алгоритмом N = 110002 = 2410 24 делится нацело на 4. По алгоритму в конце должно быть 00, а мы имеем 10 98 - не подходит 97 = 11000012 : 01 в конце добавлено алгоритмом N = 110002 = 2410 24 делится нацело на 4. По алгоритму в конце должно быть 00, а мы имеем 01 97 - не подходит 96 = 11000002 : 00 в конце добавлено алгоритмом N = 110002 = 2410 24 делится нацело на 4. По алгоритму в конце должно быть 00, у нас 00 - верно! 96 - подходит!
Результат: 96
Предлагаем посмотреть видео теоретического решения:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
5_14:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. К этой записи дописывается (дублируется) последняя цифра.
3. Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4. К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, большее 114, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение аналитическим способом:
- В постановке задания задано R > 114. R — это результат работы алгоритма. Для того, чтобы определить наименьшее возможно N, переведем сначала 114 в двоичную систему счисления и выделим в нем три добавленные по алгоритму цифры (перевод можно выполнить в консоли Питона:
bin(114))
114 = 11100102
2. В полученное числе N = 1110 дублируется последняя цифра и получается 11100.
3. Поскольку число единиц (3) — нечетное, то справа добавляется 1: 111001.
4. Т.к. в полученном наборе цифр четное число единиц, то добавляем 0: 1110010
1. N = 1110 + 1 = 1111 Работа по алгоритму: 2. 11111 - дублирование последней цифры. 3. 111111 - справа дописываем единицу, т.к. в полученном числе 5 единиц (нечетное) 4. 1111110 - дописываем ноль, т.к. в полученном числе четное число единиц.
int('1111110',2)):min R = 11111102 = 12610
✎ Решение с использованием программирования:
PascalAbc.Net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
uses school; begin var n_ := 1; while True do begin var n := n_; // дублирвание последней цифры if n mod 2 = 0 then // если четное, то в конце 0 n := 2 * n // добавляем разряд = 0 else n := 2 * n + 1; // иначе добавляем разряд = 1 for var i := 1 to 2 do begin if bin(n).CountOf('1') mod 2 = 0 then n := 2 * n // добавляем разряд = 0 else n := 2 * n + 1 // иначе добавляем разряд = 1 end; if n > 114 then begin println(n); break end; n_ += 1; end; end. |
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
n_ = 1 while True: n = n_ r = str(bin(n)) # строковое значение r = r[2:] # убираем 0b r=r+r[-1] for i in range (2): if r.count('1') % 2 == 0: r = r+'0' else: r = r+'1' r = int(r,base = 2) # в 10-ю с.с. if r > 114: print(r) break n_+= 1 |
Результат: 126
5_17: Досрочный вариант 1 ЕГЭ по информатике 2020, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
— если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы.
Например, двоичная запись 1001 числа 9 будет преобразована в 100111.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.
Укажите минимальное число N, для которого результат работы алгоритма будет больше 134. В ответе это число запишите в десятичной системе счисления.
Ответ: 33
Видео -> теоретическое решение
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_16:
Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:
1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из нового числа вычитается исходное, полученная разность выводится на экран.
Какое число нужно ввести в автомат, чтобы в результате получилось 45?
✍ Решение:
- Результатом выполнения алгоритма является число 45. Алгоритм работает в двоичной системе счисления, поэтому переведем число:
45 = 001011012
1 - 0, с учетом, что у разряда с единицей заняли. То есть бит:. _ 1 _ _ _ _ _ _ _ N инвертируемое = 0 _ _ _ _ _ _ _ N исходное 0 0 1 0 1 1 0 1 = 45 результат
1 - 0 не может в результате дать 0, так как у следующей слева единицы мы заняли. Значит, 0 - 1. Чтобы не получить единицу в ответе, необходимо у нуля тоже занять:. . _ 1 0 _ _ _ _ _ _ = 0 1 _ _ _ _ _ _ 0 0 1 0 1 1 0 1 = 45 результат
1 - 0 не может быть, так как у следующего слева нуля мы заняли.Значит
0 - 1. То есть как раз чтобы получить единицу (10 - 1 = 1), занимаем у следующих слева разрядов:. . _ 1 0 0 _ _ _ _ _ = 0 1 1 _ _ _ _ _ 0 0 1 0 1 1 0 1 = 45 результат
0 - 1 не может быть. Значит, чтобы получить в результате ноль, берем 1 - 0, у единицы должно быть занято.. . . _ 1 0 0 1 _ _ _ _ = 0 1 1 0 _ _ _ _ 0 0 1 0 1 1 0 1 = 45 результат
1 - 0 не может быть. Так как слева у единицы занято. Значит, чтобы получить в результате 1, берем 0 - 1:. . . _ 1 0 0 1 0 _ _ _ = 0 1 1 0 1 _ _ _ 0 0 1 0 1 1 0 1 = 45 результат
0 - 1 не даст в ответе единицу, значит, имеем 1 - 0:. . . _ 1 0 0 1 0 1 _ _ = 0 1 1 0 1 0 _ _ 0 0 1 0 1 1 0 1 = 45 результат
0 - 1 не может быть, значит, 1 - 0. Чтобы получить в результате 0, необходимо, чтобы у 1 было занято:. . . . _ 1 0 0 1 0 1 1 _ = 0 1 1 0 1 0 0 _ 0 0 1 0 1 1 0 1 = 45 результат
0 - 1:. . . . _ 1 0 0 1 0 1 1 0 = 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 1 = 45 результат
01101001 = 10510
Ответ: 105
Смотрите теоретический разбор задания на видео и подписывайтесь на наш канал:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
Решение заданий для темы Проверка числовой последовательности (Автомат)
5_7:
Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
- Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
- Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.
Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.
✍ Решение:
Результат: 2949
Процесс теоретического решения данного 5 задания представлен в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_8:
Автомат получает на вход четырехзначное число. По нему строится новое число по следующим правилам:
- Складываются первая и вторая, затем вторая и третья, а далее третья и четвёртая цифры исходного числа.
- Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).
Пример: Исходное число: 7531. Суммы: 7+5=12; 5+3=8; 3+1=4. Результат: 4812.
✍ Решение:
2, 5, 129:12=9+3
93**
9320.Результат: 9320
Подробное теоретическое решение данного 5 задания можно просмотреть на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_9:
Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам:
- Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
- Полученные два шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).
Пример: Исходные числа: 25, 66. Поразрядные суммы: 8, B. Результат: B8.
Какие из предложенных чисел могут быть результатом работы автомата?
Перечислите в алфавитном порядке буквы, соответствующие этим числам, без пробелов и знаков препинания.
Варианты:
A) 127
B) C6
C) BA
D) E3
E) D1
✍ Решение:
Проанализируем все варианты:
12 в шестнадцатеричной системе записывается как С.С6 разбиваем на 12 и 6. Число может быть результатом работы автомата. Исходные числа, например, 35 и 37BA разбиваем на 11 и 10. Число может быть результатом работы автомата. Исходные числа, например, 55 и 56E3 разбиваем на 14 и 3. 14=6+8, но цифры большие 6 не принимает автомат. Не подходит.D1 разбиваем на 13 и 1. 13=6+7, но цифры большие 6 не принимает автомат. Не подходит.Результат: BC
Подробное теоретическое решение данного 5 задания можно просмотреть на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_10: Задание 5 ГВЭ 11 класс 2018 год ФИПИ
Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 7 (если в числе есть цифра больше 7, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.
1. Вычисляются два шестнадцатеричных числа: сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.
Определите, какое из предложенных чисел может быть результатом работы автомата.
Варианты:
1) AD
2) 64
3) CF
4) 811
✍ Решение:
Теоретическое решение 4 задания ГВЭ 11 класса смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_15:
Автомат получает на вход натуральное число X. По этому числу строится трёхзначное число Y по следующим правилам:
1. Первая цифра числа Y (разряд сотен) – остаток от деления X на 7.
2. Вторая цифра числа Y (разряд десятков) – остаток от деления X на 2.
3. Третья цифра числа Y (разряд единиц) – остаток от деления X на 5.
Пример. Исходное число: 55. Остаток от деления на 7 равен 6; остаток от деления на 2 равен 1; остаток от деления на 5 равен 0. Результат работы автомата: 610.
Сколько существует двузначных чисел, при обработке которого автомат выдаёт результат 312?
Типовые задания для тренировки
✍ Решение:
- Обозначим каждую цифру числа Y согласно заданию:
Y = 3 1 2 x mod 7 x mod 2 x mod 5
1. x mod 2 = 1 => значит, X — нечетное число
2. x mod 5 = 2 => значит, X — либо ?2, либо ?7.
3. раз x — нечетное, то из пред. пункта получаем x = ?7
4. x mod 7 = 3 => переберем все варианты:
97 - не подходит, 87 - подходит (87 / 7 = 12, остаток = 3) 77 - не подходит, 67 - не подходит, 57 - не подходит, 47 - не подходит, 37 - не подходит, 27 - не подходит, 17 - подходит (17 / 7 = 2, остаток = 3)
Результат: 2
Продолжаем решать демоверсию ЕГЭ по информатике 2023.
Условия задач были взяты с сайта: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5
В этой статье разберём задания 16-21 из демоверсии ЕГЭ по информатике 2023.
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
Задание 16
Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n − 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?
Решение:
Если мы просто перепечатаем функцию, как мы делали на экзамене в 2022 году, то программа откажится это вычислять. Здесь слишком большая глубина рекурсии.
Тогда посмотрим внимательно на функцию. Оказывается это функция факториала. Это действие означает n! = 1*2*3*…*n.
F(2023) / F(2020) = (2023 * 2022 * 2021 * 2020!) / 2020! = 2023 * 2022 * 2021
Выражение 2020! просто сокращается. В ответе напишем 2023 * 2022 * 2021 = 8266912626.
Ответ: 8266912626
Задание 17
В файле содержится последовательность целых чисел. Элементы
последовательности могут принимать целые значения от –10 000 до 10 000
включительно. Определите количество пар последовательности, в которых
только одно число оканчивается на 3, а сумма квадратов элементов пары
не меньше квадрата максимального элемента последовательности,
оканчивающегося на 3. В ответе запишите два числа: сначала количество
найденных пар, затем максимальную из сумм квадратов элементов таких
пар. В данной задаче под парой подразумевается два идущих подряд
элемента последовательности.
Решение:
В начале нужно найти максимальное число последовательности, оканчивающегося на 3.
f=open('17.txt') mx=-10000 for s in f.readlines(): x=int(s) if abs(x)%10==3: mx = max(mx, x) print(mx)
Получается число 9973.
Напишем основную программу:
f=open('17.txt') k=0 mx=0 n1=int(f.readline()) for s in f.readlines(): n2=int(s) if ((abs(n1)%10==3) != (abs(n2)%10==3)) and (n1**2 + n2**2 >= 9973**2): k=k+1 mx = max(mx, n1**2 + n2**2) n1=n2 print(k, mx)
Как решать подобные задачи было рассказано в видеокурсе.
Здесь нужно помнить, что числа отрицательные. Поэтому при нахождении последней цифры, нужно использовать функцию модуля abs.
Так же здесь интересное логическое выражение «в которых только одно число оканчивается на 3». Это операция xor — отрицание равносильности.
Ответ:
Задание 18
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается
в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата
также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета
достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой;
это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем
минимальную.
Исходные данные представляют собой электронную таблицу размером
N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние
и внешние стены обозначены утолщенными линиями.
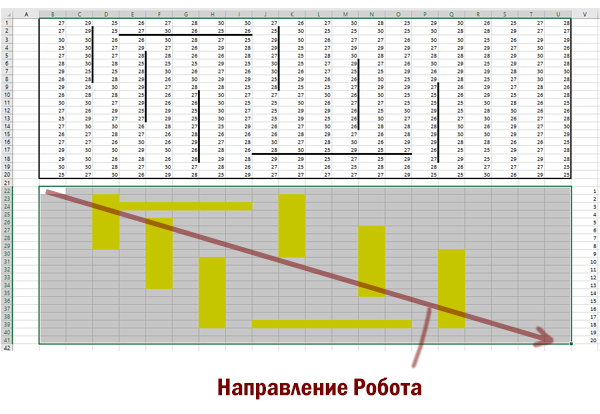
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Решение:
Открываем файл в программе Excel.
Выделим все ячейки с числами, нажмём «вырезать», используя контекстное меню. Вставим данные на 1 столбец вправо. Это делаем потому, что будем использовать для решения формулу, которая будет обращаться к ячейке слева.
Мысленно представим пространство на 1 строчку ниже, чем область, где находятся числа. Это пространство будет таким же по размерам, как и область с числами. В этом пространстве и будет наше решение.
Отметим особым цветом те ячейки, которые «спрятаны» от движения Робота стенками.
Для этих ячеек будем составлять другие формулы, в отличии от обычных ячеек.
Цвет ячейки можно поменять, нажав на кнопку «Цвет заливки» на главной вкладке программы.
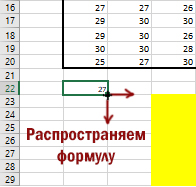
Т.к. Робот направляется из левой верхней ячейки, то мы сначала и напишем формулу для этой ячейки. Пишем для ячейки B22:
=МАКС(B21;A22)+B1
Робот в любую ячейку может прийти либо сверху, либо слева. Для подсчёта максимального количества монет, мы должны выбрать максимальное предыдущее значение. Это и делаем формула. Плюс Робот должен взять монеты с текущей клетки.
Распространим формулу на всё пространство, не трогая закрашенные клетки.
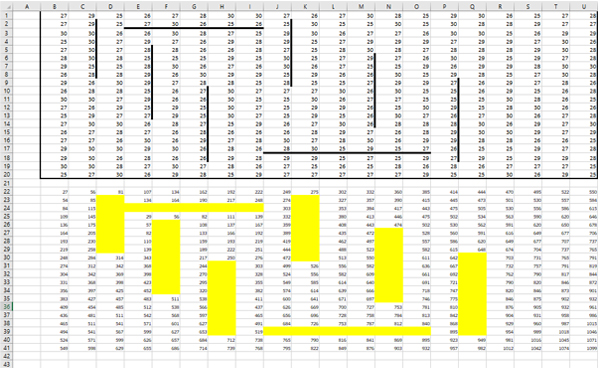
Получается такая картина:
Для вертикальных подкрашенных полосок, Робот может попасть только сверху! Поэтому пишем формулу для ячейки, к примеру, для D23:
=D22+D2
Распространяем формулу по всему закрашенному столбцу. Аналогично делаем для всех вертикальны подкрашенных полосок.
В ячейки для горизонтально подкрашенных полосок, Робот может попасть только слева! Поэтому пишем формулу, к примеру, для ячейки E24:
=D24+E3
Распространяем формулу по всей закрашенной строчке. Алагоично делаем со всеми горизонтальными полосками.
В правом нижнем углу нашего рабочего пространства получается максимальное количество монет, которое может собрать Робот. В ячейке U41 получается число 1099.
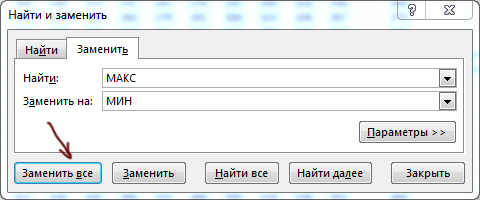
Чтобы получить минимальную возможную сумму, в главной формуле функцию МАКС нужно заменить на МИН!
Удобно воспользоваться автоматической заменой через Ctrl+F.
Минимальная сумма равна 1026.
Ответ:
Задание 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит
куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход
игрок может добавить в кучу один камень или увеличить количество камней
в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть
неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится
не менее 129. Победителем считается игрок, сделавший последний ход,
т.е. первым получивший кучу, в которой будет 29 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128.
Будем говорить, что игрок имеет выигрышную стратегию, если он может
выиграть при любых ходах противника. Описать стратегию игрока – значит
описать, какой ход он должен сделать в любой ситуации, которая ему может
встретиться при различной игре противника. В описание выигрышной
стратегии не следует включать ходы играющего по этой стратегии игрока,
не являющиеся для него безусловно выигрышными, т.е. не являющиеся
выигрышными независимо от игры противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход,
но при любом ходе Пети Ваня может выиграть своим первым ходом.
Решение:
Решим задачу с помощью шаблона на языке программирования Python. Если хотите ознакомится с аналитическим решением задач на теорию игр, можете посмотреть мои статьи по 19 Заданию, 20 Заданию, 21 Заданию. Но с помощью шаблонов на экзамене решать быстрее и легче. Об этом подходе можете найти в видеокурсе.
Введём параметр p, который будет олицетворять позицию игры (ход).
| Начальная позиция | Ход Пети | Ход Вани | Ход Пети | Ход Вани | Ход Пети | |
| p | 1 | 2 | 3 | 4 | 5 | 6 |
def F(x, p): if x>=129 and p==3: return True if x<129 and p==3: return False if x>=129: return False if p%2==1: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s)
Заводим функцию F. Т.к. у нас одна куча, то она принимает параметры: x — количество камней в куче, p-позиция игры.
Дальше описываем победу. Если x>=29 и позиция равна 3 (1 Ход Вани), то возвращаем True, что означает победу.
Если, позиция уже равна 3, но камней меньше, чем должно быть для победы, то возвращаем False (проигрыш).
Третье условие. Если кто-то выиграл, но на первых двух условиях мы не вышли из функции, то, значит, выиграл не тот, кто нам нужен, следовательно, возвращаем Fasle.
Если мы не вышли на первых трёх условиях, то, значит, продолжаем прокручивать ходы, рекурсивно запускаем функцию F.
Для нечётных p (это ходы Вани), возвращаем разные ходы через and, т.к. он должен побеждать в любом случае. При этом увеличиваем на 1 значение p.
Для чётных p (это ходы Пети), возвращаем ходы через or.
В конце перебираем все возможные значения для s через цикл for, ищём те значения, которые подходят по условию задачи.
Ответ: 64
Задание 20
Для игры, описанной в задании 19, найдите два наименьших таких значения S, при
которых у Пети есть выигрышная стратегия, причём одновременно
выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как
будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Решение:
Задача точно такая же, как и в 19 задании, только теперь обязательно должен побежать Петя на своём втором ходу (p=4), при любой игре Вани.
Пишем тот же шаблон, немного отредактировав его.
def F(x, p): if x>=129 and p==4: return True if x<129 and p==4: return False if x>=129: return False if p%2==0: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s)
Получается 32 и 63.
Ответ:
Задание 21
Для игры, описанной в задании 19, найдите минимальное значение S, при котором
одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.
Если найдено несколько значений S, в ответе запишите минимальное из них.
Решение:
Опять используем прошлый шаблон, но немного модернизируем.
def F(x, p): if x>=129 and (p==3 or p==5): return True if x<129 and p==5: return False if x>=129: return False if p%2==1: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) def F1(x, p): if x>=129 and p==3: return True if x<129 and p==3: return False if x>=129: return False if p%2==1: return F1(x+1, p+1) and F1(x*2, p+1) else: return F1(x+1, p+1) or F1(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s) print() for s in range(1, 129): if F1(s, 1): print(s)
Здесь Ваня должен выигрывать либо на первом своём ходе (p=3), либо на втором своём ходе (p=5).
Т.к. Ваня не должен гарантированно выиграть своим первым ходом, то мы создаём ещё одну функцию F1, похожую на основную функцию F, которая вычисляет, когда Ваня именно гарантированно выигрывает на своём первом ходе (p=3). И, затем, мы из тех чисел, которые получились в первой функции F, исключаем числа, которые получились во второй функции F1.
В первой функции получилось 62,64, а во второй 64. Получается ответ 62.
Ответ: 62
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
Примеры заданий ЕГЭ по информатике с решением на Паскале. На странице использованы условия задач из демо вариантов и задачника с сайта Полякова Константина Юрьевича (kpolyakov.spb.ru)
Содержание
- Задание 5
- Задание 6
- Задание 14
- Задание 15
- Задание 16
- Задание 17
- Задание 22
- Задание 24
- Задание 25
Задание 5
Демо-2022
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему
правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью результирующегочисла R.
Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.
Решение:
var n, i, b, s, k: integer; r: real; st: string; begin for n := 1 to 100 do begin k := n; //перебор исходного числа N s := 0; //сумма цифр двоичного кода r := 0; //результирующее десятичное число R st := ''; //очищаем строку двоичного кода для нового числа while k >= 1 do //цикл перевода в двоичный код исходного числа begin s := s + (k mod 2); //вычисление суммы цифр двоичного кода st := st + (k mod 2);//формирование строки двоичного кода из остатков деления на 2 k := k div 2;// деление на 2 end; st := ReverseString(st) + s mod 2; //переворачиваем код и дописываем остаток s := s + s mod 2;//вычисление суммы нового кода st := st + s mod 2;//формирование строки двоичного кода с добавлением остатка for i := 1 to Length(st) do //преобразование двоичного кода в десятичное число if st[i] = '1' then r := r + power(2, Length(st) - i); if r > 77 then begin println(n, r);break; end;//вывод найденных чисел end; end.
Задание 6
Демо-2022 Определите, при каком наибольшем введённом значении переменной s программа выведет число 64.
Решение: Используем исходный код. Добавим в него цикл перебора значений S и вывода при выполнении условия. Последнее значение и будет ответом.
var s, n, i: integer; begin for i := 1 to 510 do begin s := i; s := s div 10; n := 1; while s < 51 do begin s := s + 5; n := n * 2 end; if n = 64 then writeln(i); end; end.
Задание 14
Демо-2022 Значение арифметического выражения: 3*438+2*423+420+3*45+2*44+1 – записали в системе счисления с основанием 16. Сколько значащих нулей содержится в этой записи?
Решение:
var k,x:biginteger; begin k:=0; x:=3*4bi**38+2*4bi**23+4bi**20+3*4bi**5+2*4bi**4+1; while x>0 do begin if x mod 16=0 then k:=k+1; x:=x div 16; end; print(k) end.
Демо-2021 Значение арифметического выражения: 497 + 721 – 7 – записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
Решение:
var s, i,k6,x:integer; osn,n:biginteger; begin osn:=7; k6:=0; n:=power(osn,14)+power(osn,21)-7; while n>0 do begin if n mod 7 = 6 then k6:=k6+1; n:=n div 7; end; print(k6); end.
Демо-2020 Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 70 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
_ПОКА нашлось (2222) ИЛИ нашлось (8888)
__ЕСЛИ нашлось (2222)
___ТО заменить (2222, 88)
___ИНАЧЕ заменить (8888, 22)
__КОНЕЦ ЕСЛИ
_КОНЕЦ ПОКА
КОНЕЦ
Решение:
begin var s: string := '8' * 70; while (s.contains('2222')) or (s.contains('8888')) do begin if (s.contains('2222')) then s := s.replace('2222', '88') else s := s.replace('8888', '22'); end; writeln(s); end.
Задание 15
Демо-2021 Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9)) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решение:
// Делители var a,x, flag: integer; begin for a := 1 to 100 do begin flag := 0; for x := 1 to 1000 do if not(x mod a = 0) <= ((x mod 6 = 0) <= not (x mod 9 = 0)) = false then begin flag := 1; break; end; if flag = 0 then print(a); end; end.
К.Поляков №161 Определите наименьшее натуральное число A, такое что выражение
(X & 29 ≠ 0) → ((X & 17 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Посмотреть решение
var A, x, flag: integer; begin for A := 0 to 31 do begin flag := 0; for x := 0 to 31 do if (((x and 29) = 0) or ((x and 17) <> 0) or ((x and A) <> 0))=false then flag := 1; if flag = 0 then begin writeln(A); break; end; end; end.
Задание 16
Демо-2022 Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n + F(n − 1), если n – чётно,
F(n) = 2 × F(n − 2), если n > 1 и при этом n – нечётно.
Чему равно значение функции F(26)?
Решение:
var i, n: integer; f: array[1..100] of integer; begin print('Введите значение n'); readln(n); f[1] := 1; for i := 2 to n do if i mod 2 = 0 then f[i] := i + f[i - 1] else f[i] := 2 * f[i - 2]; print(f[n]); end.
К.Поляков №46Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = n при n ≤ 3;
F(n) = 2 · n · n + F(n – 1) при чётных n > 3;
F(n) = n · n · n + n + F(n – 1) при нечётных n > 3;
Определите количество натуральных значений n, при которых F(n) меньше, чем 107.
Посмотреть решение
var i: integer; f: array[1..1000] of integer; begin i:=3; f[1] := 1; f[2] := 2; f[3] := 3; while f[i]< 10**7 do begin i:=i+1; if i mod 2 = 0 then f[i] := 2*i*i + f[i - 1] else f[i] := i*i*i+i +f[i - 1]; end; print(i-1);// не учитываем последнее число end.
Задание 17
Демо-2022
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число делится на 3, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.Файл с данными: 17.txt
Решение:
var a,b,k,maxsum: integer; begin Assign( input, '17.txt' ); maxsum:=-20000; k:=0; readln(a); while not eof do begin readln(b); if (a mod 3 = 0) or (b mod 3 = 0) then begin k := k + 1; if a + b > maxsum then maxsum := a + b; end; a := b; end; Println( k, maxsum) end.
Задание 22
Демо-2022
Ниже на языке программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4,а потом 5.

Решение:
var x, i, L, M, Q: integer; begin for i := 9 to 50 do begin x := i; Q := 9; L := 0; while x >= Q do begin L := L + 1; x := x - Q; end; M := x; if M < L then begin M := L; L := x; end; if (L = 4) and (M = 5) then print(i); end; end.
Задание 24
Демо-2022
Текстовый файл состоит из символов P, Q, R и S. Определите максимальное количество идущих подряд символов в прилагаемом файле, среди которых нет идущих подряд символов P. Для выполнения этого задания следует написать программу.Файл с данными: 24.txt
Решение:
var i, maxlen, curlen: longint; {описание переменных} s: string; f: text;{текстовый файл} begin assign(f, '24.txt'); {исходный текстовые файл с данными} reset(f); readln(f, s);{открываем файл для чтения данных} maxlen := 1; curlen := 1; for i := 2 to Length(s) do if not ((s[i] = 'P') and (s[i-1] = 'P')) then begin curLen := curLen + 1; if curLen > maxLen then maxLen := curLen; end else curLen := 1; writeln(maxLen); close(f); { закрываем файл} end.
Задание 25
Демо-2022
Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей и у числа нет, то значение M считается равным нулю. Напишите программу, которая перебирает целые числа, большие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые пять найденных чисел и соответствующие им значения M.
Формат вывода: для каждого из пяти таких найденных чисел в отдельной строке сначала выводится само число, затем – значение М.
Строки выводятся в порядке возрастания найденных чисел.
Решение:
var d1, chislo: integer; begin for chislo := 700001 to 700100 do for d1 := 2 to chislo - 1 do if chislo mod d1 = 0 then begin if (d1 + chislo div d1) mod 10 = 8 then println(chislo, d1 + chislo div d1); break; end; end.
Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.
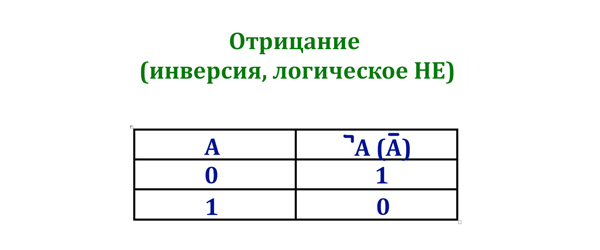
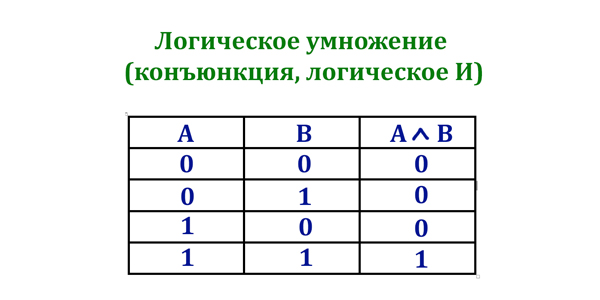
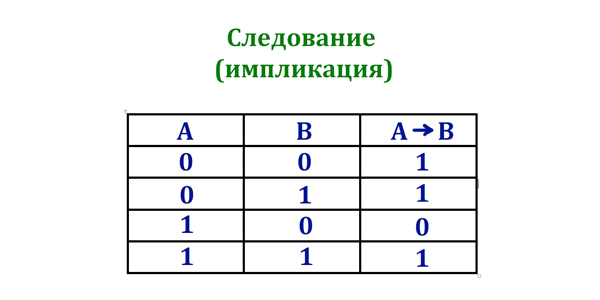
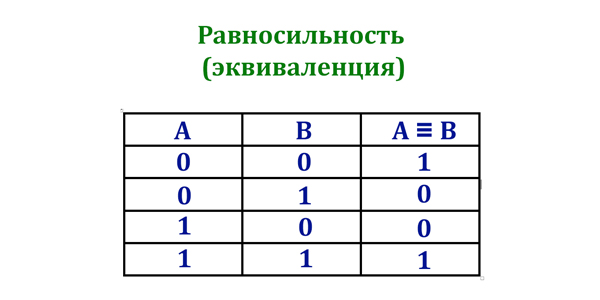
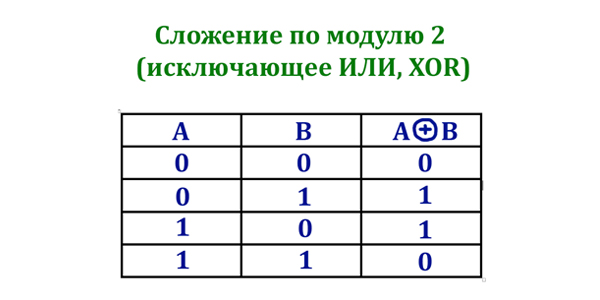
Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).
С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.
- () — операции в скобках
- ¬ — логическое отрицание
- ∧ — логическое умножение
- ∨ — логическое сложение
- ⟶ — следование
- ≡ — равнозначность
Ещё соотношения:
Передём к решению задач из ЕГЭ по информатике
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.
Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.
Задача 2 (средний уровень)
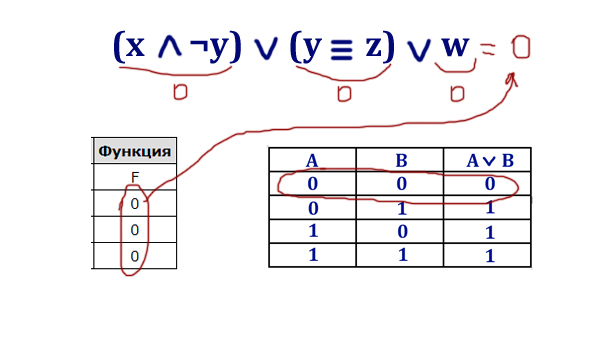
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.
Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.
Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!
Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).
Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).
Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.
Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.
Тогда ответ будет равен yxwz.
Ответ: yxwz
Мощнейший метод для решения второго задания из ЕГЭ по информатике
Задача 3 (хороший уровень)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).
Тогда каждое выражение должно равняться 0(нулю).
Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 2 4 ).
Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).
При небольшой тренировке анализ подобных выражений занимает сущие секунды!
У нас получается 4 строчки, которые удовлетворяют нашей функции:
Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).
Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.
Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец
Ответ: ywzx.
На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!
Строки с пропущенными значениями 2 задание егэ информатика как решать
Тип 2 № 14688
Логическая функция F задаётся выражением (x ∨ y) → (z ≡ x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| . | . | . | F |
| 0 | 0 | 0 | |
| 0 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| . | . | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть x = 0, тогда y = z = 1. В первой строке нет двух единиц, значит, x = 1, и эта переменная находится в первом столбце. Тогда первая строка имеет вид 1 0 0.
Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:
Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ∨ y) → (z ≡ x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы:
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, первый столбец таблицы соответствует переменной x, и в первом столбце первой строки стоит 1.
Второй столбец таблицы может соответствовать только переменной z, поскольку переменная y принимает нулевое значение только в одном наборе. Тогда третий столбец соответствует переменной y.
Тип 2 № 15097
Логическая функция F задаётся выражением (x ≡ z ) ∨ (x → (y ∧ z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
. . . F
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть . Исходя из системы (*), , тогда . В первой строке нет единицы, значит, переменная x находится в третьем столбце. Тогда первая строка имеет вид 0 0 1.
Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:
Второй вариант не удовлетворяет системе (*), а первый удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ≡ z ) ∨ (x → (y ∧ z)) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы:
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, третий столбец — это переменная x. Вторая строка соответствует набору (1, 1, 0), в котором единичное значение принимает также переменная y, следовательно, первый столбец — это переменная у, тогда второй столбец — это переменная z.
Тип 2 № 15124
Логическая функция F задаётся выражением (x ≡ y ) ∨ ((y ∨ z) → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
. . . F
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть . Исходя из системы (*), , тогда . В первой строке нет нуля, значит, переменная x находится в первом столбце. Тогда первая строка имеет вид 0 1 1.
Вторая строка должна отличаться от первой, поэтому она имеет вид 0 0 1. Рассмотрим два варианта:
Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ≡ y ) ∨ ((y ∨ z) → x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы: (0, 1, 0), (0, 1, 1).
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
В обоих наборах переменная x принимает значение 0, значит, ей может соответствовать только первый столбец таблицы. Переменная z принимает значение 1 только в одном наборе, значит, ей может соответствовать только второй столбец таблицы, тогда третий столбец соответствует переменной у.
Тип 2 № 15618
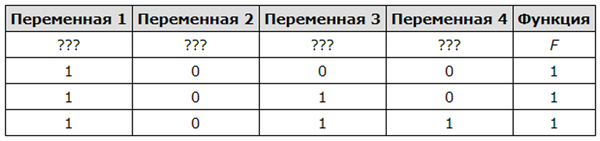
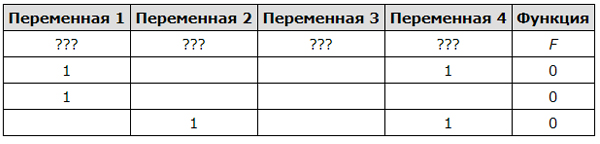
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w. На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 |
|---|---|---|---|
| . | . | . | . |
| 0 | |||
| 1 | 0 | 0 | |
| 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (без разделителей).
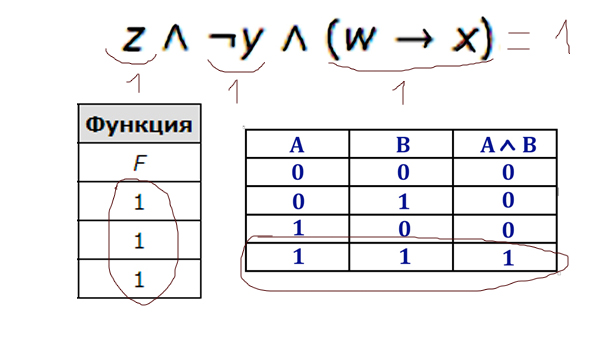
Рассмотрим данное выражение. Преобразуем логическое выражение (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w и получим систему, при которой оно ложно:
Cразу видно, что первый столбец это w, поскольку w всегда должна равняться единице. Также, ясно, что x это переменная 4, так как . Из первого выражения x ∧ ¬y и последней строчке таблицы видно, что переменная 3 это y, а вторая переменная это z.
Рассмотрим, как будет выглядеть полная таблица истинности. Переменная w всегда должна принимать значение 1, поэтому в первом столбце во всех строках будет стоять единица. Исходя из условия можно заключить, что во втором столбце в последней строке будет стоять единица, и в первых двух строках третьего столбца тоже будут стоять единицы. В первой четвёртого столбца должна стоять единица, поскольку строки в таблице истинности должны быть разными.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 |
|---|---|---|---|
| . | . | . | . |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Вариант wyzx не подходит, поскольку в первой строке функция F окажется истинной.
Приведем другое решение.
Составим таблицу истинности функции F и выпишем наборы переменных, при которых функция ложна. Для удобства обозначим эти наборы буквами:
А: (х=0, y=0, z=1, w=1)
Б: (х=0, y=1, z=0, w=1)
В: (х=1, y=1, z=0, w=1)
Заметим, что переменная w всегда должна быть равна 1, поэтому ей соответствует первый столбец заданной таблицы.
Заметим, что вторая и третья строки заданной таблицы, содержащие по два нуля, соответствуют наборам переменных А или Б, тогда первая строка соответствует набору В. Значит, в первой строке z=0, а все остальные переменные равны 1, и переменной z соответствует второй столбец заданной таблицы.
Тогда вторая строка заданной таблицы, в которой переменная z также равна 0, соответствует набору Б, в котором х=0, а остальные переменные равны 1, поэтому переменной х соответствует четвертый столбец таблицы.
Строки с пропущенными значениями 2 задание егэ информатика как решать
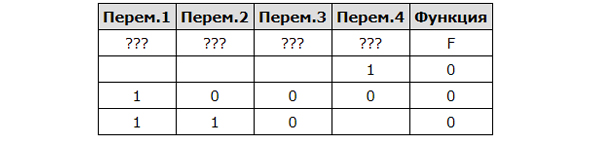
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | Функция |
| . | . | . | . | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
Логическая функция F задается выражением
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | Функция |
| . | . | . | . | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
Миша заполнял таблицу истинности функции
(¬x ∧ ¬y) ∨ (y ≡ z) ∨ w,
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| ? | ? | ? | ? | (¬x∧¬y)∨(y≡z)∨w |
|---|---|---|---|---|
| 0 | 1 | 0 | ||
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
Логическая функция F задается выражением
¬(z ∨ (y ∧ ¬x))
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Функция |
|---|---|---|---|
| . | . | . | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Видеоразбор
Логическая функция F задается выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.