На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 18 задания. Объясняется тема об обработке числовой информации в электронных таблицах.
Содержание:
- ЕГЭ по информатике 18 задание объяснение
- Решение 18 задания ЕГЭ
- Исполнитель Робот
18-е задание: «Обработка числовой информации в электронных таблицах»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение обрабатывать вещественные выражения в электронных таблицах
Решение 18 задания ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Исполнитель Робот
18 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
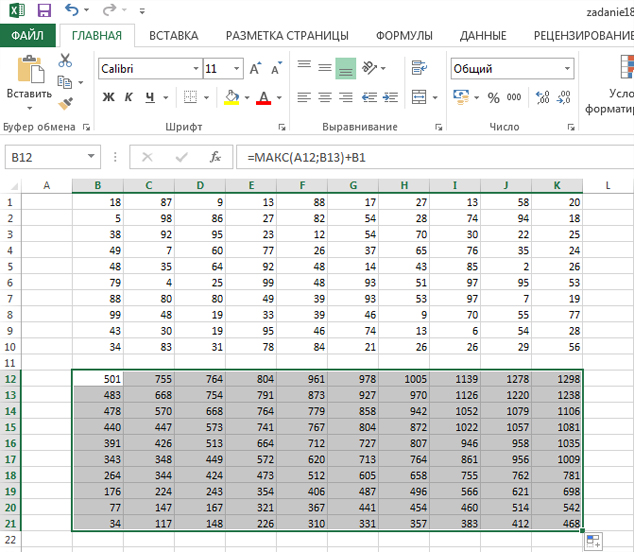
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
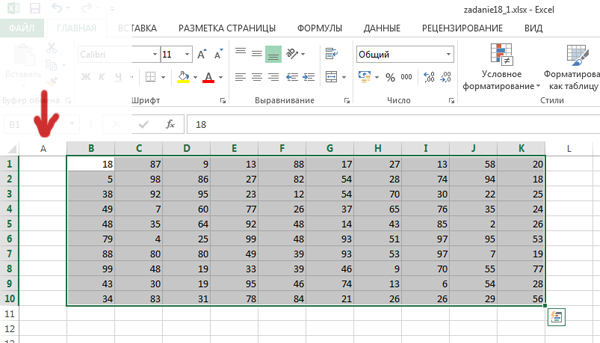
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:

Ответ: 1204 | 502
Решение подобного задания смотрите в следующем ниже разборе.
📹 YouTube здесь
Видеорешение на RuTube здесь
18_1:
Задание выполняется с использованием прилагаемых файлов
Исходные данные записаны в файле (выше) в виде электронной таблицы прямоугольной формы.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой НИЖНЕЙ клетки в правую ВЕРХНЮЮ. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
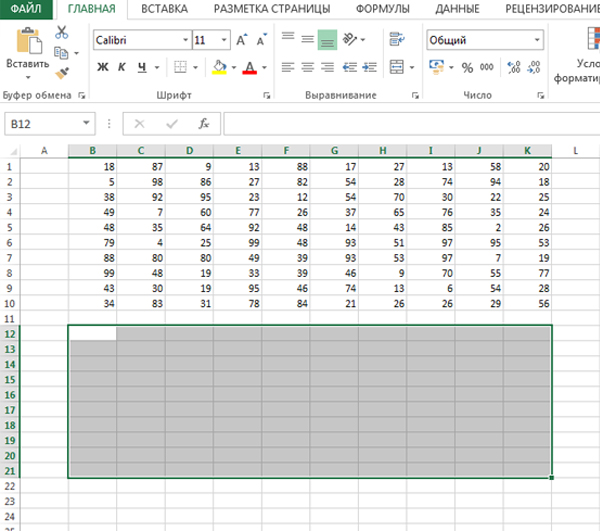
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — верхняя правая ячейка
J12результирующей таблицы. Робот просто соберет монету, которая находится в этой ячейке. Поэтому для ячейки возьмем значение из исходной таблицы. Введите формулу:
=J1
J12 Робот мог, либо двигаясь из ячейки I12, либо из J13. I12. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка I1). Ну и поскольку дальше он попадет только в ячейку J12, то необходимо прибавить значение этой ячейки. Поскольку значение уже просчитано для результирующей таблицы, то мы и будем его брать именно с результирующей таблицы. То есть введите формулу для ячейки I12:=I1+J12
I12, будет такой же и для всех оставшихся ячеек верхней строки.I12 в диапазон ячеек A12:H12:J13. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — J2) и добавим значение ячейки, в которую он пойдет дальше — ячейка J12 (берем значение из результирующей таблицы, поскольку оно уже просчитано):=J2+J12
J13 подходит для всех ячеек данного столбца.J13 в диапазон ячеек J14:J21:I12 и J13 Робот мог попасть, также двигаясь из ячейки I13. Рассмотрим ее.I13 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — I2), и затем у него альтернатива движения: либо в ячейку I12, либо в J13. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Для этого надо выбрать максимум из I12 и J13 и добавить к текущему значению. Введите формулу в I13:
=I2+МАКС(I12;J13)
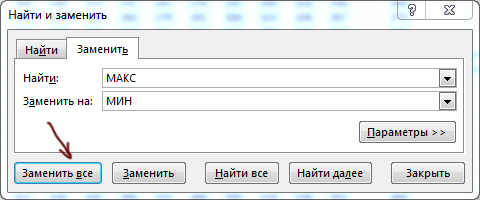
I13, использовав маркер копирования, во все оставшиеся ячейки таблицы:I13 на =I2+МИН(I12;J13).Ответ: 1133 | 522
18_2:
Задание выполняется с использованием прилагаемых файлов
При попытке зайти на клетку со стеной Робот разрушается. Исходные данные записаны в файле в виде электронной таблицы прямоугольной формы. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю, не разрушившись. Известно, что такой путь существует. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — нижняя правая ячейка
L25результирующей таблицы. Робот просто соберет монету, которая находится в этой ячейке исходной таблицы —L12. Поэтому для ячейки возьмем значение из исходной таблицы. Введите формулу:
формула для L25:
=L12
L12 Робот мог, либо двигаясь из ячейки K12, либо из L11. К12. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка K12). Ну и поскольку дальше он попадет только в ячейку L12, то необходимо прибавить значение этой ячейки.K25:=ЕСЛИ(И(L25>0;ИЛИ(K12<=100;K12>=500));K12+L25;0)
Если выполняются одновременно два условия: L25>0 И либо K12<=100 либо K12>=500, то собираем монету с текущей ячейки (K12) и добавляем монету с L25, так как там нет стены (L25>0)
K25 будет такой же и для всех оставшихся ячеек строки.K25 в диапазон ячеек A25:J25.L24. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — L11) и добавим значение ячейки, в которую он пойдет дальше — ячейка L25 (берем значение из результирующей таблицы, поскольку оно уже просчитано):=ЕСЛИ(И(L25>0;ИЛИ(L11<=100;L11>=500));L11+L25;0)
Если выполняются одновременно два условия: L25>0 И либо L11<=100 либо L11>=500, то собираем монету с текущей ячейки (L11) и добавляем монету с L25, так как там нет стены (L25>0)
L24 в диапазон ячеек L14:L23.K24 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — K11), и затем у него альтернатива движения: либо в ячейку L24, либо в K25. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Не забудем проверять значение каждой ячейки, нет ли там стены. Для этого введите формулу в K24:=ЕСЛИ(И(K11>100;K11<500);0;ЕСЛИ(И(L24=0;K25=0);0;ЕСЛИ(L24=0;K11+K25; ЕСЛИ(K25=0;K11+L24;K11+МИН(L24;K25)))))
Здесь логика формулы следующая: если текущее значение ячейки соответствует стене, то записываем 0; ИНАЧЕ — если обе ячейки, в которые может двигаться Робот, — стены, то записываем в текущую ячейку 0; ИНАЧЕ — если ячейка справа — стена, то двигаемся вниз, собирая по пути монеты; ИНАЧЕ — если ячейка снизу — стена, то двигаемся вправо, собирая по пути монеты; ИНАЧЕ — выбираем минимальное значение из соседних ячеек и собираем монеты.
K24, использовав маркер копирования, во все оставшиеся ячейки таблицы:МАКС на МИН. И скопируйте снова данную формулу во всю оставшуюся таблицу.
Ответ: 1492 640
18_3:
Задание выполняется с использованием прилагаемых файлов
Робот может двигаться только вниз и вправо. Для сбора денег у Робота есть контейнеры вместимостью 8 монет каждый. С каждой клетки Робот забирает наибольшее количество контейнеров, полностью заполненных монетами. Если контейнер не заполнен до конца, а монеты в клетке кончились, робот высыпает из него монеты перед переходом в следующую клетку. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — нижняя правая ячейка
J21результирующей таблицы. Робот просто соберет монеты, которые находится в этой ячейке исходной таблицы —J10, если наберется целое число контейнеров (значение кратное 8). Если целое число контейнеров не набирается, — то робот забирает только то, что набралось в контейнеры (8* ЧАСТНОЕ от деления монет на 8). Поэтому для ячейки возьмем значение из исходной таблицы, проверяя его на кратность 8. Введите формулу:
формула для J21:
=ЕСЛИ(ОСТАТ(J10;8)=0;J10;8*ЧАСТНОЕ(J10;8))
J20. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка J9). При этом будем проверять значение на кратность 8 и действовать так же, как описано в предыдущем пункте. Ну и поскольку дальше Робот попадет только в ячейку J21, то необходимо прибавить значение этой ячейки.формула для J20: =ЕСЛИ(ОСТАТ(J9;8)=0;J9+J21;8*ЧАСТНОЕ(J9;8)+J21)
J20 будет такой же и для всех оставшихся ячеек столбца.J20 в диапазон ячеек J12:J19.I21. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — I10). Проверим заполненность контейнеров, и добавим значение ячейки, в которую Робот пойдет дальше — ячейка J21 (берем значение из результирующей таблицы, поскольку оно уже просчитано):формула для I21:
=ЕСЛИ(ОСТАТ(I10;8)=0;I10+J21;8*ЧАСТНОЕ(I10;8)+J21)
I21 в диапазон ячеек A21:H21.I20 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — I9), проверяя заполненность контейнеров, и затем у него альтернатива движения: либо в ячейку J20, либо в I21. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Не забудем проверять значение каждой ячейки на заполненность контейнеров. Для этого введите формулу в I20:формула для I20:
=ЕСЛИ(ОСТАТ(I9;8)=0;I9+МАКС(J20;I21);8*ЧАСТНОЕ(I9;8)+МАКС(J20;I21))
I20, использовав маркер копирования, во все оставшиеся ячейки таблицы.МАКС на МИН. И скопируйте снова данную формулу во всю оставшуюся таблицу.Ответ: 1144 448
Привет! Мы добрались до 18 задания из ЕГЭ по информатике 2021.
Это задание снова решается с помощью компьютера.
Восемнадцатое задание направлено на обработку вещественных чисел с помощью таблиц. Мы с вами будет использовать программу Excel от компании Microsoft.
Перейдём к к тренировке решения 18 задания из ЕГЭ по информатике 2021.
Задача (Стандартная)
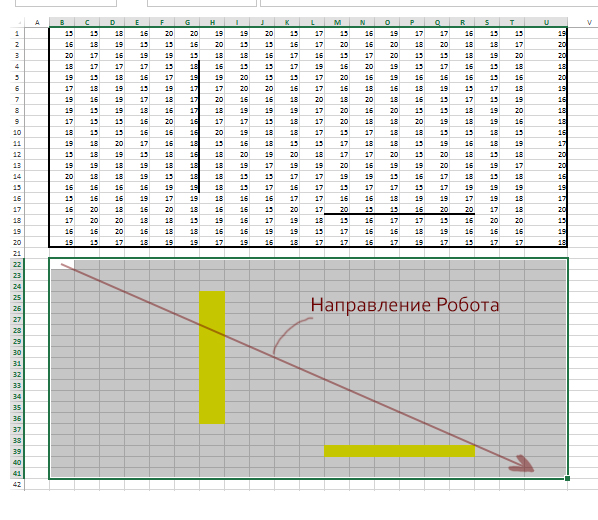
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монеты с собой; это также относится к начальной и конечной клетке маршрута Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
Решение:
Открываем файл к данной задачке.
В начале найдём максимальную сумму.
Выделяем область всех ячеек, где написаны числа, вырезаем её и вставляем на столбец правее. Это нужно для того, чтобы при составлении формулы решения не было ошибок.
Обозначим мысленно ту область, где мы будем составлять наше решение, пропустив одну или две строчки снизу. По размеру область будет такая же.
В каждой ячейке этой области будет лежать максимальная cумма, которую может собрать Робот, дойдя до этой клетки. Т.к. Робот идёт в верхнюю правую клетку, то, соответственно, в ячейке K12 будет находится нужный нам ответ.
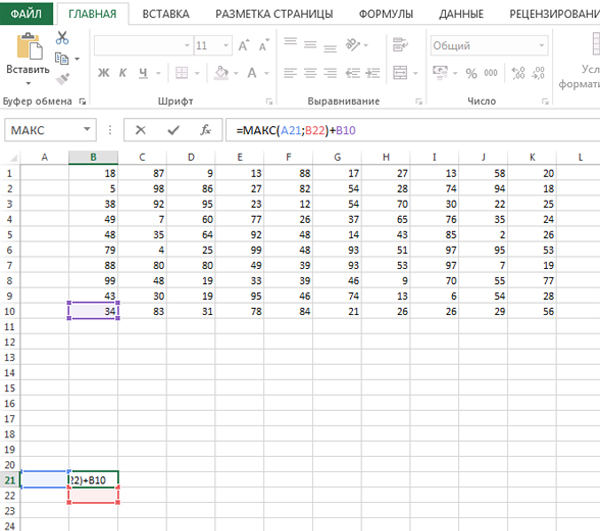
Наш Робот идёт из левой нижней клетки. Поэтому формулу, решающую эту задачу, составим сначала для ячейки B21.
Кликаем на ячейку B21 и пишем формулу:
=МАКС(A21;B22)+B10
Примечание: Чтобы в ячейке начать писать формулу, нужно поставить знак «=».
В любую ячейку нашей области можно попасть либо слева, либо снизу (Т.к. составляем формулу для любой ячейки, то не играет роли, что в данная ячейка угловая). Поэтому для ячейки B21 мы берём предыдущий результат — либо из левой ячейки, либо из правой ячейки, в зависимости от того, где собранная сумма больше.
Эту роль исполняет функция МАКС(). Она помогает выбрать откуда нужно идти, чтобы сумма всегда была максимальна.
Плюс, мы должны добавить сумму для данной ячейки к максимальной сумме предыдущей клетки. Поэтому в формулу дописываем ячейку B10
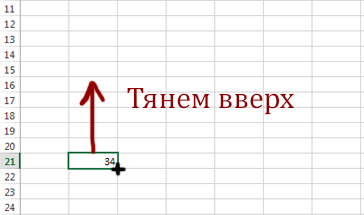
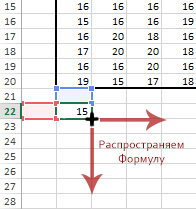
После того, как составили формулу для одной ячейки B21, можно распространить формулу на всю область.
Подносим мышку к правому нижнему углу. Как только появился чёрный крестик, кликаем левую кнопку мыши, и тянем вверх на 10 строчек вверх.
После того, как столбец готов, выделяем этот столбец, и аналогично, распространяем его на всё пространство.
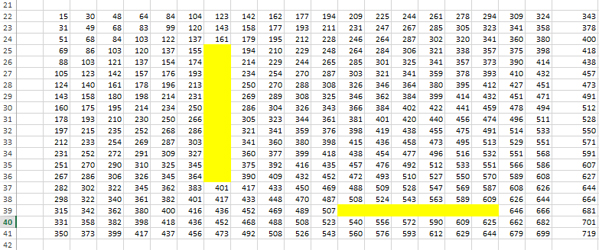
В итоге получается такая картина:
Видим, что в ячейке K12 значение 1298. Это значение нам и нужно.
Аналогичным образом ищется минимальное значение, только в формуле вместо функции МАКС будет использоваться функция МИН.
Минимальное значение получилось 589.
Ответ: 1298589
Посмотрим ещё одну интересную задачу из примерны задач ЕГЭ по информатике нового образца 2021.
Задача (со стенками)
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается
в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата
также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета
достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой;
это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем
минимальную.
Исходные данные представляют собой электронную таблицу размером
N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние
и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел
Решение:
Открываем файл в программе Excel.
Выделим все ячейки с числами, нажмём «вырезать», используя контекстное меню. Вставим данные на 1 столбец вправо. Это делаем потому, что будем использовать для решения формулу, которая будет обращаться к ячейке слева.
Мысленно представим пространство на 1 строчку ниже, чем область, где находятся числа. Это пространство будет таким же по размерам, как и область с числами. В этом пространстве и будет наше решение.
Отметим особым цветом те ячейки, которые «спрятаны» от движения Робота стенками.
Для этих ячеек будем составлять другие формулы, в отличии от обычных ячеек.
Цвет ячейки можно поменять, нажав на кнопку «Цвет заливки» на главной вкладке программы.
Т.к. Робот направляется из левой верхней ячейки, то мы сначала и напишем формулу для этой ячейки. Пишем для ячейки B22:
=МАКС(B21;A22)+B1
Робот в любую ячейку может прийти либо сверху, либо слева. Для подсчёта максимального количества монет, мы должны выбрать максимальное предыдущее значение. Это и делаем формула. Плюс Робот должен взять монеты с текущей клетки.
Распространим формулу на всё пространство, не трогая закрашенные клетки.
Получается такая картина:
В ячейки для первой закрашенной области, Робот может попасть только сверху! Поэтому пишем формулу для ячейки H25:
=H24+H4
Распространяем формулу по всему закрашенному столбцу.
В ячейки для второй закрашенной области, Робот может попасть только слева! Поэтому пишем формулу для ячейки М39:
=L39+M18
Распространяем формулу по всей закрашенной строчке.
В правом нижнем углу нашего рабочего пространства получается максимальное количество монет, которое может собрать Робот. В ячейке U41 получается число 721.
Чтобы получить минимальную возможную сумму, в главной формуле функцию МАКС нужно заменить на МИН!
Удобно воспользоваться автоматической заменой через Ctrl+F.
Минимальная сумма равна 640.
Ответ:
Задача (Два Робота)
Квадрат разлинован на N×N клеток (2 < N < 19). В каждой клетке лежат
монеты, количество которых соответствует записанному числу. Количество
монет не может быть меньше 1.
Два исполнителя – ВЕРХ и НИЗ – существуют на одинаковых полях. Первый
имеет две команды – вверх и вправо, второй – вниз и вправо, которые,
соответственно, перемещают исполнитель на одну клетку вверх, вниз или
вправо. Исполнитель ВЕРХ начинает движение в левой нижней ячейке,
исполнитель НИЗ – в левой верхней.
Откройте файл. Какой из исполнителей соберет большее количество монет в результате
своей работы, если известно, что каждый из них запрограммирован собрать
максимальное количество монет?
Исходные данные представляют собой электронную таблицу размером N×N,
каждая ячейка которой соответствует клетке квадрата.
Пример:
| 1 | 8 | 8 | 4 | 10 |
| 10 | 1 | 1 | 3 | 2 |
| 1 | 3 | 12 | 2 | 8 |
| 2 | 3 | 5 | 6 | 11 |
| 3 | 19 | 14 | 11 | 5 |
Для указанных входных данных ответом является комбинация из названия
исполнителя и количества собранных монет
ВЕРХ84
Решение:
Перенесём таблицу чисел на один столбец вправо.
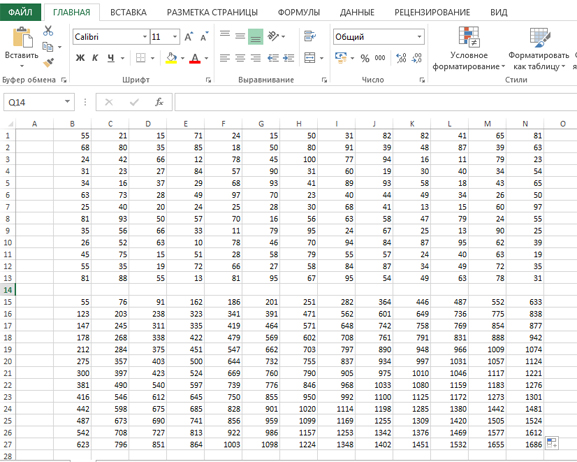
Найдём, сколько соберёт монет исполнитель ВЕРХ.
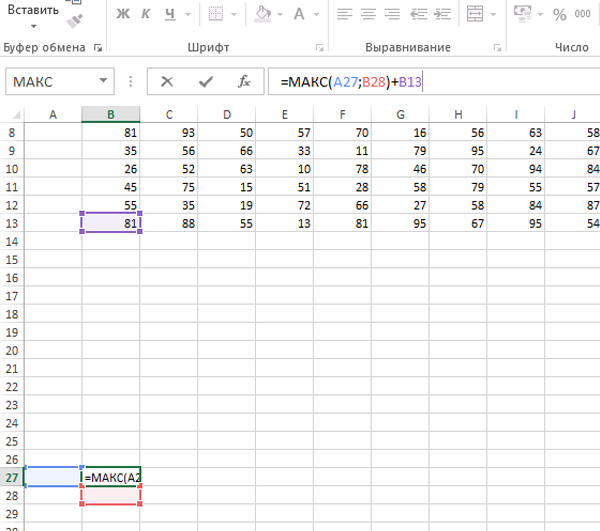
Исполнитель «ВЕРХ» начинает идти с левой нижней клетки. Поэтому первую формулу мы зададим для клетки B27. Эта ячейка является нижней левой клеткой для области, где мы будем составлять решение.
Напишем в ячейке B27:
=МАКС(A27;B28)+B13
Распространим формулу на всё пространство.
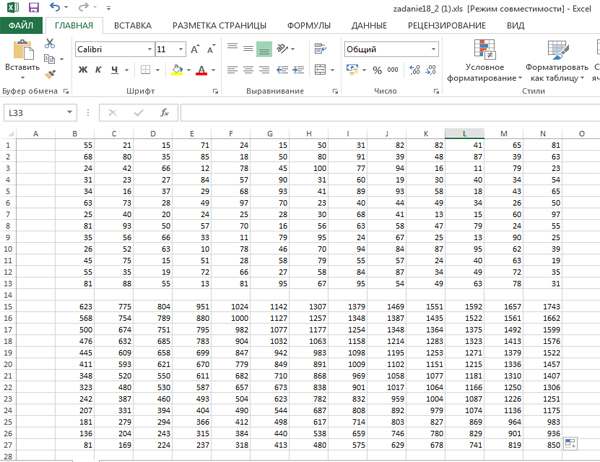
Когда исполнитель пройдёт всё поле, в ячейке N15 будет находится ответ. Максимальное количество монет, которое может собрать исполнитель ВЕРХ будет 1743.
Теперь найдём максимальное количество монет, которое может собрать исполнитель НИЗ.
Решать будем аналогичным образом, удалив все следы от предыдущего исполнителя.
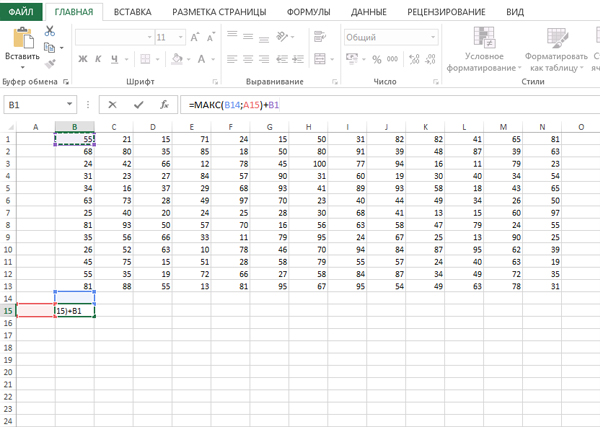
Т.к. исполнитель НИЗ стартует с левой верхней клетки, то мы сначала составим формулу для ячейки B15. Эта клетка олицетворяет левую верхнюю ячейку для области, где будет происходить решение.
=МАКС(B14;A15)+B1
В любую ячейку мы можем попасть либо сверху, либо слева. Это не относится к боковым и угловым ячейкам, но формула будет работать и для них.
При составлении максимальной суммы для любой ячейки, мы выбираем максимальное значение суммы из двух предыдущих ячеек + добавляем значение для этой ячейки.
Распространим формулу на всё пространство.
В ячейке N27 будет максимальное значение для исполнителя НИЗ. Получилось 1686.
Видим, что у исполнителя ВЕРХ получилось собрать больше монет.
Ответ: ВЕРХ1743
Спасибо за ваши советы, не знаю как без них бы я готовился к экзамену, не сдавайтесь и продолжайте помогать нам, молодёжи, удачи!
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 41 и 22.
Источник: Демонстрационная версия ЕГЭ−2021 по информатике
2
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
3
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 41 и 22.
4
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
5
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 41 и 22.
Пройти тестирование по этим заданиям
Подборка заданий №18 ЕГЭ по информатике.
30 разноплановых задач, как простых, так и сложных. Подойдет для качественного обзора всех прототипов и даже больше.
Имеются ссылки на разборы всех заданий
→ скачать задания
Примеры заданий:
Задание 18.2
Квадрат разлинован на N×N клеток (3 < N < 15), где N – нечетное число. На поле работает 4 исполнителя Грузовичок, которые начинают движение из центральной клетки. Например, для N = 5 из клетки С3. Каждый исполнитель двигается в один из углов – левый верхний, правый верхний, левый нижний или правый нижний – и может двигаться соответственно только – налево и вверх, направо и вверх, вниз и влево, вниз и вправо. Исполнители работают независимо друг от друга на своей копии поля. Каждая пройденная клетка содержит число – массу в килограммах забираемого груза. Цель исполнителя – забрать как можно больший объем груза, выраженный в килограммах.
Необходимо найти наилучшие результаты работы каждого Грузовичка. Результаты перечислить в порядке возрастания значений.
Задание 18.6
Квадрат разлинован на N×N клеток (2 < N < 19). В каждой клетке лежат монеты, количество которых соответствует записанному числу. Количество монет не может быть меньше 10. В лабиринте существуют два независимых исполнителя – Кладоискатель1 и Кладоискатель2. Каждый из них имеет две команды – влево и вниз – при выполнении которых исполнитель сдвигается либо на одну клетку влево или вниз соответственно. Движение начинается в верхней правой клетке и заканчивается с левой нижней. Известно, что каждый исполнитель запрограммирован так, чтобы собрать максимальное количество монет на своем пути. При этом сначала на поле работает исполнитель Кладоискатель1, затем Кладоискатель2. Кладоискатель2 может проходить по клеткам из лучшего маршрута для исполнителя Кладоискатель1, однако значение в этих клетках будет равно 0.
Необходимо найти результат работы обоих исполнителей, в качестве ответа указать найденные значения – сначала для исполнителя Кладоискатель1, затем для Кладоискатель2.
Источник: vk.com/inform_web
Связанные страницы:
Динамическое
программирование. Робот – сборщик монет
Разбор задания № 18 КЕГЭ 2021
Проверяемые элементы содержания:
Умение обрабатывать
вещественные выражения в электронных таблицах.
Использование инструментов
решения статистических и расчётно-графических задач.
Проверяемые
умения или способы действий: представлять и
анализировать табличную информацию
(повышенный уровень, время – 6
мин)
|
Задание повышенного уровня сложности проверяет знания и |
|||
|
использовать для расчетов в таблицах |
|||
|
таблицу значениями с использованием формул, |
|||
|
Кроме того, это задание проверяет умение применять методы динамического |
|||
|
программирования при решении задач с |
|||
|
При выполнении этого задания важно построить правильную |
|||
|
модель процесса, аккуратно описать |
|||
|
интерпретировать |
|||
|
Динамическое |
|||
|
разбиения на несколько |
|||
|
Самым простым примером будут числа Фибоначчи — чтобы |
|||
|
число в этой последовательности, нам нужно |
|||
|
первые два, затем четвертое таким же |
|||
|
далее. |
|||
|
Решение задачи динамическим программированием должно |
|||
|
● |
|||
|
условии); |
|||
|
● значение начальных состояний. |
|||
|
В задачах данного типа “динамическое программирование” |
|||
|
означает оптимальную |
|||
Общие сведения:
|
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель |
|
перемещаться по клеткам, выполняя за одно |
|
или вниз. По команде вправо Робот перемещается |
|
команде вниз – в соседнюю нижнюю. При |
|
разрушается. Перед каждым запуском Робота |
|
достоинством от 1 до 100. Посетив клетку, Робот |
|
относится |
Информационные ресурсы:
1. Теория:
Обработка числовой информации
2. Задания
для тренировки: Задания 18. Робот-сборщик монет
За да ние № 18 (ФИПИ ДЕМО КЕГЭ-2021)
|
Определите максимальную |
||||||||||||
|
собрать Робот, пройдя из левой верхней |
||||||||||||
|
два |
||||||||||||
|
Исходные данные |
||||||||||||
|
ячейка |
||||||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|||
|
1 |
51 |
21 |
93 |
48 |
45 |
100 |
67 |
39 |
18 |
29 |
||
|
2 |
57 |
43 |
97 |
51 |
92 |
10 |
93 |
32 |
19 |
58 |
||
|
3 |
63 |
16 |
31 |
16 |
78 |
88 |
90 |
72 |
37 |
67 |
||
|
4 |
10 |
57 |
64 |
25 |
96 |
50 |
81 |
65 |
91 |
69 |
||
|
5 |
99 |
43 |
95 |
7 |
40 |
76 |
18 |
34 |
5 |
65 |
||
|
6 |
35 |
19 |
71 |
77 |
64 |
38 |
62 |
56 |
10 |
2 |
||
|
7 |
100 |
57 |
27 |
26 |
51 |
33 |
100 |
11 |
53 |
1 |
||
|
8 |
11 |
79 |
49 |
46 |
37 |
69 |
80 |
31 |
25 |
39 |
||
|
9 |
22 |
71 |
20 |
23 |
11 |
12 |
39 |
16 |
64 |
34 |
||
|
10 |
4 |
25 |
87 |
84 |
30 |
48 |
77 |
13 |
40 |
33 |
Решение:
1.
В первой строке таблицы и в первом столбце вычислим значения с
нарастающим итогом, т.е.
a.
в ячейку L1 введём формулу =A1,
b.
в M1 =L1+B1, с помощью автозаполнения копируем формулу из M1
в диапазон ячеек N1:U1;
c.
в L2 =L1+A2, с помощью автозаполнения копируем
формулу из L2 в диапазон ячеек L3:L10;
2.
Для поиска максимальной суммы в ячейку M2 введём формулу
=MAX(M1;L2)+B2
3.
С помощью автозаполнения скопируем формулу из M2 в
диапазон ячеек
M2:U10. Получим таблицу:
В ячейке U10 находится искомое
число: max = 1204.
4.
Для поиска минимальной суммы в ячейку M2 введём формулу
=MIN(M1;L2)+B2
5. С помощью автозаполнения скопируем формулу из M2 в
диапазон ячеек
M2:U10. Получим таблицу:
|
Задание 18 № |
|
|
Дан квадрат 15 × 15 клеток, в каждой клетке которого |
|
|
правом верхнем углу квадрата |
|
|
одну клетку влево, вниз или по |
|
|
робот не может. Необходимо переместить |
|
|
сумма чисел в клетках, через которые прошёл |
|
|
была максимальной. |
|
|
Исходные данные |
Решение:
1. В
первой строке таблицы и в первом столбце вычислим значения с нарастающим
итогом, т.е.
a.
в ячейку O17 введём формулу =O1,
b.
в N17 =O17+N1, с помощью автозаполнения копируем (справа
налево) формулу из N17 в диапазон ячеек A17:M17;
c.
в O18 =O17+O2, с помощью автозаполнения копируем (сверху
вниз) формулу из O18 в диапазон ячеек O19:O21;
2.
Для поиска максимальной суммы в ячейку N18 введём формулу
=MAX(N17;O17;O18)+N2
3. С помощью
автозаполнения скопируем (по диагонали влево вниз) формулу из N18 в
диапазон ячеек A18:N31. Получим таблицу:
Разбор заданий № 24. Готовимся к итоговой
аттестации 2021. Лещинер, В.Р.[2]
|
Вариант № 1 |
|
|
Определите максимальную |
|
|
собрать Робот, пройдя из левой нижней |
|
|
два |
|
|
Исходные данные |
|
|
ячейка |
Решение:
1.
В последней строке таблицы и в первом столбце вычислим
значения с нарастающим итогом, т.е.
a.
в ячейку N12 введём формулу =A12,
b.
в O12 =N12+B12, с помощью автозаполнения копируем формулу
из O12 в диапазон ячеек P12:Y12;
c.
в N11 =N12+A11, с помощью автозаполнения копируем формулу
из N11 в диапазон ячеек N1:N10;
2.
Для поиска максимальной суммы в ячейку O11 введём формулу
=MAX(N11;O12)+B11
3.
С помощью автозаполнения скопируем формулу из O11 в
диапазон ячеек O1:Y11. Получим таблицу:
В ячейке Y1 находится
искомое число: max = 1439.
4.
Для поиска минимальной суммы в ячейку O11 введём формулу
=MIN(N11;O12)+B11
5. С
помощью автозаполнения скопируем формулу из O11 в диапазон ячеек O1:Y11.
Получим таблицу:
|
Вариант № 2 |
|
|
Определите максимальную |
|
|
собрать Робот, пройдя из правой нижней |
|
|
два |
|
|
Исходные данные |
|
|
ячейка |
Решение:
1.
В последней строке таблицы и в последнем столбце
вычислим значения с нарастающим итогом, т.е.
a.
в ячейку Y12 введём формулу =L12,
b.
в X12 =Y12+K12, с помощью автозаполнения копируем формулу
из X12 в диапазон ячеек N12:W12;
c.
в Y11 =Y12+L11, с помощью автозаполнения копируем формулу
из Y11 в диапазон ячеек Y1:Y10;
2.
Для поиска максимальной суммы в ячейку X11 введём формулу
=MAX(X12;Y11)+K11
3.
С помощью автозаполнения скопируем формулу из X11 в
диапазон ячеек
N1:X11. Получим таблицу:
В ячейке N1 находится
искомое число: max = 1345
4.
Для поиска минимальной суммы в ячейку X11 введём формулу
=MIN(X12;Y11)+K11
5. С помощью автозаполнения скопируем формулу из X11 в
диапазон ячеек
N1:X11. Получим таблицу:
Задание № 18.1
|
Определите максимальную |
|
собрать Робот, пройдя из правой верхней |
|
два |
|
Исходные данные |
|
ячейка |
Решение:
1. В первой строке таблицы
и в последнем столбце вычислим значения с нарастающим итогом, т.е.
a.
в ячейку U1 введём формулу =J1,
b.
в T1 =U1+L1, с помощью автозаполнения копируем формулу
из T1 в диапазон ячеек L1:S1;
c.
в U2 =U1+J2, с помощью автозаполнения копируем формулу
из U2 в диапазон ячеек U3:U10;
2. Для поиска максимальной суммы в ячейку T2 введём формулу
=MAX(T1;U2)+I2
3.
С помощью автозаполнения скопируем формулу из T2 в
диапазон ячеек L2:T10. Получим таблицу:
В ячейке L10 находится
искомое число: max = 1133.
4.
Для поиска минимальной суммы в ячейку T2 введём
формулу =MIN(T1;U2)+I2
5.
С помощью автозаполнения скопируем формулу из T2 в
диапазон ячеек L2:T10. Получим таблицу:
ЕГЭ информатика 18 задание разбор, теория, как решать.
Динамическое программирование в электронных таблицах. Робот-сборщик монет, (П) — 1 балл
Е18.16 Определите максимальную и минимальную денежные суммы
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут …
Читать далее
Е18.20 количество недоступных клеток, в которые робот не сможет попасть из-за нехватки энергии
Робот с тоит в левом н ижнем углу прямоугольного поля, в каждой клетке которого записано целое число. За один ход робот может переместиться на одну клетку вправо или на одну клетку вверх. Выходить за пределы поля робот не может. Числа показывают изменение запаса энергии робота при прохождении соответствующей клетки. Если число отрицательно, запас энергии уменьшается …
Читать далее
Е18.19 Посетив клетку, Робот забирает монету с собой
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут …
Читать далее
Е18.18 Определите количество способов, которыми Робот может попасть из левой верхней клетки в правую нижнюю.
Квадрат разлинован на МхМ клеток (1 < N < 20). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке пересечь границы квадрата (внутренние, обозначенные жирной линией, или внешние) Робот …
Читать далее
Е18.17 Проходя через клетку, Сборщик собирает все монеты, лежащие на ней
Квадрат разлинован на N×N клеток (2 < N < 21). В каждой клетке записано целое положительное число – количество монет. Исполнитель Сборщик имеет две команды ВПРАВО и ВВЕРХ, которые, соответственно, перемещают его на одну клетку вправо или на одну клетку вверх. Проходя через клетку, Сборщик собирает все монеты, лежащие на ней. На поле существуют стены, …
Читать далее
Е18.16 включается в сумму, если оно больше числа в предыдущей клетке на пути робота
Дан квадрат 15×15 клеток, в каждой клетке которого записано целое число. В левом верхнем углу квадрата стоит робот. За один ход робот может переместиться на одну клетку вправо или на одну клетку вниз. Выходить за пределы квадрата робот не может. При этом ведётся подсчёт суммы по следующим правилам: число в очередной клетке, через которую проходит …
Читать далее
Е18.15 Между соседними клетками квадрата также могут быть внутренние стены.
Между соседними клетками квадрата также могут быть внутренние стены. Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат …
Читать далее
Е18.14 За посещение клетки A взимается плата 1 монета
За посещение клетки A взимается плата 1 монета Квадрат разлинован на N x N клеток (1 < N < 20). Исполнитель Буквоед может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Буквоед перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке …
Читать далее
Е18.13 каждое следующее число отличалось от предыдущего не более чем на 10
каждое следующее число отличалось от предыдущего не более чем на 10 Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число отличалось от предыдущего не более чем на 10. Какую максимальную сумму могут иметь выбранные числа? В ответе запишите только целую часть максимально возможной суммы. Исходная последовательность записана …
Читать далее
Е18.12 Два исполнителя – ПРАВО и ЛЕВО – существуют в рамках одного поля.
Два исполнителя – ПРАВО и ЛЕВО – существуют в рамках одного поля. Квадрат разлинован на N×N клеток (2 < N < 20), N – нечетное число. В каждой клетке лежат монеты, количество которых соответствует записанному числу. Количество монет не может быть меньше 1. Два исполнителя – ПРАВО и ЛЕВО – существуют в рамках одного поля. …
Читать далее