На уроке рассмотрен разбор 27 задания ЕГЭ по информатике: дается подробное объяснение и решение задания 2017 года
Содержание:
- Объяснение задания 27 ЕГЭ по информатике
- Решение 27 заданий ЕГЭ по информатике
- Задания 2021 и более поздние
- Задания предыдущих лет на повторение
- На вход программы поступает последовательность чисел, произвести анализ пар
- Выбрать из каждой пары одно число
- Набор данных, состоящих из троек чисел
- Анализ пар, находящихся на расстоянии
27-е задание: «Анализ числовых последовательностей»
Уровень сложности
— высокий,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 2,
Примерное время выполнения
— 35 минут.
Проверяемые элементы содержания: Умение создавать собственные программы (20–40 строк) для анализа числовых последовательностей
Рекомендации по выполнению:
«О выборе языка программирования. Выбирайте тот язык, которым лучше всего владеете. Никакого повышения или снижения баллов за экзотичность языка не предусмотрено.»
Типичные ошибки и рекомендации по их предотвращению:
ФГБНУ «Федеральный институт педагогических измерений»
Работа с записями
Запись в Паскале — это сложный тип данных, который может состоять из нескольких элементов – полей; поля могут иметь различный тип.
Подробно о записях объясняется здесь.
Решение 27 заданий ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Задания 2021 и более поздние
27_1 new:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 3 и при этом была минимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число – минимально возможную сумму, соответствующую условиям задачи.
Входные данные:
Даны два входных файла: файл A (27-1a.txt) и файл B (27-1b.txt), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 100000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 10 000.
Пример входных данных:
6 1 3 5 12 6 9 5 4 3 3 1 1
Пример выходных данных для приведённого выше примера входных данных:
20
✍ Решение:
-
Язык PascalABC.NET:
Язык Python (Питон):
f = open ('27-1b.txt') # для первого ответа - 27-1a.txt n=int(f.readline()) data=f.readlines() summa=0 minim=10001 # для минимальной разницы for i in range(0, n): s = data[i].split() a=int(s[0]) b=int(s[1]) summa+=min(a,b) # сумма максимумов из пар raznitsa = abs(a-b) # разница if raznitsa % 3 != 0: minim=min(minim,raznitsa) if summa % 3 != 0: print(summa) else: print(summa + minim) # здесь добавляем! т.к. иначе берем наибольший из пары
Ответ: 67303 200157496
Задания предыдущих лет на повторение
На вход программы поступает последовательность чисел, произвести анализ пар
27_4:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
Компьютер наземной станции слежения получает от объектов-самолётов, находящихся в зоне её работы, идентификационные сигналы, представляющие собой последовательность из N целых положительных чисел. Каждый объект направляет на наземную станцию уникальное число, т. е. все числа в получаемой станцией последовательности различны. Обработка сигнала представляет собой рассмотрение всех пар различных элементов последовательности, при этом элементы пары не обязаны быть переданы непосредственно друг за другом, порядок элементов в паре не важен. Считается, что возникла одна критическая ситуация, если произведение элементов некоторой пары кратно 58.
Необходимо определить общее количество возникших критических ситуаций.
Описание входных и выходных данных
В первой строке входных данных задаётся количество чисел N (1 < N < 1000). В каждой из последующих N строк записано одно целое положительное число, не превышающее 10 000.
В качестве результата программа должна напечатать одно число: общее количество возникших критических ситуаций.
Пример входных данных:
4 2 6 29 87
Пример выходных данных для приведённого выше примера входных данных:
4
Из четырёх заданных чисел можно составить б попарных произведений:
2*6 = 12 2*29 = 58 2*87 = 174 6*29 = 174 6*87 = 522 29*87 = 2523
Из них на 58 делятся 4 произведения (выделены синим).
Требуется написать эффективную по времени и по памяти программу для решения описанной задачи.
✍ Решение:
✎ Программа эффективна по времени и по памяти (4 балла):
- Язык Паскаль (версия PascalABC):
- Язык Python (версия Python 3):
- Язык Бейсик:
- Произведение двух чисел делится на 58, если выполнено одно из следующих условий (условия не могут выполняться одновременно).
- A. Оба сомножителя делятся на 58.
- Б. Один из сомножителей делится на 58, а другой не делится.
- B. Ни один из сомножителей не делится на 58, но один сомножитель делится на 2, а другой — на 29.
- Почему именно 2 и 29?
- Берем два делителя числа 58, произведение которых дает число 58: 2*29 = 58. При этом одно из них — наименьший делитель (в нашем случае 2), а другой, не должен делиться на первый найденный делитель (29/2 <> 0).
- Условие делимости произведения на 58 можно сформулировать проще, например так:
- Но в этом случае пара сомножителей может удовлетворять обоим условиям, что затруднит подсчёт количества пар.
- При вводе чисел можно определять, делится ли каждое из них на 58, 2 и 29, и подсчитывать следующие значения:
- n58 — количество чисел, кратных 58;
- n29 —количество чисел, кратных 29, но не кратных 2 и 58;
- n2 — количество чисел, кратных 2, но не кратных 29 и 58.
- Сами числа при этом можно не хранить. Каждое число учитывается не более чем в одном из счётчиков.
- Количество пар, удовлетворяющих условию А, можно вычислить по формуле
n58*(n58 - 1)/2. - Количество пар, удовлетворяющих условию Б, можно вычислить по формуле
n58*(N - n58). - Количество пар, удовлетворяющих условию В, можно вычислить по формуле
n2 * n29. - Поэтому искомое количество пар вычисляется по формуле:
var N: integer; {количество чисел} a: integer; {очередное число} n58, n29, n2: integer; k58: integer; {количество требуемых пар} i: integer; begin readln(N); n58 := 0; n29 := 0; n2 := 0; for i := 1 to N do begin readln(a); if a mod 58 = 0 then n58 := n58 + 1 else if a mod 29 = 0 then n29 := n29 + 1 else if a mod 2 = 0 then n2 := n2 + 1; end; k58 := n58 * (n58 - 1) div 2 + n58 * (N - n58) + n2 * n29; writeln(k58) end.
n=int(input()) n58,n29,n2=0,0,0 for i in range(n): a=int(input()) if a % 28 == 0: n58+=1 elif a % 29 == 0: n29+=1 elif a % 2 == 0: n2+=1 k58=n58 * (n58-1) // 2 + n58 * (n-n58) + n2 * n29 print(k58)
N58 = 0 N2 = 0 N29 = 0 NX = 0 INPUT N FOR I = 1 TO N INPUT A IF A MOD 58 = 0 THEN N58 = N58 + 1 ELSE IF A MOD 29 = 0 THEN N29 = N29 + 1 ELSE IF A MOD 2 = 0 THEN N2 = N2 + 1 ELSE NX = NX + 1 END IF END IF END IF NEXT I K58 = N58*(N58 - 1)2 + N58*(N2 + N29 + NX) + N2*N29 PRINT K58
(один из сомножителей делится на 58)
ИЛИ
(один сомножитель делится на 2, а другой — на 29)
n58 * (n58 - 1)/2 + n58 * (N - n58) + n2 * n29
✎ Программа неэффективная (2 балла):
- Язык Паскаль (версия PascalABC):
var i, j, k, n: integer; a: array[1..1000]of integer;//очередное значение begin readln(n); for i := 1 to n do begin readln(a[i]); end; k := 0; for i := 1 to n - 1 do for j := i + 1 to n do if a[i] * a[j] mod 58 = 0 then k := k + 1; writeln(k); end.
Полный перебор: все числа сохраняются в массиве, рассматриваются все возможные пары и подсчитывается количество подходящих произведений.
27_6: Разбор 27 задания демоверсии 2018 года:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности (элементы пары не обязаны стоять в последовательности рядом, порядок элементов в паре не важен). Необходимо определить количество пар, для которых произведение элементов делится на 26.
Описание входных и выходных данных В первой строке входных данных задаётся количество чисел N (1 ≤ N ≤ 1000). В каждой из последующих N строк записано одно целое положительное число, не превышающее 10 000.
В качестве результата программа должна напечатать одно число: количество пар, в которых произведение элементов кратно 26.
Пример входных данных:
4 2 6 13 39
Пример выходных данных для приведённого выше примера входных данных:
4
Из четырёх заданных чисел можно составить 6 попарных произведений:
2·6 = 12 2·13 = 26 2·39 = 78 6·13 = 78 6·39 = 234 13·39 = 507
Из них на 26 делятся 4 произведения:
2·13=26; 2·39=78; 6·13=78; 6·39=234
Требуется написать эффективную по времени и по памяти программу для
решения описанной задачи.
✍ Решение:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
-
Произведение двух чисел делится на 26, если выполнено одно из следующих условий (условия не могут выполняться одновременно).
А. Оба сомножителя делятся на 26.
Б. Один из сомножителей делится на 26, а другой не делится.
В. Ни один из сомножителей не делится на 26, но один сомножитель делится на 2, а другой – на 13.
Примечание для проверяющего. Условие делимости произведения на 26 можно сформулировать проще, например, так:
(один из сомножителей делится на 26) ИЛИ
(один сомножитель делится на 2, а другой – на 13).
Но в этом случае пара сомножителей может удовлетворять обоим условиям, что затруднит подсчёт количества пар.
При вводе чисел можно определять, делится ли каждое из них на 26, 2 и 13, и подсчитывать следующие значения:
1) n26 – количество чисел, кратных 26;
2) n13 – количество чисел, кратных 13, но не кратных 26;
3) n2 – количество чисел, кратных 2, но не кратных 26.
Примечание для проверяющего. Сами числа при этом можно не хранить.
Каждое число учитывается не более чем в одном из счётчиков.
Количество пар, удовлетворяющих условию А, можно вычислить по формуле n26·(n26 – 1)/2.
Количество пар, удовлетворяющих условию Б, можно вычислить по формуле n26·(N – n26).
Количество пар, удовлетворяющих условию В, можно вычислить по формуле n2·n13.
Поэтому искомое количество пар вычисляется по формуле
n26·(n26 – 1)/2 + n26·(N – n26) + n2·n13
✎ Программа эффективна и по времени, и по памяти (4 балла):
Программа на языке Паскаль (версия PascalABC):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
var N: integer; {количество чисел} a: integer; {очередное число} n26, n13, n2: integer; k26: integer; {количество требуемых пар} i: integer; begin readln(N); n26 := 0;n13 := 0;n2 := 0; for i := 1 to N do begin readln(a); if a mod 26 = 0 then n26 := n26 + 1 else if a mod 13 = 0 then n13 := n13 + 1 else if a mod 2 = 0 then n2 := n2 + 1; end; k26 := n26 * (n26 - 1) div 2 + n26 * (N - n26) + n2 * n13; writeln(k26) end. |
Программа на языке Python (версия Python 3):
1 2 3 4 5 6 7 8 9 10 11 12 |
n=int(input()) n26,n13,n2=0,0,0 for i in range(n): a=int(input()) if a % 26 == 0: n56+=1 elif a % 13 == 0: n13+=1 elif a % 2 == 0: n2+=1 k26=n26 * (n26-1) // 2 + n26 * (n-n26) + n2 * n13 print(k26) |
Программа на языке Бейсик:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
N26 = 0 N2 = 0 N13 = 0 NX = 0 INPUT N FOR I = 1 TO N INPUT A IF A MOD 26 = 0 THEN N26 = N26 + 1 ELSE IF A MOD 13 = 0 THEN N13 = N13 + 1 ELSE IF A MOD 2 = 0 THEN N2 = N2 + 1 ELSE NX = NX + 1 END IF END IF END IF NEXT I K26 = N26*(N26 - 1)2 + N26*(N2 + N13 + NX) + N2*N13 PRINT K26 |
27_7: Разбор досрочного экзамена 2020 г, ФИПИ (2 вариант):
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
Дана последовательность N целых положительных чисел. Рассматриваются все пары элементов последовательности, разность которых чётна, и в этих парах, по крайней мере, одно из чисел пары делится на 19. Порядок элементов в паре неважен. Среди всех таких пар нужно найти и вывести пару с максимальной суммой элементов. Если одинаковую максимальную сумму имеет несколько пар, можно вывести
любую из них
. Если подходящих пар в последовательности нет,
нужно вывести два нуля
.
Описание входных и выходных данных
В первой строке входных данных задаётся количество чисел N (2 ≤ N ≤ 10 000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10 000.
Пример входных данных:
5 38 12 57 16 57
Пример выходных данных для приведённого выше примера входных данных:
57 57
Пояснение. Из данных пяти чисел можно составить три различные пары, удовлетворяющие условию: (38, 12), (38, 16), (57, 57). Наибольшая сумма получается в паре (57, 57). Эта пара допустима, так как число 57 встречается в исходной последовательности дважды.
Напишите эффективную по времени и памяти программу для решения этой задачи.
Программа считается эффективной по времени, если при увеличении количества исходных чисел N в k раз время работы программы увеличивается не более чем в k раз.
Программа считается эффективной по памяти, если память, необходимая для хранения всех переменных программы, не превышает 1 Кбайт и не увеличивается с ростом N.
Максимальная оценка за правильную (не содержащую синтаксических ошибок и дающую правильный ответ при любых допустимых входных данных) программу, эффективную по времени и памяти, – 4 балла.
Максимальная оценка за правильную программу, эффективную только по времени или только по памяти, – 3 балла.
Максимальная оценка за правильную программу, не удовлетворяющую требованиям эффективности, – 2 балла.
Вы можете сдать одну или две программы решения задачи. Если Вы сдадите две программы, каждая из них будет оцениваться независимо от другой, итоговой станет бо́льшая из двух оценок.
Перед текстом программы кратко опишите алгоритм решения. Укажите использованный язык программирования и его версию.
Типовые задания для тренировки
✍ Решение:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
- ✎ Программа эффективна по времени и памяти
- ✎ Правильная программа на языке C++, эффективная только по времени
- ✎ Правильная, но неэффективная программа на языке Паскаль
Язык Pascal (PascalABC):
Вариант 1:
const p = 19; var N: integer; {количество чисел} a: integer; {очередное число} m0, m1: integer; {чётный и нечётный максимумы} mp0, mp1: integer; {чётный и нечётный максимумы, кратные p} x, y: integer; {ответ – пара чисел} i: integer; begin m0 := 0; m1 := 0; mp0 := 0; mp1 := 0; x := 0; y := 0; readln(N); for i := 1 to N do begin readln(a); // для четных if a mod 2 = 0 then begin // если кратное if (a mod p = 0) and (a >= mp0) then begin if mp0 > m0 then m0:= mp0; mp0:=a end else if a > m0 then m0 := a; end else begin // для нечетных if (a mod p = 0)and(a>=mp1) then begin if mp1>m1 then m1:=mp1; mp1 := a; end else if a>m1 then m1:=a; end; end; // writeln('mp0=', mp0, 'm0=', m0); if (mp0 > 0) and (m0 > 0) then begin x := mp0; y := m0; end; // writeln('mp1=', mp1, 'm1=', m1); if (mp1 > 0) and (m1 > 0) and (mp1 + m1 > x + y) then begin x := mp1; y := m1; end; writeln('=', x, ' ', y) end.
Язык Pascal (PascalABC):
Вариант 2:
const p = 19; var n, i, x, k19n, k19chet, n19chet, n19n, m1, m2: integer; begin readln(n); {количество чисел} readln(x); {первое число} // обнуление всех переменных k19chet := 0; // четный кратный n19chet := 0; // четный некратный k19n := 0; // нечетный кратный n19n := 0; // нечетный некратный m1 := 0; m2 := 0; // максимальные // цикл до n - 1, т.к. первое число уже считали for i := 1 to n - 1 do begin // проверка, если четный и кратный if (x mod p = 0) and (x mod 2 = 0) and (x > k19chet) then begin k19chet := x; end; // проверка, если четный и некратный if (x mod p <> 0) and (x mod 2 = 0) and (x > n19chet) then begin n19chet := x; end; // проверка, если нечетный и кратный if (x mod p = 0) and (x mod 2 = 1) and (x > k19n) then begin k19n := x; end; // проверка, если нечетный и некратный if (x mod p <> 0) and (x mod 2 = 1) and (x > n19n) then begin n19n := x; end; readln(x); // считываем очередное число // если x кратно и есть такое некратное n19chet, сумма с которым была бы больше чем m1 + m2 if (x mod p = 0) and ((x + n19chet) mod 2 = 0) and (x + n19chet > m1 + m2) and (n19chet > 0) then begin m1 := x; m2 := n19chet; end; // если x кратно и есть такое некратное n19n, сумма с которым была бы больше чем m1 + m2 if (x mod p = 0) and ((x + n19n) mod 2 = 0) and (x + n19n > m1 + m2) and (n19n > 0) then begin m1 := x; m2 := n19n; end; // если есть такое кратное k19n, сумма с которым была бы четной и больше чем m1 + m2 if ((x + k19n) mod 2 = 0) and (x + k19n > m1 + m2) and (k19n > 0) then begin m1 := x; m2 := k19n; end; // если есть такое кратное k19chet, сумма с которым была бы четной и больше чем m1 + m2 if ((x + k19chet) mod 2 = 0) and (x + k19chet > m1 + m2) and (k19chet > 0) then begin m1 := x; m2 := k19chet; end; end; writeln(m1, ' ', m2) end.
:
p = 19 m0 = m1 = mp0 = mp1 = 0 N = int(input()) for i in range(N): a = int(input()) if a % 2 == 0: if a % p == 0 and a >= mp0: if mp0 > m0: m0 = mp0 mp0 = a elif a > m0: m0 = a else: if a % p == 0 and a >= mp1: if mp1 > m1: m1 = mp1 mp1 = a elif a > m1: m1 = a x = y = 0 if mp0 > 0 and m0 > 0: x = mp0; y = m0 if mp1 > 0 and m1 > 0 and mp1 + m1 > x + y: x = mp1; y = m1 print(x,y)
Ещё один путь решения – записать всю последовательность в массив и анализировать её в несколько проходов. Ниже приводится реализующая такой алгоритм программа на языке C++. В этой программе массив с исходными данными обрабатывается два раза: на первом проходе находятся индексы максимального чётного и нечётного элементов, кратных p, на втором проходе – общие чётный и нечётный максимумы. При этом элементы, выделенные как кратные при первом проходе, во время второго прохода из сравнения исключаются. Такая программа эффективна по времени (несмотря на повторную обработку массива, общее время работы пропорционально N), но неэффективна по памяти. Максимальная оценка за такую программу при отсутствии в ней синтаксических и содержательных ошибок – 3 балла.
С++:
#include <iostream> using namespace std; int main() { const int p = 19; // делитель int N; cin >> N; // количество элементов int a[N]; // элементы последовательности for (int i = 0; i < N; ++i) cin >> a[i]; int imp0 = -1, imp1 = -1; //индексы максимумов, кратных p for (int i = 0; i < N; ++i) { if (a[i] % p == 0) { if (a[i] % 2 == 0) { if (imp0 == -1 || a[i] > a[imp0]) imp0 = i; } else { if (imp1 == -1 || a[i] > a[imp1]) imp1 = i; } } } int im0 = -1, im1 = -1; // индексы общих максимумов for (int i = 0; i < N; ++i) { if (i != imp0 && i != imp1) { if (a[i] % 2 == 0) { if (im0 == -1 || a[i] > a[im0]) im0 = i; } else { if (im1 == -1 || a[i] > a[im1]) im1 = i; } } } int x = 0, y = 0; // пара чисел для ответа if (imp0 != -1 && im0 != -1) { x = a[imp0]; y = a[im0]; } if (imp1 != -1 && im1 != -1 && a[imp1] + a[im1] > x + y) { x = a[imp1]; y = a[im1]; } cout << x << ' ' << y << endl; return 0; }
Запишем все исходные числа в массив, переберём все возможные пары и выберем подходящую. Такое решение не является эффективным ни по памяти (требуемая память зависит от размера исходных данных), ни по времени (количество возможных пар, а значит, количество действий и время счёта с ростом количества исходных элементов растут квадратично). Подобная программа оценивается не выше 2 баллов.
Язык Pascal (версия PascalABC):
const p = 19; var N: integer; {количество чисел} a: array [1..10000] of integer; {исходные данные} x, y: integer; {ответ – пара чисел} i, j: integer; begin readln(N); for i := 1 to N do readln(a[i]); x := 0; y := 0; for i := 1 to N - 1 do begin for j := i + 1 to N do begin if ((a[i] - a[j]) mod 2 = 0) and ((a[i] mod p = 0) or (a[j] mod p = 0)) and (a[i] + a[j] > x + y) then begin x := a[i]; y := a[j] end end end; writeln(x, ' ', y) end.
Выбрать из каждой пары одно число
27_1:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
Задание А (более легкое, чем Б)
Имеется набор данных, состоящий из 5 пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма квадратов всех выбранных чисел была нечетной и при этом максимально возможной. Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0.
Напишите программу для решения этой задачи. В этом варианте задания оценивается только правильность программы, время работы и размер использованной памяти не имеет значения.
Максимальная оценка за правильную программу — 2 балла.
Задание Б (более сложное, чем А)
Имеется набор данных, состоящих из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма квадратов всех выбранных чисел была нечетной и при этом максимально возможной. Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0.
Напишите программу для решения этой задачи.
Постарайтесь сделать программу эффективной по времени, если время работы программы пропорционально количеству пар чисел N, т.е. при увеличении N в k раз время работы программы должно увеличиваться на более чем в k раз.
Программа считается эффективной по памяти, если размер памяти, использованной в программе для хранения данных, не зависит от числа N и не превышает 1 килобайта.
Максимальная оценка за правильную программу, эффективную по времени и по памяти, — 4 балла.
Как в варианте А, так и в варианте Б программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи (или 0, если такую сумму получить нельзя).
Например: 2 6 4 1 7 3 2 9 7 4 sum=231
✍ Решение:
- поскольку в задании указано, что «имеется набор данных, состоящих из пар…», то введем в программу переменную
nдля количества пар, значение которой будет считываться со стандартного входного потока: - объявим сами числа типа
integer, переменную цикла —i— типаintegerи дополнительные переменные, смысл которых будет объяснен ниже. Объявление сделаем в отдельных строках (так делать не обязательно), чтобы можно было ввести удобно комментарии: - так как в задании не оговаривается, что пары чисел считывается из файла, значит их необходимо считать со стандартного входного потока оператором
readln(); т.е. организуем цикл:
n:longint; {количество пар чисел};
x,y: integer; {пара чисел} max: integer; {максимальное из пары} min: integer; {минимальное из пары} sum:longint; {сумма квадратов отобранных чисел} min_kvadr:longint; {мин. нечетная разница квадратов max и min} i:integer;
for i:=1 to n do begin readln(x,y); ...
Допустим имеем пары:
2 6 4 1 7 3 2 9 7 4
2 6 4 1 7 3 2 9 7 4
if x>y then begin max:=x; min:=y end else begin max:=y;min:=x end;
2 6 - разница 32 (36 - 4)
4 1 - разница 15 (16 - 1)
7 3 - разница 40 (49 - 9)
2 9 - разница 77 (81 - 4)
7 4 - разница 33 (49 - 16)
if((max-min) mod 2 > 0) and ((sqr(max)-sqr(min)) < min_kvadr) then min_kvadr:=sqr(max) - sqr(min)
min_kvadr:=1073676289; {32 767 * 32 767 (самое большое в типе integer) }
if sum mod 2 = 0 then begin if min_kvadr = 1073676289 then sum := 0 else sum:=sum - min_kvadr end;
Эффективная программа на языке Паскаль (версия Pascal ABC):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
var n:longint; {количество пар чисел} x,y: integer; {пара чисел} max: integer; {максимальное из пары} min: integer; {минимальное из пары} sum:longint; {сумма квадратов отобранных чисел} min_kvadr:longint; {мин. нечетная разница квадратов max и min} i:integer; begin sum:=0; readln(n); min_kvadr:=1073676289; {32 767 * 32 767, самое большое integer} for i:=1 to n do begin readln(x,y); if x>y then begin max:=x; min:=y end else begin max:=y;min:=x end; sum:=sum+sqr(max); if((max-min) mod 2 > 0) and (sqr(max)-sqr(min) < min_kvadr) then min_kvadr:=sqr(max) - sqr(min) end; if sum mod 2 = 0 then begin if min_kvadr = 1073676289 then sum := 0 else sum:=sum - min_kvadr end; writeln('sum=',sum) end. |
Пример работы программы:
3 1 4 2 4 3 4 sum=41
✎ Задание А (более легкое, 2 балла максимум):
- так как в задании указано, что пар чисел ровно 5, то введем в программу константу n=5
Решение на языке Паскаль (версия PascalABC):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
const n = 5; {количество пар чисел} var x,y: longint; {пара чисел} max_sum: longint; {максимальная из сумм} sum:array [1..15]of longint; {суммы квадратов всех комбинаций чисел} i,k:longint; begin readln(x,y); sum[1]:=sqr(x); sum[2]:=sqr(y); k:=3; {счетчик для сумм} for i:=2 to n do begin readln(x,y); sum[k]:=sum[k-2]+sqr(x); {1 шаг: s3=s1+x*x}{2 шаг: s7=s4+x*x} sum[k+1]:=sum[k-2]+sqr(y); {1 шаг: s4=s1+y*y}{2 шаг: s8=s4+y*y} sum[k+2]:=sum[k-1]+sqr(x); {1 шаг: s5=s2+x*x}{2 шаг: s9=s6+x*x} sum[k+3]:=sum[k-1]+sqr(y); {1 шаг: s6=s2+y*y}{2 шаг: s10=s6+y*y} k:=k+4; end; max_sum:=sum[1]; for i:=1 to n*n do if (sum[i]>max_sum) and (sum[i] mod 2 <>0) then max_sum:=sum[i]; if (max_sum=sum[1]) and (max_sum mod 2 = 0) then max_sum:=0; writeln(max_sum) end. |
Предлагаем также посмотреть объяснение данного 27 задания на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Набор данных, состоящих из троек чисел
27_2:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
Вам предлагается два задания с похожими условиями: задание А и задание Б. Вы можете решать оба задания или одно из них по своему выбору. Задание Б более сложное, его решение оценивается выше. Итоговая оценка выставляется как максимальная из оценок за задания А и Б.
А. Имеется набор данных, состоящий из 5 троек положительных целых чисел. Необходимо выбрать из каждой тройки ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 5 и при этом была минимально возможной. Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0.
Напишите программу для решения этой задачи. В этом варианте задания оценивается только правильность программы, время работы и размер использованной памяти не имеют значения.
Максимальная оценка за правильную программу — 2 балла.
Б. Имеется набор данных, состоящий из троек положительных целых чисел. Необходимо выбрать из каждой тройки ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 5 и при этом была минимально возможной. Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0.
Постарайтесь сделать программу эффективной по времени и по используемой памяти.
Программа считается эффективной по времени, если время работы программы пропорционально количеству чисел N, т.е. при увеличении N в k раз время работы программы должно увеличиваться не более чем в k раз.
Программа считается эффективной по памяти, если размер памяти, использованной в программе для хранения данных, не зависит от числа N и не превышает 1 килобайта.
Максимальная оценка за правильную программу, эффективную по времени и по памяти, — 4 балла.
Как в варианте А, так и в варианте Б программа должна напечатать одно число — минимально возможную сумму, соответствующую условиям задачи (или 0, если такую сумму получить нельзя).
Напоминаем! не забудьте указать, к какому заданию относится каждая из представленных Вами программ.
Перед текстом программы кратко опишите Ваш алгоритм решения, укажите использованный язык программирования и его версию.
Входные данные
Для варианта А на вход программе подается 5 строк, каждая из которых содержит три натуральных числа, не превышающих 10000.
Пример входных данных для варианта А:
1 3 2 2 1 2 2 5 1 1 3 4 6 1 1
Для варианта Б на вход программе в первой строке подается количество троек чисел N (1<=N<=100000). Каждая из следующих N строк содержит три натуральных числа, не превышающих 10000.
Пример входных данных для варианта Б:
5 1 3 2 2 1 2 2 5 1 1 3 4 6 1 1
Пример выходных данных для приведенных выше примеров входных данных:
6
Типовые задания для тренировки
✍ Решение:
Чтобы получить минимально возможную сумму, будем брать из каждой тройки наименьшее число. Если полученная при этом сумма будет кратна 5, ее придется увеличить. Для этого достаточно в одной из троек, где хотя бы два числа имеют разные остатки при делении на 5, заменить ранее выбранное число на число с другим остатком от деления на 5 из той же тройки. При этом модуль разности между прежним и новым, выбранным из тройки, должен быть минимально возможным.
Пример правильной и эффективной программы для задания Б на языке Паскаль (версия PascalABC):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
const aMax = 10000;{наибольшее возможное исходное число} var N: longint; {количество троек} a, b, c, tmp: longint;{тройка чисел} s: longint;{сумма выбранных чисел} D_min: longint;{мин. разница в тройке не кратная 5} i: longint;{} begin s := 0; D_min := aMax + 1; readln(N); for i := 1 to N do begin readln(a, b, c); if (a > b) then begin tmp := a;a := b;b := tmp end; if(b > c) then begin tmp := b;b := c;c := tmp; if (a > b) then begin tmp := a;a := b;b := tmp end end; {a,b,c отсортированы по возрастанию} s := s + a; if((b - a) mod 5 > 0 ) and ((b - a) < D_min) then D_min := b - a; if((c - a) mod 5 > 0 ) and ((c - a) < D_min) then D_min := c - a end; if s mod 5 = 0 then begin if D_min > aMax then s := 0 else s := s + D_min end; writeln(s) end. |
✎ Задание А (2 балла)
В цикле перебираются все возможные суммы, и среди них ищется удовлетворяющая условию.
На языке Паскаль (версия PascalABC):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
var a: array[1..5, 1..3] of longint; i1, i2, i3, i4, i5: longint; s, sMin: longint; begin for i1 := 1 to 5 do readln(a[i1, 1], a[i1, 2], a[i1, 3]); sMin := 100000; for i1 := 1 to 3 do for i2 := 1 to 3 do for i3 := 1 to 3 do for i4 := 1 to 3 do for i5 := 1 to 3 do begin s := a[1, i1] + a[2, i2] + a[3, i3] + a[4, i4] + a[5, i5]; if (s mod 5 = 0) and (s < sMin) then sMin := s end; if (sMin = 100000) then sMin := 0; writeln(sMin) end. |
Анализ пар, находящихся на расстоянии
27_3: Разбор 27 задания демоверсии 2019 года (ФИПИ):
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности, находящихся на расстоянии не меньше чем 4 (разница в индексах элементов пары должна быть 4 или более, порядок элементов в паре неважен).
Необходимо определить количество таких пар, для которых произведение элементов делится на 29.
Описание входных и выходных данных:
В первой строке входных данных задаётся количество чисел N (4 ≤ N ≤ 1000). В каждой из последующих N строк записано одно целое положительное число, не превышающее 10 000.
В качестве результата программа должна вывести одно число: количество пар элементов, находящихся в последовательности на расстоянии не меньше чем 4, в которых произведение элементов кратно 29.
Пример входных данных:
7 58 2 3 5 4 1 29
Пример выходных данных для приведённого выше примера входных данных:
5
Из 7 заданных элементов с учётом допустимых расстояний между ними можно составить 6 произведений:
58·4 = 232 :29=8 58·1 = 58 :29=2 58·29 = 1682 :29=58 2·1 = 2 2·29 = 58 :29=2 3·29 = 87 :29=3
Из них на 29 делятся 5 произведений.
Требуется написать эффективную по времени и памяти программу для решения описанной задачи.
✍ Решение:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
✎ Программа на языке Паскаль (версия PascalABC). Программа неэффективна ни по времени, ни по памяти (2 балла):
- Перебор всех вариантов произведений:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
const s = 4;//требуемое расстояние var n, i, j, cnt: integer; a: array[1..1000] of integer; begin readln(n); cnt := 0; for i := 1 to n do readln(a[i]); for i := 1 to n - s do for j := i + s to n do if a[i] * a[j] mod 29 = 0 then cnt := cnt + 1; writeln(cnt) end. |
✎ Программа на языке Паскаль (версия PascalABC). Программа эффективна и по времени, и по памяти (4 балла):
- Если один из сомножителей делится без остатка на 29, то произведение с любым другим сомножителем тоже будет делится на 29.
- Последние рассматриваемые 4 элемента можно хранить как 4 счётчика: количество делящихся на 29 среди всех считанных чисел, всех считанных чисел без последнего, всех считанных чисел без 2 последних, всех считанных чисел без 3 последних, – и также сдвигать их после очередного шага.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
const s = 4;//требуемое расстояние var n,i: integer; n1, n2, n3, n4: integer; //хранение последних s счетчиков a_: integer; //очередное значение cnt: integer;//количество искомых пар begin readln(n); n1 := 0;n2 := 0;n3 := 0;n4 := 0; cnt := 0; for i := 1 to n do begin readln(a_); // очередное значение if i > s then if a_ mod 29 = 0 then cnt := cnt + (i - s) else cnt := cnt + n4; // сдвигаем элементы счетчика n4 := n3; n3 := n2; n2 := n1; // обновляем счетчик кратных 29 if a_ mod 29 = 0 then n1 := n1 + 1; end; writeln(cnt) end. |
Смотрите видео разбора демоверсии 2019 года задание 27:
📹 YouTube здесь
Видео на RuTube здесь
27_5:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
Датчик передаёт каждую секунду по каналу связи неотрицательное целое число, не превосходящее 1000, — текущий результат измерений. Временем, в течение которого происходит передача, можно пренебречь.
Необходимо найти в заданной серии показаний датчика минимальное чётное произведение двух показаний, между моментами передачи которых прошло не менее 8 секунд. Если получить такое произведение не удаётся, ответ считается равным -1. Общее количество показаний датчика в серии не превышает 10 000.
Вам предлагаются два задания, связанных с этой задачей: задание А и задание Б. Вы можете решать оба задания или одно из них по своему выбору.
Итоговая оценка выставляется как максимальная из оценок за задания А и Б. Если решение одного из заданий не представлено, то считается, что оценка за это задание — 0 баллов.
Задание Б является усложнённым вариантом задания А, оно содержит дополнительные требования к программе.
А. Напишите на любом языке программирования программу для решения поставленной задачи, в которой входные данные будут запоминаться в массиве, после чего будут проверены все возможные пары элементов. Перед программой укажите версию языка программирования.
ОБЯЗАТЕЛЬНО укажите, что программа является решением ЗАДАНИЯ А. Максимальная оценка за выполнение задания А — 2 балла.
Б. Напишите программу для решения поставленной задачи, которая будет эффективна как по времени, так и по памяти (или хотя бы по одной из этих характеристик). Программа считается эффективной по времени, если время работы программы пропорционально количеству полученных показаний прибора N, т. е. при увеличении N в k раз время работы программы должно увеличиваться не более чем в k раз. Программа считается эффективной по памяти, если размер памяти, использованной в программе для хранения данных, не зависит от числа А и не превышает 1 килобайта.
Перед программой укажите версию языка программирования и кратко опишите использованный алгоритм.
ОБЯЗАТЕЛЬНО укажите, что программа является решением ЗАДАНИЯ Б. Максимальная оценка за правильную программу, эффективную по времени и по памяти, — 4 балла.
Максимальная оценка за правильную программу, эффективную по времени, но неэффективную по памяти, — 3 балла.
Пример входных данных:
10 5 4 3 2 1 6 7 8 9 4
Программа должна вывести одно число — описанное в условии произведение, либо -1, если получить такое произведение не удаётся.
Пример выходных данных для приведённого выше примера входных данных:
16
✍ Решение:
* Учтите, что в данных заданиях более не требуется учитывать эффективность алгоритма (с 2021 года)!
-
✎ Задание А (решение на языке Паскаль, версия pascalABC):
Ниже приводится пример переборного решения на Паскале, неэффективного ни по памяти, ни по времени, но являющегося правильным ответом на задание А.
const s = 8;{требуемое расстояние между показаниями} var N: integer; a: array[1..10000] of integer; {все показания датчика} mp: integer; {минимальное значение произведения} i, j: integer; begin readln(N); {Ввод значений датчика} for i := 1 to N do readln(a[i]); mp := 1000 * 1000 + 1; for i := 1 to N - s do begin for j := i + s to N do begin if (a[i] * a[j] mod 2 = 0) and (a[i] * a[j] < mp) then mp := a[i] * a[j] end; end; if mp = 1000 * 1000 + 1 then mp := -1; writeln(mp) end.
✎Задание Б (решение на языке Паскаль, версия pascalABC):
Чтобы произведение было чётным, хотя бы один сомножитель должен быть чётным, поэтому при поиске подходящих произведений чётные показания прибора можно рассматривать в паре с любыми другими, а нечётные — только с чётными.
Для каждого показания с номером k, начиная с k = 9, рассмотрим все допустимые по условиям задачи пары, в которых данное показание получено вторым. Минимальное произведение из всех этих пар будет получено, если первым в паре будет взято минимальное подходящее показание среди всех, полученных от начала приёма и до показания с номером k — 8. Если очередное показание чётное, минимальное среди предыдущих может быть любым, если нечётное — только чётным.
Для получения эффективного по времени решения нужно по мере ввода данных помнить абсолютное минимальное и минимальное чётное показание на каждый момент времени, каждое вновь полученное показание умножать на соответствующий ему минимум, имевшийся на 8 элементов ранее, и выбрать минимальное из всех таких произведений. Ниже приводится пример такой программы на Паскале, эффективной по памяти и по времени.
const s = 8; {требуемое расстояние между показаниями} amax = 1001;{больше максимально возможного показания} var N: integer; a: array[1..s] of integer; {хранение s показаний датчика} a_: integer; {ввод очередного показания} ma: integer; {минимальное число без s последних} me: integer; {минимальное чётное число без s последних} mp: integer; {минимальное значение произведения} p: integer; i, j: integer; begin readln(N); {Ввод первых s чисел} for i := 1 to s do readln(a[i]); {Ввод остальных значений, поиск минимального произведения} ma := amax;me := amax;mp := amax * amax; for i := s + 1 to N do begin readln(a_); if a[1] < ma then ma := a[1]; if (a[1] mod 2 = 0) and (a[1] < me) then me := a[1]; if a_ mod 2 = 0 then p := a_ * ma else if me < amax then p := a_ * me else p := amax * amax; if (p < mp) then mp := p; {сдвигаем элементы вспомогательного массива влево} for j := 1 to s - 1 do a[j] := a[j + 1]; a[s] := a_ end; if mp = amax * amax then mp := -1; writeln(mp) end.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Исполнитель А16 преобразует число, записанное на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает его на 2.
Программа для исполнителя А16 – это последовательность команд.
Сколько существует таких программ, которые исходное число 3 преобразуют в число 12 и при этом траектория вычислений программы содержит число 10?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 16, 18.
Источник: Демонстрационная версия ЕГЭ—2017 по информатике.
2
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10203
3
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10204
4
Исполнитель Осень16 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1) Прибавить 1;
2) Прибавить 2;
3) Прибавить 4.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 4.
Программа для исполнителя Осень16 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 10, 11.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10103
5
Исполнитель Осень16 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1) Прибавить 1;
2) Прибавить 2;
3) Прибавить 3.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 3.
Программа для исполнителя Осень16 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 10, 11.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10104
Пройти тестирование по этим заданиям
ЕГЭ информатика 27 задание разбор, теория, как решать.
Создание программы для анализа числовых последовательностей, (В) — 2 балла
Е27.33 В городе M расположена кольцевая автодорога длиной в N километров
В городе M расположена кольцевая автодорога длиной в N километров с движением в обе стороны. На каждом километре автодороги расположены пункты приема мусора определенной вместимости. В пределах кольцевой дороги в одном из пунктов сборки мусора собираются поставить мусороперерабатывающий завод таким образом, чтобы стоимость доставки мусора была минимальной. Стоимость доставки мусора вычисляется, как вместимость пункта сбора …
Читать далее
Е27.32 определить количество таких подпоследовательностей, сумма элементов которых кратна 1111
Дана последовательность натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, состоящие более чем из ста элементов. Необходимо определить количество таких подпоследовательностей, сумма элементов которых кратна 1111. Входные данные Первая строка входного файла содержит целое число N – общее количество чисел в наборе. Каждая из следующих N строк содержит одно число. Гарантируется, что число в ответе не …
Читать далее
Е27.31 такие что сумма элементов каждой из них кратна k = 67
Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 67. Найдите среди них подпоследовательность с максимальной суммой. Укажите в ответе найденную максимальную сумму. Входные данные Даны два входных файла (файл А и файл В), каждый из которых содержит в первой строке количество чисел …
Читать далее
Е27.30 Необходимо определить количество её непрерывных подпоследовательностей
Дана последовательность натуральных чисел. Необходимо определить количество её непрерывных подпоследовательностей, сумма элементов которых кратна 999. Входные данные Первая строка входного файла содержит целое число N – общее количество чисел в наборе. Каждая из следующих N строк содержит одно число. Гарантируется, что общая сумма всех чисел и число в ответе не превышают 2 ∙ 109. Вам …
Читать далее
Е27.29 сумма всех выбранных чисел имела такую же последнюю цифру
Дана последовательность, которая состоит из пар натуральных чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел имела такую же последнюю цифру, как наибольшая возможная, и при этом была минимальной возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число — минимальную возможную сумму, соответствующую условиям задачи. Входные …
Читать далее
Е27.28 такие что сумма элементов каждой из них кратна k = 43
Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько, в ответе укажите количество элементов самой короткой из них. Входные данные Даны два входных файла (файл A и …
Читать далее
Е27.27 последовательности, находящихся на расстоянии не меньше чем 5
последовательности, находящихся на расстоянии не меньше чем 5 На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности, находящихся на расстоянии не меньше чем 5 (разница в индексах элементов пары должна быть 5 или более, порядок элементов в паре неважен). Необходимо определить количество таких …
Читать далее
Е27.26 чтобы сумма всех выбранных чисел не делилась на 7
чтобы сумма всех выбранных чисел не делилась на 7 Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 7 и при этом была минимально возможной. Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0. Программа должна …
Читать далее
Е27.25 чтобы сумма всех выбранных чисел делилась на 4
чтобы сумма всех выбранных чисел делилась на 4. Имеется набор данных, состоящий из троек положительных целых чисел. Необходимо выбрать из каждой тройки два числа так, чтобы сумма всех выбранных чисел делилась на 4 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число – максимально возможную сумму, соответствующую …
Читать далее
Е27.24 Определите максимально возможную сумму всех чисел в третьей группе
Определите максимально возможную сумму всех чисел в третьей группе. Набор данных состоит из троек натуральных чисел. Необходимо распределить все числа на три группы, при этом в каждую группу должно попасть ровно одно число из каждой исходной тройки. Сумма всех чисел в первой группе должна быть чётной, во второй – нечётной. Определите максимально возможную сумму всех …
Читать далее
Скачать материал

Скачать материал


- Сейчас обучается 31 человек из 21 региона


- Курс добавлен 16.12.2022
- Сейчас обучается 20 человек из 14 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
Подготовка к КЕГЭ по информатике в 2021 г.
Учитель информатики
МБУ «Лицей №6»
г.о. Тольятти
Серокурова А.А.
Мастер — класс
Разбор решения задания №23
Тольятти, 2021 -
2 слайд
Задание № 23
(повышенный уровень, время – 8 мин)
Тема: динамическое программирование.Спецификация: Умение анализировать результат исполнения алгоритма
ЕГЭ-2020: % выполнения 56,0 %
Апробация-2021: % выполнения 9,9 % -
3 слайд
Динамическое программирование
Что проверяется:
Умение анализировать результат исполнения алгоритма1.6.2. Вычислимость. Эквивалентность алгоритмических моделей.
1.1.3. Умение строить информационные модели объектов, систем и процессов в виде алгоритмов.
Что нужно знать:
динамическое программирование – это способ решения сложных задач путем сведения их к более простым задачам того же типас помощью динамического программирования решаются задачи, которые требуют полного перебор вариантов;
динамическое программирование позволяет ускорить выполнение программы за счет использования дополнительной памяти; полный перебор не требуется, поскольку запоминаются решения всех задач с меньшими значениями параметров
-
4 слайд
Типы заданий
Динамическое программирование:две команды
три команды
ограничение на траекторию
ограничение на количество команд -
5 слайд
Динамическое программирование:
две команды
(№ 3718) (А. Комков) Исполнитель Нолик преобразует число, записанное на экране в троичной системе счисления. У исполнителя есть две команды, которым присвоены номера:Вычесть 2
Обнулить младший разрядПервая команда уменьшает число на 2. Вторая команда обнуляет ненулевой младший разряд троичной записи числа. (Например, при выполнении этой команды число 21 преобразуется в число 20. Если в младшем разряде находится 0, то данная команда не выполняется).
Сколько существует программ, которые троичное число 212 преобразуют в троичное число 10?
-
6 слайд
Способ 1: Вручную таблицей
Переведем числа из троичной системы счисления в десятичную:212 => 23
10 => 3тогда команды будут такие:
1. Вычесть 2
2. Вычесть остаток от деления на 3
Ответ: 86 -
7 слайд
Способ 2: Программирование
С.С. Поляков:L=[0]*24
L[23]=1
for x in range(23,2,-1):
L[x-2] += L[x]
if x % 3 != 0:
L[(x//3)*3] += L[x]
print(L[3])
А. Комков:def f(start, end):
if start < end:
return 0
if start == end:
return 1
if start % 3 == 0:
return f(start — 2, end)
return f(start — 2, end) +
f(start- start % 3, end)
print(f(23, 3)) -
8 слайд
Динамическое программирование:
две команды
(№ 3715) (А. Комков) Исполнитель Нолик преобразует двоичное число, записанное на экране. У исполнителя есть две команды, которым присвоены номера:1. Вычесть 1
2. ОбнулитьПервая команда уменьшает число на 1. Вторая команда обнуляет все ненулевые разряды, кроме старшего (например, для исходного числа 11101 результатом работы команды будет число 10000), если таких разрядов нет, то данная команда не выполняется.
Сколько существует программ, которые исходное двоичное число 1100 преобразуют в двоичное число 100?
Ответ: 20 -
9 слайд
Динамическое программирование:
две команды
(№ 3105) У исполнителя Калькулятор две команды, которым присвоены номера:1. прибавь 1
2. увеличь каждый разряд числа на 1Например, число 23 с помощью команды 2 превратится в 34, а 29 в 39 (так как младший разряд нельзя увеличить). Если перед выполнением команды 2 какая-либо цифра равна 9, она не изменяется.
Сколько есть программ, которые число 25 преобразуют в число 51?
Ответ: 33 -
10 слайд
Динамическое программирование:
три команды
(№ 3719) (А. Комков) Исполнитель Нолик преобразует число, записанное на экране в четверичной системе счисления. У исполнителя есть три команды, которым присвоены номера:1. Прибавить 2
2. Прибавить 3
3. Добавить справа 0Первая команда увеличивает число на 2. Вторая команда увеличивает число на 3. Третья команда приписывает к записи числа справа 0, например, для числа 123 результатом работы данной команды будет являться число 1230.
Сколько существует программ, которые число 1, записанное в четверичной системе счисления, преобразуют в четверичную запись 100?
-
11 слайд
Динамическое программирование:
три команды
Переведем числа из четверичной системы счисления в десятичную:1 => 1
100 => 16Команды (для сс=4):
1. Прибавить 2
2. Прибавить 3
3. Добавить справа 0Ответ: 43
-
12 слайд
Динамическое программирование: ограничение на траекторию
(№ 2464) Исполнитель Калькулятор преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:1. Прибавить 1
2. Прибавить 3Программа для исполнителя Калькулятор – это последовательность команд.
Сколько существует программ, для которых при исходном числе 2 результатом является число 18, и при этом траектория вычислений содержит число 9 и не содержит число 14? -
13 слайд
Способ 1, 2: Вручную таблицей, подобной таблицей в Excel
В D6: C8, в D8: =D6+D7
Способ 1:
«-» долго, легко ошибиться,
много писать,
громоздко, много цифр, если опечатка,
то легко ошибиться
«+» наглядно, легко проверить
Способ 2:
«-» также громоздко
«+» считается автоматически, наглядно
Ответ: 63 -
14 слайд
Способ 3: Программирование, массив
«-» необходимо хорошо разбираться в алгоритме, большая программа
«+» программа в сочетании с предыдущими способами исключают ошибкуСпособы 1, 2, 3 отражают
одну и ту же технологию
решения
Ответ: 63 -
15 слайд
Способ 4: Дерево. От обратного
«-» если три команды или мало ограничений, то решение громоздкое
«+» меньше писатьМожно разбивать весь путь на отдельные участки
и перемножать их количество!!! -
16 слайд
Способ 5: Программирование, рекурсия
Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:Прибавить 1
Умножить на 2Сколько существует программ, для которых при исходном числе 2 результатом является число 29 и при этом траектория вычислений содержит число 14 и не содержит числа 25?
Ответ: 13
-
17 слайд
Способ 5: Программирование, рекурсия
«-» необходимо понимать алгоритм
«+» короткое решение
Ответ: 13 -
18 слайд
Способ 6: Средствами Excel
B4: =1
С4: =C2+C3
C3: = =ЕСЛИ(ОСТАТ(C1;2)=0;ПРОСМОТР(C1/2;$B$1:$N$1;$B$4:$N$4);0)Добавление знака $ происходит автоматически после выделения диапазона и нажатия клавиши F4.
B9: =N4
P8: =ЕСЛИ(ОСТАТ(P6;2)=0;ПРОСМОТР(P6/2;$B$6:$Q$6;$B$9:$Q$9);0)
Ответ: 13 -
19 слайд
Динамическое программирование: ограничение на количество команд
(№ 3448) (С.С. Поляков)
У исполнителя Калькулятор есть три команды, которым присвоены номера:1. Прибавить 1
2. Прибавить 2
3. Умножить на 2Сколько разных чисел на отрезке [34, 59] может быть получено из числа 1 с помощью программ, состоящих из 6 команд?
-
20 слайд
Способ 1: Таблица — граф
-
21 слайд
Способ 2: Программирование
‘s’ — начало, ‘x’ — цель,
‘l’ — количество команд,
‘count’ — количество чиселPython:
def func(s,x,l):
if x < s or l < 0: return 0
if x == s: return 1
K = func(s,x-1,l-1)
K += func(s,x-2,l-1)
if x % 2 == 0:
K += func(s,x//2,l-1)
return K
count = 0
for i in range(34,60):
if func(1,i,6) != 0: count += 1
print(count) -
22 слайд
Спасибо за внимание!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 681 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
- 08.06.2021
- 139
- 0
- 08.06.2021
- 135
- 0
- 08.06.2021
- 130
- 0

- 08.06.2021
- 128
- 1

Запросы на выборку данных
- Учебник: «Информатика», Босова Л.Л., Босова А.Ю.
- Тема: 1.6.4. Запросы на выборку данных
- 08.06.2021
- 141
- 4

- 08.06.2021
- 1241
- 44
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
ЕГЭ – ИНФОРМАТИКА: Задание 23
Динамическое программирование
Подготовила работу:
учитель МБОУ СОШ №7
Романова Э.Н.
Динамическое программирование – это способ решения сложных задач путём разбиения их на более простые подзадачи, сложность которых меньше исходной.
Общие сведения
Тема: Динамическое программирование
Сложность: повышенная
Максимальный балл за выполнение задания: 1 балл
Примерное время решения: 8 минут
Что проверяется: ум ение работать с графами, или с рядом чисел; умение анализировать результат исполнения алгоритма
Задание 23. ДЕМО — 2021 Открытый банк заданий ФИПИ
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
- Прибавь 1
- Умножь на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2.
Программа для исполнителя – это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 20 , и при этом траектория вычислений содержит число 10 ?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы.
Например , для программы 121 при исходном числе 7 траектория будет состоять из чисел 8,16,17 .
Итак, мы имеем
Команды:
1. +1
2. *2
Траектория: 1 10 20
Надо определить: К ПР =?
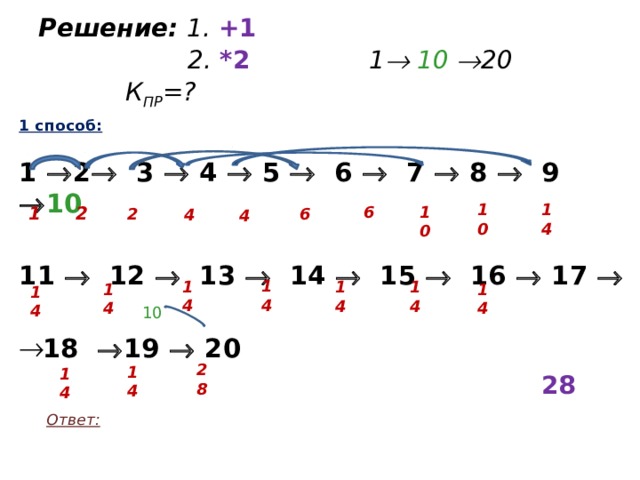
Решение: 1. +1 2. *2 1 10 20 К ПР =?
1 способ:
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17
- 18 19 20
Ответ:
14
10
10
2
6
1
2
6
4
4
14
14
14
14
14
14
14
10
28
14
14
28
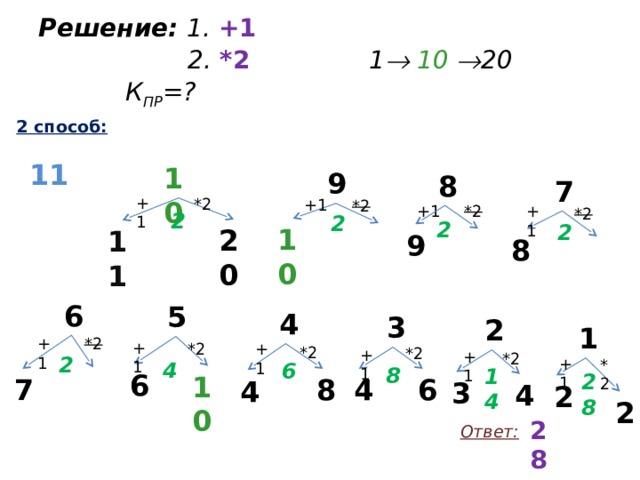
Решение: 1. +1 2. *2 1 10 20 К ПР =?
2 способ:
11
10
9
8
7
+1
*2
+1
*2
*2
+1
+1
*2
2
2
2
2
10
20
11
9
8
6
5
4
3
2
1
+1
*2
+1
*2
+1
*2
*2
+1
+1
*2
2
+1
*2
4
6
8
14
6
28
10
7
4
8
6
4
3
4
2
2
28
Ответ:
Решение: 1. +1 2. *2 1 10 20 К ПР =? 1) К ПР1 =?: 1 10 2) К ПР2 =?: 10 20 3) К ПР =К ПР1 *К ПР2
3 способ:
10
1
+1
*2
+1
*2
14
2
2
2
20
11
+1
*2
+1
1
7
3
4
12
+1
*2
4
+1
1
4
6
+1
…
*2
3
1
5
+1
+1
8
*2
2
20
6
1
1
10
+1
7
14*2=28
1
+1
8
1
+1
9
28
1
Ответ:
+1
10
Задание 23.
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
- Прибавь 1
- Умножь на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2.
Программа для исполнителя – это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 20 , и при этом траектория вычислений НЕ содержит число 10 ?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы.
Например , для программы 121 при исходном числе 7 траектория будет состоять из чисел 8,16,17 .
Итак, мы имеем
Команды:
1. +1
2. *2
Траектория: 1 10 20
Надо определить: К ПР =?
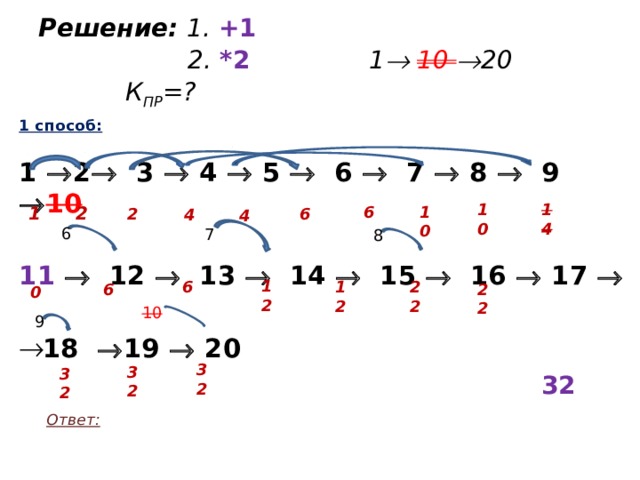
Решение: 1. +1 2. *2 1 10 20 К ПР =?
1 способ:
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17
- 18 19 20
Ответ:
14
10
10
2
6
1
2
6
4
4
6
7
8
12
6
22
12
22
6
0
10
9
32
32
32
32
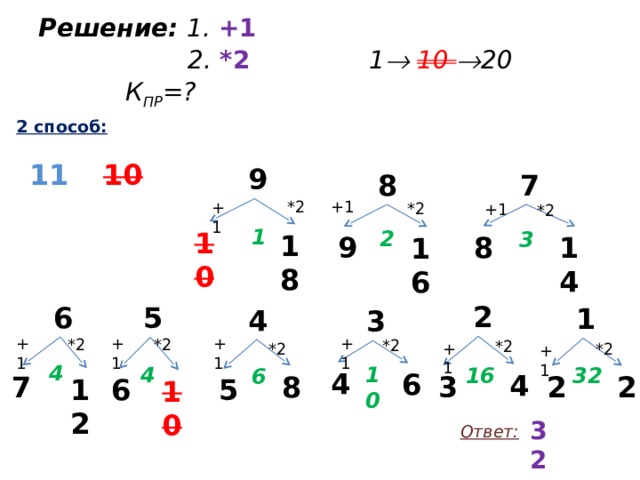
Решение: 1. +1 2. *2 1 10 20 К ПР =?
2 способ:
11
10
9
8
7
+1
*2
+1
*2
+1
*2
1
10
2
3
18
8
14
9
16
2
5
6
1
4
3
+1
+1
+1
+1
*2
*2
*2
*2
+1
*2
*2
+1
4
4
10
32
16
6
4
6
4
3
7
8
2
2
12
6
5
10
32
Ответ:
Задание 23. сайт К.Ю. Полякова https://kpolyakov.spb.ru/school/ege /
(№ 2463) Исполнитель Калькулятор преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1 2. Прибавить 3
Программа для исполнителя Калькулятор – это последовательность команд.
Сколько существует программ, для которых при исходном числе 2 результатом является число 20 , и при этом траектория вычислений содержит число 10 и не содержит число 15 ?
Итак, мы имеем
Команды:
1. +1
2. +3
Траектория: 2 10 15 20
Надо определить: К ПР =?
Решение: 1. +1 2. +3 2 10 15 20 К ПР =?
1 способ:
2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17
- 18 19 20
11
12
13
4
1
6
1
9
3
1
2
13
10
19
20
26
13
39
13
65
26
16
17
15
156
91
65
156
Ответ:
Решение: 1. +1 2. +3 2 10 15 20 К ПР =?
2 способ:
16
15
14
18
17
12
13
+1
+1
+3
+3
+3
+1
+1
+3
+1
+3
2
3
2
5
5
17
19
17
20
14
18
16
15
13
15
9
11
8
10
7
6
+1
+1
+3
+3
+1
+1
+3
+3
+1
+3
+3
+1
24
12
36
12
7
12
13
12
11
9
8
11
14
10
12
7
9
10
5
4
3
2
+1
+3
+3
+3
+1
+1
+1
+3
72
48
108
156
8
5
6
7
4
6
5
3
156
Ответ:
Решение: 1. +1 2. +3 2 10 15 20 К ПР =? Найдем: 1) К ПР1 =?: 2 10 2) К ПР2 =?: 10 15 20 3) К ПР =К ПР1 *К ПР2
2 способ:
8
2
5
6
7
3
4
+1
+3
+3
+3
+3
+1
+1
+1
+1
+3
+3
+1
13
4
9
6
2
3
6
5
7
6
3
10
4
7
8
8
5
9
16
18
15
14
17
13
+1
+3
+3
+3
+1
+3
+1
+1
2
5
3
2
20
15
18
16
17
17
19
14
12
10
11
12 * 13 = 156
+1
+3
+3
+3
+1
+1
5
7
12
15
12
13
14
11
13
156
Ответ:
Тренировочная работа Статград ЕГЭ по информатике от 22.10.20
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1 2. Умножить на 3
Программа для исполнителя – это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 1 в число 70 , и при этом траектория вычислений содержит число 22 ?
Траектория вычислений – это последовательность результатов выполнения всех команд программы.
Итак, мы имеем
Команды:
1. +1
2. *3
Траектория: 1 22 70
Надо определить: К ПР =?
Решение: 1. +1 2. *3 2 22 70 К ПР =? Найдем: 1) К ПР1 =?: 2 22 2) К ПР2 =?: 22 70 3) К ПР =К ПР1 *К ПР2
2 способ:
5
3
8
6
4
7
+1
*3
*3
+1
*3
+1
*3
+1
+1
*3
4
2
5
3
6
5
15
12
7
18
6
21
8
4
9
2
1
К ПР1 =15
+1
+1
*3
*3
15
9
3
3
2
6
К ПР2 =3
К ПР =15*3=45
23
24
22
*3
+1
*3
+1
2
3
24
66
69
23
45
Ответ:
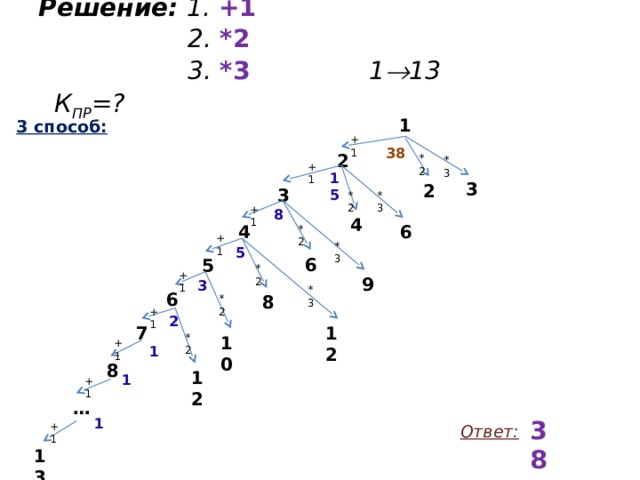
Образовательный портал для подготовки к экзаменам СДАМ ГИА : РЕШУ ЕГЭ У исполнителя Удвоитель-Утроитель три команды, которым присвоены номера:
№ 5064
1. прибавь 1
2. умножь на 2
3. умножь на 3.
Первая из них увеличивает на 1 число на экране, вторая увеличивает это число в 2 раза, третья — в 3 раза.
Программа для Удвоителя-Утроителя — это последовательность команд. Сколько существует программ, которые число 1 преобразуют в число 13?
Итак, мы имеем
Команды:
1. +1
2. *2
3. *3
Траектория: 1 13
Надо определить: К ПР =?
Решение: 1. +1 2. *2 3. *3 1 13 К ПР =?
1
3 способ:
+1
38
2
*2
*3
+1
15
3
2
3
*3
*2
+1
8
4
4
6
*2
+1
*3
5
6
5
*2
+1
9
3
*3
6
8
*2
+1
2
7
12
*2
10
+1
1
8
12
1
+1
…
1
38
+1
Ответ:
13
Возможные проблемы :
- В неверном определении начальных условий Главная, возможная, проблема (ловушка) — невнимательность. Держим внимание!
- В неверном определении начальных условий
- Главная, возможная, проблема (ловушка) — невнимательность.
- Держим внимание!
И тогда «Они НЕ будут так страшны, как могут показаться)».
НАДО ПРОСТО БОЛЬШЕ ТРЕНИРОВАТЬСЯ
Спасибо за внимание!
За это задание ты можешь получить 2 балла. На решение дается около 55 минут. Уровень сложности: высокий.
Средний процент выполнения: 14.3%
Ответом к заданию 27 по информатике может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
ДЛЯ 2022
На кольцевой дороге с двусторонним движением установлены магазины для продажи яблок. Все магазины находятся на расстоянии 1 километра друг от друга. Специальные роботы доставщики развозят яблоки со склада по этим магазинам. Длина кольцевой дороги равна N километров. Нулевой километр и N-й километр автодороги находятся в одной точке. Известно количество килограмм яблок, которое необходимо ежедневно доставлять в каждый из магазинов. Для каждого пункта яблоки возит отдельный робот доставщик. Стоимость доставки яблок вычисляется как произведение количества яблок (в килограммах) на расстояние от склада до магазина. Склад открыли в одном из магазинов таким образом, чтобы общая стоимость доставки яблок во все магазины была минимальной.
Определите минимальные расходы на доставку яблок в магазины.
Входные данные
Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество магазинов на кольцевой дороге. В каждой из следующих N строк находится число – количество килограмм яблок, необходимых для доставки в магазин (все числа натуральные, количество килограмм не превышает 1000). Числа указаны в порядке расположения магазинов на дороге, начиная с первого километра.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.
Типовой пример организации данных во входном файле
6 8 20 5 13 7 19
При таких исходных данных, если магазины установлены на каждом километре дороги, необходимо открыть склад в пункте 6. В этом случае сумма затрат на доставку составит:
1 · 7 + 0 · 19 + 1 · 8 + 2 · 20 + 3 · 5 + 2 · 13.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Решение
Для решения этого номера составим программу на языке Python
f = open('27_B.txt', 'r')
n = int(f.readline().strip())
x = [int(line) for line in f]
right = 0
left = x[0]
sum_all = 0
for i in range(1, n // 2):
sum_all += i * x[i] + i * x[-i]
right += x[i]
left += x[-i]
sum_all += (n // 2) * x[n // 2]
right += x[n // 2]
min_sum = sum_all
for i in range(1, n):
sum_all = sum_all - right + left
right = right + x[(n // 2 + i) % n] - x[i]
left = left + x[i] - x[(n // 2 + i) % n]
min_sum = min(min_sum, sum_all)
print(min_sum)
ОТВЕТ: А — 157076, В — 16371318320559
Ответ:
Задача 2
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти количество пар чисел, сумма которых кратна 26. Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — количество пар чисел, соответствующих условиям задачи. Если такую пару получить невозможно, вывести -1.
Описание входных и выходных данных
Даны два входных файла, каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10000.
Пример входных данных:
4
61
9
95
3
Пример выходных данных для приведённого выше примера входных данных:
2
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B. Без вывода ответа решение не будет засчитано.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Сумма будет кратна 26, если остатки от деления на 26 слагаемых в сумме дают 26 или 0. Воспользуемся критериальным способом решения этой задачи: будем находить количество чисел с различными остатками при делении на 26, а затем сопоставим эти группы для получения итогового ответа. Количество пар чисел, в которых оба числа кратны 26, рассчитываем по формуле $N*(N-1)/2!$, как и для чисел, кратных 26 (их количество будет храниться в элементе с индексом 26 и 0 соответственно)
Решение на Python:
file = open("file.txt", "r")
size = int(file.readline())
arr = [0] * 26
count13 = 0
for i in range(size):
val = int(file.readline())
arr[val % 26] += 1
countSum = int((arr[0] * (arr[0] - 1)) / 2 + (arr[13] * (arr[13] - 1)) / 2)
for i in range(1, 13):
countSum += arr[i] * arr[26 - i]
if countSum == 0:
print("-1")
else:
print(countSum)
file.close()
Решение на C++:
#include <iostream>
#include <fstream>
using namespace std;
int comp(int a, int b){return a < b;}
int main() {
ifstream file("file.txt");
int size; file >> size;
int arr[26]; for (int i = 0; i < 26; ++i) arr[i] = 0;
for (int i = 0; i < size; ++i) {
int val; file >> val;
arr[val % 26]++;
}
int count = (arr[0] * (arr[0] - 1))/2 + (arr[13] * (arr[13] - 1))/2;
for (int i = 1; i < 13; ++i)
count += arr[i] * arr[26 - i];
if (count == 0) cout << "-1";
else cout << count;
return 0;
}
Ответы: для файла А = 105, для файла Б = 173548026
Ответ:
Задача 3
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти количество пар, в которых произведение чисел кратно 14, а числа находятся на расстоянии не больше 10 (разность в индексах ≤ 10). Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — количество пар, соответствующее условиям задачи.
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Пример решения на Python:
f = open(‘fileB4.txt’)
N = int(f.readline())
mas = []
kol = 0
for i in range(N):
x = int(f.readline())
for y in mas:
if x * y % 14 == 0:
kol += 1
if len(mas) >= 10:
mas.pop(0)
mas.append(x)
print(kol)
f.close()
Для прикреплённого файла A программа выведет: 173
Для прикреплённого файла B программа выведет: 198081
Ответ:
Задача 4
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти наибольшее произведение пары чисел, кратное 26, числа в которой находятся на расстоянии не больше 26 (разность в индексах ≤ 26). Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — максимально возможное произведение, соответствующее условиям задачи. Если такое произведение получить невозможно, вывести -1.
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Пример решения на Python:
f = open(‘fileB7.txt’)
N = int(f.readline())
mas = []
max_pr = -1
for i in range(N):
x = int(f.readline())
for y in mas:
if x * y % 26 == 0:
if x * y > max_pr:
max_pr = x * y
if len(mas) >= 26:
mas.pop(0)
mas.append(x)
print(max_pr)
f.close()
Для прикреплённого файла A программа выведет: 94449498
Для прикреплённого файла B программа выведет: 99580416
Ответ:
Задача 5
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти количество пар, в которых произведение чисел кратно 85, а числа находятся на расстоянии не меньше 6 (разность в индексах ≥ 6). Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — количество пар, соответствующее условиям задачи.
Описание входных и выходных данных
Даны два входных файла, каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10000.
Пример входных данных:
4
14
2
8
3
Пример выходных данных для приведённого выше примера входных данных:
1
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Пример решения на Python:
def bubble_sort(a):
for i in range(len(a)):
for j in range(len(a) — 1 — i):
if a[j] < a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
f = open(«file.txt»)
i = 0
a = []
for st in f:
if i == 0:
N = int(st)
else:
n1, n2, n3 = map(int, st.split())
a.append(max(n1,n2,n3))
i += 1
bubble_sort(a)
print(a[9])
f.close()
Для прикреплённого файла программа выведет: 9952
Ответ:
Задача 6
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти наибольшее произведение пары чисел, кратное 27, числа в которой находятся на расстоянии не меньше 7 (разность в индексах ≥ 7). Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — максимально возможное произведение, соответствующее условиям задачи.Если такое произведение получить невозможно, вывести -1.
Описание входных и выходных данных
Даны два входных файла, каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10000.
Пример входных данных:
5
13
15
6
2
4
Пример выходных данных для приведённого выше примера входных данных:
52
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Пример решения на Python:
def bubble_sort(a):
for i in range(len(a)):
for j in range(len(a) — 1 — i):
if a[j] < a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
f = open(«file.txt»)
i = 0
a = []
for st in f:
if i == 0:
N = int(st)
else:
n1, n2, n3 = map(int, st.split())
a.append(max(n1,n2,n3))
i += 1
bubble_sort(a)
print(a[9])
f.close()
Для прикреплённого файла программа выведет: 9952
Ответ:
Задача 7
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти количество пар, в которых произведение чисел кратно 46. Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — количество пар, соответствующее условиям задачи.
Описание входных и выходных данных
Даны два входных файла, каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10000.
Пример входных данных:
4
92
2
8
3
Пример выходных данных для приведённого выше примера входных данных:
3
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Пример решения на Python на 1 балл:
f = open(«fileA7.txt»)
N = int(f.readline())
a = []
for i in range(N):
x = int(f.readline())
a.append(x)
f.close()
kol_par = 0
for i in range(N):
for j in range(i+1, N):
if a[i]*a[j] % 46 == 0:
kol_par += 1
print(kol_par)
Пример решения на Python на 2 балла:
f = open(«fileB7.txt»)
N = int(f.readline())
kol46 = kol23 = kol2 = kol0 = 0
for i in range(N):
x = int(f.readline())
if x % 46 == 0:
kol46 += 1
elif x % 23 == 0:
kol23 += 1
elif x % 2 == 0:
kol2 += 1
else:
kol0 += 1
f.close()
kol_par = kol46*(kol46-1)//2 + kol46*(N-kol46) + kol23*kol2
print(kol_par)
Для прикреплённого файла A программа выведет: 197
Для прикреплённого файла B программа выведет: 286112969
Ответ:
Задача 8
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти количество пар, в которых произведение чисел кратно 26. Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — количество пар, соответствующее условиям задачи.
Описание входных и выходных данных
Даны два входных файла, каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10000.
Пример входных данных:
4
14
2
8
3
Пример выходных данных для приведённого выше примера входных данных:
3
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Пример решения на Python:
def bubble_sort(a):
for i in range(len(a)):
for j in range(len(a) — 1 — i):
if a[j] < a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
f = open(«file.txt»)
i = 0
a = []
for st in f:
if i == 0:
N = int(st)
else:
n1, n2, n3 = map(int, st.split())
a.append(max(n1,n2,n3))
i += 1
bubble_sort(a)
print(a[9])
f.close()
Для прикреплённого файла программа выведет: 9952
Ответ:
Задача 9
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти наибольшее произведение пары чисел, кратное 52. Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — максимально возможное произведение, соответствующее условиям задачи.Если такое произведение получить невозможно, вывести -1.
Описание входных и выходных данных
Даны два входных файла, каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10000.
Пример входных данных:
4
13
4
2
15
Пример выходных данных для приведённого выше примера входных данных:
52
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Пример решения на Python:
def bubble_sort(a):
for i in range(len(a)):
for j in range(len(a) — 1 — i):
if a[j] < a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
f = open(«file.txt»)
i = 0
a = []
for st in f:
if i == 0:
N = int(st)
else:
n1, n2, n3 = map(int, st.split())
a.append(max(n1,n2,n3))
i += 1
bubble_sort(a)
print(a[9])
f.close()
Для прикреплённого файла программа выведет: 9952
Ответ:
Задача 10
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти наименьшее произведение пары чисел, кратное 26, числа в которой находятся на расстоянии не меньше 4 (разность в индексах ≥ 4). Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — минимально возможное произведение, соответствующее условиям задачи.Если такое произведение получить невозможно, вывести -1.
Описание входных и выходных данных
Даны два входных файла, каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10000.
Пример входных данных:
5
13
15
6
2
4
Пример выходных данных для приведённого выше примера входных данных:
52
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Пример решения на Python на 1 балл:
f = open(«file.txt»)
N = int(f.readline())
a = []
for i in range(N):
a.append(int(f.readline()))
f.close()
min_pr = 10001 * 10001
for i in range(N):
for j in range(i+1, N):
pr = a[i]*a[j]
if pr % 26 == 0 and pr < min_pr and j-i >= 4:
min_pr = pr
if min_pr == 10001 * 10001:
print(-1)
else:
print(min_pr)
Пример решения на Python на 2 балла:
f = open(«file.txt»)
N = int(f.readline())
min26 = min13 = min2 = min0 = 10001
min_pr = 10001 * 10001
queue = []
for i in range(3):
queue.append(int(f.readline()))
for i in range(3, N):
x = int(f.readline())
if x % 26 == 0:
if x * min26 < min_pr and min26 != 10001:
min_pr = x * min26
if x * min13 < min_pr and min13 != 10001:
min_pr = x * min13
if x * min2 < min_pr and min2 != 10001:
min_pr = x * min2
if x * min0 < min_pr and min0 != 10001:
min_pr = x * min0
elif x % 13 == 0:
if x * min26 < min_pr and min26 != 10001:
min_pr = x * min26
if x * min2 < min_pr and min2 != 10001:
min_pr = x * min2
elif x % 2 == 0:
if x * min26 < min_pr and min26 != 10001:
min_pr = x * min26
if x * min13 < min_pr and min13 != 10001:
min_pr = x * min13
else:
if x * min26 < min_pr and min26 != 10001:
min_pr = x * min26
if queue[0] % 26 == 0:
if queue[0] < min26:
min26 = queue[0]
elif queue[0] % 13 == 0:
if queue[0] < min13:
min13 = queue[0]
elif queue[0] % 2 == 0:
if queue[0] < min2:
min2 = queue[0]
else:
if queue[0] < min0:
min0 = queue[0]
queue[0] = queue[1]
queue[1] = queue[2]
queue[2] = x
if min_pr == 10001 * 10001:
print(-1)
else:
print(min_pr)
f.close()
Вывод для файла А: 53404
Вывод для файла B: 78
Ответ:
Задача 11
Имеется набор данных, состоящий из положительных целых чисел, все числа не превышают 10000. Количество чисел известно, но может быть очень велико. Необходимо найти количество пар чисел, произведение которых кратно 14. Под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен. Программа должна напечатать одно число — количество пар чисел, соответствующих условиям задачи.Если такое произведение получить невозможно, вывести -1.
Описание входных и выходных данных
Даны два входных файла, каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из последующих N строк записано одно натуральное число, не превышающее 10000.
Пример входных данных:
4
14
2
21
3
Пример выходных данных для приведённого выше примера входных данных:
4
В качестве ответа прикрепите код решения, а также два числа — ответ для файла А и ответ для файла B. Без вывода ответа решение не будет засчитано.
Предупреждение: для обработки файла b не следует использовать переборный алгоритм, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение
Число 14 раскладывается на множители 7 и 2. Проивзедение будет кратно 14, если один из множителей кратен 14 или числа в паре содержат простые множители 14. Воспользуемся критериальным способом решения этой задачи и разобъём входные значения на 4 группы и найдём количество значений в каждой из групп:
А. Число делится на 2 и 7;
В. Число делится на 2, не делится на 7;
С. Число не делится на 2, делится на 7;
D. Число не делится на 2, не делится на 7;
Решение на Python:
file = open("file.txt", "r")
size = int(file.readline())
countA, countB, countC, countD = (0, 0, 0, 0)
for i in range(size):
val = int(file.readline())
if val % 2 == 0 and val % 7 == 0:
countA += 1
elif val % 2 == 0 and val % 7 != 0:
countB += 1
elif val % 2 != 0 and val % 7 == 0:
countC += 1
elif val % 2 != 0 and val % 7 != 0:
countD += 1
print(int(countA * (countA - 1) / 2 + countA * countB +
countA * countC + countA * countD + countB * countC))
file.close()
Решение на C++:
#include <iostream>
#include <fstream>
using namespace std;
int main() {
ifstream file("file.txt");
int size; file >> size;
int countA = 0, countB = 0, countC = 0, countD = 0;
for (int i = 0; i < size; ++i) {
int val; file >> val;
if (val % 2 == 0 && val % 7 == 0)
countA += 1;
else if (val % 2 == 0 && val % 7 != 0)
countB += 1;
else if (val % 2 != 0 && val % 7 == 0)
countC += 1;
else if (val % 2 != 0 && val % 7 != 0)
countD += 1;
}
int count = countA * (countA - 1) / 2 + countA * countB +
countA * countC + countA * countD + countB * countC;
if (count == 0) cout << "-1";
else cout << count;
return 0;
}
Ответы: для файла А = 947, для файла Б = 990014844
Ответ:







![Способ 2: ПрограммированиеС.С. Поляков:
L=[0]*24 L[23]=1 for x in range(23... Способ 2: ПрограммированиеС.С. Поляков:
L=[0]*24 L[23]=1 for x in range(23...](https://documents.infourok.ru/3d2af76a-60e4-4299-a045-b3ffe81f639e/0/slide_07.jpg)