Егэ информатика 27228 - Помощь в подготовке к экзаменам и поступлению

Логическая функция F задаётся выражением (¬x ∨ y ∨ z) ≡ (¬y ∧ z ∧ w). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

?	?	?	F
1	1	1	1
0	0		1
1		1	1

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Спрятать решение

Решение.

Заметим, что выражение будем истинным тогда, когда обе скобки будут принимать значение 0 или 1.

Рассмотрим первую строку таблицы истинности. Заметим, что выражение будет истинным только тогда, когда переменная y будет равна 0, то есть строка будет выглядеть как 0111. Следовательно, переменной y соответствует первый столбец.

Рассмотрим вторую строку таблицы истинности. Правая скобка будет принимать значение 0. Значит, переменные y и z должны принимать значение 0, а переменная x должна принимать значение 1. Таким образом, строка будет выглядеть как 0001, а переменной x соответствует четвёртый столбец таблицы истинности.

Рассмотрим третью строку таблицы истинности. Третья строка может выглядеть как 0101, 1101 и 1111. Предположим, что переменная z соответствует второму столбцу таблицы истинности. Тогда значение выражения во всех трёх случаях будет ложным. Значит, переменная w соответствует второму столбцу таблицы истинности, а переменная z  — третьему.

Ответ: ywzx.

Приведём другое решение.

Составим таблицу истинности для выражения (¬x ∨ y ∨ z) ≡ (¬y ∧ z ∧ w) вручную или при помощи языка Python:

print(«x y z w»)

for x in range(0, 2):

for y in range(0, 2):

for z in range(0, 2):

for w in range(0, 2):

if (not(x) or y or z) == (not(y) and z and w):

print(x, y, z, w)

Далее выпишем те наборы переменных, при которых данное выражение равно 1. В наборах переменные запишем в порядке х, y, z, w. Получим следующие наборы:

(0, 0, 1, 1),

(1, 0, 0, 0),

(1, 0, 0, 1),

(1, 0, 1, 1).

Соотнесём эти наборы с представленным фрагментом таблицы истинности.

Заметим, что переменная y принимает единственное значение 0, следовательно, это первый столбец. Рассмотрим вторую строчку исходной таблицы истинности, когда в значениях три нуля, то последнее будет 1, и это будет x. Значит, последний столбец — x. Учтём, что первый набор значений можно не использовать, так как в данной таблице он не фигурирует. Тогда второй столбик, исходя из полученных наборов — w. Остаётся третий столбец — z. Получаем последовательность ywzx.

Источник

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Задания

Версия для печати и копирования в MS Word

Задания Д6 № 27228

В треугольнике ABC угол C равен 90°, Найдите

Спрятать решение

Решение.

Имеем:

Ответ: 0,28.

Аналоги к заданию № 27228: 29141 29147 29151 29143 29145 29149 Все

Спрятать решение

Сообщить об ошибке · Помощь

Ирина Викторовна Барабаш 21.12.2013 20:26

Надо вспомнить формулы, которая связывает косинус и тангенс!

Аналогичные задания: 29141 29143 29145 29147 29149 29151

Александр Иванов

Так и хочется спросить: «С кем это Вы разговариваете?»

О проекте · Редакция · Правовая информация · О рекламе

Источник

ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
АНГЛИЙСКИЙ без ГРАНИЦ

2012-07-12

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Конструктор упражнений для позвоночника!

Добавить комментарий

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

РубрикиРубрики
Задачи по номерам!

№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
МЕТКИ

БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
ОСТЕОХОНДРОЗУ-НЕТ!

Источник

Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.

Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).

С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.

() — операции в скобках
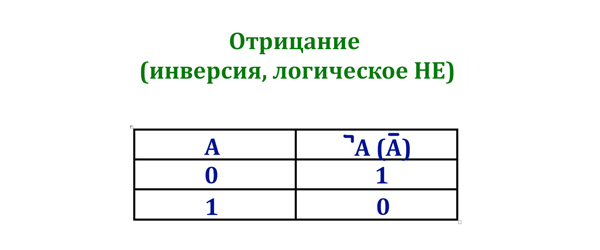
¬ — логическое отрицание
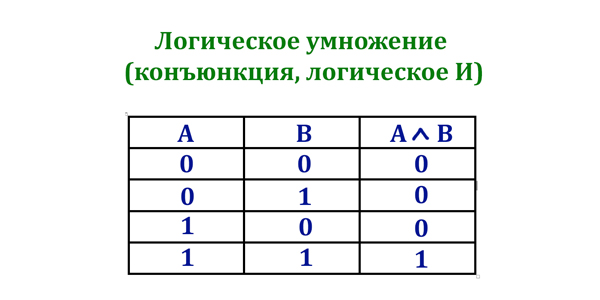
∧ — логическое умножение
∨ — логическое сложение
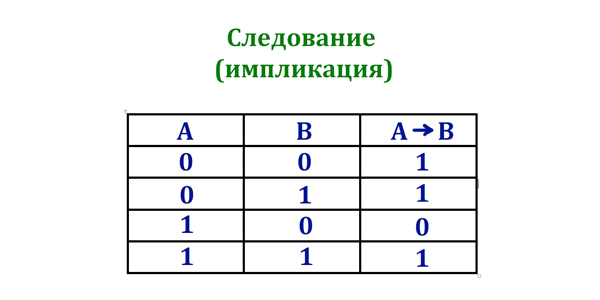
⟶ — следование
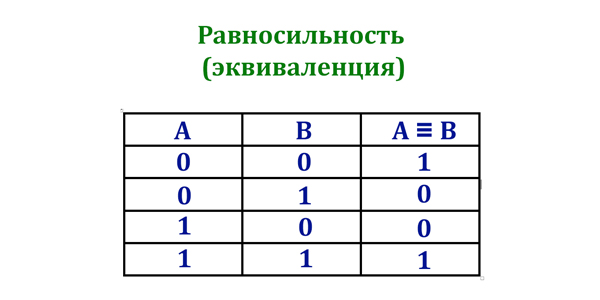
≡ — равнозначность

Ещё соотношения:

Передём к решению задач из ЕГЭ по информатике

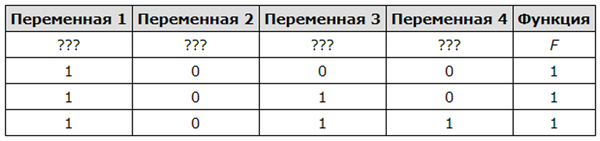
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

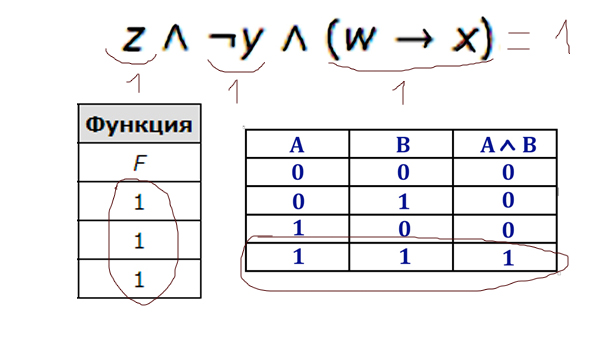
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.

Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.

Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.

Задача 2 (средний уровень)

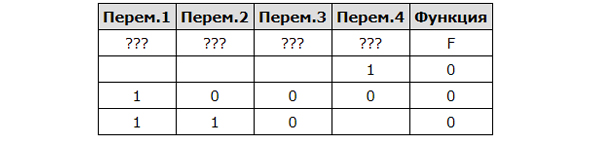
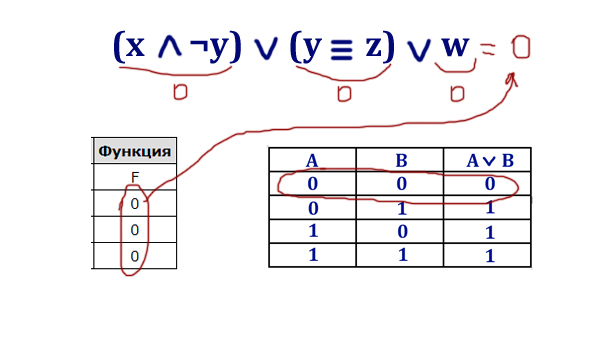
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
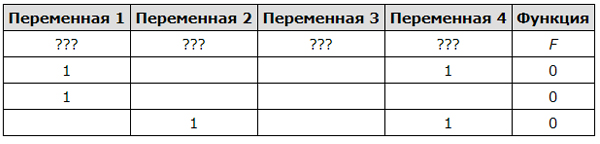
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.

Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).

Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.

Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!

Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).

Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).

Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.

Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.

Тогда ответ будет равен yxwz.

Ответ: yxwz

Мощнейший метод для решения второго задания из ЕГЭ по информатике

Задача 3 (хороший уровень)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).

Тогда каждое выражение должно равняться 0(нулю).

Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 2 4 ).

Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).

При небольшой тренировке анализ подобных выражений занимает сущие секунды!

У нас получается 4 строчки, которые удовлетворяют нашей функции:

Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).

Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.

Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец

Ответ: ywzx.

На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!

Строки с пропущенными значениями 2 задание егэ информатика как решать

Тип 2 № 14688

Логическая функция F задаётся выражением (x ∨ y) → (z ≡ x).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.

Переменная 1	Переменная 2	Переменная 3	Функция
.	.	.	F
0	0	0
0	0

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Переменная 1	Переменная 2	Функция
.	.	F
0	1	0

Данная импликация принимает значение 0 тогда и только тогда, когда

Пусть x = 0, тогда y = z = 1. В первой строке нет двух единиц, значит, x = 1, и эта переменная находится в первом столбце. Тогда первая строка имеет вид 1 0 0.

Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:

Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.

Приведем другое решение.

Составим таблицу истинности для выражения (x ∨ y) → (z ≡ x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы:

Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.

Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, первый столбец таблицы соответствует переменной x, и в первом столбце первой строки стоит 1.

Второй столбец таблицы может соответствовать только переменной z, поскольку переменная y принимает нулевое значение только в одном наборе. Тогда третий столбец соответствует переменной y.

Тип 2 № 15097

Логическая функция F задаётся выражением (x ≡ z ) ∨ (x → (y ∧ z)).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.

. . . F

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Данная импликация принимает значение 0 тогда и только тогда, когда

Пусть . Исходя из системы (*), , тогда . В первой строке нет единицы, значит, переменная x находится в третьем столбце. Тогда первая строка имеет вид 0 0 1.

Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:

Второй вариант не удовлетворяет системе (*), а первый удовлетворяет.

Приведем другое решение.

Составим таблицу истинности для выражения (x ≡ z ) ∨ (x → (y ∧ z)) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы:

Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.

Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, третий столбец — это переменная x. Вторая строка соответствует набору (1, 1, 0), в котором единичное значение принимает также переменная y, следовательно, первый столбец — это переменная у, тогда второй столбец — это переменная z.

Тип 2 № 15124

Логическая функция F задаётся выражением (x ≡ y ) ∨ ((y ∨ z) → x).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.

. . . F

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Данная импликация принимает значение 0 тогда и только тогда, когда

Пусть . Исходя из системы (*), , тогда . В первой строке нет нуля, значит, переменная x находится в первом столбце. Тогда первая строка имеет вид 0 1 1.

Вторая строка должна отличаться от первой, поэтому она имеет вид 0 0 1. Рассмотрим два варианта:

Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.

Приведем другое решение.

Составим таблицу истинности для выражения (x ≡ y ) ∨ ((y ∨ z) → x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы: (0, 1, 0), (0, 1, 1).

Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.

В обоих наборах переменная x принимает значение 0, значит, ей может соответствовать только первый столбец таблицы. Переменная z принимает значение 1 только в одном наборе, значит, ей может соответствовать только второй столбец таблицы, тогда третий столбец соответствует переменной у.

Тип 2 № 15618

Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w. На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.

Перем.1	Перем.2	Перем.3	Перем.4
.	.	.	.
0
1	0	0
1	0	0

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (без разделителей).

Рассмотрим данное выражение. Преобразуем логическое выражение (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w и получим систему, при которой оно ложно:

Cразу видно, что первый столбец это w, поскольку w всегда должна равняться единице. Также, ясно, что x это переменная 4, так как . Из первого выражения x ∧ ¬y и последней строчке таблицы видно, что переменная 3 это y, а вторая переменная это z.

Рассмотрим, как будет выглядеть полная таблица истинности. Переменная w всегда должна принимать значение 1, поэтому в первом столбце во всех строках будет стоять единица. Исходя из условия можно заключить, что во втором столбце в последней строке будет стоять единица, и в первых двух строках третьего столбца тоже будут стоять единицы. В первой четвёртого столбца должна стоять единица, поскольку строки в таблице истинности должны быть разными.

Перем. 1	Перем. 2	Перем. 3	Перем. 4
.	.	.	.
1	0	1	1
1	0	1	0
1	1	0	0

Вариант wyzx не подходит, поскольку в первой строке функция F окажется истинной.

Приведем другое решение.

Составим таблицу истинности функции F и выпишем наборы переменных, при которых функция ложна. Для удобства обозначим эти наборы буквами:

А: (х=0, y=0, z=1, w=1)

Б: (х=0, y=1, z=0, w=1)

В: (х=1, y=1, z=0, w=1)

Заметим, что переменная w всегда должна быть равна 1, поэтому ей соответствует первый столбец заданной таблицы.

Заметим, что вторая и третья строки заданной таблицы, содержащие по два нуля, соответствуют наборам переменных А или Б, тогда первая строка соответствует набору В. Значит, в первой строке z=0, а все остальные переменные равны 1, и переменной z соответствует второй столбец заданной таблицы.

Тогда вторая строка заданной таблицы, в которой переменная z также равна 0, соответствует набору Б, в котором х=0, а остальные переменные равны 1, поэтому переменной х соответствует четвертый столбец таблицы.

Строки с пропущенными значениями 2 задание егэ информатика как решать

Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

Перем. 1	Перем. 2	Перем. 3	Перем. 4	Функция
.	.	.	.	F
1	0	0	0	0
1	1	0	0	0
1	1	1	0	0

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Дан фрагмент таблицы истинности выражения F.

x1	x2	x3	x4	x5	x6	x7	F
1	0	0	1	1	1	1	0
0	1	0	0	1	0	1	1
0	1	0	1	1	0	1	0

Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7

Логическая функция F задается выражением

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.

Перем.1	Перем.2	Перем.3	Перем.4	Функция
.	.	.	.	F
0	1	0	0	1
1	1	0	0	1
1	1	0	1	1

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

Миша заполнял таблицу истинности функции
(¬x ∧ ¬y) ∨ (y ≡ z) ∨ w,
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:

?	?	?
0	1
1	1	0
1	1	0

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

Логическая функция F задается выражением
¬(z ∨ (y ∧ ¬x))

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Перем. 1	Перем. 2	Перем. 3	Функция
.	.	.	F
0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

Видеоразбор

Логическая функция F задается выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.

Источник

Продолжаем решать демоверсию ЕГЭ по информатике 2023.

Условия задач были взяты с сайта: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5

В этой статье разберём задания 22-27.

Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 16-21)

Задание 22

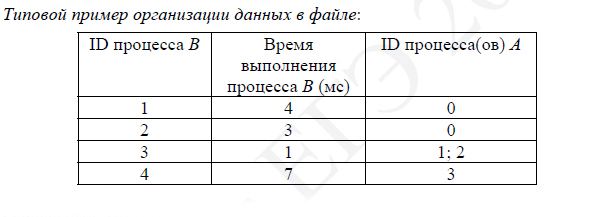
Информация о процессах представлена в файле в виде таблицы. В первой
строке таблицы указан идентификатор процесса (ID), во второй строке
таблицы – время его выполнения в миллисекундах, в третьей строке
перечислены с разделителем «;» ID процессов, от которых зависит данный
процесс. Если процесс является независимым, то в таблице указано
значение 0.

Типовой пример имеет иллюстративный характер. Для выполнения
задания используйте данные из прилагаемого файла.

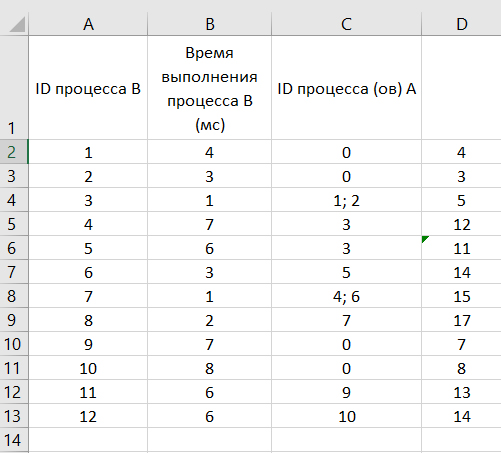
Решение:

Здесь есть процессы, которые зависят от других процесов. В столбце D вычислим время для всех процесов, с учётом зависимости.

Если процесс зависит от двух процессов, то время ожидания будет равно самому медленному из этих процессов.

В столбце D пишем для каждой строчки: время процесса + время ожидания самого медленного процесса, от которого зависит этот процесс (если такие есть).

Получается такая картина:

Система заврешить работу, когда завершится самый медленный процесс.

Ответ: 17

Задание 23

Исполнитель преобразует число на экране.

У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1
2. Умножить на 2

Программа для исполнителя – это последовательность команд.
Сколько существует программ, для которых при исходном числе 1
результатом является число 35, при этом траектория вычислений содержит
число 10 и не содержит 17?

Траектория вычислений программы – это последовательность результатов
выполнения всех команд программы. Например, для программы 121 при
исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

Решение:

Будем решать с помощью шаблона на языке Python, который был представлен в видеокурсе по подготовке к ЕГЭ по информатике.

def F(x, y):
    if x == y: return 1

    if x > y or x==17: return 0

    if x < y: return F(x+1, y) + F(x*2, y)

print(F(1, 10)*F(10, 35))

Ответ: 98

Задание 24

Текстовый файл состоит из символов A, B, C, D и O.

Определите максимальное количество идущих подряд пар символов вида

согласная + гласная

в прилагаемом файле.

Для выполнения этого задания следует написать программу.

Решение:

Подобная задача была рассмотрена в видеокурсе к ЕГЭ по информатике.

f=open('24_10.txt')
s=f.read()
s=s.replace('BA', '1')
s=s.replace('CA', '1')
s=s.replace('DA', '1')
s=s.replace('BO', '1')
s=s.replace('CO', '1')
s=s.replace('DO', '1')
k=0
kmax=0

for i in range(0, len(s)):
    if s[i]=='1':
        k=k+1
        kmax=max(k, kmax)
    else:
        k=0

print(kmax)

Ответ получается 24, но в официальном ответе 95. Дело в том, что в файле присутствует буква F, хотя в условии сказано, что файл состоит только из букв A, B, C, D и O. Следовательно, файл к задаче не верный.

Ответ: 24

Задание 25

Назовём маской числа последовательность цифр, в которой также могут
встречаться следующие символы:

– символ «?» означает ровно одну произвольную цифру;

символ «*» означает любую последовательность цифр произвольной
длины; в том числе «*» может задавать и пустую последовательность.

Например, маске 123*4?5 соответствуют числа 123405 и 12300405.
Среди натуральных чисел, не превышающих 10¹⁰, найдите все числа,
соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.

В ответе запишите в первом столбце таблицы все найденные числа
в порядке возрастания, а во втором столбце – соответствующие им
результаты деления этих чисел на 2023.

Количество строк в таблице для ответа избыточно.

Решение:

Подобная задача так же обсуждалась в видеокурсе и на обзоре реального экзамена ЕГЭ по информатике от 20.06.22

Если не учитывать звёздочку, число 1?21394 имеет семь разрядов. Максимальная верхняя граница 10¹⁰. Значит, для звёздочки есть три разряда.

#Вместо звёздочки ноль разрядов
for x in '0123456789':
    s = '1' + x + '21394'
    i=int(s)
    if i%2023==0:
        print(i, i//2023)
    
    
#Вместо звёздочки один разряд
for x in '0123456789':
    for y in '0123456789':
        s = '1' + x + '2139' + y + '4'
        i=int(s)
        if i%2023==0:
            print(i, i//2023)

#Вместо звёздочки два разряда
for x in '0123456789':
    for y in '0123456789':
        for z in '0123456789':
            s = '1' + x + '2139' + y + z + '4'
            i=int(s)
            if i%2023==0:
                print(i, i//2023)

           
#Вместо звёздочки три разряда
for x in '0123456789':
    for y in '0123456789':
        for z in '0123456789':
            for w in '0123456789':
                s = '1' + x + '2139' + y + z + w + '4'
                i=int(s)
                if i%2023==0:
                    print(i, i//2023)

Ответ:

162139404	80148
1321399324	653188
1421396214	702618
1521393104	752048

Задание 26

В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки — подарок упаковывается в одну из коробок, та в свою очередь в другую коробоку и т.д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.

Выходные данные

В первой строке входного файла находится число N — количество коробок в магазине (натуральное число, не превышающая 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое — в отдельной строке.

Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.

Типовой пример организации данных во входном файле.

5
43
40
32
40
30

Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих упаковки «матрёшки», составлят 3 единицы.

При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Решение:

f=open('26.txt')
n=int(f.readline())

a=[]

for i in range(n):
    x=int(f.readline())
    a.append(x)


a.sort(reverse=True)

k=1
p=a[0]

for i in range(1, len(a)):
    if p-a[i]>=3:
        k=k+1
        p=a[i]

print(k, p)

В начале считываем все числа в массив (список) a. Сортируем их в порядке убывания.

Приступаем собирать упаковку. Начинаем с самой большой упаковки. Большую упаковку точно можно взять в наш подарок. Переменная p — это размер последний коробки, которую мы взяли. Переменная k — количество коробок в подарке на текущий момент времени.

Если следующая коробка подходит по условию, то мы её берём в наш подарок. Кто-то может подумать, что может выгоднее взять не самую большую коробку, а предпоследнего размера. Но все размеры которые будут подходить для предпоследнего элемента, точно будут подходить и для последнего, и количество упаковок точно не будет меньше, если мы берём самую большую коробку.

Дубликаты не влияют на ответы.

Если мы начинаем с самой большой коробки, то в самом конце в переменной p окажется максимальный размер самой маленькой коробки.

Ответ:

Задание 27

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.

Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.

Входные данные

Дано два входных файла (файл А и файл B), каждый из которых в первой строке содержит число N ( 1 ≤ N ≤ 10 000 000) — количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.

В ответе укажите два числа: сначала значение искомой величины для файла A, затем — для файла B.

Типовой пример организации данных во входном файле
6
1 100
2 200
5 4
7 3
8 2
10 190

При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1*2 + 3*1 + 5*1 + 6*1 + 8*2.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных варантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Решение:

import math

f=open('27B.txt')

k=9999995

n=int(f.readline())

a=[0]*k

sm=0

for i in range(n):
    x, y = f.readline().split()
    x=int(x)
    y=int(y)
    z = math.ceil(y/36)
    a[x] = z
    sm = sm + (x-1)*z

# Вспомогательные суммы
s1=[]
s2=[]
s1.append(0)
s2.append(0)
s1.append(0)
s2.append(0)

for i in range(1, k):
    s1[1] = s1[1] + a[i]


for i in range(2, k):
    s1.append(s1[i-1] - a[i-1])
    s2.append(s2[i-1] + a[i-1])

# Ищем минимальное значение
mn=sm

for i in range(2,  k):
    sm = sm - s1[i] + s2[i]
    mn=min(mn, sm)

print(mn)

Переменная k — это количество приёмных пунктов (Т.е. длина массива a). Превая ячейка соответсвует приёмному пункту под номером 1, вторая ячейка под номером 2 и т.д. Само значение для k мы смотрим в конце файла. Например, для файла A значение напишем 999. Всего 998 приёмных пунктов, но т.к. индексы в массиве начинаются с 0, то мы должны завести 999 ячеек. Т.е. нулевая ячейка не будет никак задействована. Для файла B устанавливаем k в 9999995.

В сами ячейки массива мы поместим для каждого приёмного пункта количество контейнеров. Их легко вычислить. Если количество пробирок не нулевое, то мы должны это количество разделить на 36 и округлить в большую сторону. Количество контейниров в нашей программе для каждого приёмного пункта — это переменная z.

Пусть лаборатория расположена в первом пункте. Тогда вычислим для неё стоимость доставки:

sm1 = a[2]*1 + a[3]*2 + a[4]*3 + … + a[m]*(m-1)

Здесь m — это последний индекс массива a (m = k-1). Пусть лаборатория будет во втором пункте, тогда:

sm2= a[3]*1 + a[4]*2 + … + a[n]*(m-2) + a[1] = sm1 — (a[2] + a[3] + a[4] + … + a[m]) + a[1]

Отсюда мы понимаем, что достаточно вычислить стоимость доставки sm1 по формуле, которую нам дали в задаче, только один раз для первого пункта. Для второго пункта вычисляем: sm2 = sm1 — (a[2] + a[3] + a[4] + … + a[m]) + a[1]. Для третьего sm3 = sm2 — (a[3] + a[4] + … + a[m]) + a[2] + a[1] и т.д.

Значит, для каждого приёмного пункта i мы должны иметь уже готовую вспомагательную сумму s1[i] = a[i] + a[i+1] + …+ a[m], а так же сумму s2, т.е. сумма элементов, которые идут левее i (само a[i] уже не берётся): s2[i] = s[1] + s[2] + … + s[i-1].

Сумму s1[i] мы должны отнимать, а s2[i] прибавлять. По мерее продвижения по нашим приёмным пунктам, s1[i] будет уменьшаться, а s2[i] увеличиваться.

Но вспомогательные суммы s1[i] и s2[i] нужно тоже вычислисть, как можно эффективней. Достаточно вычислить для s1[1] и s2[1] (для первого приёмного пункта), а дальше можно воспользоваться закономерностью: s1[2] = s1[1]-a[1], s1[3] = s1[2]-a[2]…и т.д. Так же s2[2] = s[1]+a[1], s[3] = s[2]+a[2] и т.д.

s1[0] и s2[0] не нужны, они соответсвуют a[0], а она не используется при решении задачи. Значение s1[1] вычисляем «честно» с помощью цикла. Значение s2[1] = 0 (левее нет ячеек).

В самом первом цикле вычисляется значение для переменной sm — это стоимость перевозки, если лаборатория стоит в первом пункте. В последнем цикле программы вычисляем стоимоть для всех остальных приёмных пунктов, используя вышеописанные алгоритмы. И находим минимальное значение среди всех значений для переменной sm.

Ответ:

Задания 24, 26 — файлы не скачиваются, а открываются текстом в новой вкладке браузера.

Источник

Public user contributions licensed under
cc-wiki license with attribution required

Источник

В решение заданий демо-версии используется язык программирования Python.

Задание 1. Анализ информационных моделей

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число.

На графе расставим веса вершин.
Мы видим, что вершина В уникальна, имеет вес 2 и связана с двумя «тройками по весу».
Из таблицы видим, В это 4, далее видим, что «тройки по весу» это вершины 2 и 7.
7 вершина связана кроме В, еще с двумя «тройками по весу», значит D это 7, а F это 2.

Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6.
Рассуждая дальше видим, что С это 1, G это 2.

Сумма дорог BD + AF = 53 + 5 = 58

Ответ: 58

Задание 2. Построение таблиц истинности логических выражений

Миша заполнял таблицу истинности логической функции F

F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx.

¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.

y	x	z	w
0	0	1	0
0	1	1	0
1	1	1	0

Решение на Python

Ответ: YXZW

Задание выполняется с использованием прилагаемых файлов

Задание 3. Базы данных. Файловая система

В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в
магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня.

На рисунке приведена схема указанной базы данных.

Используя информацию из приведённой базы данных, определите общий вес
(в кг) крахмала картофельного, поступившего в магазины Заречного района
за период с 1 по 8 июня включительно. В ответе запишите только число.

На третьем листе книги применим фильтр по району и получим ID четырех магазинов.

На втором листе применим фильтр по товару и получим ID товара.

На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим:

Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг.

Ответ: 355

Задание 4. Кодирование и декодирование информации

По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений.

Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Ответ: 14

Задание 5. Анализ и построение алгоритмов для исполнителей

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему
новое число R следующим образом.

1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.

Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число
10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе запишите это число в десятичной системе счисления.

Минимальное R, большее 40, это 41.
В результате выполнения алгоритма число R должно либо начинаться на 10 и оканчиваться 0, либо начинаться на 11 и оканчиваться 1.
Из чисел, больших 41, это 42, 44, 46, 49, и т.д.
Мы должны найти минимальное N, из которого данное число получено.
Поскольку первые цифры заменялись, то мы видим, что данные числа могли быть получены из чисел 29, 30, 23, 16.
Из которых 16 минимальное, и меньше уже быть не может.

ИЛИ программное решение

Ответ: 16

Задание 6. Определение результатов работы простейших алгоритмов

Исполнитель Черепаха действует на плоскости с декартовой системой координат.
В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды:
Вперёд n (где n–целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Повтори 7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

ИЛИ

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки.

Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 10 Направо 90 Вперёд 20 Направо 90]
Поднять хвост
Вперёд 3 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 2 [Вперёд 70 Направо 90 Вперёд 80 Направо 90]

Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения.

Сначала нужно построить фигуру.
Это можно сделать к примеру, на тетрадном листе, при помощи библиотеки Turtle или в Excel.

Далее мы находим уравнения прямых, которыми ограничена фигура и решаем
систему уравнений программно.

ИЛИ
Фигуру можно построить программно или к примеру, в Excel.
Далее анализируем и считаем точки.

Ответ: 1 задание — 38, 2 задание — 128

Задание 7. Кодирование и декодирование информации. Передача информации

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.

I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц),

i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро)

I₁ = ν ⋅ i ⋅ t
I₂ = ν/2 ⋅ 3,5 ⋅ i ⋅ t ⋅ 2 = 3,5 ⋅ I₁

I₂ = 3,5 · 28 = 98

Ответ: 98

Задание 8. Перебор слов и системы счисления

Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6.

* * * * * — пятизначное число.
В восьмеричной системе счисления в алфавите 8 цифр: 0..7.
Первая цифра 0 быть не может.
Цифра 6 — одна, при этом стоит рядом только с четными цифрами — 0, 2 или 4.
Получим:

6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029
* 6 * * * — вариантов 2 ⋅ 3 ⋅ 7 ⋅ 7 = 294
* * 6 * * — вариантов 6 ⋅ 3 ⋅ 3 ⋅ 7 = 378
* * * 6 * — вариантов 6 ⋅ 7 ⋅ 3 ⋅ 3 = 378
* * * * 6 — вариантов 6 ⋅ 7 ⋅ 7 ⋅ 3 = 882

Ответ: 2961

Задание выполняется с использованием прилагаемых файлов

Задание 9. Работа с таблицами

Файл с данными

Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
– в строке только одно число повторяется дважды;
– среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел.
В ответе запишите только число.

Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке.

Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6.

Далее мы найдем среднее арифметическое неповторяющихся значений.

Затем найдем сумму повторяющихся значений.

Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия.

Ответ: 2241

Задание выполняется с использованием прилагаемых файлов

Задание 10. Поиск символов в текстовом редакторе

Файл с данными

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует.
В ответе запишите только число.

В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз.

Ответ: 45

Задание 11. Вычисление количества информации

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.

I = K · i, N = 2 ⁱ

ID : ****….**** – всего 250 различных символов в наборе

N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 2¹¹, значит для кодирования одного символа нужно 11 бит.

I_ID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт

I₆₅₅₃₆ = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего

Ответ: 22016

Задание 12. Выполнение алгоритмов для исполнителей

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл
    ПОКА условие
        последовательность команд
    КОНЕЦ ПОКА

выполняется, пока условие истинно.

В конструкции

    ЕСЛИ условие
        ТО команда 1
    КОНЕЦ ЕСЛИ

выполняется команда 1 (если условие истинно).

В конструкции

    ЕСЛИ условие
        ТО команда 1
        ИНАЧЕ команда 2
    КОНЕЦ ЕСЛИ

выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно).

Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>0)
ТО заменить (>0, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке. Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.

def pr(n): #функция определяет простое ли число
for i in range(2,int(n**0.5)+1):
if (n%i) == 0:
return False
return True

for n in range(100): #перебираем n
s=’>’ + 39*’0′ + n*’1′ + 39*’2′
while ‘>1’ in s or ‘>2’ in s or ‘>0’ in s:
if ‘>1’ in s:
s=s.replace(‘>1′,’22>’,1)

if ‘>2’ in s:
s=s.replace(‘>2′,’2>’,1)

if ‘>0’ in s:
s=s.replace(‘>0′,’1>’,1)

sum_s = 0
for i in s[:-1]: #считаем сумму цифр в строке
sum_s += int(i)
if pr(sum_s): #проверяем на простоту
print(n)
break

Ответ: 5

Задание 13. Поиск путей в графе

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.

Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л.

Ответ: 21

Задание 14. Кодирование чисел. Системы счисления

Операнды арифметического выражения записаны в системе счисления с основанием 15.
123x515 + 1x23315
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

for x in range(15):
s1=’123’+ str(x) +’5′
s2=’1’+ str(x) +’233′
n= int(s1,15)+ int(s2,15)

if n%14 == 0:
print(n//14)
break

Ответ: 8767

Задание 15. Преобразование логических выражений

На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
(x ∈ D) → ((¬(x ∈ C) & ¬(x ∈ A)) → ¬(x ∈ D)) истинно (т.е. принимает значение 1) при любом значении переменной х.

def deli(n,m):
if n%m == 0:
return True

for A in range(1,1000):
Ok = True
for x in range(1,10000):
Ok*=( (not(deli(x,2)) or (not(deli(x,3)))) or ((x+A)>=100) )

if Ok:
print(A)
break

Ответ: 94

Задание 16. Рекурсивные алгоритмы

Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n — 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?

F(2023) = 2023! = 2023 ⋅ 2022!

F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 =

= 8266912626

Ответ: 8266912626

Задание выполняется с использованием прилагаемых файлов

Задание 17. Проверка на делимость

Файл с данными

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых
только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

f= open(’17.txt’)
p=[int(i) for i in f]
f.close()

k = 0
PP = 0
M3 = 0

for i in p:
if (abs(i))%10 == 3:
M3 = max(i, M3)

for i in range(1,len(p)): #Осторожно, скобки!
if ( ((abs(p[i-1])%10 == 3) + ((abs(p[i])% 10 == 3)) ==1 ) and ((p[i-1]**2 + p[i]**2) >= M3**2) ):
k+=1
PP = max(PP, p[i-1]**2 + p[i]**2)

print(k,PP)

Ответ: 180 190360573

Задание выполняется с использованием прилагаемых файлов

Задание 18. Робот-сборщик монет

Файл с данными

Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.

Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:

1	8	8	4
10	1	1	3
1	3	12	2
2	3	5	6

Для указанных входных данных ответом должна быть пара чисел 41 и 22.

Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен.

Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1.

Далее делаем замену всех формул МАКС на МИН.

Ответ: 1099 1026

Задание 19. Выигрышная стратегия. Задание 1

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом.

Ответ: 64

Задание 20. Выигрышная стратегия. Задание 2

Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

Петя не может выиграть за один ход;
Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в порядке возрастания.

Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом.

Ответ: 32 63

Задание 21. Выигрышная стратегия. Задание 3

Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:

у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.

Если найдено несколько значений S, в ответе запишите минимальное из них.

Ответ: 62

Задание 22. Многопроцессорные системы

В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Типовой пример организации данных в файле:

Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла.

В независимых процессах время считается от 0,
в зависимых прибавляется к времени процесса, от которого зависит.

Ответ: 17

Задание 23. Анализ программы с циклами и условными операторами

Исполнитель преобразует число на экране.
У исполнителя есть две команды, которые обозначены латинскими буквами:
A. Прибавить 1
B. Умножить на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 35, при этом траектория вычислений содержит число 10 и не содержит 17?
Траектория вычислений программы – это последовательность результатов
выполнения всех команд программы. Например, для программы ABA при
исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

def f(x, y):
if x == y:
return 1
if x > y or x == 17:
return 0
else:
return f(x + 1, y) + f (2 * x, y)

print (f(1,10) * f(10, 35))

Ответ: 98

Задание выполняется с использованием прилагаемых файлов

Задание 24. Анализ программы с циклами и условными операторами

Файл с данными

Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная
в прилагаемом файле. Для выполнения этого задания следует написать программу.

f=open(’24.txt’)
p= f.readline()
f.close()

PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’]
M=k=0

for i in range(1, len(p), 2):
x = p[i-1] + p[i]
if x in PP:
k += 1
else:
k = 0
M=max(M,k)
print(M)

Ответ: 95

Задание 25. Анализ программы с циклами и условными операторами

Назовём маской числа последовательность цифр, в которой также могут
встречаться следующие символы:
– символ «?» означает ровно одну произвольную цифру;
– символ «*» означает любую последовательность цифр произвольной длины;
в том числе «*» может задавать и пустую последовательность.

Например, маске 123*4?5 соответствуют числа 123405 и 12300405.

Среди натуральных чисел, не превышающих 10¹⁰, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 2023. Количество строк в таблице для ответа избыточно.

Самый простой способ использовать библиотеку fnmatch.
Функция fnmatch() проверяет, соответствует ли строка шаблонной строке, возвращая True или False

или так полным перебором:

y = {»,’0′,’00’,’000′}
for x in y:
for j in range(10):
s = ‘1’ + str(j) + ‘2139’ + x + ‘4’
if int(s) % 2023 == 0:
print (s, int(s)//2023)

for x in range (1000):
for j in range(10):
s = ‘1’ + str(j) + ‘2139’ + str(x) + ‘4’
if int(s) % 2023 == 0:
print (s, int(s)//2023

Ответ: 162139404 80148
1321399324 653188
1421396214 702618
1521393104 752048

Задание выполняется с использованием прилагаемых файлов

Задание 26. Анализ программы с циклами и условными операторами

В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д.
Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Входные данные
В первой строке входного файла находится число N – количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы. При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Задание выполняется с использованием прилагаемых файлов

Задание 27. Анализ программы с циклами и условными операторами

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные

Файл А
Файл В

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.
Типовой пример организации данных во входном файле
6
1 100
2 200
5 4
7 3
8 2
10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 ∙ 2 + 3 ∙ 1 + 5 ∙ 1 + 6 ∙ 1 + 8 ∙ 2.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Ответ: 51063 5634689219329

Источник