Версия для печати и копирования в MS Word
1
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 11 символов и содержащий только символы А, Б, В, Г, Д, Е. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит. Определите, сколько байт необходимо для хранения 20 паролей.
Ответ:
2
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 21 символов и содержащий только символы A, D, F, H, X, Y, Z (таким образом, используется 7 различных символов). Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти в байтах, отводимый этой программой для записи 40 паролей.
Ответ:
3
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 23 символов и содержащий только символы A, F, G, Y, S, L (таким образом, используется 6 различных символов). Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти в байтах, отводимый этой программой для записи 50 паролей. В ответе укажите только число, слово «байт» писать не нужно.
Ответ:
4
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 12 символов и содержащий только символы А, Б, В, Г, Д, Е. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит. Определите, сколько байт необходимо для хранения 20 паролей.
Ответ:
5
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 20 символов и содержащий только символы А, Б, В, Г, Д. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит. Определите, сколько байт необходимо для хранения 50 паролей.
Ответ:
6
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 11 символов и содержащий только символы А, Б, В, Е, Ж, М, Н, Р, У, Я (таким образом, используется 10 различных символов). Каждый такой пароль в компьютерной системе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Укажите объём памяти в байтах, отводимый этой системой для записи 70 паролей.
В ответе запишите только число, слово «байт» писать не нужно.
Ответ:
7
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 9 символов и содержащий только символы А, В, И, П, Р, Ф, Э, Ю, Я (таким образом, используется 9 различных символов). Каждый такой пароль в компьютерной системе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Укажите объём памяти в байтах, отводимый этой системой для записи 12 паролей. В ответе запишите только число, слово «байт» писать не нужно.
Ответ:
8
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы А, Б, В, Г, Д, Е. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит.
Определите, сколько байт необходимо для хранения 20 паролей.
Ответ:
9
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 30 символов и содержащий только символы А, Б, В, Г, Д. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит.
Определите, сколько байт необходимо для хранения 50 паролей.
Ответ:
10
При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 9 символов и содержащий только символы A, B, C, D, E, F. Каждый такой пароль в системе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).
Определите объем памяти, отводимый системой для записи 50 паролей. (Ответ дайте в байтах.)
Ответ:
11
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 11 символов и содержащий только символы И, К, Л, М, Н. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 60 паролей. (Ответ дайте в байтах.)
Ответ:
12
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 11 символов и содержащий только символы И, К, Л, М, Н. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).
Определите объём памяти, отводимый этой программой для записи 20 паролей. (Ответ дайте в байтах.)
Ответ:
13
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы К, О, М, П, Ь, Ю, Т, Е, Р. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 30 паролей. (Ответ дайте в байтах.)
Ответ:
14
При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 15 символов и содержащий только символы Е, Г, Э, 2, 0, 1, 3. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объем памяти, отводимый этой программой для записи 30 паролей. (Ответ дайте в байтах.)
Ответ:
15
При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 15 символов и содержащий только символы Е, Г, Э, 2, 0, 1, 3. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).
Определите объем памяти, отводимый этой программой для записи 25 паролей. (Ответ дайте в байтах.)
Ответ:
16
При регистрации в компьютерной системе каждому пользователю выдаётся идентификатор, состоящий из 8 символов, первый и последний из которых — одна из 18 букв, а остальные — цифры (допускается использование 10 десятичных цифр). Каждый такой идентификатор в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование; все цифры кодируются одинаковым и минимально возможным количеством бит, все буквы также кодируются одинаковым и минимально возможным количеством бит).
Определите объём памяти, отводимый этой программой для записи 500 идентификаторов. (Ответ дайте в байтах.)
Ответ:
17
При регистрации в компьютерной системе каждому пользователю выдаётся идентификатор, состоящий из 10 символов, первый и последний из которых — одна из 18 букв, а остальные — цифры (допускается использование 10 десятичных цифр). Каждый такой идентификатор в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование; все цифры кодируются одинаковым и минимально возможным количеством бит, все буквы также кодируются одинаковым и минимально возможным количеством бит).
Определите объём памяти, отводимый этой программой для записи 25 идентификаторов. (Ответ дайте в байтах.)
Ответ:
18
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 14 символов и содержащий только символы Е, Г, Э, 2, 0, 1, 4. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).
Определите объём памяти, отводимый этой программой для записи 40 паролей. (Ответ дайте в байтах.)
Ответ:
19
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 14 символов и содержащий только символы Е, Г, Э, 2, 0, 1, 4. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).
Определите объём памяти, отводимый этой программой для записи 30 паролей. (Ответ дайте в байтах.)
Ответ:
20
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы К, Т, А, М, Р, О, Ф, Н, И. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).
Определите объём памяти, отводимый этой программой для записи 30 паролей. (Ответ дайте в байтах.)
Ответ:
21
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы И, Н, Ф, О, Р, М, А, Т, К. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 25 паролей. (Ответ дайте в байтах.)
Ответ:
22
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 16 символов и содержащий только заглавные символы среднего ряда латинской раскладки клавиатуры: A, S, D, F, G, H, J, K, L. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 20 паролей. (Ответ дайте в байтах.)
Ответ:
23
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 16 символов и содержащий только заглавные символы среднего ряда латинской раскладки клавиатуры: A, S, D, F, G, H, J, K, L. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).
Определите объём памяти, отводимый этой программой для записи 25 паролей. (Ответ дайте в байтах.)
Ответ:
24
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 11 символов. В качестве символов могут быть использованы десятичные цифры и 32 различные буквы местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение!). Под хранение каждого такого пароля на компьютере отводится одинаковое и минимально возможное целое количество байтов. При этом используется посимвольное кодирование, и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который используется для хранения 50 паролей. (Ответ дайте в байтах.)
Ответ:
25
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 9 символов. В качестве символов могут быть использованы десятичные цифры и 29 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение!). Под хранение каждого такого пароля на компьютере отводится одинаковое и минимально возможное целое количество байтов. При этом используется посимвольное кодирование, и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который используется для хранения 20 паролей. (Ответ дайте в байтах.)
Ответ:
26
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 6 символов. В качестве символов могут быть использованы десятичные цифры и 27 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение!). Под хранение каждого такого пароля на компьютере отводится одинаковое и минимально возможное целое количество байтов. При этом используется посимвольное кодирование, и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который используется для хранения 55 паролей. (Ответ дайте в байтах.)
Ответ:
27
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 8 символов. В качестве символов могут быть использованы десятичные цифры и 11 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение). Под хранение каждого такого пароля на компьютере отводится одинаковое и минимально возможное целое количество байтов. При этом используется посимвольное кодирование, и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который используется для хранения 100 паролей. (Ответ дайте в байтах.)
Ответ:
28
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 8 символов. В качестве символов могут быть использованы десятичные цифры и 30 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение). Под хранение каждого такого пароля на компьютере отводится одинаковое и минимально возможное целое количество байтов. При этом используется посимвольное кодирование, и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который используется для хранения 110 паролей. (Ответ дайте в байтах.)
Ответ:
29
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 8 символов. В качестве символов могут быть использованы десятичные цифры и 26 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение). Под хранение каждого такого пароля на компьютере отводится одинаковое и минимально возможное целое количество байтов. При этом используется посимвольное кодирование, и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который используется для хранения 70 паролей. (Ответ дайте в байтах.)
Ответ:
30
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля – ровно 7 символов. В качестве символов используются десятичные цифры и 26 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение!).
Под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов, при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который занимает хранение 65 паролей. (Ответ дайте в байтах.)
Ответ:
31
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 7 символов. В качестве символов используются десятичные цифры и 30 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение!). Под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов, при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который занимает хранение 40 паролей. (Ответ дайте в байтах.)
Ответ:
32
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 32 символов и содержащий только десятичные цифры и символы из 240-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование идентификаторов, все символы кодируют одинаковым и минимально возможным количеством бит.
Определите объём памяти (в Кбайт), необходимый для хранения 3200 идентификаторов. В ответе запишите только целое число — количество Кбайт.
Ответ:
33
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 234 символов и содержащий только десятичные цифры и символы из 1350-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит.
Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число — количество Кбайт.
Ответ:
34
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит.
Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число — количество Кбайт.
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
Задание 5205
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси – напряжение в вольтах. Определите по рисунку на сколько вольт упадет напряжение с конца 6-го по конец 56-го часа фонарика.
Ответ: 0,4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Конец 6го — 1,4В, конец 56го — 1В. Тогда разница составляет: $$1,4-1=0,4$$
Урок посвящен тому, как решать 5 задание ЕГЭ по информатике
Содержание:
- Объяснение 5 задания
- Исполнитель для возведения в квадрат, деления, умножения и сложения
- Проверка числовой последовательности на соответствие алгоритму
- Разбор 5 задания
- Решение задания про алгоритм, который строит число R
- Решение заданий для темы Проверка числовой последовательности (Автомат)
5-е задание: «Анализ алгоритмов и исполнители»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 4 минуты.
Проверяемые элементы содержания: Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд
До ЕГЭ 2021 года — это было задание № 6 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Как и в других заданиях базового уровня сложности, источником ошибок служит недостаточная внимательность и отсутствие или поверхностность самостоятельной проверки полученного ответа»
ФГБНУ «Федеральный институт педагогических измерений»
Проверка числовой последовательности на соответствие алгоритму
- для выполнения некоторых заданий необходимо повторить тему системы счисления;
- максимальное значение суммы цифр десятичного числа — это 18, так как 9 + 9 = 18;
- для проверки правильности переданного сообщения иногда вводится бит четности — дополнительный бит, которым дополняется двоичный код таким образом, чтобы в результате количество единиц стало четным: т.е. если в исходном сообщении количество единиц было четным, то добавляется 0, если нечетным — добавляется 1:
например: 310 = 112 после добавления бита четности: 110 ---- 410 = 1002 после добавления бита четности: 1001
например: 1112 - это 710 добавим 0 справа: 11102 - это 1410
Теперь будем рассматривать конкретные типовые экзаменационные варианты по информатике с объяснением их решения.
Разбор 5 задания
Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:
Решение задания про алгоритм, который строит число R
5_11:
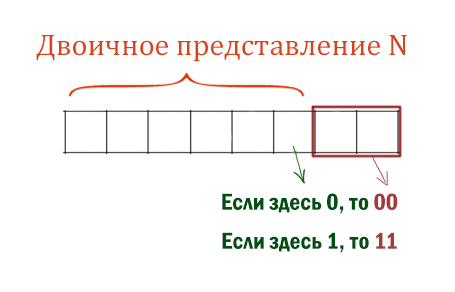
На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:
- Строится двоичная запись числа 4N.
- К этой записи дописываются справа еще два разряда по следующему правилу:
- складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
- над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись является двоичной записью искомого числа R.
Укажите такое наименьшее число N, для которого результат работы алгоритма больше 129. В ответе это число запишите в десятичной системе счисления.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение аналитическим способом:
- Заметим, что после выполнения второго пункта задания, будут получаться только четные числа! Наименьшим возможным четным числом, превышающим 129, является число 130. С ним и будем работать.
- Переведем 130 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать
bin(130). Получим:
13010 = 100000102
в обратном порядке: было 1000001 -> стало 10000010 еще раз то же самое: было 100000 -> стало 1000001
int('100000',2).1000002 = 3210
✎ Решение с использованием программирования:
PascalAbc.Net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
uses school; begin var n_ := 1; while True do begin var n := 4*n_; var ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2 n := 2 * n + ost; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряру (+ost) ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2 n := 2 * n + ost; if n > 129 then begin println(n_); break end; n_ += 1; end; end. |
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
n_ = 1 while True: n = 4*n_ r = str(bin(n)) r = r[2:] for i in range(2): if r.count('1') % 2 == 0: r+='0' else: r+='1' n = int(r, base=2) if n > 129: print(n_) break n_+=1 |
Результат: 8
Для более детального разбора предлагаем посмотреть видео теоретического решения данного 5 задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
5_12: Демоверсия ЕГЭ 2018 информатика:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
- Строится двоичная запись числа N.
- К этой записи дописываются справа ещё два разряда по следующему правилу:
- складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
- над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
✍ Решение:
- Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
- Наименьшим возможным числом, превышающим 83, является число 84. С ним и будем работать.
- Переведем 84 в двоичную систему счисления. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать
bin(84). Получим:
84 = 1010100
86 = 1010110
Результат: 86
Подробное решение данного 5 (раньше №6) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Видеорешение с программированием (PascalAnc.Net):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Аналитическое видеорешение:
📹 Видеорешение на RuTube здесь -> аналитическое решение
5_18:
Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3. Шаг 2 повторяется ещё два раза.
4. Результат переводится в десятичную систему счисления.
При каком наименьшем исходном числе N > 65 в результате работы алгоритма получится число, кратное 4?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение с использованием программирования:
PascalAbc.Net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
uses school; begin var n_ := 1; while True do begin var n := n_; for var i := 1 to 3 do begin if bin(n).CountOf('1') = bin(n).CountOf('0') then // сравниваем if n mod 2 = 0 then // если четное, то в конце 0 n := 2 * n // добавляем разряд = 0 else n := 2 * n + 1 // иначе добавляем разряд = 1 else if bin(n).CountOf('1') > bin(n).CountOf('0') then n := 2 * n else n := 2 * n + 1 end; if (n_ > 65) and (n mod 4 = 0) then begin println(n_); break end; n_ += 1; end; end. |
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
n_ = 1 while True: n = n_ r = str(bin(n)) r = r[2:] for i in range(3): if r.count('1') == r.count('0'): r+=r[-1] elif r.count('1')>r.count('0'): r+='0' else: r+='1' n = int(r, base=2) if n_ > 65 and n % 4 == 0 : print(n_,n) break n_+=1 |
Ответ: 79
5_19:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Число N переводим в двоичную запись.
2) Инвертируем все биты числа кроме первого.
3) Переводим в десятичную запись.
4) Складываем результат с исходным числом N.
Полученное число является искомым числом R.
Укажите наименьшее нечетное число N, для которого результат работы данного алгоритма больше 99. В ответе это число запишите в десятичной системе счисления.
✍ Решение:
-
✎ Решение с использованием программирования:
PascalAbc.Net:
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
n_ = 1 while True: n = n_ r = str(bin(n)) r = r[2:] for i in range(1,len(r)): if r[i]== '0': r=r[:i]+'1'+r[i+1:] else: r=r[:i]+'0'+r[i+1:] n = int(r, base=2) n+=n_ if n > 99 and n_ % 2 != 0 : print(n_,n) break n_+=1 |
Ответ: 65
5_13:
На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа еще два разряда по следующему правилу:
— если N делится нацело на 4, в конец числа (справа) дописывается сначала ноль, а затем еще один ноль;
— если N при делении на 4 дает в остатке 1, то в конец числа (справа) дописывается сначала ноль, а затем единица;
— если N при делении на 4 дает в остатке 2, то в конец числа (справа) дописывается сначала один, а затем ноль;
— если N при делении на 4 дает в остатке 3, в конец числа (справа) дописывается сначала один, а затем еще одна единица.
Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.
Укажите максимальное число R, которое меньше 100 и может являться результатом работы данного алгоритма. В ответе это число запишите
в десятичной системе счисления
.
Типовые задания для тренировки
✍ Решение:
- Поскольку требуется найти наибольшее число, то возьмем наибольшее из возможных чисел, которые < 100 — это число 99. Переведем его в двоичную систему. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать
bin(99). Получим:
99 = 11000112
1100011 N
int('11000',2)11000 = 2410
98 = 11000102 : 10 в конце добавлено алгоритмом N = 110002 = 2410 24 делится нацело на 4. По алгоритму в конце должно быть 00, а мы имеем 10 98 - не подходит 97 = 11000012 : 01 в конце добавлено алгоритмом N = 110002 = 2410 24 делится нацело на 4. По алгоритму в конце должно быть 00, а мы имеем 01 97 - не подходит 96 = 11000002 : 00 в конце добавлено алгоритмом N = 110002 = 2410 24 делится нацело на 4. По алгоритму в конце должно быть 00, у нас 00 - верно! 96 - подходит!
Результат: 96
Предлагаем посмотреть видео теоретического решения:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
5_14:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. К этой записи дописывается (дублируется) последняя цифра.
3. Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4. К полученному результату дописывается ещё один бит чётности.
Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, большее 114, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение аналитическим способом:
- В постановке задания задано R > 114. R — это результат работы алгоритма. Для того, чтобы определить наименьшее возможно N, переведем сначала 114 в двоичную систему счисления и выделим в нем три добавленные по алгоритму цифры (перевод можно выполнить в консоли Питона:
bin(114))
114 = 11100102
2. В полученное числе N = 1110 дублируется последняя цифра и получается 11100.
3. Поскольку число единиц (3) — нечетное, то справа добавляется 1: 111001.
4. Т.к. в полученном наборе цифр четное число единиц, то добавляем 0: 1110010
1. N = 1110 + 1 = 1111 Работа по алгоритму: 2. 11111 - дублирование последней цифры. 3. 111111 - справа дописываем единицу, т.к. в полученном числе 5 единиц (нечетное) 4. 1111110 - дописываем ноль, т.к. в полученном числе четное число единиц.
int('1111110',2)):min R = 11111102 = 12610
✎ Решение с использованием программирования:
PascalAbc.Net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
uses school; begin var n_ := 1; while True do begin var n := n_; // дублирвание последней цифры if n mod 2 = 0 then // если четное, то в конце 0 n := 2 * n // добавляем разряд = 0 else n := 2 * n + 1; // иначе добавляем разряд = 1 for var i := 1 to 2 do begin if bin(n).CountOf('1') mod 2 = 0 then n := 2 * n // добавляем разряд = 0 else n := 2 * n + 1 // иначе добавляем разряд = 1 end; if n > 114 then begin println(n); break end; n_ += 1; end; end. |
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
n_ = 1 while True: n = n_ r = str(bin(n)) # строковое значение r = r[2:] # убираем 0b r=r+r[-1] for i in range (2): if r.count('1') % 2 == 0: r = r+'0' else: r = r+'1' r = int(r,base = 2) # в 10-ю с.с. if r > 114: print(r) break n_+= 1 |
Результат: 126
5_17: Досрочный вариант 1 ЕГЭ по информатике 2020, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
— если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы.
Например, двоичная запись 1001 числа 9 будет преобразована в 100111.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.
Укажите минимальное число N, для которого результат работы алгоритма будет больше 134. В ответе это число запишите в десятичной системе счисления.
Ответ: 33
Видео -> теоретическое решение
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_16:
Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:
1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из нового числа вычитается исходное, полученная разность выводится на экран.
Какое число нужно ввести в автомат, чтобы в результате получилось 45?
✍ Решение:
- Результатом выполнения алгоритма является число 45. Алгоритм работает в двоичной системе счисления, поэтому переведем число:
45 = 001011012
1 - 0, с учетом, что у разряда с единицей заняли. То есть бит:. _ 1 _ _ _ _ _ _ _ N инвертируемое = 0 _ _ _ _ _ _ _ N исходное 0 0 1 0 1 1 0 1 = 45 результат
1 - 0 не может в результате дать 0, так как у следующей слева единицы мы заняли. Значит, 0 - 1. Чтобы не получить единицу в ответе, необходимо у нуля тоже занять:. . _ 1 0 _ _ _ _ _ _ = 0 1 _ _ _ _ _ _ 0 0 1 0 1 1 0 1 = 45 результат
1 - 0 не может быть, так как у следующего слева нуля мы заняли.Значит
0 - 1. То есть как раз чтобы получить единицу (10 - 1 = 1), занимаем у следующих слева разрядов:. . _ 1 0 0 _ _ _ _ _ = 0 1 1 _ _ _ _ _ 0 0 1 0 1 1 0 1 = 45 результат
0 - 1 не может быть. Значит, чтобы получить в результате ноль, берем 1 - 0, у единицы должно быть занято.. . . _ 1 0 0 1 _ _ _ _ = 0 1 1 0 _ _ _ _ 0 0 1 0 1 1 0 1 = 45 результат
1 - 0 не может быть. Так как слева у единицы занято. Значит, чтобы получить в результате 1, берем 0 - 1:. . . _ 1 0 0 1 0 _ _ _ = 0 1 1 0 1 _ _ _ 0 0 1 0 1 1 0 1 = 45 результат
0 - 1 не даст в ответе единицу, значит, имеем 1 - 0:. . . _ 1 0 0 1 0 1 _ _ = 0 1 1 0 1 0 _ _ 0 0 1 0 1 1 0 1 = 45 результат
0 - 1 не может быть, значит, 1 - 0. Чтобы получить в результате 0, необходимо, чтобы у 1 было занято:. . . . _ 1 0 0 1 0 1 1 _ = 0 1 1 0 1 0 0 _ 0 0 1 0 1 1 0 1 = 45 результат
0 - 1:. . . . _ 1 0 0 1 0 1 1 0 = 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 1 = 45 результат
01101001 = 10510
Ответ: 105
Смотрите теоретический разбор задания на видео и подписывайтесь на наш канал:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
Решение заданий для темы Проверка числовой последовательности (Автомат)
5_7:
Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.
- Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
- Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.
Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.
✍ Решение:
Результат: 2949
Процесс теоретического решения данного 5 задания представлен в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_8:
Автомат получает на вход четырехзначное число. По нему строится новое число по следующим правилам:
- Складываются первая и вторая, затем вторая и третья, а далее третья и четвёртая цифры исходного числа.
- Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).
Пример: Исходное число: 7531. Суммы: 7+5=12; 5+3=8; 3+1=4. Результат: 4812.
✍ Решение:
2, 5, 129:12=9+3
93**
9320.Результат: 9320
Подробное теоретическое решение данного 5 задания можно просмотреть на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_9:
Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам:
- Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
- Полученные два шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).
Пример: Исходные числа: 25, 66. Поразрядные суммы: 8, B. Результат: B8.
Какие из предложенных чисел могут быть результатом работы автомата?
Перечислите в алфавитном порядке буквы, соответствующие этим числам, без пробелов и знаков препинания.
Варианты:
A) 127
B) C6
C) BA
D) E3
E) D1
✍ Решение:
Проанализируем все варианты:
12 в шестнадцатеричной системе записывается как С.С6 разбиваем на 12 и 6. Число может быть результатом работы автомата. Исходные числа, например, 35 и 37BA разбиваем на 11 и 10. Число может быть результатом работы автомата. Исходные числа, например, 55 и 56E3 разбиваем на 14 и 3. 14=6+8, но цифры большие 6 не принимает автомат. Не подходит.D1 разбиваем на 13 и 1. 13=6+7, но цифры большие 6 не принимает автомат. Не подходит.Результат: BC
Подробное теоретическое решение данного 5 задания можно просмотреть на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_10: Задание 5 ГВЭ 11 класс 2018 год ФИПИ
Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 7 (если в числе есть цифра больше 7, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.
1. Вычисляются два шестнадцатеричных числа: сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.
Определите, какое из предложенных чисел может быть результатом работы автомата.
Варианты:
1) AD
2) 64
3) CF
4) 811
✍ Решение:
Теоретическое решение 4 задания ГВЭ 11 класса смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение
5_15:
Автомат получает на вход натуральное число X. По этому числу строится трёхзначное число Y по следующим правилам:
1. Первая цифра числа Y (разряд сотен) – остаток от деления X на 7.
2. Вторая цифра числа Y (разряд десятков) – остаток от деления X на 2.
3. Третья цифра числа Y (разряд единиц) – остаток от деления X на 5.
Пример. Исходное число: 55. Остаток от деления на 7 равен 6; остаток от деления на 2 равен 1; остаток от деления на 5 равен 0. Результат работы автомата: 610.
Сколько существует двузначных чисел, при обработке которого автомат выдаёт результат 312?
Типовые задания для тренировки
✍ Решение:
- Обозначим каждую цифру числа Y согласно заданию:
Y = 3 1 2 x mod 7 x mod 2 x mod 5
1. x mod 2 = 1 => значит, X — нечетное число
2. x mod 5 = 2 => значит, X — либо ?2, либо ?7.
3. раз x — нечетное, то из пред. пункта получаем x = ?7
4. x mod 7 = 3 => переберем все варианты:
97 - не подходит, 87 - подходит (87 / 7 = 12, остаток = 3) 77 - не подходит, 67 - не подходит, 57 - не подходит, 47 - не подходит, 37 - не подходит, 27 - не подходит, 17 - подходит (17 / 7 = 2, остаток = 3)
Результат: 2
В решение заданий демо-версии используется язык программирования Python.
|
Задание 1. Анализ информационных моделей На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число. |
На графе расставим веса вершин. Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6. Сумма дорог BD + AF = 53 + 5 = 58 Ответ: 58 |
||||||||||||||||||
|
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности логической функции F F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx. |
¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.
Решение на Python Ответ: YXZW |
||||||||||||||||||
Задание 3. Базы данных. Файловая система В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в На рисунке приведена схема указанной базы данных. Используя информацию из приведённой базы данных, определите общий вес |
На третьем листе книги применим фильтр по району и получим ID четырех магазинов. На втором листе применим фильтр по товару и получим ID товара. На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим: Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг. Ответ: 355 |
||||||||||||||||||
|
Задание 4. Кодирование и декодирование информации По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков? |
Ответ: 14 |
||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему 1. Строится двоичная запись числа N. Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число |
Минимальное R, большее 40, это 41. ИЛИ программное решение Ответ: 16
|
||||||||||||||||||
|
Задание 6. Определение результатов работы простейших алгоритмов Исполнитель Черепаха действует на плоскости с декартовой системой координат. Черепахе был дан для исполнения следующий алгоритм: Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения. |
Сначала нужно построить фигуру. Далее мы находим уравнения прямых, которыми ограничена фигура и решаем ИЛИ Ответ: 1 задание — 38, 2 задание — 128 |
||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно. |
I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц), i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро) I1 = ν ⋅ i ⋅ t I2 = 3,5 · 28 = 98 Ответ: 98 |
||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6. |
* * * * * — пятизначное число. 6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029 Ответ: 2961 |
||||||||||||||||||
Задание 9. Работа с таблицами Файл с данными Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: |
Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке. Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6. Далее мы найдем среднее арифметическое неповторяющихся значений. Затем найдем сумму повторяющихся значений. Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия. Ответ: 2241 |
||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе Файл с данными Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует. |
В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз. Ответ: 45 |
||||||||||||||||||
|
Задание 11. Вычисление количества информации При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт. |
I = K · i, N = 2 i ID : ****….**** – всего 250 различных символов в наборе N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 211, значит для кодирования одного символа нужно 11 бит. IID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт I65536 = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего Ответ: 22016 |
||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно. В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно). В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно). Дана программа для Редактора: |
def pr(n): #функция определяет простое ли число for n in range(100): #перебираем n if ‘>2’ in s: if ‘>0’ in s: sum_s = 0 Ответ: 5 |
||||||||||||||||||
|
Задание 13. Поиск путей в графе На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. |
Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л. Ответ: 21 |
||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Операнды арифметического выражения записаны в системе счисления с основанием 15. |
for x in range(15): if n%14 == 0: Ответ: 8767 |
||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение |
def deli(n,m): for A in range(1,1000): if Ok: Ответ: 94 |
||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n – натуральное число, |
F(2023) = 2023! = 2023 ⋅ 2022! F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 = = 8266912626 Ответ: 8266912626 |
||||||||||||||||||
Задание 17. Проверка на делимость Файл с данными В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых |
f= open(’17.txt’) k = 0 for i in p: for i in range(1,len(p)): #Осторожно, скобки! print(k,PP) Ответ: 180 190360573 |
||||||||||||||||||
Задание 18. Робот-сборщик монет Файл с данными Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел 41 и 22. |
Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен. Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1. Далее делаем замену всех формул МАКС на МИН. Ответ: 1099 1026 |
||||||||||||||||||
|
Задание 19. Выигрышная стратегия. Задание 1 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. |
При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом. Ответ: 64 |
||||||||||||||||||
|
Задание 20. Выигрышная стратегия. Задание 2 Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
Найденные значения запишите в порядке возрастания. |
Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом. Ответ: 32 63 |
||||||||||||||||||
|
Задание 21. Выигрышная стратегия. Задание 3 Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них. |
Ответ: 62 |
||||||||||||||||||
|
Задание 22. Многопроцессорные системы В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно. |
В независимых процессах время считается от 0, Ответ: 17 |
||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. |
def f(x, y): print (f(1,10) * f(10, 35)) Ответ: 98 |
||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Файл с данными Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная |
f=open(’24.txt’) PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’] for i in range(1, len(p), 2): Ответ: 95 |
||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Назовём маской числа последовательность цифр, в которой также могут Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка. |
Самый простой способ использовать библиотеку fnmatch. или так полным перебором: y = {»,’0′,’00’,’000′} for x in range (1000): Ответ: 162139404 80148 |
||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. |
|||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Файл А Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов. |
Ответ: 51063 5634689219329 |
Примеры заданий ЕГЭ по информатике с решением на Паскале. На странице использованы условия задач из демо вариантов и задачника с сайта Полякова Константина Юрьевича (kpolyakov.spb.ru)
Содержание
- Задание 5
- Задание 6
- Задание 14
- Задание 15
- Задание 16
- Задание 17
- Задание 22
- Задание 24
- Задание 25
Задание 5
Демо-2022
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему
правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью результирующегочисла R.
Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.
Решение:
var n, i, b, s, k: integer; r: real; st: string; begin for n := 1 to 100 do begin k := n; //перебор исходного числа N s := 0; //сумма цифр двоичного кода r := 0; //результирующее десятичное число R st := ''; //очищаем строку двоичного кода для нового числа while k >= 1 do //цикл перевода в двоичный код исходного числа begin s := s + (k mod 2); //вычисление суммы цифр двоичного кода st := st + (k mod 2);//формирование строки двоичного кода из остатков деления на 2 k := k div 2;// деление на 2 end; st := ReverseString(st) + s mod 2; //переворачиваем код и дописываем остаток s := s + s mod 2;//вычисление суммы нового кода st := st + s mod 2;//формирование строки двоичного кода с добавлением остатка for i := 1 to Length(st) do //преобразование двоичного кода в десятичное число if st[i] = '1' then r := r + power(2, Length(st) - i); if r > 77 then begin println(n, r);break; end;//вывод найденных чисел end; end.
Задание 6
Демо-2022 Определите, при каком наибольшем введённом значении переменной s программа выведет число 64.
Решение: Используем исходный код. Добавим в него цикл перебора значений S и вывода при выполнении условия. Последнее значение и будет ответом.
var s, n, i: integer; begin for i := 1 to 510 do begin s := i; s := s div 10; n := 1; while s < 51 do begin s := s + 5; n := n * 2 end; if n = 64 then writeln(i); end; end.
Задание 14
Демо-2022 Значение арифметического выражения: 3*438+2*423+420+3*45+2*44+1 – записали в системе счисления с основанием 16. Сколько значащих нулей содержится в этой записи?
Решение:
var k,x:biginteger; begin k:=0; x:=3*4bi**38+2*4bi**23+4bi**20+3*4bi**5+2*4bi**4+1; while x>0 do begin if x mod 16=0 then k:=k+1; x:=x div 16; end; print(k) end.
Демо-2021 Значение арифметического выражения: 497 + 721 – 7 – записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
Решение:
var s, i,k6,x:integer; osn,n:biginteger; begin osn:=7; k6:=0; n:=power(osn,14)+power(osn,21)-7; while n>0 do begin if n mod 7 = 6 then k6:=k6+1; n:=n div 7; end; print(k6); end.
Демо-2020 Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 70 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
_ПОКА нашлось (2222) ИЛИ нашлось (8888)
__ЕСЛИ нашлось (2222)
___ТО заменить (2222, 88)
___ИНАЧЕ заменить (8888, 22)
__КОНЕЦ ЕСЛИ
_КОНЕЦ ПОКА
КОНЕЦ
Решение:
begin var s: string := '8' * 70; while (s.contains('2222')) or (s.contains('8888')) do begin if (s.contains('2222')) then s := s.replace('2222', '88') else s := s.replace('8888', '22'); end; writeln(s); end.
Задание 15
Демо-2021 Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9)) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решение:
// Делители var a,x, flag: integer; begin for a := 1 to 100 do begin flag := 0; for x := 1 to 1000 do if not(x mod a = 0) <= ((x mod 6 = 0) <= not (x mod 9 = 0)) = false then begin flag := 1; break; end; if flag = 0 then print(a); end; end.
К.Поляков №161 Определите наименьшее натуральное число A, такое что выражение
(X & 29 ≠ 0) → ((X & 17 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Посмотреть решение
var A, x, flag: integer; begin for A := 0 to 31 do begin flag := 0; for x := 0 to 31 do if (((x and 29) = 0) or ((x and 17) <> 0) or ((x and A) <> 0))=false then flag := 1; if flag = 0 then begin writeln(A); break; end; end; end.
Задание 16
Демо-2022 Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n + F(n − 1), если n – чётно,
F(n) = 2 × F(n − 2), если n > 1 и при этом n – нечётно.
Чему равно значение функции F(26)?
Решение:
var i, n: integer; f: array[1..100] of integer; begin print('Введите значение n'); readln(n); f[1] := 1; for i := 2 to n do if i mod 2 = 0 then f[i] := i + f[i - 1] else f[i] := 2 * f[i - 2]; print(f[n]); end.
К.Поляков №46Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = n при n ≤ 3;
F(n) = 2 · n · n + F(n – 1) при чётных n > 3;
F(n) = n · n · n + n + F(n – 1) при нечётных n > 3;
Определите количество натуральных значений n, при которых F(n) меньше, чем 107.
Посмотреть решение
var i: integer; f: array[1..1000] of integer; begin i:=3; f[1] := 1; f[2] := 2; f[3] := 3; while f[i]< 10**7 do begin i:=i+1; if i mod 2 = 0 then f[i] := 2*i*i + f[i - 1] else f[i] := i*i*i+i +f[i - 1]; end; print(i-1);// не учитываем последнее число end.
Задание 17
Демо-2022
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число делится на 3, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.Файл с данными: 17.txt
Решение:
var a,b,k,maxsum: integer; begin Assign( input, '17.txt' ); maxsum:=-20000; k:=0; readln(a); while not eof do begin readln(b); if (a mod 3 = 0) or (b mod 3 = 0) then begin k := k + 1; if a + b > maxsum then maxsum := a + b; end; a := b; end; Println( k, maxsum) end.
Задание 22
Демо-2022
Ниже на языке программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4,а потом 5.

Решение:
var x, i, L, M, Q: integer; begin for i := 9 to 50 do begin x := i; Q := 9; L := 0; while x >= Q do begin L := L + 1; x := x - Q; end; M := x; if M < L then begin M := L; L := x; end; if (L = 4) and (M = 5) then print(i); end; end.
Задание 24
Демо-2022
Текстовый файл состоит из символов P, Q, R и S. Определите максимальное количество идущих подряд символов в прилагаемом файле, среди которых нет идущих подряд символов P. Для выполнения этого задания следует написать программу.Файл с данными: 24.txt
Решение:
var i, maxlen, curlen: longint; {описание переменных} s: string; f: text;{текстовый файл} begin assign(f, '24.txt'); {исходный текстовые файл с данными} reset(f); readln(f, s);{открываем файл для чтения данных} maxlen := 1; curlen := 1; for i := 2 to Length(s) do if not ((s[i] = 'P') and (s[i-1] = 'P')) then begin curLen := curLen + 1; if curLen > maxLen then maxLen := curLen; end else curLen := 1; writeln(maxLen); close(f); { закрываем файл} end.
Задание 25
Демо-2022
Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей и у числа нет, то значение M считается равным нулю. Напишите программу, которая перебирает целые числа, большие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые пять найденных чисел и соответствующие им значения M.
Формат вывода: для каждого из пяти таких найденных чисел в отдельной строке сначала выводится само число, затем – значение М.
Строки выводятся в порядке возрастания найденных чисел.
Решение:
var d1, chislo: integer; begin for chislo := 700001 to 700100 do for d1 := 2 to chislo - 1 do if chislo mod d1 = 0 then begin if (d1 + chislo div d1) mod 10 = 8 then println(chislo, d1 + chislo div d1); break; end; end.
Привет! В этой статье будут различные примеры решения задач из 5-ого задания ЕГЭ по информатике 2022.
Задание 5 решается не сложно, но, как всегда, нужно потренироваться решать подобные задачи, чтобы уверенно себя чувствовать на ЕГЭ по информатике 2022.
Рассмотрим классический пример.
Задача (Классическая)
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R по следующему принципу.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
а) Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.
б) Над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает 42 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.
Решение:
Решение на Python.
for n in range(1, 1000): s=format(n, 'b') s=s+str(s.count('1')%2) s=s+str(s.count('1')%2) r=int(s, 2) if r>42: print(r)
Программа будет выводить различные числа, но нас интересует самое маленькое. В ответе получается 46. Чтобы остановить поток чисел, можно нажать сочетание Ctrl + C.
В программе перебираем натуральные числа от 1 до 1000 с помощью цикла for. Каждое число подставляем в описанный алгоритм, в надежде получить в результате число r, удовлетворяющие условию задачи.
С помощью функции format переводим число n в двоичный вид. Получаем результат в виде строки s.
Чтобы найти сумму цифр получившейся двоичной записи, достаточно подсчитать количество единиц в строке s. Ведь только единицы в двоичной записи дают в сумму результат. Это можно сделать, применив функцию .count() к строке s.
Добавляем справа к строке s остаток от деления суммы цифр на 2. Остаток нужно превратить в строковый тип данных, чтобы «присоединить» к строке s справа.
Повторяем пункт Б, скопировав строку с пунктом А.
Чтобы обратно превратить строку двоичной записи в десятичное число, используем функцию int(), указав параметр 2.
В конце программы пропишем условие. Если r больше 42, то будем печатать эти значения. Остаётся выбрать минимальное число r.
Решение с помощью рассуждений.
Алгоритму на вход приходит обычное натуральное число N.
Это число преобразуется в двоичную запись (пункт 1).
Во втором пункте правил формирования нового числа сказано, что к числу, полученному в первом пункте, дописываются справа ещё два дополнительных разряда.
Про 1 дополнительный разряд указано в подпункте а): «Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.»
Если по простому сказать, то мы подсчитываем количество единиц в двоичном представлении числа N. Если количество единиц чётное, то пишем в 1 дополнительный разряд ноль, если нечётное, то пишем в 1 дополнительный разряд единицу.
Со вторым дополнительным разрядом происходит всё тоже самое, что и с первым разрядом, только когда подсчитываем количество единиц, мы так же подсчитываем и в 1-ом дополнительном разряде.
В вопросе просят указать входящее наименьшее число N, чтобы автомат выдал число R больше 42.
Возьмём наименьшее число, которое больше 42 (т.е. 43) и переведём его в двоичную систему. Это можно сделать с помощью стандартного windows калькулятора.
Вызываем калькулятор, выбираем Вид->Программист. Кликаем на отметку Dec (это означает, что мы находимся в десятичной системе) и набираем число 43. Затем кликаем на отметку Bin
Проверим число 1010112. Может ли оно быть результатом работы нашего алгоритма?
Отделяем два дополнительных разряда справа. У нас, не считая двух дополнительных разрядов, количество единиц равно двум. Количество чётное, значит, в первом дополнительном разряде должен стоять 0. А у нас стоит 1.
Следовательно, число 1010112 не может являться результатом работы алгоритма. И это число не подходит.
Проверим последующие числа. На калькуляторе можно прибавлять по 1 и получать следующее число в двоичной системе. Мы проверяем последовательно числа, чтобы не пропустить самое маленькое число.
Подходит число 1011102. Количество единиц без двух дополнительных разрядов равно трём. Число нечётное. Значит, в первом дополнительном разряде должна стоять 1. В этом числе как раз стоит 1.
Количество единиц вместе с дополнительным разрядом равно 4. Число чётное, значит, во втором дополнительном разряде должен стоять 0. У нас и стоит во втором дополнительном разряде 0. Следовательно, число 1011102 подходит по всем правилам и является наименьшим.
В десятичной системе это число 46.
Ответ: 46
Рассмотрим ещё одну интересную задачу для подготовки к ЕГЭ по информатике 2022.
Задача(Замена символов)
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) Каждый разряд этой записи заменяется двумя разрядами по следующему правилу: если в разряде стоит 0, то вместо него пишется 01; если в разряде стоит 1, то 1 заменяется на 10.
Например, двоичная запись 1010 числа 10 будет преобразована в 10011001.
Полученная таким образом запись (в ней в два раза больше разрядов, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите максимальное нечётное число R, меньшее 256, которое может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе.
Решение:
Решение на Python.
for n in range(1, 1000): s=format(n, 'b') s2='' for x in s: if x=='0': s2 = s2 + '01' else: s2 = s2 + '10' r=int(s2, 2) if r%2!=0 and r<256: print(r)
Получается наибольшее число 169.
Здесь после того, как построена строка, содержащая двоичную запись числа n, мы с помощью цикла for перебираем каждый символ и анализируем его.
Предварительно создав переменную s2 для новой строки, мы записываем в неё ’01’, если анализируемый символ является нулём, и ’10’, если единицей.
Добавляем заменённые символы справа к строке s2, таким образом, самый первые символы окажутся постепенно слева, как положено.
Далее, делаем, как в прошлой задаче.
Решение с помощью рассуждений.
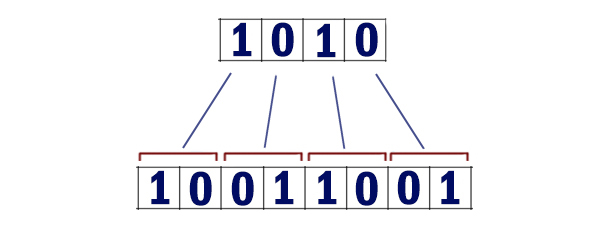
В этой задаче в начале строится двоичная запись числа N.
Каждый разряд превращается в два разряда! Единица превращается в 10. Ноль превращается в 01. На рисунке показан пример, как будет преобразовано число 10 = 10102.
Оценим первое число, которое меньше, чем 256. Это число 255.
255 = 111111112
Здесь количество разрядов равно 8. Это чётное число, значит, такое количество разрядов может быть в результате работы алгоритма. Только чётное количество разрядов может получится в результате работы алгоритма.
В старших двух разрядах должны быть цифры 10, т.к. исходное число N не может начинаться с нуля.
В остальных парах попробуем написать 10, чтобы число было как можно больше.
Получается, что число 101010102 удовлетворяет всем правилам алгоритма, является наибольшим, и оно меньше 256.
Но важный момент, нас просили в ответ записать нечётное число.
В двоичной системе число, которое оканчивается на ноль, является чётным.
В двоичной системе число, которое оканчивается на единицу, является нечётным.
Чтобы число было нечётным, изменим последние разряды на 01.
101010012 = 169
Ответ: 169
Набираем обороты в решении 5 задания из ЕГЭ по информатике 2022.
Задача(Классическая, закрепление)
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конце числа справа дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1101 будет преобразована в 110111.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа — результата работы данного алгоритма.
Укажите минимальное число N, для которого результат работы алгоритма будет больше 130. В ответе это число запишите в десятичной системе счисления.
Решение:
Решение на Python.
for n in range(1, 1000): s=format(n, 'b') if n%2==0: s=s+'00' else: s=s+'11' r=int(s, 2) if r>130: print(n)
Минимальное число n получается 33.
Обратите внимание, что здесь уже анализируем число n. Если оно чётное, то к переменной s справа дописываем ’00’, иначе ’11’. Так же в этой задаче мы печатаем в ответе само число n.
Решение с помощью рассуждений.
После перевода в двоичную систему исходного числа N, алгоритм строит новое число по следующему правилу:
Бордовым прямоугольником показаны дополнительные разряды.
Нужно найти минимальное число больше 130. Будем проверять последовательно числа, начиная с 131.
Подходит число 135. В ответе нужно указать число N. Отбросим от числа 100001112 дополнительные разряды и переведём в десятичную систему.
1000012 = 33
Ответ: 33
Похожие задачи встречались в сборнике С. С. Крылова для подготовке к ЕГЭ по информатике.
Задача (Крепкий орешек)
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Из числа N вычитается остаток от деления N на 4.
2. Строится двоичная запись полученного результата.
3. К это записи справа дописываются ещё два дополнительных разряда по следующему правилу:
а) Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.
б) Над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись является двоичной записью числа R.
Укажите наибольшее число N, для которого результат работы данного алгоритма меньше 47. В ответе число N укажите в десятичной системе.
Решение:
Первый способ. Число R должно быть меньше 47. Переведём число 46 в двоичную систему.
46 = 1011102
Результат от второго пункта не должен превышать 10112. Если результат от второго пункта будет превышать это число, то после добавления дополнительных разрядов получится число R, которое не меньше 47.
Проверим число 10112 = 11. Видим, что это число не может являться результатом пункта 2.
11 + 0 = 11 (остаток при делении 11 на 4 равен 3) —
11 + 1 = 12 (остаток при делении 12 на 4 равен 0) —
11 + 2 = 13 (остаток при делении 13 на 4 равен 1) —
11 + 3 = 14 (остаток при делении 13 на 4 равен 2) —
Здесь мы перебираем все остатки при делении на 4. Чтобы число 11 могло являться результатом пункта 2, число, помеченное зелёным цветом, должно совпадать с числом, помеченное оранжевым цветом. Стоит заметить, что если в первой строчке не совпадают числа, то и в остальных они тоже не совпадут. Верно и обратное. Если в первой строчке совпадут числа, то и для остальных остатков тоже числа будут совпадать.
Найдём, число, для которого будут совпадать эти числа, отмеченные зелёным и оранжевым цветом.
10 + 0 = 10 (остаток при делении 10 на 4 равен 2) Не подходит
9 + 0 = 9 (остаток при делении 9 на 4 равен 1) Не подходит
8 + 0 = 8 (остаток при делении 8 на 4 равен 0) Подходит!
Значит, число 8 нам подходит. Число 8 — это результат работы алгоритма в первом пункте. Нас просят найти максимальное число. Следовательно, возьмём остаток 3, чтобы исходное число N было как можно больше. Тогда N будет:
N = 8 + 3 = 11
Ответ получается 11.
Второй способ. Решим задачу с помощью Python’а.
Перебираем числа от 100 до 1 с помощью цикла for. Третий параметр «-1» в цикле for говорит о том, что мы перебираем числа в обратном порядке.
for i in range(100, 0, -1): n = i n = n - n % 4 # Выполняем первый пункт n = format(n, 'b') # Переводим в двоичную систему n = n + str(n.count('1') % 2) # Подпункт a) третьего пункта n = n + str(n.count('1') % 2) # Подпункт б) третьего пункта r = int(n, 2) # Переводим из двоичной системы в десятичную if r < 47: print(i)
В этой программе запрограммировали алгоритм, который указан в задаче. Если значение переменной r (результат работы алгоритма) меньше 47, то печатаем это значение на экран. Первое распечатанное число и есть ответ к задаче.
В переменную n по очереди подставляются числа из нашего диапазона (100-1). Команда % находит остаток от деления.
Функция count, в данном случае, подсчитывает количество единиц в строке, которая находится в переменной n.
Ответ: 11
Задача (Демо 2023)
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
a) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.
Полученная таким образом запись является двоичной записью искомого числа R.
Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе запишите это число в десятичной системе счисления.
Решение:
for n in range(1, 1000): s=format(n, 'b') if s.count('1')%2==0: s = s + '0' s = '10' + s[2:] else: s = s + '1' s = '11' + s[2:] r=int(s, 2) if r>40: print(n)
Здесь мы пишем программу, как было написано в уроке видеокурса ЕГЭ по информатике. Но, действительно, встречается и новый приём. Нужно изменить левые символы нашей строки s. Это можно сделать с помощью такой конструкции s[2:]. Таким образом, мы берём всю строку, кроме двух первых символов. Например, s=’football’, то s[2:] будет обозначать ‘otball’.
Повторим основные идеи такого подхода при решении пятого задания из ЕГЭ по информатике с помощью программирования. Перебираем числа от 1 до 999 с помощью цикла for. В этом диапазоне надеемся найти наш ответ. С помощью команды format() превращаем число в строку уже в двоичной системе. Сумма цифр в строке зависит только от количества единиц. Нули ничего не дают в сумму. Поэтому применяем функцию .count. Дальше всё делаем, как написано в условии задачи. Команда int(s, 2) превращает строку в двоичной системе в число опять в десятичной системе счисления.
Ответ: 16
Задача (Решаем с помощью Python)
Автомат обрабатывает натуральное число N > 1 по следующему алгоритму:
1) Строится двоичная запись числа N.
2) В конец записи (справа) дописывается вторая справа цифра двоичной записи.
3) В конец записи (справа) дописывается вторая слева цифра двоичной записи.
4) Результат переводится в десятичную систему.
Пример. Дано число N = 11. Алгоритм работает следующим образом.
1) Двоичная запись числа N: 11 = 10112
2) Вторая справа цифра 1, новая запись 101112.
3) Вторая слева цифра 0, новая запись 1011102.
4) Десятичное значение полученного числа 46.
При каком наименьшем числе N в результате работы алгоритма получится R > 170? В ответе запишите это число в десятичной системе счисления.
Решение:
Напишем программу на Python.
for n in range(2, 1000): s=format(n, 'b') s=s+s[-2] s=s+s[1] r=int(s, 2) if r>170: print(n)
Получается наименьшее число 43. К последнему символу можем обратится s[-1], к предпоследнему s[-2]. Но счёт слева начинается с нуля. Первый символ это s[0], второй символ s[1] и т.д.
Обратите внимание, что перебирать числа n в этой задаче начинаем с 2.
Ответ: 43
Задача(Восьмибитное число)
(А.М. Кабанов) Автомат обрабатывает натуральное число N (1≤N≤255) по следующему алгоритму:
1) Строится восьмибитная двоичная запись числа N.
2) Удаляется последняя цифра двоичной записи.
3) Запись «переворачивается», то есть читается справа налево.
4) Полученное число переводится в десятичную запись и выводится на экран.
Каково наибольшее число, меньшее 100, которое после обработки автоматом не изменится?
Решение:
for n in range(1, 256): s=format(n, 'b') # делаем 8-ое число while(len(s)<8): s='0'+s s=s[:-1] #удаляется последняя цифра s=s[::-1] #число переворачивается r=int(s, 2) if n<100 and r==n: print(n)
Ответ получается 90.
Восьмибитное число имеет длину 8 символов. После того, как перевели число n в двоичный вид, с помощью цикла while добисываем нули слева к строке s, пока длина этой строки меньше 8.
Удалить последнюю цифру можно с помощью конструкции s[:-1]. Здесь мы оставляем все цифры, начиная с первой до последней (не включительно).
Перевернуть строку можно с помощью конструкции s[::-1].
Далее решаем как обычно. Число не изменится, если входное число n равно выходному числу r.
Ответ: 90
Разберём задачу, которая была в пробном варианте от 3.02.23 в одном из регионов.
Задача(Пробник 3.02.23)
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
a) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 1;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11;
Полученная таким образом запись является двоичной записью искомого числа R.
Например, для исходного числа 610 = 1102 результатом является число 1002 = 410, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите число N, после обработки которого с помощью этого алгоритма получается наименьшее значение R, большее 49. В ответе запишите это число в десятичной системе.
Решение:
Напишем программу на языке Python.
for n in range(1, 1000): s=format(n, 'b') if s.count('1')%2==0: s = s + '0' s = '1' + s[2:] else: s = s + '1' s = '11' + s[2:] r=int(s, 2) if r>49: print(r, n)
Хитрость задачки заключается в том, что числа r возрастают неравномерно.
Нам необходимо глазами найти наименьше число r (первое число). Это число 50, а n для него равно 57.
При желании программу можно переписать следующим образом:
r_min=10**9 n_r_min = 0 for n in range(1, 1000): s=format(n, 'b') if s.count('1')%2==0: s = s + '0' s = '1' + s[2:] else: s = s + '1' s = '11' + s[2:] r=int(s, 2) if r > 49: if r < r_min: r_min=r n_r_min=n print(n_r_min)
Здесь ищется минимальное число r автоматически и для него запоминается значение n, которое пойдет в ответ.
Ответ: 57
Боковой вариант 5-ого задания из ЕГЭ по информатике.
Задача (Лучше знать)
Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам:
1. Перемножаются первая и вторая, а также третья и четвёртая цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 2465. Суммы: 2 * 4 = 8; 6 * 5 = 30. Результат: 308. Укажите наибольшее число, в результате обработки которого автомат выдаст число 124.
Решение:
В подобных задачах из ЕГЭ по информатике нумерация происходит начиная со старшего разряда.
Первое правило можно представить следующим образом:
Второе правило заключается в том, что мы «соединяем» два числа, полученных в первом пункте, причём, сначала идёт большее число, а затем меньшее.
Проанализируем число 124.
Чтобы четырёхзначное число было наибольшим, выгодно, чтобы в старшем разряде стояла 9. Но, не у числа 12, не у числа 4, нет такого делителя. Какой наибольший делитель мы можем получить? Это число 6. Число 6 является делителем 12-ти. Значит, первая цифра будет 6, а вторая цифра будет 2 (6*2=12).
Рассмотрим второе число 4. Третий разряд тоже желательно сделать побольше. Значит, в четвёртый разряд поставим 4, а в младший разряд 1 (4*1=4).
Ответ получается 6241.
Ответ: 6241
Счастливых экзаменов! Видеоролик можете посмотреть ниже!
Второе задание с заменой символом пытался сделать через команду .replace, в консоль выводились почему-то только четные числа, можете обьяснить что не так?
for unk in range(1, 1000):
unk = (bin(unk)[2:])
if «1» in unk:
unk = unk.replace(«1», «10»)
elif «0» in unk:
unk = unk.replace(«0», «01»)
R = int(unk, 2)
# if R < 256 and R % 2 != 0:
print(R)
Я так понимаю, что вы заменяете либо единицы, либо нули. А нужно в одной записи заменить и единицы, и нули. Через реплейс тоже можно решить. s=s.replace(‘1’, ‘2’) s=s.replace(‘0′, ’01’) s=s.replace(‘2′, ’10’). Т.е. мы превращаем 1 в символ, которого точно нет в строке, потом делаем замены.