Егэ информатика 5237 - Помощь в подготовке к экзаменам и поступлению

Продолжаем решать демоверсию ЕГЭ по информатике 2023.

Условия задач были взяты с сайта: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5

Видеокурс — это то, с чего лучше всего начать подготовку к ЕГЭ по информатике.

Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 16-21)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)

Задание 11

При регистрации в компьютерной системе каждому объекту присваивается
идентификатор, состоящий из 250 символов и содержащий только
десятичные цифры и символы из 1650-символьного специального алфавита.
В базе данных для хранения каждого идентификатора отведено одинаковое
и минимально возможное целое число байт. При этом используется
посимвольное кодирование идентификаторов, все символы кодируются
одинаковым и минимально возможным количеством бит.

Определите объём памяти (в Кбайт), необходимый для хранения 65 536
идентификаторов. В ответе запишите только целое число – количество
Кбайт.

Решение:

Воспользуемся формулой для 11-ого задания из ЕГЭ по информатике.

Вместо N подставляем число 1650 + 10 = 1660 (1650 символов плюс 10 цифр). Тогда

1660 < 2¹¹

Т.е. 11 бит точно хватит, чтобы закодировать 1650 символов.

В идетификаторе всего 250 ячейки. Найдём сколько будет «весить» один идетификатор: 250 * 11 = 2750 бит. Узнаем, сколько байт потребуется для одного идентификатора 2772 / 8 = 344 байт (округлили в большую сторону, чтобы точно хватило).

У нас всего 65536 идентификаторов. Тогда нам потребуется 65536 * 344 = 22544384 байт. Переведём в Кб: 22544384 / 1024 = 22016 Кб.

Ответ: 22016

Задание 12

Исполнитель Редактор получает на вход строку цифр и преобразовывает её.
Редактор может выполнять две команды, в обеих командах v и w обозначают
цепочки цифр.

А) заменить (v, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на
цепочку w. Например, выполнение команды

    заменить (111, 27)

преобразует строку 05111150 в строку 0527150.

    заменить (v, w) не меняет эту строку.

Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя
Редактор. Если она встречается, то команда возвращает логическое значение
«истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.

Цикл

    ПОКА условие
      последовательность команд
    КОНЕЦ ПОКА

выполняется, пока условие истинно.

В конструкции

    ЕСЛИ условие
      ТО команда1
      ИНАЧЕ команда2
    КОНЕЦ ЕСЛИ

выполняется команда1 (если условие истинно) или команда2 (если условие
ложно).

Дана программа для Редактора:

НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
  ЕСЛИ нашлось (>1)
    ТО заменить (>1, 22>)
  КОНЕЦ ЕСЛИ
  ЕСЛИ нашлось (>2)
    ТО заменить (>2, 2>)
  КОНЕЦ ЕСЛИ
  ЕСЛИ нашлось (>0)
    ТО заменить (>0, 1>)
  КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ

На вход приведённой выше программе поступает строка, начинающаяся
с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2»,
расположенных в произвольном порядке.

Определите наименьшее значение n, при котором сумма числовых значений
цифр строки, получившейся в результате выполнения программы, является
простым числом.

Решение:

Есть отличный разбор 12 задания в видеокурсе по подготовке к ЕГЭ по информатике.

Единица превращается в две двойки. Двойка преходим в саму себя. Ноль превращается в 1.

Изначально было 39 нулей. Значит, 39 единиц уже точно будет в строке, после выполнения программы. Так же там будет 39 двоек. Т.е., если не брать во внимание n единиц, сумма в результате будет 39 + 39 * 2 = 117.

Нужно прибавить некоторое количество чевёрок, чтобы получилось ближайшее простое число.

117 + 4*5 = 137.

Получается 5 единиц.

Ответ: 5

Задание 13

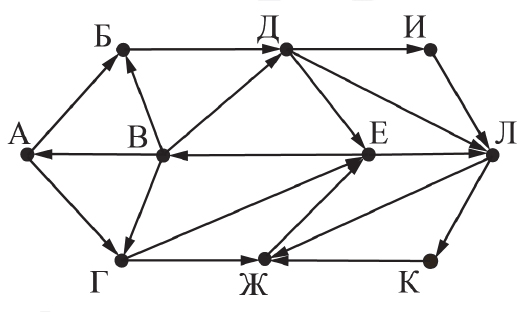
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е,
Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении,
указанном стрелкой.

Определите количество различных путей ненулевой длины, которые
начинаются и заканчиваются в городе Е, не содержат этот город в качестве
промежуточного пункта и проходят через промежуточные города не более
одного раза.

Решение:

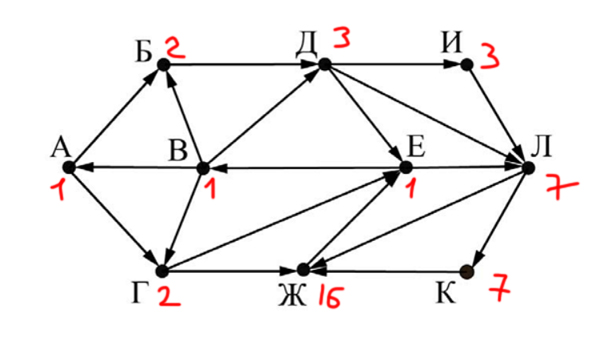
Решать будем примерно так же, как и классическую задачу. Основные идеи ни чем не отличаются.

В город Е входят города с числами: 16, 2 и 3. Значит, ответ получается 16 + 2 + 3 = 21.

Ответ: 21

Задание 14

Операнды арифметического выражения записаны в системе счисления
с основанием 15.

123×5₁₅ + 1×233₁₅

В записи чисел переменной x обозначена неизвестная цифра из алфавита
15-ричной системы счисления. Определите наименьшее значение x, при
котором значение данного арифметического выражения кратно 14. Для
найденного значения x вычислите частное от деления значения
арифметического выражения на 14 и укажите его в ответе в десятичной
системе счисления. Основание системы счисления в ответе указывать
не нужно.

Решение:

Решим с помощью программирования на языке Python.

for x in '0123456789ABCDE':
    r = int('123' + x + '5', 15) + int('1' + x + '233', 15)
    if r%14==0:
        print(r//14)
        break

Перебираем для переменной x все цифры в пятнадцатиричной системе. Вычисляем значение выражение. Функция int может перевести строку, записанную в пятнадцатиричной системе, в число.

Остаётся только найти нужное значение и остановить цикл с помощью break.

Ответ: 8767

Задание 15

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула

(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) ∨ (x + A >= 100)

тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной x ?

Решение:

Применим шаблон из видокурса ЕГЭ по информатике.

def D(n, m):
    if n%m==0: return True
    else: return False

for A in range(1, 1000):
    k=0
    for x in range(1, 10000):
        if (not(D(x, 2)) or not(D(x, 3))) or (x + A >= 100):
            k=k+1
    if k==9999:
        print(A)

Здесь в начале пишем функцию D, которая олицетворяет функцию ДЕЛ. Потом перебираем различные натуральные значения A. Если функция для какого-то значения сработает 9999 раз, то будем считать, что такое значение A нам подходит.

Самое маленькое значение получается 74.

Ответ: 94

ЕГЭ по информатике — Задание 8 (Циклы)

Добрый день! Рассмотрим 8 (восьмое) задание из Единого Государственног…

Категория: ЕГЭ Подкатегория: Информатика

Дата: 30-05-2020 в 09:55:30
0

В решении к заданию 11 вы пишите: «У нас всего 4096 идетификаторов». Пожалуй, надо исправить на «65 536 идентификаторов»…

Источник

В решение заданий демо-версии используется язык программирования Python.

Задание 1. Анализ информационных моделей

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число.

На графе расставим веса вершин.
Мы видим, что вершина В уникальна, имеет вес 2 и связана с двумя «тройками по весу».
Из таблицы видим, В это 4, далее видим, что «тройки по весу» это вершины 2 и 7.
7 вершина связана кроме В, еще с двумя «тройками по весу», значит D это 7, а F это 2.

Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6.
Рассуждая дальше видим, что С это 1, G это 2.

Сумма дорог BD + AF = 53 + 5 = 58

Ответ: 58

Задание 2. Построение таблиц истинности логических выражений

Миша заполнял таблицу истинности логической функции F

F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx.

¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.

y	x	z	w
0	0	1	0
0	1	1	0
1	1	1	0

Решение на Python

Ответ: YXZW

Задание выполняется с использованием прилагаемых файлов

Задание 3. Базы данных. Файловая система

В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в
магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня.

На рисунке приведена схема указанной базы данных.

Используя информацию из приведённой базы данных, определите общий вес
(в кг) крахмала картофельного, поступившего в магазины Заречного района
за период с 1 по 8 июня включительно. В ответе запишите только число.

На третьем листе книги применим фильтр по району и получим ID четырех магазинов.

На втором листе применим фильтр по товару и получим ID товара.

На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим:

Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг.

Ответ: 355

Задание 4. Кодирование и декодирование информации

По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений.

Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Ответ: 14

Задание 5. Анализ и построение алгоритмов для исполнителей

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему
новое число R следующим образом.

1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.

Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число
10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе запишите это число в десятичной системе счисления.

Минимальное R, большее 40, это 41.
В результате выполнения алгоритма число R должно либо начинаться на 10 и оканчиваться 0, либо начинаться на 11 и оканчиваться 1.
Из чисел, больших 41, это 42, 44, 46, 49, и т.д.
Мы должны найти минимальное N, из которого данное число получено.
Поскольку первые цифры заменялись, то мы видим, что данные числа могли быть получены из чисел 29, 30, 23, 16.
Из которых 16 минимальное, и меньше уже быть не может.

ИЛИ программное решение

Ответ: 16

Задание 6. Определение результатов работы простейших алгоритмов

Исполнитель Черепаха действует на плоскости с декартовой системой координат.
В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды:
Вперёд n (где n–целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Повтори 7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

ИЛИ

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки.

Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 10 Направо 90 Вперёд 20 Направо 90]
Поднять хвост
Вперёд 3 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 2 [Вперёд 70 Направо 90 Вперёд 80 Направо 90]

Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения.

Сначала нужно построить фигуру.
Это можно сделать к примеру, на тетрадном листе, при помощи библиотеки Turtle или в Excel.

Далее мы находим уравнения прямых, которыми ограничена фигура и решаем
систему уравнений программно.

ИЛИ
Фигуру можно построить программно или к примеру, в Excel.
Далее анализируем и считаем точки.

Ответ: 1 задание — 38, 2 задание — 128

Задание 7. Кодирование и декодирование информации. Передача информации

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.

I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц),

i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро)

I₁ = ν ⋅ i ⋅ t
I₂ = ν/2 ⋅ 3,5 ⋅ i ⋅ t ⋅ 2 = 3,5 ⋅ I₁

I₂ = 3,5 · 28 = 98

Ответ: 98

Задание 8. Перебор слов и системы счисления

Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6.

* * * * * — пятизначное число.
В восьмеричной системе счисления в алфавите 8 цифр: 0..7.
Первая цифра 0 быть не может.
Цифра 6 — одна, при этом стоит рядом только с четными цифрами — 0, 2 или 4.
Получим:

6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029
* 6 * * * — вариантов 2 ⋅ 3 ⋅ 7 ⋅ 7 = 294
* * 6 * * — вариантов 6 ⋅ 3 ⋅ 3 ⋅ 7 = 378
* * * 6 * — вариантов 6 ⋅ 7 ⋅ 3 ⋅ 3 = 378
* * * * 6 — вариантов 6 ⋅ 7 ⋅ 7 ⋅ 3 = 882

Ответ: 2961

Задание выполняется с использованием прилагаемых файлов

Задание 9. Работа с таблицами

Файл с данными

Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
– в строке только одно число повторяется дважды;
– среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел.
В ответе запишите только число.

Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке.

Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6.

Далее мы найдем среднее арифметическое неповторяющихся значений.

Затем найдем сумму повторяющихся значений.

Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия.

Ответ: 2241

Задание выполняется с использованием прилагаемых файлов

Задание 10. Поиск символов в текстовом редакторе

Файл с данными

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует.
В ответе запишите только число.

В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз.

Ответ: 45

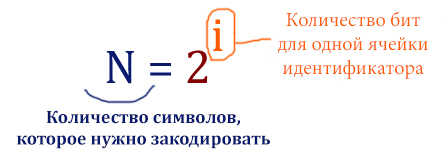
Задание 11. Вычисление количества информации

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.

I = K · i, N = 2 ⁱ

ID : ****….**** – всего 250 различных символов в наборе

N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 2¹¹, значит для кодирования одного символа нужно 11 бит.

I_ID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт

I₆₅₅₃₆ = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего

Ответ: 22016

Задание 12. Выполнение алгоритмов для исполнителей

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл
    ПОКА условие
        последовательность команд
    КОНЕЦ ПОКА

выполняется, пока условие истинно.

В конструкции

    ЕСЛИ условие
        ТО команда 1
    КОНЕЦ ЕСЛИ

выполняется команда 1 (если условие истинно).

В конструкции

    ЕСЛИ условие
        ТО команда 1
        ИНАЧЕ команда 2
    КОНЕЦ ЕСЛИ

выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно).

Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>0)
ТО заменить (>0, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке. Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.

def pr(n): #функция определяет простое ли число
for i in range(2,int(n**0.5)+1):
if (n%i) == 0:
return False
return True

for n in range(100): #перебираем n
s=’>’ + 39*’0′ + n*’1′ + 39*’2′
while ‘>1’ in s or ‘>2’ in s or ‘>0’ in s:
if ‘>1’ in s:
s=s.replace(‘>1′,’22>’,1)

if ‘>2’ in s:
s=s.replace(‘>2′,’2>’,1)

if ‘>0’ in s:
s=s.replace(‘>0′,’1>’,1)

sum_s = 0
for i in s[:-1]: #считаем сумму цифр в строке
sum_s += int(i)
if pr(sum_s): #проверяем на простоту
print(n)
break

Ответ: 5

Задание 13. Поиск путей в графе

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.

Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л.

Ответ: 21

Задание 14. Кодирование чисел. Системы счисления

Операнды арифметического выражения записаны в системе счисления с основанием 15.
123x515 + 1x23315
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

for x in range(15):
s1=’123’+ str(x) +’5′
s2=’1’+ str(x) +’233′
n= int(s1,15)+ int(s2,15)

if n%14 == 0:
print(n//14)
break

Ответ: 8767

Задание 15. Преобразование логических выражений

На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
(x ∈ D) → ((¬(x ∈ C) & ¬(x ∈ A)) → ¬(x ∈ D)) истинно (т.е. принимает значение 1) при любом значении переменной х.

def deli(n,m):
if n%m == 0:
return True

for A in range(1,1000):
Ok = True
for x in range(1,10000):
Ok*=( (not(deli(x,2)) or (not(deli(x,3)))) or ((x+A)>=100) )

if Ok:
print(A)
break

Ответ: 94

Задание 16. Рекурсивные алгоритмы

Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n — 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?

F(2023) = 2023! = 2023 ⋅ 2022!

F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 =

= 8266912626

Ответ: 8266912626

Задание выполняется с использованием прилагаемых файлов

Задание 17. Проверка на делимость

Файл с данными

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых
только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

f= open(’17.txt’)
p=[int(i) for i in f]
f.close()

k = 0
PP = 0
M3 = 0

for i in p:
if (abs(i))%10 == 3:
M3 = max(i, M3)

for i in range(1,len(p)): #Осторожно, скобки!
if ( ((abs(p[i-1])%10 == 3) + ((abs(p[i])% 10 == 3)) ==1 ) and ((p[i-1]**2 + p[i]**2) >= M3**2) ):
k+=1
PP = max(PP, p[i-1]**2 + p[i]**2)

print(k,PP)

Ответ: 180 190360573

Задание выполняется с использованием прилагаемых файлов

Задание 18. Робот-сборщик монет

Файл с данными

Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.

Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:

1	8	8	4
10	1	1	3
1	3	12	2
2	3	5	6

Для указанных входных данных ответом должна быть пара чисел 41 и 22.

Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен.

Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1.

Далее делаем замену всех формул МАКС на МИН.

Ответ: 1099 1026

Задание 19. Выигрышная стратегия. Задание 1

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом.

Ответ: 64

Задание 20. Выигрышная стратегия. Задание 2

Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

Петя не может выиграть за один ход;
Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в порядке возрастания.

Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом.

Ответ: 32 63

Задание 21. Выигрышная стратегия. Задание 3

Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:

у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.

Если найдено несколько значений S, в ответе запишите минимальное из них.

Ответ: 62

Задание 22. Многопроцессорные системы

В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Типовой пример организации данных в файле:

Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла.

В независимых процессах время считается от 0,
в зависимых прибавляется к времени процесса, от которого зависит.

Ответ: 17

Задание 23. Анализ программы с циклами и условными операторами

Исполнитель преобразует число на экране.
У исполнителя есть две команды, которые обозначены латинскими буквами:
A. Прибавить 1
B. Умножить на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 35, при этом траектория вычислений содержит число 10 и не содержит 17?
Траектория вычислений программы – это последовательность результатов
выполнения всех команд программы. Например, для программы ABA при
исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

def f(x, y):
if x == y:
return 1
if x > y or x == 17:
return 0
else:
return f(x + 1, y) + f (2 * x, y)

print (f(1,10) * f(10, 35))

Ответ: 98

Задание выполняется с использованием прилагаемых файлов

Задание 24. Анализ программы с циклами и условными операторами

Файл с данными

Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная
в прилагаемом файле. Для выполнения этого задания следует написать программу.

f=open(’24.txt’)
p= f.readline()
f.close()

PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’]
M=k=0

for i in range(1, len(p), 2):
x = p[i-1] + p[i]
if x in PP:
k += 1
else:
k = 0
M=max(M,k)
print(M)

Ответ: 95

Задание 25. Анализ программы с циклами и условными операторами

Назовём маской числа последовательность цифр, в которой также могут
встречаться следующие символы:
– символ «?» означает ровно одну произвольную цифру;
– символ «*» означает любую последовательность цифр произвольной длины;
в том числе «*» может задавать и пустую последовательность.

Например, маске 123*4?5 соответствуют числа 123405 и 12300405.

Среди натуральных чисел, не превышающих 10¹⁰, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 2023. Количество строк в таблице для ответа избыточно.

Самый простой способ использовать библиотеку fnmatch.
Функция fnmatch() проверяет, соответствует ли строка шаблонной строке, возвращая True или False

или так полным перебором:

y = {»,’0′,’00’,’000′}
for x in y:
for j in range(10):
s = ‘1’ + str(j) + ‘2139’ + x + ‘4’
if int(s) % 2023 == 0:
print (s, int(s)//2023)

for x in range (1000):
for j in range(10):
s = ‘1’ + str(j) + ‘2139’ + str(x) + ‘4’
if int(s) % 2023 == 0:
print (s, int(s)//2023

Ответ: 162139404 80148
1321399324 653188
1421396214 702618
1521393104 752048

Задание выполняется с использованием прилагаемых файлов

Задание 26. Анализ программы с циклами и условными операторами

В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д.
Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Входные данные
В первой строке входного файла находится число N – количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы. При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Задание выполняется с использованием прилагаемых файлов

Задание 27. Анализ программы с циклами и условными операторами

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные

Файл А
Файл В

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.
Типовой пример организации данных во входном файле
6
1 100
2 200
5 4
7 3
8 2
10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 ∙ 2 + 3 ∙ 1 + 5 ∙ 1 + 6 ∙ 1 + 8 ∙ 2.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Ответ: 51063 5634689219329

Источник

Урок посвящен тому, как решать 5 задание ЕГЭ по информатике

Содержание:

Объяснение 5 задания
- Исполнитель для возведения в квадрат, деления, умножения и сложения
- Проверка числовой последовательности на соответствие алгоритму
Разбор 5 задания
- Решение задания про алгоритм, который строит число R
- Решение заданий для темы Проверка числовой последовательности (Автомат)

5-е задание: «Анализ алгоритмов и исполнители»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 4 минуты.

Проверяемые элементы содержания: Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд

До ЕГЭ 2021 года — это было задание № 6 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Как и в других заданиях базового уровня сложности, источником ошибок служит недостаточная внимательность и отсутствие или поверхностность самостоятельной проверки полученного ответа»

ФГБНУ «Федеральный институт педагогических измерений»

Проверка числовой последовательности на соответствие алгоритму

для выполнения некоторых заданий необходимо повторить тему системы счисления;
максимальное значение суммы цифр десятичного числа — это 18, так как 9 + 9 = 18;
для проверки правильности переданного сообщения иногда вводится бит четности — дополнительный бит, которым дополняется двоичный код таким образом, чтобы в результате количество единиц стало четным: т.е. если в исходном сообщении количество единиц было четным, то добавляется 0, если нечетным — добавляется 1:

например: 
 3₁₀ = 11₂ 
после добавления бита четности: 110
----
 4₁₀ = 100₂ 
после добавления бита четности: 1001

добавление к двоичной записи числа нуль справа увеличивает число в 2 раза:

например:
111₂ - это 7₁₀
добавим 0 справа:
1110₂ - это 14₁₀

Теперь будем рассматривать конкретные типовые экзаменационные варианты по информатике с объяснением их решения.

Разбор 5 задания

Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:

Решение задания про алгоритм, который строит число R

5_11:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

Строится двоичная запись числа 4N.
К этой записи дописываются справа еще два разряда по следующему правилу:

складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись является двоичной записью искомого числа R.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 129. В ответе это число запишите в десятичной системе счисления.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

Заметим, что после выполнения второго пункта задания, будут получаться только четные числа! Наименьшим возможным четным числом, превышающим 129, является число 130. С ним и будем работать.
Переведем 130 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(130). Получим:

130₁₀ = 10000010₂

Это двоичное число получилось из исходного двоичного, после того как дважды был добавлен остаток от деления суммы цифр на 2. Т.е.:

в обратном порядке:
было 1000001 -> стало 10000010 
еще раз то же самое: 
было 100000 -> стало 1000001

Значит, необходимое нам двоичное число — это 100000.
Переведем 100000 в 10-ю систему. Для этого можно воспользоваться калькулятором, либо использовать интерпретатор Питона: int('100000',2).

100000₂ = 32₁₀

Так как по условию у нас 4*N, то 32 делим на 4 — > 8.

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := 4*n_;
    var ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряру (+ost)
    ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost;
    if n > 129 then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = 4*n_
    r = str(bin(n))
    r = r[2:]
    for i in range(2):
        if r.count('1') % 2 == 0:
            r+='0'
        else:
            r+='1'
 
    n = int(r, base=2)
    if n > 129:
        print(n_)
        break
    n_+=1

Результат: 8

Для более детального разбора предлагаем посмотреть видео теоретического решения данного 5 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_12: Демоверсия ЕГЭ 2018 информатика:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

Строится двоичная запись числа N.
К этой записи дописываются справа ещё два разряда по следующему правилу:
складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
Наименьшим возможным числом, превышающим 83, является число 84. С ним и будем работать.
Переведем 84 в двоичную систему счисления. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(84). Получим:

84 = 1010100

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так как оно нечетное. А мы имеем 0. Соответственно, это оно не подходит.
Возьмем следующее четное число — 86. Переведем его в двоичную систему счисления:

86 = 1010110

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так и есть: 101011. А затем добавляется 0: 1010110. Соответственно, оно подходит.

Результат: 86

Подробное решение данного 5 (раньше №6) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Видеорешение с программированием (PascalAnc.Net):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Аналитическое видеорешение:

📹 Видеорешение на RuTube здесь -> аналитическое решение

5_18:

Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3. Шаг 2 повторяется ещё два раза.
4. Результат переводится в десятичную систему счисления.

При каком наименьшем исходном числе N > 65 в результате работы алгоритма получится число, кратное 4?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
    for var i := 1 to 3 do 
    begin
      if bin(n).CountOf('1') = bin(n).CountOf('0') then // сравниваем
        if n mod 2 = 0 then // если четное, то в конце 0
          n := 2 * n  // добавляем разряд = 0
        else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
      else if bin(n).CountOf('1') > bin(n).CountOf('0') then
        n := 2 * n
      else
        n := 2 * n + 1
    end;
    if (n_ > 65) and (n mod 4 = 0) then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(3):
        if r.count('1') == r.count('0'):
            r+=r[-1] 
        elif r.count('1')>r.count('0'):
            r+='0'
        else:
            r+='1'
    n = int(r, base=2)
    if n_ > 65 and n % 4 == 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 79

5_19:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Число N переводим в двоичную запись.
2) Инвертируем все биты числа кроме первого.
3) Переводим в десятичную запись.
4) Складываем результат с исходным числом N.
Полученное число является искомым числом R.

Укажите наименьшее нечетное число N, для которого результат работы данного алгоритма больше 99. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(1,len(r)):
        if r[i]== '0':
            r=r[:i]+'1'+r[i+1:] 
        else:
            r=r[:i]+'0'+r[i+1:] 
    n = int(r, base=2)
    n+=n_
    if n > 99 and n_ % 2 != 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 65

5_13:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописываются справа еще два разряда по следующему правилу:
— если N делится нацело на 4, в конец числа (справа) дописывается сначала ноль, а затем еще один ноль;
— если N при делении на 4 дает в остатке 1, то в конец числа (справа) дописывается сначала ноль, а затем единица;
— если N при делении на 4 дает в остатке 2, то в конец числа (справа) дописывается сначала один, а затем ноль;
— если N при делении на 4 дает в остатке 3, в конец числа (справа) дописывается сначала один, а затем еще одна единица.

Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.

Укажите максимальное число R, которое меньше 100 и может являться результатом работы данного алгоритма. В ответе это число запишите

в десятичной системе счисления

Типовые задания для тренировки

✍ Решение:

Поскольку требуется найти наибольшее число, то возьмем наибольшее из возможных чисел, которые < 100 — это число 99. Переведем его в двоичную систему. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(99). Получим:

99 = 1100011₂

По алгоритму это число получилось путем добавления справа двух разрядов, значение которых зависит от исходного N:

1100011
  N

Т.е. в конце были добавлены две единицы — по алгоритму это значит, что исходное N должно в остатке при делении на 4 давать 3. Переведем найденное N в десятичную систему. Можно использовать калькулятор либо консоль пайтон: int('11000',2)

11000 = 24₁₀

24 делится на 4 нацело, т.е. в конце по алгоритму должны были добавиться два разряда — 00. У нас же в конце 11. Т.е. число 99 не подходит. Проверим следующее — 98.

98 = 1100010₂  : 10 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 10 
98 - не подходит

97 = 1100001₂ : 01 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 01 
97 - не подходит

96 = 1100000₂ : 00 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, у нас 00 - верно!
96 - подходит!

Результат: 96

Предлагаем посмотреть видео теоретического решения:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_14:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописывается (дублируется) последняя цифра.
3. Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4. К полученному результату дописывается ещё один бит чётности.

Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, большее 114, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

В постановке задания задано R > 114. R — это результат работы алгоритма. Для того, чтобы определить наименьшее возможно N, переведем сначала 114 в двоичную систему счисления и выделим в нем три добавленные по алгоритму цифры (перевод можно выполнить в консоли Питона: bin(114))

114 = 1110010₂

Проанализируем, как могло бы получиться двоичное число 114 (R) по алгоритму:

2. В полученное числе N = 1110 дублируется последняя цифра и получается 11100.
3. Поскольку число единиц (3) — нечетное, то справа добавляется 1: 111001.
4. Т.к. в полученном наборе цифр четное число единиц, то добавляем 0: 1110010

Поскольку из числа N = 1110 по алгоритму могла получиться только такая последовательность цифр (1110010), то для получения минимального R, но большего чем R = 114, увеличим в N = 1110 самый младший разряд на единицу и рассмотрим работу алгоритма с полученным числом:

1. N = 1110 + 1 = 1111

Работа по алгоритму:
2. 11111 - дублирование последней цифры.
3. 111111 - справа дописываем единицу, т.к. в полученном числе 5 единиц (нечетное)
4. 1111110 - дописываем ноль, т.к. в полученном числе четное число единиц.

Ответ нужно получить в десятичной системе счисления (для перевода можно воспользоваться интерпретатором Питона: int('1111110',2)):

min R = 1111110₂ = 126₁₀

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
          // дублирвание последней цифры
    if n mod 2 = 0 then // если четное, то в конце 0
      n := 2 * n  // добавляем разряд = 0
    else 
      n := 2 * n + 1; // иначе добавляем разряд = 1
    for var i := 1 to 2 do
    begin
      if bin(n).CountOf('1') mod 2 = 0 then
        n := 2 * n  // добавляем разряд = 0
     else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
    end;
    if n > 114 then
    begin
      println(n);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r  = str(bin(n)) # строковое значение
    r = r[2:] # убираем 0b
    r=r+r[-1]
    for i in range (2):
        if r.count('1') % 2 == 0:
            r = r+'0'
        else:
            r = r+'1'
    r = int(r,base = 2) # в 10-ю с.с.
    if r > 114:
        print(r)
        break
    n_+= 1

Результат: 126

5_17: Досрочный вариант 1 ЕГЭ по информатике 2020, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
— если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы.

Например, двоичная запись 1001 числа 9 будет преобразована в 100111.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.

Укажите минимальное число N, для которого результат работы алгоритма будет больше 134. В ответе это число запишите в десятичной системе счисления.

Ответ: 33

Видео -> теоретическое решение
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_16:

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:

1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из нового числа вычитается исходное, полученная разность выводится на экран.

Какое число нужно ввести в автомат, чтобы в результате получилось 45?

✍ Решение:

Результатом выполнения алгоритма является число 45. Алгоритм работает в двоичной системе счисления, поэтому переведем число:

45 = 00101101₂

Пронумеруем биты слева направо, начиная с единицы. Рассмотрим каждый бит отдельно, начиная с левого бита под номером 1.
1. Так как биты в уменьшаемом и вычитаемом должны быть различны, то единица в результате может получится только 1 - 0, с учетом, что у разряда с единицей заняли. То есть бит:

   .
_{_}  1 _ _ _ _ _ _ _    N инвертируемое
₌  0 _ _ _ _ _ _ _    N исходное
   0 0 1 0 1 1 0 1  = 45   результат

2. 1 - 0 не может в результате дать 0, так как у следующей слева единицы мы заняли. Значит, 0 - 1. Чтобы не получить единицу в ответе, необходимо у нуля тоже занять:

   . .
_{_}  1 0 _ _ _ _ _ _ 
₌  0 1 _ _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

3. 1 - 0 не может быть, так как у следующего слева нуля мы заняли.
Значит 0 - 1. То есть как раз чтобы получить единицу (10 - 1 = 1), занимаем у следующих слева разрядов:

   . .
_{_}  1 0 0 _ _ _ _ _ 
₌  0 1 1 _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

4. 0 - 1 не может быть. Значит, чтобы получить в результате ноль, берем 1 - 0, у единицы должно быть занято.

   . .   .
_{_}  1 0 0 1 _ _ _ _ 
₌  0 1 1 0 _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

5. 1 - 0 не может быть. Так как слева у единицы занято. Значит, чтобы получить в результате 1, берем 0 - 1:

   . .   .
_{_}  1 0 0 1 0 _ _ _ 
₌  0 1 1 0 1 _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

6. 0 - 1 не даст в ответе единицу, значит, имеем 1 - 0:

   . .   .
_{_}  1 0 0 1 0 1 _ _ 
₌  0 1 1 0 1 0 _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

7. 0 - 1 не может быть, значит, 1 - 0. Чтобы получить в результате 0, необходимо, чтобы у 1 было занято:

   . .   .     .
_{_}  1 0 0 1 0 1 1 _ 
₌  0 1 1 0 1 0 0 _ 
   0 0 1 0 1 1 0 1  = 45   результат

8. Чтобы получить 1, имеем 0 - 1:

   . .   .     .
_{_}  1 0 0 1 0 1 1 0 
₌  0 1 1 0 1 0 0 1
   0 0 1 0 1 1 0 1  = 45   результат

Полученное число (вычитаемое) и есть искомое N. Переведем его в 10-ю с.с.:

01101001 = 105₁₀

Ответ: 105

Смотрите теоретический разбор задания на видео и подписывайтесь на наш канал:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

Решение заданий для темы Проверка числовой последовательности (Автомат)

5_7:

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.

Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.

Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.

✍ Решение:

Результат: 2949

Процесс теоретического решения данного 5 задания представлен в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_8:

Автомат получает на вход четырехзначное число. По нему строится новое число по следующим правилам:

Складываются первая и вторая, затем вторая и третья, а далее третья и четвёртая цифры исходного числа.
Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).

Пример: Исходное число: 7531. Суммы: 7+5=12; 5+3=8; 3+1=4. Результат: 4812.

✍ Решение:

Число 2512 можно разбить на 2, 5, 12

Начнем с 12. Необходимо получить наибольшее число, поэтому разобьем на слагаемые с наибольшей цифрой — 9:

12=9+3

То есть первые две цифры:

 93**

В число 2 тройка не входит, значит забираем тройку из 5. Остается 2. А, значит, из состава 2 остается 0.

Получим число: 9320.

Результат: 9320

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_9:

Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам:

Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
Полученные два шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).

Пример: Исходные числа: 25, 66. Поразрядные суммы: 8, B. Результат: B8.

Какие из предложенных чисел могут быть результатом работы автомата?
Перечислите в алфавитном порядке буквы, соответствующие этим числам, без пробелов и знаков препинания.

Варианты:
A) 127
B) C6
C) BA
D) E3
E) D1

✍ Решение:

Проанализируем все варианты:

Вариант А. 127 не подходит, так как число 12 в шестнадцатеричной системе записывается как С.

Вариант В. С6 разбиваем на 12 и 6. Число может быть результатом работы автомата. Исходные числа, например, 35 и 37

Вариант С. BA разбиваем на 11 и 10. Число может быть результатом работы автомата. Исходные числа, например, 55 и 56

Вариант D. E3 разбиваем на 14 и 3. 14=6+8, но цифры большие 6 не принимает автомат. Не подходит.

Вариант E. D1 разбиваем на 13 и 1. 13=6+7, но цифры большие 6 не принимает автомат. Не подходит.

Результат: BC

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_10: Задание 5 ГВЭ 11 класс 2018 год ФИПИ

Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 7 (если в числе есть цифра больше 7, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.

1. Вычисляются два шестнадцатеричных числа: сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.

Определите, какое из предложенных чисел может быть результатом работы автомата.

Варианты:
1) AD
2) 64
3) CF
4) 811

✍ Решение:

Теоретическое решение 4 задания ГВЭ 11 класса смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_15:

Автомат получает на вход натуральное число X. По этому числу строится трёхзначное число Y по следующим правилам:
1. Первая цифра числа Y (разряд сотен) – остаток от деления X на 7.
2. Вторая цифра числа Y (разряд десятков) – остаток от деления X на 2.
3. Третья цифра числа Y (разряд единиц) – остаток от деления X на 5.

Пример. Исходное число: 55. Остаток от деления на 7 равен 6; остаток от деления на 2 равен 1; остаток от деления на 5 равен 0. Результат работы автомата: 610.

Сколько существует двузначных чисел, при обработке которого автомат выдаёт результат 312?

Типовые задания для тренировки

✍ Решение:

Обозначим каждую цифру числа Y согласно заданию:

Y =    3       1       2
^{x mod 7    x mod 2    x mod 5}

Сделаем выводы:

1. x mod 2 = 1 => значит, X — нечетное число
2. x mod 5 = 2 => значит, X — либо ?2, либо ?7.
3. раз x — нечетное, то из пред. пункта получаем x = ?7
4. x mod 7 = 3 => переберем все варианты:

97 - не подходит, 
87 - подходит (87 / 7 = 12, остаток = 3)
77 - не подходит,
67 - не подходит,
57 - не подходит,
47 - не подходит,
37 - не подходит,
27 - не подходит,
17 - подходит (17 / 7 = 2, остаток = 3)

Результат: 2

Источник

What you will learn

Научитесь мыслить логически
Изучите все необходимые особенности Python 3
Примените теорию на практике
Узнаете как можно проверить своё решение
Сможете легко решить любой прототип 27 Задания

About this course

Курс по 27 Заданию — это полноценный курс, в ходе которого мы подготовим вас ко ВСЕМ темам задания 27 с ПОЛНОГО НУЛЯ! Каждая тема будет понятна даже НОВИЧКУ, ведь обучение включает в себя :

ТЕОРИЮ по Python 3, необходимую для решения
ПРАКТИКУ с разбором — 130 прототипов
ДОМАШНЕЕ ЗАДАНИЕ с разбором — 33 прототипов
ПОДДЕРЖКУ от преподавателя и единомышленников
КОНСПЕКТЫ, которые позволят легко повторить материал
МИНИ-ЭКЗАМЕН в конце курса для проверки приобретенных навыков и полученных знаний

💖 Не стесняйтесь задавать любые вопросы в комментариях к курсу или же в нашей Беседе в VK :

👪Перейти в нашу Беседу в VK👈

✨Перейти в нашу Группу в VK👈

💯Посмотреть Отзывы Наших Учеников👈

✅ Пройдя курс ты изучишь самые оптимальные, простые, НО эффективные способы решения как простых, так и сложных 26 Заданий, используя все особенности языка программирования Python 3 и таких электронных таблиц, как Excel и LibreOffice. В курсе разобран как способ решения через табличный процессор, так и с использованием программирования.

🔥 Что тебя ждёт на курсе? 👇(Более подробное содержание в нашей группе в VK)

Блок 1 — Остатки ( Теория + Прототипы — 15 шт. + ДЗ — 14 шт. ) ~ 3 часа
Блок 2 — МЧС и ММР ( Теория + Прототипы — 10 шт. + ДЗ — 10 шт. ) ~ 2 часа 30 мин.
Блок 3 — Подмножества ( Теория + Прототипы — 3 шт. + ДЗ — 2 шт. ) ~ 1 час
Блок 4 — Префиксные Суммы ( Теория + Прототипы — 7 шт. + ДЗ — 7 шт. ) ~ 3 часа
Блок 5 — Разные Задачи ( Прототипы — 22 шт. ) ~ 4 часа 30 мин.
Блок 6 — Разные Задачи №2 ( Прототипы — 26 шт. ) ~ 7 часов 30 мин.
Блок 7 — Мини-Экзамен ( 14 Задач для Проверки Своих Знаний )

❗ ВНИМАНИЕ!

У курса нет старта. Вы можете начать его проходить в любой момент
У курса нет подписок по месяцам. После покупки курса, вы получаете доступ к нему навсегда
На курсе мы сначала рассказываем теорию, потом даём решить задачу, а после делаем видео-разбор с её решением
На курсе задания проверяются автоматически. Ждать проверки преподавателем не нужно

📚 Источники Задач :

Сайт kompege.ru
Сайт kpolyakov.spb.ru
Реальные ЕГЭ Демо-версии Досрочные волны Резервные дни Апробации
СтатГрады Авторские задачи

Whom this course is for

Курс создан для Школьников 10-11 классов, учителей и всех остальных, желающих сдавать ЕГЭ по Информатике

Initial requirements

Никакие начальные требования, кроме некоторых знаний в Python 3, не нужны. Научим решению любого вида 27 задания несколькими способами с полного нуля!

Meet the Instructors

How you will learn

При переходе к каждому новому способу решения 27 задания вы сначала получаете всю необходимую для его решения теорию, потом мы даёт вам прототип и к каждому прототипу делаем видео-разбор
После видео-разбора вас ждёт домашнее задания, к которому также прилагается видео-разбор
В комментариях вы можете посмотреть чужие решения, чтобы лучше разобраться в теме, или даже прислать своё решение
В конце курса вы сможете проверить полученные знания, решив мини-экзамен
Во время обучения у вас есть возможность задать преподавателю любой вопрос

Course content

Certificate

Сертификат Stepik =)

What you will get

Price

FAQ

Share this course

https://stepik.org/course/111154/promo

Источник

Тема 5.

Простейшие исполнители и алгоритмы

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

простейшие исполнители и алгоритмы

5.01Двоичная запись числа

5.02Бит чётности

5.03Работа с цифрами числа

5.04Нестандартные задачи

Решаем задачи

Автомат обрабатывает натуральное число N по следующему алгоритму:

1. Строится двоичная запись числа .

2. Складываются все цифры полученной двоичной записи. В конец записи (справа) дописывается остаток от деления
полученной суммы на .

3. Предыдущий пункт повторяется для записи с добавленной цифрой.

4. Результат переводится в десятичную систему и выводится на экран.

Пример. Дано число N = 13 . Алгоритм работает следующим образом:

1. Двоичная запись числа .

2. Сумма цифр двоичной записи , остаток от деления на равен , новая запись 11011 .

3. Сумма цифр полученной записи , остаток от деления на равен , новая запись 110110 .

4. На экран выводится число .

Какое наименьшее число, большее вашего балла на ЕГЭ ( 100 ), может появится на экране в результате работы
автомата?

Показать ответ и решение

for i in range(1000000):
    s = bin(i)[2::]
    s += str(s.count(’1’) % 2)
    s += str(s.count(’1’) % 2)
    if int(s, 2) > 100:
        print(int(s, 2))
        break

Аналитическое решение:

Имеется число . Все числа в двоичной записи складываются и добавляется остаток от деления на 2 этой суммы, то
есть цифра 0 или 1, значит если сумма чётна, то дописываем 0, иначе 1. Если мы дописали единичку, то количество единиц
увеличится на 1, а значит, что после этого сумма будет чётна, и уже в следующем пункте мы допишем нолик. Если мы
дописали ноль, то сумма числа не меняется, а значит в следующем пункте мы также допишем нолик. Значит число в 2 СС
заканчивается на 00 или 10.

Нам необходимо найти число, большее, чем 100, которое в 2 СС заканчивается на 00 или 10. Будем перебирать с
минимального.

Подойдет ли число ? Нет, оно кончается на 01.

Подойдет ли число ? Да, так как оно заканчивается на 10. Значит это и есть наш ответ.

Показать ответ и решение

for i in range(1000000):
    s = bin(i)[2:]
    s += str(s.count(’1’) % 2)
    s += str(s.count(’1’) % 2)
    if int(s, 2) > 1024:
        print(int(s, 2))
        break

Показать ответ и решение

for n in range(1, 1000):
    r = bin(n)[2:]
    r += r[-1]
    if bin(n)[2:].count(’1’) % 2 == 0:
        r += ’0’
    else:
        r += ’1’
    if r.count(’1’) % 2 == 0:
        r += ’0’
    else:
        r += ’1’
    if int(r, 2) > 120:
        print(n)
        break

Показать ответ и решение

Решение программой:

for i in range(1, 1000000):
    s = bin(i)[2::]
    s += ’1’
    if s.count(’1’) % 2 == 0:
        s += ’0’
    else:
        s += ’1’
    # второй if не нужен, потому что всегда будет дописываться 0
    # подумайте почему)
    if s.count(’1’) % 2 == 0:
        s += ’0’
    else:
        s += ’1’
    if int(s, 2) > 212:
        print(int(s, 2))
        break

Аналитическое решение:

Каким бы не было число, на втором шаге к нему всегда дописывается единица, так что давайте называть это число
«изначальным».

Если изначальное число имеет чётное количество единиц, то после добавления нуля количество единиц не
изменится, а потому на следующем шаге также добавится ноль. Итого к числу допишут два нуля.

Если изначально число имеет нечётное количество единиц, то после добавления единицы количество единиц
увеличится на , что означает, что количество единиц станет чётным числом, а значит на следующем шаге уже будут
добавлять ноль. Итого к числу допишут единицу и ноль.

Значит мы будем проверять только числа, которые кончаются на 100 или 110 .

Могло ли получиться число 213 ? Нет, в двоичной СС оно выглядит как , а значит получиться после
алгоритма не могло.

Могло ли получиться число 214 ? В двоичной СС оно выглядит как 11010110
2 . Так что вполне возможно. Если
откинем последние три цифры, то у нас останется число 110102 , добавим к нему единицу и получим число 1101012 , у
него чётное число единиц, а значит после работы алгоритма к нему дописали бы два нуля, но мы откинули 110 , а значит
это не то число, которое нам нужно.

Могло ли получиться число 215 ? Нет, в двоичной СС оно выглядит как , а значит получиться после
алгоритма не могло.

Могло ли получиться число 216 ? Нет, в двоичной СС оно выглядит как , а значит получиться после
алгоритма не могло.

Могло ли получиться число 217 ? Нет, в двоичной СС оно выглядит как , а значит получиться после
алгоритма не могло.

Могло ли получиться число 218 ? Нет, в двоичной СС оно выглядит как , а значит получиться после
алгоритма не могло.

Могло ли получиться число 219 ? Нет, в двоичной СС оно выглядит как , а значит получиться после
алгоритма не могло.

Могло ли получиться число 220 ? В двоичной СС оно выглядит как . Так что вполне возможно. Если
откинем последние три цифры, то у нас останется число 110112 , добавим к нему единицу и получим число 1101112 , у
него нечётное число единиц, а значит после работы алгоритма к нему дописали бы единицу и ноль, но мы откинули 100 , а
значит это не то число, которое нам нужно.

Могло ли получиться число 221 ? Нет, в двоичной СС оно выглядит как , а значит получиться после
алгоритма не могло.

Могло ли получиться число 222 ? В двоичной СС оно выглядит как . Так что вполне возможно. Если
откинем последние три цифры, то у нас останется число 110112 , добавим к нему единицу и получим число 1101112 , у
него нечётное число единиц, а значит после работы алгоритма к нему дописали бы единицу и ноль, а мы откинули как раз
110 , значит 222 – это интересующее нас число.

Показать ответ и решение

for i in range(10000):

    s = bin(i)[2::]

    if i % 2 == 0:

        s += ’11’

    else:

        s += ’00’

    x = int(s, 2) — len(bin(i)[2::])  # Длина в 2-сс числа N

    if x == 126:

        print(i)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим
образом:

1)Строится двоичная запись числа N.

2)К этой записи дописываются справа ещё два разряда по следующему правилу:

а)Дописывается справа бит чётности: 0, если в двоичном коде числа N было чётное число единиц, и 1, если
нечётное;

б)К полученному результату дописывается ещё один бит чётности

Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем
78. В ответе это число запишите в десятичной системе.

Показать ответ и решение

for i in range(1, 1000):
    s = bin(i)[2::]
    if s.count(’1’) % 2 == 0:
        s += ’0’
    else:
        s += ’1’
    if s.count(’1’) % 2 == 0:
        s += ’0’
    else:
        s += ’1’
    if int(s, 2) > 78:
        print(i)
        break

Аналитическое решение:

Если изначально число имеет нечётное количество единиц, то после добавления единицы количество единиц
увеличится на 1, что означает, что количество единиц станет чётным числом, а значит на следующем шаге уже будут
добавлять ноль. Итого к числу допишут единицу и ноль.

Значит мы будем проверять только числа, которые кончаются на или .

Могло ли получиться число ? Нет, в двоичной СС оно выглядит как , а значит получиться после
алгоритма не могло.

Могло ли получиться число 80? В двоичной СС оно выглядит как . Так что вполне возможно. Если откинем
последние две цифры, то у нас останется число 101002 , у него чётное число единиц, а значит после работы алгоритма к
нему дописали бы два нуля, но это как раз те самые цифры, которые мы откинули, значит и есть искомое
число.

На вход алгоритма подаётся натуральное число . Алгоритм строит по нему новое число R следующим
образом.

1) Строится двоичная запись числа

2) К этой записи дописываются разряды по следующему правилу:

а) если число чётное, то к двоичной записи числа в конце дописывается

б) если число нечётное, то к двоичной записи числа в конце дописывается

Полученная таким образом запись является двоичной записью искомого числа . Укажите наибольшее число
меньшее 128 , которое может получиться после обработки этого алгоритма. В ответе запишите это число в десятичной
записи.

Показать ответ и решение

Рассмотрим первое число = 127 . Переведем в двоичную сс и получим . Отрубим две последние цифры и
получим число нечетное, а значит должно было добавиться . Значит не подходит.

Похоже это число мы сразу можем угадать. У нас есть 11111
2 и к нему должно добавить 01
2 . Получаем число
. (Число 126 также не подходит т.к. )

Решение №2

ans = 0
for i in range(1000):
    s = bin(i)[2::]
    if i % 2 == 0:
        s += ’11’
    else:
        s += ’01’
    if int(s, 2) < 128:
        ans = max(ans, int(s, 2))
print(ans)

Показать ответ и решение

ans = 0
for i in range(1, 1000):
    s = bin(i)[2:]
    s += str(s.count(’1’) % 2)
    s += str(s.count(’1’) % 2)
    if int(s, 2) < 77 and int(s, 2) > ans:
        ans = int(s, 2)
print(ans)

На вход алгоритма подаётся натуральное число . Алгоритм строит по нему новое число следующим
образом.

1) Строится двоичная запись числа

2) К этой записи дописываются разряды по следующему правилу:

а) если число чётное, то к двоичной записи числа в конце дописывается

б) если число нечётное, то к двоичной записи числа в конце дописывается

Полученная таким образом запись является двоичной записью искомого числа . Укажите наибольшее число ,
меньшее 128 , которое может получиться после обработки этого алгоритма. В ответе запишите это число в десятичной
записи.

Показать ответ и решение

Решение №1

Рассмотрим первое максимально возможное число , меньшее 128 , а именно 127 . Переведем в двоичную систему
счисления и получим 1111111
2 . Уберём две последние цифры и получим нечетное число, а значит к исходному
числу должно было добавиться . Значит, число R = 127 не могло получиться в результате работы
алгоритма.

Теперь мы сразу можем угадать число . У нас есть 111112 , и к нему нужно добавить 012 . Получаем число
.

Решение №2

ans = 0
for i in range(1000):
    s = bin(i)[2::]
    if i % 2 == 0:
        s += ’11’
    else:
        s += ’01’
    if int(s, 2) < 128:
        ans = max(ans, int(s, 2))
print(ans)

Показать ответ и решение

for i in range(1, 100000):
    s = bin(i)[2:]
    s += str(s.count(’1’) % 2)
    s += str(s.count(’1’) % 2)
    r = int(s, 2)
    if r > 103:
        print(r)
        break

Показать ответ и решение

for n in range(1, 10000):
    r = bin(n)[2:]
    r = r + str(r.count(’1’) % 2)
    r = r + str(r.count(’1’) % 2)
    r = int(r, 2)
    if r > 150:
        print(r)
        break

На вход алгоритма подаётся натуральное число . Алгоритм строит по нему новое число следующим
образом.

1. Строится двоичная запись числа .

2. К этой записи дописывается единица.

3. Затем справа дописывается бит чётности: , если в двоичном коде полученного числа чётное число единиц, и ,
если нечётное.

4. К полученному результату дописывается ещё один бит чётности.

Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа ) является двоичной
записью искомого числа . Какое минимальное число , большее 168 , может быть получено в результате работы
автомата?

Показать ответ и решение

for i in range(100000):
    n = i
    s = bin(n)[2:]
    s = s + ’1’
    s = s + str(s.count(’1’) % 2)
    s = s + str(s.count(’1’) % 2)
    r = int(s, 2)
    if r > 168:
        print(r)
        break

Аналитическое решение:

Имеется число . В любом случае к нему дописывается единица, поэтому будем рассуждать, будто бы число и было
таким(с дописанной единицей) изначально. Если количество единиц чётно, то и сумма цифр числа чётна, а значит к числу
допишется ноль. Если же количество единиц нечётно, то и сумма цифр числа нечётна, а значит к числу допишется
единица. Если мы дописали единичку, то количество единиц увеличится на 1, а значит, что после этого сумма
будет чётна, и уже в следующем пункте мы допишем нолик. Если мы дописали ноль, то сумма числа не
меняется, а значит в следующем пункте мы также допишем нолик. Значит число в 2 СС заканчивается на
100 или 110 (учли, что мы изначально при любых обстоятельствах дописываем единицу, а потом 00 или
10).

Нам необходимо найти число, большее, чем 168, которое в 2 СС заканчивается на 100 или 110. Будем перебирать с
минимального.

Подойдет ли число 169 = 10101001
10 2 ? Нет, оно кончается на 001.

Подойдет ли число ? Нет, оно кончается на 010.

Подойдет ли число ? Нет, оно кончается на 011.

Подойдет ли число ? Да, так как оно заканчивается на 100. Значит это и есть наш
ответ.

Показать ответ и решение

Аналитическое решение:
Заметим, что если число единиц в двоичной записи нечётное, то в первый раз допишется единица, а затем число единиц
станет чётным, и во второй раз мы допишем ноль. Если же число единиц в двоичной записи чётное, то в первый раз мы
допишем ноль, затем количество единиц не изменится, и мы снова допишем ноль. Таким образом, в любом случае
последняя цифра числа — ноль. Напишем программу:

for i in range(1, 100):
    s = bin(i)[2::]
    a = 0
    for j in range(len(s)):
        a += int(s[j])
    if a % 2 == 0:
        s += ’00’
    else:
        s += ’10’
    if int(s, 2) > 43:
        print(int(s, 2))
        break

Источник

12 задание ЕГЭ по информатике обычно решает только половина выпускников. Оно правда такое сложное? Нет, если заранее изучить каждый из трех прототипов. Из этой статьи вы узнаете, как справиться с Редактором, Роботом и Чертежником — и как можно сделать это еще проще, используя программирование.

Прототипы задания 12 и их сложности

12 задание ЕГЭ по информатике относится к повышенному уровню сложности. На экзамене за него можно получить один первичный балл.

Это задание — часть блога «Алгоритмизация». Чтобы решить его, нужно уметь работать с алгоритмами и анализировать их. В этом задании могут встретиться три прототипа заданий: Редактор, Робот и Чертежник. Причем Редактор встречается на экзамене в последнее время чаще других прототипов.

Редактор — это прототип на работу с цепочками цифр или букв. Нам дают алгоритм и строку, содержащую некоторое количество знаков. Нужно узнать, какая строка получится после выполнения программы или посчитать количество символов в строке.

Если решать подобные задания аналитически, нужно искать закономерности изменения цепочки, чтобы получить ответ. Именно в этом и заключается сложность задания, ведь не все могут правильно найти нужную закономерность.

Робот — прототип на работу с клетчатой плоскостью и алгоритмом. Вам дают алгоритм и плоскость, содержащую 36 клеток. Нужно найти количество клеток, удовлетворяющее определенному условию. Сложность в том, что ученики начинают проверять все 36 клеток. Делать это не нужно, если проанализировать алгоритм из условия.

Чертежник — прототип на работу с алгоритмом, где исполнитель перемещается по координатной плоскости. Чаще всего в таких заданиях в алгоритме есть пропуски в командах. Нужно найти наибольшее количество повторений цикла. Сложностей обычно здесь не так много, основная — невнимательность при выполнении вычислений.

Самостоятельно подготовиться к ЕГЭ непросто. На то, чтобы разобраться со всеми темами, понадобится много времени. Но и это не решит проблему! Например, если вы запомнили какое-то решение из интернета, а оно оказалось неправильным, можно на пустом месте потерять баллы. Если хотите научиться решать все задания ЕГЭ по информатике, обратите внимание на онлайн-курсы MAXIMUM! Наши специалисты уже проанализировали сотни вариантов ЕГЭ и подготовили для вас вас максимально полезные занятия.

Приходите к нам на консультацию — вы сможете пройти диагностику по выбранным предметам ЕГЭ, поставить цели и составить стратегию подготовки, чтобы получить на экзамене высокие баллы. Все это абсолютно бесплатно!

Редактор — как решать?

Задания с прототипом «Редактор» можно решать как аналитически, так и с помощью компьютера, если у вас все хорошо с программированием. Мы рассмотрим с вами оба способа решения и убедимся, что они дают одинаковые ответы.

Пример 1 (Редактор)

Исполнитель Редактор получает на вход строку цифр и преобразовывает ее.

Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.

Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 88 идущих подряд цифр 4? В ответе запишите полученную строку.

Аналитическое решение

Алгоритм сначала заменяет в цепочке цифр все четверки на единицы. Потом начинает заменять назад единицы на четверки, но как только в цепочке образуются 3 четверки, алгоритм заменяет их на единицу. Порядок замены имеет значение при поиске ответа, поэтому его нужно обязательно учитывать. Также важно, что замена выполняется всегда в начале цепочки.

Сначала уберем по возможности все четверки из цепочки.

88 / 3 = 29 и 1 в остатке.

Получается, что из цепочки уйдет 29 блоков по 3 четверки и образуется 29 единиц, 1 четверка останется в цепочке в самом конце.

Теперь будем последовательно убирать единицы из цепочки.

29 “1” + 1 “4”

1 “4” + 27 “1” + 1 “4”

2 “4” + 25 “1” + 1 “4”

3 “4” + 23 “1” + 1 “4”

24 “1” + 1 “4”

Как только в цепочке появились 3 четверки, алгоритм заменил их назад на единицу. Суммарно из цепочки ушло 5 единиц. Это действие будет повторяться циклически, поэтому можно посчитать, сколько блоков по 5 единиц уйдет из цепочки.

29 / 5 = 5 и 4 в остатке

Получается, что в цепочке останется 4 единицы и 1 четверка.

11114 → 4114 → 444 → 1

В итоге в цепочке останется только единица.

Решение с помощью компьютера

В самом задании у нас уже написана программа. Остается перевести ее на конкретный язык программирования. Напишем программу на Python.

Она будет выглядеть следующим образом:

Создаем строку, содержащую 88 четверок. Далее запускаем цикл, который будет проверять, есть ли в строке 3 четверки или 2 единицы. Пропиваем условие и замену в строке. Важно в методе replace() указать третий параметр, который отмечает, сколько замен нужно выполнить. По умолчанию replace() сразу заменит все цифры в строке, а нам нужно выполнять замены по одной.

При запуске данной программы мы также получим ответ 1.

Ответ: 1

Пример 2 (Редактор)

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w).

Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

На вход приведенной ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 25 цифр 1, 45 цифр 2 и 10 цифр 3, расположенных в произвольном порядке.

Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы.

Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.

Аналитическое решение

Цифры 1, 2 и 3 находятся в строке в произвольном порядке. Все, что нам нужно сделать, чтобы получить ответ — это понять, сколько цифр образовалось в результате замен.

Каждую единицу алгоритм заменит на тройку. Если изначально было 25 единиц, то в результате замен образуется 25 троек, и их сумма будет равна 25 * 3 = 75.

Каждую двойку алгоритм заменит на 2 единицы. Изначально было 45 двоек, значит, в результате замен образуется 90 единиц. Их сумма будет равна 90.

Каждую тройку алгоритм заменит на 2 тройки. Было 10 троек, станет 20. Сумма составит 20 * 3 = 60.

Итоговая сумма всех цифр цепочки будет равна 75 + 90 + 60 = 225.

Решение с помощью компьютера

Перенесем алгоритм на язык программирования Python.

Получаем следующую программу:

Сначала мы задали строку, содержащую знак “>” и нужное количество всех цифр. Далее в цикле проверяем наличие знака “>” и цифр и выполняем замену. Как только программа вышла из цикла, считаем количество единиц, двоек и троек в строке — и находим сумму. При запуске программы также получается ответ 225.

В данном задании написание программы может занять больше времени, чем аналитическое решение. Поэтому всегда оценивайте временные затраты на написание кода.

Ответ: 225

Робот — как решать?

Второй прототип, который включает в себя 12 задание ЕГЭ по информатике — Робот. Этот прототип точно придётся решать аналитически, поэтому давайте разбираться, как сделать это с минимальными затратами времени.

Пример 3 (Робот)

Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа и 4 команды проверки условия.

Команды-приказы: вверх, вниз, влево, вправо

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.

Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится, и программа прервется.

Другие 4 команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно, снизу свободно, слева свободно, справа свободно

Цикл

ПОКА < условие > команда

Выполняется, пока условие истинно, иначе происходит переход на следующую строку.

Если РОБОТ начнет движение в сторону стены, то он разрушится, и программа прервется.

Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ уцелеет и остановится в той же клетке, с которой он начал движение?

НАЧАЛО

ПОКА < снизу свободно > вправо

ПОКА < справа свободно > вверх

ПОКА < сверху свободно > влево

ПОКА < слева свободно > вниз

КОНЕЦ

Решение

Чтобы не проверять все 36 клеток плоскости, нужно проанализировать программу. В алгоритме 4 цикла, но нам важен только последний. Робот будет выполнять действия и остановится только в той клетке плоскости, где слева есть стена, так как в последнем цикле мы проверяем именно это условие. Поэтому необходимо проверить только те клетки, где слева есть стена. В остальных клетках плоскости Робот просто не сможет остановиться, поэтому и начинать движение из них мы тоже не будем.

Проверяем по алгоритму 12 отмеченных клеток.

Из всех отмеченных клеток нам подойдет только клетка В5. Если начать движение из нее, Робот вернется в эту же точку. Остальные клетки не подойдут, так как Робот либо разобьется, либо остановится в другой клетке.

Ответ: 1

Прототип Чертежник — как решать?

Последний прототип, который составители включили в 12 задание ЕГЭ по информатике — это Чертежник. Здесь при решении важно правильно составить систему уравнений и найти наибольший/наименьший делитель двух чисел. Посмотрим, как это сделать.

Пример 4 (Чертежник)

Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b).

Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).

Цикл

ПОВТОРИ число РАЗ

последовательность команд

КОНЕЦ ПОВТОРИ

означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).

Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и величины смещения в первой из повторяемых команд неизвестны):

В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?

Решение

Чтобы решить это задание, необходимо обозначить неизвестными пропуски в алгоритме.

Далее составим систему уравнений. Нам известно, как перемещался Чертежник, и сказано, что он вернулся в начальную точку. Получается, его перемещение равно 0.

Теперь мы можем найти n — наибольшее количество повторений цикла. Число n должно быть делителем как 24, так и 16, то есть нам нужно найти НОД(24, 16). Он равен 8. Это и будет ответом к заданию.

Ответ: 8

Что нужно запомнить?

Если вам попадется Редактор, можете написать программу, которая найдет ответ вместо вас. Но всегда рассчитывайте, что будет рациональнее: аналитическое решение или компьютерное. Если останется время, можно проверить себя вторым способом.
Решая задание с Роботом, не нужно проверять все клетки — это долго. Проанализируйте алгоритм и проверяйте только те клетки, которые действительно могут подойти под условия.
Чтобы разобраться с Чертежником, внимательно составляйте систему уравнений. Ищите НОД, если нужно найти наибольшее количество повторений цикла.
Если в конце экзамена осталось время, вернитесь к заданию и проверьте его — ребята часто теряют баллы из-за невнимательности. Особенно рекомендую перепроверить Робота — решите его заново.

Теперь вы знаете, как решать 12 задание ЕГЭ по информатике! Обязательно прочитайте наш гайд по этому экзамену, если хотите разобраться с остальными темами и заданиями. Там вы найдете структуру экзамена, актуальные прототипы, тематические блоки и лайфхаки от наших преподавателей. Желаем удачи в подготовке 🙂

Источник