Егэ информатика деревья - Помощь в подготовке к экзаменам и поступлению

Урок посвящен тому, как решать 5 задание ЕГЭ по информатике

Содержание:

Объяснение 5 задания
- Исполнитель для возведения в квадрат, деления, умножения и сложения
- Проверка числовой последовательности на соответствие алгоритму
Разбор 5 задания
- Решение задания про алгоритм, который строит число R
- Решение заданий для темы Проверка числовой последовательности (Автомат)

5-е задание: «Анализ алгоритмов и исполнители»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 4 минуты.

Проверяемые элементы содержания: Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд

До ЕГЭ 2021 года — это было задание № 6 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Как и в других заданиях базового уровня сложности, источником ошибок служит недостаточная внимательность и отсутствие или поверхностность самостоятельной проверки полученного ответа»

ФГБНУ «Федеральный институт педагогических измерений»

Проверка числовой последовательности на соответствие алгоритму

для выполнения некоторых заданий необходимо повторить тему системы счисления;
максимальное значение суммы цифр десятичного числа — это 18, так как 9 + 9 = 18;
для проверки правильности переданного сообщения иногда вводится бит четности — дополнительный бит, которым дополняется двоичный код таким образом, чтобы в результате количество единиц стало четным: т.е. если в исходном сообщении количество единиц было четным, то добавляется 0, если нечетным — добавляется 1:

например: 
 3₁₀ = 11₂ 
после добавления бита четности: 110
----
 4₁₀ = 100₂ 
после добавления бита четности: 1001

добавление к двоичной записи числа нуль справа увеличивает число в 2 раза:

например:
111₂ - это 7₁₀
добавим 0 справа:
1110₂ - это 14₁₀

Теперь будем рассматривать конкретные типовые экзаменационные варианты по информатике с объяснением их решения.

Разбор 5 задания

Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:

Решение задания про алгоритм, который строит число R

5_11:

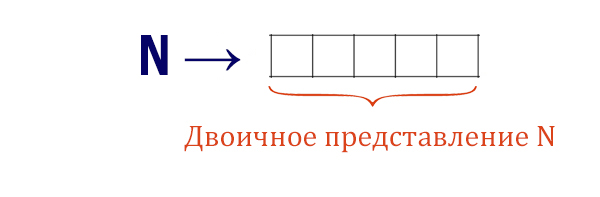
На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

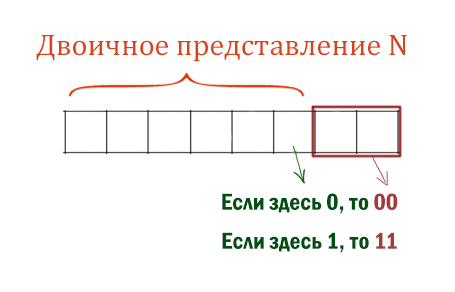
Строится двоичная запись числа 4N.
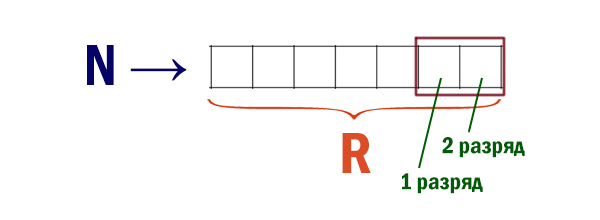
К этой записи дописываются справа еще два разряда по следующему правилу:

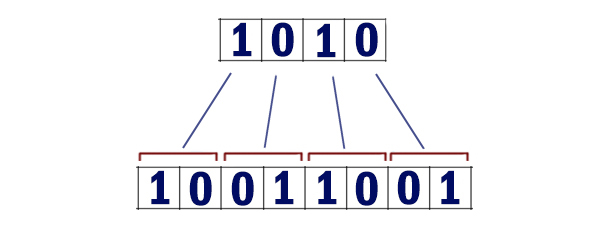
складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись является двоичной записью искомого числа R.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 129. В ответе это число запишите в десятичной системе счисления.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

Заметим, что после выполнения второго пункта задания, будут получаться только четные числа! Наименьшим возможным четным числом, превышающим 129, является число 130. С ним и будем работать.
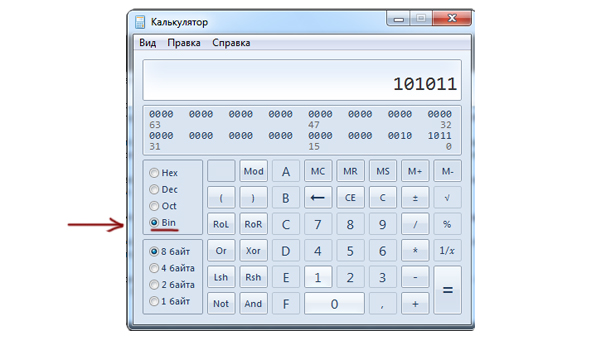
Переведем 130 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(130). Получим:

130₁₀ = 10000010₂

Это двоичное число получилось из исходного двоичного, после того как дважды был добавлен остаток от деления суммы цифр на 2. Т.е.:

в обратном порядке:
было 1000001 -> стало 10000010 
еще раз то же самое: 
было 100000 -> стало 1000001

Значит, необходимое нам двоичное число — это 100000.
Переведем 100000 в 10-ю систему. Для этого можно воспользоваться калькулятором, либо использовать интерпретатор Питона: int('100000',2).

100000₂ = 32₁₀

Так как по условию у нас 4*N, то 32 делим на 4 — > 8.

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := 4*n_;
    var ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряру (+ost)
    ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost;
    if n > 129 then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = 4*n_
    r = str(bin(n))
    r = r[2:]
    for i in range(2):
        if r.count('1') % 2 == 0:
            r+='0'
        else:
            r+='1'
 
    n = int(r, base=2)
    if n > 129:
        print(n_)
        break
    n_+=1

Результат: 8

Для более детального разбора предлагаем посмотреть видео теоретического решения данного 5 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_12: Демоверсия ЕГЭ 2018 информатика:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

Строится двоичная запись числа N.
К этой записи дописываются справа ещё два разряда по следующему правилу:
складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
Наименьшим возможным числом, превышающим 83, является число 84. С ним и будем работать.
Переведем 84 в двоичную систему счисления. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(84). Получим:

84 = 1010100

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так как оно нечетное. А мы имеем 0. Соответственно, это оно не подходит.
Возьмем следующее четное число — 86. Переведем его в двоичную систему счисления:

86 = 1010110

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так и есть: 101011. А затем добавляется 0: 1010110. Соответственно, оно подходит.

Результат: 86

Подробное решение данного 5 (раньше №6) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Видеорешение с программированием (PascalAnc.Net):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Аналитическое видеорешение:

📹 Видеорешение на RuTube здесь -> аналитическое решение

5_18:

Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3. Шаг 2 повторяется ещё два раза.
4. Результат переводится в десятичную систему счисления.

При каком наименьшем исходном числе N > 65 в результате работы алгоритма получится число, кратное 4?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
    for var i := 1 to 3 do 
    begin
      if bin(n).CountOf('1') = bin(n).CountOf('0') then // сравниваем
        if n mod 2 = 0 then // если четное, то в конце 0
          n := 2 * n  // добавляем разряд = 0
        else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
      else if bin(n).CountOf('1') > bin(n).CountOf('0') then
        n := 2 * n
      else
        n := 2 * n + 1
    end;
    if (n_ > 65) and (n mod 4 = 0) then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(3):
        if r.count('1') == r.count('0'):
            r+=r[-1] 
        elif r.count('1')>r.count('0'):
            r+='0'
        else:
            r+='1'
    n = int(r, base=2)
    if n_ > 65 and n % 4 == 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 79

5_19:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Число N переводим в двоичную запись.
2) Инвертируем все биты числа кроме первого.
3) Переводим в десятичную запись.
4) Складываем результат с исходным числом N.
Полученное число является искомым числом R.

Укажите наименьшее нечетное число N, для которого результат работы данного алгоритма больше 99. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(1,len(r)):
        if r[i]== '0':
            r=r[:i]+'1'+r[i+1:] 
        else:
            r=r[:i]+'0'+r[i+1:] 
    n = int(r, base=2)
    n+=n_
    if n > 99 and n_ % 2 != 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 65

5_13:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописываются справа еще два разряда по следующему правилу:
— если N делится нацело на 4, в конец числа (справа) дописывается сначала ноль, а затем еще один ноль;
— если N при делении на 4 дает в остатке 1, то в конец числа (справа) дописывается сначала ноль, а затем единица;
— если N при делении на 4 дает в остатке 2, то в конец числа (справа) дописывается сначала один, а затем ноль;
— если N при делении на 4 дает в остатке 3, в конец числа (справа) дописывается сначала один, а затем еще одна единица.

Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.

Укажите максимальное число R, которое меньше 100 и может являться результатом работы данного алгоритма. В ответе это число запишите

в десятичной системе счисления

Типовые задания для тренировки

✍ Решение:

Поскольку требуется найти наибольшее число, то возьмем наибольшее из возможных чисел, которые < 100 — это число 99. Переведем его в двоичную систему. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(99). Получим:

99 = 1100011₂

По алгоритму это число получилось путем добавления справа двух разрядов, значение которых зависит от исходного N:

1100011
  N

Т.е. в конце были добавлены две единицы — по алгоритму это значит, что исходное N должно в остатке при делении на 4 давать 3. Переведем найденное N в десятичную систему. Можно использовать калькулятор либо консоль пайтон: int('11000',2)

11000 = 24₁₀

24 делится на 4 нацело, т.е. в конце по алгоритму должны были добавиться два разряда — 00. У нас же в конце 11. Т.е. число 99 не подходит. Проверим следующее — 98.

98 = 1100010₂  : 10 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 10 
98 - не подходит

97 = 1100001₂ : 01 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 01 
97 - не подходит

96 = 1100000₂ : 00 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, у нас 00 - верно!
96 - подходит!

Результат: 96

Предлагаем посмотреть видео теоретического решения:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_14:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописывается (дублируется) последняя цифра.
3. Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4. К полученному результату дописывается ещё один бит чётности.

Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, большее 114, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

В постановке задания задано R > 114. R — это результат работы алгоритма. Для того, чтобы определить наименьшее возможно N, переведем сначала 114 в двоичную систему счисления и выделим в нем три добавленные по алгоритму цифры (перевод можно выполнить в консоли Питона: bin(114))

114 = 1110010₂

Проанализируем, как могло бы получиться двоичное число 114 (R) по алгоритму:

2. В полученное числе N = 1110 дублируется последняя цифра и получается 11100.
3. Поскольку число единиц (3) — нечетное, то справа добавляется 1: 111001.
4. Т.к. в полученном наборе цифр четное число единиц, то добавляем 0: 1110010

Поскольку из числа N = 1110 по алгоритму могла получиться только такая последовательность цифр (1110010), то для получения минимального R, но большего чем R = 114, увеличим в N = 1110 самый младший разряд на единицу и рассмотрим работу алгоритма с полученным числом:

1. N = 1110 + 1 = 1111

Работа по алгоритму:
2. 11111 - дублирование последней цифры.
3. 111111 - справа дописываем единицу, т.к. в полученном числе 5 единиц (нечетное)
4. 1111110 - дописываем ноль, т.к. в полученном числе четное число единиц.

Ответ нужно получить в десятичной системе счисления (для перевода можно воспользоваться интерпретатором Питона: int('1111110',2)):

min R = 1111110₂ = 126₁₀

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
          // дублирвание последней цифры
    if n mod 2 = 0 then // если четное, то в конце 0
      n := 2 * n  // добавляем разряд = 0
    else 
      n := 2 * n + 1; // иначе добавляем разряд = 1
    for var i := 1 to 2 do
    begin
      if bin(n).CountOf('1') mod 2 = 0 then
        n := 2 * n  // добавляем разряд = 0
     else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
    end;
    if n > 114 then
    begin
      println(n);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r  = str(bin(n)) # строковое значение
    r = r[2:] # убираем 0b
    r=r+r[-1]
    for i in range (2):
        if r.count('1') % 2 == 0:
            r = r+'0'
        else:
            r = r+'1'
    r = int(r,base = 2) # в 10-ю с.с.
    if r > 114:
        print(r)
        break
    n_+= 1

Результат: 126

5_17: Досрочный вариант 1 ЕГЭ по информатике 2020, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
— если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы.

Например, двоичная запись 1001 числа 9 будет преобразована в 100111.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.

Укажите минимальное число N, для которого результат работы алгоритма будет больше 134. В ответе это число запишите в десятичной системе счисления.

Ответ: 33

Видео -> теоретическое решение
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_16:

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:

1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из нового числа вычитается исходное, полученная разность выводится на экран.

Какое число нужно ввести в автомат, чтобы в результате получилось 45?

✍ Решение:

Результатом выполнения алгоритма является число 45. Алгоритм работает в двоичной системе счисления, поэтому переведем число:

45 = 00101101₂

Пронумеруем биты слева направо, начиная с единицы. Рассмотрим каждый бит отдельно, начиная с левого бита под номером 1.
1. Так как биты в уменьшаемом и вычитаемом должны быть различны, то единица в результате может получится только 1 - 0, с учетом, что у разряда с единицей заняли. То есть бит:

   .
_{_}  1 _ _ _ _ _ _ _    N инвертируемое
₌  0 _ _ _ _ _ _ _    N исходное
   0 0 1 0 1 1 0 1  = 45   результат

2. 1 - 0 не может в результате дать 0, так как у следующей слева единицы мы заняли. Значит, 0 - 1. Чтобы не получить единицу в ответе, необходимо у нуля тоже занять:

   . .
_{_}  1 0 _ _ _ _ _ _ 
₌  0 1 _ _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

3. 1 - 0 не может быть, так как у следующего слева нуля мы заняли.
Значит 0 - 1. То есть как раз чтобы получить единицу (10 - 1 = 1), занимаем у следующих слева разрядов:

   . .
_{_}  1 0 0 _ _ _ _ _ 
₌  0 1 1 _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

4. 0 - 1 не может быть. Значит, чтобы получить в результате ноль, берем 1 - 0, у единицы должно быть занято.

   . .   .
_{_}  1 0 0 1 _ _ _ _ 
₌  0 1 1 0 _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

5. 1 - 0 не может быть. Так как слева у единицы занято. Значит, чтобы получить в результате 1, берем 0 - 1:

   . .   .
_{_}  1 0 0 1 0 _ _ _ 
₌  0 1 1 0 1 _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

6. 0 - 1 не даст в ответе единицу, значит, имеем 1 - 0:

   . .   .
_{_}  1 0 0 1 0 1 _ _ 
₌  0 1 1 0 1 0 _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

7. 0 - 1 не может быть, значит, 1 - 0. Чтобы получить в результате 0, необходимо, чтобы у 1 было занято:

   . .   .     .
_{_}  1 0 0 1 0 1 1 _ 
₌  0 1 1 0 1 0 0 _ 
   0 0 1 0 1 1 0 1  = 45   результат

8. Чтобы получить 1, имеем 0 - 1:

   . .   .     .
_{_}  1 0 0 1 0 1 1 0 
₌  0 1 1 0 1 0 0 1
   0 0 1 0 1 1 0 1  = 45   результат

Полученное число (вычитаемое) и есть искомое N. Переведем его в 10-ю с.с.:

01101001 = 105₁₀

Ответ: 105

Смотрите теоретический разбор задания на видео и подписывайтесь на наш канал:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

Решение заданий для темы Проверка числовой последовательности (Автомат)

5_7:

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.

Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.

Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.

✍ Решение:

Результат: 2949

Процесс теоретического решения данного 5 задания представлен в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_8:

Автомат получает на вход четырехзначное число. По нему строится новое число по следующим правилам:

Складываются первая и вторая, затем вторая и третья, а далее третья и четвёртая цифры исходного числа.
Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).

Пример: Исходное число: 7531. Суммы: 7+5=12; 5+3=8; 3+1=4. Результат: 4812.

✍ Решение:

Число 2512 можно разбить на 2, 5, 12

Начнем с 12. Необходимо получить наибольшее число, поэтому разобьем на слагаемые с наибольшей цифрой — 9:

12=9+3

То есть первые две цифры:

 93**

В число 2 тройка не входит, значит забираем тройку из 5. Остается 2. А, значит, из состава 2 остается 0.

Получим число: 9320.

Результат: 9320

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_9:

Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам:

Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
Полученные два шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).

Пример: Исходные числа: 25, 66. Поразрядные суммы: 8, B. Результат: B8.

Какие из предложенных чисел могут быть результатом работы автомата?
Перечислите в алфавитном порядке буквы, соответствующие этим числам, без пробелов и знаков препинания.

Варианты:
A) 127
B) C6
C) BA
D) E3
E) D1

✍ Решение:

Проанализируем все варианты:

Вариант А. 127 не подходит, так как число 12 в шестнадцатеричной системе записывается как С.

Вариант В. С6 разбиваем на 12 и 6. Число может быть результатом работы автомата. Исходные числа, например, 35 и 37

Вариант С. BA разбиваем на 11 и 10. Число может быть результатом работы автомата. Исходные числа, например, 55 и 56

Вариант D. E3 разбиваем на 14 и 3. 14=6+8, но цифры большие 6 не принимает автомат. Не подходит.

Вариант E. D1 разбиваем на 13 и 1. 13=6+7, но цифры большие 6 не принимает автомат. Не подходит.

Результат: BC

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_10: Задание 5 ГВЭ 11 класс 2018 год ФИПИ

Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 7 (если в числе есть цифра больше 7, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.

1. Вычисляются два шестнадцатеричных числа: сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.

Определите, какое из предложенных чисел может быть результатом работы автомата.

Варианты:
1) AD
2) 64
3) CF
4) 811

✍ Решение:

Теоретическое решение 4 задания ГВЭ 11 класса смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_15:

Автомат получает на вход натуральное число X. По этому числу строится трёхзначное число Y по следующим правилам:
1. Первая цифра числа Y (разряд сотен) – остаток от деления X на 7.
2. Вторая цифра числа Y (разряд десятков) – остаток от деления X на 2.
3. Третья цифра числа Y (разряд единиц) – остаток от деления X на 5.

Пример. Исходное число: 55. Остаток от деления на 7 равен 6; остаток от деления на 2 равен 1; остаток от деления на 5 равен 0. Результат работы автомата: 610.

Сколько существует двузначных чисел, при обработке которого автомат выдаёт результат 312?

Типовые задания для тренировки

✍ Решение:

Обозначим каждую цифру числа Y согласно заданию:

Y =    3       1       2
^{x mod 7    x mod 2    x mod 5}

Сделаем выводы:

1. x mod 2 = 1 => значит, X — нечетное число
2. x mod 5 = 2 => значит, X — либо ?2, либо ?7.
3. раз x — нечетное, то из пред. пункта получаем x = ?7
4. x mod 7 = 3 => переберем все варианты:

97 - не подходит, 
87 - подходит (87 / 7 = 12, остаток = 3)
77 - не подходит,
67 - не подходит,
57 - не подходит,
47 - не подходит,
37 - не подходит,
27 - не подходит,
17 - подходит (17 / 7 = 2, остаток = 3)

Результат: 2

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 388 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите наибольшую длину цепочки символов, среди которых нет символов K и L, стоящих рядом.

Например, в тексте ABCAABAKLD самая длинная цепочка символов, удовлетворяющая условию  — ABCAABAK, её длина равна 8.

Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.

Задание 24

Источник: ЕГЭ−2021 по информатике 24.06.2021. Основная волна. Разные задачи

Элементами множеств А, P, Q являются натуральные числа, причём P = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21}, Q  =  {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение

((x ∈ P) → (x ∈ A)) ∨ (¬(x ∈ A) → ¬(x ∈ Q))

истинно ( т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10303

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальную длину цепочки вида XYZXYZXYZ… (составленной из фрагментов XYZ, последний фрагмент может быть неполным).

Задание 24

Текстовый файл состоит не более чем из 10⁶ символов A, B и C. Определите максимальную длину цепочки вида ABABAB… (составленной из фрагментов AB, последний фрагмент может быть неполным).

Задание 24

Текстовый файл состоит не более чем из 10⁶ символов L, D и R. Определите максимальную длину цепочки вида LDRLDRLDR… (составленной из фрагментов LDR, последний фрагмент может быть неполным).

Задание 24

Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.

Известно, что выражение

((x A) → (x P)) ∨ (¬(x Q) → ¬(x A))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наибольшее возможное количество элементов в множестве A.

Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q  =  {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.

Известно, что выражение

((x ∈ P) → (x ∈ A)) ∨ (¬(x ∈ A) → ¬(x ∈ Q))

истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых каждые два соседних различны.

Задание 24

Источник: Демонстрационная версия ЕГЭ−2021 по информатике

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня либо увеличить количество камней в куче в пять раз. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 75 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 68.

Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 68 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 67.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.

Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.

По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.

Входные данные.

Задание 26

В первой строке входного файла находятся два числа: S  — размер свободного места на диске (натуральное число, не превышающее 10 000) и N  — количество пользователей (натуральное число, не превышающее 3000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.

Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.

Пример входного файла:

100 4

При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар  — 50, поэтому ответ для приведённого примера:

2 50

Ответ:

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может

добавить в кучу один камень или

увеличить количество камней в куче в четыре раза.

Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или из 40 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче превышает 64. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 65 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 64.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

добавить в кучу один камень или

увеличить количество камней в куче в четыре раза.

В начальный момент в куче было S камней, 1 ≤ S ≤ 64.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

добавить в кучу один камень или

увеличить количество камней в куче в четыре раза.

В начальный момент в куче было S камней, 1 ≤ S ≤ 64.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

добавить в кучу один камень или

увеличить количество камней в куче в четыре раза.

Игра завершается в тот момент, когда количество камней в куче превышает 80. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 81 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 80.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

добавить в кучу один камень или

увеличить количество камней в куче в четыре раза.

В начальный момент в куче было S камней, 1 ≤ S ≤ 80.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

добавить в кучу один камень или

увеличить количество камней в куче в четыре раза.

В начальный момент в куче было S камней, 1 ≤ S ≤ 80.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы следующего стратегии игрока, которые не являются для него безусловно выигрышными.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 38. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 38 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 37.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может: добавить в кучу один камень (действие А) или утроить количество камней в куче, а затем добавить ещё один камень (действие Б). Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 31 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится более 31. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 32 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 31.

Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока  — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может: добавить в кучу один камень (действие А) или утроить количество камней в куче, а затем добавить ещё один камень (действие Б). Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 31 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится более 31. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 32 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 31.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может: добавить в кучу один камень (действие А) или утроить количество камней в куче, а затем убрать из кучи один камень (действие Б). Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 29 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится более 32. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 33 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 32.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может: добавить в кучу один камень (действие А) или утроить количество камней в куче, а затем убрать из кучи один камень (действие Б). Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 29 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится более 32. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 33 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 32.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в шесть раз. Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 60 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче превышает 365. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 366 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 365.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Игра завершается в тот момент, когда количество камней в куче превышает 361. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 362 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 360.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в 3 раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 30. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 30 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 29.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 65. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 65 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 64.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 47. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 47 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤46.

Найдите минимальное значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

— Петя не может выиграть за один ход;

— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.

Всего: 388 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Автор материалов — Лада Борисовна Есакова.

В простых играх можно найти выигрышную стратегию, расписав все возможные ходы игроков. Такая схема ходов называется деревом игры.

Все позиции в простых играх делятся на выигрышные и проигрышные.

Выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника. При этом алгоритм выбора очередного хода, приводящего к выигрышу, называется выигрышной стратегией. Считается, что игрок, обладающий выигрышной стратегией, не ошибается.

Проигрышная позиция – это такая позиция, при которой игрок, делающий первый ход, проигрывает независимо от выбора очередного хода.

Определение выигравшего игрока при заданной начальной позиции

Пример 1.

Два игрока играют в следующую игру. Перед ними лежат две кучи камней, в первой из которых 3, а во второй – 6 камней. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 24 камней. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигравшего игрока? Ответ обоснуйте.

Решение:

Для доказательства выигрыша нам достаточно привести неполное дерево игры, в котором рассмотрены все возможные ходы проигравшего игрока и одна любая, приводящая к выигрышу, последовательность ходов выигравшего игрока.

В приведенной таблице числа, разделенные запятой, соответствуют количеству камней в первой и второй кучах соответственно.

Выигрывает первый игрок. Своим первым ходом он должен добавить 2 камня в первую кучу.

Таблица содержит все возможные варианты ходов второго игрока и ходы, приводящие к победе первого.

Ответ: Выигрывает первый игрок. Своим первым ходом он должен добавить 2 камня в первую кучу.

Определение выигравшего игрока для различных начальных позиций

Пример 2.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. Например, при начальных позициях (6, 34), (7, 33), (9, 32) выигрышная стратегия есть у Пети. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.

Задание 1. Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание 2. Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание 3. Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.

Решение:

Задание 1. В начальных позициях (6, 33), (8, 32) выигрышная стратегия есть у Вани. При начальной позиции (6, 33) после первого хода Пети может получиться одна из следующих четырёх позиций: (7, 33), (12, 33), (6, 34), (6, 66). Каждая из этих позиций содержит менее 73 камней. При этом из любой из этих позиций Ваня может получить позицию, содержащую не менее 73 камней, удвоив количество камней во второй куче. Для позиции (8, 32) после первого хода Пети может получиться одна из следующих четырёх позиций: (9, 32), (16, 32), (8, 33), (8, 64). Каждая из этих позиций содержит менее 73 камней. При этом из любой из этих позиций Ваня может получить позицию, содержащую не менее 73 камней, удвоив количество камней во второй куче. Таким образом, Ваня при любом ходе Пети выигрывает своим первым ходом.

Задание 2. В начальных позициях (6, 32), (7, 32) и (8, 31) выигрышная стратегия есть у Пети. При начальной позиции (6, 32) он должен первым ходом получить позицию (6, 33), из начальных позиций (7, 32) и (8, 31) Петя после первого хода должен получить позицию (8, 32). Позиции (6, 33) и (8, 32) рассмотрены при разборе задания 1. В этих позициях выигрышная стратегия есть у игрока, который будет ходить вторым (теперь это Петя). Эта стратегия описана при разборе задания 1. Таким образом, Петя при любой игре Вани выигрывает своим вторым ходом.

Задание 3. В начальной позиции (7, 31) выигрышная стратегия есть у Вани. После первого хода Пети может возникнуть одна из четырёх позиций: (8, 31), (7, 32), (14, 31) и (7, 62). В позициях (14, 31) и (7, 62) Ваня может выиграть одним ходом, удвоив количество камней во второй куче. Позиции (8, 31) и (7, 32) были рассмотрены при разборе задания 2. В этих позициях у игрока, который должен сделать ход (теперь это Ваня), есть выигрышная стратегия. Эта стратегия описана при разборе задания 2. Таким образом, в зависимости от игры Пети Ваня выигрывает на первом или втором ходу.

Ответ:

Задание 1. Ваня выигрывает своим первым ходом.

Задание 2. Петя выигрывает своим вторым ходом.

Задание 3. Ваня выигрывает первым или вторым ходом.

Определение начальной позиции, обеспечивающей выигрыш того или иного игрока

Пример 3.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 48. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 48 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 47.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

1. а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.

б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход и (б) Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети.

3. Укажите значение S, при котором:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах — количество камней в куче.

Решение:

1. а) Петя может выиграть, если 16, …, 47. Во всех этих случаях достаточно утроить количество камней. При меньших значениях S за один ход нельзя получить кучу, в которой больше 47 камней.

б) Ваня может выиграть первым ходом (как бы ни играл Петя), если исходно в куче будет S = 15 камней. Тогда после первого хода Петя в куче будет 16 или 45 камней. В обоих случаях Ваня утраивает количество камней и выигрывает в один ход.

2. Возможные значения S: 5 и 14. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 15 камней: в первом случае утроением, во втором добавлением одного камня. Эта позиция разобрана в п. 16. В ней игрок, который будет ходить (теперь это Ваня), выиграть не может, а его противник (то есть Петя) следующим ходом выиграет.

3. Возможное значение S: 13. После первого хода Пети в куче будет 14 или 39 камней. Если в куче станет 39 камней. Ваня утроит количество камней н выиграет первым ходом. Ситуация, когда в куче 14 камней, уже разобрана в п. 2. В этой ситуации игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.

На рисунке изображено дерево игры. Выигрышные позиции подчеркнуты.

Ответ:

1. а) S от16 до 47

б) S = 15

2. S = 5 и S = 14

3. S = 13

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №26. Построение дерева игры. Поиск выигрышной стратегии» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

В теории графов , дерево – это неориентированный граф , в котором любые две вершины соединены ровно одним путем.

Корнем будет являться исходное число, а листами – число, в которое надо прийти.

Типовое задание:

У исполнителя есть команды:

Увеличить число

2. Увеличить число

Сколько существует программ, для которых при исходом числе a результатом является число b

Если строить полное дерево, оно получится очень большим. Рекомендуется применять методы динамического программирования: не считать вершины, которые уже были подсчитаны ранее.

Дополнительные ограничения мы применяем так:

Траектория вычислений содержит число n.
Разбиваем дерево решений на два дерева. Сначала находим количество программ из a в n, потом из n в a. Полученные числа перемножаем.
Траектория вычислений не содержит числа k.
В дереве не учитываем ветки, где ход идет в число k.

Рассмотрим примеры.

У исполнителя Утроитель две команды, которым присвоены номера:

1. прибавь 1

2. умножь на 3

Сколько есть программ, которые число 1 преобразуют в число 20?

У данного исполнителя две команды. Вторая более “весомая” чем первая, т.е. делает более “сильный” ход – больше увеличивает число. Поэтому будем отталкиваться от первой команды.

Само решение будет идти в два хода: сначала мы спускаемся вниз, до конечного числа. Затем обратный ход – поднимаемся до исходного числа с подсчетом количества программ.

Поскольку получить 20 из 1 прибавлением 1 можно за 19 команд, строить такое большое дерево не рационально. Из числа 7 мы уже не сможем получить 20 с помощью второй команды, мы его перепрыгнем. Значит, из 7 есть только один способ уйти в 20 — это прибавлять 1.

В дереве нижним индексом приписано количество способов получить число 20. Из всех чисел из диапазона 7..20 есть ровно один такой способ.

Из 6 мы можем попасть с помощью второй команды в число 18, которое как раз находится в этом диапазоне. Для подсчета количества программ для числа 6 мы будем складывать количество программ в числах, в которые можно попасть из 6

Продолжим подниматься вверх. Теперь мы будем опираться на уже подсчитанные значения. Такие числа выделены синим

Таким образом, получилось 12 программ.

Другой пример

Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 40 и при этом траектория вычислений содержит число 20 и не содержит число 8?

В данном задании присутствует сразу два ограничения.

Чтобы учесть, что траектория содержит число 20, мы разобьем решение на два этапа: сначала найдем количество программ из 2 в 20, затем из 20 в 40.

Второе ограничение – что нельзя в число 8 – проявит себя только в первой части решения.

При построении дерева по команде +1 мы упираемся в число 8, в которое попасть нельзя. При этом после него, т.е. из 9, мы можем все посчитать.

Все числа от 11 до 20 при умножении на 2 перепрыгивают 20, поэтому из каждого из них есть только один способ попасть в 20: это прибавлять 1.

Для числа 10 мы получаем 2 способа.

Продолжим обратный ход для чисел от 7 до 2

Для числа 7 мы получаем количество программ равное количеству программ для 14.

Второй раз нам 8 встречается при попытке умножить 4 на 2. Не забываем его проигнорировать.

В итоге, получилось 10 способов.

Теперь посчитаем способы из 20 в 40. На самом деле, их не очень много.

Итоговое количество способов это 10 * 2 = 20.

Таким образом, с помощью дерева мы получаем решение, в котором можно учесть все ограничения и относительно компактную запись. Я предпочитаю именно этот способ ручного решения, вместо табличного.

Источник

Задача 3.3.1. Два игрока, Петя и Валя, играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй — 3 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди, первый ход делает Петя. Ход состоит в том, что игрок или утраивает число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 20. Если в момент завершения игры общее число камней в двух кучах не менее 35, то выиграл Валя, в противном случае — Петя. Кто выигрывает при безошибочной игре обоих игроков? Укажите стратегию выигрывающего игрока — какой ход он должен сделать в каждой из позиций, которые могут ему встретиться при правильной игре. Докажите, что описанная стратегия — выигрышная.

Задача 3.3.2. Два игрока, Петя и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу три камня или увеличить количество камней в куче в два раза. Игра завершается тогда, когда количество камней в куче становится ≥ 33. В начальный момент в куче было S камней: 1 ≤ S ≤ 32.

Задача 3.3.3. Задание такое же, как и в предыдущей задаче. Ходы: +2, +3, *2.

Конец игры S ≤ 30. В начальный момент в куче было S камней: 1 ≤ S ≤ 29.

Задача 3.3.4. Два игрока, Петя и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может (1) добавить в кучу один камень или (2) увеличить количество камней в куче в два раза или (3) увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 30 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 36. Если при этом в куче оказалось не более 60 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 30 камней и Петя утроит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1 ≤ S ≤ 35.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при разной игре противника.

Выполните следующие задания.

1. а) При каких значениях числа S Петя может выиграть в один ход? Укажите все такие значения и соответствующие ходы Пети.

б) У кого из игроков есть выигрышная стратегия при S = 31, 32, 33, 34? Опишите выигрышные стратегии для этих случаев.

2. У кого из игроков есть выигрышная стратегия при S = 11? Опишите соответствующие выигрышные стратегии.

3. У кого из игроков есть выигрышная стратегия при S = 10? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах – количество камней в позиции.

Задача 3.3.5. Два игрока, Петя и Валя, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 55. Победителем считается игрок, сделавший последний ход, то есть этим ходом достигший 55 камней или более.

В начальный момент в первой куче было 5 камней, во второй 1 ≤ S ≤ 49

Задание 1. Укажите все значения S, при которых Петя может выиграть за один ход.

Задание 2. Сколько существует значений S, при которых Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом?

Задание 3. Укажите такое значение S, при котором одновременно выполняются два условия:

у Вали есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

у Вали нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Задача 3.3.6. Два игрока, Петя и Валя, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при разной игре противника. Например, при начальных позициях (6, 34), (7, 33), (9, 32) выигрышная стратегия есть у Пети. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.

Задание 1. Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание 2. Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание 3. Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.

Источник

Привет! В этой статье будут различные примеры решения задач из 5-ого задания ЕГЭ по информатике 2022.

Задание 5 решается не сложно, но, как всегда, нужно потренироваться решать подобные задачи, чтобы уверенно себя чувствовать на ЕГЭ по информатике 2022.

Рассмотрим классический пример.

Задача (Классическая)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R по следующему принципу.

1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
а) Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.
б) Над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Укажите минимальное число R, которое превышает 42 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.

Решение:

Решение на Python.

for n in range(1, 1000):
    s=format(n, 'b')
    s=s+str(s.count('1')%2)
    s=s+str(s.count('1')%2)
    r=int(s, 2)
    if r>42:
        print(r)

Программа будет выводить различные числа, но нас интересует самое маленькое. В ответе получается 46. Чтобы остановить поток чисел, можно нажать сочетание Ctrl + C.

В программе перебираем натуральные числа от 1 до 1000 с помощью цикла for. Каждое число подставляем в описанный алгоритм, в надежде получить в результате число r, удовлетворяющие условию задачи.

С помощью функции format переводим число n в двоичный вид. Получаем результат в виде строки s.

Чтобы найти сумму цифр получившейся двоичной записи, достаточно подсчитать количество единиц в строке s. Ведь только единицы в двоичной записи дают в сумму результат. Это можно сделать, применив функцию .count() к строке s.

Добавляем справа к строке s остаток от деления суммы цифр на 2. Остаток нужно превратить в строковый тип данных, чтобы «присоединить» к строке s справа.

Повторяем пункт Б, скопировав строку с пунктом А.

Чтобы обратно превратить строку двоичной записи в десятичное число, используем функцию int(), указав параметр 2.

В конце программы пропишем условие. Если r больше 42, то будем печатать эти значения. Остаётся выбрать минимальное число r.

Решение с помощью рассуждений.

Алгоритму на вход приходит обычное натуральное число N.

Это число преобразуется в двоичную запись (пункт 1).

Во втором пункте правил формирования нового числа сказано, что к числу, полученному в первом пункте, дописываются справа ещё два дополнительных разряда.

Про 1 дополнительный разряд указано в подпункте а): «Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.»

Если по простому сказать, то мы подсчитываем количество единиц в двоичном представлении числа N. Если количество единиц чётное, то пишем в 1 дополнительный разряд ноль, если нечётное, то пишем в 1 дополнительный разряд единицу.

Со вторым дополнительным разрядом происходит всё тоже самое, что и с первым разрядом, только когда подсчитываем количество единиц, мы так же подсчитываем и в 1-ом дополнительном разряде.

В вопросе просят указать входящее наименьшее число N, чтобы автомат выдал число R больше 42.

Возьмём наименьшее число, которое больше 42 (т.е. 43) и переведём его в двоичную систему. Это можно сделать с помощью стандартного windows калькулятора.

Вызываем калькулятор, выбираем Вид->Программист. Кликаем на отметку Dec (это означает, что мы находимся в десятичной системе) и набираем число 43. Затем кликаем на отметку Bin

Проверим число 101011₂. Может ли оно быть результатом работы нашего алгоритма?

Отделяем два дополнительных разряда справа. У нас, не считая двух дополнительных разрядов, количество единиц равно двум. Количество чётное, значит, в первом дополнительном разряде должен стоять 0. А у нас стоит 1.

Следовательно, число 101011₂ не может являться результатом работы алгоритма. И это число не подходит.

Проверим последующие числа. На калькуляторе можно прибавлять по 1 и получать следующее число в двоичной системе. Мы проверяем последовательно числа, чтобы не пропустить самое маленькое число.

Подходит число 101110₂. Количество единиц без двух дополнительных разрядов равно трём. Число нечётное. Значит, в первом дополнительном разряде должна стоять 1. В этом числе как раз стоит 1.

Количество единиц вместе с дополнительным разрядом равно 4. Число чётное, значит, во втором дополнительном разряде должен стоять 0. У нас и стоит во втором дополнительном разряде 0. Следовательно, число 101110₂ подходит по всем правилам и является наименьшим.

В десятичной системе это число 46.

Ответ: 46

Рассмотрим ещё одну интересную задачу для подготовки к ЕГЭ по информатике 2022.

Задача(Замена символов)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1) Строится двоичная запись числа N.
2) Каждый разряд этой записи заменяется двумя разрядами по следующему правилу: если в разряде стоит 0, то вместо него пишется 01; если в разряде стоит 1, то 1 заменяется на 10.
Например, двоичная запись 1010 числа 10 будет преобразована в 10011001.

Полученная таким образом запись (в ней в два раза больше разрядов, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите максимальное нечётное число R, меньшее 256, которое может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе.

Решение:

Решение на Python.

for n in range(1, 1000):
    s=format(n, 'b')
    s2=''
    for x in s:
        if x=='0':
            s2 = s2 + '01'
        else:
            s2 = s2 + '10'
    r=int(s2, 2)
    if r%2!=0 and r<256:
        print(r)

Получается наибольшее число 169.

Здесь после того, как построена строка, содержащая двоичную запись числа n, мы с помощью цикла for перебираем каждый символ и анализируем его.

Предварительно создав переменную s2 для новой строки, мы записываем в неё ’01’, если анализируемый символ является нулём, и ’10’, если единицей.

Добавляем заменённые символы справа к строке s2, таким образом, самый первые символы окажутся постепенно слева, как положено.

Далее, делаем, как в прошлой задаче.

Решение с помощью рассуждений.

В этой задаче в начале строится двоичная запись числа N.

Каждый разряд превращается в два разряда! Единица превращается в 10. Ноль превращается в 01. На рисунке показан пример, как будет преобразовано число 10 = 1010₂.

Оценим первое число, которое меньше, чем 256. Это число 255.

255 = 11111111₂

Здесь количество разрядов равно 8. Это чётное число, значит, такое количество разрядов может быть в результате работы алгоритма. Только чётное количество разрядов может получится в результате работы алгоритма.

В старших двух разрядах должны быть цифры 10, т.к. исходное число N не может начинаться с нуля.

В остальных парах попробуем написать 10, чтобы число было как можно больше.

Получается, что число 10101010₂ удовлетворяет всем правилам алгоритма, является наибольшим, и оно меньше 256.

Но важный момент, нас просили в ответ записать нечётное число.

В двоичной системе число, которое оканчивается на ноль, является чётным.

В двоичной системе число, которое оканчивается на единицу, является нечётным.

Чтобы число было нечётным, изменим последние разряды на 01.

10101001₂ = 169

Ответ: 169

Набираем обороты в решении 5 задания из ЕГЭ по информатике 2022.

Задача(Классическая, закрепление)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.

1) Строится двоичная запись числа N.

2) К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конце числа справа дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1101 будет преобразована в 110111.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа — результата работы данного алгоритма.

Укажите минимальное число N, для которого результат работы алгоритма будет больше 130. В ответе это число запишите в десятичной системе счисления.

Решение:

Решение на Python.

for n in range(1, 1000):
    s=format(n, 'b')
    
    if n%2==0:
        s=s+'00'
    else:
        s=s+'11'

    r=int(s, 2)
    if r>130:
        print(n)

Минимальное число n получается 33.

Обратите внимание, что здесь уже анализируем число n. Если оно чётное, то к переменной s справа дописываем ’00’, иначе ’11’. Так же в этой задаче мы печатаем в ответе само число n.

Решение с помощью рассуждений.

После перевода в двоичную систему исходного числа N, алгоритм строит новое число по следующему правилу:

Бордовым прямоугольником показаны дополнительные разряды.

Нужно найти минимальное число больше 130. Будем проверять последовательно числа, начиная с 131.

Подходит число 135. В ответе нужно указать число N. Отбросим от числа 10000111₂ дополнительные разряды и переведём в десятичную систему.

100001₂ = 33

Ответ: 33

Похожие задачи встречались в сборнике С. С. Крылова для подготовке к ЕГЭ по информатике.

Задача (Крепкий орешек)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Из числа N вычитается остаток от деления N на 4.

2. Строится двоичная запись полученного результата.

3. К это записи справа дописываются ещё два дополнительных разряда по следующему правилу:

а) Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.

б) Над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись является двоичной записью числа R.

Укажите наибольшее число N, для которого результат работы данного алгоритма меньше 47. В ответе число N укажите в десятичной системе.

Решение:

Первый способ. Число R должно быть меньше 47. Переведём число 46 в двоичную систему.

46 = 101110₂

Результат от второго пункта не должен превышать 1011₂. Если результат от второго пункта будет превышать это число, то после добавления дополнительных разрядов получится число R, которое не меньше 47.

Проверим число 1011₂ = 11. Видим, что это число не может являться результатом пункта 2.

11 + 0 = 11 (остаток при делении 11 на 4 равен 3) —
11 + 1 = 12 (остаток при делении 12 на 4 равен 0) —
11 + 2 = 13 (остаток при делении 13 на 4 равен 1) —
11 + 3 = 14 (остаток при делении 13 на 4 равен 2) —

Здесь мы перебираем все остатки при делении на 4. Чтобы число 11 могло являться результатом пункта 2, число, помеченное зелёным цветом, должно совпадать с числом, помеченное оранжевым цветом. Стоит заметить, что если в первой строчке не совпадают числа, то и в остальных они тоже не совпадут. Верно и обратное. Если в первой строчке совпадут числа, то и для остальных остатков тоже числа будут совпадать.

Найдём, число, для которого будут совпадать эти числа, отмеченные зелёным и оранжевым цветом.

10 + 0 = 10 (остаток при делении 10 на 4 равен 2) Не подходит

9 + 0 = 9 (остаток при делении 9 на 4 равен 1) Не подходит

8 + 0 = 8 (остаток при делении 8 на 4 равен 0) Подходит!

Значит, число 8 нам подходит. Число 8 — это результат работы алгоритма в первом пункте. Нас просят найти максимальное число. Следовательно, возьмём остаток 3, чтобы исходное число N было как можно больше. Тогда N будет:

N = 8 + 3 = 11

Ответ получается 11.

Второй способ. Решим задачу с помощью Python’а.

Перебираем числа от 100 до 1 с помощью цикла for. Третий параметр «-1» в цикле for говорит о том, что мы перебираем числа в обратном порядке.

for i in range(100, 0, -1):
    n = i
    n = n - n % 4 # Выполняем первый пункт
    n = format(n, 'b') # Переводим в двоичную систему
    n = n + str(n.count('1') % 2) # Подпункт a) третьего пункта
    n = n + str(n.count('1') % 2) # Подпункт б) третьего пункта
    r = int(n, 2) # Переводим из двоичной системы в десятичную
    if r < 47:
        print(i)

В этой программе запрограммировали алгоритм, который указан в задаче. Если значение переменной r (результат работы алгоритма) меньше 47, то печатаем это значение на экран. Первое распечатанное число и есть ответ к задаче.

В переменную n по очереди подставляются числа из нашего диапазона (100-1). Команда % находит остаток от деления.

Функция count, в данном случае, подсчитывает количество единиц в строке, которая находится в переменной n.

Ответ: 11

Задача (Демо 2023)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. Далее эта запись обрабатывается по следующему правилу:

a) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;

б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.

Полученная таким образом запись является двоичной записью искомого числа R.

Например, для исходного числа 6₁₀ = 110₂ результатом является число 1000₂ = 8₁₀, а для исходного числа 4₁₀ = 100₂ результатом является число 1101₂ = 13₁₀.

Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе запишите это число в десятичной системе счисления.

Решение:

for n in range(1, 1000):
    s=format(n, 'b')
    if s.count('1')%2==0:
        s = s + '0'
        s = '10' + s[2:]
    else:
        s = s + '1'
        s = '11' + s[2:]
    r=int(s, 2)

    if r>40:
        print(n)

Здесь мы пишем программу, как было написано в уроке видеокурса ЕГЭ по информатике. Но, действительно, встречается и новый приём. Нужно изменить левые символы нашей строки s. Это можно сделать с помощью такой конструкции s[2:]. Таким образом, мы берём всю строку, кроме двух первых символов. Например, s=’football’, то s[2:] будет обозначать ‘otball’.

Повторим основные идеи такого подхода при решении пятого задания из ЕГЭ по информатике с помощью программирования. Перебираем числа от 1 до 999 с помощью цикла for. В этом диапазоне надеемся найти наш ответ. С помощью команды format() превращаем число в строку уже в двоичной системе. Сумма цифр в строке зависит только от количества единиц. Нули ничего не дают в сумму. Поэтому применяем функцию .count. Дальше всё делаем, как написано в условии задачи. Команда int(s, 2) превращает строку в двоичной системе в число опять в десятичной системе счисления.

Ответ: 16

Задача (Решаем с помощью Python)

Автомат обрабатывает натуральное число N > 1 по следующему алгоритму:

1) Строится двоичная запись числа N.
2) В конец записи (справа) дописывается вторая справа цифра двоичной записи.
3) В конец записи (справа) дописывается вторая слева цифра двоичной записи.
4) Результат переводится в десятичную систему.

Пример. Дано число N = 11. Алгоритм работает следующим образом.
1) Двоичная запись числа N: 11 = 10112
2) Вторая справа цифра 1, новая запись 101112.
3) Вторая слева цифра 0, новая запись 1011102.
4) Десятичное значение полученного числа 46.

При каком наименьшем числе N в результате работы алгоритма получится R > 170? В ответе запишите это число в десятичной системе счисления.

Решение:

Напишем программу на Python.

for n in range(2, 1000):
    s=format(n, 'b')

    s=s+s[-2]
    s=s+s[1]

    r=int(s, 2)
    if r>170:
        print(n)

Получается наименьшее число 43. К последнему символу можем обратится s[-1], к предпоследнему s[-2]. Но счёт слева начинается с нуля. Первый символ это s[0], второй символ s[1] и т.д.

Обратите внимание, что перебирать числа n в этой задаче начинаем с 2.

Ответ: 43

Задача(Восьмибитное число)

(А.М. Кабанов) Автомат обрабатывает натуральное число N (1≤N≤255) по следующему алгоритму:

1) Строится восьмибитная двоичная запись числа N.
2) Удаляется последняя цифра двоичной записи.
3) Запись «переворачивается», то есть читается справа налево.
4) Полученное число переводится в десятичную запись и выводится на экран.

Каково наибольшее число, меньшее 100, которое после обработки автоматом не изменится?

Решение:

for n in range(1, 256):
    s=format(n, 'b')

    # делаем 8-ое число
    while(len(s)<8):
        s='0'+s

    s=s[:-1] #удаляется последняя цифра
    s=s[::-1] #число переворачивается

    r=int(s, 2)
    if n<100 and r==n:
        print(n)

Ответ получается 90.

Восьмибитное число имеет длину 8 символов. После того, как перевели число n в двоичный вид, с помощью цикла while добисываем нули слева к строке s, пока длина этой строки меньше 8.

Удалить последнюю цифру можно с помощью конструкции s[:-1]. Здесь мы оставляем все цифры, начиная с первой до последней (не включительно).

Перевернуть строку можно с помощью конструкции s[::-1].

Далее решаем как обычно. Число не изменится, если входное число n равно выходному числу r.

Ответ: 90

Разберём задачу, которая была в пробном варианте от 3.02.23 в одном из регионов.

Задача(Пробник 3.02.23)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. Далее эта запись обрабатывается по следующему правилу:

a) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 1;

б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11;

Полученная таким образом запись является двоичной записью искомого числа R.

Например, для исходного числа 6₁₀ = 110₂ результатом является число 100₂ = 4₁₀, а для исходного числа 4₁₀ = 100₂ результатом является число 1101₂ = 13₁₀.

Укажите число N, после обработки которого с помощью этого алгоритма получается наименьшее значение R, большее 49. В ответе запишите это число в десятичной системе.

Решение:

Напишем программу на языке Python.

for n in range(1, 1000):
    s=format(n, 'b')
    if s.count('1')%2==0:
        s = s + '0'
        s = '1' + s[2:]
    else:
        s = s + '1'
        s = '11' + s[2:]
    r=int(s, 2)
    if r>49:
        print(r, n)

Хитрость задачки заключается в том, что числа r возрастают неравномерно.

Нам необходимо глазами найти наименьше число r (первое число). Это число 50, а n для него равно 57.

При желании программу можно переписать следующим образом:

r_min=10**9
n_r_min = 0
for n in range(1, 1000):
    s=format(n, 'b')
    if s.count('1')%2==0:
        s = s + '0'
        s = '1' + s[2:]
    else:
        s = s + '1'
        s = '11' + s[2:]
    r=int(s, 2)
    if r > 49:
         if r < r_min:
            r_min=r
            n_r_min=n

print(n_r_min)

Здесь ищется минимальное число r автоматически и для него запоминается значение n, которое пойдет в ответ.

Ответ: 57

Боковой вариант 5-ого задания из ЕГЭ по информатике.

Задача (Лучше знать)

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам:

1. Перемножаются первая и вторая, а также третья и четвёртая цифры исходного числа.

2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 2465. Суммы: 2 * 4 = 8; 6 * 5 = 30. Результат: 308. Укажите наибольшее число, в результате обработки которого автомат выдаст число 124.

Решение:

В подобных задачах из ЕГЭ по информатике нумерация происходит начиная со старшего разряда.

Первое правило можно представить следующим образом:

Второе правило заключается в том, что мы «соединяем» два числа, полученных в первом пункте, причём, сначала идёт большее число, а затем меньшее.

Проанализируем число 124.

Чтобы четырёхзначное число было наибольшим, выгодно, чтобы в старшем разряде стояла 9. Но, не у числа 12, не у числа 4, нет такого делителя. Какой наибольший делитель мы можем получить? Это число 6. Число 6 является делителем 12-ти. Значит, первая цифра будет 6, а вторая цифра будет 2 (6*2=12).

Рассмотрим второе число 4. Третий разряд тоже желательно сделать побольше. Значит, в четвёртый разряд поставим 4, а в младший разряд 1 (4*1=4).

Ответ получается 6241.

Ответ: 6241

Счастливых экзаменов! Видеоролик можете посмотреть ниже!

Второе задание с заменой символом пытался сделать через команду .replace, в консоль выводились почему-то только четные числа, можете обьяснить что не так?

for unk in range(1, 1000):
unk = (bin(unk)[2:])

if «1» in unk:
unk = unk.replace(«1», «10»)
elif «0» in unk:
unk = unk.replace(«0», «01»)

R = int(unk, 2)
# if R < 256 and R % 2 != 0:
print(R)

Я так понимаю, что вы заменяете либо единицы, либо нули. А нужно в одной записи заменить и единицы, и нули. Через реплейс тоже можно решить. s=s.replace(‘1’, ‘2’) s=s.replace(‘0′, ’01’) s=s.replace(‘2′, ’10’). Т.е. мы превращаем 1 в символ, которого точно нет в строке, потом делаем замены.

Источник