Задания
Версия для печати и копирования в MS Word
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, И, К, Л, О, С. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 001, И — 01, С — 10. Какое наименьшее количество двоичных знаков потребуется для кодирования слова КОЛОБОК?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Спрятать решение
Решение.
Букву О закодируем кодовым словом 000, поскольку буква О повторяется в слове КОЛОБОК 3 раза. Букву К закодируем кодовым словом 110, поскольку буква К повторяется в слове КОЛОБОК 2 раза. Буквы Б и Л закодируем кодовыми словами 1110 и 1111 соответственно. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова КОЛОБОК равно 3 + 3 + 4 + 3 + 4 + 3 + 3 = 23.
Ответ: 23.
Привет! Сегодня узнаем, как решать 4 задание из ЕГЭ по информатике нового формата 2021.
Четвёртое задание из ЕГЭ по информатике раскрывает тему кодирование информации. Одним из центральных приёмов при решении задач подобного типа является построение дерева Фано. Рассмотрим на примерах этот метод.
Задача (стандартная)
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0. Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наименьшему возможному двоичному числу.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование
Решение:
Т.к. код букв должен удовлетворять условию Фано (т.е. однозначно декодироваться), то
расположим буквы, которые уже имеют код (A, B, C), на Дереве Фано.
Дерево Фано для двоичного кодирования начинается с двух направлений, которые означают 0(ноль) и 1(единицу) (цифры двоичного кодирования).
От каждого направления можно также рисовать только два направления: 0(ноль) и 1(единицу) и т.д. Для удобства будем рисовать 1(единицу) только вправо, а 0(ноль) только влево.
Получается структура похожая на дерево!
В конце каждой ветки можно располагать букву, которую мы хотим закодировать, но если мы расположили букву, от этой ветки больше нельзя делать новых ответвлений.
Такой подход позволяет однозначно декодировать сообщение, состоящее из этих букв.
Буква C заблокировала левую ветку, поэтому будем работать с правой частью нашего дерева.
Если мы расположим какую-нибудь букву на оставшуюся ветку (100), то эта ветка заблокируется, и нам некуда будет писать остальные 2 буквы. Поэтому продолжаем ветку (100) дальше.
Теперь свободно уже две ветки, а нам нужно закодировать ещё три буквы. Поэтому должны ещё раз продолжить дерево от какой-нибудь ветки.
Но уже видно, что букве F будет правильно присвоить код 1000, т.к. нам в условии сказано, что код буквы F должен соответствовать наименьшему возможному двоичному числу. Как расположить буквы D и E в данной задаче не принципиально.
Ответ: 1000.
Ещё один важный тип задания 4 из ЕГЭ по информатике нового формата 2021.
Задача (стандартная)
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, И, К, Л, С, Ц. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 00, К — 010, Л — 111. Какое наименьшее количество двоичных знаков потребуется для кодирования слова АБСЦИССА?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение:
Коды букв должны удовлетворять условию Фано. Некоторые буквы уже имеют заданные коды (Б, К, Л). Нам нужно, чтобы слово АБСЦИССА имело как можно меньше двоичных знаков. Заметим, что буква C встречается три раза, а буква A два раза, значит, этим буквам стараемся присвоить как можно меньшую длину!
Отметим на дереве Фано уже известные буквы (Б, К, Л).
У нас осталось 4 (четыре) буквы, а свободных веток 3(три), поэтому мы должны продолжить дерево. но какую ветку продолжить ?
1 вариант
Если продолжить линию 1-0, то получится такая картина :
Теперь получились 4(четыре) свободные ветки равной длины (3(трём) двоичным символам). Т.к. ветки равной длины, то не важно на какую ветку какую букву расположим.
Посчитаем общую длину слова АБСЦИССА.
3 + 2 + 3 + 3 + 3 + 3 + 3 + 3 = 23.
2 вариант
Продлим линию 1-1-0 (можно и 0-1-1, не принципиально, т.к. эти ветки имеют одинаковую длину.), то получится:
С мы присваиваем 1-0, т.к. это буква повторяется в сообщении самое большое количество раз, значит, ей присваиваем самый маленький код, чтобы всё сообщение имело наименьшую длину.
Из этих же соображений букве А присваиваем код из трёх двоичных символов 0-1-1.
Подсчитаем общее количество символов в сообщении.
3 + 2 + 2 + 4 + 4 + 2 + 2 + 3 = 22
Длина получилась меньше, чем в первом варианте. Других вариантов нет, поэтому ответ будет 22.
Ответ: 22.
Задача (не сложная)
Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется неравномерный (по длине) код: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в восьмеричный вид.
Решение:
В этой задаче ничего не сказано про условие Фано. Здесь уже все буквы закодированы, осталось написать сам код.
Задача сводится к переводу из двоичной системы в восьмеричную систему. На эту тему был урок на моём сайте.
Ответ: 151646.
На этом всё! Увидимся на следующих занятиях по подготовке к ЕГЭ по информатике.
Этого не знаю. Это просто примерные задачи, которые наиболее часто попадаются в книжках и на сайтах по подготовке к ЕГЭ по информатике.
Здравствуйте, а вот такое задание ПО КАНАЛУ СВЯЗИ ПЕРЕДАЮТСЯ СООБЩЕНИЯ, СОДЕРЖАЩИЕ ТОЛЬКО 4 БУКВЫ : А, Б, В, Г; ДЛЯ ПЕРЕДАЧИ ИСП. ДВОИЧНЫЙ КОД, ДОПУСКАЮЩИЙ ОДНОЗНАЧНОЕ ДЕКОДИРОВАНИЕ. ДЛЯ БУКВ А, Б, В ИСПОЛЬЗУЮТСЯ ТАКИЕ КОДОВЫЕ СЛОВА: А:00011, Б:1001, В: 01100.
УКАЖИТЕ КРАТЧАЙШЕЕ КОДОВОЕ СЛОВО ДЛЯ БУКВЫ Г, ПРИ КОТОРОМ КОД БУДЕТ ДОПУСКАТЬ ОДНОЗНАЧНОЕ ДЕКОДИРОВАНИЕ. ЕСЛИ ТАКИХ КОДОВ НЕСКОЛЬКО, УКАЖИТЕ КОД С НАИМЕНЬШИМ ЧИСЛОВЫМ ЗНАЧЕНИЕМ. В ответе указано число 10. Не могу понять почему. У меня 11.
Здравствуйте, а вот такое задание ПО КАНАЛУ СВЯЗИ ПЕРЕДАЮТСЯ СООБЩЕНИЯ, СОДЕРЖАЩИЕ ТОЛЬКО 4 БУКВЫ : А, Б, В, Г; ДЛЯ ПЕРЕДАЧИ ИСП. ДВОИЧНЫЙ КОД, ДОПУСКАЮЩИЙ ОДНОЗНАЧНОЕ ДЕКОДИРОВАНИЕ. ДЛЯ БУКВ А, Б, В ИСПОЛЬЗУЮТСЯ ТАКИЕ КОДОВЫЕ СЛОВА: А:00011, Б:1001, В: 01100.
УКАЖИТЕ КРАТЧАЙШЕЕ КОДОВОЕ СЛОВО ДЛЯ БУКВЫ Г, ПРИ КОТОРОМ КОД БУДЕТ ДОПУСКАТЬ ОДНОЗНАЧНОЕ ДЕКОДИРОВАНИЕ. ЕСЛИ ТАКИХ КОДОВ НЕСКОЛЬКО, УКАЖИТЕ КОД С НАИМЕНЬШИМ ЧИСЛОВЫМ ЗНАЧЕНИЕМ. В ответе указано число 10. Не могу понять почему. У меня 11.
Ольга Владимировна Сорокина, как я понимаю, суть задания в том, что здесь действует либо прямое, либо обратное условие Фано. (Примечание. Условие Фано означает, что соблюдается одно из двух условий.
Либо никакое кодовое слово не является началом другого кодового слова,
либо никакое кодовое слово не является окончанием другого кодового слова.
Это обеспечивает возможность однозначной расшифровки закодированных
сообщений.)
Поэтому 10 является ответом, так как ни один код для букв не оканчивается на 10 (срабатывает обратное условие Фано)
1. По каналу связи передаются сообщения, содержащие только десять букв: А, Б, В, Г, Д, Е, И, К, Л, М. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| Буква | Кодовое слово |
| А | 00 |
| Б | 010 |
| В | 111 |
| Г | 1100 |
| Д | 1011 |
| Буква | Кодовое слово |
| Е | 011 |
| И | 1010 |
| К | 1001 |
| Л | |
| М | 1000 |
Укажите кратчайшее кодовое слово для буквы Л. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения.
0 — нельзя, А, Б и Е начинаются с 0.
1 — нельзя, В, Г, Д, И, К и М начинаются с 1.
00 — нельзя из-за А.
01 — нельзя из-за Б и Е.
10 — нельзя из-за Д, И, К и М.
11 — нельзя из-за В и Г.
000 — нельзя из-за А.
001 — нельзя из-за А.
010 — нельзя из-за Б.
011 — нельзя из-за Е.
100 — нельзя из-за М и К.
101 — нельзя из-за Д и И.
110 — нельзя из-за Г.
111 — нельзя из-за В.
0000 — нельзя из-за А.
0001 — нельзя из-за А.
0010 — нельзя из-за А.
0011 — нельзя из-за А.
0100 — нельзя из-за Б.
0101 — нельзя из-за Б.
0110 — нельзя из-за Е.
0111 — нельзя из-за Е.
1000 — нельзя из-за М.
1001 — нельзя из-за К.
1010 — нельзя из-за И.
1011 — нельзя из-за Д.
1100 — нельзя из-за Г.
1101 — можно использовать.
1110 — нельзя из-за В.
1111 — нельзя из-за В.
Таким образом, кодовым словом для буквы Л, удовлетворяющим условию Фано, является 1101.
Ответ: 1101.
2. Для кодирования букв А, В, С, D используются четырехразрядные последовательные двоичные числа, начинающиеся с 1 (от 1001 до 1100 соответственно). Закодируйте таким образом последовательность символов CADB и запишите результат в шестнадцатеричном коде.
Решение.
Закодируем последовательность букв: CADB — 1011100111001010. Теперь разобьём это представление на четвёрки справа налево и переведём полученный набор чисел сначала в десятичный код, затем в шестнадцатеричный:
1011 1001 1100 1010 — 11 9 12 10 — B9CA.
3. Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
| a | b | c | d | e |
| 100 | 110 | 011 | 01 | 10 |
Какой набор букв закодирован двоичной строкой 1000110110110? Все буквы в последовательности — разные.
Решение.
Мы видим, что условия Фано и обратное условие Фано не выполняются, значит, код можно раскодировать неоднозначно.
Будем пробовать разные варианты, отбрасывая те, в которых получаются повторяющиеся буквы:
1) 100 011 01 10 110
Первая буква определяется однозначно, её код 100: a.
Пусть вторая буква — с, тогда следующая буква — d, потом — e и b.
Такой вариант удовлетворет условию, значит, окончательно получили ответ: acdeb.
4. По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, Н, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Г — 110, И — 01, Т — 10. Какое наименьшее количество двоичных знаков потребуется для кодирования слова БАРАБАН?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Букву А закодируем кодовым словом 000, поскольку буква А повторяется в слове БАРАБАН 3 раза. Букву Б закодируем кодовым словом 001, поскольку буква Б повторяется в слове БАРАБАН 2 раза. Буквы Р и Н закодируем кодовыми словами 1110 и 1111 соответственно. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова БАРАБАН равно 3 + 3 + 4 + 3 + 3 + 3 + 4 = 23.
Ответ: 23.
5. По каналу связи передаются сообщения, содержащие только шесть букв: А, Б, В, К, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б – 010, Т – 011. Какое наименьшее количество двоичных знаков потребуется для кодирования слова КАТАРАКТА?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Буква А повторяется в слове КАТАРАКТА чаще всего, поэтому закодируем её кодовым словом 1. Следующую букву невозможно закодировать кодовым словом длиной 2, так как будет невозможно закодировать другие буквы так, чтобы выполнялось условие Фано. Букву К закодируем кодовым словом длиной 3, например, 000. Буквы Р и В закодируем кодовыми словами 0011 и 0010. Тогда количество двоичных знаков, которые потребуются для кодирования слова КАТАРАКТА равно 4 · 1 + 2 · 3 + 2 · 3 + 4 = 20.
Ответ: 20.
6. Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.
Решение.
Сначала следует представить данные в условии числа в двоичном коде:
| О | В | Д | П | А |
| 0 | 1 | 2 | 3 | 4 |
| 00 | 01 | 10 | 11 | 100 |
Затем закодировать последовательность букв: ВОДОПАД — 010010001110010. Теперь разобьём это представление на тройки справа налево и переведём полученный набор чисел в десятичный код, затем в восьмеричный (восьмеричное предствление совпадает с десятичным при разбиении тройками)
010 010 001 110 010 — 22162.
7. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код:
А — 0; Б — 100; В — 1010; Г — 111; Д — 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать?
1) для буквы В — 101
2) это невозможно
3) для буквы В — 010
4) для буквы Б — 10
Решение.
Для однозначного декодирования получившееся в результате сокращения кодовое слово не должно быть началом никакого другого. Первый вариант ответа подходит. Третий вариант не подходит, поскольку код буквы А является началом кода буквы В. Четвёртый вариант ответа не подходит, т. к. в таком случае код буквы Б является началом кода буквы В.
Правильный ответ указан под номером: 1.
8. По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 011, Г — 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Следующая буква должна кодироваться как 11, поскольку 10 мы взять не можем. 100 взять не можем из-за Г, значит, следующая буква должна быть закодирована кодом 101. Следующая буква должна кодироваться как 000, поскольку 00 взять не можем, иначе не останется кодовых слов для оставшейся буквы, которые удовлетворяют условию Фано. Значит, последняя буква будет кодироваться как 001. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова МАГИЯ равно 2 + 3 + 3 + 3 + 3 = 14.
Ответ: 14.
9. Для кодирования букв Р, И, К, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ПАПРИКА таким способом и результат запишите шестнадцатеричным кодом.
Решение.
Сначала следует представить данные в условии числа в двоичном коде:
| Р | И | К | П | А |
| 0 | 1 | 2 | 3 | 4 |
| 00 | 01 | 10 | 11 | 100 |
Затем закодировать последовательность букв: ПАПРИКА — 1110011000110100. Теперь разобьём это представление на четвёрки справа налево и переведём полученный набор чисел сначала в десятичный код, затем в шестнадцатеричный:
1110 0110 0011 0100 — 14 6 3 4 — E634.
10. По каналу связи с помощью равномерного двоичного кода передаются сообщения, содержащие только 4 буквы: К, Л, М, Н; для кодировки букв используются кодовые слова длины 5. При этом для набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Для кодирования букв К, Л, М используются 5-битовые кодовые слова: К: 11100, Л: 01111, М: 00001. 5-битовый код для буквы Н начинается с 1 и заканчивается 0. Определите кодовое слово для буквы Н.
Решение.
Заметим, что буква K также начинается на 1 и заканчивается на 0, значит, для выполнения условия нужно, чтобы все остальные 3 бита в K и Н отличались. Поскольку в К эти три бита — 110, то в Н они будут 001, соответственно. Тогда Н: 10010.
Ответ: 10010.
11. По каналу связи передаются сообщения, содержащие только семь букв: А, Б, И, К, Л, О, С. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 001, И — 01, С — 10. Какое наименьшее количество двоичных знаков потребуется для кодирования слова КОЛОБОК?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
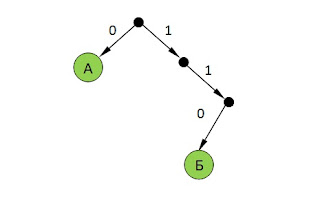
Букву О закодируем кодовым словом 000, поскольку буква О повторяется в слове КОЛОБОК 3 раза. Букву К закодируем кодовым словом 110, поскольку буква К повторяется в слове КОЛОБОК 2 раза. Буквы Б и Л закодируем кодовыми словами 1110 и 1111 соответственно. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова КОЛОБОК равно 3 + 3 + 4 + 3 + 4 + 3 + 3 = 23.
Ответ: 23.
12. Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110). Определите, какое число передавалось по каналу в виде 01100010100100100110.
Решение.
Из примера видно, что 2 знака кодируются 10 двоичными разрядами (битами), на каждую цифру отводится 5 бит. В условии сказано, что каждая цифра записывается кодом длиной 4 знака, значит, пятую цифру можно отбросить.
Разобьём двоичную запись на группы по 5 знаков: 01100 01010 01001 00110. Отбрасываем послеюднюю цифру в каждой пятёрке и переводим в десятичную запись:
0110 0101 0100 0011 — 6 5 4 3.
13. По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В используются такие кодовые слова: А — 0; Б — 110; В — 101.
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наибольшим числовым значением.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения:
0 — нельзя из-за А.
1 — нельзя, буквы Б, В начинаются с 1.
01 — нельзя из-за А.
10 — нельзя из-за В.
11 — нельзя из-за Б.
000 — нельзя из-за А.
001 — нельзя из-за А.
100 — можно использовать.
101 — нельзя из-за В.
110 — нельзя из-за Б.
111 — можно использовать.
Таким образом, поскольку, если кратчайших кодов несколько, необходимо указать код с наибольшим числовым значением, кратчайшее кодовое слово для буквы Г — 111.
Ответ: 111.
14. Для кодирования букв Д, X, Р, О, В решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ХОРОВОД таким способом и результат запишите восьмеричным кодом.
Решение.
Сначала следует представить данные в условии числа в двоичном коде:
| Д | Х | Р | О | В |
| 0 | 1 | 2 | 3 | 4 |
| 00 | 01 | 10 | 11 | 100 |
Затем закодировать последовательность букв: ХОРОВОД — 011110111001100. Теперь разобьём это представление на тройки справа налево и переведём полученный набор чисел в десятичный код, затем в восьмеричный (восьмеричное предствление совпадает с десятичным при разбиении тройками)
011 110 111 001 100 — 36714.
15. По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 011, И — 10. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ГРАММ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Для трёх букв кодовые слова уже известны, осталось подобрать для оставшихся четырёх букв такие кодовые слова, которые обеспечат наименьшее количество двоичных знаков для кодирования слова ГРАММ.
Закодируем букву М кодовым словом 00, поскольку буква М повторяется в слове ГРАММ два раза. Для буквы Г возьмём кодовое слово 110. Кодовое слово 111 взять не можем, поскольку для остальных букв не останется кодовых слов, удовлетворяющих условию Фано. Оставшиеся две буквы закодируем кодовыми словами длины 4.
Таким образом, наименьшее количество двоичных знаков, которые потребуются для кодирования слова ГРАММ, равно 3 + 4 + 3 + 2 + 2 = 14.
Ответ: 14.
16. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А — 10; Б — 11; В — 000; Г — 001; Д — 010. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать?
1) это невозможно
2) для буквы А — 0
3) для буквы В — 00
4) для буквы Д — 01
Решение.
Для однозначного декодирования получившееся в результате сокращения кодовое слово не должно быть началом никакого другого. Второй вариант ответа не подходит, поскольку код буквы А является началом кода буквы В. Третий вариант не подходит, поскольку код буквы В является началом кода буквы Г. Четвёртый вариант ответа подходит.
Правильный ответ указан под номером: 4.
17. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение.
Поскольку все однозначные и двузначные слова не подходят по условию Фано, нужно найти трехзначное слово, которое было бы максимально и удовлетряло условию. Так как 111, 101 и 110 нарушают условие Фано, то искомое слово — 010.
Ответ: 010.
Примечание.
Заметим, что двузначное кодовое слово 01 не подходит, поскольку при его использовании нельзя подобрать кодовое слово для буквы Е.
———-
Дублирует задание 13481.
18. Для кодирования сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:
Закодируйте таким образом последовательность символов ВГАГБВ и запишите результат в шестнадцатеричном коде.
Решение.
Закодируем последовательность букв: ВГАГБВ — 0100110001111010. Теперь разобьём это представление на четвёрки справа налево и переведём полученный набор чисел сначала в десятичный код, затем в шестнадцатеричный:
0100 1100 0111 1010 — 4 12 7 10 — 4С7А.
19. По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Д, Е, И, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 110, Б — 01, И — 000. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ВВЕДЕНИЕ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Букву Е закодируем кодовым словом 10, поскольку буква Е повторяется в слове ВВЕДЕНИЕ 3 раза. Букву В закодируем кодовым словом 111, поскольку буква В повторяется в слове ВВЕДЕНИЕ 2 раза. Буквы Д и Н закодируем кодовыми словами 0010 и 0011 соответственно. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова ВВЕДЕНИЕ равно 3 + 3 + 2 + 4 + 2 + 4 + 3 + 2 = 23.
Ответ: 23.
20. Для кодирования некоторой последовательности, состоящей из букв А, Б, В и Г, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Для букв А, Б, В используются такие кодовые слова: А — 010, Б — 1, В — 011.
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение.
Код не может начинаться с 1, так как Б − 1.
0 не подойдёт, так как А и В начинаются с 0.
00 же не включает в себя никакой из кодов и также не является подстрокой какого-либо кода, поэтому подойдёт.
21. По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 00, Г — 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Следующую буква должна кодироваться как 011, поскольку 01 мы взять не можем, иначе код для буквы А не будет удовлетворять условию Фано. 10 из-за Г взять не можем, тогда следующая буква будет кодироваться как 100. Следующая буква должна кодироваться как 110, поскольку 11 взять не можем, иначе не останется кодовых слов для оставшейся буквы, которые удовлетворяют условию Фано. Значит, последняя буква будет кодироваться как 111. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова МАГИЯ равно
3 + 3 + 3 + 3 + 3 = 15.
Ответ: 15.
22. Для кодирования букв О, К, Г, Д, Р решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ГОРОДОК таким способом и результат запишите восьмеричным кодом.
Решение.
Сначала следует представить данные в условии числа в двоичном коде:
| О | К | Г | Д | Р |
| 0 | 1 | 2 | 3 | 4 |
| 00 | 01 | 10 | 11 | 100 |
Затем закодировать последовательность букв: ГОРОДОК — 100010000110001. Теперь разобьём это представление на тройки справа налево и переведём полученный набор чисел в десятичный код, затем в восьмеричный (восьмеричное представление совпадает с десятичным при разбиении тройками)
100 010 000 110 001 — 42061.
23. Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
| a | b | c | d | e |
| 000 | 110 | 01 | 001 | 10 |
Какой набор букв закодирован двоичной строкой 1100000100110?
Решение.
Мы видим, что выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова, поэтому однозначно можем раскодировать сообщение с начала.
Разобьём код слева направо по данным таблицы и переведём его в буквы:
110 000 01 001 10 — b a c d e.
24. Для 6 букв латинского алфавита заданы их двоичные коды (для некоторых букв из двух бит, для некоторых – из трех). Эти коды представлены в таблице:
| A | B | C | D | E | F |
| 00 | 100 | 10 | 011 | 11 | 101 |
Какая последовательность из 6 букв закодирована двоичной строкой 011111000101100?
Решение.
Мы видим, что условия Фано и обратное условие Фано не выполняются, значит, код можно раскодировать неоднозначно.
Будем пробовать различные варианты:
1) 011 11 100 0101100
Первая буква определяется однозначно, её код 011: D.
Вторая буква также определится однозначно — E.
Пусть третья буква B, тогда следующая начинается с кода 010, но таких букв в таблице нет, значит, предположение не верно.
2) 011 11 10 00 101 100
Третья буква — С, потом — A. Мы хотим получить ещё две буквы, чтобы в сумме их было 6, тогда следующая буква — F, и последняя — B.
Окончательно получили ответ: DECAFB.
Примечание. DECACEA не подходит, так как 7 букв.
25. По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У; для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.
|
|
Укажите кратчайшее кодовое слово для буквы Р, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение.
Заметим, что невозможно подобрать однобуквенное, двухбуквенное, трёхбуквенное кодовое слово, удовлетворяющее условию Фано. Подберём четырёхбуквенное кодовое слово. Таким словом будет 1100.
Ответ: 1100.
26. Для кодирования букв А, Б, В, Г используются четырехразрядные последовательные двоичные числа от 1000 до 1011 соответственно. Закодируйте таким образом последовательность символов БГАВ и запишите результат в восьмеричном коде.
Решение.
Закодируем последовательность букв: БГАВ — 1001101110001010. Теперь разобьём это представление на тройки справа налево и переведём полученный набор чисел сначала в десятичный код,(в таком представлении восьмеричный код совпадает с десятеричным):
1 001 101 110 001 010 — 1 1 5 6 1 2.
27. Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется посимвольное кодирование: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в шестнадцатеричный вид.
Решение.
Закодируем последовательность букв: ВАГБААГВ — 1101001110100110. Теперь разобьём это представление на четвёрки справа налево и переведём полученный набор чисел сначала в десятичный код, затем в шестнадцатеричный:
1101 0011 1010 0110 — 13 3 10 6 — D3A6.
28. Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, П, Р. решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв К, Л, М, Н использовали соответственно кодовые слова 00, 01, 100, 110. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Кодовое слово для буквы П не может начинаться с 0, поскольку кодовые слова начинающиеся с 0, будут либо являться подстрокой кодовых слов для букв К и Л, либо включать в себя кодовые слова для букв К и Л. Кодовые слова 1, 10 и 11 взять не можем, поэтому букву П можно закодировать кодовыми словами 101 или 111. Возьмём кодовое слово с наименьшим числовым значением. Следовательно, букву П можно закодировать кодовым словом 101.
Ответ: 101.
29. По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0. Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наименьшему возможному двоичному числу. Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование
Решение.
Поскольку все однозначные и двузначные слова не подходят по условию Фано, значит, нужно найти трехзначное слово, которое было бы минимально и удовлетворяло условию. Это слово — 100. Однако при выборе кода 100 мы закрываем возможные варианты для D И E. Значит, трехзначные слова нам тоже не подходят, если взять четырехзначные то там мы для кодирования можем взять слово 1000. Тогда для кодирования D и E можно использовать слова 10010 и 10011.
Ответ: 1000.
30. По каналу связи передаются сообщения, содержащие только семь букв: А, Б, И, К, Л, С, Ц. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 00, К — 010, Л — 111. Какое наименьшее количество двоичных знаков потребуется для кодирования слова АБСЦИССА?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение.
Букву С закодируем кодовым словом 10, поскольку буква С повторяется в слове АБСЦИССА 3 раза. Букву А закодируем кодовым словом 011, поскольку буква А повторяется в слове АБСЦИССА 2 раза. Буквы Ц и И закодируем кодовыми словами 1101 и 1100 соответственно. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова АБСЦИССА равно 3 + 2 + 2 + 4 + 4 + 2 + 2 + 3 = 22.
Ответ: 22.
25 задание ЕГЭ информатика (Питон)
#25
for i in range(101000000, 102000000 + 1, 2):
k = 1
d = 2
while d * d < i:
if i % d == 0:
if d % 2 == 0:
k += 1
if (i//d) % 2 == 0:
k += 1
if k > 3:
break
d += 1
if d * d == i:
k += 1
if k == 3:
print(i)
Ищет среди целых чисел, принадлежащих числовому отрезку [312614; 312651], числа, имеющие ровно шесть различных натуральных делителей. Для каждого найденного числа запишите эти шесть делителей в шесть соседних столбцов на экране с новой строки. Делители в строке должны следовать в порядке возрастания.
for i in range(312614,312652):
cnt=0
v=[]
for j in range(1,i+1):
if i%j==0:
cnt+=1
v.append(j)
if cnt==6:
print(v)
Пусть M(N) – пятый по величине делитель натурального числа N без учёта самого числа и единицы. Найдите 5 наименьших натуральных чисел, превышающих 460 000 000, для которых M(N) > 0.
n=460000000
count=0
while count!=5:
n+=1
countd=0
for d in range(2,n//2+1):
if n%d==0:
coutd+=1
if countd==5:
print(n//d)
count+=1
break
Назовём натуральное число подходящим, если у него ровно 3 различных простых делителя. Например, число 180 подходящее (его простые делители – 2, 3 и 5), а число 12 – нет (у него только два различных простых делителя). Определите количество подходящих чисел, принадлежащих отрезку [10001;50000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
def PrimeDelThree(n):
SetPrimeDel = set()
prime = True
for d in range(2, n+1):
while n % d == 0:
SetPrimeDel.add(d)
prime = False
n = n // d
if n == 1:
break
else:
if (d*d>n) and prime:
break
if prime:
SetPrimeDel.add(n)
return len(SetPrimeDel)==3
(count, mn) = (0, 50_000)
for n in range (50_000, 10001-1, -1):
if PrimeDelThree(n):
count += 1
mn = n
print(count, mn)Найдите все натуральные числа, принадлежащие отрезку [35000000;40000000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
Идея. Нас интересуют числа, являющиеся четвертой степенью простого числа, возможно умноженные на некоторую степень двойки.
def isPrime(n):
d = 2
while d * d <= n:
if n % d == 0:
return False
d += 1
return True
(a, b) = (35_000_000, 40_000_000)
for n in range (a, b+1):
x = n
while x % 2 == 0:
x = x // 2 # Убираем все четные делители
if x ** 0.25 == int(x ** 0.25) and isPrime(x ** 0.25):
print(n)
n += 1
Обновлено: 09.03.2023
Ответы и задания для вариантов ИН2010201, ИН2010202 тренировочной работы №2 статград по информатике 11 класс для подготовки к ЕГЭ 2021, официальная дата проведения работы статград: 10.12.2020 (10 декабря 2020 год).
Ссылка для скачивания вариантов (ИН2010201-ИН2010202): скачать в PDF
Тренировочная работа №2 по информатике 11 класс статград 2020-2021 решать онлайн:
Сложные задания с варианта ИН2010201:
1)На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П7: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
Ответ: БДЖГВАЕ
3)Даны фрагменты двух таблиц из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. На основании имеющихся данных определите количество людей, у которых в момент достижения 50 полных лет было не меньше двух внуков и внучек.
Ответ: 3
Ответ: 20
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 60. Для Вашего удобства программа представлена на четырёх языках программирования.
Ответ: 8
7)Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 9 Мбайт. В целях экономии было решено перейти на разрешение 200 dpi и цветовую систему, содержащую 256 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Ответ: 2
8)Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой И. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Тимофей?
Ответ: 10476
9)Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений температура в 8:00 была выше среднесуточной температуры того же дня.
Ответ: 30
Ответ: 2
11)При регистрации на сервере каждый пользователь получает уникальный персональный код, состоящий из двух частей. Первая часть кода содержит 12 символов, каждый из которых может быть одной из 26 заглавных латинских букв. Вторая часть кода содержит 5 символов, каждый из которых может быть одной из 9 цифр (цифра 0 не используется). При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе. Для представления кода используют посимвольное кодирование, все символы в пределах одной части кода кодируют одинаковым минимально возможным для этой части количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Для хранения данных о 30 пользователях потребовалось 2100 байт. Сколько байтов выделено для хранения дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байтов.
Ответ: 60
13)На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П, Р, С. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункт К?
Ответ: 48
14)Значение выражения 3435 – 79 + 48 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
16)Обозначим через a mod b остаток от деления натурального числа a на натуральное число b. Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = n + F(n – 3), если n > 0 и при этом n mod 3 = 0; F(n) = n + F(n – (n mod 3)), если n mod 3 > 0. Чему равно значение функции F(22)?
17)Назовём натуральное число подходящим, если ровно два из его делителей входят в список (11, 13, 17, 19). Определите количество подходящих чисел, принадлежащих отрезку [11 000; 22 000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
18)Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число отличалось от предыдущего не более чем на 10. Какую максимальную сумму могут иметь выбранные числа?
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в четыре раза. Например, пусть в одной куче 7 камней, а в другой 9 камней; такую позицию мы будем обозначать (7, 9). За один ход из позиции (7, 9) можно получить любую из четырёх позиций: (8, 9), (28, 9), (7, 10), (7, 36). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
20)Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21)Для игры, описанной в задании 19, укажите такое значения S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22)Ниже на четырёх языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит одно число. Укажите наименьшее возможное значение x, при вводе которого программа выведет число 120.
24)Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы A. Например, в тексте ABCAABADDD после буквы A два раза стоит B, по одному разу – A и D. Для этого текста ответом будет B.
25)Рассмотрим произвольное натуральное число, представим его всеми возможными способами в виде произведения двух натуральных чисел и найдём для каждого такого произведения разность сомножителей. Например, для числа 16 получим: 16 = 16*1 = 8*2 = 4*4, множество разностей содержит числа 15, 6 и 0. Найдите все натуральные числа, принадлежащие отрезку [1 000 000; 2 000 000], у которых составленное описанным способом множество разностей будет содержать не меньше трёх элементов, не превышающих 100. В ответе перечислите найденные числа в порядке возрастания.
26)Для перевозки партии грузов различной массы выделен грузовик, но его грузоподъёмность ограничена, поэтому перевезти сразу все грузы не удастся. Грузы массой от 200 до 210 кг грузят в первую очередь. На оставшееся после этого место стараются взять как можно больше грузов. Если это можно сделать несколькими способами, выбирают тот способ, при котором самый большой из выбранных грузов имеет наибольшую массу. Если и при этом условии возможно несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй по величине груз, и т.д. Известны количество грузов, масса каждого из них и грузоподъёмность грузовика. Необходимо определить количество и общую массу грузов, которые будут вывезены при погрузке по вышеописанным правилам.
27)Набор данных состоит из троек натуральных чисел. Необходимо распределить все числа на три группы, при этом в каждую группу должно попасть ровно одно число из каждой исходной тройки. Сумма всех чисел в первой группе должна быть чётной, во второй – нечётной. Определите максимально возможную сумму всех чисел в третьей группе.
Сложные задания с варианта ИН2010202:
Ответ: 21
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 57. Для Вашего удобства программа представлена на четырёх языках программирования.
Ответ: 16
7)Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 8 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 224 = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Ответ: 27
8)Андрей составляет 6-буквенные коды из букв А, Н, Д, Р, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Андрей?
Ответ: 23625
9)Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений температура в 20:00 была ниже среднесуточной температуры того же дня.
Ответ: 28
20)Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
Ответ: 6*35
21)Для игры, описанной в задании 19, укажите такое значения S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Ответ: 34
22)Ниже на четырёх языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит одно число. Укажите наименьшее возможное значение x, при вводе которого программа выведет число 140.
Ответ: 329
24)Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы E. Например, в тексте EBCEEBEDDD после буквы E два раза стоит B, по одному разу – E и D. Для этого текста ответом будет B.
Задание 4 № 16380
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Букву О закодируем кодовым словом 000, поскольку буква О повторяется в слове КОЛОБОК 3 раза. Букву К закодируем кодовым словом 110, поскольку буква К повторяется в слове КОЛОБОК 2 раза. Буквы Б и Л закодируем кодовыми словами 1110 и 1111 соответственно. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова КОЛОБОК равно 3 + 3 + 4 + 3 + 4 + 3 + 3 = 23.
Привет! Сегодня узнаем, как решать 4 задание из ЕГЭ по информатике нового формата 2021.
Четвёртое задание из ЕГЭ по информатике раскрывает тему кодирование информации. Одним из центральных приёмов при решении задач подобного типа является построение дерева Фано. Рассмотрим на примерах этот метод.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование
Т.к. код букв должен удовлетворять условию Фано (т.е. однозначно декодироваться), то расположим буквы, которые уже имеют код (A, B, C), на Дереве Фано.
Дерево Фано для двоичного кодирования начинается с двух направлений, которые означают 0(ноль) и 1(единицу) (цифры двоичного кодирования).
От каждого направления можно также рисовать только два направления: 0(ноль) и 1(единицу) и т.д. Для удобства будем рисовать 1(единицу) только вправо, а 0(ноль) только влево.
Получается структура похожая на дерево!
В конце каждой ветки можно располагать букву, которую мы хотим закодировать, но если мы расположили букву, от этой ветки больше нельзя делать новых ответвлений.
Буква C заблокировала левую ветку, поэтому будем работать с правой частью нашего дерева.
Если мы расположим какую-нибудь букву на оставшуюся ветку (100), то эта ветка заблокируется, и нам некуда будет писать остальные 2 буквы. Поэтому продолжаем ветку (100) дальше.
Теперь свободно уже две ветки, а нам нужно закодировать ещё три буквы. Поэтому должны ещё раз продолжить дерево от какой-нибудь ветки.
Но уже видно, что букве F будет правильно присвоить код 1000, т.к. нам в условии сказано, что код буквы F должен соответствовать наименьшему возможному двоичному числу. Как расположить буквы D и E в данной задаче не принципиально.
Ответ: 1000.
Ещё один важный тип задания 4 из ЕГЭ по информатике нового формата 2021.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Коды букв должны удовлетворять условию Фано. Некоторые буквы уже имеют заданные коды (Б, К, Л). Нам нужно, чтобы слово АБСЦИССА имело как можно меньше двоичных знаков. Заметим, что буква C встречается три раза, а буква A два раза, значит, этим буквам стараемся присвоить как можно меньшую длину!
Отметим на дереве Фано уже известные буквы (Б, К, Л).
У нас осталось 4 (четыре) буквы, а свободных веток 3(три), поэтому мы должны продолжить дерево. но какую ветку продолжить ?
Если продолжить линию 1-0, то получится такая картина :
Теперь получились 4(четыре) свободные ветки равной длины (3(трём) двоичным символам). Т.к. ветки равной длины, то не важно на какую ветку какую букву расположим.
Посчитаем общую длину слова АБСЦИССА.
3 + 2 + 3 + 3 + 3 + 3 + 3 + 3 = 23.
Продлим линию 1-1-0 (можно и 0-1-1, не принципиально, т.к. эти ветки имеют одинаковую длину.), то получится:
Из этих же соображений букве А присваиваем код из трёх двоичных символов 0-1-1.
3 + 2 + 2 + 4 + 4 + 2 + 2 + 3 = 22
Длина получилась меньше, чем в первом варианте. Других вариантов нет, поэтому ответ будет 22.
В этой задаче ничего не сказано про условие Фано. Здесь уже все буквы закодированы, осталось написать сам код.
Задача сводится к переводу из двоичной системы в восьмеричную систему. На эту тему был урок на моём сайте.
Ответ: 151646.
На этом всё! Увидимся на следующих занятиях по подготовке к ЕГЭ по информатике.
ЕГЭ по информатике — Задание 15 (Лёгкое!)
Стас костюшкин 15-10-2020 в 18:48:52
Этого не знаю. Это просто примерные задачи, которые наиболее часто попадаются в книжках и на сайтах по подготовке к ЕГЭ по информатике.
Калужский Александр 15-10-2020 в 18:57:40
Глеб Цыбрий 15-11-2020 в 10:30:33
Ольга Владимировна Сорокина 05-03-2021 в 12:09:08
Ольга Владимировна Сорокина 05-03-2021 в 12:09:14
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Какое кодовое слово надо назначить для буквы М, чтобы код удовлетворял указанному условию и при этом длина слова МОЛОКО после кодирования была наименьшей? Если таких кодов несколько, укажите код с наименьшим числовым значением.
Работа состоит из 27 заданий с кратким ответом, выполняемых с помощью компьютера.
Тренировочные варианты (ИН2010201-ИН2010202): скачать в PDF
Все ответы, задания (без водяного знака) и файлы для вариантов: скачать
Тренировочные варианты по информатике 11 класс ЕГЭ 2021 ответы и задания ИН2010201 ИН2010202:
Сложные задания с варианта ИН2010201:
1)На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П7: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
2)Логическая функция F задаётся выражением: ((x → y) ≡ (w → x)) / (z → w). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
3)Даны фрагменты двух таблиц из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. На основании имеющихся данных определите количество людей, у которых в момент достижения 50 полных лет было не меньше двух внуков и внучек.
5)Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом: 1. Строится двоичная запись числа N. 2. В конец записи (справа) дописывается вторая справа цифра двоичной записи. 3. В конец записи (справа) дописывается вторая слева цифра двоичной записи. 4. Результат переводится в десятичную систему.
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 60. Для Вашего удобства программа представлена на четырёх языках программирования.
7)Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 9 Мбайт. В целях экономии было решено перейти на разрешение 200 dpi и цветовую систему, содержащую 256 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
8)Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой И. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Тимофей?
9)Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений температура в 8:00 была выше среднесуточной температуры того же дня.
11)При регистрации на сервере каждый пользователь получает уникальный персональный код, состоящий из двух частей. Первая часть кода содержит 12 символов, каждый из которых может быть одной из 26 заглавных латинских букв. Вторая часть кода содержит 5 символов, каждый из которых может быть одной из 9 цифр (цифра 0 не используется). При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе. Для представления кода используют посимвольное кодирование, все символы в пределах одной части кода кодируют одинаковым минимально возможным для этой части количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов.
Для хранения данных о 30 пользователях потребовалось 2100 байт. Сколько байтов выделено для хранения дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байтов.
13)На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П, Р, С. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункт К?
14)Значение выражения 3435 – 79 + 48 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
16)Обозначим через a mod b остаток от деления натурального числа a на натуральное число b. Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = n + F(n – 3), если n > 0 и при этом n mod 3 = 0; F(n) = n + F(n – (n mod 3)), если n mod 3 > 0. Чему равно значение функции F(22)?
17)Назовём натуральное число подходящим, если ровно два из его делителей входят в список (11, 13, 17, 19). Определите количество подходящих чисел, принадлежащих отрезку [11 000; 22 000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
18)Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число отличалось от предыдущего не более чем на 10. Какую максимальную сумму могут иметь выбранные числа? В ответе запишите только целую часть максимально возможной суммы. Исходная последовательность записана в виде одного столбца электронной таблицы.
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в четыре раза. Например, пусть в одной куче 7 камней, а в другой 9 камней; такую позицию мы будем обозначать (7, 9). За один ход из позиции (7, 9) можно получить любую из четырёх позиций: (8, 9), (28, 9), (7, 10), (7, 36).
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 91. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 91 или больше камней. В начальный момент в первой куче было 5 камней, во второй куче – S камней, 1 ≤ S ≤ 85. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
20)Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21)Для игры, описанной в задании 19, укажите такое значения S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22)Ниже на четырёх языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит одно число. Укажите наименьшее возможное значение x, при вводе которого программа выведет число 120.
23)Исполнитель преобразует число на экране. У исполнителя есть три команды, которым присвоены номера: 1. Прибавить 1 2. Прибавить 2 3. Умножить на 3 Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья – умножает на 3. Программа для исполнителя – это последовательность команд. Сколько существует программ, которые преобразуют исходное число 1 в число 27, и при этом траектория вычислений содержит число 8 и не содержит чисел 10 и 11? Траектория вычислений – это последовательность результатов выполнения всех команд программы. Например, для программы 213 при исходном числе 4 траектория будет состоять из чисел 6, 7, 21.
24)Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы A. Например, в тексте ABCAABADDD после буквы A два раза стоит B, по одному разу – A и D. Для этого текста ответом будет B.
25)Рассмотрим произвольное натуральное число, представим его всеми возможными способами в виде произведения двух натуральных чисел и найдём для каждого такого произведения разность сомножителей. Например, для числа 16 получим: 16 = 16*1 = 8*2 = 4*4, множество разностей содержит числа 15, 6 и 0. Найдите все натуральные числа, принадлежащие отрезку [1 000 000; 2 000 000], у которых составленное описанным способом множество разностей будет содержать не меньше трёх элементов, не превышающих 100. В ответе перечислите найденные числа в порядке возрастания.
26)Для перевозки партии грузов различной массы выделен грузовик, но его грузоподъёмность ограничена, поэтому перевезти сразу все грузы не удастся. Грузы массой от 200 до 210 кг грузят в первую очередь. На оставшееся после этого место стараются взять как можно больше грузов. Если это можно сделать несколькими способами, выбирают тот способ, при котором самый большой из выбранных грузов имеет наибольшую массу. Если и при этом условии возможно несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй по величине груз, и т.д. Известны количество грузов, масса каждого из них и грузоподъёмность грузовика. Необходимо определить количество и общую массу грузов, которые будут вывезены при погрузке по вышеописанным правилам.
27)Набор данных состоит из троек натуральных чисел. Необходимо распределить все числа на три группы, при этом в каждую группу должно попасть ровно одно число из каждой исходной тройки. Сумма всех чисел в первой группе должна быть чётной, во второй – нечётной. Определите максимально возможную сумму всех чисел в третьей группе.
Сложные задания с варианта ИН2010202:
5)Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом: 1. Строится двоичная запись числа N. 2. В конец записи (справа) дописывается вторая справа цифра двоичной записи. 3. В конец записи (справа) дописывается вторая слева цифра двоичной записи. 4. Результат переводится в десятичную систему.
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 57. Для Вашего удобства программа представлена на четырёх языках программирования.
7)Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 8 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 224 = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
8)Андрей составляет 6-буквенные коды из букв А, Н, Д, Р, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Андрей?
9)Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений температура в 20:00 была ниже среднесуточной температуры того же дня.
11)При регистрации на сервере каждый пользователь получает уникальный персональный код, состоящий из двух частей. Первая часть кода содержит 10 символов, каждый из которых может быть одной из 26 заглавных латинских букв. Вторая часть кода содержит 7 символов, каждый из которых может быть одной из 9 цифр (цифра 0 не используется). При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе.
Для представления кода используют посимвольное кодирование, все символы в пределах одной части кода кодируют одинаковым минимально возможным для этой части количеством битов, а для кода в целом выделяется минимально возможное целое количество байт. Для хранения данных о 40 пользователях потребовалось 2400 байтов. Сколько байт выделено для хранения дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байтов.
13)На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П, Р, С. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункт Н?
14)Значение выражения 3436 – 710 + 47 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
16)Обозначим через a mod b остаток от деления натурального числа a на натуральное число b. Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = n + F(n – 3), если n > 0 и при этом n mod 3 = 0; F(n) = n + F(n – (n mod 3)), если n mod 3 > 0. Чему равно значение функции F(26)?
17)Назовём натуральное число подходящим, если ровно два из его делителей входят в список (11, 13, 17, 19). Определите количество подходящих чисел, принадлежащих отрезку [22 000; 33 000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
18)Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число отличалось от предыдущего не более чем на 8. Какую максимальную сумму могут иметь выбранные числа? В ответе запишите только целую часть максимально возможной суммы. Исходная последовательность записана в виде одного столбца электронной таблицы.
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в четыре раза. Например, пусть в одной куче 7 камней, а в другой 9 камней; такую позицию мы будем обозначать (7, 9). За один ход из позиции (7, 9) можно получить любую из четырёх позиций: (8, 9), (28, 9), (7, 10), (7, 36). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 151. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 151 или больше камней.
20)Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21)Для игры, описанной в задании 19, укажите такое значения S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22)Ниже на четырёх языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит одно число. Укажите наименьшее возможное значение x, при вводе которого программа выведет число 140.
23)Исполнитель преобразует число на экране. У исполнителя есть три команды, которым присвоены номера: 1. Прибавить 1 2. Прибавить 2 3. Умножить на 3 Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья – умножает на 3. Программа для исполнителя – это последовательность команд. Сколько существует программ, которые преобразуют исходное число 1 в число 30, и при этом траектория вычислений содержит число 9 и не содержит чисел 11 и 12? Траектория вычислений – это последовательность результатов выполнения всех команд программы. Например, для программы 213 при исходном числе 4 траектория будет состоять из чисел 6, 7, 21.
24)Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы E. Например, в тексте EBCEEBEDDD после буквы E два раза стоит B, по одному разу – E и D. Для этого текста ответом будет B.
25)Рассмотрим произвольное натуральное число, представим его всеми возможными способами в виде произведения двух натуральных чисел и найдём для каждого такого произведения разность сомножителей. Например, для числа 16 получим: 16 = 16*1 = 8*2 = 4*4, множество разностей содержит числа 15, 6 и 0. Найдите все натуральные числа, принадлежащие отрезку [2 000 000; 3 000 000], у которых составленное описанным способом множество разностей будет содержать не меньше трёх элементов, не превышающих 115. В ответе перечислите найденные числа в порядке возрастания.
26)Для перевозки партии грузов различной массы выделен грузовик, но его грузоподъёмность ограничена, поэтому перевезти сразу все грузы не удастся. Грузы массой от 210 до 220 кг грузят в первую очередь. На оставшееся после этого место стараются взять как можно больше грузов. Если это можно сделать несколькими способами, выбирают тот способ, при котором самый большой из выбранных грузов имеет наибольшую массу.
Если и при этом условии возможно несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй по величине груз, и т.д. Известны количество грузов, масса каждого из них и грузоподъёмность грузовика. Необходимо определить количество и общую массу грузов, которые будут вывезены при погрузке по вышеописанным правилам.
Читайте также:
- Управление чувствами и эмоциями обж сообщение
- Сообщение на тему музеи франции
- Сообщение о возгорании поступило на пульт
- Сообщение о грузинских танцах
- Сообщение о лимоне домашнем
Урок посвящен тому, как решать 4 задание ЕГЭ по информатике
Содержание:
- Кодирование информации
- Кодирование и расшифровка сообщений
- Решение 4 заданий ЕГЭ
Кодирование информации
4-е задание: «Кодирование и декодирование информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 2 минуты.
Проверяемые элементы содержания: Умение кодировать и декодировать информацию
До ЕГЭ 2021 года — это было задание № 5 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Из-за невнимательного чтения условия задания экзаменуемые иногда не замечают, что требуется найти кодовое слово минимальной длины с максимальным (минимальным) числовым значением.
Кроме того, если в задании указано, что несколько букв остались без кодовых слов (как, например, в задании демоварианта), то кодовое слово для указанной буквы должно быть подобрано таким образом, чтобы осталась возможность найти кодовые слова, удовлетворяющие условию Фано, и для других букв. Так, например, если мы букву А закодируем нулём, а букву Б единицей, то букву В мы уже никак не сможем закодировать с соблюдением условия Фано, поэтому длину кодового слова для А или Б следует увеличить»
ФГБНУ «Федеральный институт педагогических измерений»
- Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
- Кодирование бывает равномерным и неравномерным:
- при равномерном кодировании всем символам соответствуют коды одинаковой длины;
- при неравномерном кодировании разным символам соответствуют коды разной длины, это затрудняет декодирование.
Пример: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодов (2).
Кодирование и расшифровка сообщений
Декодирование (расшифровка) — это восстановление сообщения из последовательности кодов.
Для решения задач с декодированием, необходимо знать условие Фано:
Условие Фано: ни одно кодовое слово не должно являться началом другого кодового слова (что обеспечивает однозначное декодирование сообщений с начала)
Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно.
- если сообщение декодируется с конца, то его можно однозначно декодировать, если выполняется обратное условие Фано:
- условие Фано – это достаточное, но не необходимое условие однозначного декодирования.
Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова
Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с концом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.
Однозначное декодирование обеспечивается:
Однозначное декодирование
Декодирование
Егифка ©:
Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:
ЕГЭ 4.1: Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).
Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.
✍ Решение:
- Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:
О -> 0 -> 00 В -> 1 -> 01 Д -> 2 -> 10 П -> 3 -> 11 А -> 4 -> 100
ВОДОПАД:010010001110010
010 010 001 110 010 ↓ ↓ ↓ ↓ ↓ 2 2 1 6 2
Результат: 22162
Теоретическое решение ЕГЭ данного задания по информатике, видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Рассмотрим еще разбор 4 задания ЕГЭ:
ЕГЭ 4.2: Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
| a | b | c | d | e |
|---|---|---|---|---|
| 000 | 110 | 01 | 001 | 10 |
Какой набор букв закодирован двоичной строкой 1100000100110?
✍ Решение:
- Во-первых, проверяем условие Фано: никакое кодовое слово не является началом другого кодового слова. Условие верно.
- Код разбиваем слева направо согласно данным, представленным в таблице. Затем переведём его в буквы:
✎ 1 вариант решения:
110 000 01 001 10 ↓ ↓ ↓ ↓ ↓ b a c d e
Результат: b a c d e.
✎ 2 вариант решения:
-
Этот вариант решения 4 задания ЕГЭ более сложен, но тоже верен.
- Сделаем дерево, согласно кодам в таблице:
- Сопоставим закодированное сообщение с кодами в дереве:
110 000 01 001 10
Результат: b a c d e.
Кроме того, вы можете посмотреть видеорешение этого задания ЕГЭ по информатике (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Решим следующее 4 задание:
ЕГЭ 4.3:
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110).
Определите, какое число передавалось по каналу в виде 01100010100100100110.
✍ Решение:
- Рассмотрим пример из условия задачи:
Было2310 Стало00101001102
0010100110 (0010 - 2, 0011 - 3)
01100 01010 01001 00110
0110 0101 0100 0011
0110 0101 0100 0011 ↓ ↓ ↓ ↓ 6 5 4 3
Ответ: 6 5 4 3
Вы можете посмотреть видеорешение этого задания ЕГЭ по информатике, теоретическое решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
ЕГЭ 4.4:
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10.
Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Подобные задания для тренировки
✍ Решение:
✎
1 вариант решения
основан на логических умозаключениях:
- Найдём самые короткие возможные кодовые слова для всех букв.
- Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
- Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
- Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.
- Суммарная длина всех четырёх кодовых слов равна:
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
✎ 2 вариант решения:
- Будем использовать дерево. Влево откладываем 0, вправо — 1:
- Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:
(Н) -> 0 -> 1 символ (К) -> 10 -> 2 символа (Л) -> 110 -> 3 символа (М) -> 111 -> 3 символа
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
Ответ: 9
4.5:
По каналу связи передаются сообщения, содержащие только 4 буквы: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова:
А: 101010, Б: 011011, В: 01000
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).
- Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.
Результат: 00
4.6:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код:
А - 01 Б - 00 В - 11 Г - 100
Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:
- Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:
- Перепишем сверху вниз получившееся кодовое слово для Д: 101
Результат: 101
Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
4.7: Демоверсия ЕГЭ 2018 информатика (ФИПИ):
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.
Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:

Результат: 1100
Подробное теоретическое решение данного 4 (раньше №5) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 Видеорешение на RuTube здесь
4.8:
По каналу связи передаются шифрованные сообщения, содержащие только четыре букв: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются кодовые слова:
А: 00011 Б: 111 В: 1010
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- Поскольку в задании явно не указано о том, что код должен удовлетворять условию Фано, то дерево нужно построить как с начала (по условию Фано), так и с конца (обратное условие Фано).
- Получившееся числовое значение кодового слова для буквы Г — 01.
- Получившееся числовое значение кодового слова для буквы Г — 00.
- После сравнения двух кодовых слов (01 и 00), код с наименьшим числовым значением — это 00.
Дерево по условию Фано (однозначно декодируется с начала):
Дерево по обратному условию Фано (однозначно декодируется с конца):
Результат: 00
4.9:
По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:
Е – 000 Д – 10 К – 111
Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.
Подобные задания для тренировки
✍ Решение:
- С помощью дерева отобразим известные коды для букв:
- В результирующем слове — ДЕДМАКАР — вде буквы А. Значит, для получения наименьшей длины необходимо для буквы А выбрать наименьший код в дереве. Учтем это и достроим дерево для остальных трех букв А, М и Р:
- Расположим буквы в порядке их следования в слове и подставим их кодовые слова:
Д Е Д М А К А Р 10 000 10 001 01 111 01 110
Результат: 20
Смотрите виде решения задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Задание 5.
Пример 1. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0, для буквы Б – кодовое слово 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение:
1) Построение дерева: условие Фано означает, что ни одно кодовое слово не совпадает с началом другого кодового слова; при этом в дереве кода все кодовые слова должны располагаться в листьях дерева, то есть в узлах, которые не имеют потомков.
2) Построим дерево для заданных кодовых слов А – 0, Б – 110:
3) Штриховыми линиями отмечены две «пустые» ветви, на которые можно «прикрепить» листья для кодовых слов буквы В и Г: 10 и 111 или 111 и 10:
4) Суммарная длина всех четырёх кодовых слов 1 + 3 + 2 + 3 = 9
Ответ: 9
Задание 9.
Пример 1. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 45 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 4 раза ниже и частотой дискретизации в 12 раз выше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд. Во сколько раз скорость пропускная способность канала в город Б больше пропускной способности канала в город А?
Решение:
1) Объем звукового файла (I) вычисляется как произведение частоты дискретизации (n) на разрешение (i) на время звучания (t) и на количество каналов записи (k) I = n i t k
2) Примем объем первого музыкального фрагмента за Х, тогда скорость передачи этого файла в город А равна Х / 45
3) После повторной оцифровки объем файла изменится Х · 1/4 · 12 = 3 Х
4) Скорость передачи файла в город Б составит 3 Х /15
5) Найдем соотношение большей скорости к меньшей ( 3 Х /15 ) : ( Х / 45 ) = 9
Ответ: 9
Задание 10.
Пример 1. Ольга составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Ольга использует 5-буквенные слова, в которых есть только буквы A, B, C, D, причём буква D может появиться на первом месте или не появиться вовсе. Сколько различных кодовых слов может использовать Ольга?
Решение:
1) На первом месте может быть использована одна из четырех букв, на остальных местах одна из трёх букв.
2) Общее число различных кодовых слов равно 4 * 3 * 3 * 3 * 3 = 324
Ответ: 324
Задание 13.
Пример 1. При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы А, Б, В, Г, Д, Е. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит. Определите, сколько байт необходимо для хранения 25 паролей.
Решение:
1) Согласно условию, в пароле можно использовать 15 символов. Для кодирования одного из 15 символов нужно выделить 3 бита памяти (они позволяют закодировать 23 = 8 варианта, достаточно, т.к. используются шесть букв А, Б, В, Г, Д, Е). Для хранения всех 15 символов пароля нужно 15 * 3 = 45 бит
2) Пароль занимает целое число байт: берем ближайшее большее (точнее, не меньшее) значение, которое кратно 8: это 48 = 6 * 8; то есть один пароль занимает 6 байт
3) Для хранения 25 паролей. необходимо 25 * 6 = 150 (байт)

.jpg?7)
.jpg?6)
.jpg?4)
.jpg?4)
.jpg?4)
.jpg?4)
.jpg?4)
.jpg?4)
.jpg?4)


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)