Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Шахматная доска состоит из 8 столбцов и 8 строк. Какое минимальное количество бит потребуется для кодирования координат одной шахматной клетки?
2
Какое минимальное количество бит потребуется для кодирования целых положительных чисел, меньших 60?
3
Двое играют в «крестики-нолики» на поле 4 на 4 клетки. Какое количество информации (в битах) получил второй игрок, узнав ход первого игрока?
4
В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?
5
В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в коробке?
Пройти тестирование по этим заданиям
«Шахматная доска»
«Шахматная доска»
Условие:
Заданы две клетки шахматной доски. Если они покрашены в один цвет, то выведи слово YES, а если в разные цвета — NO. Программа получает на вход четыре числа от 1 до 8 каждое. Они задают номер столбца и строки сначала для первой клетки,а затем для второй клетки.
Решение:
|
a=int(input()) b=int(input()) c=int(input()) d=int(input()) if (a+b)%2==(c+d)%2: print(‘YES’) else: print(‘NO’) |
Сегодня завершаем трилогию по теории игр из первой части ЕГЭ по информатике 2021.
Разберём 21 задание из ЕГЭ по информатике 2021.
Перейдём к примерным задачам из ЕГЭ по информатике 2021.
Задача (Одна куча камней)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или три камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 18 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 33. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 33 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 32.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Решение:
S0 — первоначальное количество камней в куче.
Петя не должен выиграть на своём первом ходе. Найдём при каких значениях S0 это возможно.
Петя может сделать всего 3 действия. Распишем количество камней в куче для 3-х случаев. Это количество должно быть меньше 33.
| +1 | +3 | *2 |
| S0 + 1 < 33 S0 < 32 |
S0 + 3 < 33 S0 < 30 |
2*S0 < 33 S0 < 17 (Округляем в большую сторону) |
Все случаи должны быть удовлетворены, поэтому наш ответ должен быть меньше 17.
S0 < 17
Рассмотрим 1-ый ход, который может сделать Петя в начале игры.
1. S0+1 — оставил Петя после своего первого хода.
При каких S0 Ваня может выиграть первым своим ходом ?
| +1 | +3 | *2 |
| S0 + 2 ≥ 33 S0 ≥ 31 |
S0 + 4 ≥ 33 S0 ≥ 29 |
2*S0+2 ≥ 33 2*S0 ≥ 31 S0 ≥ 16 (Округляем в большую сторону) |
Получили первого кандидата для ответа S0=16. Но если и в двух оставшихся ветках это значение пройдёт на первом ходу Вани, то мы не сможем засчитать этот ответ.
Может ли Петя выиграть вторым своим ходом ?
а) S0+1+1 = S0+2 — Ваня оставил после первого своего хода.
| +1 | +3 | *2 |
| S0 + 3 < 33 S0 < 30 |
S0 + 5 < 33 S0 < 28 |
2*S0+4 < 33 2*S0 < 29 S0 < 15 (Округляем в большую сторону) |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт a) накладывается дополнительное ограничение S0 < 15
Рассмотрим, при каких значениях S0 Ваня сможет выиграть на своём втором ходе в пункте a).
1) S0+1+1+1 = S0+3 -Петя оставил после своего второго хода.
| +1 | +3 | *2 |
| S0 + 4 ≥ 33 S0 ≥ 29 |
S0 + 6 ≥ 33 S0 ≥ 27 |
2*S0 + 6 ≥ 33 2*S0 ≥ 27 S0 ≥ 14 (Округляем в большую сторону) |
Получили значение S0 = 14, при котором Ваня может выиграть на своём втором ходе в пункте 1). Это первый кандидат для ответа.
б) S0+1+3 = S0+4 — Ваня оставил после первого своего хода.
| +1 | +3 | *2 |
| S0 + 5 < 33 S0 < 28 |
S0 + 7 < 33 S0 < 26 |
2*S0 + 8 < 33 2*S0 < 25 S0 < 13 (Округляем в большую сторону) |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт б) накладывается дополнительное ограничение S0 < 13
1) S0+4+1 = S0+5 — Петя оставил после второго хода.
| +1 | +3 | *2 |
| S0 + 6 ≥ 33 S0 ≥ 27 |
S0 + 8 ≥ 33 S0 ≥ 25 |
2*S0 + 10 ≥ 33 2*S0 ≥ 23 S0 ≥ 12 (Округляем в большую сторону) |
Получили значение S0 = 12, при котором Ваня может выиграть на своём втором ходе в пункте 1). Это пока самый приоритетный кандидат для ответа.
Если мы в пунктах 2), 3), 4) получим меньшие значения, то у Пети есть всегда возможность свернуть в пункт 1), и там уже значения меньше, чем 12, подходить не будут. Теоретически Петя в пунктах 2), 3), 4) может создать ситуацию, когда Ваня не сможет выиграть на своём втором ходе («Заблокировать» ветку б). Но мы, перед тем, как записать ответ, сделаем проверку и найдём такую возможность, если она есть.
в) 2*(S0+1) = 2*S0+2 — Ваня оставил после первого своего хода.
| +1 | +3 | *2 |
| 2*S0 + 3 < 33 2*S0 < 30 S0 < 15 |
2*S0 + 5 < 33 2*S0 < 28 S0 < 14 |
4*S0 + 4 < 33 4*S0 < 29 S0 < 8 (Округляем в меньшую сторону) |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт в) накладывается дополнительное ограничение S0 < 8
1) 2*S0+2+1 = 2*S0+3 — Петя оставил после второго хода.
| +1 | +3 | *2 |
| 2*S0 + 4 ≥ 33 2*S0 ≥ 29 S0 ≥ 15 |
2*S0 + 6 ≥ 33 2*S0 ≥ 27 S0 ≥ 14 (Округляем в большую сторону) |
4*S0 + 6 ≥ 33 4*S0 ≥ 27 S0 ≥ 7 (Округляем в большую сторону) |
Получили значение S0 = 7, при котором Ваня может выиграть на своём втором ходе в пункте 1). Это пока самый приоритетный кандидат для ответа.
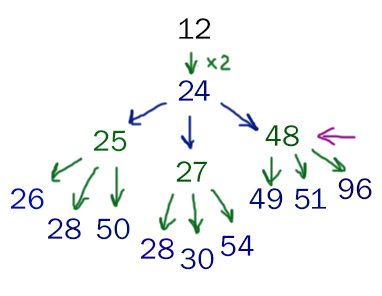
Теперь делаем проверку четырёх чисел, которые отмечены синим цветом. Проверку делаем в порядке возрастания. Если число подойдёт, то сразу записываем его в ответ.
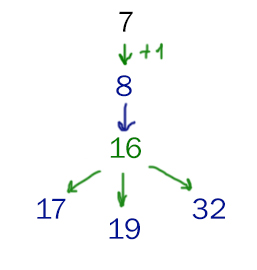
Проверяем значение S0 = 7
Проверим первую ветку, когда Петя на своём первом ходе делает +1 к куче.
Видим, что значение 7 полностью подходит в первой ветке.
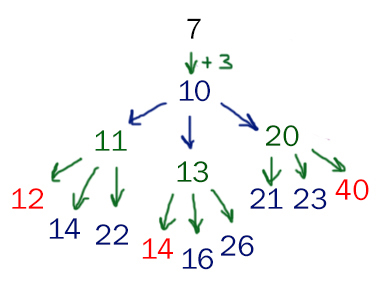
Синим цветом показаны кучки, которые оставляет Петя. Зелёным цветом показаны кучки, которые оставляет Ваня. Красным цветом показаны те ходы Пети, которые не дают Вани выиграть на втором своём ходе.
Видим, что в этой ветке значение 7 не проходит. Числа 12 и 14 не дают возможность Вани выиграть на своём втором ходе. Значение 40 уже являются выигрышным для Пети.
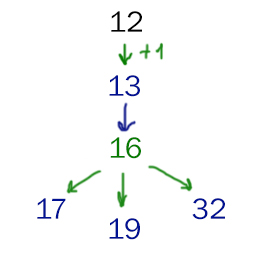
Проверяем значение S0 = 12
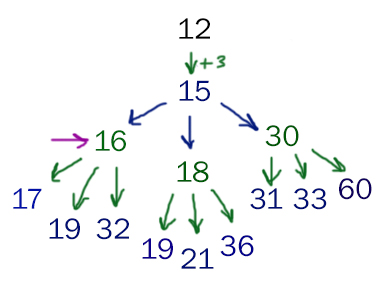
Видим, что значение 12 проходит в первой ветке. Рассмотрим вторую ветку.
Если Ваня сделает кучу, состоящую из 16 камней, то он сможет выиграть при любой игре Пети в этой ветке.
В этой ветке Ваня может выиграть на своём первом ходе! Число 48 уже является выигрышным.
Таким образом, в ответ пойдёт значение 12.
Ответ: 12
Рассмотрим более классическую задачу из 21 задания ЕГЭ по информатике 2021.
Задача (Демонстрационный вариант ЕГЭ по информатике 2021)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы,
у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было семь камней, во второй куче –
S камней; 1 ≤ S ≤ 69.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Решение:
Обозначим первую кучу за a, вторую кучу за b.
Распишем все комбинации для суммы двух куч для каждого хода:
1. a + 1 + b (Добавляем камень к первой куче)
2. a + b + 1 (Добавляем камень ко второй куче)
3. 2*a + b (Удваиваем первую кучу)
4. a + 2*b (Удваиваем вторую кучу)
S0 — первоначальное количество камней во второй куче.
a=7, b=S0 — Первоначальное положение
Петя не должен выиграть на своём первом ходе. Найдём при каких значениях S0 это возможно.
У нас эти данные должны были остаться после решения 20 задания (см в этой статье). Но распишем ещё раз, чтобы всё выкладки были перед глазами.
Петя может сделать всего 4 действия. Распишем сумму двух кучек для 4-х случаев. Эти суммы должны быть меньше 77.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 8 < 77 S0 < 69 |
S0 + 8 < 77 S0 < 69 |
S0 + 14 < 77 S0 < 63 |
2*S0 + 7 < 77 2*S0 < 70 S0 < 35 |
Все случаи должны быть удовлетворены, поэтому наш ответ должен быть меньше 35.
S0 < 35
Рассмотрим все ходы, которые может сделать Петя в начале игры.
1. a=8, b=S0 — оставил Петя после своего первого хода.
При каких S0 Ваня может выиграть первым своим ходом ?
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 9 ≥ 77 S0 ≥ 68 |
S0 + 9 ≥ 77 S0 ≥ 68 |
S0 + 16 ≥ 77 S0 ≥ 61 |
2*S0 + 8 ≥ 77 2*S0 ≥ 69 S0 ≥ 35 (Округляем в большую сторону) |
Все решения не удовлетворяют главному ограничению S0 < 35. Значит, не существует таких значений S0, при которых Ваня может выиграть своим первым ходом в данной ветке.
Может ли Петя выиграть вторым своим ходом ?
а) a=9(8+1), b=S0 — Ваня оставил после первого своего хода.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 10 < 77 S0 < 67 |
S0 + 10 < 77 S0 < 67 |
S0 + 18 < 77 S0 < 59 |
2*S0 + 9 < 77 2*S0 < 68 S0 < 34 |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт a) накладывается дополнительное ограничение S0 < 34
Рассмотрим, при каких значениях S0 Ваня сможет выиграть на своём втором ходе в пункте a).
1) a=10, b=S0 -Петя оставил после своего второго хода.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 11 ≥ 77 S0 ≥ 66 |
S0 + 11 ≥ 77 S0 ≥ 66 |
S0 + 20 ≥ 77 S0 ≥ 57 |
2*S0 + 10 ≥ 77 2*S0 ≥ 67 S0 ≥ 34 Округляем в большую сторону |
Видим, что Ваня не может выиграть на своём втором ходе в пункте a). Значения не проходят ограничение S0 < 34.
Петя всегда может ходить a=10, b=S0 и «блокировать» пункт a).
б) a=8, b=S0+1 — Ваня оставил после первого своего хода.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 10 < 77 S0 < 67 |
S0 + 10 < 77 S0 < 67 |
S0 + 17 < 77 S0 < 60 |
2*S0 + 10 < 77 2*S0 < 67 S0 < 34 (Округляем в большую сторону) |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт б) накладывается дополнительное ограничение S0 < 34
1) a=9(8+1), b=S0+1 — Петя оставил после второго хода.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 11 ≥ 77 S0 ≥ 66 |
S0 + 11 ≥ 77 S0 ≥ 66 |
S0 + 19 ≥ 77 S0 ≥ 58 |
2*S0 + 11 ≥ 77 2*S0 ≥ 66 S0 ≥ 33 |
Получили значение S0 = 33, при котором Ваня может выиграть на своём втором ходе в пункте 1). Это первый кандидат для ответа.
Если мы в пунктах 2), 3), 4) получим меньшие значения, то у Пети есть всегда возможность свернуть в пункт 1), и там уже значения меньше, чем 33, подходить не будут. Теоретически Петя в пунктах 2), 3), 4) может создать ситуацию, когда Ваня не сможет выиграть на своём втором ходе («Заблокировать» ветку б). Но мы, перед тем, как записать ответ, сделаем проверку и найдём такую возможность, если она есть.
в) a=16, b=S0 — Ваня оставил после первого своего хода.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 17 < 77 S0 < 60 |
S0 + 17 < 77 S0 < 60 |
S0 + 32 < 77 S0 < 45 |
2*S0 + 16 < 77 2*S0 < 61 S0 < 31 (Округляем в большую сторону) |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт в) накладывается дополнительное ограничение S0 < 31
1) a=17(16+1), b=S0 — Петя оставил после второго хода.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| S0 + 18 ≥ 77 S0 ≥ 59 |
S0 + 18 ≥ 77 S0 ≥ 59 |
S0 + 34 ≥ 77 S0 ≥ 43 |
2*S0 + 17 ≥ 77 2*S0 ≥ 60 S0 ≥ 30 |
Получили значение S0 = 30. Ещё один кандидат для ответа. Даже более приоритетный, потому что нам нужно найти наименьшее значение S0, при котором будут выполняться условия задачи.
г) a=8, b=2*S0 — Ваня оставил после первого своего хода.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| 2*S0 + 9 < 77 2*S0 < 68 S0 < 34 |
2*S0 + 9 < 77 2*S0 < 68 S0 < 34 |
2*S0 + 16 < 77 2*S0 < 61 S0 < 31 Округляем в большую сторону |
4*S0 + 8 < 77 4*S0 < 69 S0 < 18 Округляем в большую сторону |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт г) накладывается дополнительное ограничение S0 < 18
1) a=9, b=2*S0 — Петя оставил после второго хода.
| a+1+b | a + b+1 | 2*a + b | a + 2*b |
| 2*S0 + 10 ≥ 77 2*S0 ≥ 67 S0 ≥ 34 (Округляем в большую сторону) |
2*S0 + 10 ≥ 77 2*S0 ≥ 67 S0 ≥ 34 (Округляем в большую сторону) |
2*S0 + 18 ≥ 77 2*S0 ≥ 59 S0≥30 (Округляем в большую сторону) |
4*S0 + 9 ≥ 77 4*S0 ≥ 68 S0 ≥ 17 |
Получили значение S0 = 17. Ещё один кандидат на ответ. Это значение самое приоритетное.
Теперь делаем проверку трёх чисел, которые отмечены синим цветом. Проверку делаем в порядке возрастания. Если число подойдёт, то сразу записываем его в ответ.
Первый ход Пети, при котором он прибавляем к первой куче единицу мы уже исследовали. Начинаем со второй возможности Пети прибавить 1 ко второй куче.
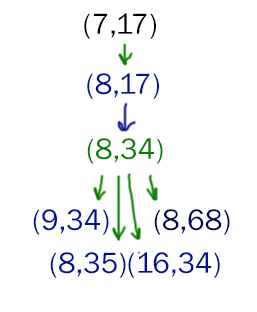
Проверяем значение S0 = 17
Проверим первую ветку, когда Петя прибавляет 1 к первой куче.
Синим цветом показаны кучки, которые оставляет Петя. Зелёным цветом показаны кучки, которые оставляет Ваня.
Мы рассматриваем именно тот пункт г), который и принёс нам значение 17. Видим, что это значение полность подходит в первой ветке.
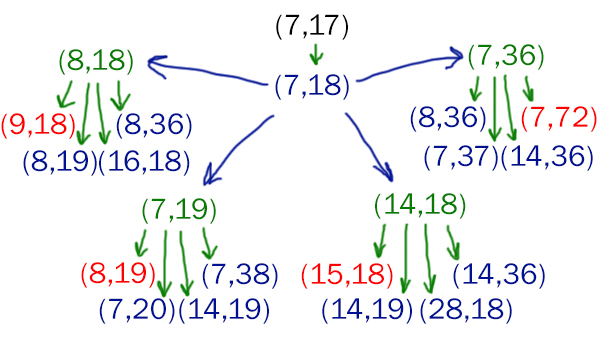
Проверим вторую ветку.
Красным цветом показаны те ходы Пети, которые не дают Вани выиграть на втором своём ходе.
(9,18), (8,19), (15,18) — эти точки не дают Вани выиграть. (7, 72) — Петя сам выигрывает на своём втором ходе.
Что бы ни делал Ваня, он не может выиграть на втором своём ходе. Значит, значение 17 нам не подходит.
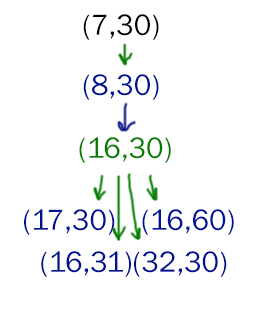
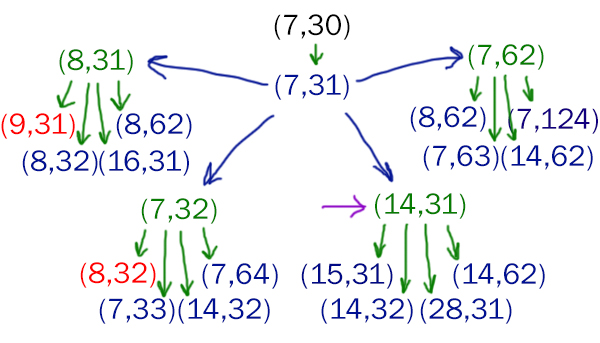
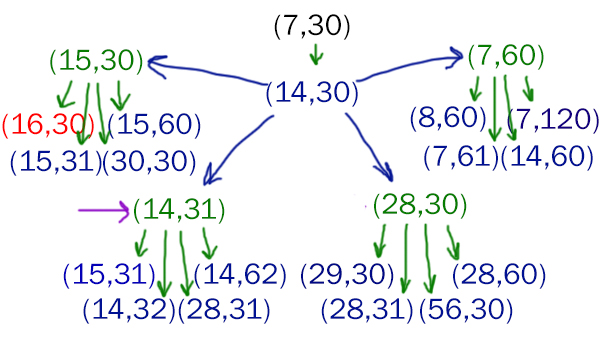
Проверяем значение S0 = 30
Проверим первую ветку, когда Петя прибавляет 1 к первой куче.
Видим, значение 30 в первой ветке подходит полностью.
Видим, если Ваня пойдёт (14,31), то он сможет выиграть на втором своём ходе при любом втором ходе Пети!
Проверим что будет, если Петя на своём первом ходе увеличит первую кучу в два раза.
Видим, и в этой ветке, если Ваня пойдёт (14,31), то он сможет выиграть на втором своём ходе при любом втором ходе Пети!
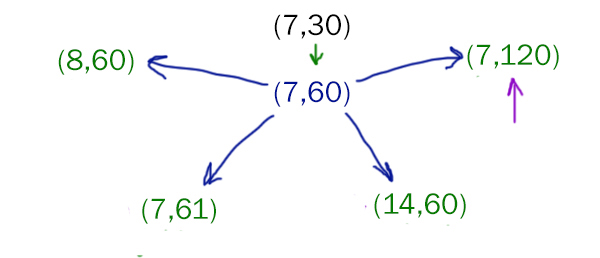
Проверим что будет, если Петя на своём первом ходе увеличит вторую кучу в два раза.
Видим, что Ваня в этой ветке может выиграть на первом своём ходе!
Мы пришли к выводу: Значение S0=30 нас полностью устраивает. Значение S0=33 проверять не будем, т.к. нас просили найти наименьшее значение.
Ответ: 30
Решим ещё одну задачу 21 задания из тренировочных вариантов ЕГЭ по информатике 2021.
Задача (На закрепление)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в четыре раза. Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (24, 9), (6, 10), (6, 36). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 61. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 61 или больше камней.
В начальный момент в первой куче было 3 камня, во второй куче — S камней, 1 ≤ S ≤ 57.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, то есть не гарантируют выигрыш независимо от игры противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Решение:
Обозначим первую кучу за a, вторую кучу за b.
Распишем все комбинации для суммы двух куч для каждого хода:
1. a + 1 + b (Добавляем камень к первой куче)
2. a + b + 1 (Добавляем камень ко второй куче)
3. 4*a + b (Увеличиваем первую кучу в 4 раза)
4. a + 4*b (Увеличиваем вторую кучу в 4 раза)
S0 — первоначальное количество камней во второй куче.
a=3, b=S0 — Первоначальное положение
Петя не должен выиграть на своём первом ходе. Найдём при каких значениях S0 это возможно.
Петя может сделать всего 4 действия. Распишем сумму двух кучек для 4-х случаев. Эти суммы должны быть меньше 61.
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| S0 + 4 < 61 S0 < 57 |
S0 + 4 < 61 S0 < 57 |
S0 + 12 < 61 S0 < 49 |
4*S0 + 3 < 61 4*S0 < 58 S0 < 15 (Округляем в большую сторону) |
Все случаи должны быть удовлетворены, поэтому наш ответ должен быть меньше 15.
S0 < 15
Рассмотрим 1-ый ход, который может сделать Петя в начале игры.
1. a=4(3+1), b=S0 — оставил Петя после своего первого хода.
При каких S0 Ваня может выиграть первым своим ходом ?
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| S0 + 5 ≥ 61 S0 ≥ 56 |
S0 + 5 ≥ 61 S0 ≥ 56 |
S0 + 16 ≥ 61 S0 ≥ 45 |
4*S0 + 4 ≥ 61 4*S0 ≥ 57 S0 ≥ 15 (Округляем в большую сторону) |
Все решения не удовлетворяют главному ограничению S0 < 15. Значит, не существует таких значений S0, при которых Ваня может выиграть своим первым ходом в данной ветке.
Может ли Петя выиграть вторым своим ходом ?
а) a=5(4+1), b=S0 — Ваня оставил после первого своего хода.
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| S0 + 6 < 61 S0 < 55 |
S0 + 6 < 61 S0 < 55 |
S0 + 20 < 61 S0 < 41 |
4*S0 + 5 < 61 4*S0 < 56 S0 < 14 |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт a) накладывается дополнительное ограничение S0 < 14
Рассмотрим, при каких значениях S0 Ваня сможет выиграть на своём втором ходе в пункте a).
1) a=6(5+1), b=S0 -Петя оставил после своего второго хода.
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| S0 + 7 ≥ 61 S0 ≥ 54 |
S0 + 7 ≥ 61 S0 ≥ 54 |
S0 + 24 ≥ 61 S0 ≥ 37 |
4*S0 + 6 ≥ 61 4*S0 ≥ 55 S0 ≥ 14 Округляем в большую сторону |
Видим, что Ваня не может выиграть на своём втором ходе в пункте a). Значения не проходят ограничение S0 < 14.
Петя всегда может ходить a=6, b=S0 и «блокировать» пункт a).
б) a=4, b=S0+1 — Ваня оставил после первого своего хода.
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| S0 + 6 < 61 S0 < 55 |
S0 + 6 < 61 S0 < 55 |
S0 + 17 < 61 S0 < 44 |
4*S0 + 8 < 61 4*S0 < 53 S0 < 14 (Округляем в большую сторону) |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт б) накладывается дополнительное ограничение S0 < 14
1) a=5(4+1), b=S0+1 — Петя оставил после второго хода.
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| S0 + 7 ≥ 61 S0 ≥ 54 |
S0 + 7 ≥ 61 S0 ≥ 54 |
S0 + 21 ≥ 61 S0 ≥ 40 |
4*S0 + 9 ≥ 61 4*S0 ≥ 52 S0 ≥ 13 |
Получили значение S0 = 13, при котором Ваня может выиграть на своём втором ходе в пункте 1). Это первый кандидат для ответа.
Если мы в пунктах 2), 3), 4) получим меньшие значения, то у Пети есть всегда возможность свернуть в пункт 1), и там уже значения меньше, чем 13, подходить не будут. Теоретически Петя в пунктах 2), 3), 4) может создать ситуацию, когда Ваня не сможет выиграть на своём втором ходе («Заблокировать» ветку б). Но мы, перед тем, как записать ответ, сделаем проверку и найдём такую возможность, если она есть.
в) a=16, b=S0 — Ваня оставил после первого своего хода.
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| S0 + 17 < 61 S0 < 44 |
S0 + 17 < 61 S0 < 44 |
S0 + 64 < 61 | — |
Видим, что Петя выигрывает в ветке в), если первую кучку умножит на 4.
г) a=4, b=4*S0 — Ваня оставил после первого своего хода.
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| 4*S0 + 5 < 61 4*S0 < 56 S0 < 14 |
4*S0 + 5 < 61 4*S0 < 56 S0 < 14 |
4*S0 + 16 < 61 4*S0 < 45 S0 < 12 Округляем в большую сторону |
16*S0 + 4 < 61 16*S0 < 57 S0 < 4 Округляем в большую сторону |
Видим, чтобы Петя не выиграл своим вторым ходом, на пункт г) накладывается дополнительное ограничение S0 < 4
1) a=5, b=4*S0 — Петя оставил после второго хода.
| a+1+b | a + b+1 | 4*a + b | a + 4*b |
| 4*S0 + 6 ≥ 61 4*S0 ≥ 55 S0 ≥ 14 (Округляем в большую сторону) |
4*S0 + 6 ≥ 61 4*S0 ≥ 55 S0 ≥ 14 (Округляем в большую сторону) |
4*S0 + 20 ≥ 61 4*S0 ≥ 41 S0≥11 (Округляем в большую сторону) |
16*S0 + 5 ≥ 61 16*S0 ≥ 56 S0 ≥ 4 |
Видим, что пункт г) не даёт решений.
В ответ мож
Условие: В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Шахматы | Теннис | 7770 |
| Теннис | 5500 |
| Шахматы & Теннис | 1000 |
Какое количество страниц (в тысячах) будет найдено по запросу
Шахматы?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение: Через Ответ(Z) будем обозначать множество страниц, найденных по запросу Z, а через N(Z) – размер множества Ответ(Z), то есть количество страниц, найденных по запросу Z. В этих обозначениях множество Ответ(X&Y) = это пересечение множеств Ответ(X) и Ответ(Y), а множество Ответ(X | Y) – объединение Ответ(X) и Ответ(Y).
Если по запросу Шахматы | Теннис было найдено 7770 страниц, то среди них были страницы, содержавшие либо оба этих слова, либо только одно из них. Так как страниц, содержащих оба эти слова, было найдено ровно 1000, то из 5500 страниц, содержащих слово «Теннис», 1000 содержит также слово «Шахматы», а 4500 – не содержат этого слова. Поэтому из общего количества 7770 страниц, надо вычесть 4500, на которых есть слово «Теннис», но нет слова «Шахматы». Полученное число в 3270 страниц и будет результатом запроса «Шахматы» и, соответственно, ответом на задание.
Ответ:3270
Замечание. Приведенные рассуждения отражают следующий простой факт из теории множеств. Применительно к нашей задаче его можно записать так. Для любых запросов X и Y выполнено:
N(X | Y) = N(X)+N(Y) – N(X&Y)
Что думаете?
На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 20 задания. Объясняется тема о поиске выигрышной стратегии.
20-е задание: «Поиск выигрышной стратегии»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение найти выигрышную стратегию игры
До ЕГЭ 2021 года — это частично входило в задание № 26 ЕГЭ
Выполнение 20 задания ЕГЭ
20_1: Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Для игры, описанной в предыдущем задании, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
Найденные значения запишите в ответе в порядке возрастания.
Ответ: 31 | 34
Решение подобного задания смотрите на видео:
Видео
Время выполнения-2 мин, уровень сложности-повышенный
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Шахматы | Теннис | 7770 |
| Теннис | 5500 |
| Шахматы & Теннис | 1000 |
Какое количество страниц (в тысячах) будет найдено по запросу Шахматы?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ответ: 3270
Решение:
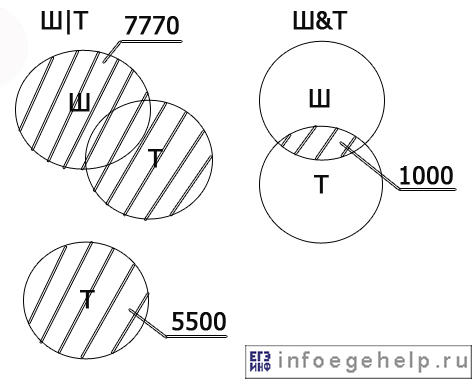
Изобразим запросы в виде диаграмм Эйлера-Венна.
Запрос «Шахматы» обозначим символом «Ш», «Теннис» — символом «Т».
Ш=(Ш|Т)-Т+(Ш&Т)=7770-5500+1000=3270.
Перейти к другим задачам.
Доклад учителя информатики ГБОУ СОШ №1021 Курчавовой Е.В. на тему:
«Информатика + шахматы: от Е2-Е4 до ЕГЭ»
Новый стандарт образования призывает нас нацелить обучающий процесс не на получение учащимися определенной суммы знаний, а на освоение ими универсальных учебных действий через межпредметные связи. Главное — научить ребенка учиться и активировать его способность к саморазвитию.
Курс информатики и ИКТ в нашей школе ориентирован на системно-деятельностный подход к обучению. Чтобы открыть возможность для самостоятельной работы учащихся, а так же сделать её индивидуальной необходимо создать такую обучающую среду, в которой ребенок будет максимально компетентен и мотивирован. То есть он должен в полной мере владеть инструментарием и набором правил, и решать актуальные и интересные для себя задачи. Также необходимо учитывать возрастные особенности учащихся. Сохраняя учебную деятельность как ведущую, можно эффективно использовать элементы игровой деятельности. Ведь она интересна детям.
Курс информатики в начальной школе изучается по программе пропедевтического курса информатики 3-4 кл. (авт. А.С.Семенов Т.А.Рудченко), 2010. В основу построения данного курса положен ряд принципов:
ясные правила игры;
графические и телесные объекты как главные объекты учебной деятельности;
введение всего спектра основных понятий современной информатики и математики на материале наглядных примеров, а не в виде формальных определений для заучивания;
использование естественных языков как основной области реальных приложений математических конструкций.
Основными темами данного курса являются:
Правила игры
Базисные объекты и их свойства
Цепочка
Мешок
Логические значения утверждений
Язык
Алгоритмы. Исполнитель Робик
Дерево
Игры с полной информацией
Математическое представление информации
Решение практических задач
ИКТ-компетентность. Решение практических задач
ИКТ-компетентность. Клавиатурный ввод
Преподавая информатику в 3-4 классах, я обратила внимание на группу ребят, у которых появилась явная положительная динамика относительно своего прежнего уровня. У одних при решении типовых, а у других при решении трудных задач. Явно повысился уровень самостоятельности, изобретательности. Ребята чаще стали выходить к доске, с удовольствием давали на проверку домашние задания, увеличился объем работы на уроке, повысилось внимание и работоспособность детей. Оказалось, что эти ребята посещают кружок по шахматам.
Информатика – это наука о способах получения, накопления, хранения, преобразования и передачи информации и не сводится лишь к овладению навыками работы на компьютере. Основная задача научить ребенка работать с информацией, развить алгоритмическое и логическое мышление. При изучении предмета уже в начальной школе речь идет о знакомстве с графами, комбинаторными задачами, логическими играми с выигрышной стратегией. К тому же необходимо научить ребенка отвечать на вопрос «как решить задачу, которую раньше не решали», используя поиск закономерностей и аналогий, правдоподобные догадки, творческое мышление. Это зачастую вызывает определенные сложности у некоторых учеников. Вы наверняка не раз замечали, что, несмотря на одинаковые программы и условия обучения, разные школьники имеют неодинаковые знания, различные показатели успеваемости, по-разному относятся к учебным обязанностям, то есть фактически получают неодинаковый уровень развития. Потому что ребенок не может действовать только по указаниям и требованиям учителя. Также очень важен склад формирующейся личности. Если у ребенка появляется боязнь неуспешности в учебе, то он испытывает стресс и как следствие удаляется от учебной деятельности вообще и научно-познавательной в частности. В такой ситуации педагогу важно создать наиболее комфортную учебно-воспитательную среду, в которой возможна наиболее полная самореализация ребенка. Еще одной причиной сложностей является очень небольшое количество часов, предусмотренное федеральными образовательными стандартами на изучение предмета информатика как такового, без учета компьютерных технологий.
Недостатки в усвоении материала младшими школьниками можно преодолеть, если развивать в них нравственные и волевые качества: старание, упорство, трудолюбие, настойчивость, ответственность.
Не каждая деятельность обладает развивающей функцией, а только та, которая затрагивает потенциальные возможности ученика, вызывает его творческую познавательную активность, активизирует логическое и алгоритмическое мышление.
Доктор психологических наук Нина Фёдоровна Талызина пишет «…до сих пор нет конкретной программы логических приемов мышления, которые должны быть сформированы при изучении данного предмета, в связи с чем работа над развитием мышления в школе идет стихийно, и большинство учащихся не овладевает начальными приемами мышления даже в старших классах… Традиционное школьное образование тренирует сравнительно ограниченный набор навыков мышления, необходимый для чтения, письма, говорения, математических операций, и очень мало делаем для выработки умений высшего типа – рассуждать логично, критично, творчески, контекстуально, аргументированно, диалогично. В результате в мышлении начинается перекос [Талызина Н.Ф1988 г.175с.].
Такой развивающей функцией обладает игра в шахматы. Василий Александрович Сухомлинский особенно выделял роль шахмат в воспитании культуры мышления и умственном развитии младшего школьника. «Шахматы – превосходная школа последовательного логического мышления. Без шахмат невозможно себе представить полноценного воспитания умственных способностей и памяти. Игра в шахматы должна войти в жизнь начальной школы как один из элементов умственной культуры».[21]
Анализ таких авторских программ по информатике для начальной школы, как «Информатика в играх и задачах» Горячев, пропедевтическая программа курса информатики 3-4 классы А.С.Семенов,Т.А.Рудченко, показал, что уже на этом уровне изучаются: теория алгоритмов, теория графов, теория множеств, теории игр, искусственный интеллект, объекты и системы, закономерности, теория управления и т . д. Это абсолютно необходимо для пропедевтики тех базовых знаний, которые учащиеся будут получать в старших классах. Игра в шахматы позволяет наглядно рассматривать вышеуказанный материал, тем самым позволяя достичь эффекта, о котором писал Джеймс Максвелл: «Нет лучше способа сообщения уму знаний, чем метод преподнесения их в возможно более разнообразных формах». Ведь на чисто шахматные объекты можно посмотреть с позиций различных наук. Обыкновенное шахматное поле можно рассматривать и как единицу шахматного пространства, и как элемент множества полей, образующих линию, и как множество, являющееся пересечением вертикали и горизонтали, которые, по сути, тоже являются множествами. Также его можно представить как элемент кодирования или как точку в системе координат. В программы начальной школы включаются некоторые элементы логики и алгоритмизации, которая является общим фундаментом информатики и шахмат. Поэтому совершенно неудивительно, что шахматы повышают успеваемость учеников по информатике. Удобно рассматривать теорию графов, используя простейшие деревья расчета вариантов. Ребра графа – шахматные ходы, вершины – шахматные позиции, получившиеся в результате этих ходов. Если рассматривать шахматную доску как совокупность полей и комплекта шахматных фигур, то можно обсуждать теорию множеств. Именно шахматы выбрали моделью для развития искусственного интеллекта.
В информатике часто встречаются задачи по управлению ресурсами, связанные с наличием противоречий для достижения цели. Например, задача о волке, козе и капусте, или о рыцарях и оруженосцах, которых необходимо переправить на другой берег, соблюдая определенные условия и т.д. Это задачи на последовательность логического мышления, превосходной школой которого, по словам В.А. Сухомлинского, являются шахматы. В этих задачах тоже присутствуют ходы — операции перевозки через реку и позиции – положение пассажиров по обе стороны реки после каждого хода. Шахматы являются не только логической, но и очень занимательной игрой. Исследования психолога Нины Фёдоровны Талызиной о влиянии занятий шахматами на развитие младших школьников показало, что «целенаправленное формирование основных приемов шахматной игры существенно повышает уровень логического мышления детей, а тем самым и их успехи в овладении школьными предметами» [22]. Шахматы дают возможность ребенку почувствовать себя властелином, главнокомандующим армией, президентом, то есть человеком, способным управлять. Ведь деятельность шахматиста и управленца очень похожа. Шахматы учат управлять ресурсами, причем любыми: экономическими, военными, информационными и т.д. Эта игра учит принимать решения.
Изучение информатики в школе организовано «по спирали». На пропедевтическом уровне изучаются основные направления, которые на следующей ступени изучаются более глубоко, задачи усложняются, включаются некоторые новые понятия. Китайская мудрость гласит: «Я услышал и забыл. Я увидел и запомнил. Я сделал и понял». Изучая шахматы параллельно с информатикой, можно многие сложные темы показать просто и наглядно. Поэтому было бы неплохо организовать шахматный кружок для средней и старшей школы.
Статистика утверждает, что среди учеников, показывающих лучшие результаты ЕГЭ по информатике, как правило, есть шахматисты – победители и призеры городских и окружных соревнований. И это понятно, ведь для сдачи ЕГЭ необходимо обладать не только знаниями, но и выдержкой, скоростью мышления, трудолюбием и выносливостью. Все эти качества шахматист приобретает во время занятий и соревнований. Перед тем как сделать ход, необходимо проанализировать, оценить ситуацию, задавая себе десятки вопросов. Постоянные тренировки позволяют лучше других давать ответы на вопросы в единицу времени.
Оризон Свит Марден говорил: «Внутри каждого человека есть дремлющие силы; силы, способные удивить его самого, так как он зачастую и не предполагает, что обладает ими; силы, способные перевернуть жизнь стоит их только поднять из глубин и привести в действие».
А от себя добавлю, что помочь в этом нам могут шахматы. Играйте в шахматы, друзья!
1. Возрастные и индивидуальные особенности образного мышления учащихся / Под ред. И.С.Якиманской. — М., 1989.
2. Вопросы психологии способностей школьников /Под рук. В.А.Крутецкого. — М., 1964.
3. Горячев А.В. Информатика в играх и задачах. – В сб. Программы общеобразовательных учреждений. Начальные классы (1- 4). В двух частях, часть I. – М.: Просвещение, 2002. – с.309 – 318.
4. Дергачева, Л.М. Информатика в начальной школе [Текст] / Л.М. Дергачева, М.В. Шиленкова, Т.С. Ягодкина.– М.: Образование и Информатика, 2008.– (Информатика в школе; № 8/2008).
5. Информатика -1: Математические основы мышления и коммуникации: Книга для учителя. – М.: Институт новых технологий образования, 1999. – 76 с.
6. Калмыкова З.И. Продуктивное мышление как основа обучаемости. — М., 1981. Якиманская И. С. Принцип активности в педагогической психологии // Вопросы психологии. -1989. — №6.
7. Кузнецов А.А., Семенов А.Л., Уваров А.Ю. О проекте концепции образовательной области. “Информатика и информационные технологии” – Информатика, №17, 2001.
8. Левченко, И.В. Общие вопросы методики обучения информатике в средней школе [Текст] : Учеб. пособие для студентов вузов и университетов / И.В. Левченко, Н.Н. Самылкина.– М.: МГПУ, 2003.
9. Леонтович, А.В. Исследовательская деятельность учащихся (сборник статей) [Электронный документ] / МГДД(Ю)Т; А.В. Леонтович.– (http://www.researcher.ru/methodics/teor/f_1abucy/a_1abujp.html?xsl:print=1). 15.01.2010.
10. Сухомлинский В.А. Сердце отдаю детям. – Киев: Радянска школа, 1974.
11. Талызина Н.Ф. Формирование познавательной деятельности младших школьников. – М.: Просвещение, 1988-175с.
12. Тимофеев А.А.»Концепция обучения шахматам в начальной школе» (Проект) Электронный документ http://chess555.narod.ru/tim2.htm
13. Чередов, И.М. Методы обучения как условия развития активности и самостоятельности учащихся [Текст] / И.М. Чередов; Под ред. И.М. Чередова.– Омск, 2000.
14. Якиманская И. С. Принцип активности в педагогической психологии // Вопросы психологии. -1989. — №6.