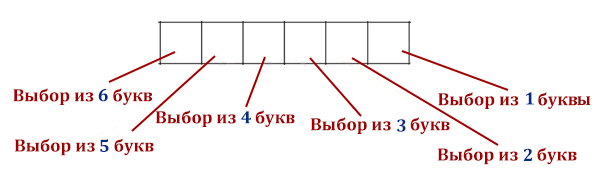
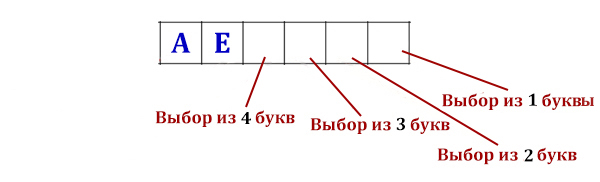
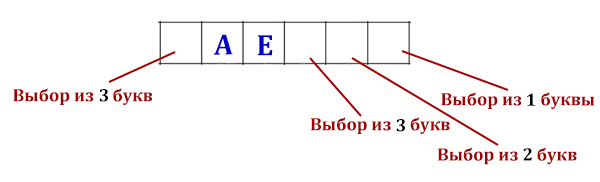
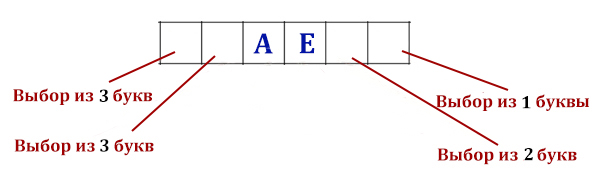
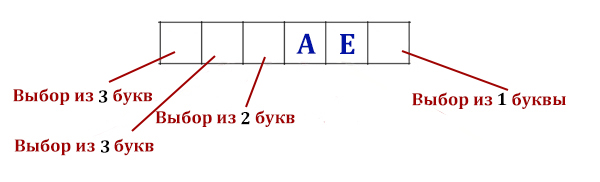
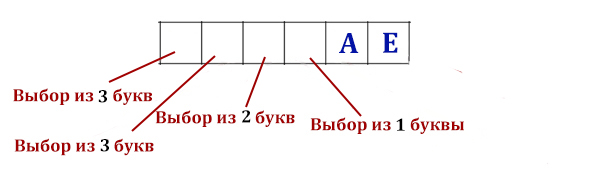
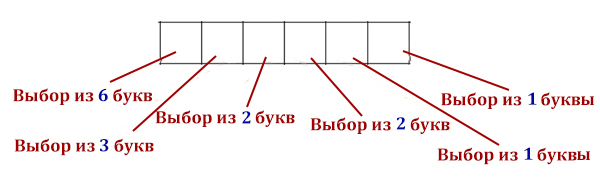
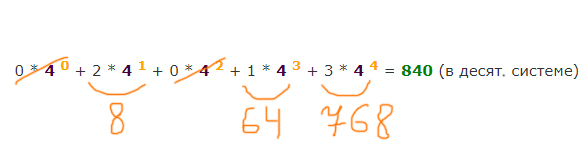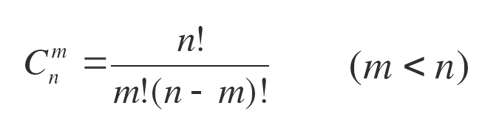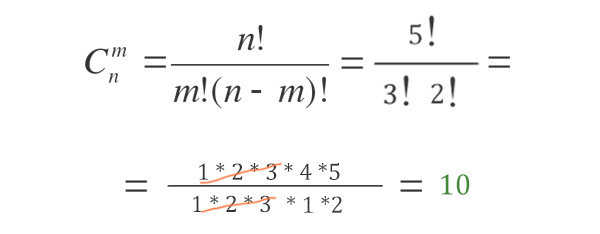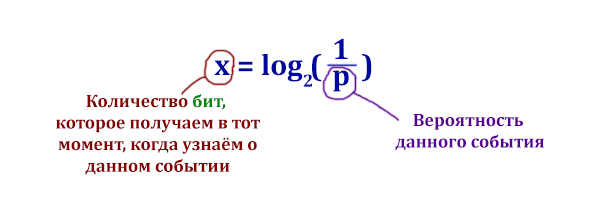Егэ информатика задание 8 лемур - Помощь в подготовке к экзаменам и поступлению

Все четырёхбуквенные слова, в составе которых могут быть только буквы Л, Е, М, У, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1. Ниже приведено начало списка.

1.  ЕЕЕЕ

2.  ЕЕЕЛ

3.  ЕЕЕМ

4.  ЕЕЕР

5.  ЕЕЕУ

6.  ЕЕЛЕ

…

Под каким номером в списке идёт первое слово, которое начинается с буквы Л?

Решение.

Из пяти букв можно составить 5⁴ = 625 четырёхбуквенных слов. Т. к. слова идут в алфавитном порядке, то первая одна пятая часть букв (125 шт) начинаются с «Е», вторая часть (тоже 125)  — с «Л», третья  — с «М», четвёртая  — с «Р», последняя  — с «У», то есть первая буква меняется через каждые 125 слов. Т. е. со слова с номером 126 первой буквой будет Л.

Ответ: 126.

Приведём другое решение на языке Python.

a = {0: «Е», 1: «Л», 2: «М», 3: «Р», 4: «У»}

k = 0

for i in range(0, len(a)):

for j in range(0, len(a)):

for g in range(0, len(a)):

for m in range(0, len(a)):

k += 1

if a[i] == «Л»:

print(k) # Возьмем первое число, которое выведет программа

Источник

Содержание

Разбор демоверсии ЕГЭ по информатике 2022 (6-10 Задание)
Все четырехбуквенные слова в составе которых могут быть только буквы лемур
Демоверсия ЕГЭ 2022 по информатике + видеоразбор
Изменения ЕГЭ 2022 по информатике
Видеоразбор всех изменений
Примеры заданий из демоверсии ЕГЭ 2022
Задание 4
Задание 8
Задание 16
Видеоразбор демоверсии ЕГЭ 2022
Все четырехбуквенные слова в составе которых могут быть только буквы лемур
Все четырехбуквенные слова в составе которых могут быть только буквы лемур

Разбор демоверсии ЕГЭ по информатике 2022 (6-10 Задание)

Продолжаем разбор демонстрационного варианта ЕГЭ по информатике 2022.

В этой статье разберём с 6-ого по 10 задание.

Удачи на ЕГЭ по информатике 2022!

Определите, при каком наибольшем введённом значении переменной s программа выведет число 64. Для Вашего удобства программа представлена на четырёх языках программирования.

Паскаль	Python	Алгоритмический язык
C++

Решим задачу методом перебора на языке программирования Python.

Нас спрашивают, какое наибольшее число должен ввести пользователь программы, чтобы программа распечатала число 64. Мы будем подставлять каждое число в диапазоне, к примеру, от 1 до 1000 и попробуем получить на выходе число 64.

Делаем это с помощью цикла. Как только в переменной n будет значение 64, мы печатаем переменную i

Видим, что максимальное число, которое даёт нужный результат это 259.

Для хранения произвольного растрового изображения размером 128 × 320 пикселей отведено 20 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

Решение:

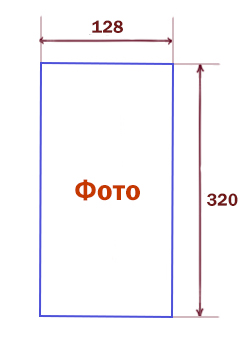
Узнаем, сколько информации будет весить один пиксель (одна точка).

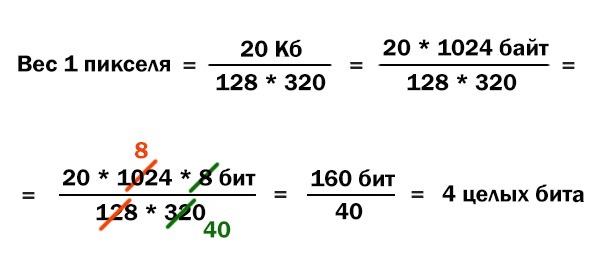
Теперь воспользуемся главной формулой для 7 задания из ЕГЭ по информатике.

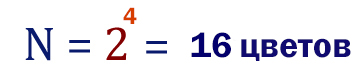
Ответ: 16

Все четырёхбуквенные слова, в составе которых могут быть только буквы Л, Е, М, У, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.

Ниже приведено начало списка.

Под каким номером в списке идёт первое слово, которое начинается с буквы Л?

Закодируем в правом столбце буквы цифрами, начиная с нуля.

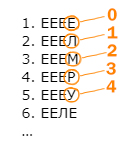
Дальше кодирование прекращаем, т.к. буквы начинают повторяться.

Если представить список в виде цифр, то получится счёт в пятеричной системе, ведь у нас пять цифр.

1. 0000
2. 0001
3. 0002
4. 0003
5. 0004
6. 0010

В вопросе спрашивают про первое слово, которое начинается с буквы Л. А мы понимаем, что спрашивают про число 1000₅ в пятеричной системе, потому что это первое число, которое начинается с 1. Длина числа равна 4, т.к. длина слов равна 4.

Переведём число 1000₅ из пятеричной системы в нашу родную десятичную систему.

0*5 0 + 0*5 1 + 0*5 2 + 1*5 3 = 125

А порядковый номер (столбец слева) отличается от счёта в пятеричной системе на 1. Порядковый номер на 1 больше. Поэтому в ответе напишем 126.

Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел может являться сторонами треугольника, то есть удовлетворяет неравенству треугольника.

В ответе запишите только число.

Неравенство треугольника заключается в том, что каждая сторона должна быть меньше, чем сумма двух других сторон.

Напротив тех строчек, которые удовлетворяют этому неравенству будем ставить 1, остальным ставим 0.

Сформируем формулу для первой строчки. Кликаем в ячейку D1 и нажимаем кнопку Вставить функцию.

Выбираем функцию ЕСЛИ. Пишем логическое выражение:

И(A1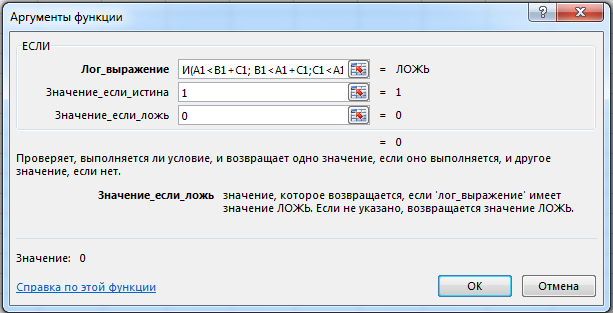

Если одновременно выполняются три условия, то в ячейку идёт 1, иначе 0.

Распространим формулу на весь столбец. Подведём курсор к правому нижнему углу. Как только загорелся чёрный крестик, кликаем два раза, и формула должна распространится на весь столбец.

Возле тех строчек, которые удовлетворяют условию, будут нули, возле тех, которые нет, будут единицы.

Найдём сумму столбца D. Это и будет количество троек, которые подходят в нашей задаче.

Кликаем по ячейке E1, нажимаем Вставить функцию и выбираем функцию СУММ. Там выбираем столбец D мышкой.

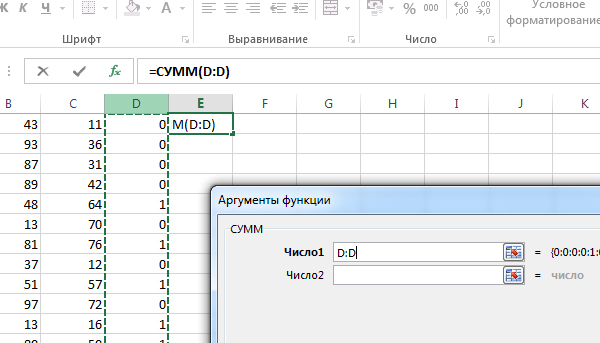
Нажимаем ОК, получается 2453.

С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «долг» или «Долг» в тексте романа в стихах А.С. Пушкина «Евгений Онегин». Другие формы слова «долг», такие как «долги», «долгами» и т.д., учитывать не следует. В ответе укажите только число.

Открываем соответствующий файл в программе Word. На вкладке «Главная» находится кнопка «Найти«. Кликаем по чёрному треугольнику возле этой кнопки и выбираем «Расширенный поиск«.

На вкладке «Главная» находится кнопка «Найти«. Кликаем по чёрному треугольнику возле этой кнопки и выбираем «Расширенный поиск«.

Далее, нажимаем кнопку «Больше>>«.

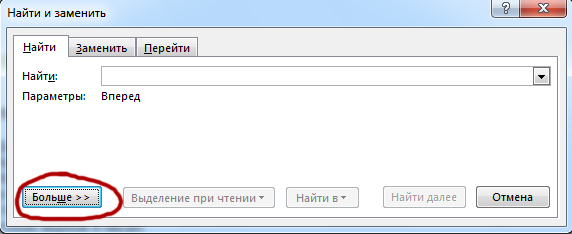
Теперь у нас есть все инструменты, чтобы решить 10 задание из ЕГЭ по информатике 2022.

В поле «Найти» пишем наше слово «долг«. Галочку «Учитывать регистр» не ставим, т.к. слово может быть и с большой буквы. Но ставим галочку «Только слово целом«.

Источник

Все четырехбуквенные слова в составе которых могут быть только буквы лемур

Все 4-буквенные слова, составленные из букв М, У, Х, А записаны в алфавитном порядке и пронумерованы.

Запишите слово, которое стоит под номером 254.

Всего из четырёх букв можно составить 4 4 = 256 4-хбуквенных слов.

Запишем буквы в алфавитном порядке: А, М, У, Х. Очевидно, что последнее слово ХХХХ. Тогда слово с номером 255 запишется как ХХХУ, 254 — ХХХМ.

Все 4-буквенные слова, составленные из букв К, Л, Р, Т, записаны в алфавитном порядке и пронумерованы.

Запишите слово, которое стоит под номером 67.

Заменим буквы К, Л, Р, Т на 0, 1, 2, 3.

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в четверичной системе счисления в порядке возрастания. Тогда на 67 месте будет стоять число 66 (т. к. первое число 0). Переведём число 66 в четверичную систему:

66₁₀ = 1 · 4 3 + 0 · 4 2 + 0 · 4 1 + 2 = 1002₄.

В четверичной системе 66 запишется как 1002. Произведём обратную замену и получим ЛККР.

Все 4-буквенные слова, составленные из букв В, Л, Т, У, записаны в алфавитном порядке и пронумерованы.

Запишите слово, которое стоит под номером 98.

Заменим буквы В, Л, Т, У на 0, 1, 2, 3 соответственно.

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в четверичной системе счисления в порядке возрастания. Тогда на 98-м месте будет стоять число 97 (т. к. первое число 0). Переведём число 97 в четверичную систему:

97₁₀ = 4 3 + 2 * 4 2 + 1 = 1201₄

Произведём обратную замену и получим ЛТВЛ.

Все 4-буквенные слова, составленные из букв В, Л, Т, У, записаны в алфавитном порядке и пронумерованы.

Запишите слово, которое стоит под номером 75.

Заменим буквы В, Л, Т, У на 0, 1, 2, 3 соответственно.

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в четверичной системе счисления в порядке возрастания. Тогда на 75-м месте будет стоять число 74 (т. к. первое число 0). Переведём число 74 в четверичную систему:

74₁₀ = 4 3 + 2 * 4 1 + 2 = 1022₄

Произведём обратную замену и получим ЛВТТ.

Все 4-буквенные слова, составленные из букв Д, Е, К, О, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1. Ниже приведено начало списка.

Под каким номером в списке идёт первое слово, которое начинается с буквы K?

Заменим буквы Д, Е, К, О, Р на 0, 1, 2, 3, 4 соответственно (для них порядок очевиден — по возрастанию).

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в пятеричной системе счисления в порядке возрастания. Первое слово, начинающееся с «К» — 2000 переведём его в десятичную: 2 · 5 3 + 0 · 5 2 + 0 · 5 1 + 0 · 5 0 = 250.

Не забудем о том, что есть слово номер 1, записывающееся как 0, а значит, 250 — число, соответствующее номеру 251.

Все 4-буквенные слова, составленные из букв А, И, О, У, Э, записаны в алфавитном порядке и пронумерованы.

Под каким номером стоит ИААЭ?

Заменим буквы А, И, О, У, Э на 0, 1, 2, 3, 4 соответственно (для них порядок очевиден — по возрастанию).

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в пятеричной системе счисления в порядке возрастания. Слово ИААЭ можно представить в виде: 1004₅ = 129₁₀. Так как порядковый номер на единицу больше, получаем ответ: 130.

Все 4-буквенные слова, составленные из букв В, И, Р, Т, записаны в алфавитном порядке.

Запишите слово, которое стоит на 249-м месте от начала списка.

Заменим буквы В, И, Р, Т на 0, 1, 2, 3 (для них порядок очевиден – по возрастанию).

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в четверичной системе счисления в порядке возрастания. Тогда на 249 месте будет стоять число 248 (т. к. первое число 0). Переведём число 248 в четверичную систему (деля и снося остаток справа налево):

В четверичной системе 248 запишется как 3320. Произведём обратную замену и получим ТТРВ.

Все 4-буквенные слова, составленные из букв М, А, Р, Т, записаны в алфавитном порядке.

Запишите слово, которое стоит на 250-м месте от начала списка.

Заменим буквы А, М, Р, Т на 0, 1, 2, 3. Заметим, что буквы должны заменяться на числовые коды в алфавитном порядке, а не в том порядке, в котором они перечислены в задании.

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в четверичной системе счисления в порядке возрастания. Тогда на 250 месте будет стоять число 249 (т. к. первое число 0). Переведём число 249 в четверичную систему (деля и снося остаток справа налево):

В четверичной системе 249 запишется как 3321. Произведём обратную замену и получим ТТРМ.

Все 4-буквенные слова, составленные из букв С, Л, О, Н записаны в алфавитном порядке и пронумерованы.

Запишите слово, которое стоит под номером 250.

Заменим буквы Л, Н, О, С на 0, 1, 2, 3 (для них порядок очевиден – по возрастанию).

Выпишем начало списка, заменив буквы на цифры:

В четверичной системе 249 запишется как 3321. Произведём обратную замену и получим ССОН.

Все 4-буквенные слова, составленные из букв В, Н, Р, Т, записаны в алфавитном порядке и пронумерованы.

Запишите слово, которое стоит под номером 250.

Заменим буквы В, Н, Р, Т на 0, 1, 2, 3 (для них порядок — по возрастанию).

Выпишем начало списка, заменив буквы на цифры:

В четверичной системе 249 запишется как 3321. Произведём обратную замену и получим ТТРН.

Все 4-буквенные слова, составленные из букв В, Н, Р, Т, записаны в алфавитном порядке и пронумерованы.

Запишите слово, которое стоит под номером 251.

Заменим буквы В, Н, Р, Т на 0, 1, 2, 3 (для них порядок — по возрастанию).

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в четверичной системе счисления в порядке возрастания. Тогда на 251 месте будет стоять число 250 (т. к. первое число 0). Переведём число 250 в четверичную систему (деля и снося остаток справа налево):

В четверичной системе 250 запишется как 3322. Произведём обратную замену и получим ТТРР.

Все 4-буквенные слова, составленные из букв Н, Р, Т, У, записаны в алфавитном порядке. Вот начало списка:

Запишите слово, которое стоит на 215-м месте от начала списка.

Заменим буквы Н, Р, Т, У, на 0, 1, 2, 3 соответственно.

Выпишем начало списка, заменив буквы на цифры:

Полученная запись есть числа, записанные в четверичной системе счисления в порядке возрастания. Тогда на 215-м месте будет стоять число 214 (т. к. первое число 0). Переведём число 214 в четверичную систему:

В четверичной системе 214 запишется как 3112. Произведём обратную замену и получим УРРТ.

Все 4-буквенные слова, составленные из букв М, У, Х, А записаны в алфавитном порядке и пронумерованы.

Напишите номер слова ХУХХ

Пусть букве А соответствует 0, М—1, У —2 и Х—3.

Тогда данный список слов станет последовательно записанным рядом чисел в четверичной системе исчисления.

Слово ХУХХ станет числом 3233. Переведём его в десятичную систему: 3233 = 3 * 4 3 + 2 * 4 2 + 3 * 4 1 + 3 = 3 * 64 + 2 * 16 + 12 + 3 = 192 + 32 + 15 = 239.

Не забудем также про слово АААА (в четверичной системе это 0), которое является первым, поэтому нужный нам номер 239 + 1 = 240.

Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И, записаны в алфавитном порядке и пронумерованы, начиная с 1.

Ниже приведено начало списка.

Под каким номером в списке идёт первое слово, которое начинается с буквы О?

Из пяти букв можно составить 5 4 = 625 четырёхбуквенных слов. Т. к. слова идут в алфавитном порядке, то первая одна пятая часть букв (125 шт) начинаются с «И», вторая часть (тоже 125) – с «К», третья — с «Н», четвёртая — с «О», последняя — с «Т» то есть первая буква меняется через 125 слов. Т. е. со слова с номером 376 первой буквой будет О.

Вася составляет 4-буквенные слова, в которых есть только буквы Б, Е, Л, К, А, причём буква Б используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

Пусть Б стоит в слове на первом месте. Тогда на каждое из оставшихся 3 мест можно поставить независимо одну из 4 букв. То есть всего варианта.

Таким образом, Б можно по очереди поставить на все 4 мест, в каждом случае получая 64 варианта.

Итого получается слов.

Источник

Демоверсия ЕГЭ 2022 по информатике + видеоразбор

Обновление 15.11.2021

Официальная демоверсия ЕГЭ для 2022 года по информатике + спецификация + кодификатор для этого варианта. Автор-составитель: ФИПИ.

Документы по актуальной демоверсии ЕГЭ 2022 по информатике

Изменения ЕГЭ 2022 по информатике

Видеоразбор всех изменений

Текущая версия уже идёт как «предварительные варианты», которые (как правило) не меняются.

Оставляйте свои комментарии ниже. Задавайте вопросы!

Примеры заданий из демоверсии ЕГЭ 2022

Задание 4

Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность
однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся
букв П и Р кодовые слова неизвестны.

Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько,
укажите код с наименьшим числовым значением.

Задание 8

Ниже приведено начало списка.

Под каким номером в списке идёт первое слово, которое начинается с буквы Л?

Задание 16

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = n + F(n − 1), если n чётно,

F(n) = 2 × F(n − 2), если n > 1 и при этом n нечётно.

Чему равно значение функции F(26)?

Видеоразбор демоверсии ЕГЭ 2022

Источник

Все четырехбуквенные слова в составе которых могут быть только буквы лемур

Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

На первом месте может стоять две буквы: Е или Э, на остальных — три. Таким образом, можно составить 2 · 3 · 3 · 3 · 3 = 162 слова.

Сколько слов длины 6, начинающихся с согласной буквы, можно составить из букв Г, О, Д? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

На первом месте может стоять две буквы: Г или Д, на остальных — три буквы. Таким образом, можно составить 2 · 3 5 = 486 слов.

Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

В конце может стоять две буквы: И или А, а в начале — буквы З и М. Таким образом, можно составить 2 · 4 3 · 2 = 256 слов.

Вася составляет 5-буквенные слова, в которых есть только буквы С, Л, О, Н, причём буква С используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

Пусть С стоит в слове на первом месте. Тогда на каждое из оставшихся 4 мест можно поставить независимо одну из 3 букв. То есть всего вариант.

Таким образом, С можно по очереди поставить на все 5 мест, в каждом случае получая 81 вариант.

Итого получается слов.

Источник

Все четырехбуквенные слова в составе которых могут быть только буквы лемур

Два сторожевых отряда, расположенных на большом расстоянии друг от друга, условились передавать друг другу сообщения при помощи сигнальных ракет красного и зеленого цвета. Сколько различных сообщений можно передать таким способом, запустив только 3 ракеты?

Мы имеем 2 возможных события (запуск ракеты), одно событие по сути есть символ, а всё сообщение есть просто 3-буквенное слово. Из M = 2 различных символов можно составить Q = M N слов длиной N = 3, т. е. 2 3 = 8 слов.

Сколько сообщений мог бы передавать светофор, если бы у него одновременно горели сразу три «глаза», а каждый из них мог бы менять цвет и становиться либо красным, либо желтым, либо зеленым?

Один цвет по сути есть символ, а всё сообщение есть просто 3-буквенное слово. Из M = 3 различных символов можно составить Q = M N слов длиной N = 3, т. е. 3 3 = 27 слов.

В детскую игрушку «Набор юного шпиона» входят два одинаковых комплекта из четырех флажков различных цветов. Сколько различных тайных сообщений можно передать этими флажками, условившись менять выставленный флажок каждые пять минут и наблюдая за процессом 15 минут? Наблюдатель видит вынос первого флажка и две перемены флажка. При этом возможна смена флажка на флажок того же цвета.

Каждое событие длится 5 минут, поэтому в сообщении длиной 15 минут будет N = 3 события. Одно событие по сути есть символ, а всё сообщение есть просто 3-буквенное слово.

Имеется 4 различных флажка, значит, 4 символа. Из M = 4 различных символов можно составить Q = M N слов длиной N = 3, т. е. 4 3 = 64 слова.

Примечание. Цвета меняются по очереди, т. е. не нужно иметь три флажка одного цвета.

В этой задаче возможны в одной коробке 2, 3, 4 одинаковых флажка?

Внимательно читайте условие: «. входят два одинаковых комплекта из четырех флажков различных цветов.» То есть флажков каждого цвета два в одной коробке.

Два туристских лагеря, расположенных по разные стороны реки, условились передавать друг другу сообщения при помощи цветных фонариков красного и зеленого цвета, зажигая или гася их на одну минуту. Каждую минуту наблюдатель с другого берега может зафиксировать одно из трех событий: светит красный фонарик, светит зеленый фонарик, не светит ни один фонарик. Сколько различных сообщений длиной в пять минут можно передать таким способом?

Каждое событие длится 1 минуту, поэтому в сообщении длиной пять минут будет N=5 событий. Одно событие по сути есть символ, а всё сообщение есть просто 5-буквенное слово.

Мы имеем 3 возможных события. Из M=3 различных символов можно составить Q = M N слов длиной N = 5, т. е. 3 5 = 243 слова.

Источник

Сегодня на повестке дня 8 задание из ЕГЭ по информатике 2021. Данный тип заданий включает в себя нахождение количества вариантов, элементы комбинаторики и другие математические понятия.

Перейдём к практике решения задач задания 8 ЕГЭ по информатике 2021.

Задача (Классика)

Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…

Запишите слово, стоящее на 248-м месте от начала списка.

Решение:

Обозначим условно А — 0, Е — 1, И — 2, О — 3.

Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом правом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.

Теперь запишем список с помощью цифр.

1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
…

Получился обычный счёт в четверичной системе!! (всего используются 4 цифры: 0, 1, 2, 3). А слева нумерация показывает соответствие нашей десятичной системе. Но все числа десятичной системы в этой таблице соответствия сдвинуты на 1, ведь мы должны были начать с нуля.

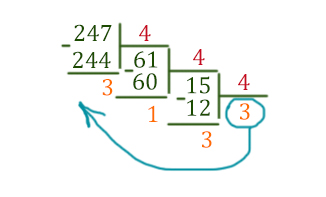
Нас просят записать слово стоящее на 248, т.е. если была обычная таблица соответствия чисел десятичной системы и четверичной системы, слово стоящее на 248 месте, находилось бы на 247 (248 — 1) месте. Значит, наше искомое четверичное число соответствует 247 в десятичной системе.

Переведём число 247 в четверичную систему!

Получилось число 3313₄ в четверичной системе. Сделаем обратное декодирование в буквы. Таким образом, ответ будет ООЕО.

Ответы: ООЕО

Ещё одна похожая задача 8 задания из примерных вариантов ЕГЭ по информатике, но другой вариации.

Задача (Классика, Другая вариация)

Все 5-буквенные слова, составленные из букв А, Р, У, К записаны в алфавитном порядке. Вот начало списка:

1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА

Решение:

Закодируем буквы цифрами: А — 0, К — 1, Р — 2, У — 3. Здесь как раз буквы даны не в том порядке, как они идут в самом правом столбце. Но мы должны кодировать именно в том порядке, как буквы идут в самом правом столбце.

У нас получилось четыре цифры! Значит снова можно слова превратить в таблицу соответствия между десятичной системой и четверичной системой. Но десятичная система смещена на 1 позицию.

1. 00000
2. 00001
3. 00002
4. 00003
5. 00010
……

Выписываем данное нам слово и посмотрим, какое число в четверичной системе было бы, если бы у нас были в место слов числа в четверичной системе!

Получили число в четверичной системе 31020₄. Узнаем, какое число в десятичной системе соответствовало этому числу, если бы была обычная таблица соответствия. Для этого переведём число 31020₄ из четверичной системы в десятичную. Перевод делаем по аналогии перевода из двоичной системы в десятичную.

Но помним, что у нас нумерация идёт на 1 быстрее, нежели мы бы поставили десятичные числа, как в таблице соответствия, потому что нумерация начинается не с нуля, а с 1. Поэтому к числу 840 нужно прибавить 1, и в ответе будет 841

Ответ: 841

Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)

Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И,
записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.

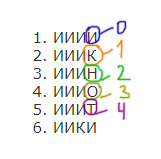
1. ИИИИ
2. ИИИК
3. ИИИН
4. ИИИО
5. ИИИТ
6. ИИКИ
…

Под каким номером в списке идёт первое слово, которое начинается
с буквы О?

Решение:

Закодируем буквы цифрами.

Получилось 5 цифр ( 0, 1, 2, 3, 4 ), значит, будем работать в пятеричной системе.

Нужно найти номер первого слова, которое начинается с буквы О. Если говорить на языке пятеричных чисел, то нужно найти номер числа 3000₅. Мы «забиваем нулями», чтобы число было четырёхразрядное, т.к. слова 4-х буквенные. Именно нулями, потому что нужно именно первое слово найти.

Теперь, как в предыдущей задаче, переведём число 3000₅ из пятеричной системы в десятичную.

0 * 5 ⁰ + 0 * 5 ¹ + 0 * 5 ² +
3 * 5 ³ = 375 (в десят. системе)

Но опять же должны прибавить 1 к числу 375, т.к. нумерация отличается от десятичных чисел на 1 в большую сторону.

Ответ: 376

Задача (Досрочная волна 2020 ЕГЭ по информатике, вариант 1)

Вася составляет 5-буквенные слова, в которых есть только буквы В, О, Л, К,
причём буква В используется в каждом слове ровно 1 раз. Каждая из других
допустимых букв может встречаться в слове любое количество раз или
не встречаться совсем. Словом считается любая допустимая
последовательность букв, не обязательно осмысленная. Сколько существует
таких слов, которые может написать Вася?

Решение:

Для начала решим вводную подзадачу.

Пусть у нас есть те же буквы В, О, Л, К, каждая из букв может встречаться в слове любое количество раз или
не встречаться совсем. Сколько можно составить 5-буквенных слов ?

Т.е буквы могут повторяться!

Например

Такая конструкция сильно напоминает перебор чисел, где вместо цифр используются буквы.

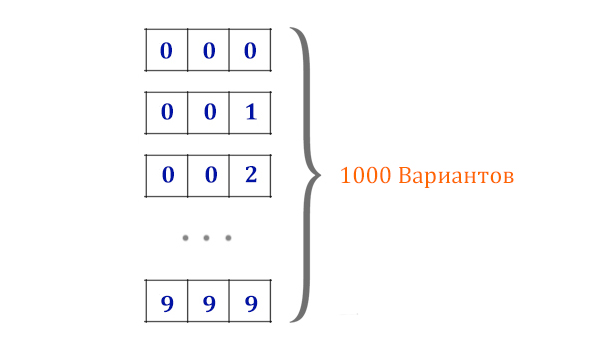
Рассмотрим перебор трёхразрядных чисел. Вместо 5 букв теперь можно использовать 10 цифр ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ). Цифры так же могут повторяться. Сколько получится вариантов ?

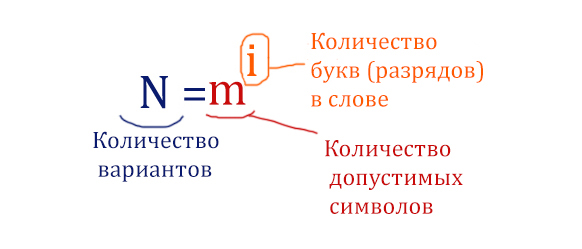
Выведем общую формулу для количества вариантов, когда символы могут повторяться!

Для трёхразрядных чисел от 000 до 999:

N = 10³ = 1000 вариантов.

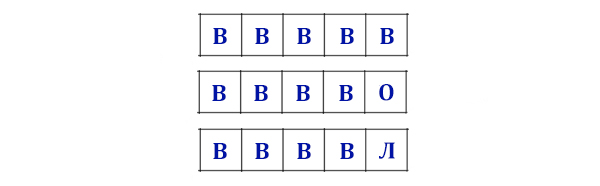
Вернёмся к пятибуквенным словам и нашей подзадаче. Здесь количество букв (разрядов) в слове равно 5, количество допустимых символов равно 4 ( В, О, Л, К ).

N = 4⁵ = 1024 вариантов.

Вернёмся к изначальной задаче. Сначала найдём количество вариантов, когда буква В находится в самой левой ячейке!

Применим формулу! Здесь слово сократилось до четырёхразрядного. А количество букв для использования 3 (О, Л, К).

N = 3⁴ = 81 комбинация.

Но буква В так же может стоять во второй ячейке слева. Этот случай тоже даст 81 других комбинаций. Буква В может стоять в каждой из 5-ти ячеек, и везде будет получатся 81 комбинация.

Таким образом, окончательный ответ будет:

N = 81 * 5 = 405 различных вариантов.

Ответ: 405

Разобравшись с этой задачей, больше половины тренировочных задач десятого задания из различных книг и сайтов по подготовке к ЕГЭ по информатике будут решаться, как по маслу!

Задача(Закрепление формулы)

Рассматриваются символьные последовательности длины 5 в шестибуквенном алфавите {У, Ч, Е, Н, И, К}. Сколько существует таких последовательностей, которые начинаются с буквы У и заканчиваются буквой К?

Решение:

Применим главную формулу 8 задания из ЕГЭ по информатике

N = mⁱ = 6³ = 216

Здесь буквы могут изменяться на 3 ячейках! Значит, в формуле i=3. Количество допустимых символов, которые можно поставить в каждую ячейку равно 6. Значит, в формуле m=6.

В ответе будет 216.

Примечание: Здесь можно использовать все буквы в каждой ячейке, включая У и К. В некоторых задачах их уже использовать нельзя, т.е. сказано, что буквы У и К используются один раз в слове. Тогда в формуле m, будет на 2 единицы меньше. Нужно внимательно читать задачу!

Ответ: 216

Задача (Демонстрационный вариант ЕГЭ по информатике, 2019)

Вася составляет 5-буквенные слова, в которых есть только буквы З, И, М, А,
причём в каждом слове есть ровно одна гласная буква и она встречается
ровно 1 раз. Каждая из допустимых согласных букв может встречаться
в слове любое количество раз или не встречаться совсем. Словом считается
любая допустимая последовательность букв, не обязательно осмысленная.
Сколько существует таких слов, которые может написать Вася?

Решение:

Рассмотрим количество вариантов, когда гласная И стоит в первом месте!

Подсчитаем количество слов с помощью супер-формулы

N = mⁱ = 2⁴ = 16

Длина изменяющихся ячеек равна 4, а количество допустимых букв равно 2.

Но буква И может стоять не только на первом месте. Она так же может стоять и на 2, и на 3, и на 4, и на 5 месте. Каждый такое случай добавляет столько же новых слов.

Значит, при использовании только буквы И будет количество слов 16 * 5 = 80. Ещё столько же слов добавится, если в словах вместо буквы И будет использоваться буква А. Поэтому окончательный ответ будет 80 * 2 = 160

Ответ: 160

Отработаем главную формулу 8 задания из ЕГЭ по информатике.

Задача (Развиваем понимание формулы!)

Решение:

Рассмотрим, какие варианты могут быть, если у нас на первом месте стоит согласная, а на последнем месте гласная

Получилось 4 разных случая. Подсчитаем, сколько слов можно составить при одном случае.

N = mⁱ = 4³ = 64

Длина изменяющихся ячеек равна 3, а количество возможных букв 4.

Но т.к. таких случая у нас четыре, то ответ будет 4 * 64 = 256

Ответ: 256

Рассмотрим важнейший «метод умножения» при решении 8 задания из ЕГЭ по информатике.

Задача (Другой метод решения!!)

Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз , при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?

Решение:

Эта задача отличается от уже разобранных тем, что каждую букву можно использовать один раз. В этой задаче удобнее воспользоваться немного другим методом решения! «Методом умножения»!

Решим вводную подзадачу (без дополнительных ограничений).

Сколькими способами можно составить 6-x буквенное слово из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз .

Чтобы найти возможные варианты, перемножаем для каждой ячейки количество букв из которых у нас есть выбор!

N = 6 * 5 * 4 * 3 * 2 * 1 = 720

Вернёмся к изначальной задаче!

В начале подсчитаем «методом умножения» количество слов, не обращая внимание, на условие, в котором сказано, что слово не может содержать сочетание АЕ.

N = 5 * 5 * 4 * 3 * 2 * 1 = 600

В формуле стоят почти все те же самые числа, как и в вводном примере, только первый множитель не 6, а 5. Это произошло из-за того, что у нас в задаче слово не может начинаться на букву Й. Значит, выбор на первую позицию будет не из 6 букв, а из 5.

Но в 600 комбинаций входят и те случаи, когда в слове присутствует сочетание АЕ. Теперь найдём сколько таких слов, где присутствует сочетание АЕ

Узнаем количество вариантов в каждом таком случае.

N1 = 4 * 3 * 2 * 1 = 24

На первом месте мы не можем использовать букву Й, поэтому мы на первом месте выбираем из 3 букв.

N2 = 3 * 3 * 2 * 1 = 18

Аналогично предыдущему случаю.

N3 = 3 * 3 * 2 * 1 = 18

N4 = 3 * 3 * 2 * 1 = 18

N5 = 3 * 3 * 2 * 1 = 18

Всего слов с сочетанием АЕ будет

24 + 18 + 18 + 18 + 18 = 96

Значит, всего слов, которые удовлетворяют условию задаче будет

N = 600 — 96 = 504

Примечание: Метод умножения можно было использовать и в задачах, которые мы рассмотрели ранее. Например, в задаче «Закрепление формулы» в первой свободной ячейке выбираем из 6 букв, во второй свободной ячейке тоже из 6 букв, и в третий свободной ячейке тоже можно использовать 6 букв. Значит, по методу умножения получается N = 6 * 6 * 6 = 6³ = 216

Ответ: 504

Задача (Закрепления «метода умножения»)

Полина составляет 6-буквенные коды из букв П, О, Л, И, Н, А. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Полина?

Решение:

Опять сказано, что каждая буква используется 1 раз, следовательно, нужно применять «метод умножения».

На первое место можно выбрать из 6 букв, предположим, мы выберем согласную. Тогда на второе место нужно выбирать из 3 гласных. Потом опять должна идти согласная, но их у нас осталось только 2. Далее, на следующее место выбираем из 2 гласных букв. И на предпоследнее место выбирается 1 согласная, а на последнее место остаётся 1 гласная.

Т.к. количество гласных букв и согласных одинаковое, и равно трём, то если мы бы начали делать «метод умножения» с гласной буквы, количество вариантов бы не поменялось.

N = 6 * 3 * 2 * 2 * 1 * 1 = 72

Ответ: 72

Задача (Азбука Морзе)

Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее трёх и не более четырёх сигналов (точек и тире) ?

Решение:

Зная формулу, без проблем решим данную примерную задачу из ЕГЭ по информатике.

У нас есть 2 символа, которые можно использовать: точка и тире. Фраза, что сообщение может иметь «не менее трёх и не более четырёх сигналов», означает, что сообщения могут быть длиною 3 символа и длиною 4 символа.

Подсчитаем общее количество вариантов.

N = 2³ + 2⁴ = 8 + 16 = 24 комбинаций.

Значит, для 24 различных символов (цифр, букв, знаков пунктуации и т.д.) мы найдём различные комбинации, чтобы их закодировать

Ответ: 24

Задача (Обратная предыдущей)

Световое табло состоит из цветных индикаторов. Каждый индикатор может окрашиваться в четыре цвета: белый, черный, желтый и красный. Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 300 различных сигналов?

Решение:

Нам нужно закодировать 300 различных вариантов! Имеются 4 различных лампочки! (Они имеют смысл, как количество допустимых символов!) На этот раз нужно узнать количество лампочек (количество разрядов, «длину слова»). Применяем формулу.

N = 4^x = 300

Не найдётся такое целое x, чтобы равенство стало верным. Поэтому берём целое минимальное x такое, чтобы 4^x больше 300.

4⁵ = 1024

Пять лампочек на табло хватит, чтобы закодировать 300 сигналов, но, к сожалению, много комбинаций просто не пригодится!

Ответ: 5

Задача (Важная!)

Нужно выбрать в подарок 3 книги из 5. Сколькими способами можно выбрать ?

Решение:

На рисунке показано две комбинации, как можно выбрать в подарок 3 книги из 5.

Данную задачку нужно решать используя формулу сочетаний из раздела комбинаторика.

n — количество книг, из которых мы выбираем подарок, m — количество книг, которое мы хотим выбрать, C — количество вариантов (способов).

Восклицательный знак — это факториал!

Факториалом числа «n» (условное обозначение n!- читается как «эн» — факториал) называется произведение чисел от 1 до «n»

Примечание: При использовании формулы сочетаний, не важен порядок, в котором мы выбираем одни и те же книги. Это будет один и тот же вариант.

Ответ: 10

Следующая задача часто встречается в книгах по подготовке к ЕГЭ по информатике.

Задача (Главная формула + сочетания)

Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 5. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 встречается ровно три раза, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?

Решение:

В начале нужно посчитать, сколькими способами на 5-ти ячейках можно расположить 3 единицы!

Обратите внимание, как будто мы выбираем 3 книги в подарок из 5 возможных! Значит, опять применяем формулу сочетаний из комбинаторики. Мы вычисляли уже её точно с такими же числами в прошлой задаче, количество вариантов равно 10.

Подсчитаем, сколько вариантов кодового замка можно составить при одном определённом расположении трёх единиц.

Применим формулу, есть две ячейки, в которых изменяются цифры, а в каждой ячейке может быть одна из 4 цифр.

N = mⁱ = 4² = 16

Т.к. различных вариантов, как расположить единицы на 5 ячейках равно 10, то ответ будет 16 * 10 = 160

Ответ: 160

Ещё одна задача из примерных вариантов по подготовке к ЕГЭ по информатике.

Задача (Таблица соревнований)

Для записи результатов соревнований используется таблица, в которой для каждой из 20-ти команд по каждому из 10-ти видов состязаний записано 1, 2 или 3 (если команда заняла соответствующее место в этом состязании) или прочерк (если не заняла призовое место или не участвовала). Какое количество информации (бит) содержит таблица ?

Решение:

Есть таблица с 20 командами и для каждой команды есть результат по 10-ти видам состязаний.

	1 команда	2 команда	3 команда	…	20 команда
1 дисциплина	1	—	1	…	3
2 дисциплина	—	2	1	…	2
…	…	…	…	…	…
10 дисциплина	1	1	2	…	—

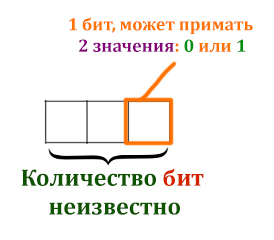
В каждой ячейке может быть 4 различных значения ( 1, 2, 3, — ). Нужно узнать, сколько бит занимает одна ячейка таблицы. Один бит может быть либо единицей, либо нулём.

Сделав рисунок, задача обрела привычные очертания.

Как будто мы решаем задачу с перебором слов. Но здесь длина слова неизвестна, а количество вариантов, которое должно получится уже дано и равно 4 (четырём). Применим главную формулу из 10 задания из ЕГЭ по информатике.

N = mⁱ = 2ⁱ = 4

i=2 бита (длина равна «2 буквам», если воспринимать задачу, как со словами.)

Одна ячейка таблицы весит 2 бита. Найдём количество ячеек во всей таблице соревнований.

Всего ячеек = 20 * 10 = 200

Тогда вся таблица будет весит:

V = 2 бита * 200 = 400 бит.

Ответ: 400

Формула Шеннона

Задача (Формула Шеннона)

В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?

Решение:

Данную задачу нужно решать по формуле Шеннона

Найдём вероятность p того, что вытащили чёрный шарик.

p = (количество чёрных шаров) / (количество всех шаров) = 8 / (24 + = 8 / 32 = 1 /4

p = 1 / 4

Применим формулу Шеннона.

x = log₂(4)
2^x = 4

x = 2 бита

Ответ: 2

Доброго времени суток ! Помогите пожалуйста решить задачу .) Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?

В закрытом ящике находится 32 карандаша, некоторые из них синего цвета. Наугад вынимается один карандаш. Сообщение «этот карандаш – НЕ синий» несёт 4 бита информации. Сколько синих карандашей в ящике?
Был бы очень рад , если вы разберете и эту задачку

Добрый день. Полностью разобрал этот номер, но наткнулся на один интересный пример. Объясните доступным языком, пожалуйста. На решу егэ вообще не понял их решение:

Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Т должна входить в код не менее одного раза, а буква Й — не более одного раза. Сколько различных кодов может составить Тимофей? (ответ: 8006)

Добрый день! Подскажите пожалуйста, как решить следующую задачу: Сколько существует чисел, шестнадцатеричная запись которых содержит 3 цифры, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом.

Петя составляет семибуквенные слова перестановкой букв слова АССАСИН. Сколько всего различных слов может составить Петя? Мое решение: 21 вариант с буквой А, 35- с буквой С, и 4 на буквы И и Н. Всего 60 и умножаем на 7. Получается 420. Не уверена, что применила верный алгоритм. Прокомментируйте, пожалуйста, решение

Можете заказать решение задачи через раздел «связь».

В Задаче (Другой метод решения!!) допущена ошибка в решении, ведь 24 + 18 + 18 + 18 + 18 = 114,значит N = 600 — 114 = 486!

Добрый день! Помогите пожалуйста решить задачку
Сколько чисел длиной 6 можно составить, если известно, что цифры идут в порядке убывания, при этом четные и нечетные цифры чередуются?

У меня только один вопрос. Почему в школах на уроках информатики вместо действительно полезного изучения какого нибудь языка программирования, заставляют заниматься вот этой вот ересью и решать какое по счету слово напишет Вася? Я могу только составить в ответ на это только слова которые нельзя здесь писать. От таких знаний и занятий ни один ребенок не захочет стать программистом, потому что это непонятно, и неизвестно зачем уметь решать такие задачи. Я сам программист с 10 летним стажем не смог объяснить ребенку как решать некоторые задачи и самое главное, я не знаю зачем дети должны уметь это решать.

Дмитрий, согласен с Вами. Особенно 11 задание и формула Шеннона. Надо либо излагать задание корректно, либо исключить вообще: «В корзине лежат черные и белые шары. Среди них 18 черных шаров. Сообщение о том, что достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине?» — для двух состояний достаточно одного бита.

marvell special for u

c = 0
from itertools import*
for i in permutations(‘МАТВЕЙ’, r=6):
i = ».join(i)
if i[0] != ‘Й’ and i.count(‘АЕ’) == 0:
print(i)
c += 1
print(c)

Источник

Содержание:

Решение 8 задания
- Сколько вариантов шифра или кодовых слов
- Сколько существует n-значных чисел, записанных в m-ной системе счисления
- Список в алфавитном порядке
- Вероятность событий

8-е задание: «Измерение количества информации»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 4 минуты.

Проверяемые элементы содержания: Знание о методах измерения количества информации

До ЕГЭ 2021 года — это было задание № 10 ЕГЭ

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Сколько вариантов шифра или кодовых слов

8_1:

Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 6.

Сколько различных вариантов шифра можно задать, если известно, что цифра 1 должна встречаться в коде ровно 1 раз, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?

Типовые задания для тренировки

Ответ: 3125

✍ Показать решение:

✎ Решение теоретическое:

Формула нахождения количества различных сообщений:

Q = N^L

Итак, что у нас дано из этой формулы:
Длина сообщения (L) = 5 символов
Мощность алфавита (N) = 6 (цифры от 1 до 6).
Но так как цифра 1 встречается по условию ровно один раз, а остальные 5 цифр — любое количество раз, то будем считать, что N = 5 (цифры от 2 до 6, исключая 1).
Найдем количество вариантов для одного случая, а именно: когда единица стоит на первом месте, а остальные 5 цифр размещаем на четыре позиции:

1 5 5 5 5 - 1 * Q = 5⁴ = 625

Найдем количество вариантов двумя разными способами (можно выбрать любой из них):
✎ 1 способ. Найдем количество вариантов методом перебора:

Методом перебора найдем количество вариантов размещения:

1 5 5 5 5 - 1 * Q=5⁴ = 625
5 1 5 5 5 - 1 * Q=5⁴ = 625
5 5 1 5 5 - 1 * Q=5⁴ = 625
5 5 5 1 5 - 1 * Q=5⁴ = 625
5 5 5 5 1 - 1 * Q=5⁴ = 625

получили 5 вариантов;

✎ 2 способ. Найдем количество вариантов при помощи формулы комбинаторики:

[ C{binom{4}{5}}= frac{5!}{4!(5-4)!} = 5 ]

получили 5 вариантов, так же как и в первом способе;
В итоге получили 625 вариантов на каждый из пяти случаев, т.е.:

625 * 5 = 3125

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := '123456';
  foreach var s1 in str do
    foreach var s2 in str do
      foreach var s3 in str do
        foreach var s4 in str do
          foreach var s5 in str do
          begin
            if (s1 + s2 + s3 + s4 + s5).CountOf('1') = 1 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='123456'.Cartesian(5) 
.where(w->w.countOf('1')=1)// кол-во '1' в слове
.count.print

Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='123456'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
        for s5 in str:
          if (s1+s2+s3+s4+s5).count('1')==1:
            n+=1
print(n)

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_2:

Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является либо буквой (A или B) или цифрой (1, 2 или 3).

Сколько различных вариантов шифра можно задать, если известно, что в коде присутствует ровно одна буква, а все другие символы являются цифрами?

Ответ: 810

✍ Показать решение:

✎ Решение теоретическое:

Формула нахождения количества различных сообщений:

Q = N^L

Посчитаем количество возможных шифров для одного из вариантов (например, когда буквы находятся на первой позиции). Так как цифры (1, 2, 3) могут занимать 4 позиции из пяти, а две буквы (А и В) одну из позиций, значит:

Q = 2 * 3⁴ = 162

Имеем 162 вариантов шифра для слова, в котором буквы могут стоять на первой позиции:

AB  123 123 123 123 = 162

Получим все варианты размещения:

"2" означает одна из двух букв: А или B, "3" - одна из трех цифр:

2 3 3 3 3 -> Q = 2 * 3⁴ = 162
3 2 3 3 3 -> Q = 2 * 3⁴ = 162
3 3 2 3 3 -> Q = 2 * 3⁴ = 162
3 3 3 2 3 -> Q = 2 * 3⁴ = 162
3 3 3 3 2 -> Q = 2 * 3⁴ = 162

Получили 5 вариантов с размещением букв А и B.
Осталось умножить:

5 * 162 = 810

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'AB123';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5];
            if (res.CountOf('A') = 1) and (res.CountOf('B') = 0) 
            or (res.CountOf('B') = 1) and (res.CountOf('A') = 0) then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='АВ123'.Cartesian(5) 
.where(w->w.count(letter -> letter in 'АВ')=1)// кол-во букв в слове
.count.print

Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='AB123'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
        for s5 in str:
          if ((s1+s2+s3+s4+s5).count('A')==1 and (s1+s2+s3+s4+s5).count('B')==0) 
          or ((s1+s2+s3+s4+s5).count('B')==1 and (s1+s2+s3+s4+s5).count('A')==0):
            n+=1
print(n)

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_3:

Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, Б, В, Г, Д и Е, причём буква Г появляется ровно 1 раз и только на первом или последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.

Сколько различных кодовых слов может использовать Олег?

Ответ: 250

✍ Показать решение:

✎ Решение теоретическое:

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
Рассмотрим варианты, когда буква Г встречается на первом или последнем месте:

Г ? ? ? = 1 * 5 * 5 * 5 = 5³ = 125 
? ? ? Г = 5 * 5 * 5 * 1 = 5³ = 125

Вместо знаков ? может стоять одна из пяти букв (А, Б, В, Д, Е), т.к. буква Г там стоять не может
Теперь суммируем количество найденных вариантов:

125 + 125 = 250

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'АБВГДЕ';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4];
            if (res[1]='Г') and (res[2]<>'Г') and (res[3]<>'Г') and (res[4]<>'Г')
            or (res[1]<>'Г') and (res[2]<>'Г') and (res[3]<>'Г') and (res[4]='Г') then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='АБВГДЕ'.Cartesian(4)
.where(w->(w.countOf('Г')=1)and((w.First='Г')or(w.Last='Г'))) // или: 
// .where(w->(w.countOf('Г')=1)and(w[1]<>'Г')and(w[2]<>'Г'))
.count.print

Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='АБВГДЕ'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
        if (s1 =='Г') and (s2!='Г') and (s3!='Г') and (s4!='Г') 
        or (s1 !='Г') and (s2!='Г') and (s3!='Г') and (s4=='Г'):
            n+=1
print(n)

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_4:

Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является одной из букв X, Y или Z.

Сколько различных вариантов шифра можно задать, если известно, что буква X должна встречаться в коде ровно 2 раза, а каждая из других допустимых букв может встречаться в шифре любое количество раз или не встречаться совсем?

Типовые задания для тренировки

Ответ: 80

✍ Показать решение:

✎ Решение теоретическое:

Формула нахождения количества различных сообщений:

Q = N^L

Итак, что у нас дано из этой формулы:
Начальная мощность алфавита (N) = 3 (буквы X, Y, Z). Но так как буква X встречается ровно два раза, то мы ее рассмотрим отдельно, а остальные 2 буквы — встречаются любое количество раз, значит, будем считать, что:

N = 3 - 1 = 2 (Y и Z)

Исходя из предыдущего пункта, длина сообщения тоже сократится:

(L) = 5 - 2 = 3 символа (остальные два символа отведем на размещение X)

Количество различных сообщений (вариантов шифра) = Q = ?
Т.е. для одного варианта размещения (для одного варианта шифра) имеем:

X X ? ? ? -> 1² * Q = 2³ = 8

Согласно условию получим следующие варианты размещения:

✎1 способ. Перебор всех вариантов:

X X ? ? ? - 1² * Q = 2³ = 8
X ? X ? ? - 1² * Q = 2³ = 8
X ? ? X ? - 1² * Q = 2³ = 8
X ? ? ? X - 1² * Q = 2³ = 8
? X X ? ? - 1² * Q = 2³ = 8
? X ? X ? - 1² * Q = 2³ = 8
? X ? ? X - 1² * Q = 2³ = 8
? ? X X ? - 1² * Q = 2³ = 8
? ? X ? X - 1² * Q = 2³ = 8
? ? ? X X - 1² * Q = 2³ = 8

✎ 2 способ. При помощи формулы поиска числа сочетаний:

[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]

Число сочетаний из n элементов по k элементов:

[ C{binom{2}{5}}= frac{5!}{2!(5-2)!} = frac{120}{12} = 10 ]

* Факториал числа: n! = 0 * 1 * 2 * 3 * .. * n

Количество вариантов найдено верно, т.к. результат обоих способов = 10. В итоге получаем:

8 * 10 = 80

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'xyz';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5];
            if res.countOf('x') = 2 then // или if res.Count(y -> y = 'x') = 2 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='XYZ'.Cartesian(5)
.where(w->w.countOf('X')=2)
.count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='xyz'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
        for s5 in str:
          if (s1+s2+s3+s4+s5).count('x') == 2:
            n+=1
print(n)

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_5:

Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв ОСЕНЬ? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

Типовые задания для тренировки

Ответ: 500

✍ Показать решение:

✎ Решение теоретическое:

Из букв слова ОСЕНЬ имеем 2 гласных буквы (О, Е) и 2 согласных буквы (С, Н). Буква мягкий знак «нейтральна».
Подсчитаем количество букв на каждой из 5 позиций:

2   5   5   5   2
^{СН   все  все  все   ОЕ}

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
Т.е. количество вариантов равно произведению полученных чисел:

N = 2 * 5 * 5 * 5 * 2 = 500

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'ОСЕНЬ';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5];
            if ((res[1] = 'С') or (res[1] = 'Н')) and ((res[5] = 'О') or (res[5] = 'Е')) then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

1	'ОСЕНЬ'.Cartesian(5).Where(w->w[0] in 'СН').Where(w->w[4] in 'ОЕ').Count.Print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

str = 'ОСЕНЬ'
n = 0
for s1 in str:
    for s2 in str: 
        for s3 in str:
            for s4 in str:
                for s5 in str:
                    res = s1 + s2 + s3 + s4
                    if (s1 == 'С' or s1 == 'Н') and (s5 == 'О' or s5 == 'Е'):
                        n += 1
print(n)

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_6:

Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.

Ответ: 175

✍ Показать решение:

✎ Решение теоретическое:

✎ 1 способ:

Количество вариантов различных слов вычислим по формуле:

N = n1 * n2 * n3 * …
где

n1 — количество вариантов выбора первой буквы и т.п.
Рассмотрим все варианты расположения буквы Е:

1. Е ? ? ? или 
2. ? Е ? ? или 
3. ? ? Е ? или
4. ? ? ? Е 

Где вопросительный знак означает любую букву из Л, Е, Т, О.

Подсчитаем по формуле количество слов для варианта 1:

Е ? ? ? = 1 * 4 * 4 * 4 = 64

т.е. на первой позиции - только 1 буква - Е, на каждой последующей - одна из четырех букв Л, Е, Т, О.

Подсчитаем по формуле количество слов для варианта 2; учтем, что на первой позиции букву Е мы уже посчитали для первого варианта!:

? Е ? ? = 3 * 1 * 4 * 4 = 48

Подсчитаем по формуле количество слов для варианта 3; учтем, что на первой и второй позициях букву Е мы уже посчитали в предыдущих вариантах!:

? ? Е ? = 3 * 3 * 1 * 4 = 36

Подсчитаем по формуле количество слов для варианта 4; учтем, что на первой, второй и третьей позициях букву Е мы уже посчитали в предыдущих вариантах:

? ? ? Е = 3 * 3 * 3 * 1 = 27

Поскольку у нас каждый вариант связан операцией логическое ИЛИ, то теперь суммируем все варианты:

64 + 48 + 36 + 27 = 175

Результат: 175
✎ 2 способ:

Так как по условию буква Е встретится хотя бы 1 раз, значит, можно утверждать, что не может быть такого, чтобы буква Е не встретилась бы ни одного раза.
Таким образом, рассчитаем случай, когда буква Е встречается все 4 раза (т.е. все случаи) и отнимем от результата невозможный случай: когда буква Е не встретится ни одного раза:

1. Буква Е используется 4 раза (т.е. на всех позициях):
4 * 4 * 4 * 4 = 256

2. Буква Е не используется совсем (т.е. только 3 буквы):
3 * 3 * 3 * 3 = 81

Вычтем из первого варианта невозможный вариант № 2:

256 - 81 = 175

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'ЛЕТО';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4];
            if res.countOf('Е') >= 1 then // или if res.Count(y -> y = 'Е') >= 1 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='лето'.Cartesian(4).where(w->w.countOf('е')>=1).count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='ЛЕТО'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
          if (s1+s2+s3+s4).count('Е') >= 1:
            n+=1
print(n)

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_7:

Вася составляет 4-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.

Ответ: 113

✍ Показать решение:

✎ Решение теоретическое:

Количество возможных вариантов слов вычислим по формуле:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
Сначала по формуле получим все варианты для всех пяти букв, включая букву Р:

5 * 5 * 5 * 5 = 5⁴ = 625

Из общего количества вариантов нам необходимо исключить те варианты, где Р не встречается вообще и Р встречается только 1 раз. Найдем их последовательно:
1. Буква Р не встречается совсем:

4 * 4 * 4 * 4 = 4⁴ = 256

2. Буква Р встречается только один раз:

р ? ? ? = 1 * 4 * 4 * 4 = 4³
? р ? ? = 4 * 1 * 4 * 4 = 4³
? ? р ? = 4 * 4 * 1 * 4 = 4³
? ? ? р = 4 * 4 * 4 * 1 = 4³

Получим  4³ * 4 = 256

Теперь вычтем из общего количества найденные варианты (№ 1 и № 2):

625 - 256 - 256 = 113

✎ Решение с использованием программирования:

PascalABC.net (традиционный):

begin
  var n := 0;
  var str := 'КАТЕР';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4];
            if res.CountOf('Р') >= 2 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (LINQ):

1 2	## var d:='катер'.Cartesian(4).where(w->w.countOf('р')>=2).count.print

Python:

n=0
str='КАТЕР'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
          if (s1+s2+s3+s4).count('Р') >= 2:
            n+=1
print(n)

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_8:

Вася составляет 4-буквенные слова, в которых есть только буквы К, О, М, А, Р, причём буква А используется в них не более 3-х раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.

Ответ: 624

✍ Показать решение:

✎ Решение теоретическое:

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы,
n2 — количество вариантов выбора второй буквы и т.п.
Так как буква А по условию используется не более 3-х раз, это значит, что она используется либо 3 раза, либо 2 раза, либо 1 раз, либо не используется совсем. Рассмотрим все эти варианты отдельно.
1. Буква А используется 3 раза:

А А А _  -> 1 * 1 * 1 * 4 = 4
А А _ А  -> 1 * 1 * 4 * А = 4
А _ А А  -> 1 * 4 * 1 * 1 = 4
_ А А А  -> 4 * 1 * 1 * 1 = 4

Итого получаем 4 варианта, в которых вместо символа _ может быть любая из 4 букв: К О М Р. Значит, имеем:

 4 * 4 = 16 вариантов

2. Буква А используется 2 раза:

А А _ _  -> 1 * 1 * 4 * 4 = 16
А _ А _  -> 1 * 4 * 1 * 4 = 16
А _ _ А  -> 1 * 4 * 4 * 1 = 16
_ А А _  -> 4 * 1 * 1 * 4 = 16
_ А _ А  -> 4 * 1 * 4 * 1 = 16
_ _ А А  -> 4 * 4 * 1 * 1 = 16

Итого получаем 6 вариантов, в которых вместо символа _ может быть любая из 4 букв: К О М Р. Значит имеем:

 16 * 6 = 96 вариантов

3. Буква А используется 1 раз:

А _ _ _  -> 1 * 4 * 4 * 4 = 64
_ А _ _  -> = 64
_ _ А _  -> = 64
_ _ _ А  -> = 64

Итого имеем:

64 * 4 = 256 вариантов

Буква А используется 0 раз:

_ _ _ _ -> 4⁴ = 256

Суммируем результаты всех трех случаев:

16 + 96 + 256 + 256 = 624

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'КОМАР';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4];
            if res.CountOf('А') <=3 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

1
2
3

##
var d:='комар'.Cartesian(4)
.where(w->w.countOf('а')<=3).count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

str = 'КОМАР'
n = 0
for s1 in str:
    for s2 in str: 
        for s3 in str:
            for s4 in str:
                res = s1 + s2 + s3 + s4
                if res.count('А')<=3:
                    n += 1
print(n)

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_10:

Сколько существует различных символьных последовательностей длины 3 в четырёхбуквенном алфавите {A,B,C,D}, если известно, что одним из соседей A обязательно является D, а буквы B и C никогда не соседствуют друг с другом?

Ответ: 29

✍ Показать решение:

✎ Решение теоретическое:

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы,
n2 — количество вариантов выбора второй буквы и т.п.
Будем рассматривать варианты, расставляя каждую букву последовательно по алфавиту, начиная с первой буквы. При этом будем учитывать указанные ограничения для букв А, B и С:

Начинаем с A: A D 4_ABCD = 1 * 1 * 4 = 4 
Начинаем с B: B A D, B B 2_BD, B D 4_ABCD = 7
Начинаем с C: C A D, C C 2_CD, C D 4_ABCD = 7
Начинаем с D: D A 3_BCD, D B 2_BD, D C 2_CD, D D 4_ABCD = 11

Теперь суммируем количество найденных вариантов:

4 + 7 + 7 + 11 = 29

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_22:

Лена составляет 5-буквенные слова из букв Я, С, Н, О, В, И, Д, Е, Ц, причём слово должно начинаться с согласной и заканчиваться гласной. Первая и последняя буквы слова встречаются в нем только один раз; остальные буквы могут повторяться.

Сколько слов может составить Лена?

Ответ: 6860

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='ясновидец'.Cartesian(5) 
.where(l->(l[0] in 'снвдц') and (l[4] in 'яоие'))// учитываем гласные и согласные
.where(l->(l.countOf(l[0])=1)and(l.countOf(l[4])=1))//учитываем, что они не повторяются
.count.print

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var str := 'ЯСНОВИДЕЦ';
  var n := 0;
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var slovo := str[s1] + str[s2] + str[s3] + str[s4] + str[s5];
            if (slovo[1] in 'СНВДЦ') and (slovo[5] in 'ЯОИЕ') then
              if (slovo[1] <> slovo[2]) and (slovo[1] <> slovo[3]) and (slovo[1] <> slovo[4])            
              and (slovo[1] <> slovo[5]) and (slovo[5] <> slovo[1]) and (slovo[5] <> slovo[2]) 
              and (slovo[5] <> slovo[3]) and (slovo[5] <> slovo[4]) then
              begin
                n += 1
              end;
          end;
  print(n)
end.

Python:

С++:

Результат: 6860

8_11:

Из букв С, Р, Е, Д, А составляются трехбуквенные комбинации по следующему правилу – в комбинации не может быть подряд идущих гласных и одинаковых букв.

Например, комбинации ААР или ЕСС не являются допустимыми.

Сколько всего комбинаций можно составить, используя это правило?

Ответ: 66

✍ Показать решение:

✎ Решение теоретическое:

Рассмотрим два варианта: когда слово начинается с гласной буквы, и когда оно начинается с согласной.

1. С гласной:

1.1
2 3 2 = 2 * 3 * 2 = 12
^{гл с  с}

1.2
2 3 2 = 2 * 3 * 2 = 12
^{гл с гл}

2. С согласной:

2.1
3  2  2 = 3 * 2 * 2 = 12
с  с  с

2.2
3  2  3 = 3 * 2 * 3 = 18
с гл  с

2.3
3  2  2 = 3 * 2 * 2 = 12
с  с  гл

Подсчитаем общее количество вариантов:

12 + 12 + 12 + 18 + 12 = 66

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

### 
'среда'.cart(3)// 
 .Select(w -> w.JoinToString('')) // собираем в строку;
 .where(w->w.Pairwise.All((a,b) -> a+b not in 'еае'))
 .where(w->w.Pairwise.All((a,b) -> a<>b))
 .count.print

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'СРЕДА';
  var glas := 'ЕА';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
      begin
        var res := str[s1] + str[s2] + str[s3];
        // условие для подряд идущих гласных
        if not ((res[1] in glas) and (res[2] in glas) or
           (res[2] in glas) and (res[3] in glas)) then
        // условие для подряд идущих одинаковых букв
          if not ((res[1] = res[2]) or (res[2] = res[3])) then
            n += 1;
      end;
  print(n)
end.

Python:

str = 'СРЕДА'
glas = 'ЕА'
n = 0
for s1 in str:
    for s2 in str: 
        for s3 in str:
            res = s1 + s2 + s3 
            if not (s1 in glas and s2 in glas or
           s2 in glas and s3 in glas) :
                if not (s1 == s2 or s2 == s3) :
                    n += 1
print(n)

С++:

8_12:

Дано слово КОРАБЛИКИ. Таня решила составлять новые 5-буквенные слова из букв этого слова по следующим правилам:
1) слово начинается с гласной буквы;
2) гласные и согласные буквы в слове должны чередоваться;
3) буквы в слове не должны повторяться.

Ответ: 72

✍ Показать решение:

✎ Решение теоретическое:

Учтем, что в слове КОРАБЛИКИ две буквы К и две И.
Всего в слове 4 гласных, но поскольку две буквы И, то необходимо считать только 3 гласных.
Всего в слове 5 согласных, однако две из них — буквы К, поэтому считать следует 4 согласных.
Посчитаем количество согласных и гласных для каждой из 5 позиций слова, учитывая, что с каждой последующей буквой количество используемых гласных/согласных уменьшается. Под позициями приведем пример букв:

гл   с   гл   с   гл  
3    4    2   3    1
^{оаи   крбл   оа   крб    и}

Количество слов вычисляется как произведение полученных чисел:

3 * 4 * 2 * 3 * 1 = 72

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

###
'кораблики'
.Cart(5)
.select(w->w.JoinToString(''))
.Distinct //Обязательно!
.where(w-> w.First in 'оаи')
.where(w->w.Pairwise.All((a,b)->not ((a in 'оаи') and (b in 'оаи')) and not( ( a in'крбл') and (b in 'крбл' ))))
.where(w->'корабли'.All(c->w.countOf(c)<=1))
.count.print

Python:

С++:

Результат: 72

8_21:

Ксюша составляет слова, меняя местами буквы в слове МИМИКРИЯ.
Сколько различных слов, включая исходное, может составить Ксюша?

Ответ: 3360

Показать решение:

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var str := 'МИМИКРИЯ';
  var set1: set of string;
  set1 := [];
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do 
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do 
          for var s5 := 1 to length(str) do  
            for var s6 := 1 to length(str) do
              for var s7 := 1 to length(str) do  
                for var s8 := 1 to length(str) do 
                begin
                  var slovo := str[s1] + str[s2] + str[s3] + str[s4] + str[s5] 
                              + str[s6] + str[s7] + str[s8];
                  if (slovo.CountOf('М') = 2) and (slovo.CountOf('И') = 3)
                  and (slovo.CountOf('К') = 1)
                  and (slovo.CountOf('Р') = 1)
                  and (slovo.CountOf('Я') = 1) then
                    include(set1, slovo);
                end;
  print(set1.count);
end.

Смысл решения в использовании типа множества (set). При добавлении новых элементов к множеству исключаются повторения.

PascalABC.net (использование LINQ, быстрое решение):

### 
 'МИМИКРИЯ'.Permutations // перестановки букв
 .Select(w->w.JoinToString('')) // собираем в строку
 .Distinct  // выбираем уникальные
 .Count.Print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

📹 Видео (программный способ)
📹 Видеорешение на RuTube здесь (программное решение)

8_19:

Петя составляет шестибуквенные слова

перестановкой букв

слова АДЖИКА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?

Типовые задания для тренировки

Ответ: 240

✍ Показать решение:

✎ Решение теоретическое:

Посчитаем количество слов без двух подряд одинаковых букв. Будем считать относительно буквы А, которых две в заданном слове АДЖИКА. Буквы не могут повторяться, поэтому их кол-во в каждом варианте будет уменьшается:

А*А*** = 4*3*2*1 = 24 слова с данным расположением буквы А. 
А**А** = 4*3*2*1 = 24
А***А* = 4*3*2*1
А****А = ...
*А*А**
*А**А*
*А***А
**А*А*
**А**А
***А*А

Получили 10 вариантов, и в каждом из них можно составить по 24 слова.
Таким образом, получим общее количество слов:

10 * 24 = 240

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var s: set of string;
  s := [];
  var str := 'АДЖИКА';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
            for var s6 := 1 to length(str) do
            begin
              var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5] + str[s6];
              if (res.CountOf('А') = 2) and (res.CountOf('Д') = 1) 
                  and (res.CountOf('Ж') = 1) and (res.CountOf('И') = 1) 
                  and (res.CountOf('К') = 1) then
                  if (res[1] <> res[2]) and (res[2] <> res[3]) and (res[3] <> res[4]) 
                      and (res[4] <> res[5]) and (res[5] <> res[6]) then
                  include(s, res);
            end;
  print(s.count)
end.

Смысл решения в использовании типа — множества (set). При добавлении новых элементов к множеству исключаются повторения.

PascalABC.net (использование LINQ, быстрое решение):

### 
'аджика'.Permutations
 .Select(w -> w.JoinToString('')) // собираем в строку;
 .distinct // исключаем дубли
 .where(s -> not ('аа' in s)) // исключаем две подряд буквы 'а'
 .count.pr

Python:

С++:

8_20:

Маша составляет 7-буквенные коды из букв В, Е, Н, Т, И, Л, Ь. Каждую букву нужно использовать

ровно 1 раз

, при этом код буква Ь не может стоять на последнем месте и между гласными. Сколько различных кодов может составить Маша?

Типовые задания для тренировки

Ответ: 4080

Показать решение:

✎ Решение теоретическое:

Выполним задание следующим образом: 1. посчитаем общее количество слов, не учитывая никакие ограничения. 2. Затем посчитаем случаи, которые необходимо исключить. 3. Вычтем из результата пункта 1 результат пункта 2.

Общее количество независимо от ограничений (учтем, что буквы не должны повторяться):

7 6 5 4 3 2 1 - количество возможных вариантов букв на семи позициях

ИТОГО:
7! = 5040 слов

Посчитаем варианты, которые необходимо исключить. Их будет несколько:

а) буква ь — на последнем месте:

6 5 4 3 2 1 Ь = 6! = 720

б) буква ь — между гласными:

И Ь Е 4 3 2 1  = 24 варианта
Так как буквы смещаются по всем позициям, то получим (4 И Ь Е 3 2 1, ...):
24 * 5 = 120
Е Ь И 4 3 2 1  = 24 варианта
24 * 5 = 120

Посчитаем количество слов, согласно условию задачи:

5040 - 720 - 120 - 120 = 4080

✎ Решение с использованием программирования:
Стоит заметить, что теоретическое решение занимает меньше времени, чем программный способ!

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'ВЕНТИЛЬ';
  var glas := 'ЕИ';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
            for var s6 := 1 to length(str) do
              for var s7 := 1 to length(str) do
              begin
                var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5] + str[s6] + str[s7];
                if (res.CountOf('В') = 1) and (res.CountOf('Е') = 1) 
                    and (res.CountOf('Н') = 1) and (res.CountOf('Т') = 1) 
                    and (res.CountOf('И') = 1) and (res.CountOf('Л') = 1)
                    and (res.CountOf('Ь') = 1) then
                  if not (res[7] = 'Ь') then
                    if not ((res[1] in glas) and (res[3] in glas) and (res[2] = 'Ь') or
                        (res[2] in glas) and (res[4] in glas) and (res[3] = 'Ь') or
                        (res[3] in glas) and (res[5] in glas) and (res[4] = 'Ь') or
                        (res[4] in glas) and (res[6] in glas) and (res[5] = 'Ь') or
                        (res[5] in glas) and (res[7] in glas) and (res[6] = 'Ь')) then
                      n += 1
              end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

### 
'вентиль'.Permutations// здесь можно без distinct, т.к. буквы не повторяются
 .Select(w -> w.JoinToString('')) // собираем в строку
 .where(s -> not ('еьи' in s) and not ('иье' in s) and (s.last <> 'ь'))
.Count.Print

Python:

С++:

8_23:

Артур составляет 6-буквенные коды перестановкой букв слова ВОРОТА. При этом нельзя ставить рядом две гласные.
Сколько различных кодов может составить Артур?

Ответ: 72

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, спортивное прогр-е):

###
'ВОРОТА'.prm
.Sel(w->w.ToS('')).dst
.Wh(w-> not w.Pairwise.Any((a,b)->a+b in 'АООАА'))
.Cnt.pr

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Ответ: 72

Сколько существует n-значных чисел, записанных в m-ной системе счисления

Разбор 8 задания экзамена ЕГЭ 2020 г. (со слов учащегося):

Сколько существует восьмизначных чисел, записанных в восьмеричной системе счисления, в которых все цифры различны и рядом не могут стоять 2 чётные или 2 нечётные цифры?

Типовые задания для тренировки

Ответ: 1008

✍ Показать решение:

✎ Решение теоретическое:

Выпишем все четные и нечетные цифры, которые могут использоваться в 8-й с.с.:

четные: 0, 2, 4, 6 - итого 4 цифры
нечетные: 1, 3, 5, 7 - итого 4 цифры

Рассмотрим два случая построения числа по заданию: 1) начиная с четной цифры и 2) начиная с нечетной цифры. Изобразим схематично числа, указывая сверху возможное количество цифр на разряд:

1) с четной цифры:
3  4  3  3  2  2  1  1 = 3*4*3*3*2*2*1*1 = 432
ч  н  ч  н  ч  н  ч  н

Самый старший разряд не может быть равен 0 (поэтому 3 цифры из 4 возможных), так как разряд просто потеряется, и число станет семизначным). Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.

2) с нечетной цифры:
4  4  3  3  2  2  1  1 = 4*4*3*3*2*2*1*1 = 576
н  ч  н  ч  н  ч  н  ч

Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.

Сложим количество вариантов в обеих случаях:

432 + 576 = 1008

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

###
'01234567'.Permutations // т.к. цифр итак 8 штук
.where(w->w.First<>'0') // первая цифра не может быть 0
.where(w->w.Pairwise.All((a,b)-> (a.ToDigit + b.ToDigit).IsOdd)) // проверка пар четных и нечетных
.count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Список в алфавитном порядке

8_13:

Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Ниже приведено начало списка:

1. ААААА
2. ААААО
3. ААААУ
4. АААОА
…

Запишите слово, которое стоит под номером 242 от начала списка.

Ответ: УУУУО

✍ Показать решение:

✎ Решение теоретическое:

Данное задание лучше решать следующим образом. Подставим вместо букв цифры (А -> 0, О -> 1, У -> 2):

Видим, что каждая последующее число получается путем прибавления в столбик единицы к предыдущему числу. В троичной системе счисления! Т.к. цифр всего три.
Порядковый номер, написанный рядом с пунктом, всегда на единицу больше располагающейся рядом цифры в троичной системе счисления.
Значит, пункту под номером 242 будет соответствовать число 241 в троичной системе счисления.
Переведем 241 в 3-ю систему делением на 3:

        ^{остатки}
241 | 3 | 1
 80 | 3 | 2
 26 | 3 | 2
  8 | 3 | 2
  2 |   |

Перепишем остатки снизу вверх: 22221, им соответствуют буквы УУУУО

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='АОУ'.Order // сортируем по алфавиту
.Cartesian(5)
.Numerate.print

Смотрим слова и находим по номеру нужное слово:

… (241,[У,У,У,У,А]) (242,[У,У,У,У,О]) (243,[У,У,У,У,У])

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

📹 Видео (теоретический способ)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8 (10) задание. Демоверсия ЕГЭ 2018 информатика:

Все 4-буквенные слова, составленные из букв Д, Е, К, О, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.

1. ДДДД
2. ДДДЕ
3. ДДДК
4. ДДДО
5. ДДДР
6. ДДЕД
…

Под каким номером в списке идёт первое слово, которое начинается с буквы K?

Ответ: 251

✍ Показать решение:

✎ Решение теоретическое:

Подставим вместо букв цифры (Д -> 0, Е -> 1, К -> 2, О -> 3, Р -> 4):

Видим, что каждое последующее число получается путем прибавления единицы в столбик к предыдущему (в пятеричной системе счисления! т.к. цифр всего пять).
Порядковый номер, написанный рядом с пунктом, всегда на единицу больше располагающейся рядом цифры в пятеричной системе счисления.
Определим число, которое получится, если мы в начале слова поставим букву К (остальные должны остаться нулями, т.к. числа идут по порядку, а нам необходимо первое, начинающееся с К):

K -> 2 -> 2000

Полученное число — 2000 — необходимо перевести из пятеричной системы счисления в десятичную, чтобы узнать порядковый номер:

По формуле разложения числа по степеням основания:

2000₅ = 2 * 5³ + 0 * 2² + 0 + 0 = 2 * 125 = 250₁₀

Поскольку порядковый номер числа всегда на единицу больше самого числа, то имеем 251.

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

###
var d:='декор'.Order // сортируем по алфавиту
.Cartesian(4) // d - массива из массивов символов 
.Numerate // нумерация
.where((i,w)->w[0] = 'к') // рассматриваем и номер и слово
.first[0].print // выводим именно номер

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_15:

Все 4-буквенные слова, составленные из букв П, Р, С, Т, записаны в алфавитном порядке.
Вот начало списка:

1. ПППП
2. ПППР
3. ПППС
4. ПППТ
5. ППРП
... ...

Ответ: 65

📹 Видео
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_16:

Все четырёхбуквенные слова, составленные из букв В, Е, Г, А, Н записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:

1. АААА
2. АААВ
3. АААГ
4. АААЕ
5. АААН
6. ААВА
…

Под каким номером в списке идёт первое слово, в котором нет буквы А?

Ответ: 157

✍ Показать решение:

✎ Решение теоретическое:

Пронумерованный список начинается со всех букв А. Представим, что А — 0, В — 1, Г — 2, Е — 3, Н — 4. Получим следующий список:

Такой список представляет из себя увеличивающиеся числа 5-й системы счисления.
Так как букве А соответствует 0, то первое (самое младшее) четырехзначное число без нуля — это 1111.
Чтобы вычислить под каким номером стоит данное число, переведем его в 10-ю систему и прибавим к результату единицу (так как порядковые номера в списке на единицу больше самих чисел):

1111₅ = 1 * 5³ + 1 * 5² + 1 * 5¹ + 1 * 5⁰ = 156
156 + 1 = 157

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

###
var d:='веган'.Order // сортируем по алфавиту
.Cartesian(4) // d - массива из массивов символов
.Select(x->x.JoinToString(''))// d - массив из строк 
.Numerate // нумерация
.where((i,w)->'а' not in w) // рассматриваем и номер и слово
.first[0].print // выводим именно номер

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

📹 Видео (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)

Вероятность событий

8_17:

За четверть Василий Пупкин получил 20 оценок. Сообщение о том, что он вчера получил четверку, несет 2 бита информации.

Сколько четверок получил Василий за четверть?

Ответ: 5

✍ Показать решение:

Для решения данного задания необходимо вспомнить две формулы:

1. Формула Шеннона:

x = log₂(1/p)

x - количество информации в сообщении о событии
p - вероятность события

2. Формула вероятности случайного события:

p(A) = m/n

m - число случаев, способствующих событию А
n - общее число равновозможных случаев

Подставим в первую формулу известное значение — вероятность того, что Василий получил четверку:

2 = log₂(1/p);
    => 
1/p = 4; 
    =>
p = 1/4

Затем подставим известное по условию значение в формулу вероятности случайного события:

p = ?/20

Поскольку p мы уже нашли, подставим найденное значение и найдем искомое число — количество четверок за четверть:

1/4 = ?/20

? = 1/4 * 20 = 5

📹 Видео
📹 Видеорешение на RuTube здесь (теоретическое решение)

Источник

18850. Все четырёхбуквенные слова, в составе которых могут быть только буквы Л, Е, М, У, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ЕЕЕЕ
2. ЕЕЕЛ
3. ЕЕЕМ
4. ЕЕЕР
5. ЕЕЕУ
6. ЕЕЛЕ
…
Под каким номером в списке идёт первое слово, которое начинается с буквы Л?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 18850.

18877. Все 3-буквенные слова, составленные из ЛАТИНСКИХ букв K, O, T, записаны в алфавитном порядке и пронумерованы. Вот начало списка:

      1. KKK
      2. KKO
      3. KKT
      4. KOK
      ...

Запишите слово, которое стоит под номером 22.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 18877.

18904. Миша составляет 6-буквенные коды из букв Б, А, Н, К, И, Р. Каждая допустимая гласная буква может входить в код не более одного раза. Сколько кодов может составить Миша?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 18904.

18931. Вася составляет 5-буквенные слова, в которых есть только буквы А, Р, Б, У, З, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 18931.

18958. Все 4-буквенные слова, составленные из букв ‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’, ‘G’, ‘H’, записаны в алфавитном порядке и пронумерованы. Вот начало списка:

      1. AAAA
      2. AAAB
      3. AAAC
      4. AAAD
      5. AAAE
      6. AAAF
      7. AAAG
      8. AAAH
      9. AABA
      ...

Под каким номером стоит слово DDFA?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 18958.

18985. Все 5-буквенные слова, составленные из букв ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’, записаны в алфавитном порядке. Вот начало списка:

      1. aaaaa
      2. aaaab
      3. aaaac
      4. aaaad
      5. aaaae
      6. aaaaf
      7. aaaag
      8. aaaba
      ...

Запишите слово, которое стоит на 12769-м месте от начала списка.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 18985.

19012. Миша составляет 6-буквенные коды из букв Б, А, Н, К, И, Р. Каждая допустимая гласная буква может входить в код не более одного раза. Сколько кодов может составить Миша?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19012.

19039. Все 3-буквенные слова, составленные из ЛАТИНСКИХ букв K, O, T, записаны в алфавитном порядке и пронумерованы. Вот начало списка:

       1. KKK
       2. KKO
       3. KKT
       4. KOK
       ...

Запишите слово, которое стоит под номером 22.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19039.

19066. Юля составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Юля использует трёхбуквенные слова, в которых могут быть только буквы О, С, Е, Н, Ь, причём буква С появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Юля?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19066.

19093. Птенчик составляет 7-буквенные слова, в которых есть только буквы К, У, Р, С, причём буква С используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может составить птенчик?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19093.

Для вас приятно генерировать тесты, создавайте их почаще

За правильное выполненное задание получишь 1 балл. На решение отводится примерно 4 минуты.

если слово состоит из L букв, причем есть n₁ вариантов выбора первой буквы, n₂ вариантов выбора второй буквы и т.д., то число возможных слов вычисляется как произведение N = n₁ · n₂ · … · n_L
если слово состоит из L букв, причем каждая буква может быть выбрана n способами, то число возможных слов вычисляется как N = n^L

Ниже приведено начало списка.

ИИИИ
ИИИК
ИИИН
ИИИО
ИИИТ
ИИКИ

…

Под каким номером в списке идёт первое слово, которое начинается с буквы О?

ДДДД
ДДДЕ
ДДДК
ДДДО
ДДДР
ДДЕД

…
Под каким номером в списке идёт первое слово, которое начинается с буквы K?

Все 6-буквенные слова, составленные из букв С, А, Й, Т, записаны в алфавитном порядке и пронумерованы, начиная с 1. Ниже приведено начало списка.

СССCСС
CCCСCТ
CCCCСЙ
CCCCСА
CCCСТС

…
Под каким номером в списке идёт слово ТСАСАТ?

Все 5-буквенные слова, составленные из букв К, А, Р, Т, записаны в алфавитном порядке и пронумерованы, начиная с 1. Ниже приведено начало списка.

ККККK
KKKKА
KKKKТ
KKKKР
КККАК

…
Под каким номером в списке идёт слово РРРТК?

Все 5-буквенные слова, составленные из букв Д, У, Б, записаны в алфавитном порядке и пронумерованы, начиная с 1. Ниже приведено начало списка.

ДДДДД
ДДДДУ
ДДДДБ
ДДДУД

…
Под каким номером в списке идёт первое слово, которое начинается с буквы Б и оканчивается на букву У?

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 85.3%
Ответом к заданию 8 по информатике может быть цифра (число) или слово.

Задача 1

Саша составляет шестибуквенные слова, в которых есть только буквы А, М, О, К, Т и С, причём в каждом слове буква Т используется один или два раза и при этом может стоять только на первом или на втором местах, а буква О встречается в слове ровно 2 раза, на пятом и шестом месте. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.

Сколько существует таких слов, которые может написать Саша?

Решение

Поскольку на двух последних позициях обязательно стоит буква О, там всегда ровно один вариант расстановки букв. Количество вариантов зависит только от первых 4-х символов. Дальше будем считать именно для 4-х символов.

Рассмотрим все варианты расстановки буквы Т:

1. Буква Т встречается ровно 2 раза на первом и втором месте. Тогда на 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4 = 16 вариантов.

2. Буква Т встречается ровно 1 раз на первом месте. Тогда на 2, 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4·4 = 64 варианта.

3. Буква Т встречается ровно 1 раз на втором месте. Тогда на 1, 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4·4 = 64 варианта.

Всего вариантов: 64+64+16 = 144.

Ответ: 144

Ответ: 144

Показать решение

Полный курс

Задача 2

Саша составляет шестизначные числа, в которых есть только цифры 1, 2 и 3, причём цифра 1 используется в каждом числе не более двух раз и при этом может стоять только на первом или втором местах. Каждая из других допустимых цифр может встречаться в числе любое количество раз или не встречаться совсем. Сколько существует таких чисел, которые может написать Саша?

Решение

1) без цифры 1: 2*2*2*2*2*2=64
2) с одной 1 на первом месте: 1*2*2*2*2*2=32
3) с одной 1 на втором месте: 2*1*2*2*2*2=32
1) с двумя 1: 1*1*2*2*2*2=16
Итого: 64+32+32+16=144

Ответ: 144

Показать решение

Полный курс

Задача 3

Саша составляет пятибуквенные слова, в которых есть только буквы А, Б, В, Г, Д, Е, причём в каждом слове буква Г используется ровно 2 раза. Каждая из других допустимых букв может встречаться любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.

Сколько существует таких слов, которые может написать Саша?

Решение

Количество перестановок букв Т на 5 позициях = 10. можно вычислить по формуле n!/(n-m)! где n — это количество позиций (в данном случае 5), а m — количество букв, которые необходимо расположить (в данном случае 2 буквы Т). по формуле получается 20, но у нас абсолютно одинаковые элементы (буквы Т) поэтому делим на факториал 2, чтобы не учитывать повторы.

На каждой из оставшихся трёх позиций в слове могут стоять по 5 букв — итого 125 комбинаций.

В итоге: для каждого из 10 вариантов расположения букв Т получается по 125 комбинаций оставшихся трёх букв: 10 * 125 = 1250.

Ответ: 1250

Показать решение

Полный курс

Задача 4

Аня составляет 5-буквенные слова, в которых встречаются только буквы А, Б, В. Причем буква A может встречаться только первой или последней (двух букв А в слове быть не может), но при этом должна присутствовать обязательно. Каждая из других допустимых букв может встречаться в слове на любом месте или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная.

Сколько существует таких слов, которые может написать Аня?

Решение

Поскольку буква А должна стоять либо на первом, либо на последнем месте (должна встретиться в слове, но не на обеих позициях), то получаем такие комбинации размещения букв:
A 2 2 2 2 = 16 слов
2 2 2 2 A = 16 слов
Итого: 16+16=32 слова

Ответ: 32

Показать решение

Полный курс

Задача 5

Все пятибуквенные слова, составленные из букв А, Л, Е, Т, Б записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. ААААА
2. ААААБ
3. ААААЕ
4. ААААЛ
5. ААААТ
6. АААБА
. . .

Под каким номером в списке идёт первое слово, которое начинается с буквы Л и заканчивается буквой Т?

Решение

Каждому слову поставим в соответствие пятизначное число в пятеричной системе счисления. Для этого каждой букве поставим в соответствие цифру в том порядке, в котором она появляетс в списке.

А — 0, Б — 1, Е — 2, Л — 3, Т — 4

Первое слово, которое начинается на Л — это слово ЛАААА и заканчивающееся на Т — то есть ЛАААТ. Этому слову соответствует число $30004_5$ = $1879_10$, которое стоит под номером 1880.

Ответ: 1880

Показать решение

Полный курс

Задача 6

Все шестибуквенные слова, составленные из букв Б, Л, О, Т записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. ББББББ
2. БББББЛ
3. БББББО
4. БББББТ
5. ББББЛБ
6. ББББЛЛ
. . .

Под каким номером стоит слово БОЛОТО?

Решение

Для составления слов используются 4 различных буквы. Поставим в соответствие каждой из букв цифры системы счисления с основанием 4 (с учётом порядка их следования в алфавите): Б — 0, Л — 1, О — 2, Т — 3.

Тогда упорядоченной по алфавиту последовательности слов

1. ББББББ
2. БББББЛ
3. БББББО
4. БББББТ
5. ББББЛБ
6. ББББЛЛ
. . .

будут соответствовать числа в системе счисления с основанием 4:

1. 000000₄ = 0₁₀
2. 000001₄ = 1₁₀
3. 000002₄ = 2₁₀
4. 000003₄ = 3₁₀
5. 000010₄= 4₁₀
5. 000011₄ = 5₁₀
. . .

Слову БОЛОТО будет соответствовать число 021232₄. Переведём это число из системы счисления с основанием 4 в десятичную.

021232₄ = 0 · 4⁵ + 2 · 4⁴ + 1 · 4³ + 2 · 4² + 3 · 4¹ + 2 · 4⁰ = 622₁₀.

Заметим, что соответствующая последовательность чисел, записанных в десятичной системе счисления, на 1 меньше номера строки, содержащей данное число. Значит, десятичное число 622 будет находиться на 623-м месте.

Ответ: 623

Показать решение

Полный курс

Задача 7

Саша составляет 6-значные числа, в которых есть только цифры 1, 2, 3 и 4 причём цифра 1 используется в каждом числе ровно 1 раз. Каждое из других допустимых цифр может встречаться в числе любое количество раз или не встречаться совсем. Сколько существует таких чисел, которые может написать Саша?

Решение

Пусть цифра 1 стоит в числе на первом месте. Тогда на оставшихся 5 местах может стоять одна из оставшихся цифр 2, 3 или 4. Причём каждая из этих цифр может встречаться в числе любое количество раз. Таким образом нам нужно определить количество 5-значных чисел, состоящих из трёх цифр.

Если M — количество символов в некотором алфавите (мощность алфавита), K — количество всех возможных «слов» (символьных цепочек) длиной N , то = M^N.

Следовательно, количество пятизначных чисел, состоящих из трёх цифр, равно 3⁵ = 243. А значит такое же количество 6-значных чисел, в которых на первом месте стоит цифра 1, а на остальных местах цифры 2, 3 или 4, возможно с повтором.

Рассуждая аналогичным образом, мы получим, что такое же количество чисел в 6-значных числах, в которых цифра 1 на втором, третьем, четвёртом, пятом и шестом местах.

То есть всего искомых чисел 6 · 243 = 1458.

Ответ: 1458

Показать решение

Полный курс

Задача 8

Саша составляет четырёхбуквенные слова, в которых есть только буквы Е, Д, О, Н и К, причём в каждом слове буква О используется ровно 2 раза. Каждое из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.

Сколько существует таких слов, которые может написать Саша?

Показать решение

Полный курс

Задача 9

Саша составляет трёхбуквенные слова, в которых есть только буквы E, C, B, Н, К и У, причём в каждом слове буква К используется ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.

Сколько существует таких слов, которые может написать Саша?

Показать решение

Полный курс

Задача 10

Все шестибуквенные слова, составленные из букв М, Н, О, П, Р, записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. ММММММ

2. МММММН

3. МММММО

4. МММММП

5. МММММР

6. ММММНМ

. . .

Укажите слово, которое стоит под номером 267.

Показать решение

Полный курс

Задача 11

Все пятибуквенные слова, составленные из букв А, М, Н, Т, У, записаны в алфавитном порядке и пронумерованы. Вот начало списка:

Введите ответ в поле ввода

Решение
→

Источник

Разбор 8 задания ЕГЭ 2017 года по информатике из проекта демоверсии. Это задание базового уровня сложности. Примерное время выполнения задания 3 минуты.

Проверяемые элементы содержания: знание основных конструкций языка программирования, понятия переменной, оператора присваивания. Элементы содержания, проверяемые на ЕГЭ: основные конструкции языка программирования, система программирования.

Определите, какое число будет напечатано в результате выполнения программы, записанной ниже на пяти языках программирования.

Ответ: ________

Разбор 8 задания ЕГЭ 2017:

Нужно определить значение переменной s в результате выполнения программы.

Что мы имеем:

1) Начальное значение переменной n=1, переменной s=0.
2) Цикл в программе будет выполняться пока выполняется условие n<=150.
3) После окончания цикла выводится значение переменной s.
4) С каждым шагом цикла s увеличивается на 30 — s := s + 30 n увеличивается в 5 раз — n := n * 5.
5) Цикл закончится, как только n станет меньше или равно 150 (пока выполняется условие n<=150).
6) Таким образом цикл выполнится 4 раза (для n равной 1, 5, 25 и 125).

Таким образом к начальному значению s=0 прибавиться 30*4=120 — это и есть наш ответ.

Ответ: 120

Опубликовано: 22.09.2016
Обновлено: 12.03.2020

Источник

Лада Есакова, преподаватель информатики и математики, автор книги «Информатика. Полный курс подготовки к ЕГЭ».

Добрый день, дорогие друзья! С вами я, Есакова Лада, преподаватель информатики с 20-летним стажем.
Сегодня разберем основы комбинаторики и буквенные цепочки.

Задача:
«Все 4-буквенные слова, составленные из букв В, Н, Р, Т, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ВВВВ
2. ВВВН
3. ВВВР
4. ВВВТ
5. ВВНВ
………
Запишите слово, которое стоит под номером 251.»

Обозначим В = 0, Н = 1, Р = 2, Т = 3 и получим вот такой ряд:

1. 0000
2. 0001
3. 0002
4. 0003
5. 0010

Это числовой ряд в четверичной системе исчисления. Нам нужно найти слово, которое стоит под номером 251.

Здесь важный нюанс, на котором часто ребята теряют балл. На первом месте стоит 0, то есть номер строчки на единицу больше самого числа. Поэтому на 251 месте у нас будет стоять число на единицу меньше – 250, но только в четверичной системе исчисления.

Переведем 250 в четверичную систему. Будем делить столбиком. У нас получается 250 = 3322₄. Теперь переводим цифры в буквы — ТТРР. Вот такой ответ должен получиться.
Вот такие буквенные цепочки – это, по сути, числовые ряды.

Следующая задача:
«Все 6-буквенные слова, составленные из букв С, В, Е, Т, записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. ВВВВВВ
2. ВВВВВЕ
3. ВВВВВС
4. ВВВВВТ
5. ВВВВЕВ
………
Под каким номером стоит первое из слов, которое начинается с буквы Т?»

Здесь есть еще одна ловушка: нам сказали, что все 6-буквенные слова составлены из этих букв, и очень хочется пронумеровать букву в том же порядке, в котором они представлены – С = 0, В = 1, Е = 2, Т = 3. Вот здесь-то и ошибка.

Если посмотрим на числовой ряд, то увидим, что на первой строчке у нас стоит В, значит, она будет равна 0. Далее появляется Е, значит, она равна 1, С = 2 и Т = 3.

И снова у нас четверичная система исчисления. Необходимо определить, под каким номером стоит первое из слов, которое начинается с буквы Т. Перефразирую вопрос: под каким номером стоит четверичное число, которое начинается на 3? Значит, оно должно выглядеть как 300000. Это число стоит на месте, которое на единицу больше, чем оно само, но в десятичной записи. Необходимо это число, 300000, из четверичной системы перевести в десятичную.

300000₄=3*4⁵=3*1024=3072

У нас получается число 3072, а номер строки на единицу больше, то есть номер строки будет 3073. Это и есть ответ задачи.

С такими цифровыми цепочками на сегодня мы закончим. Перейдем к более интересной теме, к элементам комбинаторики, хотя это громко сказано, потому что там от комбинаторики только одна маленькая формула.

Чтобы понять, о чем я сейчас буду говорить, давайте представим такую ситуацию: допустим, надоело нам жить в Москве и решили переехать на необитаемый остров. Для связи с внешним миром мы запасли некоторое количество цветных флажков, которые мы можем прикрепить к флагштокам и при необходимости подать сигнал. У нас есть два флагштока и флажки только двух цветов: красные и синие. Что же при помощи этого мы можем сообщить во внешний мир?

Мы можем составить 4 комбинации:

Если нам этого не хватает, мы можем добавить флажки еще одного цвета. Допустим, у нас еще есть зеленые флажки, и мы можем составить следующие комбинации:

У нас получилось 9 комбинаций.

Если же все-таки у нас флажки только двух цветов, третьего нет, у нас есть другой путь увеличить количество комбинаций, увеличив количество флагштоков. Получаем следующие комбинации:

и их получилось 8 штук.

Мы видим, что количество сообщений, которые мы можем передать внешнему миру, зависит от двух параметров: от количества букв в нашем алфавите (или, в нашем случае, от разных цветов флажков) и от длины слова (или от количества флагштоков).

Количество слов, которые мы можем закодировать, равно количеству букв в нашем алфавите (еще это называется мощностью алфавита) в степени «длина слова» A=aⁱ

«Сколько различных символов можно закодировать, используя код азбуки Морзе длиной не менее четырех и не более пяти сигналов (точек и тире)?»

Если я делаю слово из четырех сигналов, то таких слов я могу сделать 2⁴, если я делаю из пяти сигналов, то таких слов я могу придумать 2⁵. А в задаче как раз этот интервал, то есть и те, и те мне подойдут. Вот столько разных слов я могу составить 2⁴ + 2⁵ = 48.

«Коля составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует свое кодовое слово. В качестве кодовых слов Коля использует 4-буквенные слова, в которых есть буквы А, Б, В, Г, Д, причем буква Д появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Коля?»

Не буду мудрить, придумывать какие-то сложные формулы, а просто распишу, как буква Д может встречаться ровно один раз. Это выглядит так

Д — — —
— Д — —
— — Д —
— — — Д

то есть она может встретиться на каком-то из четырех мест. На остальных трех местах может стоять все, кроме Д, то есть 4 любые буквы по трем позициям, 4³. И так в каждом ряду. Все это сложим и получим 4*4³=4⁴=256

«Паша составляет таблицу кодовых слов для передачи сообщений. В качестве кодовых слов Паша использует 4-буквенные слова, в которых есть только буквы А, Б, В, Г, Д, Е, Ж. При этом первая буква кодового слова – это буква Д, Е или Ж, а далее в кодовом слове буквы Д, Е и Ж не встречаются. Сколько различных кодов может использовать Паша?»

У нас получается такой вид

Д — — —
Е — — —
Ж — — —

А в остальных местах используются остальные буквы, кроме Д, Е и Ж. Получаем 3*4³=3*64=192

«Герасим составляет 7-буквенные коды из букв Г, Е, Р, А, С, И, М. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Герасим?»

Тут немного схитрим. Необходимо обязательно чередовать гласные и согласные, а для этого посмотрим, сколько у нас гласных. 3. А согласных 4. Поэтому на гласную начать слово я не могу, иначе их не хватит на все слово, и согласные где-то обязательно повторятся. Поэтому слово будет выглядеть таким образом: согласная – гласная – согласная – гласная – согласная – гласная – согласная.

Далее каждую букву я должна использовать ровно один раз.

Вначале состава слова согласных у нас 4, гласных – 3, далее согласных остается 3, т.к. одну я уже использовала, а согласных – 2, затем согласных 2, гласных – одна и согласная осталась одна. Теперь мы перемножаем все эти цифры

и получаем 144.

«Ольга составляет 5-буквенные коды из букв О, Л, Ь, Г, А. Каждую букву нужно использовать ровно 1 раз, при этом Ь нельзя ставить первым и нельзя ставить после гласной. Сколько различных кодов может составить Ольга?»

Давайте пойдем от противного: посчитаем все варианты, а потом выбросим те, которые нам запретили, но сразу выкинем вариант с мягким знаком на первом месте. То есть на первом месте мы можем поставить 4 различные буквы. На втором месте могу поставить все, кроме этой буквы, но зато мы можем добавить Ь, то есть тоже 4. Две буквы уже использовали. Осталось 3, 2 и 1. Все это перемножаю и получаю 96. То есть это все возможные слова, где используется буквы по одному разу, но только не начинающиеся на Ь.

Теперь из этого числа нужно выбросить ситуации, когда Ь стоит после гласной. Это, например, вот так

О Ь — — —
— О Ь — —
— — О Ь —
— — — О Ь

Таких слов 24

О Ь — — — 3*2*1
— О Ь — — 3*2*1
— — О Ь — 3*2*1
— — — О Ь 3*2*1
——
24

Абсолютно такая же ситуация с буквой А

А Ь — — —
— А Ь — —
— — А Ь —
— — — А Ь
———
24

И их тоже 24. То есть 96-48=48.

На этом прощаемся. Если вопросов нет, пока!

Все видео по информатике

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «8 Задание ЕГЭ 2021 | Комбинаторика» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник