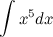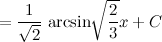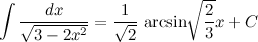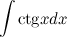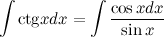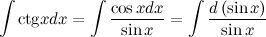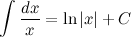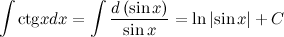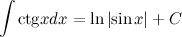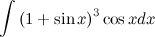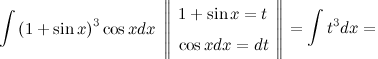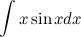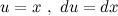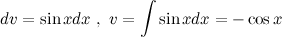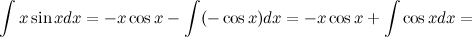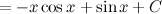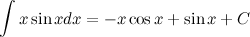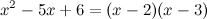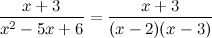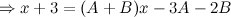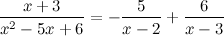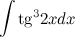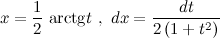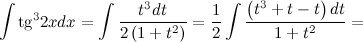Егэ интегралы примеры


Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Математика профильного уровня

Сайты, меню, вход, новости

Каталог заданий.
Первообразная


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

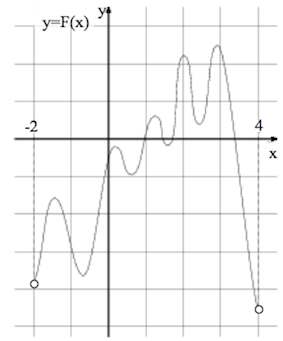
На рисунке изображён график функции y  =  F(x)  — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)  =  0 на отрезке [−2; 4].

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.

2

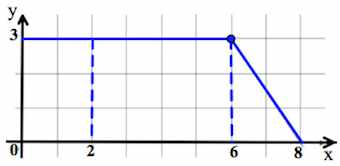
На рисунке изображён график некоторой функции y=f левая круглая скобка x правая круглая скобка (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x)  — одна из первообразных функции f(x).

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1.

3

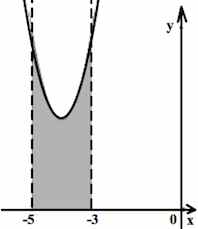
На рисунке изображён график функции y = f(x). Функция F левая круглая скобка x правая круглая скобка =x в кубе плюс 30x в квадрате плюс 302x минус дробь: числитель: 15, знаменатель: 8 конец дроби   — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

4

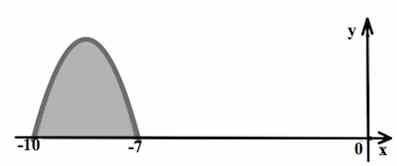
На рисунке изображён график некоторой функции y = f(x). Функция F левая круглая скобка x правая круглая скобка = минус x в кубе минус 27x в квадрате минус 240x минус 8  — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

Пройти тестирование по этим заданиям

Источник

Алгоритм решения интегралов

Неопределённым интегралом функции называется множество всех первообразных этой функции.

Первообразной функции называется такая функция, производная которой равна исходной функции, т.е., если F(x) – первообразная функции f(x), то:

F'(x) = f(x)

Операция интегрирования является операцией обратной операции дифференцирования.

Определённым интегралом функции на отрезке [a, b] называется разность первообразных функции, вычисленных на концах этого отрезка.

Определённый интеграл вычисляется при помощи формулы Ньютона-Лейбница:

    [int_a^b f(x) dx = F(b) - F(a)]

Для нахождения интегралов функций, используются свойства интегралов, а также таблица интегралов.

Таблица основных интегралов

Таблица основных интегралов, C – постоянная величина

    [int 0cdot dx = C]

    [int dx = x + C]

    [int x^{n}dx = frac{x^{n + 1}}{n + 1} + C, (n = const, n neq -1)]

    [int frac{dx}{x^{n}} = -frac{1}{n - 1}cdotfrac{1}{x^{n-1}} + C, (n = const, n neq -1)]

    [int frac{dx}{sqrt{x}} = 2sqrt{x} + C]

    [int frac{dx}{x} = ln{|x|} + C]

    [int a^{x}dx = frac{a^{x}}{ln a} + C, (a > 0, a neq 1)]

    [int e^{x}dx = e^{x} + C]

    [int sin{x}dx = -cos{x} + C]

    [int cos{x}dx = sin{x} + C]

    [int tg{x}dx = -ln|cos{x}| + C]

    [int ctg{x}dx = ln|sin{x}| + C]

    [int frac{dx}{cos^{2}x} = tg{x} + C]

    [int frac{dx}{sin^{2}x} = - ctg{x} + C]

    [int frac{dx}{1 + x^{2}} = arctg{x} + C]

    [int frac{dx}{sqrt{1 - x^{2}}} = arcsin{x} + C]

    [int frac{dx}{1 - x^{2}} = frac{1}{2}cdotlnleft | frac{1 + x}{1 - x} right | + C]

    [int frac{dx}{sqrt{x^{2} pm a^{2}}} = ln | x + sqrt{x^{2} pm a^{2}} | + C]

    [int sh{x}dx = ch{x} + C]

    [int ch{x}dx = sh{x} + C]

    [int frac{dx}{ ch^{2}x} = th{x} + C]

    [int frac{dx}{ sh^{2}x} = - cth{x} + C]

Примеры решений интегралов

Задача

Вычислить интеграл:

    [int xdx]

Решение

По таблице интегралов находим:

    [int xdx = frac{x^{2}}{d2} + C]

Ответ

    [int xdx = frac{x^{2}}{d2} + C]

Задача

Вычислить интеграл:

    [int sqrt{x}dx]

Решение

По таблице интегралов находим:

    [int sqrt{x}dx = int x^{frac{1}{2}}dx = frac{x^{frac{3}{2}}}{frac{3}{2}} = frac{2}{3}xsqrt{x} + C]

Ответ

    [int sqrt{x}dx = frac{2}{3}xsqrt{x} + C]

Задача

Вычислить интеграл:

    [int frac{dx}{sqrt{x}}]

Решение

По таблице интегралов находим:

    [int frac{dx}{sqrt{x}} = 2sqrt{x} + C]

Ответ

    [int frac{dx}{sqrt{x}} = 2sqrt{x} + C]

Задача

Вычислить интеграл:

    [int 7x^{5}dx]

Решение

Вынося постоянный множитель 7 за знак интеграла, по таблице интегралов находим:

    [int 7x^{5}dx = 7int x^{5}dx = 7cdotfrac{x^{6}}{6} + C]

Ответ

    [int 7x^{5}dx = 7cdotfrac{x^{6}}{6} + C]

Задача

Вычислить интеграл:

    [int (x^{3} + 5x)dx]

Решение

Интеграл суммы равен сумме интегралов, поэтому:

    [int (x^{3} + 5x)dx = int (x^{3})dx + int (5x)dx = frac{x^{4}}{4} + 5cdotfrac{x^{2}}{2} + C = frac{x^{4} + 10x^{2}}{4} + C]

Ответ

    [int (x^{3} + 5x)dx = frac{x^{4} + 10x^{2}}{4} + C]

Задача

Вычислить интеграл:

    [int (x^{4} - x^{2} + 4)dx]

Решение

Интеграл суммы равен сумме интегралов, поэтому:

    [int (x^{4} - x^{2} + 4)dx = int (x^{4})dx - int (x^{2})dx + int (4)dx = frac{x^{5}}{5} - frac{x^{3}}{3} + 4x + C]

Ответ

    [int (x^{4} - x^{2} + 4)dx = frac{x^{5}}{5} - frac{x^{3}}{3} + 4x + C]

Задача

Вычислить интеграл:

    [int sqrt[n]{x}dx]

Решение

Преобразуя подынтегральную функцию к виду степенной, находим её интеграл по таблице интегралов:

    [int sqrt[n]{x}dx = int {x}^{frac{1}{n}}dx = frac{x^{frac{n + 1}{n}}}{frac{n + 1}{n}} + C = frac{ncdot x^{frac{n + 1}{n}}}{n + 1} + C = frac{n}{n + 1}xsqrt[n]{x} + C]

Ответ

    [int sqrt[n]{x}dx = frac{n}{n + 1}xsqrt[n]{x} + C]

Задача

Вычислить интеграл:

    [int sqrt[n]{x^{m}}dx]

Решение

Преобразуя подынтегральную функцию к виду степенной, находим её интеграл по таблице интегралов:

    [int sqrt[n]{x}dx = int {x}^{frac{m}{n}}dx = frac{x^{frac{m + n}{n}}}{frac{m + n}{n}} + C = frac{ncdot x^{frac{m + n}{n}}}{m + n} + C = frac{n}{m + n}xsqrt[n]{x^{m}} + C]

Ответ

    [int sqrt[n]{x}dx = frac{n}{m + n}xsqrt[n]{x^{m}} + C]

Задача

Вычислить интеграл:

    [int (frac{3}{x^{5}} - frac{2}{x^{4}} + frac{1}{x^{3}})dx]

Решение

Интеграл суммы равен сумме интегралов, поэтому:

    [int (frac{3}{x^{5}} - frac{2}{x^{4}} + frac{1}{x^{3}})dx = int (frac{3}{x^{5}})dx - int (frac{2}{x^{4}})dx + int (frac{1}{x^{3}})dx]

Далее найдём каждый интеграл суммы:

    [int (frac{3}{x^{5}})dx = 3frac{x^{-4}}{-4} + C = -frac{3}{4}cdotfrac{1}{x^{4}} + C]

    [int (frac{2}{x^{4}})dx = 2frac{x^{-3}}{-3} + + C = - frac{2}{3}cdotfrac{1}{x^{3}} + C]

    [int (frac{1}{x^{3}})dx = frac{x^{-2}}{-2} + C = - frac{1}{2}cdotfrac{1}{x^{2}} + C]

Ответ

    [int (frac{3}{x^{5}} - frac{2}{x^{4}} + frac{1}{x^{3}})dx = -frac{3}{4}cdotfrac{1}{x^{4}} + frac{2}{3}cdotfrac{1}{x^{3}} - frac{1}{2}cdotfrac{1}{x^{2}} + C]

Задача

Вычислить интеграл:

    [int (sin{x} + cos{x})dx]

Решение

Интеграл суммы равен сумме интегралов, поэтому:

    [int (sin{x} + cos{x})dx = int (sin{x})dx + int (cos{x})dx]

Далее, применяя таблицу интегралов, находим интегралы функций синус и косинус:

    [int (sin{x})dx + int (cos{x})dx = -cos{x} + sin{x} + C]

Ответ

    [int (sin{x} + cos{x})dx = -cos{x} + sin{x} + C]

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Первообразная функции»

Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры на плоскости: вычисление величин с использованием углов

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №1164

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).

График функции y=f(x), являющийся ломаной линией, составленной из трёх прямолинейных отрезков

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.

Её площадь равна frac{4+3}{2}cdot 3=10,5.

Ответ

10,5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1158

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].

График функции y= F(x) - одной из первообразных функции f(x), на интервале (-5; 5)

Показать решение

Решение

Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).

Ответ

7

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1155

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).

График функции у=f(x) являющийся ломаной линией, составленной из трёх прямолинейных отрезков

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.

Её площадь равна frac{5+3}{2}cdot 3=12.

Ответ

12

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1149

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].

График функции y=F(x) — одной из первообразных некоторой функции f(x) на интервале (-5; 4)

Показать решение

Решение

Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 3], в которых производная функции F(x) равна нулю.

Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).

Ответ

5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1146

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).

Найдите площадь заштрихованной фигуры.

График некоторой функции y=f(x) с известной первообразной и заштрихованной фигурой

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.

Ответ

10

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №907

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

График функции y=f(x) с заштрихованной областью

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).

Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.

Ответ

12

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №307

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

График некоторой функции y=f(x) с заштрихованной фигурой

Показать решение

Решение

По формуле Ньютона-Лейбница S=F(-1)-F(-5).

F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.

F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.

F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.

Ответ

576

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №306

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).

График функции y=f(x)

Показать решение

Решение

F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.

Трапеция, ограниченная графиком функции y=f(x) и прямыми.

Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.

Ответ

7

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №104

Тип задания: 7
Тема:
Первообразная функции

Условие

На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.

График дифференцируемой функции y=f(x)

Показать решение

Решение

На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:

intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)

Подставим значение первообразной из условия и получим площадь фигуры:

F(-1)-F(-4)=

=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=

=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5

Ответ

4,5

Задание №103

Тип задания: 7
Тема:
Первообразная функции

Условие

Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].

Первообразная y=F(x) функции y=f(x)

Показать решение

Решение

Формула первообразной имеет следующий вид:

f(x) = F'(x)

По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.

Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.

На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.

Первообразная y=F(x) функции y=f(x)

Ответ

3

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Примеры решения задач с интегралами

Интеграл функции является основным понятием интегрального исчисления.
Интеграл широко используется при решении целого ряда задач по математике, физике и в других науках.
Именно поэтому мы собрали на сайте более 100 примеров решения интегралов и постоянно добавляем новые! Список тем находится в правом меню.

Перед изучением примеров вычисления интегралов советуем вам прочитать теоретический материал по теме:
определения, свойства и таблицу интегралов, методы их вычисления и
другой материал по интегралам.

Таблица интегралов

Основные ссылки — таблица интегралов и
примеры решений (10 шт).

Пример

Задание. Вычислить неопределенный интеграл

Решение. Для решения данного интеграла не нужно использовать свойства неопределенных интегралов, достаточно формулы интеграла степенной функции:

В нашем случае 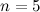, тогда искомый интеграл равен:

Ответ.

Больше примеров решений →

Метод непосредственного интегрирования

Основные ссылки — метод непосредственного интегрирования и
примеры решений (10 шт).

Пример

Задание. Вычислить неопределенный интеграл

Решение. Преобразуем подынтегральное выражение. Для этого вынесем из знаменателя
за знак интеграла

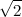
далее, используя таблицу интегралов (Формула №11), получим

Ответ.

Больше примеров решений →

Внесение под знак дифференциала

Основные ссылки — внесение под знак дифференциала и
примеры решений (10 шт).

Пример

Задание. Вычислить неопределенный интеграл

Решение. Распишем подынтегральную сумму, используя тригонометрические функции (определение котангенса)

Внесем 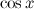под знак дифференциала:

Полученный интеграл можно вычислить, используя табличный интеграл

В результате получим

Ответ.

Больше примеров решений →

Интегрирование заменой переменной

Основные ссылки — интегрирование заменой переменной и
примеры решений (10 шт).

Пример

Задание. Найти неопределенный интеграл

Решение. Введем замену 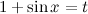и полученный интеграл находим как интеграл от степенной функции:

Сделаем обратную замену

Ответ.

Больше примеров решений →

Интегрирование по частям

Основные ссылки — интегрирование по частям и
примеры решений (10 шт).

Пример

Задание. Найти неопределенный интеграл

Решение. Воспользуемся методом интегрирования по частям. Для этого положим

Подставим это в формулу для интегрирования по частям, затем воспользуемся формулой интеграла косинуса из таблицы интегралов

Ответ.

Больше примеров решений →

Метод неопределенных коэффициентов

Основные ссылки — метод неопределенных коэффициентов и
примеры решений (10 шт).

Пример

Задание. Разложить рациональную дробь
на простые дроби.

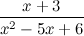
Решение. Так как корнями знаменателя являются значения
,
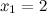
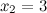
, то его можно разложить на множители следующим образом:

А тогда

Искомое разложение имеет вид:

Приводим к общему знаменателю в правой части равенства и приравниваем числители:

Приравнивая коэффициенты, при соответствующих степенях, получаем:

Отсюда, искомое разложение:

Ответ.  

Больше примеров решений →

Интегрирование тригонометрических функций

Основные ссылки — универсальная тригонометрическая подстановка и
примеры решений (10 шт).

Пример

Задание. Найти неопределенный интеграл

Решение. Для вычисления исходного интеграла введем тригонометрическую замену 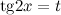, тогда

Подставляя это в искомый интеграл, получим

Сделаем обратную замену

Ответ.

Больше примеров решений →

Вы поняли, как решать? Нет?

Другие примеры

  • Примеры решения задач с логарифмами
  • Решение СЛАУ 3-его порядка методом Гаусса, пример № 5
  • Решение СЛАУ 3-его порядка методом Гаусса, пример № 1
  • Решение СЛАУ 3-его порядка методом Гаусса, пример № 11

    • Калькулятор стоимости

    Рассчитайте цену решения ваших задач

    Ошибка

    Ошибка

    Закрыть

    Калькулятор
    стоимости

    Решение контрольной

    от 300 рублей
    *

    * Точная стоимость будет определена после загрузки задания для исполнителя

    +Загрузить файл


    Файлы doc, pdf, xls, jpg, png не более 5 МБ.

    Ошибка

    Ошибка

Источник

Интегралы на ЕГЭ. Первообразные элементарных функций

Вы в школе уже прошли интегралы? Поняли эту тему?:)

А вы знали, что в ЕГЭ тоже могут попасться интегралы? Да-да, открываем кодификатор и видим: 

4.3 Первообразная и интеграл

– 4.3.1 Первообразные элементарных функций

– 4.3.2 Примеры применения интеграла в физике и геометрии)

Но не волнуйтесь. В школьной программе интегралы – не сложные. Это не проблема, это скорее возможность получить легкие баллы!!!

И это значит, что пора смотреть наше видео.

Интегралы на ЕГЭ. Первообразные элементарных функций

В этом видео мы расскажем вам, какие типы задач на интегралы и первообразную могут быть в ЕГЭ, и научим их решать.

И да, в институте без знания производной и интегралов делать нечего. Совсем. Там не будет времени разбираться с ней, так что лучше займитесь ей сейчас.

Важно: перед этим уроком повторите производную! 

Ведь проходить интегралы без производной – это как вычислять арксинус, не зная, что такое синус:)

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Алексей Шевчук – ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 – WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org – email для записи

  • тысячи учеников, поступивших в лучшие ВУЗы страны
  • автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
  • закончил МФТИ, преподавал на малом физтехе;
  • репетиторский стаж – c 2003 года;
  • в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
  • отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.

Что думаете об интегралах на ЕГЭ?

Попадутся или нет на экзамене?

Насколько сложно понять и научиться решать задачи именно для вас?

Будете ли вы учить эту тему перед ЕГЭ.

Напишите нам в комментариях прямо сейчас.

Источник

10
Авг 2013

Категория: 07 Производная, ПО

07. Первообразная

2013-08-10
2022-09-11

Задача 1. На рисунке изображён график некоторой функции y=f(x)  (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)-F(2), где F(x)  — одна из первообразных функции f(x).

у

Решение: + показать


Задача 2. На рисунке изображён график некоторой функции  y=f(x). Функция F(x)=x^3+12x^2+51x-3 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

ed

Решение: + показать


Задача 3. На рисунке изображён график некоторой функции y=f(x). Функция F(x)=-frac{4}{9}x^3-frac{34}{3}x^2-frac{280}{3}x-frac{18}{5} — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

u

Решение: + показать


Задача 4. На рисунке изображён график функции y=F(x) – одной из первообразных некоторой функции f(x), определённой на интервале (-2;4). Пользуясь рисунком, определите количество решений уравнения f(x)=0  на отрезке [-1;3].

r

Решение: + показать


колоЗагляните –> + показать

тест

Вы можете пройти тест «Первообразная»

Автор: egeMax |

комментариев 7

Источник

Первообразной для функции $f(x)$ называется такая функция $F(x)$, для которой выполняется равенство: $F'(x)=f(x)$

Таблица первообразных

Первообразная нуля равна $С$

Функция Первообразная
$f(x)=k$ $F(x)=kx+C$
$f(x)=x^m, m≠-1$ $F(x)={x^{m+1}}/{m+1}+C$
$f(x)={1}/{x}$ $F(x)=ln|x|+C$
$f(x)=e^x$ $F(x)=e^x+C$
$f(x)=a^x$ $F(x)={a^x}/{lna}+C$
$f(x)=sinx$ $F(x)-cosx+C$
$f(x)=cosx$ $F(x)=sinx+C$
$f(x)={1}/{sin^2x}$ $F(x)=-ctgx+C$
$f(x)={1}/{cos^2x}$ $F(x)=tgx+C$
$f(x)=√x$ $F(x)={2x√x}/{3}+C$
$f(x)={1}/{√x}$ $F(x)=2√x+C$

Если $y=F(x)$ – это первообразная для функции $y=f(x)$ на промежутке $Х$, то $у$ $у=f(x)$ бесконечно много первообразных и все они имеют вид $y=F(x)+C$

Правила вычисления первообразных:

  1. Первообразная суммы равна сумме первообразных. Если $F(x)$ — первообразная для $f(x)$, а $G(x)$ – первообразная для $g(x)$, то $F(x)+G(x)$ — первообразная для $f(x)+g(x)$.
  2. Постоянный множитель выносится за знак первообразной. Если $F(x)$ — первообразная для $f(x)$, а $k$ – постоянная величина, то $k$ $F(x)$ — первообразная для $k$ $f(x)$.
  3. Если $F(x)$ — первообразная для $f(x)$, $а, k, b$ — постоянные величины, причем $k≠0$, то ${1}/{k}$ $F(kx+b)$ — это первообразная для $f(kx+b)$.

Пример:

Найти первообразную для функции $f(x)=2sin⁡x+{4}/{x}-{cos⁡x}/{3}$.

Решение:

Чтобы было проще найти первообразную от функции, выделим коэффициенты каждого слагаемого

$f(x)=2sin⁡x+{4}/{x}-{cos⁡x}/{3}=2∙sin⁡x+4∙{1}/{x}-{1/3}∙cos⁡x$

Далее, воспользовавшись таблицей первообразных, найдем первообразную для каждой функции, входящих в состав $f(x)$

$f_1=sin⁡x$

$f_2={1}/{x}$

$f_3=cos⁡x$

Для $f_1=sin⁡x$ первообразная равна $F_1=-cos⁡x$

Для $f_2={1}/{x}$ первообразная равна $F_2=ln⁡|x|$

Для $f_2=cos⁡x$ первообразная равна $F_3=sin⁡x$

По первому правилу вычисления первообразных получаем:

$F(x)=2F_1+4F_2-{1}/{3}F_3=2∙(-cos⁡x)+4∙ln⁡|x|-{1}/{3}∙sin⁡x$

Итак, общий вид первообразной для заданной функции

$F(x)=-2cos⁡x+4ln⁡|x|-{sin x}/{3}+C$

Связь между графиками функции и ее первообразной:

  1. Если график функции $f (x) > 0$ на промежутке, то график ее первообразной $F(x)$ возрастает на этом промежутке.
  2. Если график функции $f (x) < 0$ на промежутке, то график ее первообразной $F(x)$ убывает на этом промежутке.
  3. Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий (или наоборот).

Пример:

На рисунке изображен график функции $y=F(x)$ – одной из первообразных некоторой функции $f(x)$, определенной на интервале $(-3;5)$. Пользуясь рисунком, определите количество решений $f(x)=0$ на отрезке $(-2;2]$

Если $f(x)=0$, то график ее первообразной $F(x)$ в этой точке меняется с возрастающего на убывающий(или наоборот).

Выделим отрезок $(-2;2]$ и отметим на нем экстремумы.

У нас получилось $6$ таких точек.

Ответ: $6$

Неопределенный интеграл

Если функция $у=f(x)$ имеет на промежутке $Х$ первообразную $у=F(x)$, то множество всех первообразных $у=F(x)+С$, называют неопределенным интегралом функции $у=f(x)$ и записывают:

$∫f(x)dx$

Определенный интеграл – это интеграл с пределами интегрирования (на отрезке)

$∫_a^bf(x)dx$, где $a,b$ — пределы интегрирования

Площадь криволинейной трапеции или геометрический смысл первообразной

Площадь $S$ фигуры, ограниченной осью $Oх$, прямыми $х=а$ и $х=b$ и графиком неотрицательной функции $у=f(x)$ на отрезке $[a;b]$, находится по формуле

$S=∫_a^bf(x)dx$ 

Формула Ньютона — Лейбница

Если функция $у=f(x)$ непрерывна на отрезке $[a;b]$, то справедливо равенство

$∫_a^bf(x)dx=F(x)|_a^b=F(b)-F(a)$, где $F(x)$ — первообразная для $f(x)$

Пример:

На рисунке изображен график некоторой функции $у=f(x)$. Одна из первообразных этой функции равна $F(x)={2х^3}/{3}-2х^2-1$. Найдите площадь заштрихованной фигуры.

Решение:

Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках $1$ и $-2$

$S=F(1)-F(-2)$

Первообразная нам известна, следовательно, осталось только подставить в нее значения и вычислить

$F(1)={2∙1}/{3}-2∙1-1={2}/{3}-2-1={2}/{3}-3$

$F(-2)={2(-2)^3}/{3}-2(-2)^2-1={2∙(-8)}/{3}-8-1=-{16}/{3}-9$

$S={2}/{3}-3-(-{16}/{3}-9)={2}/{3}-3+{16}/{3}+9={18}/{3}+6=6+6=12$

Ответ: $12$

Источник

Понравилась статья? Поделить с друзьями:
  • Егэ индивидуальные авторские слова
  • Егэ индивидуальное предпринимательство
  • Егэ или огэ что страшнее
  • Егэ или огэ как правильно
  • Егэ или егэ как правильно писать