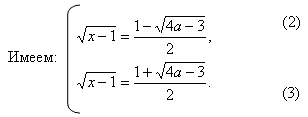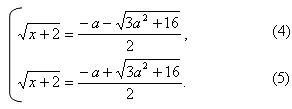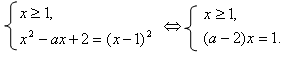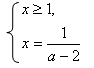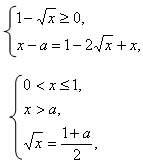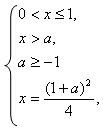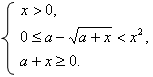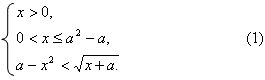Егэ иррациональные уравнения с параметром

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 255    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 255    1–20 | 21–40 | 41–60 | 61–80 …

Цель: Познакомить обучающихся с решением иррациональных уравнений и неравенств с параметром. Способствовать развитию навыка решения задач.

Содержание занятий.

Задачи с параметром даются в текстах ЕГЭ.

Фактически задача с одним параметром содержит не одну неизвестную , а две — и параметр Множество решений такого уравнения — это множество пар чисел , подстановка которых в уравнение обращает его в верное равенство. Аналогично, множество решений неравенства с неизвестной  и параметром

 — множество пар чисел (, обращающих его в верное числовое неравенство. На I этапе решения классифицируются типы уравнений и неравенств для каждого значения параметра, а на II этапе – решаются не одно, а несколько уравнений (неравенств) каждого типа. Выделенные два этапа не обязательно идут в строгой последовательности I, II. В процессе решения они могут «переплетаться».

Пример №1 Решить уравнение

Решение. Перепишем уравнение в виде:

 (1)

и рассмотрим его как квадратное относительно . Находим дискриминант уравнения D=. Уравнение (1) имеет решение только в случае, если .

Заметим, что уравнение (2) имеет решение тогда и только тогда, когда , т. е. при  . Решив уравнения (2) и (3), получим при

                         

Таким образом, приходим к следующему ответу:

при  уравнение имеет два корня: х1 и х2 ; при  уравнение имеет один корень: х2; при  решений нет.

Пример №2 Решить уравнение

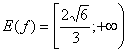
Решение. Функция  определена и возрастает на промежутке . Наименьшее значение она принимает в точке ; . Следовательно, при  уравнение  имеет единственное решение, при  решений нет.

Итак, пусть . Переписав уравнение в виде

, (1)

возведём обе его части в квадрат:

. (2)

Уравнение (2) является следствием (1). Перепишем его в виде:

 (3)

Уравнение (3) является квадратным относительно . Решив его, получаем совокупность двух уравнений:

При  уравнение (4) решений не имеет, а уравнение (5) имеет один корень

.

Так как при любом  исходное уравнение имеет один корень, и притом только один, то найденный корень и является корнем исходного уравнения.

Ответ: При  , при  решений нет.

Пример №3. Решить уравнение

Решение. Уравнение равносильно системе

При  система решений не имеет, при  получим

Заметив, что  при  приходим к ответу: при   при  3 решений нет.

Графическое решение

Пример №4

Решить уравнение

Решение. 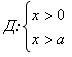, на множестве Д уравнение  равносильно исходному.

Уравнение  равносильно системе

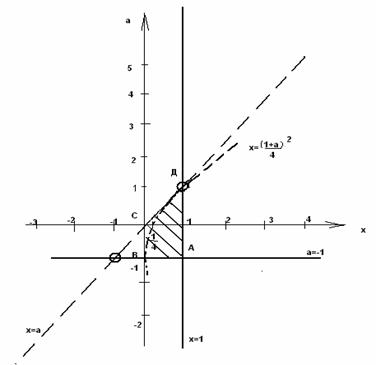
Изобразим на плоскости (х;а) график функции  — это парабола с минимумом в точке , пересекающая ось  в точке

Укажем также области плоскости (х;а), в которых выполняются неравенства системы

1.  — полуплоскость ниже прямой , не включая эту прямую;
2.  вертикальная полоса между прямыми  и  включающая правую границу;
3.  полуплоскость выше прямой  включая эту прямую.

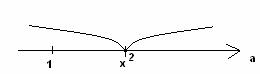
Таким образом, исходное уравнение имеет решение при указанных условиях, иллюстрирующееся частью параболы, заключённой внутри трапеции АВСД, т. е. при .

При всех остальных действительных значениях  решения нет.

Ответ:  при

Решений нет при

Пример №5.

Для любого значения  решите неравенство

.

Решение. Во-первых, заметим, что левая часть неравенства представляет собой квадратный трёхчлен относительно  с корнями

 так что левая часть раскладывается на множители

. (1)

Во-вторых, при  имеем особый случай: , решением которого является .

В- третьих, заметим, что значение разности во второй скобке положительно при . Так что при  неравенство (1) можно переписать в виде

.

При  в (1) значение суммы в первой скобке положительно, то есть (1) можно переписать в виде неравенства

.

Наконец, заметим, что  входит в последний случай.

Осталось скомпоновать

Ответ: если , то ;

Если  то .

Пример №6 Для каждого значения  решите неравенство

Решение. При  неравенство не выполняется и оно равносильно системе неравенств

Рассмотрим второе  При  нет решений, а для  имеем  Первое из этих неравенств заведомо выполнено (и ). Получаем систему

Двойное неравенство этой системы непротиворечиво лишь при условии  при условии  приводит к условию .

Итак, остаётся решить последнее неравенство системы (1) при . Основная идея – решаем неравенство относительно , объявляя на время  параметром.

1. Если , то есть  — уже решение.
2. Если же , то есть , то

. (1/)

Дискриминант квадратного трёхчлена

,

а его корни  и . Заметим, что очевидно  при х > 0. Значит, решения неравенства (1/) суть

.

Здесь первое неравенство следует из неравенства . Остаётся  для любого  (

При  решение последнего неравенства составляют промежутки

 

С учётом  очевидно, остаётся лишь второй промежуток.

Наконец, убедимся, что при

<.

 

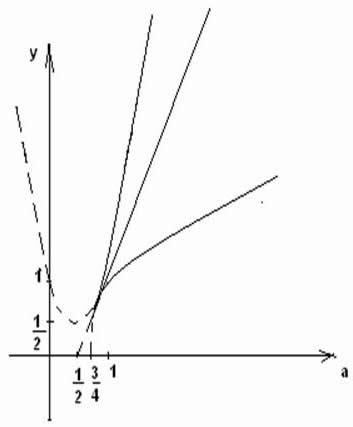
Установим двойное неравенство

При  каждое из них сводиться к неравенству  (легко проверить!). Остаётся лишь записать

Ответ: если , то решений нет ;

если , то .

Задачи для самостоятельной работы 

11 апреля 2021

В закладки

Обсудить

Жалоба

Решение иррациональных уравнений и систем уравнений с параметром

Иррациональными уравнениями называются уравнения, содержащие переменную под знаком радикала (корня) или под знаком возведения в дробную степень. При этом, степень корня может быть произвольной.

riu.docx
riu.pdf

Автор: Канаева Ирина Витальевна.

Решение иррациональных уравнений и систем уравнений с параметром

Иррациональными уравнениями называются уравнения, содержащие переменную под знаком радикала (корня) или под знаком возведения в дробную степень. При этом, степень корня может быть произвольной.

Контрольная работа по русской литературе второй половины 19 века

Н.С. Лесков, М.Е. Салтыков-Щедрин, Ф.М. Достоевский.

Банковская задача (дифференцированные платежи)

На занятии обсуждаем критерии оценивания задания №15, виды задач на кредиты, а так же рассматриваем процесс построения математической модели для задач на кредиты с дифференцированными платежами.

Контрольная работа по теме: «Россия при Екатерине II (1762-1796 гг.)»

Тестовая работа разработана на основе УМК А.В. Торкунова (§17-23). Состоит из 2-х вариантов, в каждом 23 вопроса.

Задачи с параметрами по теме: Иррациональные уравнения и неравенства.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

МАОУ ЛИЦЕЙ №44 г. Липецка

Учитель математики: Скорикова Людмила Алексеевна.

Уроки математики в 11 классе

Задачи с параметрами

по теме: Иррациональные уравнения и неравенства.

Углубить знания учащихся по теме иррациональные уравнения и неравенства.

Показать как одна из линий курса математики средней школы “Уравнения и неравенства с параметрами” реализуются в содержании ЕГЭ.

Развивать практические навыки в решении иррациональных неравенств с параметрами.

Развивать логическое мышление, математическую речь, навыки самостоятельной работы, самоконтроля.

Воспитывать познавательный интерес, творческие способности, ответственное отношение. Повысить уровень подготовленности учащихся к сдаче ЕГЭ по математике.

Задачи с параметрами представляют для учащихся наибольшую сложность. Большинство учащихся либо не справляются с такими задачами, либо приводят громоздкое решение без всякой логической стройности. Многие же задачи можно решать различными способами. Решению задач с параметрами в школе уделяется мало внимания. Устранить этот пробел можно на внеклассных занятиях.

Предлагаю занятие по теме: «Иррациональные уравнения и неравенства с параметрами», которое расширит и углубит базовую основу общеобразовательной программы по математике и поможет повысить уровень подготовленности учащихся к сдаче ЕГЭ.

Универсальных указаний по решению задач с параметрами дать нельзя. При решении задач с параметрами приходится рассматривать различные случаи, в зависимости от значений параметров, и методы решения задач различны. Но знание некоторых правил и алгоритмов решения необходимо.

Взяты эти задания из различных источников. Большинство из этих заданий предлагалось на вступительных экзаменах в ВУЗах.

Используются аналитические и графические способы решения уравнений и неравенств.

В конце рассматриваемой темы даются задания для самостоятельной работы.

Данный материал может быть полезным учителям математики, абитуриентам, школьникам.

Иррациональные уравнения и неравенства.

При решении иррациональных уравнений с параметрами пользуются общими формулами. Пусть f и q – некоторые функции, , тогда:

1). , f ≥ 0; q ≥ 0.

2). , f ≥ 0; q > 0.

3). , q ≥ 0.

4). , , q ≠ 0.

5). , fq ≥0.

Применяя эти формулы нужно иметь в виду, что ОДЗ левой и правой частей каждой из них могут быть различными. Для каждой формулы ОДЗ правой части может быть шире ОДЗ левой.

Отсюда следует, что преобразования уравнения с формальным использованием формул «слева-направо» приводят к уравнению, являющемуся следствием исходного. В этом случае могут появиться посторонние корни уравнения.

Преобразование уравнений с формальным использованием данных формул «справа-налево» недопустимы, т.к. возможно сужение ОДЗ исходного уравнения, а следовательно, и потеря корней.

Уравнение вида , равносильно системе:

Решить уравнение .

Заданное уравнение равносильно системе:

=> =>

Находим значения а, при которых

Ответ:

Решить уравнение .

Заданное уравнение равносильно системе:

=>

,

х ₁ , х ₂ являются действительными числами при а ≤ 9/16. При значениях а > 9/16 решений нет.

Удовлетворим неравенства х ≥ а и х ≥ ½.

а) ≥ ½

≥ а

Если а ≤ 9/16, то 8а-5 справедливо при всех допустимых а.

б).

а ≥ ½ (а ≤ 9/16)

Следовательно, х ₂ является решением исходного уравнения при ½ ≤ а ≤ 9/16

Ответ: , если а , если ½ ≤ а ≤ 9/16; нет решений, если а>9/16.

Решить уравнение

ОДЗ: х – а ≥ 0, х ≥ а

Если а = 1, то х ₁ = х ₁ = 1.

Если а ₁ = 1 удовлетворяет условию ОДЗ х ≥ а, т.е. является корнем уравнения.

Если а > 1, то х ₁ = 1 не удовлетворяет условию х ≥ а, т.е. является посторонним корнем.

Ответ: 1) если а ₁ = 1; х ₂ = а; 2) если а ≥ 1, то х = а.

При каких а уравнение имеет один корень?

Корень будет единственным, если а=4; если одно из двух значений (4 и а) является посторонним корнем, а именно х = а. Это произойдет при условии, что х = а не входит в область определения уравнения х ≥ 0, т.е. при а

Ответ: а = 4 или а

Найти минимальное целое положительное значение параметра а, при котором уравнение имеет различные положительные корни.

ах -8 ≥ 0, х ≥ 8/а, х > 0, а > 0

D =

, . А = 17 – минимальное целое число.

Найти все значения параметра а, при которых корни уравнения принадлежат отрезку [2;17].

Пусть

, t ≥ 0, х — 1 = t 2

,

,

1) => => =>

2) => =>

3) => => =>

Ответ: .

Решить уравнение .

х ≥ 2

(х + 1)(х — 2) = а; х 2 – х – 2 = а, х 2 – х – 2 – а = 0.

, .

Множеству х ≥ 2 принадлежит только корень х ₂ .

Ответ: при а ≥ 0 .

Решить уравнение .

. Так как , то m > 0. Пусть у = , тогда х = у 2 + 3, и исходное уравнение равносильно системе уравнений:

т.е. ,

, , .

Ответ: при m m >3 решений нет, при .

Решить уравнение .

Пусть , тогда ,

, , а т.к. t > 0, то ,

, , . ( а > ¼)

х = .

Ответ: х = при а > ¼.

Найти все значения параметра а, при которых уравнение имеет решение.

Если изобразить графики функций и , то очевидно, что они пересекаются (и исходное уравнение имеет решение) при .

При каких значениях а решением неравенства является промежуток [2;18)?

х 2 , т.к. , то

а = 7 – не подходит в ОДЗ.

Решить неравенство , где а – параметр.

При любом значении а, если правая часть х + а – 1

При х ≥ 1 – а равносильная система имеет вид :

=> (*)

Рассмотрим возможные случаи:

Если а > 1, то 1 – а ≤ х . Объединяя с множеством х .

Если а = 1, то х ≥ 1 – решение системы (*). Объединяя с множеством х

Ответ: , если а > 1; , если а ≤ 1.

Решить уравнение

Из данного уравнения следует:

1 – х 2 = х 2 + 2ах + а 2 ,

2х 2 + 2ах + а 2 — 1 = 0.

D /4 = 2 – а 2 . D > 0 при |a| .

Затем если изобразить графики функций и , то видно как меняется количество решений в зависимости от значений а.

Ответ: при нет решений; при и одно решение; при два решения.

1). Решить уравнение .

Ответ: .

2). Найти левый и правый края области значений параметра а, в которой уравнение имеет различные положительные корни.

, х > 0, а ≥ 0.

D = 49 – 4 a 2 > 0

а = -3, 5 не входит в ОДЗ.

3). Решить уравнение .

Данное уравнение равносильно системе:

=>

При а = 2 второе уравнение имеет вид , т.е. .

При а ≠ 2 .

Выясним, при каких значениях а найденное значение х удовлетворяет неравенству х ≥ -1.

.

Ответ: при а ≤ 1/3 и а > 2 ; при 1/3

4). Найти все значения параметра а, при которых корни уравнения принадлежит отрезку [-4;44].

Ответ: .

5). При всех а решить неравенство .

ОДЗ:

а). Если а ≤ 0, то данное неравенство справедливо при всех .

б). Если а > 0, то данное неравенство равносильно системе неравенств.

=> .

Ответ: при ; при .

Математика. Иррациональные уравнения и неравенства с параметрами.

Иррациональными называются уравнения, в которых переменная содержится под знаком корня.

Иррациональное уравнение, как правило, сводится к равносильной системе, содержащей уравнения и неравенства.

1.

Из двух систем выбирают ту, которая решается проще.

2.

12
Фев 2014

Категория: 17 (С6) Параметры*ПараметрТ/P A. Ларина

C5 (№20) с ловушкой, не попадитесь!

2014-02-12
2015-09-05

Автор: egeMax |

комментария 4