Егэ исследование произведений решу - Помощь в подготовке к экзаменам и поступлению

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Исследование произведений

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 11 № 26691

Найдите наименьшее значение функции на отрезке

Аналоги к заданию № 26691: 3383 69993 3385 3387 3389 3391 3393 3395 3397 3399 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 26710

Найдите точку минимума функции

Аналоги к заданию № 26710: 3773 3781 70837 548382 3775 3777 3779 3783 3785 3787 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 26711

Найдите точку максимума функции

Аналоги к заданию № 26711: 3791 70887 509578 3793 3795 3797 3799 3801 3803 3805 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 11 № 26712

Найдите точку минимума функции

Аналоги к заданию № 26712: 3811 70937 3813 3815 3817 3819 3821 3823 3825 3827 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 11 № 26713

Найдите точку максимума функции

Аналоги к заданию № 26713: 3829 70987 3831 3833 3835 3837 3839 3841 3843 3845 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Исследование произведений»

Открытый банк заданий по теме исследование произведений. Задания B12 из ЕГЭ по математике (профильный уровень)

Тригонометрические уравнения

Задание №1136

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите наибольшее значение функции y=(7x^2-56x+56)e^x на отрезке [-3; 2].

Показать решение

Решение

Найдём производную исходной функции по формуле производной произведения y’= (7x^2-56x+56)’e^x,+ (7x^2-56x+56)left(e^xright)’= (14x-56)e^x+(7x^2-56x+56)e^x= (7x^2-42x)e^x= 7x(x-6)e^x. Вычислим нули производной: y’=0;

7x(x-6)e^x=0,

x_1=0, x_2=6.

Расставим знаки производной и определим промежутки монотонности исходной функции на заданном отрезке.

Из рисунка видно, что на отрезке [-3; 0] исходная функция возрастает, а на отрезке [0; 2] — убывает. Таким образом, наибольшее значение на отрезке [-3; 2] достигается при x=0 и равно y(0)= 7cdot 0^2-56cdot 0+56=56.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1134

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите точку минимума функции y=(x+8)^2e^{x+52}.

Показать решение

Решение

Будем находить точку минимума функции с помощью производной. Найдём производную заданной функции, пользуясь формулами производной произведения, производной x^alpha и e^x:

y'(x)= left((x+8)^2right)’e^{x+52}+(x+8)^2left(e^{x+52}right)’= 2(x+8)e^{x+52}+(x+8)^2e^{x+52}= (x+8)e^{x+52}(2+x+8)= (x+8)(x+10)e^{x+52}.

Расставим знаки производной и определим промежутки монотонности исходной функции. e^{x+52}>0 при любом x. y’=0 при x=-8, x=-10.

Из рисунка видно, что функция y=(x+8)^2e^{x+52} имеет единственную точку минимума x=-8.

Ответ

-8

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1129

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите наименьшее значение функции y=(5x^2-70x+70)e^{x-12} на отрезке [10; 15].

Показать решение

Решение

Найдём производную исходной функции по формуле производной произведения

y’= (5x^2-70x+70)’e^{x-12},+ (5x^2-70x+70)left(e^{x-12}right)’= (10x-70)e^{x-12},+ (5x^2-70x+70)e^{x-12}= (5x^2-60x)e^{x-12}= 5x(x-12)e^{x-12}.

Вычислим нули производной: y’=0;

5x(x-12)e^{x-12}=0,

x_1=0, x_2=12.

Расставим знаки производной и определим промежутки монотонности исходной функции на заданном отрезке.

Из рисунка видно, что на отрезке [10; 12] исходная функция убывает, а на отрезке [12; 15] — возрастает. Таким образом, наименьшее значение на отрезке [10; 15] достигается при x=12 и равно y(12)= (5cdot 12^2-70cdot 12+70)e^{12-12}= -50.

Ответ

-50

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1127

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите точку максимума функции y=(x+3)^2e^{x-2016}.

Показать решение

Решение

Будем находить точку максимума функции с помощью производной. Найдём производную заданной функции, пользуясь формулами производной произведения, производной x^alpha и e^x:

y'(x)= left((x+3)^2right)’e^{x-2016}+(x+3)^2left(e^{x-2016}right)’= 2(x+3)e^{x-2016}+(x+3)^2e^{x-2016}= (x+3)e^{x-2016}(2+x+3)= (x+3)(x+5)e^{x-2016}.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Так как e^{x-2016}>0 для любого x, то y’=0 при x=-3, x=-5.

Из рисунка видно, что функция y=(x+3)^2e^{x-2016} имеет единственную точку максимума x=-5.

Ответ

-5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1121

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите наименьшее значение функции y=(x-11)e^{x-10} на отрезке [8; 14].

Показать решение

Решение

Найдём производную исходной функции по формуле производной произведения:

y’= (x-11)’e^{x-10}+(x-11)left(e^{x-10}right)’= e^{x-10}+(x-11)e^{x-10}= (x-10)e^{x-10}.

Вычислим нули производной: y’=0;

(x-10)e^{x-10}=0;

x=10.

Заметим, что при x<10 выполняется неравенство y'<0, при x>10 выполняется неравенство y’>0. Значит, функция y=(x-11)e^{x-10} возрастает при x>10 и убывает при x<10.

Значение x=10 принадлежит отрезку [8; 14], наименьшее значение на указанном отрезке достигается при x=10 и равно y(10)= (10-11)e^{10-10}= -1.

Ответ

-1

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1117

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите точку минимума функции y=(x-9)e^{2x+5}.

Показать решение

Решение

Найдём производную исходной функции, воспользовавшись формулой производной произведения:

y'(x)= (x-9)’e^{2x+5}+(x-9)left(e^{2x+5}right)’= e^{2x+5}+(x-9)cdot2e^{2x+5}= (1+2x-18)e^{2x+5}= (2x-17)e^{2x+5}.

y'(x)=0 при x=8,5.

При этом:

y'(x)<0 при x<8,5,

y'(x)>0 при x>8,5.

Таким образом, x=8,5 является единственной точкой минимума.

Ответ

8,5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №956

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите наибольшее значение функции y=(51-x)e^{x-50} на отрезке [42; 70].

Показать решение

Решение

Найдём производную исходной функции по формуле производной произведения

y’= (51-x)’e^{x-50}+(51-x)left ( e^{x-50} right )’= -e^{x-50}+(51-x)e^{x-50}= (50-x)e^{x-50}.

Найдём нули производной: y’=0.

(50-x)e^{x-50}=0,

x=50.

Заметим, что при x<50 выполняется неравенство y’>0, при x>50 выполняется неравенство y'<0. Значит, функция y=(51-x)e^{x-50} возрастает при x<50 и убывает при x>50.

Значение x=50 принадлежит отрезку [42; 70], наибольшее значение на указанном отрезке достигается при x=50 и равно y(50)=(51-50)e^{50-50}=1.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №954

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите точку максимума функции y=(8-x)e^{x+12}.

Показать решение

Решение

Найдём производную исходной функции, воспользовавшись формулой производной произведения:

y'(x)= (8-x)’e^{x+12}+(8-x)left ( e^{x+12} right )’= -e^{x+12}+(8-x)e^{x+12}= (7-x)e^{x+12}.

y'(x)=0 при x=7. При этом y'(x)>0 при x<7, y'(x)<0 при x>7.

Таким образом, x=7 является единственной точкой максимума.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №146

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите точку минимума функции y=(x-1)cdot e^2x.

Показать решение

Решение

Вычислим производную функции.

y’=(x-1)’cdot e^{2x}+(x-1)cdot(e^{2x})’= e^{2x}+2(x-1)cdot e^{2x}= (2x-1)cdot e^{2x}

Найдем точки экстремума, в которых производная функции обращается в нуль.

(2x-1)cdot e^{2x}=0

x=0,5

На числовой оси расставим знаки производной и посмотрим как ведет себя функция.

При переходе через точку x = 0,5 производная меняет знак с минуса на плюс. Значит x = 0,5 – точка минимума функции.

Ответ

0,5

Задание №130

Тип задания: 12
Тема:
Исследование произведений

Условие

Найдите наибольшее значение функции y=(x^2+12x+33)e^{-3-x} на отрезке [−7; 0].

Показать решение

Решение

Вычислим производную функции.

y’=(2x+12)cdot e^{-3-x}+(x^2+12x+33)cdot e^{-3-x}cdot(-1)

y’=e^{-3-x}(2x+12-x^2-12x-33)

y’=(-x^2-10x-21)e^{-3-x}

y’=-(x^2+10x+21)e^{-3-x}

Найдем точки экстремума, в которых производная функции обращается в нуль.

(x^2+10x+21)e^{-3-x}=0

Решим квадратное уравнение x^2+10x+21=0:

D=100-84=16

x_{1,2}=frac{-10pm4}{2}

x_1=-3; enspace x_2=-7

На числовой оси отложим граничные точки отрезка, точки экстремума и посмотрим как ведет себя функция.

При переходе через точку x = −3 производная меняет знак с плюса на минус. Значит x = −3 – точка максимума функции.

Ответ

-3

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Наиболее эффективная подготовка к ЕГЭ по литературе 2023 года – это последовательная подготовка по заданиям, расположенным от простого к сложному. Чтобы ее осуществить, Многомудрый Литрекон проанализирует каждый из 12 вопросов, которые достанутся Вам уже этим летом. Наши задачи – определить, что собой представляет задание, выяснить, что от нас требуется, и выработать рекомендации по его выполнению и подготовке, исходя из критериев оценивания.

Содержание:

1 Задание 1
2 Задание 2
3 Задание 3
4 Задание 4
5 Задание 5
6 Задание 6
7 Задание 7
8 Задание 8
9 Задание 9
10 Задание 10
11 Задание 11
12 Задание 12

Задание 1

Как правило, это одно из самых простых заданий ЕГЭ. Нужно всего лишь указать жанр, направление или род представленного текста. Отрывки берутся из очень популярных книг, мимо которых просто невозможно пройти в период подготовки. В помощь Вам обновленный список литературы на ЕГЭ.

Сделать его не составляет труда. Для этого нужно всего лишь напрячь память или пойти методом исключения: не может такой смешной отрывок быть частью трагедии.

Задание 2

Второй вопрос посвящен, как правило, проверке знания содержания произведения, процитированного в первой части. Экзаменаторы интересуются, как зовут героев, где происходит действие и т.д. За него дают один балл.

Подготовиться позволит только чтение основных произведений из кодификатора. Чтобы запомнить все значимые события, изготовьте свои шпаргалки. Примером послужит таблица:

Название книги

Главные герои

Место действия

Синопсис

«Горе от Ума»,

А.С. Грибоедов

Александр Чацкий — главный герой

Софья Фамусова — главная героиня

Павел Фамусов — отец главной героини и антипод Чацкого

Алексей Молчалин — возлюбленный главной героини

Москва, дом Фамусова

Чацкий приезжает из заграничного путешествия и находит московские нравы предосудительными. Он осуждает крепостное право, галломанию, кумовство и казнокрадство на службе, невежество. Он намерен добиться руки Софьи, но ее сердце занято карьеристом Молчалиным, которому нужна не она, а повышение. Невольно оскорбив избранника Софьи, Чацкий попадает к ней в немилость. Героиня распространяет слух о сумасшествии Чацкого. Разочаровавшись в свете и своей любви, Александр уезжает.

Задание 3

Это задание будет посложнее, ведь оно проверяет знание нескольких произведений одного и того же автора. Некоторых героев, как назло, выбирают из второстепенных. Поэтому действовать приходится методом исключения, а то и вовсе ненаучного тыка.

Однако поверхностное знание сюжета и объема помогает установить истину: например, в «Ночи перед рождеством» второстепенных героев совсем не много, значит, нужно присмотреться к «Мертвым душам» — там больше. Кроме того, подсказку дали сами составители заданий. Прозвище «кувшинное рыло» в 19 веке обозначало взяточника. Какое произведение Гоголя посвящено этой теме? Из оставшихся только «Мертвые души», но никак не «Ночь перед Рождеством». Такого рода рассуждения помогут Вам справиться даже тогда, когда Вы знаете далеко не все.

Подготовиться поможет только чтение книг из списка. Ускорить подготовку позволяет прослушивание аудиокниг в свободное время.

Задание 4

Термины учить никто не любит, а придется. Задание 4 посвящено именно этой неприятной необходимости. Вот основная теория для экзамена по литературе.

Суть вопроса в том, чтобы подобрать термины, подходящие по смыслу. Ответ заложен в выдержке из текста, ее нужно проанализировать. Даже если Вы не знаете термины, поможет обыкновенная логика.

Что можно «разрешать» в произведении? Конфликт, это устойчивая форма употребления этих двух слов.
Что может использовать автор, чтобы сообщить нечто важное о героях и обстановке? Только ремарку, ничего большего не остается.

Даже если знать термины поверхностно, эту задачу решить вполне реально. Не волнуйтесь и действуйте вдумчиво.

Задание 5

Мини-сочинение нужно написать по одному из двух предложенных вопросов. Это развёрнутый ответ, который должен всесторонне раскрыть поставленную тему. За него дадут 6 баллов.

Поскольку задание сложное и «дорогое», Литрекон подготовил для него отдельный разбор с примерами, теорией, клише и критериями оценки.

Задание 6

6 задание еще выгоднее для выпускника. Целых 8 первичных баллов, подумать только! Но есть и подвохи: сравнительный анализ делать сложнее, чем предыдущую работу, так как произведение для сопоставления нужно выбрать из багажа собственных знаний. Но далеко не каждый выпускник обстоятельно собирается в дорогу…

Чтобы проработать это мини-сочинение на ЕГЭ, используйте разбор задания 6 от Многомудрого Литрекона. Там Вы найдете примеры из демоверсии 2023, клише и шаблоны, теорию и критерии оценки.

Задание 7

Суть задания — подобрать правильные термины, ориентируясь на выдержку из текста. Подсказки даны в тексте задания, ничего сложного, но…

В 7 задании важно правильно понять текст. Многие выпускники нервничают, спешат, а потому неверно понимают суть прочитанного. Например, в демоверсии ученики охотно ставят на первое место «сонет», забыв о том, что спрашивают их о РОДЕ литературы, а не о ЖАНРЕ стихотворения. Такая мелочь может погубить даже знающего человека, которому сложно концентрироваться в стрессовых обстоятельствах.

Все термины кратко рассмотрены в статье «Теория для ЕГЭ по литературе».

Задание 8

Восьмое задание посвящено проверке знания таких терминов, как размер, римфа, рифмовка стихотворения. Все они рассмотрены в подробном разборе задания 10.

В подготовке к этому заданию без заучивания терминов не обойтись. Но нужно не зубрить, а понимать, иначе Вы не разберетесь на практике. Поэтому отрабатывайте практические аспекты теории: сколько должно быть слогов, где должны быть ударения, как посчитать? Все это есть в разборе.

Задание 9

Средства языковой выразительности, которые проверяются в задании 9 на ЕГЭ по литературе, перечислены в подборке. Важно отличать их друг от друга и находить в тексте. Порой методом исключения можно отсеять то, чего явно нет в стихотворении, но полагаться лишь на него не стоит. Примеры и практика помогут освоить этот материал в достаточной степени.

Подготовка к заданию 9 должна состоять не только из изучения СХВ, но и из практического применения знаний. Пока не научитесь отличать эпитет от метафоры с первого взгляда, не забрасывайте эту тему.

Задание 10

Для этого мини-сочинения, которое принесет выпускнику 6 баллов, Литрекон тоже сочинил целый разбор, где изложил примеры, теорию, критерии и клише для быстрого написания работ. Освоить этот формат можно довольно быстро, если сосредоточиться и больше практиковаться.

ЕГЭ по литературе ориентирован на практику. Заучить определения и пару стихотворений вовсе не достаточно. Поэтому тренируйтесь ежедневно, чтобы довести навык до автоматизма.

Задание 11

План задания 11, примеры из демоверсии, клише и шаблоны, а также теория расположены в разборе задания 11. Выпускникам тоже нужно структурировать свою подготовку таким образом, уделив больше времени и стараний развернутым ответам и изучив каждое задание в отдельности. Все-таки за базовые вопросы дают по одному баллу, а тут на кону 8! Разница существенная.

Чтобы эффективно распорядиться своим временем, выполняйте не целые варианты ЕГЭ, а те части, которые вызывают наиболее беспокойство и стоят затраченных усилий.

Задание 12

Задание 12 — самое сложное, но в то же время наиболее выгодное. К нему нужно готовиться очень тщательно. Прежде всего, практиковаться в написании по определённому шаблону, чтобы легче было придерживаться структуры и не растекаться мыслью по древу. Даже самый способные ученики прогорают на том, что пытаются вместить всю свою креативность в текст, который должен быть строго регламентирован. Если Ваши ценные мысли сочтут далекими от темы, то за эссе поставят 0 баллов.

Написать его помогает четкий план:

Вступление: перефразированная формулировка задания и переход к аргументам.
Основная часть: 2-3 примера из текста (текстов). Каждый пример состоит из тезиса, обоснования (деталь, цитата, обстоятельство), мини-вывода. Все они должны отвечать на заданный вопрос. Если тема, например, сопоставление героев-антиподов, то каждый пример должен быть посвящен разнице их точек зрения. Сначала пишем, в чем разница, потом о том, как и чем это подтверждается в тексте, а потом резюмируем суть столкновения идей.
Заключение: перефразированная формулировка задания и вывод из написанного: герои отличаются друг от друга тем-то и тем-то, это противостояние позволило автору выразить то и вот это.

Многомудрый Литрекон уже подготовил примеры сочинения 12 на ЕГЭ по литературе и критерии оценки.

Вот советы по выбору тем:

Не берите тему, если не помните все необходимое. Выстроить предварительный план и набросать зачатки аргументов — не проблема, а ее решение. Только так можно убедиться, что Вы готовы. Иначе осознание, что тема выбрана не та, придет уже тогда, когда большая часть будет написана.
Если не знаете подробно сферу искусства из пятой темы, не берите ее, ведь иначе не сможете раскрыть ее полностью.
Коварна и тема по лирике. Там нужно три примера из разных произведений, с привлечением цитат по памяти могут возникнуть проблемы, так что не стоит рисковать, если в себе не уверены.

Прочитав весь список литературы и проработав термины, Вы без особого беспокойства осилите ЕГЭ по литературе. Разбор Вам поможет, как и все остальные материалы на сайте. Ни пуха, ни пера!

Источник

ТОП речевых ошибок в сочинении ЕГЭ

Сочинение ЕГЭ 2023 на 24 балла

Интерактивное пособие для подготовки к сочинению

АНАЛИЗ ТЕКСТА

Пособие «Анализ текста. Задание 1-3, 22-26 ЕГЭ»

300+ аргументов к итоговому

Навигатор-ЕГЭ 2023. Сочинение

Интерактивный чек-лист

Навигатор-ЕГЭ 2023. Тест

Интерактивный чек-лист

Учимся формулировать

проблему, комментарий, авторскую позицию, обоснование

Исключения и трудности ЕГЭ

ИСКЛЮЧИТЬ/ЗАМЕНИТЬ

300+ заданий 6 ЕГЭ

200+ аргументов для сочинения ОГЭ

ОГЭ-навигатор 2023

Чек-лист подготовки к ОГЭ по русскому языку 2023

СКИДКА

1000 НАРЕЧИЙ

Слитно, раздельно, через дефис

Проверка сочинения ЕГЭ

Источник

Задание 2355

Найдите точку максимума функции: $$y=-frac{x^{2}+324}{x}$$

Ответ: 18

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=-frac{x^{2}+324}{x}$$

$${y}’=-frac{{(x^{2}+324)}’cdot x-{x}'(x^{2}+324)}{x^{2}}=-frac{2xcdot x-x^{2}-324}{x^{2}}=-frac{x^{2}-324}{x^{2}}=frac{324-x^{2}}{x^{2}}=0$$

$$x=pm 18$$

$$xneq 0$$

Точка минимума: -18

Точка максимума: 18

Задание 2497

Найдите наименьшее значение функции $$y=(x-8)^{2}(x-1)+10$$ на отрезке [6; 14].

Ответ: 10

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=(x-8)^{2}(x-1)+10$$ $$y{}’=2(x-8)^{2}(x-1)+(x-8)^{2}=$$ $$=2(x^{2}-9x+8)+x^{2}-16x+64=$$ $$=2x^{2}-18x+16+x^{2}-16x+64=$$ $$=3x^{2}-34x+80=0$$ $$D=1156-960=196=14^{2}$$ $$x_{1}=frac{34+14}{6}=8$$ $$x_{2}=frac{34-14}{6}=frac{10}{3}$$ $$y(8)=(8-8)^{2}(8-1)+10=10$$

Задание 3033

Найдите точку максимума функции $$y=frac{16}{x}-x^{2}+9$$

Ответ: -2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=frac{16}{x}-x^{2}+9$$ $$y’=-frac{16}{x^{2}}-2x=0$$ $$frac{-16-2x^{3}}{x^{2}}=0$$ $$xneq 0$$ $$x=-2$$

Задание 3075

Найдите наибольшее значение функции $$f(x)=(x+4)^{2}(x+3)$$ на отрезке [‐5; ‐3,5].

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$f'(x)=2(x+4)(x+3)+(x+4)^{2}=$$$$2(x^{2}+7x+12)+x^{2}+8x+16=$$$$3x^{2}+22x+40=0$$

$$D=484-480=4$$

$$x_{1}=frac{-22+2}{6}=-frac{20}{6}$$

$$x_{1}=frac{-22-2}{6}=-4$$

$$f(-4)=(-4+4)^{2}(-4+3)=0$$

Задание 3202

Найдите точку минимума функции: $$y=-frac{x^{2}+676}{x}$$

Ответ: -26

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y’=-(frac{(x^{2}+676)’cdot x-x'(x^{2}+676)}{x^{2}})=$$ $$=-(frac{2x^{2}-x^{2}+676}{x^{2}})=$$ $$=-frac{x^{2}-676}{x^{2}}=frac{676-x^{2}}{x^{2}}$$

Задание 3423

Найдите наименьшее значение функции: $$y=-frac{4x^{2}+4x+7}{4x^{2}+4x+3}$$

Ответ: -3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=-frac{4x^{2}+4x+7}{4x^{2}+4x+3}=-(1+frac{4}{4x^{2}+4x+3})$$ $$Rightarrow 4x^{2}+4x+3Rightarrow f(x)$$ y будет наименьшим, если $$f(x)$$ будет наименьшим: $$x_{0}=-frac{4}{4cdot2}=-0,5$$ $$f(-0,5)=4cdotfrac{1}{4}-4cdotfrac{1}{2}+3=1-2+3=2$$ $$y_{min}=-(1+frac{4}{2})=-3$$

Задание 3859

Найдите наименьшее значение функции $$y=frac{x^{2}-6x+36}{x}$$ на отрезке $$[3;9]$$

Ответ: 6

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y’=frac{(2x-6)x-x^{2}+6x-36}{x^{2}}=$$

$$=frac{2x^{2}-6x-x^{2}+6x-36}{x^{2}}=$$

$$=frac{x^{2}-36}{x^{2}}$$

$$f_{min}=f(6)=frac{6^{2}-6cdot6+36}{6}=6$$

Задание 4817

Найдите наибольшее значение функции $$y=frac{x^{2}+7x+49}{x}$$ на отрезке [-14;-1]

Ответ: -7

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную данной функции:$$y’=frac{(2x+7)*x-(x^{2}+7x+49)}{x^{2}}=$$$$frac{2x^{2}+7x-x^{2}-7x-49}{x^{2}}=$$$$frac{x^{2}-49}{x^{2}}=0$$ Начертим координатную прямую, отметим полученные точки, и растравим знаки производной:

Как видим, -7 — точка максимума, следовательно, на заданном по условию промежутке в этой точке и будет максимальное значение функции:

$$y(-7)=frac{(-7)^{2}+7*(-7)+49}{-7}=-7$$

Задание 5055

Найдите наибольшее значение функции $$y=frac{x^{3}+x^{2}+9}{x}-x^{2}$$ на отрезке $$[-9;-1$$]

Ответ: -6

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=frac{x^{3}+x^{2}+9}{x}-x^{2}=$$ $$x^{2}+x+frac{9}{x}-x^{2}=x+frac{9}{x}$$; $$y’=1-frac{9}{x^{x}}=0$$; $$frac{x^{2}-9}{x^{2}}=0$$ $$Leftrightarrow$$ $$x=pm3$$;

$$y(-3)=frac{(-3)^{3}+(-3)^{2}+9}{-3}-(-3)^{2}=frac{-27+9+9}{-3}-9=3-9=-6$$

Задание 5192

Найдите наибольшее значение функции $$y=frac{250+50x-x^{3}}{x}$$ на отрезке $$[-10;-1]$$

Ответ: -25

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=frac{250+50x-x^{3}}{x}$$; $$y’=frac{(50-3x^{2})x-(250+50x-x^{3})}{x^{2}}=$$ $$frac{50x-3x^{3}-250-50x+x^{3}}{x^{2}}=$$ $$frac{-2x^{3}-250}{x^{2}}=0$$; $$x^{3}=-125$$ $$Rightarrow$$ $$x=-5$$;

$$y(-5)=frac{250+50cdot(-5)-(-5)^{3}}{(-5)}=frac{125}{-5}=-25$$

Задание 5335

Найдите наименьшее значение функции $$y=frac{x^{2}-8x+64}{x}$$ на отрезке [4;18].

Ответ: 8

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную данной функции и приравняем ее к нулю: $$y’=frac{(x^{2}-8x+64)’x-x'(x^{2}-8x+64)}{x^{2}}=0$$ $$y’=frac{2x^{2}-8x-x^{2}+8x-64}{x^{2}}=0$$ $$frac{x^{2}-64}{x^{2}}=0$$ $$x_{1}=-8 ; x_{2}=8$$ Отметим полученные значения на координатной прямой и расставим знаки производной, получим, что $$x_{2}$$ является точкой минимума. Тогда наименьшее значение функции на заданном отрезке будет именно в этой точке: $$y(8)=frac{8^{2}-8*8+64}{8}=8$$

Задание 7321

Найдите наименьшее значение функции $$y=-frac{4x^{2}+4x+7}{4x^{2}+4x+3}$$

Ответ: -3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Преобразуем данную функцию: $$y=-frac{4x^{2}+4x+7}{4x^{2}+4x+3}=$$$$-(1+frac{4}{4x^{2}+4x+3})=$$$$-1-frac{4}{4x^{2}+4x+3}$$

Найдем производную: $$y^{‘}=-frac{4^{‘}(4x^{2}+4x+3)-(4x^{2}+4x+3)^{‘}*4}{(4x^{2}+4x+3)^{2}}=0$$$$Rightarrow$$ $$frac{(8x+4)*4}{4x^{2}+4x+3}=0$$$$Rightarrow$$ $$8x+4=0Rightarrow$$ $$x=-frac{1}{2}$$

$$y(-2)=-frac{4*frac{1}{4}+4(-frac{1}{2})+7}{4*frac{1}{4}+4(-frac{1}{2})+3}=$$$$-frac{6}{2}=-3$$

Задание 8679

Найдите точку минимума функции $$y=x+frac{25}{x}$$

Ответ: 5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8716

Найдите точку максимума функции $$y=x^{3}+18x^{2}+81x+23$$

Ответ: -9

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8777

Найдите точку минимума функции $$y=frac{162}{x}+2x+7$$

Ответ: 9

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Источник

Исследование функций. В этой статье мы поговорим о задачах, в которых рассматриваются функции и в условии стоят вопросы связанные с их исследованием. Рассмотрим основные теоретические моменты, которые необходимо знать и понимать для их решения.

Это целая группа задач входящих в ЕГЭ по математике. Обычно ставится вопрос о нахождении точек максимума (минимума) или определения наибольшего (наименьшего) значения функции на заданном интервале. Рассматриваются:

— Степенные и иррациональные функции.

— Рациональные функции.

— Исследование произведений и частных.

— Логарифмические функции.

— Тригонометрические функции.

Если вы поняли теорию пределов, понятие производной, свойства производной для исследования графиков функций и её геометрический смысл, то такие задачи никакого затруднения у вас не вызовут и вы решите их с лёгкостью.

Информация ниже — это теоретические моменты, понимание которых позволит осознать, как решать подобные задачи. Постараюсь изложить их именно так, чтобы даже тот, кто эту тему пропустил или изучил слабо, смог без особых затруднений решать подобные задачи.

В задачах данной группы, как уже сказано, требуется найти либо точку минимума (максимума) функции, либо наибольшее (наименьшее) значение функции на интервале.

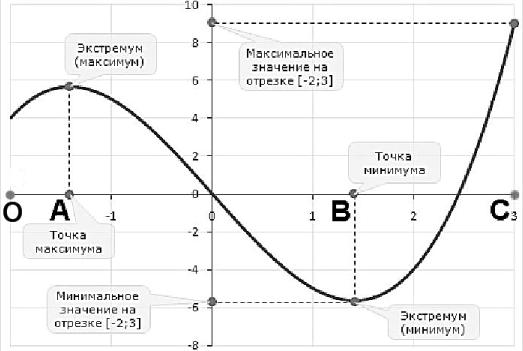
Точки минимума, максимума. Свойства производной.

Рассмотрим график функции:

Точка А – это точка максимума, на интервале от О до А функция возрастает, на интервале от А до В убывает.

Точка В – это точка минимума, на интервале от А до В функция убывает, на интервале от В до С возрастает.

В данных точках (А и В) производная обращается в нуль (равна нулю).

Касательные в этих точках параллельны оси ox.

Добавлю, что точки, в которых функция меняет своё поведение с возрастания на убывание (и наоборот, с убывания на возрастание), называются экстремумами.

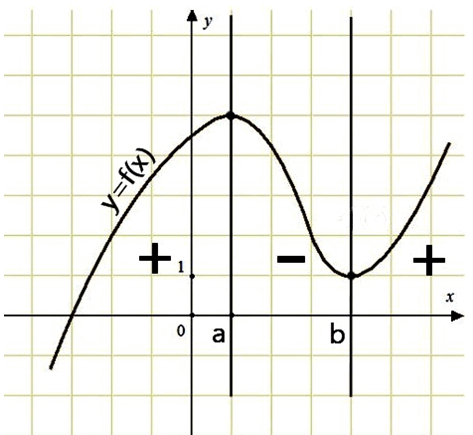
Важный момент:

1. Производная на интервалах возрастания имеет положительный знак (при подстановке значения из интервала в производную получается положительное число).

Значит, если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.

2. На интервалах убывания производная имеет отрицательный знак (при подстановке значения из интервала в выражение производной получается отрицательное число).

Значит, если производная в определённой точке из некоторого интервала имеет отрицательное значение, то график функции на этом интервале убывает.

Это надо чётко уяснить!!!

Таким образом, вычислив производную и приравняв её к нулю, можно найти точки, которые разбивают числовую ось на интервалы. На каждом из этих интервалов можно определить знак производной и далее сделать вывод о её возрастании или убывании.

*Отдельно следует сказать о точках, в которых производая не существует. Например, можем получить производную, знаменатель которой при определённом х обращается в нуль. Понятно, что при таком х производная не существует. Так вот, данную точку также необходимо учитывать при определени интервалов возрастания (убывания).

Функция в точках, где производная равна нулю меняет свой знак не всегда. Об этом будет отдельная статья. На самом ЕГЭ таких задач не будет.

Вышеизложенные свойства необходимы для исследования поведения функции на возрастание и убывание.

Что ещё необходимо знать для решения оговоренных задач: таблицу производных и правила дифференцирования. Без этого никак. Это базовые знания, в теме производной. Производные элементарных функций вы должны знать на отлично.

Вычисляя производную сложной функции f(g(x)), представьте, что функция g(x) это переменная и далее вычисляйте производную f’(g(x)) по табличным формулам как обычную производную от переменной. Затем полученный результат умножьте на производную функции g(x).

Посмотрите видеоурок Максима Семенихина о сложной функции:

Исследование функций

Задачи на нахождение точек максимума и минимума

Алгоритм нахождения точек максимума (минимума) функции:

1. Находим производную функции f’(x).

2. Находим нули производной (приравниванием производную к нулю f’(x)=0 и решаем полученное уравнение). Также находим точки в которых производная не существует (в частности это касается дробно-рациональных функций).

3. Отмечаем полученные значения на числовой прямой и определяем знаки производной на этих интервалах путём подстановки значений из интервалов в выражение производной.

4. Далее делаем вывод.

Вывод будет один из двух:

1. Точка максимума это точка, в которой производная меняет значение с положительного на отрицательное.

2. Точка минимума это точка, в которой производная меняет значение с отрицательного на положительное.

Задачи на нахождение наибольшего или наименьшего значения

функции на интервале.

В другом типе задач требуется найти наибольшее или наименьшее значение функции на заданном интервале.

Алгоритм нахождения наибольшего (наименьшего) значения функции:

1. Определяем, есть ли точки максимума (минимума). Для этого находим производную f’(x), затем решаем f’(x)=0 (пункты 1 и 2 из предыдущего алгоритма).

2. Определяем, принадлежат ли полученные точки заданному интервалу и записываем лежащие в его пределах.

3. Подставляем в исходную функцию (не в производную, а в данную в условии) границы данного интервала и точки (максимума-минимума), лежащие в пределах интервала (п.2).

4. Вычисляем значения функции.

5. Выбираем из полученных наибольшее (наименьше) значение, в зависимости от того, какой вопрос был поставлен в задаче и далее записываем ответ.

Вопрос: для чего в задачах на нахождение наибольшего (наименьшего) значения функции необходимо искать точки максимума (минимума)?

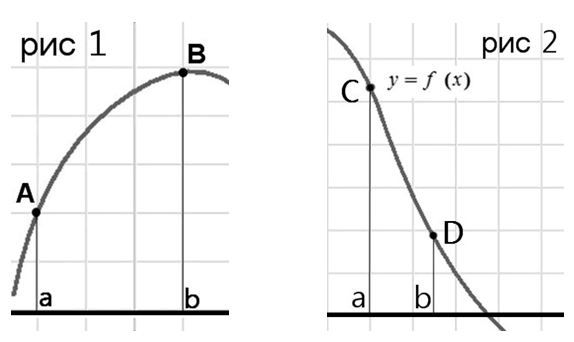
Ответ лучше всего это проиллюстрировать, посмотрите схематичное изображение графиков, задаваемых функций:

В случаях 1 и 2 достаточно подставить границы интервала, чтобы определить наибольшее или наименьшее значение функции. В случаях 3 и 4 необходимо найти нули функции (точки максимума-минимума). Если мы подставим границы интервала (не находя нули функции), то получим неверный ответ, это видно по графикам.

И всё дело в том, что мы по заданной функции не можем увидеть как выглядит график на интервале (имеет ли он максимум или минимум в пределах интервала). Потому находите нули функции обязательно!!!

Если уравнение f’(x)=0 не будет иметь решения, это значит, что точек максимума-минимума нет (рисунок 1,2), и для нахождения поставленной задачи в данную функцию подставляем только границы интервала.

Ещё один важный момент. Помните, что ответом должно быть целое число или конечная десятичная дробь. При вычислении наибольшего и наименьшего значения функции вы будете получать выражения с числом е и Пи, а также выражения с корнем. Запомните, что до конца вам их вычислять не нужно, и так понятно, что результат таких выражений ответом являться не будет. Если возникнет желание вычислить такое значение, то сделайте это (числа: е ≈ 2,71 Пи ≈ 3,14 ).

Много написал, запутал наверное? По конкретным примерам вы увидите, что всё просто.

Далее хочу открыть вам маленький секрет. Дело в том, что многие задания можно решить без знания свойств производной и даже без правил дифференцирования. Об этих нюансах я вам обязательно расскажу и покажу как это делается? не пропустите!

Но тогда зачем же я вообще изложил теорию и ещё сказал, что её нужно знать обязательно. Всё верно – знать надо. Если её поймёте, тогда никакая задача в этой теме в тупик вас не поставит.

Те «хитрости», о которых вы узнаете, помогут вам при решении конкретных (некоторых) прототипов задач. Как дополнительный инструмент эти приёмы использовать, конечно, удобно. Задачу можно решить в 2-3 раза быстрее и сэкономить время на решение части С.

Всего доброго!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.

Источник

В подготовке к ЕГЭ по литературе есть нюанс — нужно прочитать большой объем литературы. Мы решили упростить вашу подготовку и сделали подборку из: сайтов, YouTube-каналов, подкастов, кратких содержаний произведений, биографии, книг, фильмов и приложений.

Всех приветствуем! На связи «Сотка» — онлайн-школа, которая подготовила к экзаменам больше 60.000 учеников👇

Ниже вы увидите список из 21 ссылки с ресурсами.
Нажмите на ссылку, чтобы узнать подробнее о ресурсе.
Нажмите кнопку «назад» в браузере, чтобы вернутся к списку.

Сайты:

ФИПИ
Официальный сайт Рособрнадзора
Калькулятор баллов
Решу ЕГЭ
Яндекс.ЕГЭ
Русская литература
Literaturus
Российская электронная школа
Курс по литературе от Яндекса
Русская историческая библиотека
Полка
Брифли
Список фильмов школьной программы по литературе

YouTube:

My Book
Учи стихи легко
Любовь Гогина
Literatura_100
Литбез

Подкасты:

Ликвидация безграмотности
Книжный базар

Приложения:

ЕГЭ.Литература

🗿Бонус:

Действенные советы для подготовки к ЕГЭ по литературе
Бесплатные ресурсы для подготовки по другим предметам

Подготовка к ЕГЭ по литературе: базовые сервисы

Начинать подготовку к любому предмету нужно с базовых сервисов. Они не только упростят подготовку к экзаменам, но и помогут ознакомиться с порядком проведения ЕГЭ.

ФИПИ — задумывались когда-то: кто разрабатывает КИМы по всем экзаменам, устанавливает правила и добавляет в ЕГЭ нововведения? Этим занимается Федеральный институт педагогических измерений. Коротко — ФИПИ. На сайте ФИПИ вы можете ознакомиться со свежими КИМами и проследить за новостями из мира ЕГЭ.

Подготовка к ЕГЭ по литературе | ФИПИ

Официальный сайт Рособрнадзора — если ФИПИ разрабатывает ЕГЭ, то Рособрнадзор следит за порядком на экзаменах. На их сайте вы можете не только ознакомиться с правилами, но и посмотреть расписание экзаменов.

Подготовка к ЕГЭ по литературе | Рособрнадзор

Калькулятор баллов — этот сайт мы даем вам на будущее. Как только успешно сдадите ЕГЭ по всем трем предметам на максимальные баллы, зайдите на этот сайт. Здесь вы можете посчитать всю сумму баллов и посмотреть, в какие университеты проходите на бюджетной основе.

Подготовка к ЕГЭ по литературе | Калькулятор баллов

Подготовка к ЕГЭ по литературе: сайты

Решу ЕГЭ — чем больше вы решите тестов, тем легче будет вам на экзамене. Тренироваться можно на сайте «Решу ЕГЭ» — это классика жанра.

Подготовка к ЕГЭ по литературе | Решу-ЕГЭ

Яндекс.ЕГЭ — если «Решу ЕГЭ» вам надоест, всегда найдется альтернатива. Мы обычно выбираем «Яндекс.ЕГЭ». Там удобный интерфейс и приятный дизайн. А за выполнение тестов дают достижения, которые только придают мотивации. Кстати, вы можете не только решать тесты на этой сайте, но и смотреть баллы и свои ошибки.

Подготовка к ЕГЭ по литературе | Яндекс-ЕГЭ

Русская литература — библиотека, в которой собраны большинство произведений из русской литературы. Ничего лишнего. Присутствует все, что пригодится на экзамене. Можно смотреть биографии авторов, можно искать произведения и даже «гуглить» героев и смотреть, в каких произведениях они были.

Подготовка к ЕГЭ по литературе | Русская литература

Literaturus — подробные анализы произведений, краткие содержания, характеристики героев, цитаты — все это вы найдете на сайте Literaturus. После того, как вы прочитаете краткое содержание, на сайте можно решить небольшой тест и проверить, насколько вы усвоили произведение.

Подготовка к ЕГЭ по литературе | Literaturus

Российская электронная школа — вся программа литературы за 11 лет есть на этом сайте. Вы просто включаете урок по нужной теме, смотрите его, а затем решаете тест для того, чтобы проверить себя. Уроки рассортированы по классам и разделам. Сайт очень полезен и поможет ускорить подготовку к ЕГЭ по литературе.

Подготовка к ЕГЭ по литературе | Электронная школа

Курс по литературе от Яндекса — курсов много не бывает. И чем больше вы посмотрите уроков, тем шире будет ваш кругозор и легче станет на экзамене. На этот раз предлагаем пройти курс от Яндекса. Они записали 15 качественных уроков, которые помогут подготовиться к ЕГЭ по литературе.

Подготовка к ЕГЭ по литературе | Курс по Яндекса

Русская историческая библиотека — на этом сайте вы найдете краткие содержания большинства произведений из русской и зарубежной литературы. На сайте вы также найдете статьи по литературе, анализы произведений, биографии писателей и зарактеристики героев.

Подготовка к ЕГЭ по литературе | Историческая библиотека

Полка — как только вы откроете сайт, то окажетесь перед настоящей книжной полкой. Выбирайте любое произведение и смотрите его подробный анализ. Сайт сделан красиво и качественно, а самое главное — он очень полезен при подготовке к ЕГЭ по литературе. Кстати, на сайте есть также статьи и подкасты по литературе.

Подготовка к ЕГЭ по литературе | Полка

Брифли — еще один полезный сайт, на котором вы можете прочитать краткие пересказы большинства произведений, как зарубежных так и отечественных. Уникальная особенность сайта в том, что на нем есть не только пересказы произведений, но и краткие содержания всех глав. Это будет удобно для тех, кто хочет более подробно изучить детали и глубже познакомиться с творчеством многих авторов.

Подготовка к ЕГЭ по литературе | Брифли

Список фильмов школьной программы по литературе — книга всегда интереснее. Но иногда полезно после прочтения книги посмотреть ее экранизацию. Так произведения усваиваются и запоминаются лучше. На этом сайте собраны все фильмы по отечественным произведениям из школьной программы литературы.

Подготовка к ЕГЭ по литературе | Список фильмов

Подготовка к ЕГЭ по литературе: YouTube-каналы и видео-лекции

My Book — краткие содержания популярных произведений, интересные факты и случаи из литературы, разборы и многое другое вы найдете на канале My Book. Канал создан при поддержке популярного сервиса Литрес, поэтому за качество видео и информации, которую в них дают, можете не беспокоиться.

Подготовка к ЕГЭ по литературе | My book

Учи стихи легко — для того, чтобы сдать ЕГЭ по литературе на высокий балл, вам просто необходимо знать стихотворения. Есть хорошая новость: заучивать стихи не придется. Зайдите на этот канал, включите видео и занимайтесь своими делами. Таким способом стихотворения будут легко запоминаться. Попробуйте, мы лично проверяли.

Подготовка к ЕГЭ по литературе | Учи стихи легко

Любовь Гогина — разборы сочинений, анализы, лекции и пересказы произведений. Все это вы найдете на канале Любви Гогиной. Мы прикрепили целый плейлист, в котором больше 170 видео. Включайте, смотрите и готовьтесь к ЕГЭ по литературе.

Подготовка к ЕГЭ по литературе | Любовь Гогина

Literatura_100 — лайфхаки, шпаргалки, разговоры по душам на тему сдачи ЕГЭ по литературе и многое другое вы найдете на канале Literatura_100. Сам канал создан вокруг идеи сдачи ЕГЭ по литературе на 100 баллов. И мы уверены, что он отлично поможет вам сдать экзамен на такой высокий балл.

Подготовка к ЕГЭ по литературе | Literatura_100

Литбез — очень интересный и полезный канал, на котором вы найдете не только емкие и интересные пересказы произведений, но и классные ролики, которые помогут вам подготовиться к ЕГЭ по литературе.

Подготовка к ЕГЭ по литературе | Литбез

Подготовка к ЕГЭ по литературе: подкасты

Ликвидация безграмотности — думаем, по названию понятно, о чем будут подкасты. И вправду, подкасты отлично справляются с тем, чтобы сделать человека более грамотным. Многие записи затрагивают не только литературу, но и русский язык, что еще сильнее расширит кругозор.

Подготовка к ЕГЭ по литературе | Подкасты

Книжный базар — в серии подкастов говорят о литературе, советуют что почитать, проводят анализы и разборы. Кстати, в подкастах встречается довольно разная литература, вам должно понравиться.

Подготовка к ЕГЭ по литературе | Книжный базар

Подготовка к ЕГЭ по литературе: приложения

ЕГЭ. Литература (Android, iOS) — приложение, в котором вы можете не только почитать теорию и порешать тесты, но и почитать краткие содержания произведений, их разборы и анализы. Приложение заменяет большинство сайтов и сервисов, которые мы давали выше.

Подготовка к ЕГЭ по литературе | ЕГЭ-литература

Советы для успешной подготовки к ЕГЭ по литератере:

Не уходите, это еще не все. Теперь у вас есть список полезных сервисов, которые помогут подготовиться к ЕГЭ по литературе и сдать экзамен на максимальный балл.

Но остался один вопрос: как эффективнее всего воспользоваться этими сервисами и с чего начать?

Мы подготовили для вас специальный раздел с советами. Они помогут сэкономить ваше время, и вы поймете, как должна проходить эффективная подготовка.

Советы от онлайн-школы «Сотка»👇

Как можно больше читайте. Вам нужно набивать базу прочитанных произведений, чтобы сдать экзамен стало легче.
Читайте краткие пересказы. Иногда прочитанные произведения забываются. Чтобы не перечитывать книгу заново, прочтите качественные краткие пересказы. Мы дали вам несколько сервисов, в которых собраны краткие содержания на многие произведения.
Не забывайте про тесты. Теория теорией, но про тесты забывать не стоит. Чем больше вы их решите, тем опять же — вам будет легче на экзамене.
Работайте над ошибками. На сайте «Решу ЕГЭ» и «Яндекс. ЕГЭ» после того, как вы решили тест, можно сразу же просмотреть свои ошибки. Так вот, работайте больше над теми заданиями, в которых вы чаще всего ошибаетесь.
Выберите 2-3 YouTube канала. На слух информация воспринимается лучше, да и чтобы подготовка не наскучила, советуем разбавлять обычное чтение просмотров полезных видеороликов по литературе.
Учите стихи. На экзамене есть задания, которые вы не решите без знания стихотворений. Чтобы стихи запоминались и усваивались быстрее, мы добавили в подборку специальный канал. Учи стихи легко.

Мы уверены, что вы сдадите экзамены на максимальный балл и поступите на бюджет в тот ВУЗ, в который хотите.

💙 С заботой, ваша «Сотка».

Ресурсы для подготовки по другим предметам

Курсы ЕГЭ: 33 бесплатных сайта

Статья содержит информацию о курсах ЕГЭ по различным предметам, включая: литературу, математику, химию, русский язык, обществознание, информатику, физику, английский язык и биологию. Все курсы ЕГЭ являются бесплатными. Материал регулярно обновляется — сохраняйте в закладки.

Курсы ЕГЭ | youtube.com/c/devinf74

ЕГЭ 2023: расписание, изменения, бесплатные лекции

В статье вы найдете всю необходимую информацию по теме ЕГЭ 2023: расписание, баллы, изменения, а также бесплатные ресурсы для подготовки по любому предмету. Статья регулярно обновляется, поэтому смело добавляйте ее в Закладки.

ЕГЭ 2023 | @abitunet

Подготовка к ЕГЭ: 139 бесплатных сайтов

В статье вы найдете 139 бесплатных ресурсов для подготовки к ЕГЭ по следующим предметам: математика, русский язык, обществознание, информатика, физика, английский язык, литература, химия, биология. Статья регулярно обновляется — добавляйте в закладки.

Подготовка к ЕГЭ | zygotebody.com

🗣Уверены, что это далеко не полный список полезных сайтов для подготовки к ЕГЭ по литературе, поэтому будет рады, если вы поделитесь своими рекомендациями в комментариях👇

Источник