Егэ ивт 16 задание - Помощь в подготовке к экзаменам и поступлению

На уроке рассматривается решение 16 задания ЕГЭ по информатике про рекурсивные алгоритмы

Рекомендации по выполнению:

«Для успешного выполнения этого задания следует аккуратно произвести трассировку
предложенной рекурсивной функции»

Типичные ошибки и рекомендации по их предотвращению:

«Крайне важно отслеживать правильность возврата выполнения программы в нужную точку для
каждого рекурсивного вызова»

ФГБНУ «Федеральный институт педагогических измерений»

Для начала, разберем некоторые определения.

Процедура (функция)– это вспомогательный алгоритм (фрагмент кода программы), который служит для выполнения определенных действий.

Предназначена для:

выполнения одинаковых действий в различных местах одной и той же программы;

разбивки программы (или другой процедуры или функции) на подзадачи для улучшения читаемости кода;

Особенности программирования процедур (функций):

подпрограммы располагаются всегда выше основной программы:

сначала составляется заголовок процедуры или функции, в котором перечисляются формальные параметры, они обозначаются идентификаторами, как переменные (т.к. формальные параметры могут меняться, также как переменные):

var x,y:integer;
{ заголовок процедуры 
с формальными переменными x и y:}
procedure Sum(x,y:integer); 
begin
 ...
end;
// основная программа
begin
  ...
end.

var x,y:integer;
{ заголовок функции 
с формальными переменными x и y:}
function Sum(x,y:integer): integer; 
begin
  ...
end;
// основная программа
begin
 ...
end.

в месте вызова процедуры в круглых скобках указываются фактические параметры (числовые значения либо арифметические выражения) в том же порядке:

функция вызывается немного иначе:

{ заголовок процедуры 
с формальными переменными x и y:}
procedure Sum(x,y:integer); 
begin
 ...
end;
// основная программа
begin
  Sum(100,200)
end.

{ заголовок функции 
с формальными переменными x и y:}
function Sum(x,y:integer): integer; 
begin
  ...
end;
// основная программа
begin
 write (Sum(100,200))
end.

компилятор не будет выполнять процедуру (функцию) до момента ее вызова в основной программе;

пример работы процедуры и функции для сложения двух значений (порядок действий компилятора указан числами):

var x,y:integer;
procedure Sum(x,y:integer); 
begin
//3. Выводим сумму двух запрошенных чисел
  write(x+y); 
end;
begin
// 1. запрашиваем два числа
 readln(x,y);
// 2. передаем запрошенные числа в процедуру 
 Sum(x,y)  
end.

var x,y:integer;
function Sum(x,y:integer): integer; 
begin
{3. Суммируем два числа и присваиваем 
значение функции:}
  Sum:=x+y;
end;
begin
// 1. запрашиваем два числа
 readln(x,y);
{2. передаем запрошенные числа 
в функцию и выводим результат:} 
 write (Sum(x,y))
end.

Подробное описание работы с процедурами можно найти, перейдя по ссылке.

Рекурсивной называется процедура, вызывающая сама себя:

procedure row(n:integer);
begin
     if n >=1 then begin
        write (n, ' ');
        row(n-1)
     end;
end;
begin
    row(10);
end.

Для использования рекурсии, необходимо задать:

условие остановки рекурсии (обычно, в виде условного оператора):
рекуррентную формулу (обычно, вызов самой себя с измененным параметром):

Подробное описание работы с рекурсивными процедурами и функциями в Паскале можно найти здесь.

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Решение по рекуррентной формуле

16_13:

Алгоритм вычисления значений функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1; G(1) = 1;
F(n) = F(n–1) + 3·G(n–1), при n >=2 
G(n) = F(n–1) - 2·G(n–1), при n >=2

Чему равна сумма цифр значения F(18)?

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET:

function F(n: integer): integer; forward;
function G(n: integer): integer; forward;
 
function F(n: integer): integer;
begin
  if n = 1 then
    F := 1  // или result := 1
  else if n >= 2 then
    F := F(n - 1) + 3 * G(n - 1) 
    // или result := F(n - 1) + 3 * G(n - 1)
end;
 
function G(n: integer): integer;
begin
  if n = 1 then
    G := 1  // или result := 1
  else if n >= 2 then
    G := F(n - 1) - 2 * G(n - 1)
    // или result := F(n - 1) - 2 * G(n - 1)
end;
 
begin
  var res := F(18);
  var s := 0;
  while res > 0 do
  begin
    s := s + (res mod 10);
    res := res div 10;
  end;
  print(s)
end.

Питон:

def F( n ):
    if n == 1: 
        return 1
    elif (n >= 2):
        return F(n-1)+3*G(n-1)
def G( n ):
    if n == 1: 
        return 1
    elif (n >= 2):
        return F(n-1)-2*G(n-1)
 
res = F(18)
s = 0
while res > 0:
    s += res%10
    res = res // 10
print(s)

C++:

Результат: 46

16_1:

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1
F(n) = F(n–1) * (n + 2), при n > 1

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET (решение №1):

function F(n: integer): integer;
begin
  if n = 1 then
    F := 1
  else if n > 1 then
    F := F(n - 1) * (n + 2)
end;
 
begin
  print(F(5))
end.

PascalABC.NET (решение №2):

function F(n:integer):integer:=
 n=1 ? 1
 :  F(n-1) * (n+2);
 
begin
  print(F(5))
end.

Питон:

def F( n ):
    if n == 1: 
        return 1
    elif (n > 1):
        return F(n-1)*(n+2)
print (F(5))

C++:

✎ Решение теоретическое (методом с конца к началу):

Из условия задания мы имеем рекуррентную формулу: F(n–1) * (n + 2) и условие остановки рекурсии: n > 1.
Поскольку рекуррентная формула уже задана, то остается подставить в нее начальный параметр — число 5:

F(5) = F(4) * 7

Теперь применим эту формулу для всех вызываемых вложенных функций, вплоть до F(1) (при котором «сработает» остановка рекурсии). Получим:

F(5) = F(4) * 7
       F(4) = F(3) * 6
              F(3) = F(2) * 5
                     F(2) = F(1) * 4
                              1

На F(2) необходимо остановиться, так как действует условие остановки рекурсии: формула работает для n > 1. Также учтем, что по условию F(1) = 1.
Теперь с конца к началу перепишем все получившиеся сомножители и перемножим их:

1 * 4 * 5 * 6 * 7 = 840

Результат: 840

16_2:

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(0) = 1, F(1) = 1
F(n) = 2 * F(n–1) + F(n-2), при n > 1

Чему равно значение функции F(6)? В ответе запишите только целое число.

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET (решение №2):

function F(n:integer):integer;
begin
  if (n = 0) or (n = 1) then result:=1
  else if n>1 then result:=2*F(n-1) + F(n-2);
end;
begin
  print(F(6))
end.

✎ Решение 1. Теоретическое (метод решения с начала к концу):

Из условия задания мы имеем рекуррентную формулу: 2 * F(n–1) + F(n-2) и условие остановки рекурсии: n > 1.
Из заданной рекуррентной формулы видим, что функция зависит от предыдущей функции (F(n–1)) и от пред-предыдущей функции (F(n-2)).
Так как первые два значения заданы (F(0) = 1, F(1) = 1), то можно построить таблицу последующих значений, двигаясь к числу 6:

n	0	1	2	3	4	5	6
F(n) ^{2*F(n – 1)+F(n — 2)}	1	1	2*1+1 =3	2*3+1 =7	2*7+3 =17	2*17+7 =41	2*41+17 =99

Таким образом, получаем, что при вызове функции F(6) результатом будет число 99

✎ Решение 2. Теоретическое (метод решения с конца к началу):

Поскольку рекуррентная формула уже задана, то остается подставить в нее начальный параметр — число 6:

F(6) = 2*F(5) + F(4)

Теперь применим эту формулу для всех вызываемых вложенных функций, вплоть до F(2) (F(1) и F(0) известны из условия задачи). Получим:

F(6) = 2*F(5) + F(4)
       F(5) = 2*F(4) + F(3)
              F(4) = 2*F(3) + F(2)
                     F(3) = 2*F(2) + F(1)
                              F(2) = 2*F(1) + F(0) = 2*1+1 = 3
                                        1       1

Теперь с конца к началу перепишем все получившиеся значения функций:

F(6) = 2*F(5) + F(4) = 2*41 + 17 = 99
       F(5) = 2*F(4) + F(3) + 2*17+7 = 41 ↑
              F(4) = 2*F(3) + F(2) = 2*7+3 = 17 ↑
                     F(3) = 2*F(2) + F(1) = 2*3+1 = 7 ↑
                              F(2) = 2*F(1) + F(0) = 2*1+1 = 3 ↑  
                                        1       1

Результат: 99

Решение данного задания 16 также можно посмотреть в видеоуроке (теоретическое):

📹 YouTube здесь

16_10:

Алгоритм вычисления значений функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1; G(1) = 1;
F(n) = F(n–1) – G(n–1), 
G(n) = F(n–1) + 2*G(n–1), при n >= 2

Чему равно значение величины F(5)/G(5)?
В ответе запишите только целое число.

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET:

function F(n: integer): integer; forward;
function G(n: integer): integer; forward;
 
function F(n:integer):integer;
begin
  if n = 1 then result:=1
  else if n>=2 then result:=F(n-1) - G(n-1);
end;
 
function G(n:integer):integer;
begin
  if n = 1 then result:=1
  else if n>=2 then result:=F(n-1) + 2*G(n-1);
end;
begin
  print(F(5)/G(5))
end.

✎ Решение теоретическое:

Решим задание с вызова функций F(5) и G(5). Будем получать формулы последовательно для F(5), F(4), …, F(1), G(5), G(4), …, G(1). Дойдя до известных значений F(1) = 1 и G(1) = 1, подставим их в полученные формулы:

F(5) = F(4) – G(4)
G(5) = F(4) + 2*G(4)
	F(4) = F(3) – G(3)  
	G(4) = F(3) + 2*G(3) 
		F(3) = F(2) – G(2) 
		G(3) = F(2) + 2*G(2) 
			F(2) = F(1) – G(1) 
			G(2) = F(1) + 2*G(1) 
                               F(1) = 1; G(1) = 1;

F(2) = F(1) – G(1) = 1 - 1 = 0
G(2) = F(1) + 2*G(1) = 1 + 2 = 3
F(3) = F(2) – G(2) = 0 - 3 = -3
G(3) = F(2) + 2*G(2) = 0 + 6 = 6
F(4) = F(3) – G(3) = -3 - 6 = -9 
G(4) = F(3) + 2*G(3) = -3 + 12 = 9
F(5) = F(4) – G(4) = -9 - 9 = -18
G(5) = F(4) + 2*G(4) = -9 + 18 = 9

Итого:

F(5)/G(5) = -18/9 = -2

Ответ: -2

Что вернет функция. Сколько символов «звездочка». Какова сумма чисел

16_9:

Что вернет функция F, если ее вызвать с аргументом 6?

Паскаль:

function f(a:word):longword;
begin
  if a>0 then
    f := f(a-1)*a;
  else
    f:=1;
end;

Бейсик:

FUNCTION F(a)
  IF a > 0 THEN
     F = F(a - 1) * a
  ELSE
     F = 1;
  END IF
END FUNCTION

Python:

def F(a):
    if a > 0:
        return F(a - 1) * a
    else:
        return 1

С++:

int F(int a);
int F(int a) {
  if (a > 0)
    return F(a - 1) * a;
  else
    return 1;
}

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET:

function f(a:word):longword;
begin
  if a>0 then
    f := f(a-1)*a
  else
    f:=1;
end;
begin
  print(f(6))
end.

✎ Решение теоретическое:
Рассмотрим алгоритм функции:

Если аргумент функции, т.е. a, равен единице, то функция возвращает в программу значение 1, иначе вызывается функция с аргументом a — 1 и результат этой функции умножается на a.
Это рекурсивный алгоритм вычисления факториала числа. Чтобы удостовериться в этом, выполним трассировку функции с аргументом = 6:

F(6):
6 > 0, то F(5)*6
F(5):
5 > 0, то F(4)*5
F(4):
4 > 0, то F(3)*4
F(3):
3 > 0, то F(2)*3
F(2):
2 > 0, то F(1)*2
F(1): 
1 > 0, то F(0)*1
F(0):
0 > 0 - нет, то F(0) = 1

Теперь подставляем значения, двигаясь вверх по прописанному алгоритму:
F(1)= F(0)*1 = 1*1 = 1
F(2)= F(1)*2 = 1*2 = 2
F(3)= F(2)*3 = 2*3 = 6
F(4)= F(3)*4 = 6*4 = 24
F(5)= F(4)*5 = 24*5 = 120
F(6)= F(5)*6 = 120*6 = 720

Т.е. 6! = 720

Ответ: 720

16_3:

Ниже записаны две рекурсивные функции (процедуры): F и G.
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(18)?

Паскаль:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
 
procedure F(n: integer);
begin
  write('*');
  if n > 10 then F(n - 2) else G(n);
end;
 
procedure G(n: integer);
begin
  write('**');
  if n > 0 then F(n - 3);
end;

Бейсик:

DECLARE SUB F(n)
DECLARE SUB G(n)
SUB F(n)
  PRINT "*"
  IF n > 10 THEN
     F(n - 2)
  ELSE
     G(n)
  END IF
END SUB
SUB G(n)
  PRINT "**"
  IF n > 0 THEN
     F(n - 3)
  END IF
END SUB

Python:

def F(n):
  print("*")
  if n > 10:
    F(n - 2)
  else:
    G(n)
def G(n):
  print("**")
  if n > 0:
    F(n - 3)

С++:

void F(int n) {
  std::cout << "*";
  if (n > 10) {
    F(n - 2);
  }
  else {
    G(n);
  }
}
void G(int n) {
  std::cout << "**";
  if (n > 0)
    F(n - 3);
}

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
var k:=0; // объявление глобальной переменной-счетчика 
procedure F(n: integer);
begin
  write('*');
  k+=1; // увеличение счетчика
  if n > 10 then F(n - 2) else G(n);
end;
 
procedure G(n: integer);
begin
  write('**');
  k+=2;// увеличение счетчика
  if n > 0 then F(n - 3);
end;
begin
 f(18);
 print(k) // вывод счетчика
end.

✎ Решение теоретическое:

Для удобства восприятия задания, выпишем рекуррентные формулы и условия остановки рекурсии для двух процедур:

Для F:
*
F(n - 2) при n > 10
G(n) при n <= 10

Для G:
**
F(n - 3) при n > 0

✎ Способ 1:

Выпишем последовательность вызовов процедур, начиная с указанного в задании F(18):

F(18) -> F(16) -> F(14) -> F(12) -> F(10) -> G(10) -> 
F(7) -> G(7) -> F(4) -> G(4) -> F(1) -> G(1) -> F(-2) -> G(-2)

Обратим внимание, что независимо от условия процедура F выводит на экран одну *, а процедура G выводит две *. Посчитаем для последовательности вызовов итоговую сумму звездочек: 9F + 5G = 9*1 + 5*2 = 19

Результат: 19

✎ Способ 2:

Рассмотрим пошагово выполнение программы при вызове F(18):

1 шаг: F(18)
       *    F(16)
2 шаг:      *    F(14)
3 шаг:           *    F(12)
4 шаг:                *    F(10)
5 шаг:                     *    G(10)
6 шаг:                          **   F(7)
7 шаг:                                *  G(7)
8 шаг:                                   **  F(4)
9 шаг:                                       *    G(4)
10 шаг:                                           **   F(1)
11 шаг:                                                *   G(1)
12 шаг:                                                    **   F(-2)
13 шаг:                                                         *   G(-2)
14 шаг:                                                             **

Посчитаем количество звездочек: 19

Результат: 19

Пошаговое аналитическое решение данного 16 задания ЕГЭ по информатике доступно в видеоуроке:

📹 YouTube здесь

Видеорешение на RuTube здесь

16_12:

Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(5)?

Паскаль:

procedure F(n: integer);
begin
 writeln('*');
 if n > 0 then begin
   F(n-2);
   F(n div 2);
   F(n div 2);
 end
end;

Бейсик:

DECLARE SUB F(n)
SUB F(n)
  PRINT '*'
  IF n > 0 THEN
     F(n - 2)
     F(n  2)
     F(n  2)
  END IF
END SUB

Python:

def F(n):
  print('*')
  if n > 0:    
    F(n-2)
    F(n // 2)
    F(n // 2)

С++:

void F(int n) {
  std::cout << ″*″;
  if (n > 0) {
    F(n - 2);
    F(n / 2);
    F(n / 2);
  }
}

✍ Решение:

В начале каждого вызова независимо от условия на экран выводится «звездочка». Кроме того, если условие n > 0 истинно, то функция вызывается еще три раза с разными аргументами. Таким образом, каждая функция выводит на экран либо одну звездочку (если условие ложно), либо 4 звездочки если условие истинно.
Схематично рассмотрим вызов каждой функции, начиная с функции F(5). Дойдя до F(0), для которой условие будет ложно, будем подставлять полученное количество «звездочек», двигаясь опять к F(5):

F(5) = одна '*', F(3), F(2), F(2)
F(3) = одна '*', F(1), F(1), F(1)
F(2) = одна '*', F(0), F(1), F(1)
F(1) = одна '*', F(-1), F(0), F(0)
F(0) = одна '*' = 1  (условие ложно)
F(-1) = одна '*' = 1 (условие ложно)
---
Движение обратно:
F(1) = одна '*', F(-1), F(0), F(0) = 1 + 1 + 1 + 1 = 4 '*'
F(2) = одна '*', F(0), F(1), F(1) = 1 + 1 + 4 + 4 = 10 '*'
F(3) = одна '*', F(1), F(1), F(1) = 1 + 4 + 4 + 4 = 13 '*'
F(5) = одна '*', F(3), F(2), F(2) = 1 + 13 + 10 + 10 = 34 '*'

Ответ: 34

16_4:

Ниже записаны две рекурсивные функции (процедуры): F и G.
Какова сумма чисел, напечатанных на экране при выполнении вызова F(17)?

Паскаль:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
 
procedure F(n: integer);
begin
  writeln(n);
  if n mod 2  =0 then F(n div 2) 
  else G((n - 1) div 2);
end;
 
procedure G(n: integer);
begin
  writeln (n); 
  if n > 0 then F(n);
end;

Бейсик:

DECLARE SUB F(n)
DECLARE SUB G(n)
SUB F(n)
  PRINT n
  IF n MOD 2 = 0 THEN
     F(n  2)
  ELSE
     G ( (n - 1)  2)
  END IF
END SUB
SUB G(n)
  PRINT n
  IF n > 0 THEN
     F(n)
  END IF
END SUB

Python:

def F(n):
  print(n)
  if n % 2 == 0:
    F(n // 2)
  else:
    G((n - 1) // 2)
def G(n):
  print(n)
  if n > 0:
    F(n)

С++:

void F(int n) {
  std::cout << n << endl;
  if (n % 2 == 0) {
    F(n / 2);
  }
  else {
    G((n - 1) / 2) ;
  }
}
void G(int n) {
  std::cout << n << endl;
  if (n > 0)
    F(n);
}

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
var sum:=0; // сумматор
procedure F(n: integer);
begin
  writeln(n);
  sum+=n; // добавляем число в сумматор
  if n mod 2  =0 then F(n div 2) 
  else G((n - 1) div 2);
end;
 
procedure G(n: integer);
begin
  writeln (n); 
  sum+=n; // добавляем число в сумматор
  if n > 0 then F(n);
end;
begin
  F(17);
  print('sum =',sum)
end.

✎ Решение теоретическое:

Для удобства восприятия задания, выпишем рекуррентные формулы и условия остановки рекурсии для двух процедур:

Для F:
n
F(n div 2) при n - четное (n mod 2 = 0)
G((n - 1) div 2) при n - нечетное

Для G:
n
F(n) при n > 0

Выпишем последовательность вызовов процедур, начиная с указанного в задании F(17).
Обратим внимание, что независимо от условия как процедура F выводит на экран n, так и процедура G выводит n.

F(17) -> n - нечетное, G(8) вывод 17
G(8) -> F(8)                вывод 8
F(8) -> n - четное, F(4)    вывод 8
F(4) -> n - четное, F(2)    вывод 4 
F(2) -> n - четное, F(1)    вывод 2
F(1) -> n - нечетное, G(0)  вывод 1
G(0)                        вывод 0

Сумма:

17 + 8 + 8 + 4 + 2 + 1 + 0 = 40

Результат: 40

16_5:

Ниже записаны две рекурсивные функции (процедуры): F и G.
Чему будет равно значение, вычисленное при выполнении вызова F(6)?

Паскаль:

function F(n: integer):integer; forward;
function G(n: integer):integer; forward;
function F(n:integer):integer;
begin
 if (n > 2) then
   F:= F(n - 1) + G(n - 2)
 else F:= n;
end;
function G(n:integer):integer;
begin
 if (n > 2)then
   G:= G(n - 1) + F(n -2)
 else G:= n+1;
end;

Бейсик:

FUNCTION F(n)
  IF n > 2 THEN
     F = F(n - 1) + G(n - 2)
  ELSE
     F = n;
  END IF
END FUNCTION 
FUNCTION G(n)
  IF n > 2 THEN
     G = G(n - 1) + F(n -2)
  ELSE
     G = n+1;
  END IF
END FUNCTION

Python:

def F(n):
    if n > 2:
        return F(n - 1) + G(n - 2)
    else:
        return n
def G(n):
    if n > 2:
        return G(n - 1) + F(n - 2)
    else:
        return n+1

С++:

int F(int n);
int G(int n);
int F(int n) {
  if (n > 2)
    return F(n - 1) + G(n - 2);
  else
    return n;
}
int G(int n) {
  if (n > 2)
    return G(n - 1) + F(n - 2);
  else
    return n + 1;
}

Типовые задания для тренировки

✍ Решение:

Результат: 17

Предлагаем посмотреть видеоразбор данного аналитического решения:

📹 YouTube здесь

Видеорешение на RuTube здесь

С каким аргументом?

16_8:

Вызов представленной ниже рекурсивной функции приводит к появлению на экране чисел и точек. С каким минимальным натуральным аргументом а нужно вызвать эту функцию, чтобы в результате на экране появилось 5 точек (не обязательно подряд, между точками могут встречаться числа)?

Паскаль:

function gz(a:integer):integer;
var p:integer;
begin
  if a<1 then begin 
   gz:=1; exit; 
  end;
  if a mod 3=0 then begin
   write('...');
   p:=gz(a div 3)+gz(a div 4);
  end
  else begin
    write('.');
    p:=gz(a div 4);
  end;
  write(p);
  gz:=2; 
end;

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
var sum:=0; // сумматор
procedure F(n: integer);
begin
  writeln(n);
  sum+=n; // добавляем число в сумматор
  if n mod 2  =0 then F(n div 2) 
  else G((n - 1) div 2);
end;
 
procedure G(n: integer);
begin
  writeln (n); 
  sum+=n; // добавляем число в сумматор
  if n > 0 then F(n);
end;
begin
  F(17);
  print('sum =',sum)
end.

Результат: 6

Смотрите подробное аналитическое решение:

📹 YouTube здесь

📹 Видеорешение на RuTube здесь (аналитическое)

Не актуально для компьютерного ЕГЭ

Все числа, которые будут напечатаны на экране, в том же порядке

16_6: Демоверсия ЕГЭ 2018 информатика:

Ниже на пяти языках программирования записан рекурсивный алгоритм F.
Паскаль:

procedure F(n: integer);
begin
if n > 0 then
begin
  write(n);
  F(n - 3);
  F(n div 3)
end
end;

Бейсик:

SUB F(n)
  IF n > 0 THEN
     PRINT n
     F(n - 3)
     F(n  3)
  END IF
END SUB

Python:

def F(n):
  if n > 0:
     print(n)
     F(n - 3)
     F(n // 3)

С++:

void F(int n){
  if (n > 0){
    std::cout <<n;
    F(n - 3);
    F(n / 3);
  }
}

Запишите подряд без пробелов и разделителей все числа, которые будут напечатаны на экране при выполнении вызова F(9). Числа должны быть записаны в том же порядке, в котором они выводятся на экран.

Похожие задания для тренировки

✍ Решение:

В данном фрагменте программы рекурсивная процедура вызывает саму себя дважды.
Благодаря условию, находящемуся в процедуре (if n > 0 — условие остановки рекурсии), обеспечивается выход из рекурсии и не происходит «зацикливания».
Выполнение процедур закончится, когда в каждой из вызванных процедур выполнятся по две внутренние процедуры, и условие if n > 0 перестанет работать (т.е. когда параметр процедуры n станет <= 0).
div — целочисленное деление, т.е., например:

5 div 2 = 2
1 div 2 = 0

Отобразим пошагово выполнение каждой процедуры, двигаясь сверху вниз и оставляя отступы слева с каждым новым шагом. В каждой строке будем отображать порядковый номер шага. Под вызовом каждой процедуры разместим именно те действия, которые происходят в данной процедуре:

   F(9)
1: 9  F(6)    (9 - 3 = 6)
2:     6   F(3)    (6 - 3 = 3)
3:          3    F(0)    (3 - 3 = 0, условие не работает)
4:         F(1)  (3 div 3 = 1)
5:          1    F(-2)    (1 - 3 = -2, условие не работает)
6:         F(0)    (1 div 3 = 0, условие не работает)
7:    F(2) (6 div 3 = 2)
8:     2   F(-1)    (2 - 3 = -1, условие не работает)
9:    F(0)    (2 div 3 = 0, условие не работает)
10:F(3)  (9 div 3 = 3)
11:3  F(0)     (3 - 3 = 0, условие не работает) 
12:F(1)  (3 div 3 = 1)   
13: 1   F(-2)     (1 - 3 = -2, условие не работает)

Выделены те числа, которые выводятся на экран. Подчеркнуты те процедуры, в которых условие не работает, соответственно, ничего на экран не выводится.
Перепишем по порядку все выводимые на экран числа сверху вниз: 9631231

Результат: 9631231

Подробное решение 16 (11) задания демоверсии ЕГЭ 2018 года смотрите на видео:
📹 Видео 1 способ
📹 Видеорешение на RuTube здесь

2 способ:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

16_7:

Ниже записан рекурсивный алгоритм F. Запишите подряд без пробелов и разделителей все числа, которые будут напечатаны на экране при выполнении вызова F(130).
Числа должны быть записаны в том же порядке, в котором они выводятся на экран.

Паскаль:

procedure F(n: integer);
begin
  if n > 1 then
  begin
    write(n);
    F(n div 10);
    F(n - 40)
   end
end;

Бейсик:

SUB F(n)
  IF n > 1 THEN
     PRINT n
     F(n  10)
     F(n - 40)
  END IF
END SUB

Python:

def F(n):
  if n > 1:
     print(n)
     F(n // 10)
     F(n - 40)

С++:

void F(int n){
  if (n > 1){
    std::cout <<n;
    F(n / 10);
    F(n - 40);
  }
}

✍ Решение:

В данном фрагменте программы рекурсивная процедура F вызывает саму себя дважды.
В процедуре находится условие if n > 1 — условие остановки рекурсии, благодаря которому обеспечивается выход из рекурсии и не происходит «зацикливания».
Выполнение фрагмента программы закончится, когда в каждой из вызванных процедур выполнятся по две внутренние процедуры, и условие if n > 1 перестанет работать (т.е. когда параметр процедуры n станет <= 1).
div — целочисленное деление, т.е., например:

5 div 3 = 1
1 div 3 = 0

Выполним трассировку кода процедуры: двигаться будем пошагово сверху вниз, оставляя отступы слева с каждым новым шагом. В каждой строке будем отображать порядковый номер шага. Под вызовом каждой процедуры разместим именно те действия, которые происходят в данной процедуре:

   F(130) 130  
1: ➥  F(13) (130 div 10 = 13) 13
2:           ➥ F(1) условие не работает! 1 ≤ 0
3:           ➥ F(-27) условие не работает! -27 ≤ 0
4: ➥  F(90) (130 - 40 = 90) 90        
5:           ➥ F(9) (90 div 10 = 9) 9
6:                    ➥ F(0) условие не работает! 0 ≤ 0
7:                    ➥ F(-31) условие не работает! -31 ≤ 0
8:           ➥  F(50) (90 - 40 = 50) 50
9:                     ➥  F(5) (50 div 10 = 5) 5
10:                              ➥ F(0) условие не работает! 0 ≤ 0
11:                              ➥ F(-35) условие не работает! -35 ≤ 0
12:                    ➥  F(10) (50 - 40 = 10) 10
13:                              ➥ F(1) условие не работает! 1 ≤ 0
14:                              ➥ F(-30) условие не работает! -30 ≤ 0

Выделены красным цветом те числа, которые выводятся на экран. Подчеркнуты те процедуры, в которых условие не работает, соответственно, ничего на экран не выводится.
Перепишем сверху вниз все выводимые на экран числа: 1301390950510

Результат: 1301390950510

Предлагаем посмотреть видео разбора задания:
📹 YouTube здесь

📹 Видеорешение на RuTube здесь

16_11:

Определите, что выведет на экран программа при вызове F(5).

Паскаль:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
procedure F(n: integer);
begin
  if n > 2 then
   begin
    write(n);
    F(n - 1);
    G(n - 2);
   end
  else
    write(n+2);
end;
procedure G(n: integer);
begin
  write(n);
  if n > 2 then
   begin
    G(n - 1);
    F(n - 2);
   end;
end;

Бейсик:

DECLARE SUB F(n)
DECLARE SUB G(n)
SUB F(n)
  IF n > 2 THEN
     PRINT n
     F(n - 1)
     G(n - 2)
  ELSE
     PRINT n+2
  END IF
END SUB
SUB G(n)
  PRINT n
  IF n > 2 THEN
     G(n - 1)
     F(n - 2)
  END IF
END SUB

Python:

def F(n):
    if n > 2:
        print(n, end='')
        F(n - 1)
        G(n - 2)
    else:
        print(n+2, end='')
 
def G(n):
    print(n, end='')
    if n > 2:
        G(n - 1)
        F(n - 2)

С++:

void G(int n);
void F(int n) {
	if (n > 2) {
	  std::cout << n;
	  F(n - 1);
	  G(n - 2);		
	  }
	else
	  std::cout << n+2;
}
void G(int n) {
	std::cout << n;
	if (n > 2) {
	  G(n - 1);
	  F(n - 2);
	  } 
}

Типовые задания для тренировки

✍ Решение:

При истинности условия функция F также, как и функция G «запускает» еще две функции: функция F: 1)F(n — 1) и 2)G(n — 2), а функция G: 1)G(n — 1) и 2)F(n — 2).
Рассмотрим последовательно алгоритм работы функций, нумеруя вызовы функций. Для удобства будем делать отступы для каждой функции. Таким образом, для вызова каждой функции должно быть два внутренних вызова:

F(5) = 5 (на экране)
1) F(n - 1), т.е. F(4)
    F(4) = 4(на экране)
    1) F(n - 1), т.е. F(3)
           F(3) = 3(на экране)
           1) F(n - 1), т.е. F(2)
                  F(2) = n + 2 = 4 (на экране) (блок else)
           2) G(n - 2), т.е. G(1)
   	          G(1) = 1 (на экране)
    2) G(n - 2), т.е. G(2)
	   G(2) = 2 (на экране)
2) G(n - 2), т.е. G(3)
    G(3) = 3 (на экране)
    1)G(n - 1), т.е. G(2)
           G(2) = 2 (на экране)
    2) F(n - 2), т.е. F(1)
           F(1) = n + 2 = 3 (на экране) (блок else)

Перепишем сверху вниз все цифры, выведенные на экран:

543412323

Ответ: 543412323

Источник

Шестнадцатое задание из ЕГЭ по информатике 2022 даётся на рекурсию.

Это задание нужно делать с помощью компьютера.

В программировании рекурсией называется процесс, когда функция вызывает сама себя или, когда две функции попарно вызывают друг друга.

Мы будем писать все программы на языке программирования Python.

Что такое Функция в языке программирования Python ?

Функция – это подпрограмма, результатом работы которой может является определенное значение.

Рассмотрим пример функции, которая суммирует два числа!

def F(x, y):
    s = x + y
    return s

a = int(input())
b = int(input())

r = F(a, b)

print(r)

Здесь функция F, которая суммирует два числа.

В главной части программы запрашиваются два числа с клавиатуры: a и b! Эти два числа передаются в функцию F. В функции эти числа кладутся в локальные переменные x и y. Сумма переменных x и y записывается в переменную s. Переменная s возвращается, как результат работы функции F.

Результат работы функции будет помещён в переменную r (в строке r = F(a, b)) в основной части программы.

Таким образом, в переменной r будет сумма двух переменных a и b.

Функции позволяют сократить программный код для однотипных расчётов.

Тренировочные задачи 16 задания из ЕГЭ по информатике 2023

Задача (Стандартная)

Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:

F(n) = 1 при n = 1;
F(n) = n + F(n − 1), если n – чётно,
F(n) = 3 × F(n − 2), если n > 1 и при этом n – нечётно.

Чему равно значение функции F(25)?

Решение:

Напишем программу для решения данной задачи. В начале опишем все правила, которые даны в условии задачи для функции. В основной части программы запустим эту функцию.

# Сама функция
def F(n):
    if n==1: return 1
    if n%2==0: return n+F(n-1)
    if n>1 and n%2!=0: return 3*F(n-2)
    
# Основная часть программы
print(F(25))

После запуска рекурсивной функции программа выведет ответ 531441.

Выражение n%2 != 0 (остаток от деления на «2» не равен нулю) обозначает нечётное число. Выражение n%2==0 обозначает чётное число.

Ответ: 531441

Продолжаем тренировку по подготовке к 16 заданию ЕГЭ по информатике 2022.

Задача (Продолжаем подготовку)

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1
F(2) = 3
F(n) = F(n–1) * n + F(n–2) * (n – 1) , при n > 2

Чему равно значение функции F(8)? В ответе запишите только натуральное число.

Решение:

# Сама функция
def F(n):
    if n==1: return 1
    if n==2: return 3
    if n>2: return F(n-1)*n + F(n-2)*(n-1)
    
# Основная часть программы
print(F(8))

Ответ получается 148329.

Ответ: 148329

Закрепляющий пример на рекурсию 16 задания из ЕГЭ по информатике 2022.

Задача(Две функции)

Алгоритм вычисления значения функций F(n) и G(n), где n — натуральное число, задан следующими соотношениями:

F(n) = 0, если n <= 2,
F(n) = G(n — 2), если n > 2

G(n) = 0, n <= 1,
G(n) = F(n — 1) + n, если n > 1

Чему равно значение функции F(8)? В ответе запишите только натуральное число.

Решение:

# Сами функции
def F(n):
    if n<=2: return 0
    if n>2: return G(n-2)

def G(n):
    if n<=1: return 0
    if n>1: return F(n-1)+n

# Основная часть программы
print(F(8))

Получается ответ 9.

Ответ: 9

Задача (Количество значений)

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = 2*n*n*n + 1, при n > 25
F(n) = F(n+2) + 2*F(n+3), при n ≤ 25

Определите количество натуральных значений n из отрезка [1; 1000], для которых значение F(n) кратно 11.

Решение:

# Сама функция
def F(n):
    if n>25: return 2*n*n*n + 1
    if n<=25: return F(n+2) + 2*F(n+3)

k=0

# Перебираем диапазон
for i in range(1, 1001):
    if F(i)%11==0:
        k=k+1

print(k)

В начале формируем функцию F. Затем перебираем числа из диапазона от 1 до 1000. Каждое число подставляем в функцию F. Если значение функции F делится на 11, то мы зачитываем такое значение i.

В ответе получается 91.

Ответ: 91

Задача (Используем глобальную переменную)

Решение:

При решении этой задачи можно применить глобальную переменную.

def F(n):
    global s
    s=s+1
    if n>=1:
        s=s+1
        F(n-1)
        F(n-2)
        s=s+1

s=0
F(35)
print(s)

Здесь внутри функции заводим глобальную переменную s, которая будет подсчитывать количество напечатанных звёздочек. Теперь эту переменную видно при любом вызове функции, и при каждом вызове функции она будет одна и та же переменная. Вместо печати звёздочек пишем конструкцию s=s+1.

В основной части программы перед первым запуском функции переменной s присваиваем 0.

Программа может немного медленно работать из-за большой глубины рекурсии, но через минуту выведет число 96631265.

Ответ: 96631265

Новые тенденции

В последнее время мы видим тенденцию в 16 задании из ЕГЭ по информатике 2023, что теперь мало переписать функцию и её запустить. Необходимо подумать, как можно преобразовать то рекурсивное выражение, которое нужно вычислить.

Задача (Новое веяние)

(К. Багдасарян) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = 2, если n = 1,
F(n) = 2 · F(n – 1), если n > 1.

Чему равно значение выражения F(1900)/2¹⁸⁹⁰ ?

Решение:

1 Способ (Аналитическое решение)

Если мы просто перепишем функцию и попытаемся вычислить выражение F(1900)/2¹⁸⁹⁰, то получим ошибку RecursionError: maximum recursion depth exceeded. Возникает она из-за слишком большой цепочки вызовов функции.

В подобных задачах нужно попытаться самому упростить выражение, которое пытаемся вычислить. Посмотрим, что из себя представляет функция.

F(1900) = 2*F(1899) = 2*2*F(1898) = … 2¹⁹⁰⁰

Тогда

F(1900)/2¹⁸⁹⁰ = 2¹⁹⁰⁰/2¹⁸⁹⁰ = 2¹⁰ = 1024

Получается 1024.

2 Способ (Через lru_cache)

Чтобы уменьшить цепочку вызовов функции, можно использовать инструмент lru_cache.

from functools import lru_cache

@lru_cache(None)
def F(n):
    if n==1: return 2
    if n>1: return 2*F(n-1)

for i in range(2, 1900):
    F(i)

print(F(1900)/2**1890)

В задаче функция опирается на значение функции от n-1 и т.д. За счёт этого происходят длинные вычисления для каждого числа n.

Использовав инструмент lru_cache, мы пробегаемся в цикле по значениям n в возрастающем порядке, и для каждого значения сохраняем результаты функции. Таким образом, вычисляя очередное значение, программа опирается на уже готовый результат, тем самым цепочка вызовов функции будет маленькой.

Ответ: 1024

Задача(Новое веяние, закрепление)

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

F(n) = 1 при n ≤ 2;
F(n) = n * F(n-2), если n > 2.

Чему равно значение выражение F(3000)/F(2996) ?

Решение:

1 Способ (Аналитическое решение)

Начнём расписывать F(3000).

F(3000) = 3000*F(2998) = 3000*2998*F(2996)

Получается:

F(3000)/F(2996) = 3000*2998*F(2996)/F(2996) = 3000*2998 = 8994000

2 Способ (Через lru_cache)

from functools import lru_cache

@lru_cache(None)
def F(n):
    if n<=2: return 1
    if n>2: return n*F(n-2)

for i in range(2, 3000):
    F(i)

print(F(3000)/F(2996))

Ответ: 8994000

Задача (Вперёд к победе!)

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

F(n) = 1 при n=1;
F(n) = 2 при n=2;
F(n) = n*(n-1) + F(n-1) + F(n-2), если n > 2.

Чему равно значение функции F(2023) — F(2021) — 2*F(2020) — F(2019)?

Решение:

1 Способ (Аналитическое решение)

F(2023) = 2023*2022 + F(2022) + F(2021) =
= 2023*2022 + 2022*2021 + F(2021) + F(2020) + F(2021) =
=2023*2022 + 2022*2021 + 2021*2020 + F(2020) + F(2019) + F(2020) + F(2021) =
2023*2022 + 2022*2021 + 2021*2020 + 2*F(2020) + F(2019) + F(2021) =
2023*2022 + 2022*2021 + 2021*2020 + F(2021) + 2*F(2020) + F(2019)

Если подставим полученный результат в выражение, которое нужно найти, то получим:

2023*2022 + 2022*2021 + 2021*2020 = 12259388

2 Способ (Через lru_cache)

from functools import lru_cache

@lru_cache(None)
def F(n):
    if n==1: return 1
    if n==2: return 2
    if n>2: return n*(n-1) + F(n-1) + F(n-2)

for i in range(2, 2023):
    F(i)

print(F(2023) - F(2021) -2*F(2020) - F(2019))

Ответ: 12259388

Удачи при решении 16 задания из ЕГЭ по информатике 2022.

А если промежуток намного больше будет? например не [1, 1000], а [1,500 000 000]? пк зависнет просто.. можно кроме как разбивать промежуток много на разных программ решить такую задачу?

Ниже на пяти языках программирования записан рекурсивный алгоритм F.
def F(n):
  print(n)
  if n > 0:
  F(n — 1)
  F(n — 3)
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(5)?
А можете показать как это через python решать ?

Источник

Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = F(n–1) * n, при n >1

Чему равно значение функции F(5)? В ответе запишите только натуральное число.

Источник: Демонстрационная версия ЕГЭ—2013 по информатике.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 3

F(n) = F(n–1) * (n–1), при n >1

Чему равно значение функции F(6)?

В ответе запишите только натуральное число.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = 5*F(n–1) + 3*n, при n >1

Чему равно значение функции F(4)?

В ответе запишите только натуральное число.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = F(n–1) * F(n–1) − F(n–1) * n + 2 * n, при n >1

Чему равно значение функции F(4)?

В ответе запишите только натуральное число.

Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 0

F(n) = F(n–1) + n, при n >1

G(1) = 1

G(n) = G(n–1) * n, при n >1

Чему равно значение функции F(5) + G(5)?

В ответе запишите только натуральное число.

Пройти тестирование по этим заданиям

Источник

За это задание ты можешь получить 1 балл. На решение дается около 2 минут. Уровень сложности: повышенный.
Средний процент выполнения: 54.9%
Ответом к заданию 16 по информатике может быть цифра (число) или слово.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Функция F(n), где n — натуральное число, вычисляется по следующему правилу:

F(n) = n, при n < 4;

F(n) = F(n-3)*3, при n > 3 кратном трём;

F(n) = F(n-1)+7, при n > 3, которое даёт остаток 1 при делении на 3;

F(n) = F(n-2)+n, при n > 3, которое даёт остаток 2 при делении на 3.

Чему равно значение функции F(28)?

Для выполнения задания рекомендуется написать программу.

Решение

Перепишем правило вычисления функции в рекуррентную функцию на языке Python:

def f(n):

if n < 4:

return n

elif n % 3 == 0:

return f(n-3)*3

elif n % 3 == 1:

return f(n-1)+7

else:

return f(n-2)+n

print(f(28))

При запуске программа выдаст ответ: 19690

Ответ: 19690

Задача 2

Функция F(n), где n — натуральное число, вычисляется по следующему правилу:

F(n) = n, при n < 4;

F(n) = F(n-3)*3, при n > 3 кратном трём;

F(n) = F(n-1)+7, при n > 3, которое даёт остаток 1 при делении на 3;

F(n) = F(n-2)+n, при n > 3, которое даёт остаток 2 при делении на 3.

Чему равно значение функции F(25)?

Для выполнения задания рекомендуется написать программу.

Решение

Перепишем правило вычисления функции в рекуррентную функцию на языке Python:

def f(n):

if n < 4:

return n

elif n % 3 == 0:

return f(n-3)*3

elif n % 3 == 1:

return f(n-1)+7

else:

return f(n-2)+n

print(f(25))

Решение на С++:

#include <iostream>
using namespace std;int f(int n){
    if (n < 4)
        return n;
    else if (n % 3 == 0)
        return f(n-3)*3;
    else if (n % 3 == 1)
        return f(n-1)+7;
    else
        return f(n-2)+n;
}
int main() {
    cout << f(25);
    return 0;
}

При запуске программа выдаст ответ: 6568

Ответ: 6568

Задача 3

Функция F(n), где n — натуральное число, вычисляется по следующему правилу:

F(n) = n, при n < 2;

F(n) = F(n-2)+n, при n > 1 чётном

F(n) = F(n-1)+2*F(n-3), при n > 1 нечётном

Чему равно значение функции F(199)?

Для выполнения задания рекомендуется написать программу.

Решение

Перепишем правило вычисления функции в рекуррентную функцию на языке Python:

def f(n):

if n < 2:

return n

elif n % 2 == 0:

return f(n-2)+n

else:

return f(n-1)+2*f(n-3)

print(f(199))

При запуске программа выдаст ответ: 29304

Ответ: 29304

Задача 4

Функция F(n), где n — натуральное число, вычисляется по следующему правилу:

F(n) = n, при n < 2;

F(n) = F(n-1)+F(n-3), при n > 1 чётном

F(n) = F(n-2)*n, при n > 1 нечётном

Чему равно значение функции F(10)?

Для выполнения задания рекомендуется написать программу.

Решение

Перепишем правило вычисления функции в рекуррентную функцию на языке Python:

def f(n):

if n < 2:

return n

elif n % 2 == 0:

return f(n-1)+f(n-3)

else:

return f(n-2)*n

print(f(10))

При запуске программа выдаст ответ: 1050

Ответ: 1050

Задача 5

Функция F(n), где n — натуральное число, вычисляется по следующему правилу:

F(n) = n, при n ≤ 2;

F(n) = F(n-1)*(n-2), при n > 2

Чему равно значение функции F(8)?

Для выполнения задания рекомендуется написать программу.

Решение

Перепишем правило вычисления функции в рекуррентную функцию на языке Python:

def f(n):

if n <= 2:

return n

else:

return f(n-1)*(n-2)

print(f(8))

При запуске программа выдаст ответ: 1440

Ответ: 1440

Задача 6

Функция F(n), где n — натуральное число, вычисляется по следующему правилу:

F(n) = 1, при n ≤ 2;

F(n) = F(n-1)+F(n-2), при n > 2

Чему равно значение функции F(19)?

Для выполнения задания рекомендуется написать программу.

Решение

Перепишем правило вычисления функции в рекуррентную функцию на языке Python:

def f(n):

if n <= 2:

return 1

else:

return f(n-1)+f(n-2)

print(f(19))

При запуске программа выдаст ответ: 4181

Ответ: 4181

Задача 7

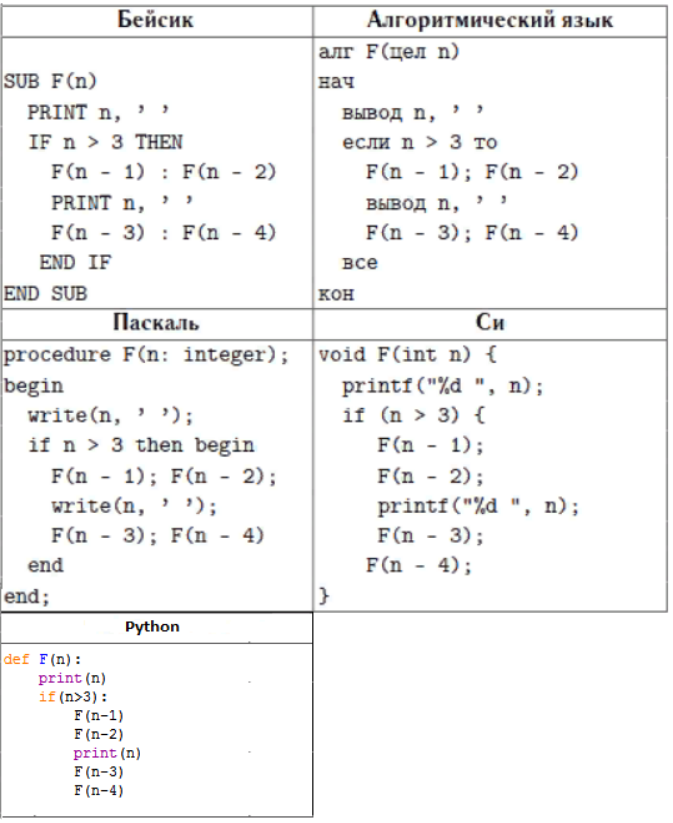
На рисунке на различных языках программирования записан рекурсивный алгоритм F.

Определите сумму чисел, напечатанных на экране при выполнении вызова F(4)?

Решение

Поскольку нам необходимо посчитать сумму чисел, порядок вызова функций не имеет значения. Заметим, что первый вывод печатает на экране все параметры n, с которыми вызываются функции, а второй печатает параметр n, только если он больше 3. Изначальная F(4) вызовет 4 функции: F(3), F(2), F(1), F(0).

Итого, будут вызваны функции: F(4), F(3), F(2), F(1), F(0), причём для F(4) вывод на экран произойдёт дважды. Итоговая сумма чисел: 4+4+3+2+1+0=14

Ответ: 14.

Ответ: 14

Задача 8

На картинке на различных языках программирования записан рекурсивный алгоритм F. Сколько чисел будет выведено в консоль при выполнении вызова функции F(8)?

Решение

Решение при помощи программы на языке С++:

#include <iostream>
using namespace std;int f(int n){
    if (n > 2) {
        cout << n;
        f(n - 2);
        f(n - 3);
    }
}
int main() {
    cout << f(8);
    return 0;
}

Программ выведет на экран число из 6 цифр: 864353

Ответ: 6

Задача 9

Функция F(n), где n — натуральное число, вычисляется по следующему правилу:

F(n) = n, при n < 4;

F(n) = F(n-3)*3, при n > 3 кратном трём;

F(n) = F(n-1)+7, при n > 3, которое даёт остаток 1 при делении на 3;

F(n) = F(n-2)+n, при n > 3, которое даёт остаток 2 при делении на 3.

Чему равно значение функции F(22)?

Для выполнения задания рекомендуется написать программу.

Решение

Перепишем правило вычисления функции в рекуррентную функцию на языке Python:

def f(n):

if n < 4:

return n

elif n % 3 == 0:

return f(n-3)*3

elif n % 3 == 1:

return f(n-1)+7

else:

return f(n-2)+n

print(f(22))

При запуске программа выдаст ответ: 2194

Ответ: 2194

Задача 10

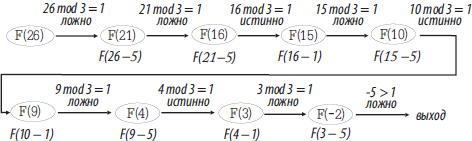
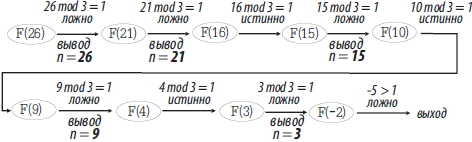
На рисунке на различных языках программирования записан рекурсивный алгоритм F. Определите, сколько чисел будет напечатано на экране при выполнении вызова F(26).

Решение

На рисунке представлена схема выполнения вызова процедуры F(26) в виде дерева.

Согласно алгоритма, вывод чисел на экран осуществляется, когда остаток от деления n на 3 не равен 1.

Количество чисел напечатанных на экране (26, 21, 15, 9, 3) : 5

Ответ: 5

Задача 11

На рисунке на различных языках программирования записан рекурсивный алгоритм F.

Определите, сколько чисел будет напечатано на экране при выполнении вызова F(6).

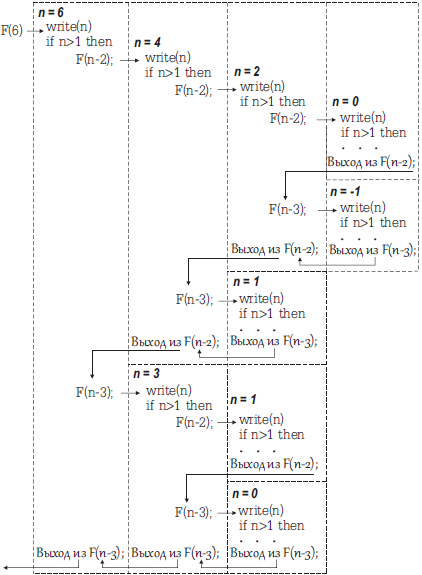
Решение

При вызове функции F(6) выполняется подпрограмма, в которой переменная n принимает значение 6. Каждый раз при вызове процедур F(n — 2) и F(n — 3) в качестве фактического параметра n в них передаётся текущее значение этой переменной. На рисунке участки, ограниченные пунктиром, демонстрируют область видимости соответствующего значения переменной n.

Каждый раз, возвращаясь из процедуры, переменная n принимает значение, которое было до вызова данной процедуры. Например, если процедура F(n — 2) была вызвана при n = 6, то, попадая в процедуру, переменная n примет значение 4(= 6 − 2). После выхода из этой процедуры значение переменной n вновь будет равно 6.

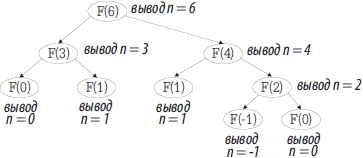
На рисунке представлена схема выполнения вызова процедуры F(6) в виде дерева.

В данном случае осуществляется вертикальный обход дерева в прямом (префиксном) порядке. То есть сначала просматривается вершина, затем правое поддерево, затем левое поддерево.

Согласно алгоритму, сразу после входа в процедуру осуществляется вывод на экран переменной n. Следовательно, при выполнении вызова F(6) на экране будет отображена последовательность чисел: 6 4 2 0 -1 1 3 1 0. На экране будет напечатано 9 чисел.

Ответ: 9

Е16.28 Чему равно значение выражения F(2023) / F(2020)?

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = n × F(n − 1), если n > 1. Чему равно значение выражения F(2023) / F(2020)? Ответ: Демонстрационный вариант ЕГЭ 2023 г. – задание №16

Е16.27 Укажите наименьшее значение a, для которого F(a, 0) = 1392781243

Обозначим частное от деления целочисленного натурального числа a на натуральное число b как a div b, а остаток как a mod b. Например, 13 div 3 = 4, 13 mod 3 = 1. Алгоритм вычисления значения функции F(a, b), где a и b – целые неотрицательные числа, задан следующими соотношениями: F(0, b) = b; F(a, …

Е16.26 Чему равно значение функции F(42)?

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = 3 × n + F(n — 2), если n > 1 и при этом n нечётно, F(n) = 4 × F(n / 2), если n > 1 и при этом n чётно. Чему …

Е16.25 Укажите количество таких значений n < 1 000 000 000, для которых F(n) = 2.

Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = F(n – 1) + 1, если n нечётно; F(n) = F(n/2), если n > 0 и при этом n чётно. Укажите количество таких значений n < 1 000 000 000, для которых F(n) = 2. СтатГрад …

Е16.24 являющихся результатом вызова функции для значений n в диапазоне [40; 50]

Алгоритм вычисления функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:

F(n) = n + 3, при n ≤ 3

F(n) = F(n – 2) + n, при n > 3 и четном значении F(n—1),

F(n) = F(n – 2) + 2· n, при n > 3 и нечетном значении F(n—1)

Определите сумму значений, являющихся результатом вызова функции для значений n в диапазоне [40; 50]. Ответ: Е. Джобс

Е16.23 F(n) = F(n – 1) – F(n – 2) + 3n, при n > 1 и n – четно

Алгоритм вычисления функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:

F(0) = 1, F(1) = 3

F(n) = F(n – 1) – F(n – 2) + 3n, при n > 1 и n – четно

F(n) = F(n – 2) – F(n – 3) + 2n, при n > 1 и n – нечетно

Чему равно значение функции F(40)? В ответе запишите только целое число Ответ: Е. Джобс

Е16.22 Сколько существует таких чисел n, что 1 ≤ n ≤ 500 и F(n) = 8

Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = F(n/2), если n > 0 и при этом n чётно; F(n) = 1 + F(n – 1), если n нечётно. Сколько существует таких чисел n, что 1 ≤ n ≤ 500 и F(n) = 8? Ответ: …

Е16.21 F(n) = 1 при n ≤ 1; F(n) = n · F(n – 1) при чётных n > 1;

Алгоритм вычисления функции F(n) задан следующими соотношениями: F(n) = 1 при n ≤ 1; F(n) = n · F(n – 1) при чётных n > 1; F(n) = n + F(n – 2) при нечётных n > 1; Определите значение F(84). Ответ: Тренировочный вариант от 16.11.2020 «Евгений Джобс»

Е16.20 для которых сумма цифр значения F(n) равна 27.

Алгоритм вычисления функции F(n) задан следующими соотношениями: F(n) = n · n + 5 · n + 4, при n > 30 F(n) = F(n+1) + 3 · F(n+4), при чётных n ≤ 30 F(n) = 2 · F(n+2) + F(n+5), при нечётных n ≤ 30 Определите количество натуральных значений n из отрезка [1; 1000], …

Е16.19 F(0) = 0; F(n) = n + F(n – 3), если n > 0 и при этом n mod 3 = 0;

F(0) = 0; F(n) = n + F(n – 3), если n > 0 и при этом n mod 3 = 0; F(n) = n + F(n – (n mod 3)), если n mod 3 > 0. Чему равно значение функции F(25)? Обозначим через a mod b остаток от деления натурального числа a на натуральное …

Источник

Информатика. ЕГЭ

Задания для подготовки

Задачи разных лет из реальных экзаменов, демо-вариантов, сборников задач и других источников

Задание 16. Информатика. Статград-22-1-1

Алгоритм вычисления значения функции ( F(n) ), где ( n ) — целое неотрицательное число, задан следующими соотношениями:

( F(0) = 0;)
( F(n) = F(n/2), ) если ( n>0) и при этом ( n ) чётно;
( F(n) = 1 + F(n-1), ) если ( n ) нечётно.

Сколько существует таких чисел ( n ), что ( 1 leqslant n leqslant 500 ) и ( F(n) = 8 )?

Показать решение…

Задание 16. Информатика. Статград-22-1-2

( F(0) = 0;)
( F(n) = F(n/2), ) если ( n>0) и при этом ( n ) чётно;
( F(n) = 1 + F(n-1), ) если ( n ) нечётно.

Сколько существует таких чисел ( n ), что ( 1 leqslant n leqslant 900 ) и ( F(n) = 9 )?

Показать решение…

Задание 16. Информатике. Статград-22-2-1

Обозначим остаток от деления натурального числа ( a ) на натуральное число (b) как ( a mod b).

( F(0) = 0;)
( F(n) = F(n-1) + 1, ) если ( n>0) и при этом ( nmod 3 = 2);
( F(n) = F((n — n mod 3) / 3), ) если ( n > 0 ) и при этом ( n mod 3 < 2 ).

Укажите наименьшее возможное ( n ), для которого ( F(n) = 6 ).

Показать решение…

Задание 16. Информатика. Статград-22-2-2

Обозначим остаток от деления натурального числа ( a ) на натуральное число (b) как ( a mod b).

( F(0) = 0;)
( F(n) = F(n-1) + 1, ) если ( n>0) и при этом ( nmod 3 = 2);
( F(n) = F((n — n mod 3) / 3), ) если ( n > 0 ) и при этом ( n mod 3 < 2 ).

Укажите наименьшее возможное ( n ), для которого ( F(n) = 5 ).

Показать решение…

Задание 16. Информатика. Статград-22-3-1

Алгоритм вычисления значения функции (F(n)), где ( n ) — целое неотрицательное число, задан следующими соотношениями:

( F(0) = 0);
( F(n) = F(n-1) + 1), если (n) нечётно;
( F(n) = F(n/2)), если ( n >0) и при этом ( n ) чётно.

Укажите количество таких значений ( n < 1~000~000~000), для которых ( F(n) = 2).

Показать решение…

Источник

: ЕГЭ по информатике

Полезный материал для подготовки к ЕГЭ по информатике — отработка заданий 16 и 18.

Источник: vk.com/itege ma

Задание 16 — Знание позиционных систем счисления (повышенный уровень сложности)

Теория + пример разбора заданий.

→ Скачать материал — EGE-INF-16

Задание 16 из демоверсии 2020 года:

Сколько единиц содержится в двоичной записи значения выражения:

48 + 28 – 8?

Ответ: ___________________________.

Задание 18 — Знание основных понятий и законов математической логики (повышенный уровень сложности)

Разработка содержит нужные формулы, разбор 6 видов задач с ответами, задания для самостоятельного решения.

→ Скачать материал — EGE-INF-18

Задание 18 из демоверсии 2020 года:

Для какого наименьшего целого неотрицательного числа А выражение

(x + 2y < A) / (y > x) / (x > 30)

тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?

Ответ: ___________________________.

Смотрите также:

Источник

Решение по рекуррентной формуле

Что вернет функция. Сколько символов «звездочка». Какова сумма чисел

С каким аргументом?

Не актуально для компьютерного ЕГЭ

Что такое Функция в языке программирования Python ?

Тренировочные задачи 16 задания из ЕГЭ по информатике 2023

Новые тенденции

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Задача 10

Решение

Задача 11

Решение

Рекомендуемые курсы подготовки

Е16.28 Чему равно значение выражения F(2023) / F(2020)?

Е16.27 Укажите наименьшее значение a, для которого F(a, 0) = 1392781243

Е16.26 Чему равно значение функции F(42)?

Е16.25 Укажите количество таких значений n < 1 000 000 000, для которых F(n) = 2.

Е16.24 являющихся результатом вызова функции для значений n в диапазоне [40; 50]

Е16.23 F(n) = F(n – 1) – F(n – 2) + 3n, при n > 1 и n – четно

Е16.22 Сколько существует таких чисел n, что 1 ≤ n ≤ 500 и F(n) = 8

Е16.21 F(n) = 1 при n ≤ 1; F(n) = n · F(n – 1) при чётных n > 1;

Е16.20 для которых сумма цифр значения F(n) равна 27.

Е16.19 F(0) = 0; F(n) = n + F(n – 3), если n > 0 и при этом n mod 3 = 0;

Информатика. ЕГЭ

Задания для подготовки

Задание 16. Информатика. Статград-22-1-1

Задание 16. Информатика. Статград-22-1-2

Задание 16. Информатике. Статград-22-2-1

Задание 16. Информатика. Статград-22-2-2

Задание 16. Информатика. Статград-22-3-1