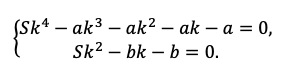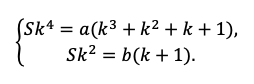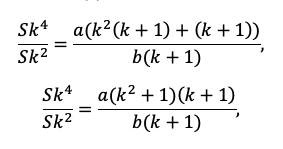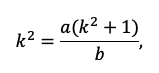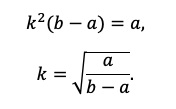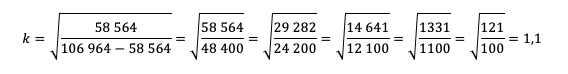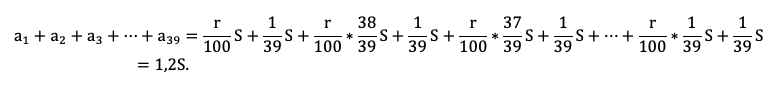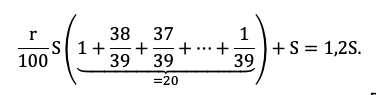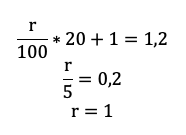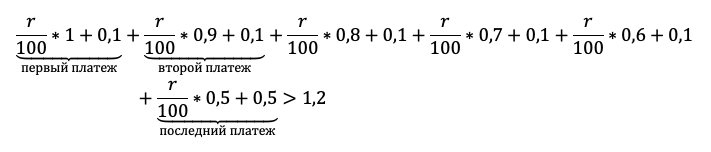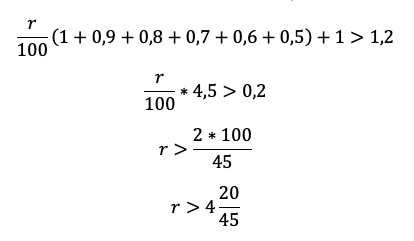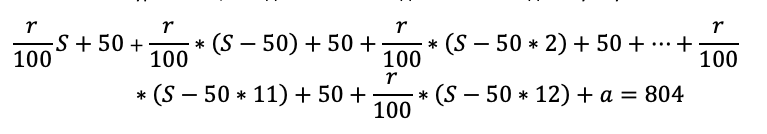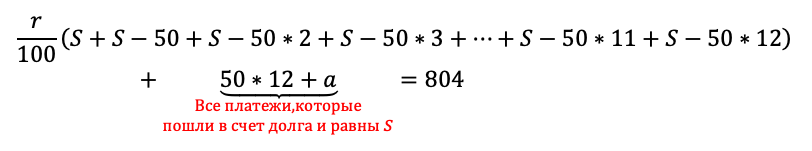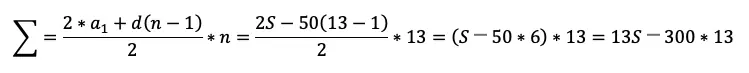В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!
Прототипы для 17-го номера делятся на три большие группы:
- банковские задачи,
- на ценные бумаги,
- задачи на оптимальный выбор.
В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.
Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.
- Как работает процент по кредиту?
- На какую сумму начисляется?
- Из каких частей состоит платеж?
- Как уменьшается долг?
На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!
Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.
С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике
Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:
- Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
- Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
- Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.
Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.
Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.
Тип 1. Равные платежи
Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
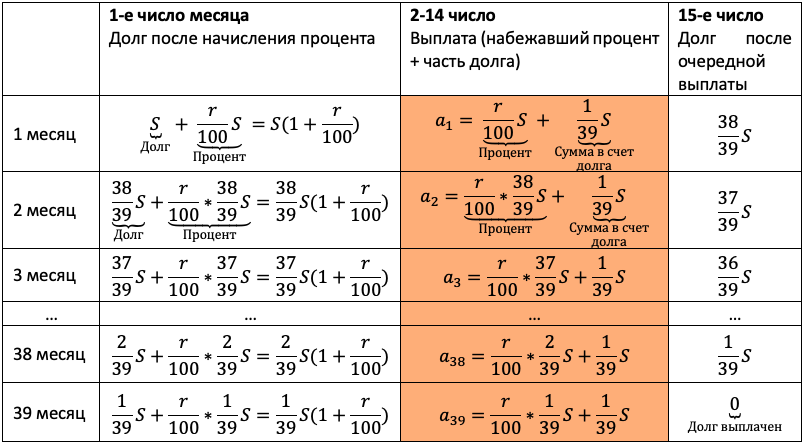
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!
Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.
Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.
Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!
Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.
Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:
Наше решение не зависит от суммы кредита, S сокращается.
По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:
Пожалуй, все, проще уже некуда. Подставляем значения!
Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.
Вспоминаем, что k=1+r/100, а найти нам надо r.
Ответ: 10%.
Не забудьте после решения расставить акценты в задаче:
Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.
Тип 2. Равномерно убывающий долг
В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:
Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:
Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:
Приведем подобные, вынесем общий множитель за скобку:
Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:
Ответ: 1%.
И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.
Тип 3. Долг, убывающий согласно табличке
Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг(в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.
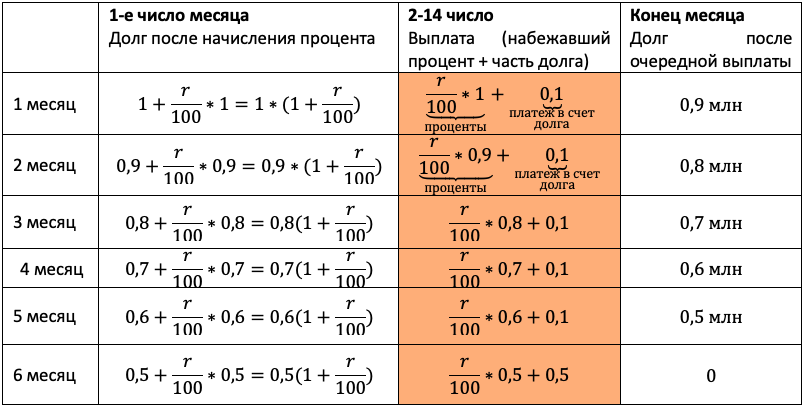
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:
Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.
Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.
«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:
Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.
Приведем подобные и вынесем общие множители за скобку:
Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.
Ответ: 5%.
Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.
Тип 4. Погашение кредита в два этапа.
По сути, это та же прошлая задача, но месяцев больше
В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!
15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.
Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.
Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.
Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:
Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:
Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.
Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:
Посчитаем эту сумму:
Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!
Ответ: 700 тысяч.
Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.
Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике
Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:
- Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
- Повторите типы задач и механизм распределения платежа на проценты и долг;
- Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
- Проговорите, что математическая модель должна точно отражать условие задачи.
Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.
За что дают баллы?
Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.
17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.
Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.
Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:
А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.
Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.
Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.
ГОТОВИМСЯ
К ЕГЭ ПО МАТЕМАТИКЕ ЭКОНОМИЧЕСКИЕ ЗАДАЧИ
I.
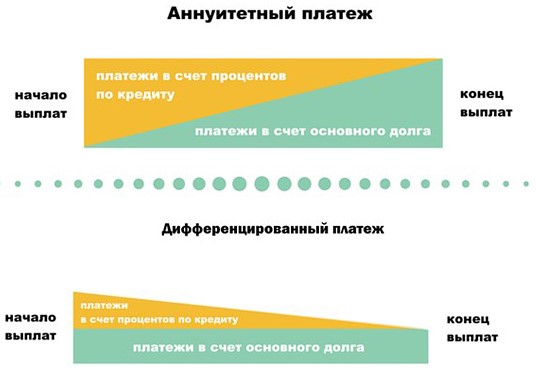
АННУИТЕТНЫЕ ПЛАТЕЖИ
Определение.
Аннуитетный платёж –
вариант ежемесячного (ежегодного) платежа по кредиту, когда размер ежемесячного
(ежегодного) платежа остается постоянным на всем периоде кредитования..
При решении экономических задач на
аннуитетные платежи примем следующие обозначения величин:
S – сумма кредита,
х – ежегодный (ежемесячный)
платёж,
r –
процентная ставка,
p = 1 + .
n – срок кредитования.
Решение задач на аннуитетные платежи удобно оформлять в
виде таблицы. Рассмотрим примеры решения задач.
Задача 1.
В июле 2021 года
планируется взять кредит в банке на некоторую сумму. Условия его возврата
таковы:
§ каждый
январь долг увеличивается на 20% по сравнению с концом предыдущего года;
§ с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет
выплачено банку, если известно, что кредит будет полностью погашен тремя
равными платежами (то есть за три года) и общая сумма выплат после полного
погашения кредита на 96500 рублей больше суммы, взятой в кредит?
Решение.
Пусть S
рублей – сумма кредита,
r = 20 %, тогда p
= 1 + 20/100 = 1,2.
n = 3
года.
х – годовой
платёж,
тогда 3х
– общая сумма платежа за 3 года,
3х – S = 96500.
Заполним таблицу:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
х |
р S – х |
|
2 |
р S – х |
p2 S –p х |
х |
p2 S –p х – х |
|
3 |
p2 S –p х – х |
p3 S –p2 х – pх |
x |
p3 S –p2 х – pх – x |
В
последней ячейке таблицы мы получили уравнение:
p3
S – p2 х – pх – x = 0.
Подставим вместо S выражение 3х – 96500.
p3
∙ (3х –
96500) – p2 х – pх – x = 0.
3p3∙ х – 96500 p3–
p2 х – pх – x = 0.
Теперь выразим из этого уравнения переменную х:
х
∙ (3p3
– p2 – p – 1) = 96500 p3,
х = =
.
3х = .
Подставив p = 1,2,
получим общую сумму выплат за три года:
3х = 324000
рублей.
Ответ:
324000 рублей.
Задача 2.
В июле планируется
взять кредит в банке на сумму 1 000 000 рублей. Условия его возврата таковы:
§ каждый
январь долг увеличивается на 10% по сравнению с концом предыдущего года;
§ с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
§ ежегодные
выплаты не превышают 300 000 рублей.
На какое минимальное
число рублей сумма выплат может превышать размер кредита?
Решение.
S =
1 000 000 рублей – сумма кредита,
r = 10 %, тогда p
= 1 + 10/100 = 1,1.
Для того, чтобы переплаты были минимальными, нужно,
чтобы сумма ежегодных выплат принимала наибольшую возможную сумму. Поэтому
примем х = 300 000 рублей, за исключением последнего
платежа, сумма которого может быть меньше предыдущих платежей.
Заполним таблицу:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
1 |
1,1 ∙ 1 000 |
300 000 |
1 100 000 – 300 000 = = 800 000 |
|
2 |
800 000 |
1,1 ∙ 800 000 = = 880 000 |
300 000 |
880 000 – 300 000 = = 580 000 |
|
3 |
580 000 |
1,1 ∙ 580 000 = = 638 000 |
300 000 |
638 000 – 300 000 = = 338 000 |
|
4 |
338 000 |
1,1 ∙ 338 000 = = 371 800 |
300 000 |
371 800 – 300 000 = = 71800 |
|
5 |
71 800 |
1,1 ∙ 71 800 = = 78 980 |
78 980 |
78 980 – 78 980 = 0. |
Общая сумма выплат равна:
4 ∙
300 000 + 78 980 = 1 278 980 (рублей).
Наименьшее значение переплат за весь срок кредитования:
1 278 980
– 1 000 000 = 278 980 (рублей).
Ответ:
278 980 рублей
Задача 3 (для самостоятельного решения).
В июле планируется
взять кредит в банке на сумму 1 000 000 рублей. Условия его возврата таковы:
§ каждый
январь долг увеличивается на 20% по сравнению с концом предыдущего года;
§ с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
§ ежегодные
выплаты не превышают 400 000 рублей.
На какое минимальное
число рублей сумма выплат может превышать размер кредита?
Ответ:
526 400 рублей.
Задача 4.
31 декабря 2020 года
Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5 % годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (т.е. увеличивает долг на 14,5 %), затем
Дмитрий переводит в банк х рублей. Какой должна быть сумма х,
чтобы Дмитрий выплатил долг двумя равными платежами (т.е. за два года)?
Решение.
S =
4 290 000 рублей,
r = 14,5%, тогда p
= 1,145.
n = 2 года.
х – годовой
платёж,
Заполним таблицу:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
х |
р S – х |
|
2 |
р S – х |
p2 S –p х |
х |
p2 S –p х – |
В
последней ячейке таблицы мы получили уравнение:
p2 S – pх –
x = 0.
Выразим
из этого уравнения х:
p2 S – х ∙ (p + 1) = 0,
p2 S = х ∙ (p + 1),
х = ,
Подставим
числа, данные в условии задачи, вместо букв S и p:
х = = 2 622 050.
Ответ:
2 622 050 рублей.
Задача 5 (для самостоятельного решения).
31 декабря 2020 года Алексей
взял в банке 6 902 000 рублей в кредит под 12,5 % годовых. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет проценты
на оставшуюся сумму долга (т.е. увеличивает долг на 12,5 %), затем Алексей
переводит в банк х рублей. Какой должна быть сумма х,
чтобы Алексей выплатил долг четырьмя равными платежами (т.е. за четыре года)?
Ответ:
2 296 350 рублей.
Задача 6.
31 декабря 2020 года Ярослав
взял в банке некоторую сумму в кредит под 12,5 % годовых. Схема выплаты кредита
следующая: 31 декабря каждого следующего года банк начисляет проценты на
оставшуюся сумму долга (т.е. увеличивает долг на 12,5 %), затем Ярослав
переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав
в банке, если он выплатил долг четырьмя равными платежами (т.е. за четыре
года)?
Решение.
Пусть S рублей
– сумма, взятая в кредит,
r = 12,5%, тогда p
= 1,125.
n = 4 года.
х =
2 132 325 рублей – ежегодные платежи,
Заполним таблицу:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
х |
р S – х |
|
2 |
р S – х |
p2 S –p х |
х |
p2 S –p х – х = |
|
3 |
p2 S –p х – х |
p3 S –p2 х – pх |
x |
p3 S –p2 х – pх – x = 0 |
|
4 |
p3 S –p2 х – pх – x |
p4 S –p3 х – p2 х –px |
х |
p4 S –p3 х – p2 х –px – x = 0 |
В
последней ячейке таблицы мы получили уравнение:
p4 S –p3 х – p2 х –px – x = 0.
Выразим
из этого уравнения S:
p4
S – х ∙ (p3 + p2
+ p + 1) = 0,
p4
S = х ∙ (p3 + p2
+ p + 1),
S = ,
Подставим
числа, данные в условии задачи, вместо букв x и p:
х = = 6 409 000.
Ответ:
6 409 000 рублей.
Задача 7 (для самостоятельного решения).
В июле планируется
взять кредит в банке на некоторую сумму. Условия его возврата таковы:
§ каждый
январь долг увеличивается на 10% по сравнению с концом предыдущего года;
§ с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга,
равную 399 300 рублей.
Сколько рублей было
взято в банке, если известно, что кредит был полностью погашен тремя равными
платежами (т.е. за три года)?
Ответ:
993 000 рублей.
Задача 8 (для самостоятельного решения).
В июле планируется
взять кредит в банке на некоторую сумму. Условия его возврата таковы:
§ каждый
январь долг увеличивается на 20% по сравнению с концом предыдущего года;
§ с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга,
равную 207 360 рублей.
Сколько рублей было
взято в банке, если известно, что кредит был полностью погашен четырьмя равными
платежами (т.е. за четыре года)?
Ответ:
536 800 рублей.
Задача 9.
31 декабря 2020 года
Тимофей взял в банке 7 007 000 рублей в кредит под 20 % годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (т.е. увеличивает долг на 20 %), затем
Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных
платежа. На сколько рублей меньше он бы отдал банку, сели бы смог выплатить
долг за 2 равных платежа?
Решение.
S =
7 007 000 рублей,
r = 20%, тогда p
= 1,2.
n1 = 3 года,
n2 = 2 года.
х рублей –
ежегодные платежи.
1) Заполним
таблицу для n1 = 3:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
х |
р S – х |
|
2 |
р S – х |
p2 S –p х |
х |
p2 S –p х – х = |
|
3 |
p2 S –p х – х |
p3 S –p2 х – pх |
x |
p3 S –p2 х – pх – x |
В последней ячейке таблицы мы получили уравнение:
p3 S – p2 х –px – x = 0.
Выразим из этого уравнения переменную х:
p3 S – х ∙ (p2
+ p + 1) = 0,
p3 S = х ∙ (p2
+ p + 1),
х = ,
3х = =
= 9 979 200.
2) Заполним
таблицу для n2 = 2:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
х |
р S – х |
|
2 |
р S – х |
p2 S –p х |
х |
p2 S –p х – |
В последней ячейке таблицы мы получили уравнение:
p2 S – px – x = 0.
Выразим из этого уравнения переменную х:
p2 S – х ∙ (p + 1) = 0,
p2 S = х ∙ (p + 1),
х = ,
2х = =
= 9 172 800.
3) 9 979 200
– 9 172 800 = 806 400 (рублей).
Ответ:
806 400 рублей.
Задача 10 (для самостоятельного решения).
31 декабря 2020 года Савелий
взял в банке 7 378 000 рублей в кредит под 12,5 % годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (т.е. увеличивает долг на 12,5 %), затем Савелий
переводит в банк платёж. Весь долг Савелий выплатил за 3 равных платежа. На
сколько рублей меньше он бы отдал банку, сели бы смог выплатить долг за 2
равных платежа?
Ответ:
506 250 рублей.
Задача 11.
В июле планируется
взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:
§ каждый
январь долг увеличивается на r % по сравнению
с концом предыдущего года;
§ с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Известно, что кредит
был полностью погашен за два года, причём в первый год было переведено
75 000 рублей, а во второй год – 46 000 рублей. Найдите число r.
Решение.
Заполним таблицу:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
75 000 |
р S – 75 000 |
|
2 |
р S – 75 000 |
p2 S – |
46 000 |
p2 S – 75 000 p – 46 000 = 0 |
В последней ячейке таблицы мы получили уравнение:
p2
S – 75 000 p
– 46 000 = 0.
Поскольку
S
= 100 000, то получаем квадратное уравнение:
100 000
p2
– 75 000 p
– 46 000 = 0,
100
p2
– 75 p – 46 = 0,
Положительный
корень этого уравнения равен:
p
= 1,15,
откуда
r
= 15 %.
Ответ:
15 %.
Задача 12 (для самостоятельного решения).
В июле планируется
взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:
§ каждый
январь долг увеличивается на r % по сравнению
с концом предыдущего года;
§ с февраля
по июнь каждого года необходимо выплатить одним платежом часть долга.
Известно, что кредит
был полностью погашен за два года, причём в первый год было переведено
68 000 рублей, а во второй год – 59 000 рублей. Найдите число r.
Ответ:
18 %.
Задача 13.
Дмитрий взял кредит в
банке на сумму 270 200 рублей. Схема выплаты кредита такова: в конце
каждого года банк увеличивает на 10 % оставшуюся сумму долга, а затем Дмитрий
переводит в банк свой очередной платёж. Известно, что Дмитрий погасил кредит за
три года, причём каждый его следующий платёж был ровно втрое больше
предыдущего. Какую сумму Дмитрий заплатил в первый раз? Ответ дайте в рублях.
Решение.
Заполним таблицу:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
х |
р S – х |
|
2 |
р S – х |
p2 S –p х |
3х |
p2 S –p х – 3х |
|
3 |
p2 S –p х –3 х |
p3 S –p2 х – 3pх |
9x |
p3 S –p2 х – 3pх – 9x = 0 |
В последней ячейке таблицы мы получили уравнение:
p3
S –p2
х – 3pх
– 9x = 0.
Выразим из этого уравнения переменную х:
p3
S – х ∙ (p2 +
3p + 9) = 0,
p3
S = х ∙ (p2 +
3p + 9),
х = ,
х = = 26 620.
Ответ:
26 620 рублей.
Задача 14 (для самостоятельного решения).
Георгий взял кредит в
банке на сумму 270 200 рублей. Схема выплаты кредита такова: в конце
каждого года банк увеличивает на 10 % оставшуюся сумму долга, а затем Георгий
переводит в банк свой очередной платёж. Известно, что Георгий погасил кредит за
три года, причём каждый его следующий платёж был ровно вдвое меньше
предыдущего. Какую сумму Георгий заплатил в третий раз? Ответ дайте в рублях.
Ответ:
133 100 рублей.
Задача 15.
В июле планируется
взять кредит в банке на некоторую сумму. Условия его возврата таковы:
§ каждый
январь долг увеличивается на r % по сравнению
с концом предыдущего года;
§ с
февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Известно, что если
каждый год выплачивать по 292 820 рублей, то кредит будет полностью
погашен за четыре года, а если ежегодно выплачивать по 534 820 рублей, то
кредит будет полностью погашен за два года. Найдите число r.
Решение.
Пусть S рублей –
сумма кредита,
n1 = 4 года, при этом
х = 292 820 рублей – ежегодные платежи,
n2 = 2 года,
при
этом у = 534 820 рублей – ежегодные платежи.
1) Заполним
таблицу для n1 = 4:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
х |
р S – х |
|
2 |
р S – х |
p2 S –p х |
х |
p2 S –p х – х = |
|
3 |
p2 S –p х – х |
p3 S –p2 х – pх |
x |
p3 S –p2 х – pх – x |
|
4 |
p3 S –p2 х – pх – x |
p4 S –p3 х – p2х – px |
x |
p4 S –p3 х – p2х – px – x = 0 |
2) Заполним
таблицу для n2 = 2:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
р S |
у |
р S – у |
|
2 |
р S – у |
p2 S –p у |
у |
p2 S –p у – у |
В последних ячейках таблиц мы получили два уравнения:
p4 S –p3 х – p2х – px – x = 0 и p2 S –p у – у = 0.
Умножим второе уравнение на p2, а затем
вычтем из него первое уравнение:
(p3 у – p3 х) + (p2 у – p2 х) – (pх + х) =
0,
p3 (у – х) +
p2 (у – х) –
х (p + 1) = 0,
p2 (у – х) (p + 1) = х
(p + 1).
Поскольку p – число
положительное, то число (p + 1) – также
является положительным числом. Поэтому обе части уравнения можно разделить на
(p + 1).
p2 (у – х) =
х,
p2 = ,
p2 = = 1,21.
p = 1,1.
Значит,
r
= 10 %.
Ответ:
10 %.
Задача 16 (для самостоятельного решения).
В июле планируется
взять кредит в банке на некоторую сумму. Условия его возврата таковы:
§ каждый
январь долг увеличивается на r % по сравнению
с концом предыдущего года;
§ с февраля
по июнь каждого года необходимо выплатить одним платежом часть долга.
Известно, что если
каждый год выплачивать по 216 000 рублей, то кредит будет полностью
погашен за четыре года, а если ежегодно выплачивать по 366 000 рублей, то
кредит будет полностью погашен за два года. Найдите число r.
Ответ:
20 %.
Задача 17.
Планируется выдать
льготный кредит на целое число миллионов рублей на пять лет. В середине каждого
года действия кредита долг заёмщика возрастает на 10 % по сравнению с началом
года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по
кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го
годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью.
Найдите наибольший размер кредита (в млн. рублей), при котором общая сумма
выплат заёмщика будет меньше 8 млн. рублей.
Решение.
r = 10%, тогда p
= 1,1.
Заполним
таблицу:
|
Год |
Долг до начисления процентов (млн. руб.) |
Долг после начисления процентов (млн. руб.) |
Выплаты (млн. руб.) |
Долг после выплаты (млн. руб.) |
|
1 |
S |
р S |
р S — S |
S |
|
2 |
S |
р S |
р S — S |
S |
|
3 |
S |
р S |
р S — S |
S |
|
4 |
S |
р S |
x |
р S – x |
|
5 |
р S – x |
p2х – px |
x |
p2х – px – x = 0 |
1) Рассмотрим
уравнение в последней ячейке таблицы:
p2х
– px – x = 0.
Выразим
из этого уравнения х:
p2х
– х (p +1) = 0,
p2х
= х (p +1),
х
= =
=
.
2)
Общая сумма выплат равна:
3
∙
(р S – S) + 2х
= 3 ∙ (р
S – S) + 2S ∙ = S ∙
(3p – 3 + 2 ∙ ) = … = S ∙
.
По
условию, эта сумма меньше 8 млн. рублей, тогда
S
∙ < 8,
S
< ≈ 5,508…
При
этом S – целое
число миллионов рублей. Значит, S = 5 (млн. рублей).
Ответ:
5 млн. рублей.
Задача 18 (для самостоятельного решения).
Планируется выдать
льготный кредит на целое число миллионов рублей на пять лет. В середине каждого
года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом
года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по
кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го
годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью.
Найдите наименьший размер кредита (в млн. рублей), при котором общая сумма
выплат заёмщика превысит 10 млн. рублей.
Ответ:
6 млн. рублей.
Задача 19.
Гражданин Гусев взял
кредит в банке, рассчитывая погасить долг равными ежегодными платежами, каждый
из которых (кроме, возможно, последнего) составляет половину суммы S,
взятой в кредит. Схема выплаты кредита следующая: в конце каждого года банк
увеличивает на 25 % оставшуюся сумму долга, а затем гражданин Гусев переводит в
банк очередной платёж. После двух лет выплат банк снизил процентную ставку до
20 % годовых, и гражданин Гусев внёс третий платёж. Четвёртым платежом долг был
полностью погашен. Сколько процентов от первоначальной суммы S
составлял четвёртый платёж по кредиту гражданина Гусева?
Решение.
r1 = 25%, тогда p1 = 1,25.
r2 = 20%, тогда p2 = 1,2.
Заполним
таблицу:
|
Год |
Долг до начисления процентов (руб.) |
Долг после начисления процентов (руб.) |
Выплаты (руб.) |
Долг после выплаты (руб.) |
|
1 |
S |
1,25 S |
0,5 S |
1,25 S – 0,5 S = 0,75 S |
|
2 |
0,75 S |
1,25 ∙ 0,75 ∙ S = = |
0,5 S |
0,9375 ∙ S – 0,5 ∙ S = = 0,4375 ∙ S |
|
3 |
0,4375 ∙ S |
1,2 ∙ 0,4375 ∙ S = 0,525 ∙ S |
0,5 S |
0,525 S — 0,5 S = = |
|
4 |
0,025 S |
1,2 ∙ 0,025 ∙ S = = 0,03 ∙ S |
0,03 ∙ S |
0,03 ∙ S – |
= 0,03 = 3 %.
Ответ:
3 %.
Всего: 258 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
15‐го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 10% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 8 млн.
Савелий хочет взять в кредит 1,4 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Савелий взять кредит, чтобы ежегодные выплаты были не более 330 тысяч рублей?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
Источник: А. Ларин. Тренировочный вариант № 322 (часть C).
1 января 2015 года Тарас Павлович взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая — 1 числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Тарас Павлович переводит в банк платёж. На какое минимальное количество месяцев Тарас Павлович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С).
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С)., Задания 17 (С4) ЕГЭ 2015
В июле планируется взять кредит на сумму 2 320 500 рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?
Наш добрый герой В. взял в банке кредит в размере 20 192 020 рублей по очень знакомой схеме:
— в конце очередного месяца пользования кредитом банк начисляет проценты за пользование заемными средствами по специальной ставке данного варианта 2,96%;
— в этот же день клиент выплачивает часть долга и сумму начисленных процентов;
— после выплаты долг должен быть на одну и ту же величину меньше долга на конец предыдущего месяца.
Но дальше все пошло не по сценарию. Наш герой решил каждый месяц, начиная с первого, платить банку сверх прочего дополнительную сумму на погашение долга, при этом долг по‐прежнему ежемесячно уменьшался на одну и ту же величину (бóльшую, чем планировалось изначально) до полного погашения. В итоге срок кредита сократился на 52%. На какое наименьшее число процентов могла уменьшиться при этом переплата банку?
Источник: А. Ларин. Тренировочный вариант № 296.
Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк от всей суммы, которую он должен банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму, на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
Источник: А. Ларин: Тренировочный вариант № 85.
31 декабря 2014 года Никита взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Никита переводит очередной транш. Если он будет платить каждый год по 2 073 600 рублей, то выплатит долг за 4 года. Если по 3 513 600 рублей, то за 2 года. Под какой процент Никита взял деньги в банке?
15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015 по математике. Основная волна 04.06.2015. Вариант 1 (Часть С)., Задания 17 (С4) ЕГЭ 2015
В начале года фирма «Жилстройсервис» выбирает банк для получения кредита среди нескольких банков, кредитующих под разные проценты. Полученным кредитом фирма фирма планирует распорядится следующим образом: 75% кредита направить на строительство коттеджей, а остальные 25% на оказание риэлтерских услуг населению. Первый проект может принести прибыль в размере от 36% до 44% годовых, а второй — от 20% до 24% годовых. В конце года фирма должна вернуть кредит банку с процентами и при этом рассчитывает на чистую прибыль от указанных видов деятельности от не менее 13%, но и не более 21% годовых от всего полученного кредита. Какими должны быть наименьшая и наибольшая процентные ставки кредитования выбираемых банков, чтобы фирма гарантированно обеспечила себе указанный выше уровень прибыли.
Источник: А. Ларин: Тренировочный вариант № 157.
В январе 2020 года Борис взял кредит в банке на сумму 4 200 000 рублей. По договору с банком Борис должен был погасить долг двумя равными платежами в феврале 2021 года и феврале 2022 года, при условии, что в январе 2021 года и январе 2022 года сумма оставшегося долга увеличивается на 10%. В феврале 2021 года Борис сделал первую выплату в соответствии с договором. После этого ему удалось договориться с банком о рефинансировании кредита и уменьшить процент, на который сумма долга вырастет в январе 2022 года, до 7%. Какую сумму сэкономит Борис на рефинансировании своего кредита?
Источник: Пробный вариант ЕГЭ по математике 18.03.21 Санкт-Петербург. Вариант №1
В январе 2020 года Василий взял кредит в банке на сумму 3 300 000 рублей. По договору с банком Василий должен был погасить долг двумя равными платежами в феврале 2021 года и феврале 2022 года, при условии, что в январе 2021 года и январе 2022 года сумма оставшегося долга увеличивается на 20%. В феврале 2021 года Василий сделал первую выплату в соответствии с договором. После этого ему удалось договориться с банком о рефинансировании кредита и уменьшить процент, на который сумма долга вырастет в январе 2022 года, до 16%. Какую сумму сэкономит Василий на рефинансировании своего кредита?
Источник: А. Ларин. Тренировочный вариант № 348., Пробный вариант ЕГЭ по математике 18.03.21 Санкт-Петербург. Вариант №2
Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?
В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в млн рублей) |
S | 0,7S | 0,4S | 0 |
Найдите наибольшее значение S, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
Источник: Задания 17 (С5) ЕГЭ 2016
15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
− 1-го числа k-ого месяца долг возрастёт на 1% по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число k-того месяца необходимо выплатить часть долга;
− 15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит?
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 402 (C часть).
В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 825 тыс рублей?
Источник: РЕШУ ЕГЭ
В июле 2018 года планируется взять кредит в банке на шесть лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 2% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите S, если общая сумма выплат после полного погашения кредита составила 327 тысяч рублей.
Всего: 258 1–20 | 21–40 | 41–60 | 61–80 …
Всего: 23 1–20 | 21–23
Добавить в вариант
Задания Д22 C3 № 5722
Опираясь на обществоведческие знания, объясните смысл понятия «кредит». Какие причины, препятствующие получению кредита в банке, названы в тексте? Какие дополнительные источники финансирования указаны в тексте (укажите два источника)?
Показать
1
Какую характерную черту (проблему) малого бизнеса называют авторы? Какие два объяснения существования этой проблемы они указывают?
2
Назовите три меры, которые авторы текста указывают как необходимые для оказания поддержки малому бизнесу. На основании знаний обществоведческого курса приведите две меры по поддержке малого бизнеса, не указанные в тексте.
3
Опираясь на знания обществоведческого курса, назовите три объяснения роли малого бизнеса в современной экономике. Проиллюстрируйте одно из объяснений примером.
4
Задания Д22 C3 № 6545
Какие причины, препятствующие получению кредита в банке, названы в тексте? Какие дополнительные источники финансирования указаны в тексте (укажите два источника)?
Используя обществоведческие знания, объясните смысл понятия «кредит».
(В объяснении смысла / определении понятия должно быть указано не менее двух существенных признаков. Объяснение/определение может быть дано в одном или нескольких распространённых предложениях.)
Показать
1
Какую характерную черту (проблему) малого бизнеса называют авторы? Какие два объяснения существования этой проблемы они указывают?
2
Назовите три меры, которые авторы текста указывают как необходимые для оказания поддержки малому бизнесу. На основании знаний обществоведческого курса приведите две меры по поддержке малого бизнеса, не указанные в тексте.
3
Опираясь на знания обществоведческого курса, назовите три объяснения роли малого бизнеса в современной экономике. Проиллюстрируйте одно из объяснений примером.
4
Задания Д22 C3 № 5722
Опираясь на обществоведческие знания, объясните смысл понятия «кредит». Какие причины, препятствующие получению кредита в банке, названы в тексте? Какие дополнительные источники финансирования указаны в тексте (укажите два источника)?
Анастасии 15 лет. Найдите в приведённом ниже списке действия, которые она вправе осуществлять самостоятельно в соответствии с Гражданским кодексом РФ. Запишите цифры, под которыми они указаны. Цифры укажите в порядке возрастания.
1) распоряжаться авторским гонораром за опубликованную статью собственного сочинения
2) заключать мелкие бытовые сделки
3) взять кредит под залог недвижимости
4) управлять подаренным ей отцом автомобилем
5) устроиться на работу в летнее кафе
6) внести за работу в летнем трудовом лагере зарплату на счёт в банке
В тексте упомянуто использование денег в качестве посредника в обмене товаров. Как в экономической науке называют эту функцию денег? Назовите и проиллюстрируйте примером любые две другие функции денег. (Сначала называйте функцию, а затем — пример, иначе ответ не будет засчитан как верный.)
Показать
1
Какие четыре эпохи, связанные с изменением формы денег, отмечены в тексте? Как автор отвечает на вопрос о том, чем определяется стоимость денег?
Источник: ЕГЭ 2015 по обществознанию. (часть С, вариант 711)
2
В тексте описан безналичный денежный оборот, который является приоритетным в современной экономике. Используя текст, обществоведческие знания и факты общественной жизни, укажите любые три преимущества использования безналичных денег.
Источник: ЕГЭ 2015 по обществознанию. (часть С, вариант 711)
3
К какому виду товаров отнесены в тексте бумажные деньги? Приведите пояснение автора. Опираясь на обществоведческие знания, назовите какой-либо недостаток бумажных денег в масштабе макроэкономики.
Источник: ЕГЭ 2015 по обществознанию. (часть С, вариант 711)
Источник: ЕГЭ 2015 по обществознанию. (часть С, вариант 711)
В какой из приведённых ситуаций речь идёт об ипотечном кредите?
1) Гражданка М. взяла в банке кредит на покупку норковой шубы.
2) Гражданин Н. оформил кредит под залог недвижимости.
3) Торговая сеть получила в коммерческом банке кредит на закупку товаров.
4) Государственное предприятие получило кредит на закупку оборудования.
Предметная область: Экономика. Финансовые институты, банковская система
В какой из приведённых ситуаций речь идёт об ипотечном кредите?
1) Гражданка М. взяла в банке кредит на покупку норковой шубы.
2) Гражданин Н. оформил кредит на приобретение квартиры.
3) Государственное предприятие получило кредит на закупку оборудования.
4) Торговая сеть получила в коммерческом банке кредит на закупку товаров.
Предметная область: Экономика. Финансовые институты, банковская система
Источник: ЕГЭ по обществознанию 10.06.2013. Основная волна. Центр. Вариант 2.
В каком из приведённых примеров речь идёт о потребительском кредите?
1) Супруги Ивановы взяли в банке кредит на оплату летнего отдыха.
2) Супруги Петровы взяли кредит на покупку загородного дома под залог будущего строения.
3) В связи с дефицитом государственного бюджета правительство прибегло к заимствованиям на внешнем рынке.
4) Индивидуальный предприниматель Лисицын взял кредит для открытия новых торговых точек.
Предметная область: Экономика. Финансовые институты, банковская система
Верны ли следующие суждения о налогах?
А. Налоги являются добровольными выплатами граждан и фирм в пользу государства.
Б. Большинство налогов имеют невозвратный характер.
1) верно только А
2) верно только Б
3) верны оба суждения
4) оба суждения неверны
Предметная область: Экономика. Налоги
Источник: Демонстрационная версия ЕГЭ—2013 по обществознанию.
Верны ли следующие суждения о потребительском кредите?
А. Снижение банками процента по потребительским кредитам способствует повышению спроса на электронику и бытовую технику.
Б. В расширении системы потребительского кредитования, прежде всего, заинтересованы крупные торговые сети.
1) верно только А
2) верно только Б
3) верны оба суждения
4) оба суждения неверны
Предметная область: Экономика. Финансовые институты, банковская система
Вид потребительского кредита —
1) предоставление государственного кредита оборонному предприятию
2) кредитование банками крупных торговых сетей
3) выделение банком кредитной линии для предприятия
4) выделение средств гражданину на приобретение автомобиля
Предметная область: Экономика. Финансовые институты, банковская система
Источник: ЕГЭ по обществознанию 10.06.2013. Основная волна. Центр. Вариант 6.
Верны ли следующие суждения об ипотечном кредите?
А. Повышение ставки ипотечного кредитования приводит к снижению объема продаж на рынке недвижимости.
Б. Льготные ставки ипотечного кредитования обычно предоставляются молодым семьям и военнослужащим.
1) верно только А
2) верно только Б
3) верны оба суждения
4) оба суждения неверны
Предметная область: Экономика. Финансовые институты, банковская система
Задания Д6 № 968
Основным источником дохода коммерческого банка является
1) сдача в аренду недвижимости
2) оплата населением коммунальных услуг
3) налоговые отчисления
4) плата за предоставляемый кредит
Предметная область: Экономика. Финансовые институты, банковская система
Выберите из перечня функции, присущие только Центральному банку, и запишите цифры, под которыми они указаны.
1) проведение расчетов и платежей в хозяйстве
2) посредничество в кредите между домохозяйствами и владельцами свободных денежных средств
3) аккумуляция и мобилизация денежного капитала
4) управление золотовалютными запасами страны
5) поддержание устойчивости курса рубля
6) осуществление денежной эмиссии
Выберите верные суждения об издержках в краткосрочном периоде и запишите цифры, под которыми они указаны.
1) К постоянным издержкам в краткосрочном периоде относят процент банку за кредит, плату за охрану помещения.
2) Переменные издержки в краткосрочном периоде непосредственно зависят от объёма производимой продукции.
3) Себестоимостью продукции называют сумму постоянных издержек.
4) К переменным издержкам в краткосрочном периоде относят страховые взносы на бизнес.
5) Издержки — это денежная оценка затрат всех ресурсов, задействованных в производстве.
Источник: ЕГЭ — 2019. Досрочная волна
Задания Д6 № 488
К функциям центрального банка в отличие от коммерческих банков относится
1) проведение расчетов и платежей в хозяйстве
2) посредничество в кредите
3) аккумуляция и мобилизация денежного капитала
4) управление золотовалютными запасами страны
Предметная область: Экономика. Финансовые институты, банковская система
Задания Д6 № 524
Какие затраты можно отнести к переменным затратам?
1) затраты на аппарат управления
2) затраты на аренду здания
3) выплата банку процентов за кредит
4) сдельная заработная плата рабочих
Предметная область: Экономика. Постоянные и переменные затраты
Какое из приведённых ниже понятий объединяет три других?
1) обмен валюты
2) депозит
3) коммерческий банк
4) потребительский кредит
Предметная область: Экономика. Финансовые институты, банковская система
Источник: ЕГЭ по обществознанию 10.06.2013. Основная волна. Дальний Восток. Вариант 4.
Задания Д26 C6 № 9858
Проиллюстрируйте тремя примерами влияние финансовой стабильности в стране на успешность экономической деятельности индивидов и фирм (предприятий).
Какие три функции предпринимательства приводят авторы? Перечислите их с опорой на текст. Проиллюстрируйте каждую из них конкретным примером.
Показать
1
Какое определение предпринимательства дают авторы? При каком типе экономики хозяйственная деятельность принимает характер бизнеса?
2
Авторы подчёркивают, что функции предпринимателя в качестве субъекта рыночной экономики состоят в нахождении и формировании спроса на продукты и услуги, продажи товаров с максимальной прибылью. Приведите три примера предпринимательских решений, приводящих к максимизации прибыли.
3
Задания Д22 C3 № 3280
Авторы сравнивают деятельность предпринимателя с деятельностью менеджера. Опираясь на авторский текст и знания обществоведческого курса, проведите сравнение деятельности предпринимателя и деятельности менеджера, указав две общие и две различные позиции. Опираясь на обществоведческие знания, объясните смысл понятия «менеджмент».
В условиях высокой инфляции правительство страны Н. пошло на сокращение расходных статей бюджета, повысило учетную ставку банковского процента. Антиинфляционные меры государству необходимо предпринимать, так как инфляция
1) приводит к обесценению национальной валюты
2) способствует возрастанию бюджетного профицита
3) делает невозможным проведение девальвации
4) содействует возрастанию внешнеторгового сальдо
Предметная область: Экономика. Виды, причины и последствия инфляции
Всего: 23 1–20 | 21–23

Экспресс-тренинг
Подготовка к ЕГЭ-2023 по профильной математике в кратчайшие сроки!
До экзамена осталось совсем немного времени! Закрепите свои знания! Понятная теория и эффективные тренажеры с объяснением! Ваш ребенок успеет подготовиться к экзамену!

Кредиты. Дифференцированная и аннуитетная схемы платежей
Кредиты. Дифференцированная и аннуитетная схемы платежей
Здравствуйте!
Текстовые задачи с экономическим содержанием, темой которых являются банковские кредиты, сравнительно недавно появились в содержании экзамена по математике. Тем не менее, в реальных вариантах КИМ ЕГЭ они встречаются чаще других.
Для решения таких задач вам необходимо познакомиться с двумя математическими моделями, лежащими в основе наиболее распространенных схем выплат по банковским кредитам — дифференцированной и аннуитетной. Эти модели представлены на слайдах.
Рекомендуем вам перед тем, как изучать теоретический материал по теме «Банковские кредиты», повторить определения арифметической и геометрической прогрессий и формулы суммы n последовательных членов каждой из прогрессий – они вам понадобятся.
Арифметическая прогрессия
Последовательность чисел an такая, что
где d — разность арифметической прогрессии.
Сумма Sn=a1+a2+…+an n первых членов арифметической прогрессии вычисляется по формуле:
Sn=a1+an2⋅n=2a1+d(n−1)2⋅n.
Геометрическая прогрессия
Последовательность чисел bn такая, что
где q — знаменатель геометрической прогрессии.
Сумма Sn=b1+b2+…+bn n первых членов геометрической прогрессии вычисляется по формуле:
Формула бесконечной суммы при q∈(−1,1):
S=b11−q
На слайдах также представлены примеры разобранных задач. Обратите внимание на два различных подхода, которые чаще всего используются при решении задач.
Первый подход состоит в использовании готовых формул, полученных при исследовании математической модели.
Второй — в пошаговом вычислении размеров каждого из очередных платежей при выплате кредита и размеров оставшихся задолженностей.
Следите за обновлениями на сайте и подписывайтесь на наш канал в Ютьюбе и группу Вконтакте!
|
VI районная научно-исследовательская конференция обучающихся обучающихся общеобразовательных организаций Октябрьского муниципального района |
|
Финансовая математика в задачах ЕГЭ. Решение задач на кредиты |
|
Исследовательская работа по математике |
Автор работы: Кутепова Анна, ученица 10 класса
Руководитель: Моторина Ольга Робертовна, преподаватель математики «МОУ ОСОШ №1»
с. Октябрьское, 2022 г.
СОДЕРЖАНИЕ
Введение 2
Банковские кредиты и математика 4
Схемы решения экономических задач на кредиты 8
- Задача на определение величины выплаты/дифференцированные платежи 8
- Задача на определение ежегодной (ежемесячной) выплаты /аннуитетные платежи 10
- Определение величины процента ставки кредита /долг, убывающий согласно таблице в условие задачи 12
- Задача на определение суммы кредита/аннуитетные платежи 14
- Нахождение количества лет (месяцев) выплаты кредита /дифференцированные платежи 16
Заключение 20
Список информационных источников 22
Введение
В современном, информационно-развитом мире, встречаются люди, которые не умеют правильно распоряжаться своими финансами и контролировать свои доходы и расходы. В этих случаях необходима финансовая грамотность, ведь благодаря данным знаниям мы сможем не только управлять деньгами, правильно инвестировать свои средства, но также будем в безопасности во время сложных жизненных обстоятельств и не потеряем свои доходы. Наша жизнь сегодня настоятельно требует, чтобы каждый человек имел развитое экономическое мышление и был готов к жизни в условиях рыночных отношений. Финансовая грамотность необходима при решении экономических задач в ЕГЭ профильного уровня по математике. Данные задания проверяют практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
Учащиеся при подходе к итоговой аттестации в 9-х и 11-х классах сталкиваются с проблемой решения задач на проценты, а они есть и в ОГЭ и в ЕГЭ. На данный момент я являюсь ученицей 10 класса. В следующем году мне предстоит сдать ЕГЭ. Я уже ознакомлена с заданиями данного экзамена и знаю, что среди них есть задачи экономической направленности повышенного уровня сложности, которые в курсе старшей общеобразовательной школы не рассматриваются. Для меня стал актуален вопрос о том, каким образом подойти к решению таких задач. Кроме того я выбрала эту тему еще и потому, что в 7 классе мной был выполнен проект «Сам себе финансист: проценты и скидки».В этой исследовательской работе я хочу углубить и расширить свои знания в области финансовой математики. На выбор темы повлияло и то, что в будущем я планирую поступить на экономический факультет ВУЗа.
Тема моей работы: Финансовая математика в экономических задачах ЕГЭ. Решение задач на кредиты.
Гипотеза: Не смотря многообразие типов экономических задач профильного экзамена по математике, их можно классифицировать и вывести единую схему решения.
Цель работы: Изучить основные типы экономических задач на кредиты ЕГЭ по профильной математике и научиться их решать.
Задачи:
- Изучить теоретические аспекты решения экономических задач;
- Познакомиться с прототипами экономических задач, представленных в открытом банке заданий ЕГЭ;
- Создать обучающую презентацию по различным типам задач на кредиты.
Объект исследования: Экономические задачи на кредиты №15 в ЕГЭ.
Предмет исследования: Схемы и алгоритмы решения задач на кредиты.
Методы исследования:
- Изучение и анализ литературы и интернет-источников по данной теме.
- Математическое моделирование
- Классификация
- Анализ
Банковские кредиты и математика
Финансовая математика – раздел прикладной математики, имеющий дело с математическими задачами, связанными с экономическими расчётами.
В единый государственный экзамен по математике (ЕГЭ) профильного уровня экономические задачи были включены в 2015 г. Это задания высокого уровня сложности с практическим содержанием, проверяющее навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
Экономические задачи предполагают:
- Умение работать с процентами, частями и долями.
- Владение понятием «Математическая модель».
- Умение строить математическую модель задачи.
- Владение вычислительными навыками.
- Умение применять математические методы для решения содержательных задач из различных областей науки и практики.
- Умение интерпретировать полученный результат, учитывать реальные ограничения.
Экономические задачи под номером 15 в ЕГЭ по профильной математике делятся на три основные группы:
- Задачи на кредиты.
- Задачи на вклады и ценные бумаги.
- Задачи на оптимальный выбор.
Данную работу я посвятила разбору примеров задач первого типа.
Банковский кредит – денежная сумма, предоставляемая банком на определённый срок и на определённых условиях; определённая технология удовлетворения заявленной заёмщикомфинансовой потребности.
Потребность в кредите возникает при оплате значительныхпо стоимости объектов потребления без предварительного накопления достаточных ресурсов, необходимости обеспечения своевременных платежей по товарам, приобретенным в рассрочку, оплате эксклюзивных покупок случайного характера, кассовых разрывах при замене старых объектов потребления на новые, покрытии потерь при наступлении рисков, оплате значительных расходов и т. д.
Понимание и структурирование данных условия задачи – важный шаг на пути правильного ее решения. Для упорядочивания данных условия задачи я использовала таблицы, хотя это и не единственный способ решения 15-го задания, можно использовать и другие методы: последовательности, прикладные методы. Метод решения текстовых задач с помощью таблиц универсальный, знаком каждому школьнику. С помощью таблицможно выработать единый алгоритм решения большинства банковских задач.
В решениях, представленных в работе задач,мною будут использоваться следующие обозначения:
выплатить кредит
Кредитные операции играют основную роль в деятельности банков. Экономические задачи, конечно, несколько упрощают реальную ситуацию, в жизни банковские операции по кредитам значительно сложнее, тем не менее, именно они дают начальные представления о действиях в мире финансов. При решении экономических задач не обойтись без вычисления процентов, при этом используются «простые» и «сложные проценты». Задачи простые проценты изучаются в школьном курсе математике и включены в тестовую часть заданий профильного экзамена. Вычислять же «сложные проценты» приходится в тех случаях, когда в задаче идет речь о величине, подверженной поэтапному изменению. При этом каждый раз ее изменениесоставляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе.Существуют разные формулы, по которым происходит вычисление сложных процентов. При выдаче кредитов на срок n проценты могут, например, начисляться по формуле:

Проанализировав условия задач на кредиты профильного ЕГЭ, я обнаружила, что классифицировать задачи можно разными способами:
- По типу ежемесячных (ежегодных) платежей.
- Разделить на простые (используется одна формула) или сложные (применяются несколько формул, используются системы, неравенства).
- По неизвестной величине, которую требуется найти в условии (процентной ставке, величине выплаты, суммы кредита и др.)
По типу платежей задачи ЕГЭ задачами самыми распространенными являются задачи на фиксированный, аннуитетный и дифференцированный платежи.
Фиксированный платеж – это платеж, величина которого четко определена в задаче.
Аннуитетный платеж– это платеж, которыйустанавливается в равной сумме через равные промежутки времени, то есть остаётся постоянным на всём периоде кредитования. Ежемесячный платёж, при аннуитетной схеме погашения кредита состоит из двух частей. Первая часть платежа идёт на погашение процентов за пользование кредитом, авторая часть идёт на погашение суммы долга. Главная особенность таких платежей в том, что вначале ежемесячный платеж практически полностью состоит из суммы процентов, тогда как основной долг заемщика не уменьшается. Постепенно это соотношение выравнивается: если первое времязаемщик гасит в основном проценты, то потом основные средства идут в счет погашения задолженности.
Дифференцированный платеж – это способ ежемесячного платежа по кредиту, при котором размер ежемесячной выплаты по погашению кредита постепенно уменьшается к концу периода кредитования. Ежемесячный платёж, как и при аннуитетной схеме погашения кредита, складывается тоже из двух составляющих. Но в дифференцированной схеме первая часть называется основным платежом, размер которого не изменяется на всём сроке кредитования. Этот платёж идет на погашение основного долга по кредиту. Вторая часть платежа непостоянная, она уменьшается к концу срока кредитования. Данная часть платежа при дифференцированной схеме идет на погашение процентов по кредиту. При дифференцированной схеме погашения кредита, ежемесячный платеж рассчитывается как сумма основного платежа и проценты, начисляемые на оставшийся размер долга. Естественно, что оставшийся размер долга уменьшается к концу срока кредитования, отсюда и получается уменьшение размера ежемесячной выплаты.
Схемы решения экономических задач на кредиты
В практической части своей работы я представляюпримеры решений нескольких задач на кредиты. Это задачи на нахождение: процентной ставки, суммы долга, суммы переплаты, ежегодных (ежемесячных, еженедельных т.д.) выплат, определения срока кредитования.
-
Задача на определение величины выплаты
/дифференцированные платежи
15-го января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку в первые 12 месяцев?
Решение:
Фраза «15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца» — это означает, что каждый месяц мы должны выплачивать часть начального долга 

|
№ мес. |
Начальная сумма, млн. руб. |
Сумма начисленных процентов, млн. руб. |
Выплата, млн. руб. |
Конечная сумма, млн. руб. |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
24 |
… |
… |
… |
0 |
Первая сумма 



Ответ: 1 866 000 рублей
Примеры задач банка ЕГЭ на определение величины выплаты:
1. В июле планируется взять кредит в банке на сумму 28 млн. рублей на некоторыйсрок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июльпредыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн. рублей?
2. В июле планируется взять кредит в банке на сумму 9 млн. рублей на некоторый срок(целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июльпредыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн. рублей?
-
Задача на определение ежегодной (ежемесячной) выплаты/аннуитетные платежи
В июле планируется взять кредит на сумму 6409000 рублей. Условия его возврата таковы:
— Каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года.
— С февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен двумя равными платежами.
Решение:
|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
1 год |
|
|
x |
|
|
2 год |
|
|
x |
|
Ответ: 3817125 руб.
Примеры задач банка ЕГЭна определение ежегодной (ежемесячной) выплаты:
- В июле планируется взять кредит на сумму 8052000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?
-
Определение величины процента ставки кредита /долг, убывающий согласно таблице в условие задачи
15-го января планируется взять кредит в банке на шесть месяцев в размере 
– 1-го числа каждого месяца долг увеличивается на

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:
|
Дата |
|
|
|
|
|
|
|
|
Долг (млн. руб.) |
|
|
|
|
|
|
|
Найдите наибольшее значение
Решение:
|
|
Начальная сумма, млн. руб. |
Сумма долга после начисления процентов,млн. руб. |
Выплата, млн. руб. |
Конечная сумма,млн. руб. |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что общая сумма выплат меньше 1,2 млн. руб., составим и решим неравенство:
Ответ: 7%
Примеры задач банка ЕГЭна определение величины процента ставки кредита:
- 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн. руб.) |
1 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн. рублей.
- В июле планируется взять кредит в банке на сумму 4,5 млн. рублей на срок 9 лет. Условия его возврата таковы:
– каждый январь долг возрастает на r % по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн. рублей, а наименьший – не менее 0,6 млн рублей.
-
Задача на определение суммы кредита
/аннуитетные платежи
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 156 060 рублей больше суммы, взятой в кредит?
Решение:
|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим величину ежегодной выплаты, решив уравнение относительно x:
Известно, что сумма трех выплат на 156060 руб. больше суммы кредита:
Ответ: 239 400руб.
Примеры задач банка ЕГЭна определение суммы кредита:
- В июле 2020 года планируется взять кредит в банке на сумму 419 375 рублей. Условия его возврата таковы:
– каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года)?
- В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 40 980 рублей больше суммы, взятой в кредит?
-
Нахождение количества лет (месяцев) выплаты кредита/дифференцированные платежи
В июле планируется взять кредит в банке на сумму 5 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн. рублей?
Решение:
«В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года» — это означает, что каждый год мы должны выплачивать часть начального долга 

|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
Сложим все платежи, чтобы определить общую сумму выплат по кредиту:
Сложив все слагаемые 


Выражение в скобках – арифметическая прогрессия.Найдём её сумму по формуле:
Подставим полученную сумму в выражение для нахождения общей выплаты:
Вместо буквенных символов подставим известные нам значения величин и найдем n:
Ответ: 4 года
Примеры задач банка ЕГЭна нахождение срокавыплаты кредита:
- В июле планируется взять кредит в банке на сумму 14 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 24,5 млн. рублей?
- В июле планируется взять кредит в банке на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн. рублей?
Заключение
Подводя итоги своей работы, целью которой было познакомиться с типами задач с экономическим содержанием и научиться решать задачи на кредиты, я считаю, что мне удалось достичь этой цели, хотя есть еще к чему стремиться, так как предстоит изучить и задачи других видов.
Проанализировав условия и решения банковских задач, я пришла к заключению, что в большинстве случаев схему решения можно использовать таблицу такого вида:
В ходе своего исследования, разбирая примеры задач и решая задачи самостоятельно, я заметила, что:
- Практически все экономические задачи из банка ЕГЭ можно разделить на несколько основных видов
- Решение экономических задач можно выполнять по одному алгоритму, а именно:
- Занести данные условия задачи в таблицу.
- Составить уравнение или неравенство (систему уравнений/неравенств).
- В ходе решения появится формула, с помощью которой будет найден ответ на вопрос задачи.
Моя гипотеза о том, что, несмотря на сложность и многообразие типов экономических задач их можно классифицировать и вывести единую схему решения, подтвердилась. Я убедилась в ее истинности на примере изучения задач на кредиты.Работу по изучению экономических задач буду продолжать и дальше, так как впереди экзамен по профильной математике и, кроме того, считаю, что решение таких задач позволило мне лучше разобраться в базовых понятиях банковских процессов, что будет полезно мне в моей будущей профессии.
Думаю, что эта работа будет полезна ученикам 10 и 11 класса, учителям для подготовки к ЕГЭ профильного уровня по математике. В ходе работы мною была создана презентация с примерами задач на кредиты и их подробными решениями. Эту презентацию можно предложить ребятам для самостоятельной подготовки, кроме решенных примеров она содержит задачи из банка ЕГЭ по математике.
Список информационных источников
- Лукашин Ю.П. Финансовая математика / Московский международный институт эконометрики, информатики, финансов и права. — М., 2003. https://kpsu.ru/upload/medialibrary/606/606fd86fd3cd2272b6f1f3f1b0e4f96c.pdf
- https://ru.wikipedia.org
- https://ege.sdamgia.ru/
- http://fipi.ru/
- Курс лекций по финансовой математике https://lfirmal.com/predmet-finansovaya-matematika/
- Материалы для подготовки к ЕГЭ по математике https://www.time4math.ru/ege
Кредит – это ссуда в денежной или товарной форме, предоставляемая кредитором заёмщику.
Функции кредита
- регулирующая – кредит способствует непрерывному процессу производства, способен формировать сбалансированную экономику.
- перераспределительная – удовлетворение временных потребностей юридических и физических лиц за счёт временно свободных денежных средств других лиц
- стимулирующая – кредит стимулирует заёмщика к трудовой деятельности, которая поможет ему вернуть кредит.
Принципы кредитования
- возвратность – кредит будет возвращён кредитору
- срочность– кредит выдаётся на определённый срок
- платность – кредит возвращается с процентами
- гарантированность – государство гарантирует защиту прав обеих сторон
- обеспеченность – защищает кредитора от невозврата кредитов.
Виды обеспечения ссуд:
- Материальные ценности, оформленные под залог
- Гарантии посредников — поручителей
- Страховые полисы
Заёмщик – организация или физическое лицо, берущее кредит в банке.
Кредитор – кто предоставляет кредит.
Кредитное соглашение – договор между кредитором и заёмщиком, составленный в письменной форме, в котором оговариваются условия предоставления и возвращения кредита.
Дифференцированность кредита – это различный подход банков к заёмщикам от их реальных возможностей погасить ссуду ( первоклассные и сомнительные)
Платёжеспособность – способность заёмщика погасить кредит в срок с процентами.
Виды кредита
По способу кредитования
- коммерческий ( натуральный)- предприниматели кредитуют друг у друга при покупке и продаже товаров .Он осуществляется в товарной форме, выдаётся вексель – долговое обязательство заёмщика уплатить сумму с процентами в определённый срок.
- банковский ( денежный) – банки выдают денежные ссуды .
По целевому назначению
- потребительский – для приобретения потребительских товаров с отсрочкой платежа
- ипотечный – долгосрочная ссуда на приобретение жилья под залог имущества
- ростовщический – выдаётся под очень высокие проценты ( до 300%)
По кредиторам и вкладчикам
- государственный — выдаётся государством или местными органами власти
- международный – кредитные отношения между государствами, межгосударственными банками и корпорациями
По срокам выплаты
- краткосрочный (до года)
- среднесрочный ( от года до 5 лет)
- долгосрочный (свыше 5 лет)
Новые формы кредита
- Лизинг (англ. leasing от англ. to lease — сдать в аренду) – долгосрочная аренда движимого и недвижимого имущества (кредит этот всегда долгосрочный)
- Факторинг (англ.factoring от англ. factor — посредник, торговый агент)– посредническая операция банка по взысканию денежных средств с должников своего клиента и управление его долговыми требованиями.
- Форфейтинг (англ.forfaiting от фр. à forfait — целиком, общей суммой) – это приобретение финансовым агентом ( форфейтором) обязательства заёмщика перед кредитором.
Тенденции развития системы кредитования в РФ
- наблюдается отток иностранного капитала из российской экономики в связи с напряжённой международной обстановкой.
- замораживание счетов российских вкладчиков в иностранных банках увеличивает степень доверия к банкам России.
- увеличение спроса на краткосрочные кредиты и кредиты по ипотеке.
- продолжение государственной поддержки банков, предоставление кредитов на укрепление банковской системы.
- Увеличение объёмов кредитования из федерального бюджета.
- создание благоприятных условий для кредитования среднего и малого бизнеса (снижение процентной ставки, увеличение суммы кредита и срока его выплаты)
- улучшение требований к заёмщику
- снижение ставок по кредитам в крупных российских банках, увеличение доверия к ним со стороны граждан.
- предоставление кредитов по ипотеке на длительный срок (от 10 до 25 лет)
Таким образом, устойчивость кредитной системы – одно их условий эффективного развития страны в целом.
Страхование
Страхование – финансовое обеспечение от возможного ущерба.
Функции страхования
- рисковая – возмещение убытков
- предупредительная – проведение мер по предупреждению, страхового случая, минимизации ущерба при этом
- контрольная – строго целевое назначение средств из страхового фонда.
- сберегательная – проведение особого вида страхования — накопительного, когда организация предлагает страховую защиту и одновременно выполняет роль сберегательного учреждения.
Страховая деятельность – сфера деятельности по страхованию физических и юридических лиц.
Цель страховой деятельности : обеспечение защиты имущественных интересов физических и юридических лиц РФ при наступлении страхового случая.
Задачи организации страхования
- проведение единой, целенаправленной политики по организации страхования
- установление принципов страхования
- формирование механизма страхования
Принципы страхования
- свободный выбор страховщиком — страхователя и вида страхования
- наличие страхового интереса – то есть наличие собственности, опасности пр.
- страхование риска – то есть страхуется событие, произошедшее случайно, а не спровоцировано страховщиком.
- наивысшее доверие сторон
- выплата страхового возмещения, максимальная добросовестность со стороны страхователя
Виды страхования
По объекту страхования
—личное (жизни, от несчастных случаев, медицинское)
—имущественное (транспорт, грузы, финансовые риски, имущество)
—ответственности (заемщика за непогашение кредита, владельцев автотранспортных средств)
По форме вовлечения в систему страховых отношений
- обязательное – осуществляется в силу закона, страховая защита связана с интересами общества.
- добровольное – добровольное заключение договора между страховщиком и страхователем.
Обязательное страхование:
- медицинское
- государственное личное страхование госслужащих
- личное страхование за счет работодателя граждан, занимающихся опасной для жизни деятельностью
- страхование жизни и здоровья членов экипажей самолетов;
- страхование пассажиров
- страхование ответственности при причинении вреда при строительстве
- противопожарное страхование
По страхователям
- государственное – страховщиком выступает государство
- негосударственное — страховщиком выступают негосударственные юридические лица, предусмотренные законом.
Страховой полис — документ, удостоверяющий процесс страхования юридического или физического лица.
Страховой случай – это событие, предусмотренное договором страхования или законом, с наступлением которого страховщик обязан выплатить страхователю или третьим лицам сумму, указанную в договоре.
Материал подготовила: Мельникова Вера Александровна
.
17. Сложные задачи прикладного характера
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи про банковский кредит: другие схемы платежей
Задание
1
#1211
Уровень задания: Легче ЕГЭ
Валентина Яковлевна решила взять кредит в банке на (565,000) рублей под (25 %) годовых сроком на три года. Каждый год Валентина Яковлевна вносит платеж по кредиту после начисления процентов. Причем платеж в первый год в два раза меньше платежа во второй год и в три раза меньше платежа в третий год. Сколько рублей составит переплата Валентины Яковлевны по кредиту?
Составим таблицу (суммы долга запишем в тыс. рублей): [begin{array}{|l|c|c|}
hline text{Год} & text{Сумма долга до начисления }% & text{Сумма долга после начисления }% text{ и платежа}
hline 1 & 565 & 1,25cdot 565 — x
hline 2 & 1,25cdot 565-x & 1,25(1,25cdot 565-x)-2x
hline 3 & 1,25(1,25cdot 565-x)-2x & 1,25(1,25(1,25cdot 565-x)-2x)-3x
hline
end{array}]
где (x, 2x, 3x) тыс. рублей – платежи по кредиту.
Тогда имеем: (1,25(1,25(1,25cdot 565-x)-2x)-3x=0 Rightarrow
x=dfrac{1,25^3cdot 565}{1,25^2+2cdot 1,25+3}=156,25) тыс.рублей.
Таким образом, переплата равна ((x+2x+3x)-565 =372,5) тыс.руб. или (372,500) рублей.
Ответ:
(372,500) рублей.
Задание
2
#4043
Уровень задания: Равен ЕГЭ
В конце сентября 2016 года планируется взять кредит в банке на год. Условия его возврата таковы:
— в течение первого месяца каждого квартала долг увеличивается на (6%) по сравнению с долгом на конец предыдущего квартала;
— в течение второго месяца каждого квартала необходимо выплатить одним платежом часть долга;
— долг на начало каждого квартала должен составлять часть кредита в соответствии со следующей таблицей: [begin{array}{|l|c|c|c|c|}
hline text{Квартал} & 1 & 2 & 3 & 4
hline text{Долг (в процентах)} & 100 & 75 & 40 & 0
hline end{array}] На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
(Задача от подписчиков)
Пусть кредит составил (A) рублей. Тогда:
– в первый месяц первого квартала до начисления процентов долг равен (A), после начисления процентов долг составил (1,06A);
– в первый месяц второго квартала до начисления процентов долг равен (0,75A), после начисления процентов долг составил (1,06cdot 0,75A);
– в первый месяц третьего квартала до начисления процентов долг равен (0,4A), после начисления процентов долг составил (1,06cdot 0,4A);
– в первый месяц четвертого квартала долг равен (0).
Таким образом, в первом квартале был сделан платеж в размере (B_1=1,06A-0,75A); во втором квартале платеж (B_2=1,06cdot
0,75A-0,4A); в третьем (B_3=1,06cdot 0,4A-0). Следовательно, общая сумма выплат составила: [V=B_1+B_2+B_3=(1,06A-0,75A)+(1,06cdot 0,75A-0,4A)+(1,06cdot 0,4A-0)] Необходимо найти, на сколько процентов общая сумма выплат больше кредита, или, что то же самое, сколько процентов составила переплата (общая сумма выплат минус сумма кредита) от кредита: [dfrac{V-A}{A}cdot 100%] Найдем [begin{aligned}
&dfrac{V-A}{A}=dfrac{A(1,06-0,75+1,06cdot 0,75-0,4+1,06cdot
0,4-1)}A=[2ex]
&=1,06(1+0,75+0,4)-(1+0,75+0,4)=(1+0,75+0,4)(1,06-1)=1,25cdot
0,06=0,129 end{aligned}] Следовательно, ответ: [0,129cdot 100%=12,9%.]
Ответ:
12,9(%)
Задание
3
#3919
Уровень задания: Равен ЕГЭ
В июле 2017 года планируется взять кредит в банке на сумму (250,000) рулей. Условия его возврата таковы:
— каждый январь долг возрастает на (r%) по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.
Найдите число (r), если известно, что кредит был полностью погашен за два года, причем в первый год было переведено (150,000) рублей, во второй год – (180,000) рублей.
Если (r) – количество начисляемых процентов, то (y=(100+r):100=1+0,01r) – коэффициент, на который умножается сумма долга после начисления процентов. Составим таблицу (ведя все вычисления в тыс. рублей): [begin{array}{|l|c|c|c|}
hline text {Год}&text{Долг до начисления }% & text{Долг после
начисления }
%&text{Выплата}
hline 1 & 250 & 250y & 150
hline 2 & 250y-150 & (250y-150)y & 180
hline end{array}] Так как после второй выплаты долг банку должен быть равен нулю, то получаем уравнение [(250y-150)y-180=0quadLeftrightarrowquad
25y^2-15y-18=0quadRightarrowquad y=dfrac65] (отрицательный корень мы не рассматриваем, так как (r>0), следовательно, и (y>0))
Таким образом, [1+0,01r=dfrac65quadRightarrowquad r=20]
Ответ:
20
Задание
4
#1212
Уровень задания: Равен ЕГЭ
В январе банк предоставляет кредиты на сумму (A) рублей на (6) лет на следующих условиях:
– в ноябре каждого года, начиная с первого (когда был взят кредит) сумма долга возрастает на некоторое целое число (y) процентов;
– в декабре каждого года, начиная с первого, клиент должен внести платеж в счет погашения части текущего долга;
– платежи подбираются так, чтобы в январе каждого года сумма долга менялась соответственно таблице:
[begin{array}{|c|c|c|c|c|c|c|}
hline 1 text{ год} & 2text{ год} & 3text{ год} & 4text{ год} & 5text{ год} & 6text{ год} & 7text{ год}
hline A & 0,8A & 0,65A & 0,4A & 0,35A & 0,2A & 0
hline
end{array}]
Какой наибольший процент годовых должен выставить банк, чтобы переплата клиента не превысила половину от суммы взятого кредита?
Обозначим за (t=dfrac{100+y}{100}).
В ноябре (1)-ого года сумма долга составит (tcdot A) рублей. Т.к. после выплаты долг должен уменьшиться до (0,8A), то выплата составит: (tcdot A-0,8A).
Выпишем выплаты по кредиту в течение всех шести лет: [begin{array}{|c|c|c|c|c|c|}
hline 1 text{ год} & 2text{ год} & 3text{ год} & 4text{ год} & 5text{ год} & 6text{ год}
hline tA-0,8A & tcdot0,8A-0,65A & tcdot0,65A-0,4A &tcdot0,4A-0,35A & tcdot0,35A-0,2A & tcdot0,2A
hline
end{array}]
Тогда переплата составит: ((tcdot
A-0,8A+tcdot0,8A-0,65A+tcdot0,65A-0,4A+tcdot0,4A-0,35A+tcdot0,35A-0,2A+)
(+tcdot0,2A-0)-A=3,4A(t-1)=dfrac{3,4Ay}{100})
Т.к. переплата не должна превышать половины суммы кредита, то:
(dfrac{3,4Ay}{100} leq dfrac{A}{2} Rightarrow y leq
14dfrac{12}{17} Rightarrow) наибольшее целое (y=14%).
Ответ:
(14%).
Задание
5
#1213
Уровень задания: Равен ЕГЭ
Студент Миша не смог поступить на бюджет в Университет и поэтому был вынужден взять образовательный кредит сроком на (10) лет. Условия пользования образовательным кредитом таковы:
– в течение первых пяти лет (пока Миша учится в Университете) гасить кредит не нужно, но за пользование кредитом банк начисляет проценты;
– каждый год в течение обучения банк перечисляет на счет Университета сумму в размере (327,680) рублей, равную стоимости годового обучения в Университете;
– один раз в конце года в течение первых пяти лет (после зачисления денег на счет Университета) банк начисляет (12,5 %) на сумму, которую на этот момент клиент должен банку;
– с (6)-ого по (10)-ый года клиент обязан устроиться на работу и выплачивать кредит равными платежами раз в полгода.
Чему равен этот платеж?
Составим таблицу для первых пяти лет, обозначив за (A=327680) рублей: [begin{array}{|l|c|c|}
hline text{Год} & text{Сумма долга до начисления }% & text{Сумма долга после начисления }%
hline 1& A & 1,125A
hline 2& 1,125A+A & 1,125(1,125A+A)
hline 3& 1,125(1,125A+A)+A & 1,125(1,125(1,125A+A)+A)
hline 4& 1,125(1,125(1,125A+A)+ & 1,125(1,125(1,125(1,125A+A)+
&+A)+A&+A)+A)
hline 5& 1,125(1,125(1,125(1,125A+A)+ & 1,125(1,125(1,125(1,125(1,125A+A)+
&+A)+A)+A&+A)+A)+A)
hline
end{array}]
Таким образом, по окончании Университета Миша будет должен банку
(1,125(1,125(1,125(1,125(1,125A+A)+A)+A)+A)=)
(=1,125A(1,125^4+1,125^3+1,125^2+1,125+1)=B)
Т.к. в последующие годы проценты банк не начисляет, а платежи Миша вносит каждые полгода, то каждый платеж равен (dfrac{B}{10}). Для удобства вычисления заметим, что (1,125=dfrac{9}{8} Rightarrow) (используя формулу суммы геометрической прогрессии)
(dfrac{B}{10}=dfrac{9cdot left(dfrac{9^5}{8^5}-1right)}{8cdot
dfrac{1}{8}}cdot Acdot dfrac{1}{10}=236,529) рублей.
Ответ:
(236,529) рублей.
Задание
6
#2067
Уровень задания: Равен ЕГЭ
На последние два года обучения в университете студент взял образовательный кредит. Условия пользования кредитом таковы:
– в сентябре каждого года в течение обучения студента банк перечисляет на счет университета сумму, равную стоимости годового обучения в университете;
– один раз в ноябре каждого года пользования кредитом банк начисляет (20 %) на текущий долг клиента;
– каждый год в течение обучения в декабре студент вносит некоторую сумму (одну и ту же) в счет погашения кредита;
– после окончания обучения в течение еще двух лет банк продолжает в ноябре каждого года начислять (20%) на оставшуюся сумму долга, но теперь студент обязан выплачивать кредит равными платежами, в пять раз превышающими платеж во время обучения.
Сколько рублей составит переплата по такому кредиту, если год обучения в университете стоит (402,500) рублей?
Обозначим за (A=402,500) рублей.
Заметим, что в итоге кредит был выдан на 4 года, причем в течение первых двух лет студент учится, а в течение последних двух – уже нет. Пусть (x) – это платеж банку в первые 2 года, тогда (5x) – платеж банку в последние два года. Если банк начисляет (20%) на текущий долг, то этот долг увеличивается в (frac{120}{100}=1,2) раза.
Заметим также, что в сентябре второго года долг банку увеличится на стоимость годового обучения, то есть на (A).
Составим таблицу:
[begin{array}{|l|c|c|c|c|}
hline text{Год} & text{Сумма долга до } & text{Сумма долга после}& text{Сумма долга} & text{Платеж}
& text{начисления }% & text{начисления }% & text{после платежа} &
hline 1& A & 1,2A & 1,2A-x & x
hline 2& 1,2A-x+A & 1,2((1,2+1)A-x) & 1,2((1,2+1)A-x)-x=B & x
hline 3& B & 1,2B & 1,2B-5x & 5x
hline 4& 1,2B-5x & 1,2(1,2B-5x) & 1,2(1,2B-5x)-5x & 5x
hline
end{array}]
Т.к. в конце 4-ого года кредит закрыт, то долг банку будет равен нулю, то есть
[1,2(1,2B-5x)-5x=0 quad Leftrightarrow quad 1,2^2B-5xcdot 2,2=0]
Т.к. (B=1,2((1,2+1)A-x)-x=1,2(1,2+1)A-x(1,2+1)=1,2cdot 2,2A-2,2x), то:
[1,2^3cdot 2,2A-1,2^2cdot 2,2x-5cdot 2,2x=0 quad Leftrightarrow quad 1,2^3A-x(1,2^2+5)=0 quad Leftrightarrow quad
x=dfrac{1,2^3A}{1,2^2+5}]
Заметим, что за все годы пользования кредитом студент выплатил банку (x+x+5x+5x=12x) рублей, а взял в кредит — две стоимости годового обучения в университете, то есть взял (2A). Значит, переплата равна [R=12x-2A=2(6x-A)=2Acdot left(dfrac{6cdot 1,2^3}{1,2^2+5}-1right)=491,000]
Ответ:
(491000)
Задание
7
#2313
Уровень задания: Равен ЕГЭ
В банке в честь Дня труда действует следующее предложение по выдаче кредита:
— кредит выдается сроком на 5 лет под (10%) годовых;
— в первый, третий и пятый годы после начисления процентов на текущую сумму долга клиент обязан внести некоторый платеж, одинаковый во все эти три года;
— во второй и четвертый годы после начисления процентов на текущую сумму долга клиент выплачивает только проценты по кредиту.
Какое максимальное целое число тысяч рублей в кредит может позволить себе взять трудоголик Лера, если она знает, что переплата по кредиту не должна превысить (100) тысяч рублей?
Пусть Лера взяла в кредит (A) тысяч рублей, а платеж, который она вносила в первый, третий и пятый годы, равен (x) тысяч рублей. Составим таблицу:
[small{begin{array}{|l|c|c|c|c|}
hline text{Год}&text{Сумма долга до} &text{Сумма долга после} &text{Сумма платежа}&text{Сумма долга}
&text{начисления }% &text{начисления }% & &text{после платежа}
hline 1& A & 1,1A & x & 1,1A-x
hline 2& 1,1A-x & 1,1A-x+0,1(1,1A-x) & 0,1(1,1A-x) & 1,1A-x
hline 3& 1,1A-x & 1,1(1,1A-x) & x & 1,1(1,1A-x)-x
hline 4& 1,1(1,1A-x)-x & 1,1(1,1A-x)-x+ &
0,1(1,1(1,1A- & 1,1(1,1A-x)-x
&&+0,1(1,1(1,1A-x)-x)&-x)-x)&
hline 5& 1,1(1,1A-x)-x & 1,1(1,1(1,1A-x)-x) & x &
1,1(1,1(1,1A-x)-x)-x
hline
end{array}}]
Заметим, что в те годы, когда платеж составлял (x), мы записывали сумму долга после начисления процентов как (1,1cdot)долг; а в те годы, где платеж равнялся начисленным процентам — как долг(+0,1cdot)долг. Это было сделано лишь для удобства.
Т.к. в последний, пятый, год кредит был погашен, то [1,1(1,1(1,1A-x)-x)-x=0 quad Rightarrow quad 1,1^3A-x(1,1^2+1,1+1)=0]
По условию задачи переплата не должна превысить (100) тысяч рублей. Вычислим переплату (для этого нужно из общей суммы всех выплат вычесть сумму кредита):
[3x+0,1(1,1A-x)+0,1(1,1(1,1A-x)-x)-A=2,69x-0,769A]
Таким образом, получаем следующее неравенство:
[2,69x-0,769Aleqslant 100]
Подставим в это неравенство выраженное из уравнения (x=dfrac{1,1^3cdot A}{1,1^2+1,1+1}):
[2,69cdot dfrac{1,1^3cdot A}{1,1^2+1,1+1}-0,769Aleqslant 100 quad Leftrightarrow quad
Aleqslant dfrac{66200}{207}=319,8…]
Т.к. (A) – целое число тысяч рублей, то наибольшее подходящее (A=319) тысяч рублей.
Ответ: 319

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задание № 27620
Совершеннолетние граждане имеют возможность брать различные кредиты. Чаще всего граждане оформляют потребительские и ипотечные кредиты.
Приведите по одному примеру, иллюстрирующему оформление каждого вида кредита.
Ответ запишите на бланке ответов № 2, указав номер задания.
Показать ответ
Комментарий:
Правильный ответ может содержать следующие элементы:
1) потребительский: гражданка М. оформила потребительский кредит под 5% годовых на покупку стиральной машинки.
2) ипотечный: гражданка М. оформила ипотечный кредит на двухкомнатную квартиру с ежемесячным платежом — 15000 рублей.
Могут быт приведены иные, близких по смыслу, примеры
Ответ:
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
Основные формулы в задачах на вклады и кредиты
12 марта 2015
Сегодня мы немного отвлечемся от стандартных логарифмов, интегралов, тригонометрии и т.д., а вместе этого рассмотрим более жизненную задачу из ЕГЭ по математике, которая имеет прямое отношение к нашей отсталой российской сырьевой экономике. А если быть точным, мы рассмотрим задачу про вклады, проценты и кредиты. Потому что именно задачи с процентами с недавних пор добавлены во вторую часть единого государственного экзамена по математике. Сразу оговорюсь, что за решение этой задачи согласно спецификациям ЕГЭ предлагается сразу три первичных балла, т. е. экзаменаторы считают эту задачу одной из самых сложных.
Вместе с тем, для решения любой из указанных задач из ЕГЭ по математике необходимо знать всего лишь две формулы, каждая из которых вполне доступна любому школьному выпускнику, однако по непонятным мне причинам эти формулы начисто игнорируются как школьными учителями, так и составителями всевозможных задач для подготовки к ЕГЭ. Поэтому сегодня я не просто расскажу вам, что это за формулы и как их применять, а выведу каждую из этих формул буквально у вас на глазах, взяв за основу задачи из открытого банка ЕГЭ по математике.
Поэтому урок получился довольно объемный, довольно содержательный, поэтому устраивайтесь поудобнее, и мы начинаем.
Вкладываем деньги в банк
Прежде всего, хотелось бы сделать небольшое лирическое отступление, связанное с финансами, банками, кредитами и вкладами, на основании которых мы и получим те формулы, которые будем использовать для решения данной задачи. Итак, давайте немного отвлечемся от экзаменов, от предстоящих школьных проблем, и посмотрим в будущее.
Допустим, вы выросли и собираетесь покупать квартиру. Допустим, вы собираетесь покупать не какую-то плохую квартиру на окраине, а хорошую качественную квартиру за 20 миллионов рублей. При этом также предположим, что вы устроились на более-менее нормальную работу и зарабатываете по 300 тысяч рублей в месяц. В этом случае за год вы сможете отложить примерно три миллиона рублей. Разумеется, зарабатывая по 300 тысяч рублей в месяц, за год у вас получится чуть большая сумма — 3600000 — но эти 600000 пусть будут потрачены на еду, на одежду и на прочие ежедневные бытовые радости. Итого вводные данные таковы: необходимо заработать двадцать миллионов рублей, у нас же в распоряжении имеется лишь три миллиона рублей в год. Возникает естественный вопрос: сколько лет нам необходимо откладывать по три миллиона, чтобы получить эти самые двадцать миллионов. Считается это элементарно:
[frac{20}{3}=6,….to 7]
Однако как мы уже с вами отмечали, вы зарабатываете 300 тысяч рублей в месяц, это значит, что вы умные люди и не будете откладывать деньги «под подушку», а отнесете их в банк. И, следовательно, ежегодно на те вклады, которые вы принесете в банк, будут начисляться проценты. Допустим, вы выберете надежный, но при этом более-менее прибыльный банк, и поэтому ваши вклады ежегодно будут расти на 15% годовых. Другими словами можно сказать, что сумма на ваших счетах ежегодно будет увеличиваться в 1,15 раза. Напомню формулу:
[Ktext{%} to 1+frac{K}{100}]
Давайте посчитаем, сколько денег будет на ваших счетах после каждого года:
В первый год, когда вы только начнете откладывать деньги, никакие проценты не накопятся, т. е. в конце года вы отложите три миллиона рублей:
[3m]
В конце второго года на те три миллиона рублей, которые остались с первого года, уже будут начислены проценты, т.е. нам нужно умножить на 1,15. Однако в течение второго года вы также доложили еще три миллиона рублей. Разумеется, на эти три миллиона еще не были начислены проценты, потому что к концу второго года эти три миллиона только появились на счету:
[3mcdot 1,15+3m]
Итак, третий год. В конце третьего года на эту сумму будут начислены проценты, т. е. необходимо всю эту сумму умножить на 1,15. И опять же, в течение всего года вы усердно работали и еще отложили три миллиона рублей:
[left( 3mcdot 1,15+3m right)cdot 1,15+3m]
Давайте рассчитаем еще четвертый год. Опять же, вся сумма, которая оказалась у нас к концу третьего года, умножается на 1,15, т.е. на всю сумму будут начислены проценты. В том числе, будут начислены проценты на проценты. И к этой сумме добавляется еще три миллиона, потому что в течение четвертого года вы также работали и также откладывали деньги:
[left( left( 3mcdot 1,15+3m right)cdot 1,15+3m right)cdot 1,15+3m]
А теперь давайте раскроем скобки и посмотрим, какая у нас будет сумма к концу четвертого года откладывания денег:
[begin{align}& left( left( 3mcdot 1,15+3m right)cdot 1,15+3m right)cdot 1,15+3m= \& =left( 3mcdot {{1,15}^{2}}+3mcdot 1,15+3m right)cdot 1,15+3m= \& =3mcdot {{1,15}^{3}}+3mcdot {{1,15}^{2}}+3mcdot 1,15+3m= \& =3mleft( {{1,15}^{3}}+{{1,15}^{2}}+1,15+1 right)= \& =3mleft( 1+1,15+{{1,15}^{2}}+{{1,15}^{3}} right) \end{align}]
Как видим, в скобках у нас стоят элементы геометрической прогрессии, т. е. у нас стоит сумма элементов геометрической прогрессии.
Напомню, что если геометрическая прогрессия задана элементом ${{b}_{1}}$, а также знаменателем $q$, то сумма элементов будет считаться по следующей формуле:
[{{S}_{n}}={{b}_{1}}cdot frac{{{q}^{n}}-1}{q-1}]
Эту формулу обязательно нужно знать и четко применять.
Обратите внимание: формула n-го элемента звучит следующим образом:
[{{b}_{n}}={{b}_{1}}cdot {{q}^{n-1}}]
Из-за этой степени многие ученики путаются. В сумме у нас стоит просто nдля суммы n-элементов, а сам n-й элемент имеет степень $n-1$. Другими словами, если мы сейчас попытаемся посчитать сумму геометрической прогрессии, то нужно учитывать следующее:
[begin{align}& {{b}_{1}}=1 \& q=1,15 \end{align}]
Теперь мы можем посчитать сумму:
[{{S}_{4}}=1cdot frac{{{1,15}^{4}}-1}{1,15-1}]
Посчитаем числитель отдельно:
[{{1,15}^{4}}={{left( {{1,15}^{2}} right)}^{2}}={{left( 1,3225 right)}^{2}}=1,74900625approx 1,75]
Итого, возвращаясь к сумме геометрической прогрессии, мы получим:
[{{S}_{4}}=1cdot frac{1,75-1}{0,15}=frac{0,75}{0,15}=frac{75}{15}=5]
В итоге мы получаем, что за четыре года накоплений наша исходная сумма увеличится не в четыре раза, как если бы мы не клали деньги в банк, а в пять раз, т. е. пятнадцать миллионов. Давайте запишем это отдельно:
4 года → 5 раз
Забегая вперед, скажу, что если бы мы копили не четыре года, а пять лет, то в итоге наша сумма накоплений увеличилась бы в 6,7 раза:
5 лет → 6,7 раз
Другими словами, к концу пятого года мы бы получили на счету следующую сумму:
[6,7cdot 3=20,1]
Т. е. к концу пятого года накоплений с учетом процентов по вкладу мы бы уже получили свыше двадцати миллионов рублей. Таким образом, общий счет накоплений за счет банковских процентов снизился бы с почти семи лет до пяти лет, т. е. почти на два года.
Таким образом, даже, несмотря на то, что банк начисляет достаточно низкий процент на наши вклады (15%), уже через пять лет эти самые 15% дают прибавку, существенно превышающую наш ежегодный заработок. При этом основной мультипликационный эффект приходится на последние годы и даже, скорее, на последний год накоплений.
К чему я это все писал? Разумеется, не к тому, чтобы агитировать вас нести деньги в банк. Потому что если вы действительно хотите приумножить свои сбережения, то вкладывать их нужно не в банк, а в реально действующий бизнес, где эти самые проценты, т. е. рентабельность в условиях российской экономики редко опускается ниже 30%, т. е. вдвое больше банковских вкладов.
А вот что действительно полезно во всех этих рассуждениях, так это формула, которая позволяет нам найти итоговую сумму вклада через размер ежегодных платежей, а также через проценты, которые начисляет банк. Так и запишем:
[text{Vklad}=text{platezh}frac{{{text{%}}^{n}}-1}{text{%}-1}]
Сам по себе % считается по следующей формуле:
[Ktext{%}to 1+frac{K}{100}]
Эту формулу также необходимо знать, как и основную формулу суммы вклада. А, в свою очередь, основная формула способна значительно сократить вычисления в тех задачах с процентами, где требуется посчитать именно вклад.
Почему стоит пользоваться формулами, а не таблицами?
У многих наверняка возникнет вопрос, а к чему вообще все эти сложности, нельзя ли просто расписать каждый год в табличке, как это делают во многих учебниках, посчитать отдельно каждый год, а затем посчитать общую сумму вклада? Конечно, можно вообще забыть про сумму геометрической прогрессии и все считать с помощью классических табличек — так сделано в большинстве сборников для подготовки к ЕГЭ. Однако, во-первых, резко увеличивается объем вычислений, а во-вторых, как следствие, увеличивается вероятность допустить ошибку.
Да и вообще, использовать таблицы вместо этой замечательной формулы — это то же самое, что на стройке копать траншеи руками вместо того, чтобы использовать стоящий рядом и полностью работающий экскаватор.
Ну, или то же самое, что умножить пятерку на десятку не с помощью таблицы умножения, а складывать пятерку с самой собой десять раз подряд. Впрочем, это я уже отвлекся, поэтому еще раз повторю самую главную мысль: если есть какой-то способ упростить и сократить вычисления, то именно этим способом и надо воспользоваться.
Проценты по кредитам
С вкладами мы разобрались, поэтому переходим к следующей теме, а именно — к процентам по кредитам.
Итак, пока вы копите деньги, скрупулезно планируете свой бюджет, думаете о своей будущей квартире, ваш одноклассник, а нынче простой безработный, решил жить сегодняшним днем и просто взял кредит. При этом он еще будет подкалывать и смеяться над вами, мол, у него кредитный телефон и подержанный автомобиль, взятый в кредит, а вы до сих пор ездите на метро и пользуетесь старым кнопочным телефоном. Разумеется, за все эти дешевые «понты» вашему бывшему однокласснику придется дорого расплатится. Насколько дорого — вот это именно сейчас мы и посчитаем.
Для начала краткая вводная информация. Допустим, ваш бывший одноклассник взял два миллиона рублей в кредит. При этом согласно договору он должен платить xрублей в месяц. Допустим, что кредит он взял по ставке 20% годовых, что в нынешних условиях выглядит вполне прилично. Кроме того, предположим, что срок кредита составляет всего три месяца. Давайте попробуем связать все эти величины в одну формулу.
Итак, в самом начале, как только ваш бывший одноклассник вышел из банка у него в кармане два миллиона, и это и есть его долг. При этом не год прошел, и не месяц, а это только самое начало:
[2m]
Затем спустя один месяц на сумму задолженности будут начислены проценты. Как мы уже знаем для вычисления процентов достаточно умножить исходную задолженность на коэффициент, который считается по следующей формуле:
[Ktext{%}to 1+frac{K}{100}]
В нашем случае речь идет о ставке 20% годовых, т. е. мы можем записать:
[1+frac{20}{100}=1,2]
Это коэффициент суммы, которая будет начисляться в год. Однако наш одноклассник не очень умный и он не читал договор, и на деле кредит ему выдали не под 20% в год, а под 20% в месяц. И уже к концу первого месяца на эту сумму будут начислены проценты, и она увеличится в 1,2 раза. Сразу после этого человеку будет необходимо оплатить оговоренную сумму, т. е. xрублей в месяц:
[2mcdot 1,2- x]
Далее к концу второго месяца уже на эту сумму будут вновь начислены проценты:
[left( 2mcdot 1,2- xright)cdot 1,2-x]
И вновь наш паренек вносит платеж в размере $x$ рублей.
Затем к концу третьего месяца сумма его задолженности еще раз увеличивается на 20%:
[left( left( 2mcdot 1,2- xright)cdot 1,2- xright)1,2- x]
И по условию за три месяца он должен полностью расплатиться, т. е. после внесения последнего третьего платежа его объем задолженности должен быть равен нулю. Мы можем записать такое уравнение:
[left( left( 2mcdot 1,2- xright)cdot 1,2- xright)1,2 — x=0]
Давайте решать:
[begin{align}& left( 2mcdot {{1,2}^{2}}- xcdot 1,2- xright)cdot 1,2- x=0 \& 2mcdot {{1,2}^{3}}- xcdot {{1,2}^{2}}- xcdot 1,2- x=0 \& 2mcdot {{1,2}^{3}}=cdot {{1,2}^{2}}+cdot 1,2+ \& 2mcdot {{1,2}^{3}}=left( {{1,2}^{2}}+1,2+1 right) \end{align}]
Перед нами вновь геометрическая прогрессия, а точнее, сумма трех элементов геометрической прогрессии. Давайте перепишем ее в порядке возрастания элементов:
[2mcdot {{1,2}^{3}}=left( 1+1,2+{{1,2}^{2}} right)]
Теперь нам нужно найти сумму трех элементов геометрической прогрессии. Давайте запишем:
[begin{align}& {{b}_{1}}=1; \& q=1,2 \end{align}]
Теперь найдем сумму геометрической прогрессии:
[{{S}_{3}}=1cdot frac{{{1,2}^{3}}-1}{1,2-1}]
Следует напомнить, что сумма геометрической прогрессии с такими параметрами $left( {{b}_{1}};q right)$ считается по формуле:
[{{S}_{n}}={{b}_{1}}cdot frac{{{q}^{n}}-1}{q-1}]
Вот этой формулой мы только что и воспользовались. Подставляем эту формулу в наше выражение:
[2mcdot {{1,2}^{3}}=cdot frac{{{1,2}^{3}}-1}{1,2-1}]
Для дальнейших вычислений нам следует узнать, чему равна ${{1,2}^{3}}$. К сожалению, в этом случае мы уже не можем расписать как в прошлый раз в виде двойного квадрата, но зато можем посчитать так:
[begin{align}& {{1,2}^{3}}={{1,2}^{2}}cdot 1,2 \& {{1,2}^{3}}=1,44cdot 1,2 \& {{1,2}^{3}}=1,728 \end{align}]
Переписываем наше выражение:
[2mcdot 1,728=cdot frac{0,728}{0,2}]
Это классическое линейное выражение. Давайте вернемся к следующей формуле:
[2cdot {{1,2}^{3}}=cdot frac{{{1,2}^{3}}-1}{1,2-1}]
По сути, если обобщить ее, то мы получим формулу, связывающую проценты, кредиты, платежи и сроки. Формула звучит следующим образом:
[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]
Вот она, самая главная формула сегодняшнего видеоурока, с помощью которой считается не менее 80% всех экономических задач из ЕГЭ по математике во второй части.
Чаще всего в реальных задачах у вас будет спрашиваться платеж, либо чуть реже кредит, т. е. общая сумма задолженности, которая была у нашего одноклассника в самом начале платежей. В более сложных задачах вас попросят найти процент, ну а совсем сложных, которые мы разберем в отдельном видеоуроке от вас попросят найти сроки, в течение которых при данных параметрах кредита и платежа наш безработный одноклассник сможет полностью расплатится с банком.
Возможно, кто-то сейчас подумает, что я являюсь яростным противником кредитов, финансов и вообще банковской системы. Так вот, ничего подобного! Напротив, я считаю, что кредитные инструменты очень полезны и крайне необходимы нашей экономике, но только при условии, что кредит берется на развитие бизнеса. В крайнем случае, можно взять кредит на покупку жилья, т. е. ипотеку либо на неотложное медицинское лечение — все, других причин взять кредит просто не существует. А всевозможные безработные, которые берут кредиты на покупку «понтов» и при этом совершенно не задумываются о последствиях в итоге и становятся причиной кризисов и проблем в нашей экономике.
Возвращаясь к теме сегодняшнего урока, хотел бы отметить, что знать эту формулу, связывающую кредиты платежи и проценты, также необходимо как и сумму геометрической прогрессии. Именно с помощью этих формул решаются реальные экономические задачи из ЕГЭ по математике. Ну, а теперь, когда вы все это прекрасно знаете, когда понимаете, что такое кредит и почему его не стоит брать, переходим к решению реальных экономических задач из ЕГЭ по математике.
Решаем реальные задачи из ЕГЭ по математике
Пример № 1
Итак, первая задача:
31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т .е. увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами (т .е. за четыре года)?
Итак, это задача про кредит, поэтому сразу записываем нашу формулу:
[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]
Кредит нам известен — 9282000 рублей.
С процентами мы сейчас разберемся. У нас речь идет о 10% в задаче. Следовательно, мы можем их перевести:
[10text{%}to 1+frac{10}{100}=1,1]
Мы можем составить уравнение:
[9289000cdot {{1,1}^{4}}=xcdot frac{{{1,1}^{4}}-1}{1,1-1}]
У нас получилось обычное линейное уравнение относительно $x$, хотя с достаточно грозными коэффициентами. Давайте попробуем его решить. Для начала найдем выражение ${{1,1}^{4}}$:
$begin{align}& {{1,1}^{4}}={{left( {{1,1}^{2}} right)}^{2}} \& 1,1cdot 1,1=1,21 \& {{1,1}^{4}}=1,4641 \end{align}$
Теперь перепишем уравнение:
[begin{align}& 9289000cdot 1,4641=xcdot frac{1,4641-1}{0,1} \& 9282000cdot 1,4641=xcdot frac{0,4641}{0,1}|:10000 \& 9282000cdot frac{14641}{10000}=xcdot frac{4641}{1000} \& frac{9282cdot 14641}{10}=xcdot frac{4641}{1000}|:frac{4641}{1000} \& x=frac{9282cdot 14641}{10}cdot frac{1000}{4641} \& x=frac{2cdot 14641cdot 1000}{10} \& x=200cdot 14641 \& x=2928200 \end{align}][]
Все, наша задача с процентами решена.
Разумеется, что это была лишь самая простая задача с процентами из ЕГЭ по математике. В настоящем экзамене такой задачи, скорее всего, не будет. А если и будет, то считайте, что вам очень повезло. Ну, а для тех, кто любит считать и не любит рисковать, переходим к следующим более сложным задачам.
Пример № 2
31 декабря 2014 года Степан взял в банке 4004000 рублей в кредит под 20% годовых. Схема выплаты кредиты следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е.) увеличивает долг на 20%), затем Степан производит в банк платеж. Весь долг Степан выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа.
Перед нами задача про кредиты, поэтому записываем нашу формулу:
[][kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]
Что нам известно? Во-первых, нам известен общий кредит. Также нам известны проценты. Давайте найдем коэффициент:
[20%to 1+frac{20}{100}=1,2]
Что касается $n$, то нужно внимательно прочитать условие задачи. Т. е. сначала нам необходимо посчитать, сколько он заплатил за три года, т. е. $n=3$, а затем выполнить еще раз те же самые действия но рассчитать платежи за два года. Давайте запишем уравнение для того случай, когда платеж выплачивается за три года:
[4004000cdot {{1,2}^{3}}=xcdot frac{{{1,2}^{3}}-1}{1,2-1}]
Давайте решать это уравнение. Но для начала найдем выражение ${{1,2}^{3}}$:
[begin{align}& {{1,2}^{3}}=1,2cdot {{1,2}^{2}} \& {{1,2}^{3}}=1,44cdot 1,2 \& {{1,2}^{3}}=1,728 \end{align}]
Переписываем наше выражение:
[begin{align}& 4004000cdot 1,728=xcdot frac{1,728-1}{0,2} \& 4004000cdot frac{1728}{1000}=xcdot frac{728}{200}|:frac{728}{200} \& x=frac{4004cdot 1728cdot 200}{728} \& x=frac{4004cdot 216cdot 200}{91} \& x=44cdot 216cdot 200 \& x=8800cdot 216 \& x=1900800 \end{align}]
Итого, наш платеж составит 1900800 рублей. Однако обратите внимании: в задаче от нас требовалось найти не ежемесячный платеж, а сколько всего Степан заплатит за три равных платежа, т. е. за все время пользования кредитом. Поэтому полученную величину необходимо еще раз умножить на три. Давайте посчитаем:
[3x=5702400]
Итого за три равных платежа Степан заплатит 5702400 рублей. Вот во сколько ему обойдется пользование кредитом в течение трех лет.
Теперь рассмотрим вторую ситуацию, когда Степан поднапрягся, собрался и выплатил весь кредит не за три, а за два равных платежа. Записываем все ту же нашу формулу:
[begin{align}& 4004000cdot {{1,2}^{2}}=xcdot frac{{{1,2}^{2}}-1}{1,2-1} \& 4004000cdot frac{144}{100}=xcdot frac{11}{5}|cdot frac{5}{11} \& x=frac{40040cdot 144cdot 5}{11} \& x=3640cdot 144cdot 5=3640cdot 720 \& x=2620800 \end{align}]
Но это еще не все, потому что сейчас мы посчитали лишь один из двух платежей, поэтому всего Степан заплатит ровно в два раза больше:
[2x=5241600]
Прекрасно, вот теперь мы и приблизились к окончательному ответу. Но обратите внимание: ни в коем случае мы еще не получили окончательный ответ, потому что за три года платежей Степан заплатит 5702400 рублей, а за два года платежей он заплатит 5241600 рублей, т. е. чуть-чуть поменьше. Насколько меньше? Чтобы это узнать, нужно из первого размера платежей вычесть второй размер платежей:
[5702400-5241600=460800]
Итого окончательный ответ — 460800 рублей. Именно сколько сэкономит Степан, если будет платить не три года, а два.
Как видите, формула, связывающая проценты, сроки и платежи, существенно упрощает вычисления по сравнению с классическими таблицами и, к сожалению, по непонятным причинам в большинстве сборников задач, тем не менее, до сих пор используются именно таблицы.
Отдельно хотел бы обратить ваше внимание на срок, на который взят кредит, и размером ежемесячных платежей. Дело в том, что эта связь напрямую не просматривается из тех формул, которые мы записали, однако ее понимание необходимо для быстрого и эффективного решения настоящих задач на экзамене. На самом деле эта связь очень проста: чем на больший срок берется кредит, тем меньшая сумма будет в ежемесячных платежах, но тем большая сумма накопится за все время пользования кредитом. И наоборот: чем меньше срок, тем больше ежемесячный платеж, однако при этом меньше итоговая переплата и меньше общая стоимость кредита.
Разумеется, все эти утверждения будут равны лишь при условии, что сумма кредита и процентная ставка в обоих случаях одна и та же. В общем, пока просто запомните этот факт — он будет использоваться для решения самых сложных задач на эту тему, а пока мы разберем более простую задачу, где как раз и требуется найти общую сумму исходного кредита.
Пример № 3
Итак, еще одна задача на кредит и по совместительству последняя задача в сегодняшнем видеоуроке.
31 декабря 2014 года Василий взял в банке некоторую сумму в кредит под 13% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 13%), затем Василий переводит в банк 5 107 600 рублей. Какую сумму взял Василий в банке, если он выплатил долг двумя равными платежами (за два года)?
Итак, в первую очередь, эта задача вновь про кредиты, поэтому записываем нашу замечательную формулу:
[kreditcdot {{%}^{n}}=platezhcdot frac{{{%}^{n}}-1}{%-1}]
Посмотрим, что нам известно из условия задачи. Во-первых, платеж — он равен 5107600 рублей в год. Во вторых проценты, поэтому мы можем найти коэффициент:
[13%to 1+frac{13}{100}=1,13]
Кроме того, согласно условию задачи Василий взял в банке кредит на два года, т.е. выплатил двумя равными платежами, следовательно, $n=2$. Давайте все подставим и также заметим, что кредит нам неизвестен, т.е. та сумма, которую он взял, и обозначим ее за $x$. Получим:
[xcdot {{1,13}^{2}}=5107600cdot frac{{{1,13}^{2}}-1}{1,13-1}]
Знаменатель мы можем тут же посчитать — это будет 1,13, а вот в числителе, а также слева перед переменной $x$ у нас стоит коэффициент ${{1,13}^{2}}$. Предлагаю посчитать данное выражение отдельно:
[{{1,13}^{2}}=1,2769]
Перепишем наше уравнение с учетом этого факта:
[begin{align}& xcdot frac{12769}{10000}=5107600cdot frac{1,2769-1}{0,13} \& xcdot frac{12769}{10000}=frac{5107600cdot 2769}{1300}|:frac{12769}{10000} \& x=frac{51076cdot 2769}{13}cdot frac{10000}{12769} \& x=4cdot 213cdot 10000 \& x=8520000 \end{align}]
Все, это и есть окончательный ответ. Именно такую сумму Василий взял в кредит в самом начале.
Теперь понятно, почему в этой задаче нам предлагается взять кредит лишь на два года, потому что здесь фигурируют двузначные проценты, а именно 13%, которые в квадрате дают уже довольно «зверское» число. Но и это еще не предел — в следующем отдельном уроке мы рассмотрим более сложные задачи, где будет требоваться найти срок кредита, а ставка будет составлять один, два или три процента.
В общем, учитесь решать задачи на вклады и кредиты, готовьтесь к экзаменам и сдавайте их «отлично». А если что-то непонятно в материалах сегодняшнего видеоурока, то не стесняйтесь — пишите, звоните, и я постараюсь вам помочь.
Смотрите также:
- Задача на производительность труда
- ЕГЭ по математике 2016: задача про кредиты с фиксированным платежом
- Тест к уроку «Что такое логарифм» (тяжелый)
- Комбинированные задачи B12
- Как решать задачи про летающие камни?
- Задача C1: тригонометрия и показательная функция — 1 вариант