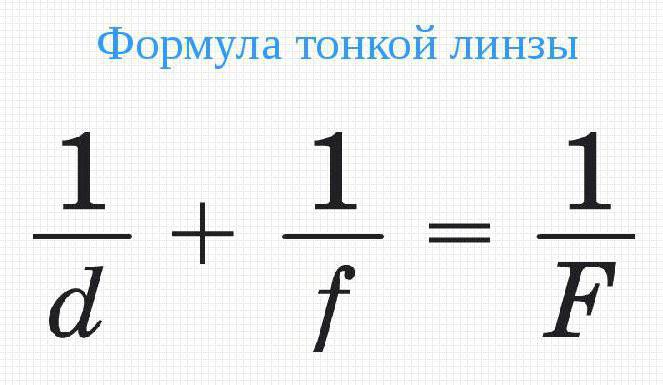в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 225 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Небольшой предмет находится на главной оптической оси тонкой собирающей линзы, на двойном фокусном расстоянии от нее. Как изменятся при удалении предмета от линзы следующие три величины: размер изображения, его расстояние от линзы, оптическая сила линзы?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Размер
изображения |
Расстояние
изображения от линзы |
Оптическая
сила линзы |
Фокусное расстояние тонкой собирающей линзы равно F. На главной оптической оси слева от линзы на расстоянии a = 2,5F от неё находится точечный источник света. Горизонтальная ось Ox совпадает с главной оптической осью линзы.
Выберите все верные утверждения.
1) Изображение точечного источника света будет находиться справа от линзы на расстоянии b > a от неё.
2) Если линзу переместить вдоль главной оптической оси так, что расстояние от точечного источника света до линзы уменьшится на величину l = F , то изображение источника будет находиться справа от линзы на расстоянии b > a от неё.
3) Если линзу переместить вдоль главной оптической оси так, что расстояние от точечного источника света до линзы станет равным 3,5F, то изображение источника будет находиться справа от линзы на расстоянии b > a от неё.
4) Если линзу сместить перпендикулярно главной оптической оси, не изменяя расстояния a от точечного источника света до линзы, то оптическая сила линзы не изменится.
5) Если линзу повернуть относительно главной оптической оси на угол α, то изображение точечного источника света повернется относительно оси Ox на угол 2α.
Небольшой предмет располагают на расстоянии a от тонкой собирающей линзы и получают с её помощью изображение этого предмета, расположенное на расстоянии b от линзы. На рисунке изображены графики зависимостей b от a для двух тонких собирающих линз 1 и 2.
Выберите все верные утверждения на основании анализа представленных графиков.
1) Фокусное расстояние линзы 2 равно 14 см.
2) Фокусное расстояние линзы 1 меньше фокусного расстояния линзы 2 на 0,5 см.
3) Оптическая сила линзы 1 меньше оптической силы линзы 2.
4) Если предмет расположен на расстоянии 10 см от линзы 2, то изображение этого предмета будет увеличено в 2 раза.
5) При одинаковом расстоянии от линз до предметов линза 2 будет давать изображение с бóльшим увеличением.
Небольшой предмет располагают на расстоянии a от тонкой собирающей линзы и получают с её помощью изображение этого предмета, расположенное на расстоянии b от линзы. На рисунке изображены графики зависимостей b от a для двух тонких собирающих линз 1 и 2.
Выберите все верные утверждения на основании анализа представленных графиков.
1) Фокусное расстояние линзы 1 равно 3 см.
2) Фокусное расстояние линзы 1 больше фокусного расстояния линзы 2 на 1,5 см.
3) Оптическая сила линзы 1 больше оптической силы линзы 2.
4) Если предмет расположен на расстоянии 5 см от линзы 1, то изображение этого предмета будет увеличено в 2 раза.
5) При одинаковом расстоянии от линз до предметов линза 1 будет давать изображение с меньшим увеличением.
На оптической скамье установлена тонкая собирающая линза с фокусным расстоянием F, а слева от неё на расстоянии d > F от линзы помещён предмет (стрелка, перпендикулярная оси). В линзе получилось действительное изображение высотой h. Затем справа от этой линзы поместили на расстоянии F от неё вторую такую же линзу. Главные оптические оси линз совпадали. Правее второй линзы получилось новое изображение исходного предмета высотой h′. Изобразите на чертеже ход лучей в системе из двух линз, постройте новое изображение предмета и вычислите отношение
На оптической оси тонкой собирающей линзы с фокусным расстоянием F = 10 см слева от неё на расстоянии a = 3F/2 = 15 см находится точечный источник света S. За линзой справа от неё на расстоянии F = 10 см расположено плоское зеркало, перпендикулярное оси линзы. На каком расстоянии от источника находится его изображение S‘ в данной оптической системе?
К решению приложите рисунок с изображением хода лучей от S до S‘.
Точечный источник света удаляется от тонкой собирающей линзы, двигаясь вдоль её главной оптической оси. Фокусное расстояние линзы равно 10 см. На рисунке показан график зависимости расстояния x между источником и линзой от времени t.
Из приведённого ниже списка выберите все верные утверждения.
1) В момент времени t0 = 0 с изображение источника в линзе было мнимым и находилось в фокальной плоскости линзы.
2) Изображение источника в линзе в любой момент времени действительное.
3) В момент времени t = 25 с увеличение линзы меньше единицы.
4) Изображение источника в линзе движется с постоянной скоростью в течение всего времени наблюдения.
5) В момент времени t = 10 с пучок световых лучей, прошедших через линзу, становится параллельным её главной оптической оси.
При изучении законов геометрической оптики ученик расположил небольшой предмет на расстоянии 50 см от тонкой собирающей линзы. Оптическая сила линзы равна 2,5 дптр. После этого он стал перемещать предмет вдоль главной оптической оси линзы. Выберите все верные утверждения о результатах этого опыта. В ответе укажите их номера.
1) Фокусное расстояние линзы равно 25 см.
2) Первоначальное изображение предмета получилось действительным и увеличенным.
3) При перемещении предмета на 15 см ближе к линзе изображение предмета стало мнимым.
4) Первоначально изображение предмета находилось на расстоянии 2,5 м от линзы.
5) При перемещении предмета на 30 см дальше от линзы размер изображения предмета уменьшился.
Середина светящегося отрезка АВ находится на расстоянии 20 см от центра тонкой собирающей линзы с фокусным расстоянием 10 см на главной оптический оси (см. рис.). Линия OO’, совпадающая с координатной осью OX, является главной оптической осью линзы. Координатная ось OY лежит в плоскости линзы. Отрезок AB находится в плоскости OXY.
Из приведённого ниже списка выберите все правильные утверждения.
1) Расстояние вдоль оси OX от линзы до точки А меньше, чем расстояние вдоль оси OX от линзы до изображения точки А.
2) Расстояние вдоль оси OX от линзы до точки В меньше, чем расстояние вдоль оси OX от линзы до изображения точки В.
3) При вращении отрезка AB вокруг его середины в плоскости рисунка против часовой стрелки изображение будет поворачиваться по часовой стрелке.
4) Расстояние вдоль оси OY от главной оптической оси до точки В равно расстоянию вдоль оси OY от главной оптической оси до изображения точки В.
5) Размер изображения равен размеру светящегося объекта.
На главной оптической оси тонкой собирающей линзы с фокусным расстоянием F = 10 см на расстоянии d = 30 см от линзы находится точечный источник света S. За линзой в её фокальной плоскости расположено плоское зеркало, отражающая поверхность которого направлена в сторону линзы. Рассчитайте, на каком расстоянии от линзы находится изображение источника в данной оптической системе, и сделайте чертёж, поясняющий расчёт.
При изучении законов геометрической оптики ученик расположил небольшой предмет на расстоянии 50 см от тонкой собирающей линзы. Оптическая сила линзы равна 2,5 дптр. После этого он стал перемещать предмет вдоль главной оптической оси линзы. Выберите все верные утверждения о результатах этого опыта. В ответе укажите их номера.
1) Первоначально изображение предмета находилось на расстоянии 2 м от линзы.
2) Первоначальное изображение предмета получилось мнимым и увеличенным.
3) При перемещении предмета на 20 см ближе к линзе изображение предмета стало уменьшенным.
4) Фокусное расстояние линзы равно 40 см.
5) При перемещении предмета на 30 см дальше от линзы размер изображения предмета стал равен размеру самого предмета.
Точечный источник света S расположен на главной оптической оси рассеивающей линзы в её фокусе. Оптическая сила линзы
дптр (см. рисунок). На какое расстояние сместится изображение источника, если линзу повернуть на угол
относительно оси, перпендикулярной плоскости рисунка и проходящей через оптический центр линзы?
Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи
Равнобедренный прямоугольный треугольник ABC площадью 50 см
расположен перед тонкой собирающей линзой так, что его катет АС лежит на главной оптической оси линзы. Фокусное расстояние линзы 50 см. Вершина прямого угла С лежит дальше от центра линзы, чем вершина острого угла А. Расстояние от центра линзы до точки А равно удвоенному фокусному расстоянию линзы (см. рисунок). Постройте изображение треугольника и найдите площадь получившейся фигуры.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 1., ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 5.
Равнобедренный прямоугольный треугольник ABC площадью 50 см
расположен перед тонкой собирающей линзой так, что его катет АС лежит на главной оптической оси линзы. Фокусное расстояние линзы равно 50 см. Вершина прямого угла С лежит ближе к центру линзы, чем вершина острого угла А. Расстояние от центра линзы до точки А равно удвоенному фокусному расстоянию линзы (см. рисунок). Постройте изображение треугольника и найдите площадь получившейся фигуры.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 3.
В распоряжении ученика были тонкая собирающая линза, лампочка и экран. Ученик устанавливал лампочку на разных расстояниях a от линзы на её главной оптической оси, и затем получал чёткое изображение лампочки, устанавливая экран на соответствующем расстоянии b от линзы. По результатам своих экспериментов он построил зависимость, изображённую на рисунке. Определите по этой зависимости фокусное расстояние линзы и её оптическую силу.
1) Фокусное расстояние линзы равно F = 10 cм.
2) Оптическая сила линзы равна D = 20 дптр.
3) Фокусное расстояние линзы равно F = 4 см.
4) Оптическая сила линзы равна D = 2 дптр.
5) Фокусное расстояние линзы равно F = 5 cм.
С помощью тонкой линзы на экране получают изображение объекта AB, расположенного параллельно ей. После чего линзу закрывают ободком из чёрного картона. Нарисуйте ход лучей и объясните, что произойдёт с изображением на экране.
Источник: ЕГЭ по физике 24.06.2016. Основная волна, резервная волна. Вариант 1. (Часть С)
Точечный источник света приближается к тонкой собирающей линзе, двигаясь вдоль её главной оптической оси. Фокусное расстояние линзы равно 10 см. На рисунке показан график зависимости расстояния x между источником и линзой от времени t.
Из приведённого ниже списка выберите все верные утверждения.
1) В момент времени t0 = 0 с изображение источника в линзе было действительным и находилось на расстоянии более 10 см линзы.
2) Изображение источника в линзе в любой момент времени действительное.
3) В момент времени t = 20 с увеличение линзы по модулю превышает единицу.
4) Изображение источника в линзе движется с постоянной скоростью всё время наблюдения.
5) В момент времени t = 10 с пучок световых лучей, прошедших через линзу, становится параллельным её главной оптической оси.
По разные стороны от линзы на главной оптической оси расположены два источника света. Они дают изображение в одной точке. Один из источников располагается на расстоянии x = 20 см от линзы. Оптическая сила линзы равна 3,5 дптр. Найдите расстояние между источниками L. Сделайте два рисунка с построением хода лучей в линзе.
Источник: ЕГЭ по физике 13.07.2020. Основная волна. ЦФО. Часть C. Вариант 2
Два точечных источника света находятся на главной оптической оси тонкой собирающей линзы на расстоянии L = 1 м друг от друга. Линза находится между ними. Расстояние от линзы до одного из источников x = 20 см. Изображения обоих источников получились в одной точке. Найдите оптическую силу линзы. Постройте на отдельных рисунках изображения двух источников в линзе, указав ход лучей.
Источник: Демонстрационная версия ЕГЭ—2022 по физике
Предмет находится перед собирающей линзой между фокусным и двойным фокусным расстоянием. Как изменятся расстояние от линзы до его изображения, линейный размер изображения предмета и вид изображения (мнимое или действительное) при перемещении предмета на расстояние больше двойного фокусного ()?
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Расстояние от линзы до изображения предмета
Б) Линейный размер изображения предмета
В) Вид изображения предмета
ИЗМЕНЕНИЕ ВЕЛИЧИНЫ
1) Увеличивается
2) Уменьшается
3) Не изменится
Всего: 225 1–20 | 21–40 | 41–60 | 61–80 …
Задачи по геометрической оптике не такие уж и сложные, если уделить их разбору немного временени. Сегодня в нашей регулярной рубрике «Физика для чайников» рассмотрим несколько примеров задач на тонкие линзы.
Хотите быть в курсе актуальных новостей, связанных с учебой? Присоединяйтесь к нам в телеграме! А тем, кто хочет получать скидки и бонусы, рекомендуем заглянуть на наш второй канал для клиентов.
Тонкая линза: задачи
Чтобы успешно решать задачи по геометрической оптике на тему «Тонкие линзы», нужно знать всего лишь пару формулу. Правда, формул много не бывает, и мы собрали их вместе: пригодятся в решении задач по другим темам. А тем, кто не знает, как вообще подступиться к задачам по физике, рекомендуем почитать общую памятку по решению.
Задача №1. Формула тонкой линзы
Условие
Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?
Решение
Линза является собирающей (оптическая сила положительна). Запишем формулу тонкой линзы:
1F=1d+1f
Учтем, что F=1D, подставим значения из условия, и запишем:
2,5=10,5+1+ff=2 м
Ответ: 2м
Задача №2. Формула тонкой линзы
Условие
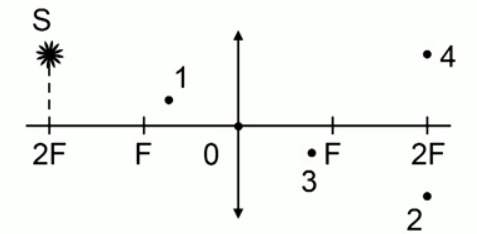
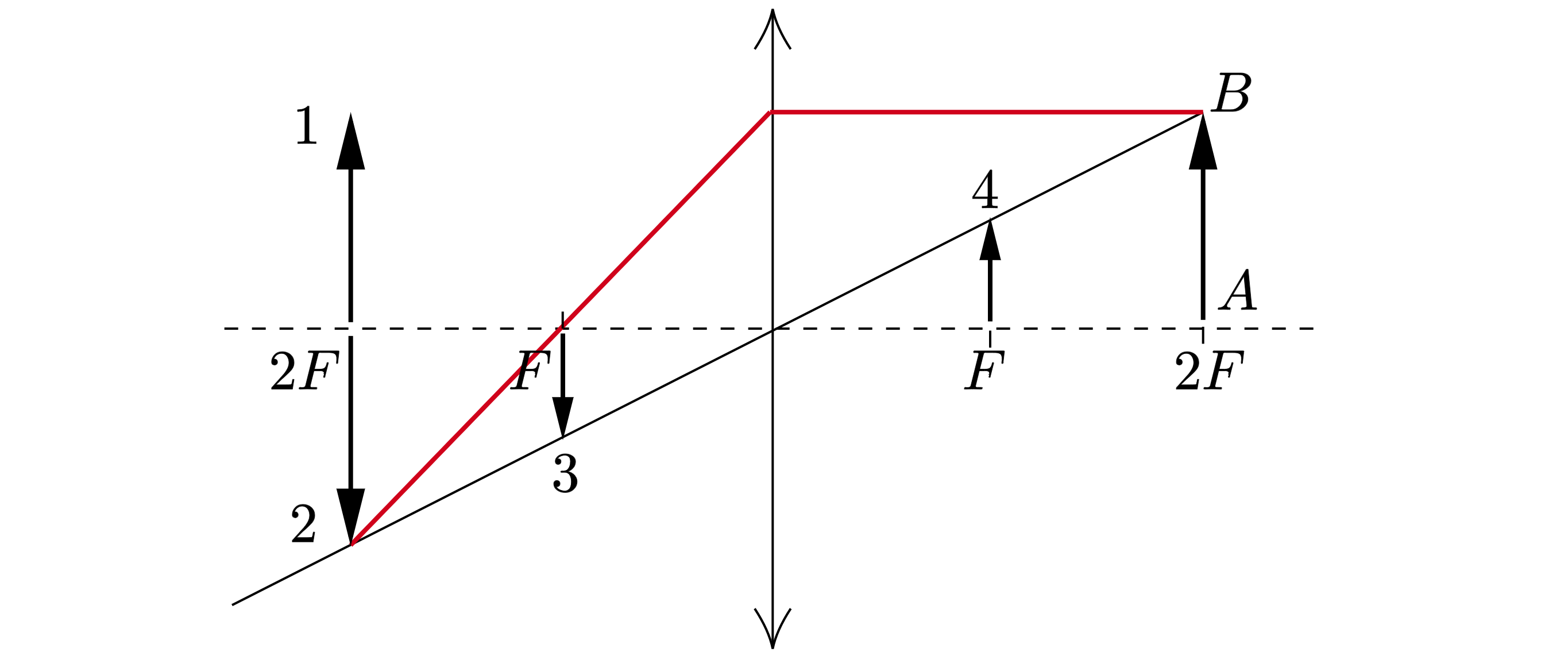
Светящаяся точка лежит в плоскости, проходящей через двойной фокус тонкой линзы, у которой указана главная оптическая ось. Определите, какая из четырех точек на чертеже соответствует правильному изображению светящейся точки.
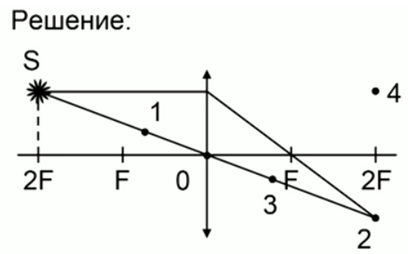
Решение
Как видим, на рисунке изображена собирающая линза с оптическим центром в точке 0. Светящася точка S находится от линзы на расстоянии, равном двум фокусам.
Построим изображение точки: один луч проходит через оптический центр линзы, а второй луч, параллельный главной оптической оси, после преломления проходит через фокус. Точка пересечения лучей на расстоянии двойного фокуса и будет являться изображением точки S.
Ответ: изображению точки S соответствует точка 2.
Денное решение получено геометрическим путем, но его можно проверить, используя формулу линзы. Подставим в нее 2F вместо d, и получим тот же результат.
Задача №3. Формула тонкой линзы
Условие
Предмет высотой 3 см находится на расстоянии 40 см от собирающей тонкой линзы. Определите высоту изображения, если оптическая сила линзы равна 4 диоптриям.
Решение
Запишем форумулу тонкой собирающей линзы и формулу увеличения линзы:
1F=1d+1f ; Г=Hh=fd
Перепишем эти соотношения, с учетом того, что F=1D
H=h·fd1f=D-1d
Отсюда найдем f:
f=dD·d-1
Осталось подставить значения в формулу для H и вычислить:
H=hdD·d-1=0,03·0,44·0,4-1=0,05 м
Ответ: 0,05 м.
Задача №4. Формула тонкой линзы
Условие
Предмет имеет высоту 2 см. Какое фокусное расстояние должна иметь линза, расположенная на расстоянии f=4 м от экрана, чтобы изображение предмета на экране имело высоту H=1 м?
Решение
Фокусное расстояние найдем из формулы линзы:
1F=1d+1fF=fdd+f
Запишем формулу увеличения линзы и выразим d:
Г=Hh=fd ; d=fhH
Запишем окончательный ответ:
F=hfH+h≈0,08 м
Ответ: 0,08 м.
Задача №5. Формула тонкой линзы
Условие
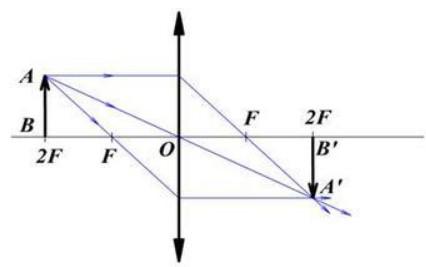
Постройте изображение отрезка AB, расположенного перед собирающей линзой так, что расстояние от предмета до линзы d=2F. Каким будет изображение?
Решение
Посторим изображение в соответствии с правилами геометрической оптики:
Данное изображение:
- действительное;
- перевернутое;
- равное предмету.
Ответ: см. выше.
Вопросы на тему «Тонкая линза»
Вопрос 1. Какое равенство называют формулой тонкой линзы?
Ответ. Формула тонкой линзы имеет следующий вид:
1F=1d+1±f
Здесь:
- F – фокусное расстояние;
- d – расстояние от линзы до предмета;
- f – расстояние от линзы до изображения.
Вопрос 2. В чем разница в формуле линзы для собирающей и рассеивающей линз?
Ответ. Для собирающей линзы f берется положительным, а для рассеивающей – отрицательным. Соответственно, собирающая линза строит действительное изображение, а рассеивающая – мнимое.
Вопрос 3. Что такое фокусное расстоняние линзы?
Ответ. Фокусное расстояние линзы – это расстояние между ее оптическим центром и главным фокусом.
Вопрос 4. Что такое оптическая сила линзы?
Ответ. Оптическая сила – это величина, обратная фокусному расстоянию. Она характеризует преломляющую способность линзы.
Вопрос 5. Может ли оптическая сила линзы быть отрицательной?
Ответ. Да. Для рассеивающей линзы оптическая сила берется со знаком минус.
Проблемы с решением задач или других заданий? Обращайтесь в профессиональный сервис помощи учащимся!
Тема 14.
Оптика. Электромагнитные колебания и волны
14
.
04
Геометрическая оптика (Линзы)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
оптика. электромагнитные колебания и волны
14.01Колебательный контур
14.02Переменный ток
14.03Геометрическая оптика (Законы отражения и преломления)
14.04Геометрическая оптика (Линзы)
14.05Волновая оптика
Решаем задачи
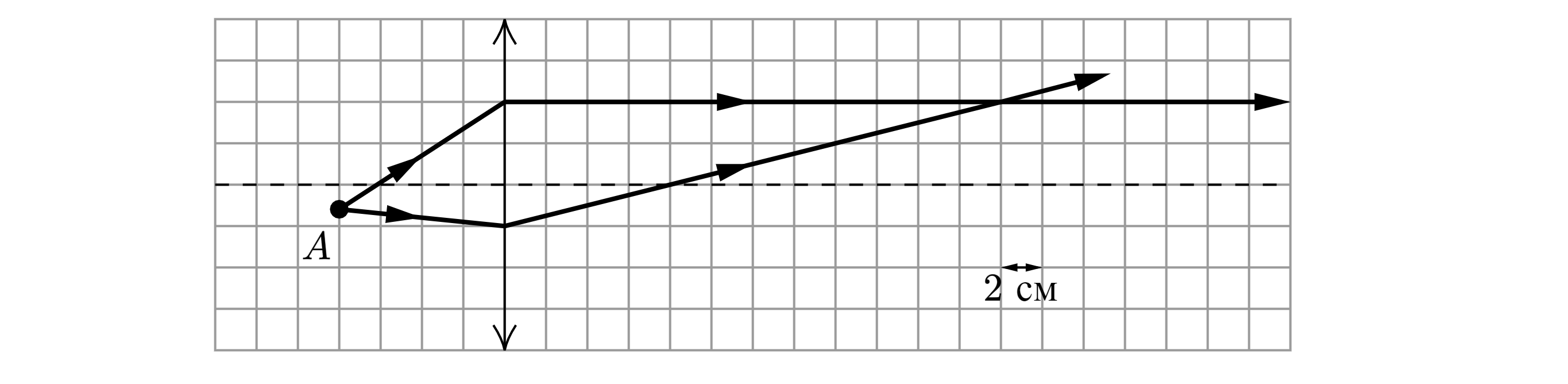
На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу.
Каково фокусное расстояние этой линзы? Ответ дайте в сантиметрах.
Показать ответ и решение
Найдем фокусное расстояние линзы из рисунка. Для того, чтобы луч после преломления в тонкой линзе шел параллельно главной
оптической оси, он должен проходить через фокус линзы, в данном случае луч пересекает главную оптическую ось на расстоянии 4
клетки от линзы, то есть 40 см.
Два точечных источника света находятся на расстоянии 32 см друг от друга. Где между ними надо поместить собирающую линзу,
чтобы изображения обоих источников оказались в одной точке? Фокусное расстояние линзы равно 12 см. Найдите расстояние от
источников до линзы, в ответе укажите наименьшее значение в см.
Показать ответ и решение
Для того, чтобы изображения двух источников, расположенных по разную сторону собирающей линзы, оказались в одной точке,
необходимо, чтобы одно изображение было действительным, а другое мнимым, пусть это изображение источника номер 2. Пусть
расстояние от первого источника до линзы , от второго
,
– расстояние от линзы до изображения,
– фокусное
расстояние, – расстояние между источниками.
Запишем формулу тонкой линзы для каждого из источников:
Отсюда
По условию , тогда
Или
Тогда
В ответ пойдёт 8 см.
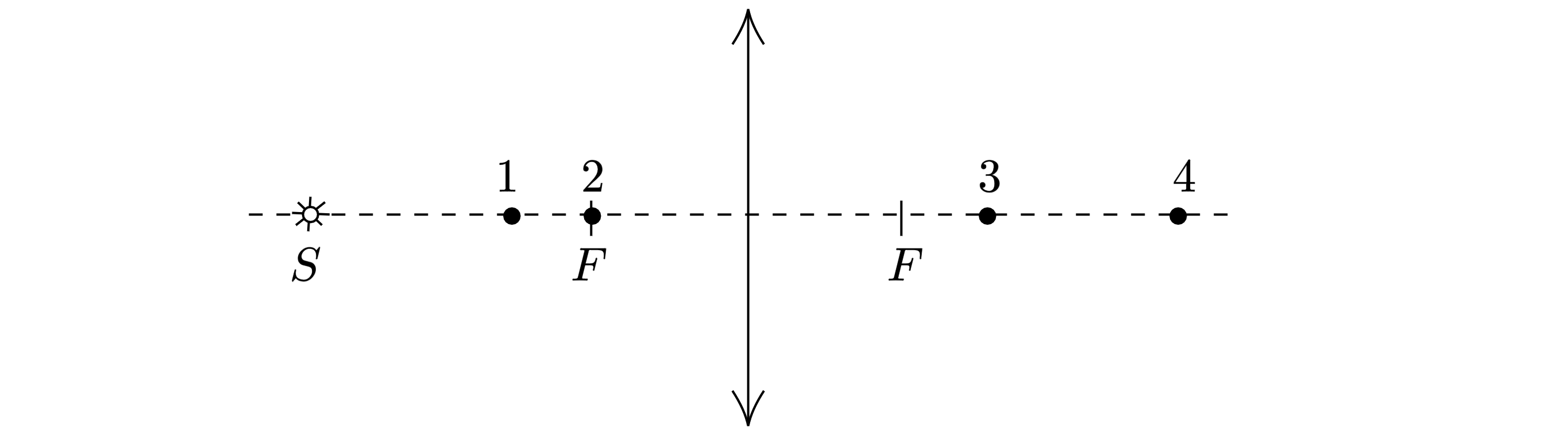
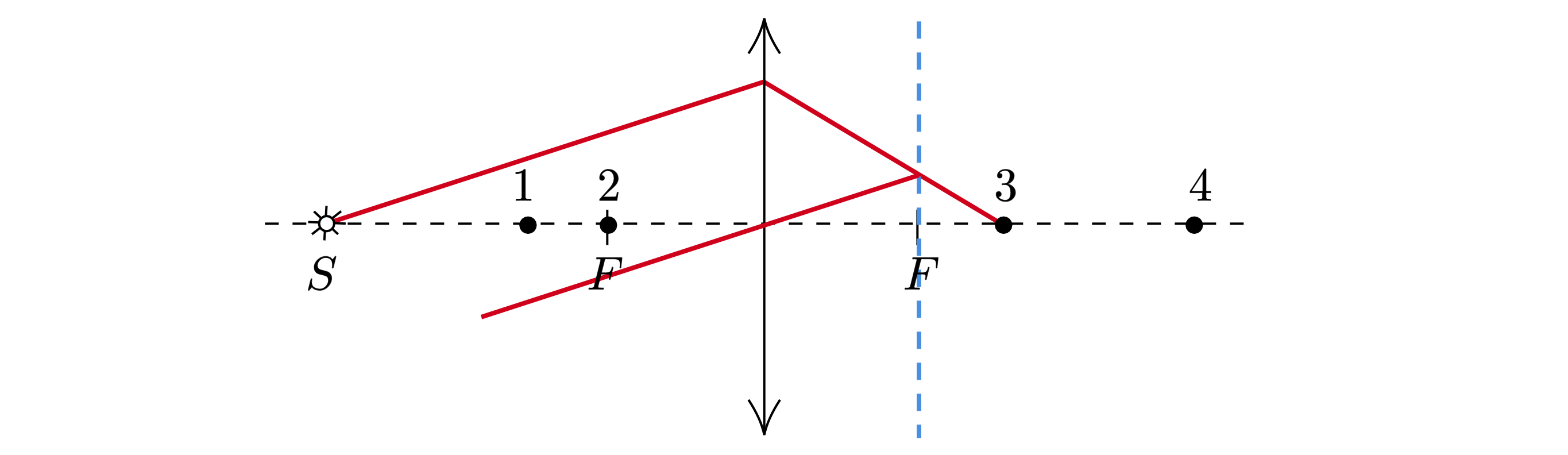
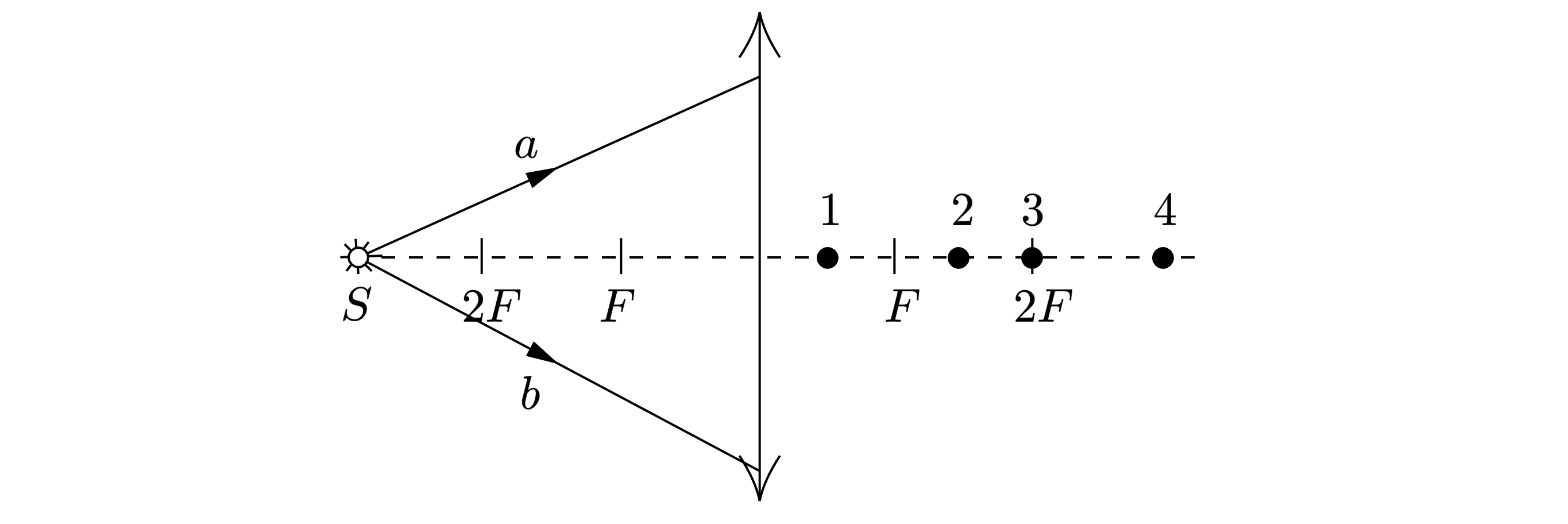
Какая из точек (1, 2, 3 или 4) является изображением точки S, создаваемым тонкой собирающей линзой с фокусным расстоянием F
(см. рисунок)
Показать ответ и решение
Проведём луч под некоторым углом к главной оптической оси (см .рис.). Также проведём луч через центр линзы параллельно
первому, при этом он не преломляется (см. рис.). Пересечение двух лучей даст побочный фокус, а продолжение первого луча –
искомую точку
В данном случае это точка 3
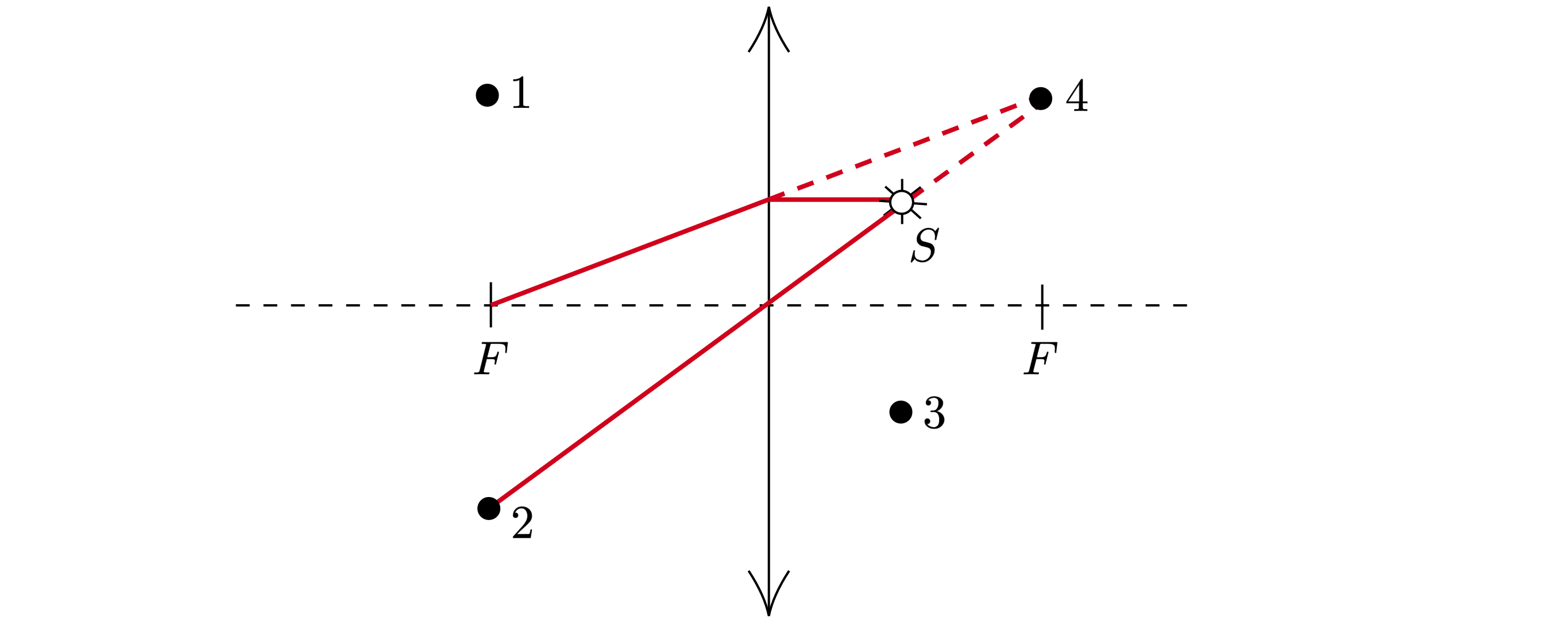
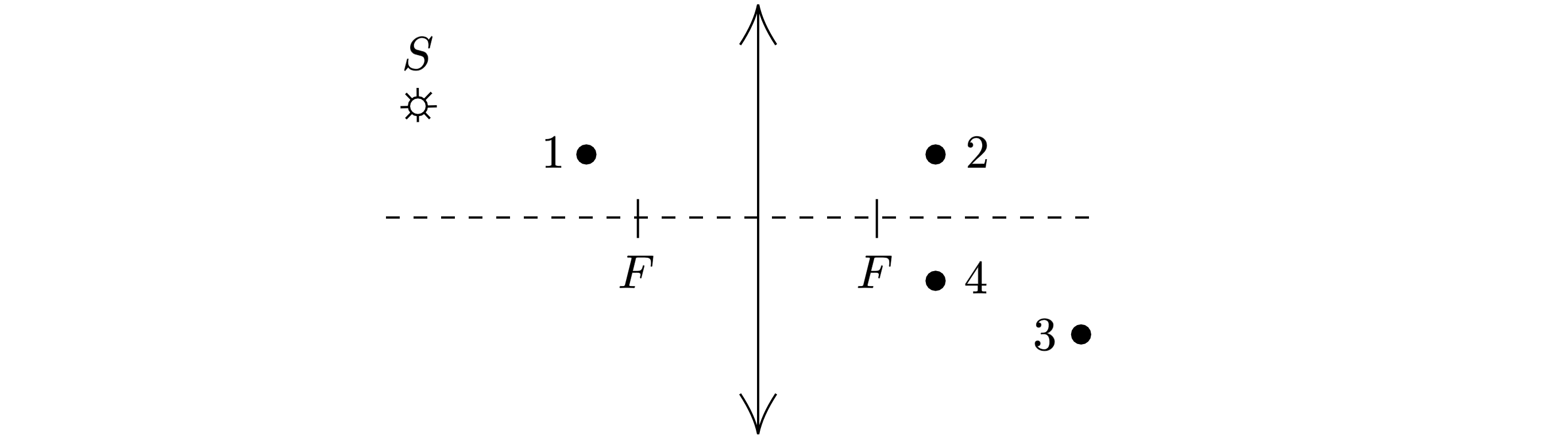
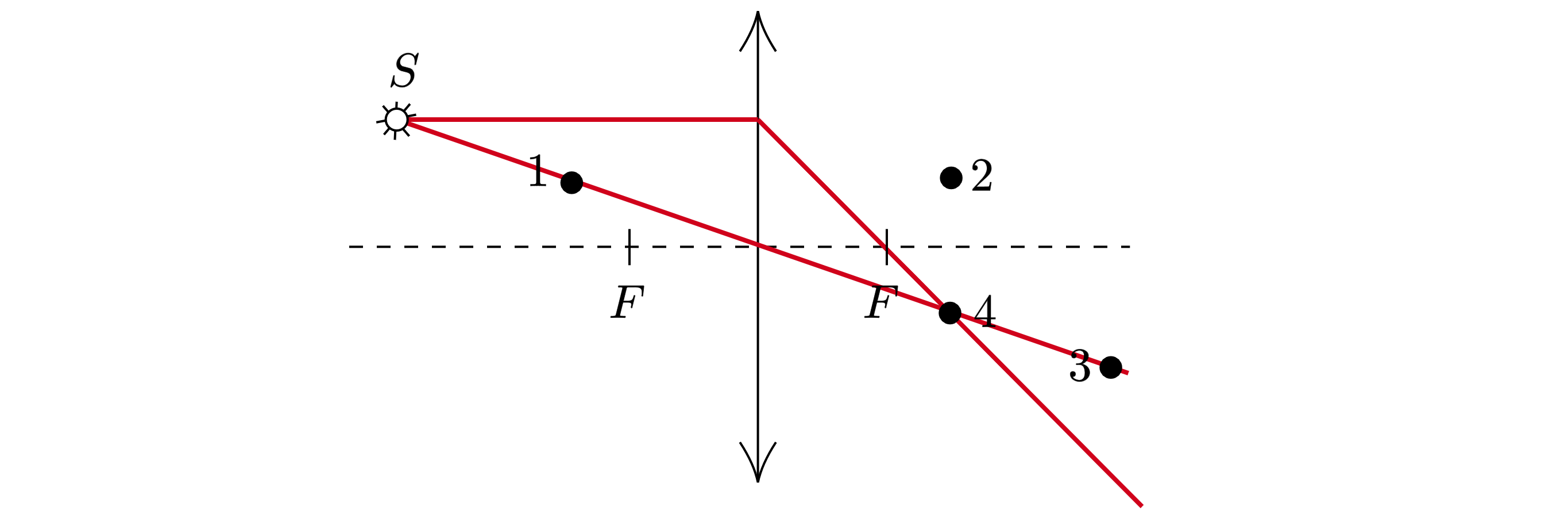
Какая из точек (1, 2, 3 или 4) является изображением точки S, создаваемым тонкой собирающей линзой с фокусным расстоянием F
(см. рисунок)
Показать ответ и решение
Проведём луч, параллельно главной оптической оси, после преломления он должен пройти через фокус линзы (см .рис.). Также
проведём луч через центр линзы, при этом он не преломляется (см. рис.). Пересечение двух лучей даст изображение
точки
В данном случае это точка 4
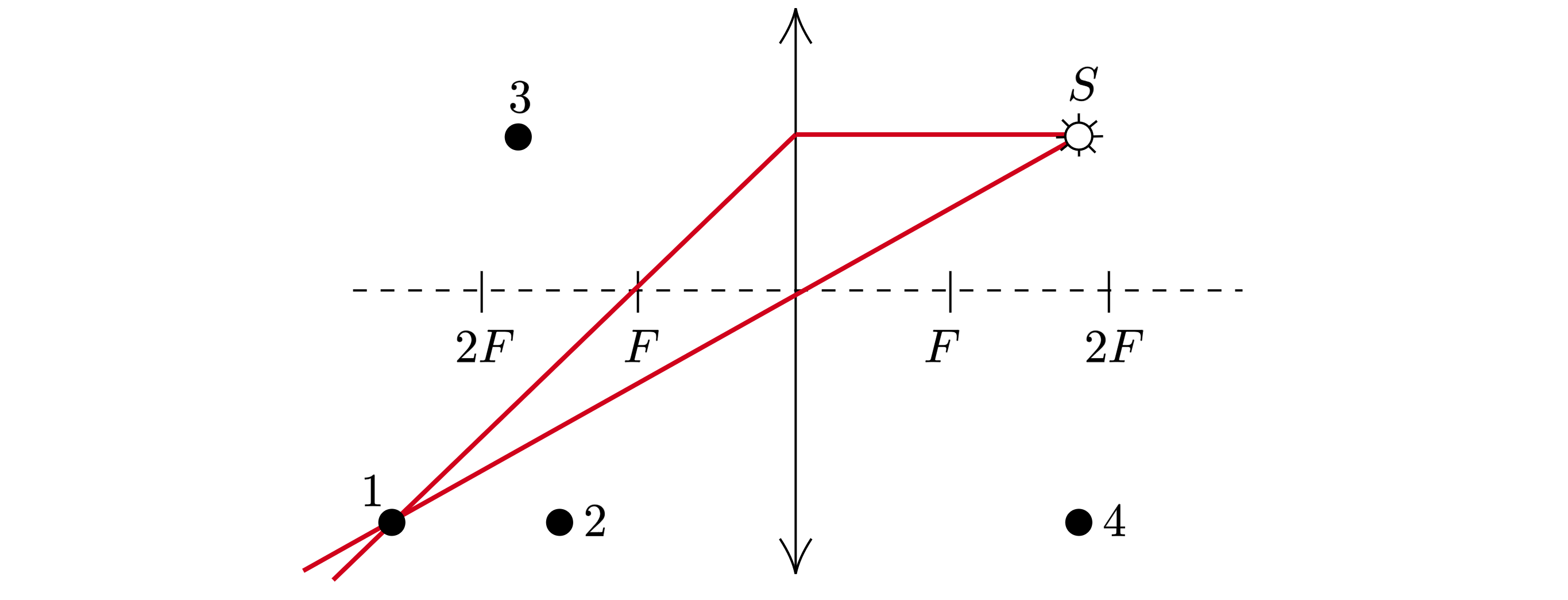
Какая из точек (1, 2, 3 или 4) является изображением точки S, создаваемым тонкой собирающей линзой с фокусным расстоянием F
(см. рисунок)
Показать ответ и решение
Проведём луч, параллельно главной оптической оси, после преломления он должен пройти через фокус линзы (см .рис.). Также
проведём луч через центр линзы, при этом он не преломляется (см. рис.). Пересечение двух лучей даст изображение
точки
В данном случае это точка 1
На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу.
Какова оптическая сила линзы? Ответ дайте в диоптриях.
Показать ответ и решение
Найдем фокусное расстояние линзы из рисунка. Луч до преломления, значит, после преломления луч пересекает главную
оптическую ось в фокусе линзы. В данном случае луч пересекает главную оптическую ось на расстоянии 5 клетки от линзы, то есть
5 см или 0,05 м. Оптическая сила линзы равна:
На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу.
Каково фокусное расстояние (в см) этой линзы?
Показать ответ и решение
Найдем фокусное расстояние линзы из рисунка. Для того, чтобы луч после преломления в тонкой линзе шел параллельно главной
оптической оси, он должен проходить через фокус линзы, в данном случае луч пересекает главную оптическую ось на расстоянии 3
клетки от линзы, то есть 6 см. Также найдём фокусное расстояние из формулы тонкой линзы. Нам известно расстояние предмета
от линзы 4 клетки или
см, нам известно расстояние изображения от линзы 12 клеток или
см. Применим формулу
тонкой линзы
Отсюда выразим фокусное расстояние
От точечного источника света , находящегося на главной оптической оси тонкой собирающей линзы с фокусным расстоянием
на расстоянии от неё, распространяются два луча:
и
, как показано на рисунке.
В какой точке: 1, 2, 3 или 4 – пересекутся эти лучи после преломления линзой?
Показать ответ и решение
Луч, проходящий под произвольным углом к главной оптической оси через центр тонкой линзы, преломляясь в ней, является
продолжением самого себя и называется побочной оптической осью. Проведём через центр линзы параллельные лучам и
(см.
рисунок)
На уровне лучи с одной стороны от главной оптической оси должны пересечься в одной точке (красные линии на рисунке).
Тогда продолжив лучи увидим, что лучи пересекаются в точке 2.
Какая из точек (1, 2, 3 или 4) является изображением точки S, создаваемым тонкой собирающей линзой с фокусным расстоянием F
(см. рисунок)
Показать ответ и решение
Проведём луч, параллельно главной оптической оси, после преломления он должен пройти через фокус линзы (см .рис.). Также
проведём луч через центр линзы, при этом он не преломляется (см. рис.). Пересечение двух лучей даст изображение
точки
В данном случае это точка 4
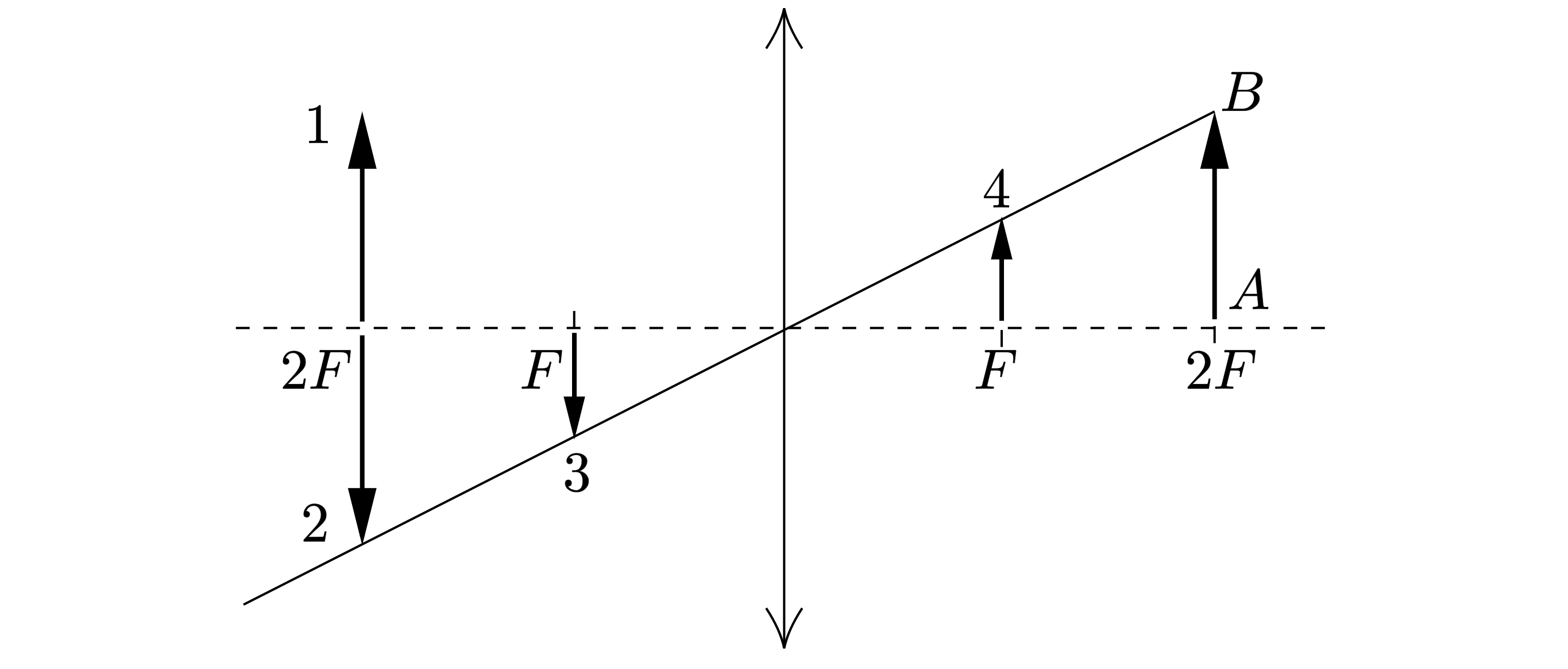
Какому из предметов 1-4 соответствует изображение АВ в тонкой линзе с фокусным расстоянием F?
Показать ответ и решение
Проведём луч, параллельно главной оптической оси, после преломления он должен пройти через фокус линзы (см
.рис.).
Пересечение красного и черного лучей даст искомое изображение
Предмет находится на расстоянии 20 см от собирающей линзы с фокусным расстоянием 15 см. Найдите расстояние (в см) от
изображения до линзы.
Показать ответ и решение
Формула тонкой линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Расстояние от предмета до рассеивающей линзы с фокусным расстоянием 4 см равно 12 см. Найдите расстояние (в см) от
изображения до предмета.
Показать ответ и решение
Формула тонкой линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Расстояние от предмета до изображения
Собирающая линза с фокусным расстоянием 10 см формирует мнимое изображение на расстоянии 15 см от линзы. На каком
расстоянии (в см) от этого изображения находится предмет?
Показать ответ и решение
Формула тонкой линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Расстояние от предмета до изображения см
Фокусное расстояние объектива проекционного фонаря 25 см. Какое увеличение диапозитива дает
фонарь, если экран удален от объектива на расстояние 200 см?
Показать ответ и решение
Формула тонкой линзы для собирающей линзы(объектива):
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы (расстояние от экрана до объектива)
Увеличение диапозитива:
На каком расстоянии (в см) от собирающей линзы с фокусным расстоянием 30 см следует поместить
предмет, чтобы получить действительное изображение, увеличенное в 3 раза?
Показать ответ и решение
Увеличение линзы:
Формула тонкой линзы для собирающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Расстояние от предмета до собирающей линзы составляет 1,25 от фокусного расстояния. Найдите
увеличение линзы.
Показать ответ и решение
Формула тонкой линзы для собирающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Увеличение линзы:
Расстояние между предметом и его увеличенным в 5 раз мнимым изображением 80 см. Найдите
расстояние (в см) от предмета до линзы.
Показать ответ и решение
Расстояние от предмета до линзы
Рассеивающая линза с фокусным расстоянием 8 см уменьшает предмет в два раза. Найдите расстояние
(в см) от предмета до линзы.
Показать ответ и решение
Формула тонкой линзы для рассеивающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Иголка высотой 3 см расположена перпендикулярно главной оптической оси тонкой собирающей линзы
на расстоянии 40 см от линзы. Оптическая сила линзы 4 дптр. Чему равна высота изображения иголки?
Ответ приведите в метрах.
Показать ответ и решение
Определим фокусное расстояние по формуле:
Сделаем рисунок
Формула тонкой линзы:
Увеличение линзы:
Расстояние от изображения до рассеивающей линзы составляет 0,75 фокусного расстояния. Во сколько
раз больше фокусного расстояние от предмета до линзы?
Показать ответ и решение
Формула тонкой линзы для данного случая:
где – фокусное расстояние,
– расстояние от предмета до линзы
– растояние от изображения до линзы,
Сейчас речь пойдет о геометрической оптике. В этом разделе много времени уделяется такому объекту, как линза. Ведь она может быть разной. При этом формула тонкой линзы одна на все случаи. Только нужно знать, как ее правильно применить.
Виды линз
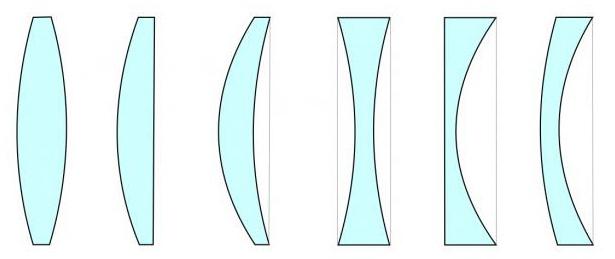
Ею всегда является прозрачное для световых лучей тело, которое имеет особенную форму. Внешний вид объекта диктуют две сферические поверхности. Одну из них допускается заменить на плоскую.
Причем у линзы может оказаться толще середина или края. В первом случае она будет называться выпуклой, во втором — вогнутой. Причем в зависимости от того, как сочетаются вогнутые, выпуклые и плоские поверхности, линзы тоже могут быть разными. А именно: двояковыпуклыми и двояковогнутыми, плосковыпуклыми и плосковогнутыми, выпукло-вогнутыми и вогнуто-выпуклыми.
В обычных условиях эти объекты используются в воздухе. Изготавливают их из вещества, оптическая плотность которого больше, чем у воздуха. Поэтому выпуклая линза будет собирающей, а вогнутая — рассеивающей.
Общие характеристики
До того, как говорить о формуле тонкой линзы, нужно определиться с основными понятиями. Их обязательно нужно знать. Поскольку к ним постоянно будут обращаться различные задачи.
Главная оптическая ось — это прямая. Она проведена через центры обеих сферических поверхностей и определяет место, где находится центр линзы. Существуют еще дополнительные оптические оси. Они проводятся через точку, являющуюся центром линзы, но не содержат центры сферических поверхностей.
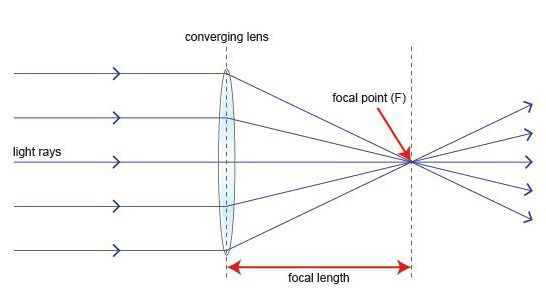
В формуле тонкой линзы есть величина, определяющая ее фокусное расстояние. Так, фокусом является точка на главной оптической оси. В ней пересекаются лучи, идущие параллельно указанной оси.
Причем фокусов у каждой тонкой линзы всегда два. Они расположены по обе стороны от ее поверхностей. Оба фокуса у собирающей действительные. У рассеивающей — мнимые.
Расстояние от линзы до точки фокуса — это фокусное расстояние (буква F). Причем его значение может быть положительным (в случае собирающей) или отрицательным (для рассеивающей).
С фокусным расстоянием связана еще одна характеристика — оптическая сила. Ее принято обозначать D. Ее значение всегда — величина, обратная фокусу, то есть D = 1/F. Измеряется оптическая сила в диоптриях (сокращенно, дптр).
Какие еще обозначения есть в формуле тонкой линзы
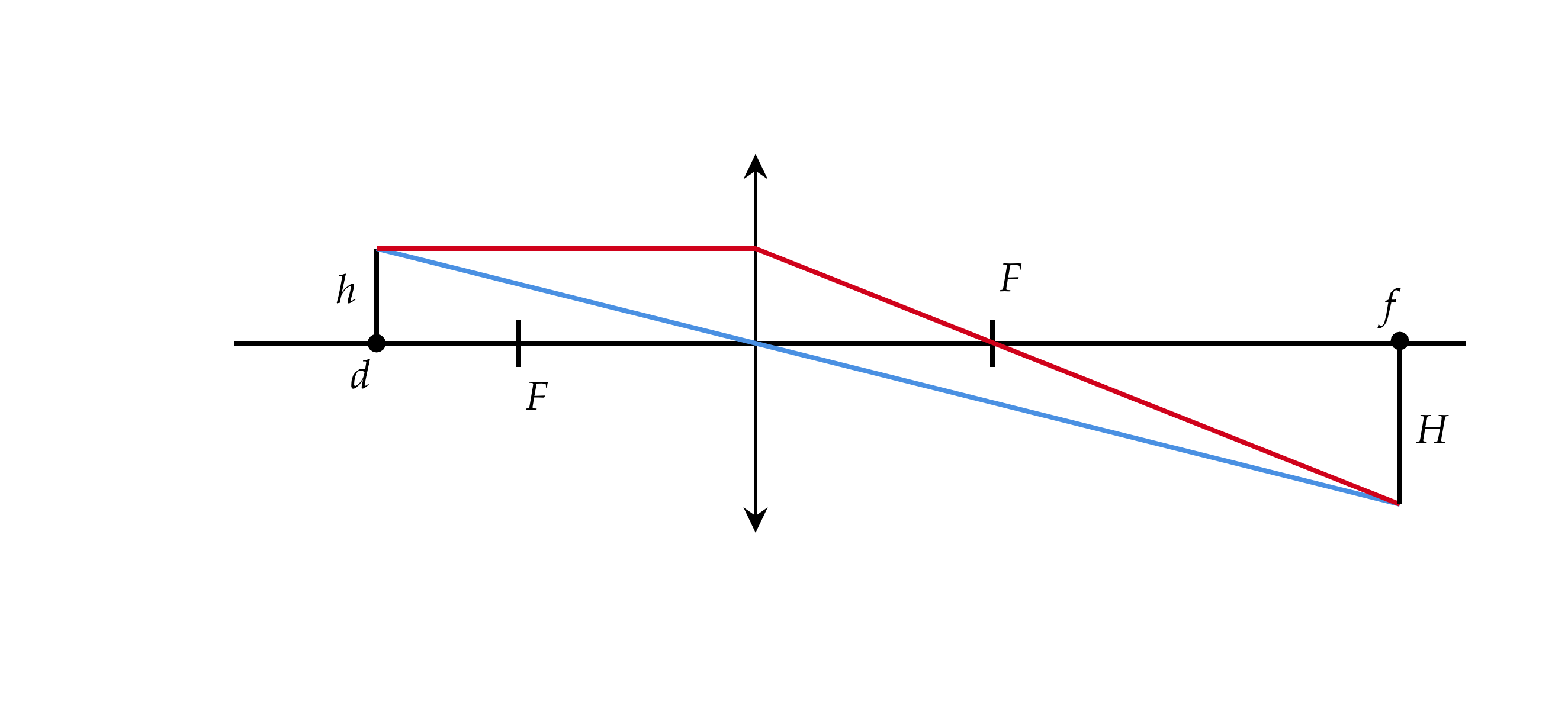
Помимо уже указанного фокусного расстояния, потребуется знать несколько расстояний и размеров. Для всех видов линз они одинаковые и представлены в таблице.
| Обозначение | Название |
| d | расстояние до предмета |
| h | высота изучаемого предмета |
| f | расстояние до изображения |
| H | высота получившегося изображения |
Все указанные расстояния и высоты принято измерять в метрах.
В физике с формулой тонкой линзы связано еще понятие увеличения. Оно определяется как отношение размеров изображения к высоте предмета, то есть H/h. Его можно обозначить буквой Г.
Что нужно для построения изображения в тонкой линзе
Это необходимо знать, чтобы получить формулу тонкой линзы, собирающей или рассеивающей. Чертеж начинается с того, что обе линзы имеют свое схематическое изображение. Обе они выглядят как отрезок. Только у собирающей на его концах стрелки направлены наружу, а у рассеивающей — внутрь этого отрезка.
Теперь к этому отрезку необходимо провести перпендикуляр к его середине. Так будет изображена главная оптическая ось. На ней с обеих сторон от линзы на одинаковом расстоянии полагается отметить фокусы.
Предмет, изображение которого требуется построить, рисуется в виде стрелки. Она показывает, где находится верх предмета. В общем случае предмет помещается параллельно линзе.
Как построить изображение в тонкой линзе
Для того чтобы построить изображение предмета, достаточно найти точки концов изображения, а потом их соединить. Каждая из этих двух точек может получиться от пересечения двух лучей. Наиболее простыми в построении являются два из них.
-
Идущий из указанной точки параллельно главной оптической оси. После соприкосновения с линзой он идет через главный фокус. Если речь идет о собирающей линзе, то этот фокус находится за линзой и луч идет через него. Когда рассматривается рассеивающая, то луч нужно провести так, чтобы его продолжение проходило через фокус перед линзой.
-
Идущий непосредственно через оптический центр линзы. Он не изменяет за ней своего направления.
Бывают ситуации, когда предмет поставлен перпендикулярно главной оптической оси и заканчивается на ней. Тогда достаточно построить изображение точки, которая соответствует краю стрелки, не лежащей на оси. А потом провести из нее перпендикуляр к оси. Это и будет изображение предмета.
Пересечение построенных точек дает изображение. В тонкой собирающей линзе получается действительное изображение. То есть оно получается непосредственно на пересечении лучей. Исключением является ситуация, когда предмет помещен между линзой и фокусом (как в лупе), тогда изображение оказывается мнимым. У рассеивающей же оно всегда получается мнимым. Ведь оно получается на пересечении не самих лучей, а их продолжений.
Действительное изображение принято чертить сплошной линией. А вот мнимое — пунктиром. Связано это с тем, что первое на самом деле там присутствует, а второе только видится.
Вывод формулы тонкой линзы
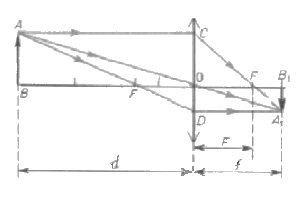
Это удобно сделать на основе чертежа, иллюстрирующего построение действительного изображения в собирающей линзе. Обозначение отрезков указано на чертеже.
Раздел оптики не зря называется геометрической. Потребуются знания именно из этого раздела математики. Для начала необходимо рассмотреть треугольники АОВ и А1ОВ1. Они подобны, поскольку в них имеется по два равных угла (прямые и вертикальные). Из их подобия следует, что модули отрезков А1В1 и АВ относятся как модули отрезков ОВ1 и ОВ.
Подобными (на основании того же принципа по двум углам) оказываются еще два треугольника: COF и A1FB1. В них равны отношения уже таких модулей отрезков: А1В1 с СО и FB1с OF. Исходя из построения равными будут отрезки АВ и СО. Поэтому левые части указанных равенств отношений одинаковые. Поэтому равны и правые. То есть ОВ1 / ОВ равно FB1/ OF.
В указанном равенстве отрезки, обозначенные точками, можно заменить на соответствующие физические понятия. Так ОВ1 — это расстояние от линзы до изображения. ОВ является расстоянием от предмета до линзы. OF — фокусное расстояние. А отрезок FB1 равен разности расстояния до изображения и фокуса. Поэтому его можно переписать по-другому:
f / d = (f – F) / F или Ff = df – dF.
Для вывода формулы тонкой линзы последнее равенство необходимо разделить на dfF. Тогда получается:
1/ d + 1/f = 1/F.
Это у есть формула тонкой собирающей линзы. У рассеивающей фокусное расстояние отрицательное. Это приводит к изменению равенства. Правда, оно незначительное. Просто в формуле тонкой рассеивающей линзы стоит минус перед отношением 1/F. То есть:
1/ d + 1/f = — 1/F.
Задача о нахождении увеличения линзы
Условие. Фокусное расстояние собирающей линзы равно 0,26 м. Требуется вычислить ее увеличение, если предмет находится на расстоянии 30 см.
Решение. Его начать стоит с введения обозначений и перевода единиц в Си. Так, известны d = 30 см = 0,3 м и F = 0,26 м. Теперь нужно выбрать формулы, основная из них та, которая указана для увеличения, вторая — для тонкой собирающей линзы.
Их нужно как-то объединить. Для этого придется рассмотреть чертеж построения изображения в собирающей линзе. Из подобных треугольников видно, что Г = H/h= f/d. То есть для того, чтобы найти увеличение, придется вычислить отношение расстояния до изображения к расстоянию до предмета.
Второе известно. А вот расстояние до изображения полагается вывести из формулы, указанной ранее. Получается, что
f = dF / (d — F).
Теперь эти две формулы необходимо объединить.
Г = dF / (d(d — F)) = F / (d — F).
В этот момент решение задачи на формулу тонкой линзы сводится к элементарным расчетам. Осталось подставить известные величины:
Г = 0,26 / (0,3 — 0,26) = 0,26 / 0,04 = 6,5.
Ответ: линза дает увеличение в 6,5 раз.
Задача, в которой нужно найти фокус
Условие. Лампа расположена в одном метре от собирающей линзы. Изображение ее спирали получается на экране, отстоящем от линзы на 25 см. Вычислите фокусное расстояние указанной линзы.
Решение. В данные полагается записать такие величины: d =1 м и f = 25 см = 0,25 м. Этих сведений достаточно, чтобы из формулы тонкой линзы вычислить фокусное расстояние.
Так 1/F = 1/1 + 1/0,25 = 1 + 4 = 5. Но в задаче требуется узнать фокус, а не оптическую силу. Поэтому остается только разделить 1 на 5, и получится фокусное расстояние:
F = 1/5 = 0,2 м.
Ответ: фокусное расстояние собирающей линзы равно 0,2 м.
Задача о нахождении расстояния до изображения
Условие. Свечку поставили на расстоянии 15 см от собирающей линзы. Ее оптическая сила равна 10 дптр. Экран за линзой поставлен так, что на нем получается четкое изображение свечи. Чему равно это расстояние?
Решение. В краткую запись полагается записать такие данные: d = 15 см = 0,15 м, D = 10 дптр. Формулу, выведенную выше, нужно записать с небольшим изменением. А именно, в правой части равенства поставить D вместо 1/F.
После нескольких преобразований получается такая формула для расстояния от линзы до изображения:
f = d / (dD — 1).
Теперь необходимо подставить все числа и сосчитать. Получается такое значение для f: 0,3 м.
Ответ: расстояние от линзы до экрана равно 0,3 м.
Задача о расстоянии между предметом и его изображением
Условие. Предмет и его изображение отстоят друг от друга на 11 см. Собирающая линза дает увеличение в 3 раза. Найти ее фокусное расстояние.
Решение. Расстояние между предметом и его изображением удобно обозначить буквой L = 72 см = 0,72 м. Увеличение Г = 3.
Здесь возможны две ситуации. Первая — предмет стоит за фокусом, то есть изображение получается действительное. Во второй — предмет между фокусом и линзой. Тогда изображение с той же стороны, что и предмет, причем мнимое.
Рассмотрим первую ситуацию. Предмет и изображение находятся по разные стороны от собирающей линзы. Здесь можно записать такую формулу: L = d + f. Вторым уравнением полагается записать: Г = f / d. Необходимо решить систему этих уравнений с двумя неизвестными. Для этого заменить L на 0,72 м, а Г на 3.
Из второго уравнения получается, что f = 3d. Тогда первое преобразуется так: 0,72 = 4d. Из него легко сосчитать d = 0,18 (м). Теперь легко определить f = 0,54 (м).
Осталось воспользоваться формулой тонкой линзы, чтобы вычислить фокусное расстояние. F = (0,18 * 0,54) / (0,18 + 0,54) = 0,135 (м). Это ответ для первого случая.
Во второй ситуации — изображение мнимое, и формула для L будет другой: L = f — d. Второе уравнение для системы будет тем же. Аналогично рассуждая, получим, что d = 0,36 (м), а f = 1,08 (м). Подобный расчет фокусного расстояния даст такой результат: 0,54 (м).
Ответ: фокусное расстояние линзы равно 0,135 м или 0,54 м.
Вместо заключения
Ход лучей в тонкой линзе — это важное практическое приложение геометрической оптики. Ведь их используют во многих приборах от простой лупы до точных микроскопов и телескопов. Поэтому знать о них необходимо.
Выведенная формула тонкой линзы позволяет решать множество задач. Причем она позволяет делать выводы о том, какое изображение дают разные виды линз. При этом достаточно знать ее фокусное расстояние и расстояние до предмета.
Предлагаю вашему вниманию несколько задач, в которых обязательно присутствуют две линзы. Линзы могут быть – обе — собирающими, и собирающей в комбинации с рассеивающей.
Задача 1.
Две собирающие линзы с фокусными расстояниями см и
см расположены вдоль общей главной оптической оси на расстоянии
см друг от друга. Где следует поместить точечный источник света, чтобы идущие от него лучи по прохождении обеих линз образовали пучок лучей, параллельных главной оптической оси?
Решение.
К задаче 1
Чтобы лучи после системы линз шли параллельным потоком, необходимо, чтобы после первой линзы лучи прошли бы через фокус второй. То есть изображение, даваемое первой линзой, должно попасть в фокус второй (на расстоянии 20 см от первой). Тогда запишем формулу линзы для первой:
Понятно, что первой может стоять линза с фокусным расстоянием 15 см. Тогда расчет немного изменится:
Ответ: 30 см или 60 см
Задача 2.
На собирающую линзу с фокусным расстоянием см падает параллельный пучок лучей. Где следует поместить рассеивающую линзу с фокусным расстоянием
см, чтобы пучок лучей после прохождения двух линз остался параллельным?
К задаче 2
Решение. Ход световых лучей обратим. Если бы лучи падали на рассеивающую линзу слева параллельным потоком, то они далее рассеивались и шли бы за линзой расходящимся потоком. То есть, чтобы обеспечить параллельный ход лучей за линзой, нужно, чтобы фокус рассеивающей линзы совпадал с фокусным расстоянием собирающей. Тогда падающий на рассеивающую линзу сходящийся поток лучей преобразуется ею в параллельный.
Ответ 25 см.
Задача 3.
Система состоит из двух линз с одинаковыми по модулю фокусными расстояниями. Одна из линз собирающая, другая рассеивающая. Линзы расположены на одной оси на некотором расстоянии друг от друга. Известно, что если поменять линзы местами, то действительное изображение Луны, даваемое этой системой, сместится на см. Найдите фокусное расстояние каждой из линз.
Решение. Пусть первой стоит рассеивающая линза, а затем собирающая. Сначала ход лучей был таким:
Рисунок 1 к задаче 3
Для собирающей линзы тогда
Откуда
Теперь поменяем линзы местами (действительное изображение может получиться только, если на рассеивающую линзу падает сходящийся пучок, то есть при мнимом предмете):
Запишем уравнение для рассеивающей линзы.
Как видно из обеих картинок, изображение переместилось на расстояние :
Откуда
Ответ 10 см
Задача 4.
Собирающая линза дает на экране изображение светящейся точки
, лежащей на главной оптической оси. Между линзой и экраном на расстоянии
см от экрана поместили рассеивающую линзу. Отодвигая экран от рассеивающей линзы, получили новое изображение
светящейся точки
. При этом расстояние нового положения экрана от рассеивающей линзы равно
см.
Определите фокусное расстояние F рассеивающей линзы и ее оптическую силу в диоптриях.
Решение.
К задаче 4
Запишем уравнение линзы (рассеивающей)
Здесь снова использована обратимость световых лучей (показана с помощью зеленого луча).
Ответ: фокусное расстояние 30 см, оптическая сила -3,3 дптр.
Задача 5.
Параллельный пучок света падает перпендикулярно на собирающую линзу, оптическая сила которой дптр. На расстоянии 20 см от нее находится рассеивающая линза с оптической силой
дптр. Диаметр линз равен 5 см. На расстоянии 30 см от рассеивающей линзы расположен экран Э. Каков диаметр светлого пятна, создаваемого линзами, на экране?
Решение. Определим фокусные расстояния линз.
Значит, задние фокусы обеих линз совпадают! А это означает, что, как и во второй задаче, падающий на рассеивающую линзу сходящийся поток лучей преобразуется ею в параллельный.
К задаче 5
Если бы рассеивающей линзы не было, то ширина светового пучка в месте ее установки была бы вдвое уже диаметра линзы – из подобия треугольников. Поэтому диаметр светлого пятна будет равен 2,5 см.
Ответ: 2,5 см.
Задача 6.
Две собирающие линзы с оптическими силами дптр и
дптр расположены на расстоянии
см друг от друга. Найдите, используя построение в линзах, где находится изображение предмета, расположенного на расстоянии
см от первой линзы, и поперечное увеличение системы.
Решение. Фокусное расстояние первой линзы равно 20 см.
Поэтому предмет расположен в двойном фокусе и его изображение получится тоже в двойном фокусе, то есть в 20 см от второй линзы. Составим уравнение линзы для второй:
Изображение получится в метре от второй линзы. Так как первая линза не увеличивает, то увеличение системы равно увеличению второй линзы. А это
Ответ: изображение получится в 1 м от второй линзы; увеличение системы равно 5.
3 комментария
Николай
✉️
11.02.2022 19:12:39
Здравствуйте, Анна!
Мне кажется, что задача 3 решена неверно.
По условию задачи в обоих случаях система дает действительное изображение. У вас во втором случае, когда свет сначала падает на собирающую линзу, а после нее падает расходящимся пучком на рассеивающую линзу, в принципе не может получиться действительное изображение.
Задача имеет решение только в случае, когда расстояние между линзами меньше фокусного расстояния.
Николай
✉️
11.02.2022 19:15:19
Не нашел возможности прикрепить файл с верным решением. Если интересно, могу прислать. Ответ тот же, что и у вас. Так как вы допустили две ошибки (чертеж и знаки в формуле линзы), в результате получили верный ответ.
Анна Валерьевна
✨
14.02.2022 08:26:50
Спасибо! Конечно, вы абсолютно правы. Исправила.
Данную презентацию можно использовать при решении задач на уроке и при подготовке к ЕГЭ.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение задач по теме: «Линзы» (подготока к ЕГЭ)»
Тонкие линзы. Построение изображений.
-
Собирающая линза: действительное изображение точки.
-
Собирающая линза: действительное изображение предмета.
-
Собирающая линза: мнимое изображение точки.
-
Собирающая линза: мнимое изображение предмета.
-
Собирающая линза: предмет в фокальной плоскости.
-
Рассеивающая линза: мнимое изображение точки.
-
Рассеивающая линза: мнимое изображение предмета.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: построение изображений в линзах, формула тонкой линзы.
Правила хода лучей в тонких линзах, сформулированные в предыдущей теме, приводят нас к важнейшему утверждению.
Теорема об изображении. Если перед линзой находится светящаяся точка , то после преломления в линзе все лучи (или их продолжения) пересекаются в одной точке
.
| Напомним ещё раз, что это касается не вообще всех лучей, а только параксиальных, то есть образующих малые углы с главной оптической осью. В предыдущей теме мы договорились, что рассматриваем только параксиальные лучи. Лишь для них работают наши правила хода лучей сквозь тонкие линзы. |
Точка называется изображением точки
.
Если в точке пересекаются сами преломлённые лучи, то изображение называется действительным. Оно может быть получено на экране, так как в точке
концентрируется энергия световых лучей.
Если же в точке пересекаются не сами преломлённые лучи, а их продолжения (так бывает, когда преломлённые лучи расходятся после линзы), то изображение называется мнимым. Его нельзя получить на экране, поскольку в точке
не сосредоточено никакой энергии. Мнимое изображение, напомним, возникает благодаря особенности нашего мозга — достраивать расходящиеся лучи до их мнимого пересечения и видеть в этом пересечении светящуюся точку.Мнимое изображение существует лишь в нашем сознании.
Теорема об изображении служит основой построения изображений в тонких линзах. Мы докажем эту теорему как для собирающей, так и для рассеивающей линзы.
к оглавлению ▴
Собирающая линза: действительное изображение точки.
Сперва рассмотрим собирающую линзу. Пусть — расстояние от точки
до линзы,
— фокусное расстояние линзы. Имеются два принципиально разных случая:
и
(а также промежуточный случай
). Мы разберём эти случаи поочерёдно; в каждом из них мы
обсудим свойства изображений точечного источника и протяжённого объекта.
Первый случай: . Точечный источник света
расположен дальше от линзы, чем левая фокальная плоскость (рис. 1).
 |
| Рис. 1. Случай a>f: действительное изображение точки S |
Луч , идущий через оптический центр, не преломляется. Мы возьмём произвольный луч
, построим точку
, в которой преломлённый луч пересекается с лучом
, а затем покажем, что положение точки
не зависит от выбора луча
(иными словами, точка
является одной и той же для всевозможных лучей
). Тем самым окажется, что все лучи, исходящие из точки
, после преломления в линзе пересекаются в точке
и теорема об изображении будет доказана для рассматриваемого случая
.
Точку мы найдём, построив дальнейший ход луча
. Делать это мы умеем: параллельно лучу
проводим побочную оптическую ось
до пересечения с фокальной плоскостью в побочном фокусе
, после чего проводим преломлённый луч
до пересечения с лучом
в точке
.
Теперь будем искать расстояние от точки
до линзы. Мы покажем, что это расстояние выражается только через
и
, т. е. определяется лишь положением источника и свойствами линзы, и не зависит тем самым от конкретного луча
.
Опустим перпендикуляры и
на главную оптическую ось. Проведём также
параллельно главной оптической оси, т. е. перпендикулярно линзе. Получим три пары подобных треугольников:
, (1)
, (2)
. (3)
В результате имеем следующую цепочку равенств (номер формулы над знаком равенства указывает, из какой пары подобных треугольников данное равенство получено).
(4)
Но , так что соотношение (4) переписывается в виде:
. (5)
Отсюда находим искомое расстояние от точки до линзы:
. (6)
Как видим, оно и в самом деле не зависит от выбора луча . Следовательно, любой луч
после преломления в линзе пройдёт через построенную нами точку
, и эта точка будет действительным изображением источника
Теорема об изображении в данном случае доказана.
Практическая важность теоремы об изображении состоит вот в чём. Коль скоро все лучи источника пересекаются после линзы в одной точке — его изображении
— то для построения изображения достаточно взять два наиболее удобных луча. Какие именно?
Если источник не лежит на главной оптической оси, то в качестве удобных лучей годятся следующие:
— луч, идущий через оптический центр линзы — он не преломляется;
— луч, параллельный главной оптической оси — после преломления он идёт через фокус.
Построение изображения с помощью этих лучей показано на рис. 2.
 |
| Рис. 2. Построение изображения точки S, не лежащей на главной оптической оси |
Если же точка лежит на главной оптической оси, то удобный луч остаётся лишь один — идущий вдоль главной оптической оси. В качестве второго луча приходится брать «неудобный» (рис. 3).
 |
| Рис. 3. Построение изображения точки S, лежащей на главной оптической оси |
Посмотрим ещё раз на выражение ( 5). Его можно записать в несколько ином виде, более симпатичном и запоминающемся. Перенесём сначала единицу влево:
Теперь разделим обе части этого равенства на a:
(7)
Соотношение (7) называется формулой тонкой линзы (или просто формулой линзы). Пока что формула линзы получена для случая собирающей линзы и для . В дальнейшем мы выведем модификации этой формулы для остальных случаев.
Теперь вернёмся к соотношению (6). Его важность не исчерпывается тем, что оно доказывает теорему об изображении. Мы видим также, что не зависит от расстояния
(рис. 1, 2) между источником
и главной оптической осью!
Это означает, что какую бы точку отрезка
мы ни взяли, её изображение будет находиться на одном и том же расстоянии
от линзы. Оно будет лежать на отрезке
— а именно, на пересечении отрезка
с лучом
, который пойдёт сквозь линзу без преломления. В частности, изображением точки
будет точка
.
Тем самым мы установили важный факт: изображением отрезка лужит отрезок
. Отныне исходный отрезок, изображение которого нас интересует, мы называем предметом и обозначаем на рисунках красной стрелочкой. Направление стрелки нам понадобится для того, чтобы следить — прямым или перевёрнутым получается изображение.
к оглавлению ▴
Перейдём к рассмотрению изображений предметов. Напомним, что пока мы находимся в рамках случая . Здесь можно выделить три характерных ситуации.
1. . Изображение предмета является действительным, перевёрнутым, увеличенным (рис. 4; двойной фокус обозначен
). Из формулы линзы следует, что в этом случае будет
(почему?).
Такая ситуация реализуется, например, в диапроекторах и киноаппаратах — эти оптические приборы дают на экране увеличенное изображение того, что находится на плёнке. Если вам доводилось показывать слайды, то вы знаете, что слайд нужно вставлять в проектор перевёрнутым — чтобы изображение на экране выглядело правильно, а не получилось вверх ногами.
Отношение размера изображения к размеру предмета называется линейным увеличением линзы и обозначается Г — (это заглавная греческая «гамма»):
.
Из подобия треугольников и
получим:
. (8)
Формула (8) применяется во многих задачах, где фигурирует линейное увеличение линзы.
2. . В этом случае из формулы (6) находим, что и
. Линейное увеличение линзы согласно (8) равно единице, т. е. размер изображения равен размеру предмета (рис. 5).
 |
| Рис. 5.a=2f: размер изображения равен размеру предмета |
3. . В этом случае из формулы линзы следует, что
(почему?). Линейное увеличение линзы будет меньше единицы — изображение действительное, перевёрнутое, уменьшенное (рис. 6).
 |
| Рис. 6.a>2f: изображение действительное, перевёрнутое, уменьшенное |
Данная ситуация является обычной для многих оптических приборов: фотоаппаратов, биноклей, телескопов — словом, тех, в которых получают изображения удалённых объектов. По мере удаления предмета от линзы его изображение уменьшается в размерах и приближается к фокальной плоскости.
Рассмотрение первого случая нами полностью закончено. Переходим ко второму случаю. Он уже не будет столь объёмным.
к оглавлению ▴
Собирающая линза: мнимое изображение точки.
Второй случай: . Точечный источник света
расположен между линзой и фокальной плоскостью (рис. 7).
 |
| Рис. 7. Случай a < f: мнимое изображение точки |
Наряду с лучом , идущим без преломления, мы снова рассматриваем произвольный луч
. Однако теперь на выходе из линзы получаются два расходящихся луча
и
. Наш глаз продолжит эти лучи до пересечения в точке
.
Теорема об изображении утверждает, что точка будет одной и той же для всех лучей
, исходящих из точки
. Мы опять докажем это с помощью трёх пар подобных треугольников:
Снова обозначая через расстояние от
до линзы, имеем соответствующую цепочку равенств (вы уже без труда в ней разберётесь):
. (9)
Отсюда
. (10)
Величина не зависит от луча
, что и доказывает теорему об изображении для нашего случая
. Итак,
— мнимое изображение источника
. Если точка
не лежит на главной оптической оси, то для построения изображения
удобнее всего брать луч, идущий через оптический центр, и луч, параллельный главной оптической оси (рис. 8).
 |
| Рис. 8. Построение изображения точки S, не лежащей на главной оптической оси |
Ну а если точка лежит на главной оптической оси, то деваться некуда — придётся довольствоваться лучом, падающим на линзу наклонно (рис. 9).
 |
| Рис. 9. Построение изображения точки S, лежащей на главной оптической оси |
Соотношение (9) приводит нас к варианту формулы линзы для рассматриваемого случая . Сначала переписываем это соотношение в виде:
,
а затем делим обе части полученного равенства на a:
. (11)
Сравнивая (7) и (11), мы видим небольшую разницу: перед слагаемым стоит знак плюс, если изображение действительное, и знак минус, если изображение мнимое.
Величина , вычисляемая по формуле (10), не зависит также от расстояния
между точкой
и главной оптической осью. Как и выше (вспомните рассуждение с точкой
), это означает, что изображением отрезка
на рис. 9 будет отрезок
.
к оглавлению ▴
Учитывая это, мы легко строим изображение предмета, находящегося между линзой и фокальной плоскостью (рис. 10). Оно получается мнимым, прямым и увеличенным.
Такое изображение вы наблюдаете, когда разглядываете мелкий предмет в увеличительное стекло — лупу. Случай полностью разобран. Как видите, он качественно отличается от нашего первого случая
. Это не удивительно — ведь между ними лежит промежуточный «катастрофический» случай
.
к оглавлению ▴
Собирающая линза: предмет в фокальной плоскости.
Промежуточный случай:. Источник света
расположен в фокальной плоскости линзы (рис. 11).
Как мы помним из предыдущего раздела, лучи параллельного пучка после преломления в собирающей линзе пересекутся в фокальной плоскости — а именно, в главном фокусе, если пучок падает перпендикулярно линзе, и в побочном фокусе при наклонном падении пучка. Воспользовавшись обратимостью хода лучей, мы заключаем, что все лучи источника , расположенного в фокальной плоскости, после выхода из линзы пойдут параллельно друг другу.
 |
| Рис. 11. a=f: изображение отсутствует |
Где же изображение точки ? Изображения нет. Впрочем, никто не запрещает нам считать, что параллельные лучи пересекаются в бесконечно удалённой точке. Тогда теорема об изображении сохраняет свою силу и в данном случае — изображение
находится на бесконечности.
Соответственно, если предмет целиком расположен в фокальной плоскости, изображение этого предмета будет находиться на бесконечности (или, что то же самое, будет отсутствовать).
Итак, мы полностью рассмотрели построение изображений в собирающей линзе.
к оглавлению ▴
Рассеивающая линза: мнимое изображение точки.
К счастью, здесь нет такого разнообразия ситуаций, как для собирающей линзы. Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.
Снова берём луч и произвольный луч
(рис. 12). На выходе из линзы имеем два расходящихся луча
и
, которые наш глаз достраивает до пересечения в точке
.
 |
| Рис. 12. Мнимое изображение точки S в рассеивающей линзе |
Нам снова предстоит доказать теорему об изображении — о том, что точка будет одной и той же для всех лучей
. Действуем с помощью всё тех же трёх пар подобных треугольников:
.
Имеем:
(12)
Отсюда
. (13)
Величина b не зависит от луча span
, поэтому продолжения всех преломлённых лучей span
пересекутся в точке
— мнимом изображении точки
. Теорема об изображении тем самым полностью доказана.
Вспомним, что для собирающей линзы мы получили аналогичные формулы (6) и (10). В случае их знаменатель обращался в нуль (изображение уходило на бесконечность), и поэтому данный случай разграничивал принципиально разные ситуации
и
.
А вот у формулы (13) знаменатель не обращается в нуль ни при каком a. Стало быть, для рассеивающей линзы не существует качественно разных ситуаций расположения источника — случай тут, как мы и сказали выше, имеется только один.
Если точка не лежит на главной оптической оси, то для построения её изображения удобны два луча: один идёт через оптический центр, другой — параллельно главной оптической оси (рис. 13).
 |
| Рис. 13. Построение изображения точки S, не лежащей на главной оптической оси |
Если же точка лежит на главной оптической оси, то второй луч приходится брать произвольным (рис. 14).
 |
| Рис. 14. Построение изображения точки S, лежащей на главной оптической оси |
Соотношение (13) даёт нам ещё один вариант формулы линзы. Сначала перепишем:
,
а потом разделим обе части полученного равенства на a:
(14)
Так выглядит формула линзы для рассеивающей линзы.
Три формулы линзы (7), (11) и (14) можно записать единообразно:
если соблюдать следующую договорённость о знаках:
— для мнимого изображения величина считается отрицательной;
— для рассеивающей линзы величина считается отрицательной.
Это очень удобно и охватывает все рассмотренные случаи.
к оглавлению ▴
Величина , вычисляемая по формуле (13), опять-таки не зависит от расстояния
между точкой
и главной оптической осью. Это снова даёт нам возможность построить изображение предмета
, которое на сей раз получается мнимым, прямым и уменьшенным (рис. 15).
 |
| Рис. 15. Изображение мнимое, прямое, уменьшенное |
Разберем задачи ЕГЭ по теме: Тонкие линзы. Построение изображений.
1. Тонкая собирающая линза с фокусным расстоянием F находится между двумя точечными источниками света на расстоянии d=15 см от одного из них. Источники расположены на главной оптической оси на расстоянии L=22,5 см друг от друга. Найдите фокусное расстояние линзы, если их изображения получились в одной точке. Ответ выразите в сантиметрах.
Дано:
= 15 см = 0,15 м
= 22,5 см=0,225 м
Найти:
Фокусное расстояние F — ?
Решение:
Тонкая собирающая линза дает различные виды изображений: увеличенные (уменьшенные), прямые (обратные), действительные (мнимые). Характеристика изображения зависит от расстояния от предмета до линзы, т.е. от соотношения d и F.
Так как в задаче говорится о получении изображений в одной точке, то один из точечных источников должен находиться за фокусом линзы – он дает действительное изображение. Второй точечный источник должен находиться перед фокусом – он дает мнимое изображение.
На рис. 1 представлено получение изображения для точечного источника света , находящегося на расстоянии больше фокусного,
— изображение точечного источника света
.
На рис. 2 представлено получение изображения для точечного источника света , находящегося на расстоянии меньше фокусного,
— изображение точечного источника света
.
После создания модели, поясняющей условие этой задачи, можно переходить к её решению. Для этого надо применить формулу тонкой линзы для двух случаев. С учетом правила знаков , так как изображение в первом случае действительное, во втором – мнимое.
Сложим эти два уравнения и учтем, что Так как изображения в двух случаях получались в одной точке, то
Определим, что (м).
(м)
(см).
Ответ: 10
2. Какая из точек (1, 2, 3 или 4) является изображением точки S, созданным тонкой собирающей линзой с фокусным расстоянием F (см. рисунок)?
Решение:
Для получения изображения точечного источника S необходимо осуществить построение двух любых лучей, исходящих от этого источника. Самым «удобным» лучом является луч, проходящий через оптический центр линзы. Такие лучи, после прохождения через линзу, не меняют своего направления. На рисунке таким лучом является луч 1-1ʹ.
Второй и третий лучи от точечного источника S попадают на линзу произвольно. Дальнейший ход таких лучей определяется следующим алгоритмом:
- необходимо построить побочные оптические оси, параллельные падающим лучам (на рисунке они проведены пунктирной линией);
- провести фокальную плоскость и найти точки пересечения этой плоскости с побочными оптическими осями;
- продолжить ход световых лучей после прохождения через линзу (на рисунке это лучи 2ʹ и 3ʹ).
Поэтому изображением точечного источника S (точки S) будет являться точка 2.
При решении этой задачи мы рассмотрели ход трех лучей сквозь линзу, для получения ответа достаточно взять любую комбинацию лучей (1-1ʹ и 2 — 2ʹ) или (1-1ʹ и 3 — 3ʹ ).
Ответ: 2
3. Спираль лампочки расположена вблизи главной оптической оси тонкой рассеивающей линзы на расстоянии а от неё перпендикулярно этой оси, причем , где F – модуль фокусного расстояния линзы. Затем рассеивающую линзу заменили на собирающую с фокусным расстоянием F. Установите соответствие между видом линзы, использованной в опыте, и свойствами даваемого ею изображения.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| Виды линз | Свойства изображения |
| А) линза рассеивающая | 1) мнимое, прямое, уменьшенное |
| Б) линза собирающая | 2) мнимое, перевёрнутое, увеличенное |
| 3) действительное, перевёрнутое, увеличенное | |
| 4) действительное, прямое, увеличенное |
Решение
Решение подобных задач опирается на умение строить изображения протяженных (имеющих размеры) предметов при прохождении лучей через линзу.
Рис.1
На рис.1 выполнено построение изображения предмета АВ в тонкой собирающей линзе. Для этого применялись следующие лучи:
1-1ʹ — луч, проходящий через оптический центр, не преломляется;
2 — 2ʹ — луч, падающий на линзу параллельно главной оптической оси, после преломления идет через фокус, расположенный за линзой .
Полученное изображение АʹВʹ имеет следующие характеристики:
увеличенное (размер изображения превышает размер предмета),
перевернутое (направления стрелок АВ и АʹВʹ противоположны),
действительное (предмет и его изображения находятся по разные стороны от линзы).
Рис.2
На рис.2 выполнено построение изображения предмета АВ в тонкой рассеивающей линзе. Для этого применялись следующие лучи:
1-1ʹ — луч, проходящий через оптический центр, не преломляется;
2 — 2ʹ — луч, падающий на линзу параллельно главной оптической оси, после преломления идет через фокус, расположенный перед линзой .
Полученное изображение АʹВʹ имеет следующие характеристики:
уменьшенное (размер изображения меньше размера предмета),
прямое (направления стрелок АВ и АʹВʹ совпадают),
мнимое (предмет и его изображения находятся с одной стороны от линзы).
Полученные изображения и их характеристики приводят к следующему ответу:
4. На рисунке показан ход лучей от точечного источника света S через тонкую линзу. Какова оптическая сила этой линзы? (Ответ дать в диоптриях.)
Решение:
На рисунке представлен ход световых лучей от точечного источника света S. Луч, проходящий через оптический центр, не меняет своего направления. Второй луч, идущий параллельно главной оптической оси, после преломления идет через фокус. Это позволяет определить фокусное расстояние линзы. Согласно рисунку, оно равно двум клеткам. С учётом указанного масштаба, длина одной клетки равна 4 см. Таким образом, фокусное расстояние этой линзы F=8 см = 0,08 м.
Так как оптическая сила линзы (дптр).
Ответ: 12,5
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Тонкие линзы. Построение изображений.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023