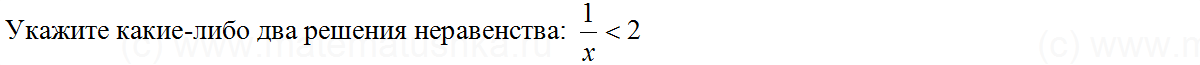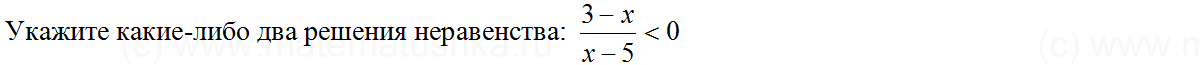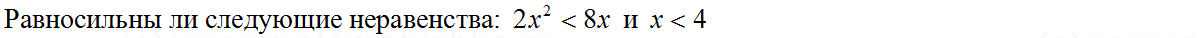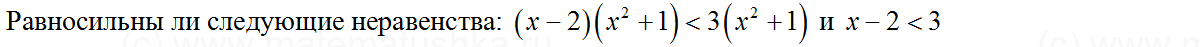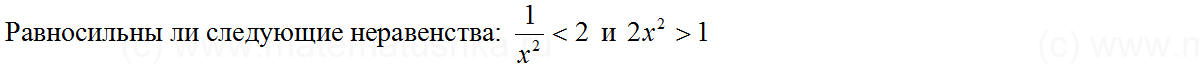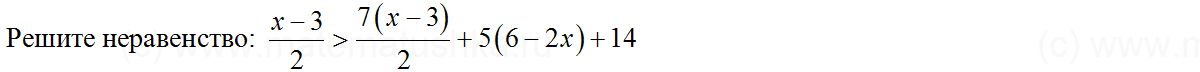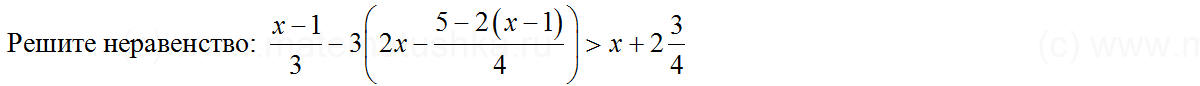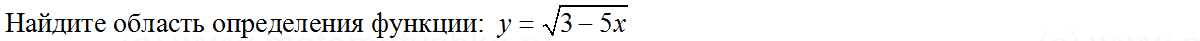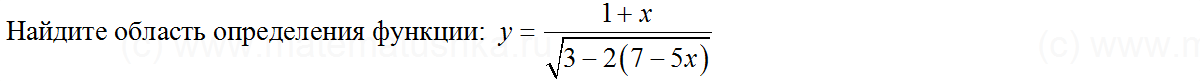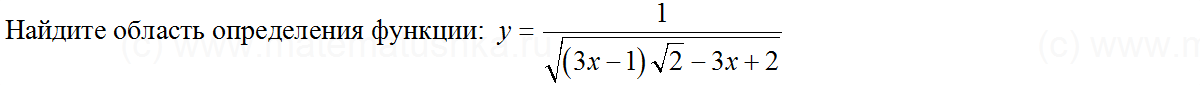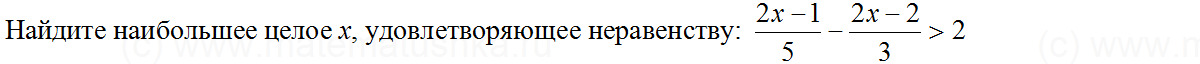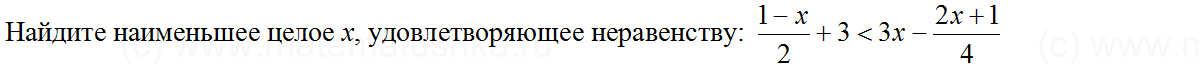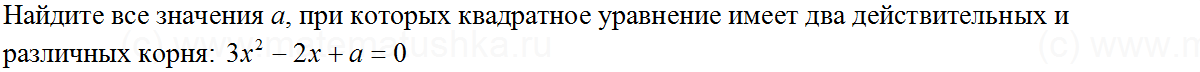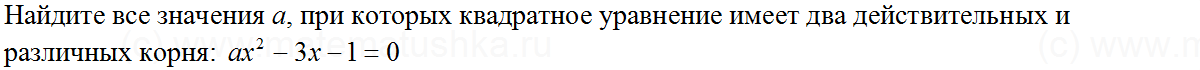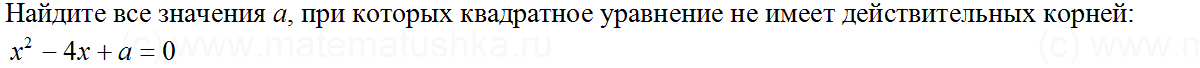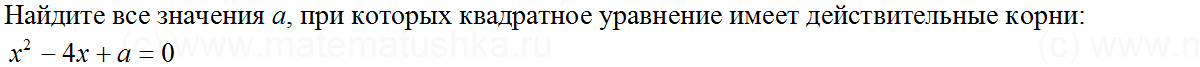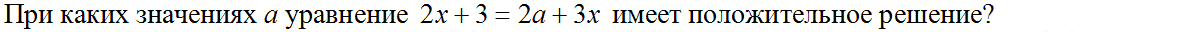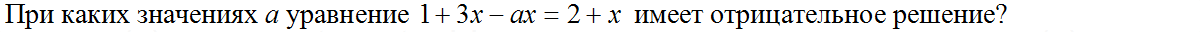Егэ математика решение неравенств с одной переменной

Укажите регион, чтобы мы точнее рассчитали условия доставки

Начните вводить название города, страны, индекс, а мы подскажем

Например: 
Москва,
Санкт-Петербург,
Новосибирск,
Екатеринбург,
Нижний Новгород,
Краснодар,
Челябинск,
Кемерово,
Тюмень,
Красноярск,
Казань,
Пермь,
Ростов-на-Дону,
Самара,
Омск

Задачи ЕГЭ по математике

---

 

Содержание

1.     Критерии оценивания выполнения задания №14	3
2.     Что можно  ожидать  в качестве задания 14 на экзамене?	3
3.     Основные методы решений неравенств	3
4.     Справочный материал	4
5.     Практикум по решению задач типа: — Квадратичные неравенства — Иррациональные неравенства — Неравенства с модулем — Показательные неравенства на ЕГЭ по математике — Логарифмические неравенства — Неравенства. Метод замены множителя (метод рационализации)	12 20 24 26 31 42
6.     Задания с решением 7.     Задачи для самостоятельного решения	51 56
8.     Примеры оценивания экзаменационных работ	58

1.     Критерии оценивания задания №14 ЕГЭ

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Обоснованно получен ответ, отличающийся от верного исключением точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

2.    
Что
можно ожидать в качестве задания 14 на экзамене?

·       
Рациональные неравенства 

·       
Неравенства, содержащие
радикалы 

·       
Показательные неравенства  

·       
Логарифмические неравенства  

·       
Неравенства с логарифмами
по переменному основанию   

·       
Неравенства с модулем  

·       
Смешанные неравенства

3.     Основные методы решений неравенств

·       
метод равносильных
переходов;

·       
метод замены;

·       
метод
интервалов и обобщенный метод интервалов;

·       
решение неравенства
на промежутках;

·       
метод
рационализации;

·       
метод оценки (графический способ).

4.     Справочный материал

5.    
Практикум по решению задач типа:

1.     Квадратичные неравенства

Квадратичная
функция, или парабола, — это функция вида

Вспомним
свойства этой функции:

Координаты вершины параболы: 

Если , ветви вверх

Если , ветви вниз

Точки пересечения с осью X:  и 

где  и  — корни квадратного
уравнения 

Точка пересечения с осью Y: М (0; с).

Вспомним также, как выражение  раскладывается
на множители.

где  и  — корни квадратного уравнения 

1. Решить неравенство

x² < 400

Давайте решим это неравенство с помощью
графика. Изобразим схематично график функции y = x² и отметим
все значения x, для которых y < 400.

Теперь мы видим правильный ответ: x ∈ (−20; 20).

Запомним: извлекать корень из неравенства
нельзя. Такого действия просто нет.

2. Решить  неравенство: 

Переносим всё в левую часть неравенства.
Раскладываем левую часть на множители.

Рисуем ось X. Рисуем параболу  с ветвями вверх.

Эта парабола пересекает ось X в точках — 4 и
4. Отмечаем знаки выражения в левой части на каждом интервале.

Записываем ответ:

3. Решить неравенство: x² − 3x − 10 ≥
0.

Графиком функции y = x² − 3x − 10
служит парабола, ветви которой направлены вверх. Решая квадратное уравнение x² − 3x − 10 =
0, находим x₁ = −2 и x₂ = 5 — в этих точках
парабола пересекает ось X. Нарисуем схематично нашу параболу:

Мы видим, что при x ∈ (−2; 5) значения функции отрицательны (график проходит
ниже оси X). В точках −2 и 5 функция обращается в нуль, а при x < −2 и
x > 5 значения функции положительны. Следовательно, наше неравенство
выполняется при .

4. Решить неравенство: x² + 2x + 4
> 0.

Ветви параболы y = x² + 2x + 4
направлены вверх. Дискриминант отрицателен, т. е. уравнение x² + 2x + 4 = 0
не имеет корней. Стало быть, нет и точек пересечения параболы с осью X.

Раз ветви параболы направлены вверх и она не
пересекает ось X — значит, парабола расположена над осью X.

Получается, что значения функции положительны
при всех возможных x. Иными словами, решения нашего неравенства — это все
действительные числа.

Ответ: .

5. Следующее квадратичное неравенство: 

Разложим его левую часть на множители.

Получим: 

И больше ничего не пишем. Рисуем ось X.
Рисуем параболу  с ветвями вверх.

Эта парабола пересекает ось X в точках 1 и 5.
Отмечаем знаки выражения в левой части на каждом интервале.

Записываем ответ:

Соберем в одну таблицу примеры решения
различных квадратичных неравенств.

Метод
интервалов – простой способ решения
дробно-рациональных неравенств. Так называются неравенства, содержащие
рациональные (или дробно-рациональные) выражения, зависящие от переменной.

1. Рассмотрим,
например, такое неравенство

В левой части этого неравенства –
дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни
синусов, ни логарифмов – только рациональные выражения. В правой – нуль.

Метод интервалов основан на следующем
свойстве дробно-рациональной функции.

Дробно-рациональная
функция может менять знак только в тех точках, в которых она равна нулю или не
существует.

Найдем нули функции в левой части нашего неравенства.
Для этого разложим числитель на множители. Напомним, как раскладывается на
множители квадратный трехчлен, то есть выражение вида  .

, где  и  — корни
квадратного уравнения .

Получим:

Рисуем ось  и расставляем точки, в которых
числитель и знаменатель обращаются в нуль.

Нули знаменателя  и  — выколотые
точки, так как в этих точках функция в левой части неравенства не определена
(на нуль делить нельзя). Нули числителя  и  — закрашены,
так как неравенство нестрогое. При  и  наше
неравенство выполняется, так как обе его части равны нулю.

Эти точки разбивают ось  на  промежутков.

Определим знак дробно-рациональной функции в
левой части нашего неравенства на каждом из этих промежутков. Мы помним,
что дробно-рациональная
функция может менять знак только в тех точках, в которых она равна нулю или не
существует. Это значит, что на каждом из промежутков между
точками, где числитель или знаменатель обращаются в нуль, знак выражения в
левой части неравенства будет постоянным — либо «плюс», либо
«минус».

И поэтому для определения знака функции на
каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку.
Ту, которая нам удобна.
 . Возьмем,
например,  и
проверим знак выражения  в левой части неравенства. Каждая из
«скобок» отрицательная. Левая часть имеет знак .

 Следующий
промежуток: .
Проверим знак при . Получаем, что левая часть поменяла знак на .

 .
Возьмем .
При  выражение
положительно — следовательно, оно положительно на всем промежутке от  до .

 При  левая
часть неравенства отрицательна. 

 И,
наконец, .
Подставим  и
проверим знак выражения в левой части неравенства. Каждая «скобочка»
положительна. Следовательно, левая часть имеет знак .

Мы нашли, на каких промежутках
выражение  положительно. Осталось записать ответ:

Ответ: .

Обратите внимание: знаки на промежутках
чередуются. Это произошло потому, что при
переходе через каждую точку ровно один из линейных множителей поменял знак, а
остальные сохранили его неизменным.

Мы видим, что метод интервалов очень прост.
Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к
виду:

, или ,
или ,
или .

(в левой части — дробно-рациональная функция,
в правой — нуль).

Затем — отмечаем на числовой прямой точки, в
которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых
дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения  в
любой точке, принадлежащей данному промежутку. После этого — записываем ответ.
Вот и всё.

Но возникает вопрос: всегда ли знаки
чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки
механически и бездумно.

2. Рассмотрим
еще одно неравенство.

Снова расставляем точки на оси . Точки  и  — выколотые,
поскольку это нули знаменателя. Точка  — тоже выколота, поскольку
неравенство строгое.

При  числитель положителен,
оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число
с данного промежутка, например, . Левая часть имеет знак :

При  числитель
положителен; первый множитель в знаменателе положителен, второй множитель
отрицателен. Левая часть имеет знак :

При  ситуация та же!
Числитель положителен, первый множитель в знаменателе положителен, второй
отрицателен. Левая часть имеет знак :

Наконец, при  все
множители положительны, и левая часть имеет знак :

Ответ: .

Почему нарушилось чередование знаков? Потому
что при переходе через точку  «ответственный» за неё множитель  не изменил знак.
Следовательно, не изменила знак и вся левая часть нашего неравенства.

Вывод: если линейный множитель  стоит в чётной степени (например,
в квадрате), то при переходе через точку  знак выражения в левой части не
меняется. В случае нечётной степени знак, разумеется, меняется.

3. Рассмотрим
более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:

Левая часть та же, что и в предыдущей задаче.
Та же будет и картина знаков:

Может, и ответ будет тем же? Нет! Добавляется
решение  Это
происходит потому, что при  и левая, и правая части неравенства равны нулю —
следовательно, эта точка является решением.

Ответ: .

4. Что делать,
если числитель или знаменатель не удается разложить на линейные множители?
Рассмотрим такое неравенство:

Квадратный трехчлен  на
множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и
хорошо! Это значит, что знак выражения  при всех  одинаков, а конкретно — положителен. И теперь мы можем поделить обе
части нашего неравенства на величину , положительную при
всех . Придём к равносильному неравенству:

— которое легко решается методом интервалов.

Обратите внимание — мы поделили обе части
неравенства на величину, о которой точно знали, что она положительна. Конечно,
в общем случае не стоит умножать или делить неравенство на переменную величину,
знак которой неизвестен.

5. Рассмотрим еще
одно неравенство, на вид совсем простое:

Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь  может
быть как положительным, так и отрицательным. А мы знаем, что если обе части
неравенства умножить на отрицательную величину — знак неравенства меняется.

Мы поступим по другому — соберём всё в одной
части и приведём к общему знаменателю. В правой части останется нуль:

И после этого —
применим метод
интервалов.

2.    
Иррациональные
неравенства

Так называются неравенства, содержащие знак
корня.

В решении иррациональных неравенств главное –
логика и внимательность.

Напоминаем, что решение лучше всего
записывать в виде цепочки равносильных переходов.

1.Решите неравенство 

Правая часть неравенства неотрицательна:
 (по определению корня квадратного).

Поскольку  левая часть
положительна: 

Выражение под корнем должно быть
неотрицательным. Неравенство равносильно системе:

Ответ: (5;+∞)

2.Решите неравенство .

Как вы думаете – это неравенство такое же,
как предыдущее, или отличается от него? Ведь здесь правая часть может быть и
положительной, и отрицательной, и равной нулю. И надо рассмотреть все эти
случаи.

1) Пусть правая часть неравенства
неотрицательна. И левая тоже неотрицательна (по определению арифметического
квадратного корня). И подкоренное выражение неотрицательно. Значит, при  обе части неравенства можно возвести в квадрат.

Получим:

Разложим выражение  на множители. Корни уравнения  – это  и .

Получаем систему:

2) Пусть теперь правая часть неравенства
отрицательна. Если  то
неравенство выполняется. В самом деле,  по
определению. Значит, 

Нам нужно только, чтобы подкоренное выражение
было неотрицательно: .

Получим:

Объединим полученные интервалы и запишем
ответ.

Ответ: .

3.Решите неравенство 

Ответ: 

4.Решите неравенство 

Ответ:  

5.Решите неравенство 

Сделаем замену , тогда 

Ответ: 

3.    
Неравенства
с модулем

1. Решить неравенство  2|x − 4| +
|3x + 5| ≥ 16.

1) x ≥ 4. Имеем:

Полученное неравенство выполняется при всех
рассматриваемых x ≥ 4. Иными словами, все числа из промежутка [4; +∞) являются
решениями нашего неравенства.

2)  Имеем
в данном случае:

Учитывая, в каком промежутке мы сейчас
находимся, получаем в качестве решений исходного неравенства множество [3; 4].

3) .
Имеем:

Так как − ,
то все значения x из полученного промежутка  служат
решениями исходного неравенства.

Остаётся объединить множества решений,
полученные в трёх рассмотренных случаях.

Ответ: 

2.Решить неравенство  |x² − 2x − 3|
< 3x − 3.

Заметим, что метод интервалов здесь проходит
весьма безболезненно по той причине, что корни квадратного трёхчлена под
модулем — целые числа. А если дискриминант не будет точным квадратом?
Замените, например, под модулем −3 на −5. Объём вычислительной
работы тогда существенно возрастёт.

Мы покажем вам другой способ решения этой
задачи, не зависящий от капризов дискриминанта.

Наше неравенство имеет вид |A| < B.
Очевидны следующие утверждения.

• Если B ≤ 0, то неравенство не имеет
решений.

• Если B > 0, то неравенство равносильно
двойному неравенству −B < A < B или, что то же самое, системе

Иными словами, мы берём пересечение множества
решений данной системы с множеством решений неравенства B > 0, то есть
решаем систему

В нашей задаче получаем:

Изобразим множества решений этих неравенств
на рисунке. Чёрным цветом показаны решения первого (двойного) неравенства;
зелёный цвет — решения совокупности; синий цвет — решения последнего
неравенства системы.

Решением системы служит пересечение этих
множеств, т. е. множество, над которым присутствуют линии всех трёх
цветов. Оно заштриховано.

Ответ: (2; 5).

 

4.    
Показательные
неравенства на ЕГЭ по математике

Знакомство с этой темой мы начнем с самых
простых показательных неравенств.

1. 2^x > 8

Так же, как и при решении простейших
показательных уравнений, представим правую часть в виде степени числа 2:

2^x > 2³

Когда я спрашиваю школьников, что делать дальше,
они обычно отвечают: «Убрать основания!» Я не против такой формулировки, просто
надо четко представлять себе, почему мы так делаем. А для этого — вспомним, как
выглядит график показательной функции y = 2^x.

Видим, что эта функция монотонно возрастает, то есть большему значению x
отвечает большее значение y. И наоборот, если 2^x₁ > 2^x₂, то x₁ > x₂ . Итак, от
неравенства 2^x > 2³ можно перейти к
алгебраическому неравенству x > 3.

Ответ: .

2. Следующее неравенство:

2^x > 7

Так же, как и в предыдущем примере,
представим правую часть в виде значения показательной функции. Как это сделать?
С помощью логарифма, конечно:
7 = 2^log₂7.

Получаем:

2^x > 2^log₂7;

x > log₂7.

3. Еще одно неравенство:

Здесь правую часть удобно представить
как .

.

Вспомним, как выглядит график функции :

Эта функция монотонно убывает (так как
основание степени меньше единицы), поэтому большее значение функции
соответствует меньшему значению аргумента. То есть из неравенства  следует,
что x < 4. Знак неравенства меняется!

4. Решите неравенство 

Умножим обе части неравенства на 

Сделаем замену  Получили квадратичное неравенство
относительно переменной t.

Внимание. Сначала
решаем неравенство относительно переменной t. Только после этого возвращаемся к
переменной х. Запомнили?

Разложим левую часть неравенства на
множители.

где  и  — корни квадратного уравнения  Получим:

Только теперь
возвращаемся к переменной х.

 «Отбрасываем»
основания степеней и получаем ответ.

Ответ: 

5. Решите
неравенство:

Сделаем замену переменной:

Обратите внимание, что возвращаться к
переменной х еще рано. Сначала решим неравенство с переменой t методом интервалов:

Поскольку  получим:

Тогда

Обратите внимание, как мы представили 4 и 9 в
виде степеней с основанием 7. Мы применили основное логарифмическое тождество.

Ответ: 

5.    Решить неравенство
 4^x − 2 · 5^2x − 10^x > 0.

Заметим, что 4^x = 2^2x, 10^x=5^x·2^x, и запишем
неравенство в виде:
2^2x − 5^x·2^x − 2 · 5^2x > 0.

Разделим обе части на положительную величину
5^2x и обозначим .
Получим квадратное неравенство:

t² − t − 2 >
0.

Кроме того, t > 0.

Графиком функции y = t² − t − 2
является парабола, ветви которой направлены вверх. Решая квадратное уравнение t² − t − 2 = 0,
получим t₁ = −1, t₂ = 2. В этих точках
наша парабола пересекает ось t.

Отметим на
числовой прямой промежутки, являющиеся решениями неравенств t² − t − 2 >
0 и t > 0.

Видим, что обоим неравенствам удовлетворяют значения t > 2.

Но решение еще не закончено! Нам нужно
вернуться к переменной x. Вспомним, что  и
получим:

Представим 2 в виде степени с
основанием :

Получим: x < 

7. Решите неравенство 

Здесь присутствуют степени с основаниями 3 и
5. Поделим на 3 обе части неравенства:

Возьмем логарифмы от левой и правой частей
неравенства по основанию 3.

Логарифм произведения запишем как сумму
логарифмов.

Разложим на множители 

Ответ: 

6.    
Логарифмические
неравенства

Решая логарифмические неравенства, мы
пользуемся свойством монотонности логарифмической функции. Также мы используем
определение логарифма и основные логарифмические формулы.

Давайте повторим, что такое логарифмы:

Логарифм положительного
числа  по основанию  —
это показатель степени, в которую надо возвести , чтобы
получить .

При этом 

Основное логарифмическое
тождество:

Основные формулы для
логарифмов:

 (Логарифм
произведения равен сумме логарифмов)

 (Логарифм частного
равен разности логарифмов)

 (Формула для логарифма степени)

Формула перехода к новому основанию:

Алгоритм решения
логарифмических неравенств

Можно сказать, что логарифмические
неравенства решаются по определенному алгоритму. Нам нужно записать область
допустимых значений (ОДЗ) неравенства. Привести неравенство к виду  Знак
здесь может быть любой:  Важно,
чтобы слева и справа в неравенстве находились логарифмы по одному и тому же
основанию.

И после этого «отбрасываем» логарифмы! При этом,
если основание степени , знак неравенства
остается тем же. Если основание такое, что  знак неравенства меняется на
противоположный.

Конечно, мы не просто «отбрасываем»
логарифмы. Мы пользуемся свойством монотонности логарифмической функции. Если
основание логарифма больше единицы, логарифмическая функция монотонно
возрастает, и тогда большему значению х соответствует большее значение
выражения .

Если основание больше нуля и меньше единицы,
логарифмическая функция монотонно убывает. Большему значению аргумента х будет
соответствовать меньшее значение 

Важное замечание: лучше всего записывать
решение в виде цепочки равносильных переходов.

Перейдем к практике. Как всегда, начнем с
самых простых неравенств.

1. Рассмотрим неравенство log₃x > log₃5.
Поскольку логарифмы определены только для положительных чисел, необходимо,
чтобы x был положительным. Условие x > 0 называется областью допустимых
значений (ОДЗ) данного неравенства. Только при таких x неравенство имеет смысл.

Что делать дальше? Стандартный ответ, который
дают школьники, — «Отбросить логарифмы!»

Что ж, эта формулировка лихо звучит и легко
запоминается. Но почему мы все-таки можем это сделать?

Мы люди, мы обладаем интеллектом. Наш разум
устроен так, что все логичное, понятное, имеющее внутреннюю структуру
запоминается и применяется намного лучше, чем случайные и не связанные между
собой факты. Вот почему важно не механически вызубрить правила, как
дрессированная собачка-математик, а действовать осознанно.

Так почему же мы все-таки «отбрасываем
логарифмы»?

Ответ простой: если основание больше единицы
(как в нашем случае), логарифмическая функция монотонно возрастает,
значит, большему значению x соответствует большее значение y и из
неравенства log₃x₁ > log₃x₂ следует, что
x₁ > x₂.

Обратите внимание, мы перешли к алгебраическому неравенству, и знак неравенства
при этом — сохраняется.

Итак, x > 5.

Следующее логарифмическое неравенство тоже
простое.

2. log₅(15 + 3x) > log₅2x

Начнём с области допустимых значений.
Логарифмы определены только для положительных чисел, поэтому

Решая эту систему, получим: x > 0.

Теперь от логарифмического неравенства
перейдем к алгебраическому — «отбросим» логарифмы. Поскольку основание
логарифма больше единицы, знак неравенства при этом сохраняется.

15 + 3x > 2x.

Получаем: x > −15.

Итак,

Ответ: x > 0.

А что же будет, если основание логарифма
меньше единицы? Легко догадаться, что в этом случае при переходе к
алгебраическому неравенству знак неравенства будет меняться.

Приведем пример.

3. 

Запишем ОДЗ. Выражения, от которых берутся
логарифмы, должны быть положительно, то есть

Решая эту систему, получим: x > 4,5.

Поскольку ,
логарифмическая функция с основанием  монотонно
убывает. А это значит, что большему значению функции отвечает меньшее значение
аргумента:

И если ,
то
2x − 9 ≤ x.

Получим, что x ≤ 9.

Учитывая, что x > 4,5, запишем ответ:

x ∈ (4,5; 9].

В следующей задаче показательное неравенство
сводится к квадратному. Так что тему «квадратные неравенства» рекомендуем
повторить.

Теперь более сложные неравенства:

4. Решите неравенство 

Ответ: 

5. Решите неравенство 

ОДЗ: 

Если , то . Нам повезло! Мы знаем, что основание логарифма
больше единицы для всех значений х, входящих в ОДЗ.

Сделаем замену 

Обратите внимание, что сначала мы полностью
решаем неравенство относительно новой переменной t. И только после этого
возвращаемся к переменной x. Запомните это и не ошибайтесь на экзамене!

Ответ: 

6. 

Запомним правило: если в уравнении или
неравенстве присутствуют корни, дроби или логарифмы — решение надо начинать с
области допустимых значений. Поскольку основание логарифма должно быть
положительно и не равно единице, получим систему условий:

Упростим эту систему:

Это область допустимых значений неравенства.

Мы видим, что переменная содержится в
основании логарифма. Перейдем к постоянному основанию. Напомним, что

В данном случае удобно перейти к основанию 4.

Сделаем замену 

Упростим неравенство и решим его методом интервалов:

Упростим неравенство и решим его методом
интервалов:

Итак, 

Вернемся к переменной x:

Мы добавили условие x >
0 (из ОДЗ).

Ответ: 

7. Следующая задача тоже решается с помощью
метода интервалов

Как всегда,
решение логарифмического неравенства начинаем с области допустимых значений. В
данном случае

Это условие
обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само
неравенство. Запишем левую часть как логарифм по основанию 3:

Правую
часть тоже можно записать как логарифм по основанию 3, а затем перейти к
алгебраическому неравенству:

Видим,
что условие  (то
есть ОДЗ) теперь выполняется автоматически. Что ж, это упрощает решение
неравенства.

Решаем
неравенство методом интервалов:

Ответ: 

Получилось? Что же, повышаем уровень
сложности:

8. Решите неравенство:

Выражение 5^—x2навязчиво
повторяется в условии задачи. А это значит, что можно сделать замену:

Поскольку показательная функция принимает
только положительные значения, t >
0. Тогда

Неравенство примет вид:

Уже лучше. Найдем область допустимых значений
неравенства. Мы уже сказали, что t >
0. Кроме того, (t −
3) (5⁹ · t −
1) > 0

Если это условие выполнено, то и
частное  будет
положительным.

А еще выражение под логарифмом в правой части
неравенства должно быть положительно, то есть (625t − 2)².

Это означает, что 625t − 2 ≠ 0, то
есть 

Аккуратно запишем ОДЗ

и решим получившуюся систему, применяя метод
интервалов.

Итак, 

Ну что ж, полдела сделано — разобрались с
ОДЗ. Решаем само неравенство. Сумму логарифмов в левой части представим как
логарифм произведения:

«Отбросим» логарифмы. Знак неравенства
сохраняется.

Перенесем все в левую часть и разложим по
известной формуле разности квадратов:

Вспомним,
что  (это
ОДЗ неравенства) и найдем пересечение полученных промежутков.

Получим,
что 

Вернемся к переменной x

Поскольку 

Ответ: 

9. Еще один прием, упрощающий решение
логарифмических неравенств, — переход к постоянному основанию. Покажем, как
использовать переход к другому основанию и обобщенный метод интервалов.

Запишем ОДЗ:

Воспользуемся
формулой  и
перейдем к основанию 10:

Применим
обобщенный метод интервалов. Выражение в левой части неравенства можно записать
как функцию

Эта функция может
менять знак в точках, где она равна нулю или не существует.

Выражение lg |x − 3| равно нулю, если |x − 3| = 1, то
есть x =
4 или x =
2.

Выражение lg (|x| − 2) равно нулю, если |x| = 3, то есть в точках 3 и
−3.

Отметим эти точки на числовой прямой, с
учетом ОДЗ неравенства.

Найдем знак
функции g(x) на
каждом из промежутков, на которые эти точки разбивают область допустимых
значений. Точно так же мы решали методом интервалов обычные рациональные
неравенства.

Ответ: 

10. А в следующей задаче спрятаны целых две
ловушки для невнимательных абитуриентов.

Запишем ОДЗ:

Итак,  Это
ОДЗ.

Обратите внимание, что .

Это пригодится вам при решении неравенства.

Упростим исходное неравенство:

Теперь главное – не спешить. Мы уже говорили,
что задача непростая – в ней расставлены ловушки. В первую вы попадете, если
напишете, что  Ведь
выражение  в данном
случае не имеет смысла, поскольку x <
18.

Как же быть? Вспомним, что (x — 18)²=(18 — x)². Тогда:

Вторая ловушка –
попроще. Запись  означает,
что сначала надо вычислить логарифм, а потом возвести полученное выражение в
квадрат. Поэтому:

Дальше – всё просто. Сделаем замену 

Выражение в левой части этого неравенства не
может быть отрицательным, поэтому t =
2. Тогда

 — не удовлетворяет
ОДЗ;

Ответ: 2.

Мы рассмотрели основные
приемы решения логарифмических неравенств — от простейших до сложных, которые
решаются с помощью обобщенного метода интервалов. Однако есть еще один
интересный метод, помогающий справиться и показательными, и с логарифмическими,
и с многими другими видами неравенств. Это метод рационализации (замены
множителя).

7.    
Метод
рационализации неравенства

Полезный прием для решения сложных неравенств
на ЕГЭ по математике – метод
рационализации неравенства. Другое название — метод замены множителя.
Это один из тех секретов, о которых ученику рассказывает репетитор. В учебниках
о таком не написано.

Суть метода в том, чтобы от неравенства,
содержащего в качестве множителей сложные показательные или логарифмические
выражения, перейти к равносильному ему более простому рациональному неравенству.

Давайте для начала вспомним, что такое
равносильные уравнения (или неравенства) В школьной программе этот важный
вопрос почти не обсуждается. Поэтому запишем определение.

Равносильными называются уравнения, множества
решений которых совпадают.

Заметим, что внешне уравнения могут быть и не
похожи друг на друга.

Например, уравнения (x − 3)² = 0 и x − 3 = 0 равносильны.
Число 3 является единственным решением и того, и другого.

Уравнения  и  также равносильны.
Оба они не имеют решений. Другими словами, множество решений каждого из них –
пусто.

Уравнения  и  не
являются равносильными. Решением первого уравнения

является только x = 5. Решения второго
– два числа: x =
5 и x =
1. Получается, что возведение обеих частей уравнения в квадрат в общем случае
приводит к уравнению, неравносильному исходному.

Аналогичное определение – для неравенств.

Равносильными называются неравенства,
множества решений которых совпадают.
Например, неравенства  и  равносильны
– ведь множества их решений совпадают. В этом легко убедиться с помощью метода
интервалов.

Неравенства  и  также
равносильны при . Заметим, что
внешне эти неравенства не похожи – одно из них логарифмическое, другое
алгебраическое.

Другими словами, при x > 0
неравенства  и  имеют одинаковые
решения. Если какое-

либо число x > 0 является решением одного из них,
то оно будет и решением второго.

А это значит, что при любом x > 0
выражение  будет
иметь такой же знак, как и выражение x −
5. Следовательно, если в какое-либо сложное неравенство входит в качестве
множителя выражение  то
при выполнении условия x >
0 его можно заменить на более простое x −
5 и получить неравенство, равносильное исходному.

Вот ключевой момент. На этом и основан метод
рационализации – замены множителей, содержащих сложные логарифмические или
показательные выражения, на более простые алгебраические множители.

Например, выражение вида ,
где f и g – функции от x, a – число, можно
заменить на более простое (f −
g) (a −
1) – конечно, при условии, что f(x) >
0 и g(x) >
0. Доказательство легко провести самостоятельно.

А сейчас – самое главное: волшебная таблица,
позволяющая заменять сложные логарифмические (или показательные) множители в
неравенствах на более простые. Эта таблица является ключом к задаче С3. Вот
увидите, она выручит вас на ЕГЭ по математике:

Конечно же, все выражения, которые содержат
логарифмы, существуют при f,
g, h > 0 и h ≠
1.

Когда на ЕГЭ по математике вы применяете
метод рационализации (замены множителя), — обязательно поясните, что вы им
воспользовались. И не забудьте доказать соответствующую формулу. Иначе можно
потерять балл.

Обратите внимание, что мы говорим о замене
множителя в неравенствах вида  Знак здесь
может быть любой: >, ≥, ≤. Правая часть обязательно должна быть равна
нулю. И заменяем мы именно множитель (а не слагаемое, например). Иначе ничего
не получится.

Перейдем к практике – к решению задач из
вариантов ЕГЭ по математике Профильного уровня.

1. 

ОДЗ неравенства: 

Применим метод рационализации. В соответствии
с нашей таблицей, множитель  заменим на
(2 − x −
1)(x + 2 −
1). Множитель вида  заменим на
(x + 3 − 1)(3
− x −
1). Таким образом, от логарифмического неравенства мы перешли к рациональному:

(1 − x) (x + 1) (x + 2) (2 − x) ≤ 0

Решим его методом интервалов:

Ответ: 

2. 

Начнем с ОДЗ.

Заметим, что выражение  положительно
при x ∈ ОДЗ. Умножим обе
части неравенства на это выражение.
Упростим числитель правой части неравенства:

Поделим обе части неравенства на 5^x > 0:

Неравенство уже намного проще, чем исходное.
Но основания степеней разные! Чтобы применить метод рационализации, нам
придется представить 2^x −
1 в
виде степени с основанием 3.

Неравенство примет
вид:

 Воспользуемся методом замены множителя.
Множитель вида h ^f −h ^g можно
заменить на (h −
1) (f − g). Да и
логарифм в знаменателе можно заменить на выражение x + 1.

Оценим . Это необходимо
сделать, чтобы правильно расставить точки на числовой прямой.

Ответ: 

3. 

Постараемся упростить это
неравенство. Область допустимых значений

Отсюда
следует, что x > 0. Это хорошо, потому что при данных
значениях x выражение x + 1 строго положительно,
следовательно, мы можем умножить на него обе части неравенства. Да и на x² тоже
можно умножить обе части неравенства, и тогда оно станет проще

Преобразуем
числители выражений в левой и правой части и сделаем замену log₂x = t

Теперь
обе части неравенства можно сократить на 5^t >
0.

Поскольку , выражение
2^t−1 можно
записать как 3^(t−1)·log₃2

Заметим,
что log₃2 − 2 < 0.

Мы получили квадратичное
неравенство относительно t. Решим его:

Итак, t ≥
1 или t ≤ log₃2 − 2.
Вернемся к переменной x:

 или 

Ответ: 

4. Еще одна задача из той
же серии.

Запишем ОДЗ:

Умножим обе части
неравенства на .
Постараемся упростить числители выражений в левой и правой части.

Поделим обе части
неравенства на 

Хорошо
бы сделать замену. Пусть log₂(4x)
= t. Тогда:

Неравенство
примет вид:

Мы уже знаем, как представить число 7 в виде степени числа 2: 

Применим
метод рационализации.

Оценим 

4
< 7 < 8;

 или   

Ответ: 

5. Еще одна
задача-страшилка из того же сборника:

Начнем с ОДЗ. Условий
будет много – все выражения под логарифмами должны быть положительны, все
основания логарифмов положительны и не равны единице, и еще знаменатель не
равен нулю

Применим в левой части
неравенства формулу перехода к другому основанию

Последовательно
применим метод замены множителя, то есть метод рационализации.
Напомним, что множитель log _h f можно
заменить на (h-1)( f-1), а множитель (log _h f —
1) — на (h — 1)( f — h).

Поскольку  при x ∈
ОДЗ, а  > 0
при всех x, получим:

С учетом ОДЗ:

Ответ: x ∈
(-5; -3]

Посмотрим, чем поможет
метод замены множителя в решении сложного показательного неравенства.

6. Решите
неравенство:

Числитель дроби в левой
части — однородное выражение, где каждое слагаемое имеет степень 2х. Поделим
обе части неравенства на 

Получим:

Поскольку  , поделим обе части
неравенства на 

Применяя метод
рационализации, множитель вида  заменяем на

 Получим:

Остается решить
неравенство методом интервалов. Но как сравнить  и  ?

Что больше? Давайте
представим  как логарифм с
основанием 

Значит, 

Ответ: 

7. Теперь логарифмическое
неравенство. Обратите внимание, что здесь лучше всего записывать решение в виде
цепочки равносильных переходов. И само неравенство, которое мы упрощаем, и
область его допустимых значений мы записываем в одну систему. И решаем ее.

Решите
неравенство:

Мы объединили в систему и
область допустимых значений, и само неравенство. Применим формулу логарифма
частного, учитывая, что 

Используем также
условия 

Обратите внимание, как мы
применили формулу для логарифма степени. Строго говоря, 

Поскольку 

Согласно методу замены
множителя, выражение  заменим

на 

Получим систему:

Решить ее легко.

Ответ: 

6. Задания с решениями

1)Логарифмические
неравенства.

Неравенства, рациональные относительно
логарифмической функции, решаемые введением замены.

Задание 1.

Решите неравенство: 

Решение. Заметим, что  тогда
пусть  решим
рациональное неравенство:

Вернёмся к исходной переменной, получим:

Ответ: 

Задание 2.

Решите неравенство 

Решение. Пусть  решим рациональное
неравенство:

Вернёмся к исходной переменной, получим: 

Ответ: 

Неравенства смешанного типа. Целые и рациональные неравенства с
иррациональными коэффициентами.

Задание 3.

Решите неравенство: 

Решение. Решим
неравенство, перейдя к равносильной системе:

Условий существования логарифмов в левой части неравенства
достаточно для соблюдения ОДЗ, ввиду знака неравенства.

Ответ: 

Логарифмические неравенства, неравенства с
модулем, область определения неравенства.

Задание 4.

Решите неравенство 

Решение. Запишем исходное неравенство в виде:

Рассмотрим первый случай:

Рассмотрим второй случай:

Ответ: 

Задание 5  Решить неравенство.

1) .

Решение. ОДЗ:  Обозначим . Тогда получим уравнение

 С учетом ОДЗ , получаем

                           ////////////////////

                    0,5                     4                   х

           ////////////////////////////////////////////////////

      0                                                         
х

Ответ: .

6) Решите неравенство .

Решение. ОДЗ:

 

Исходное неравенство записываем в виде . Это неравенство равносильно
совокупности двух систем

Изобразим решение системы (1)

                 ////////////////////

                              1                   х   
          

///////////////////////////////////              //////

                                     1            2    
х

Изобразим решение системы (2)

                 /////////////////////////////////////

               1                                        х        
     

                  //////////////////

               1                   2                  х

Объединяя
решение систем (1) и (2), получаем ответ.

Ответ:

7)
Решите неравенство .

Решение.
Решение, как обычно, начнем с нахождения ОДЗ:

Перенесем
все члены неравенства в левую часть, получим

 

 Полученное неравенство решим методом интервалов  или  . Заметим, что  , так как

                +                             —
                      +

//////////////////////////////  
                         ////////////////////

                       
                                         х

         ///////////////////////////////////////////////////////////////////

      0 
                                                                       х

С
учетом ОДЗ получаем ответ.

Ответ:

Найти область определения функции

.

Решение.

 

                        
//////////////////////////////////////

                    
2                                        х              

          
///////////////////////

     
-2                         4                          х

Ответ:

7.Задания для
самостоятельного решения

Задание 1

Решите неравенство 

Ответ: 

Задание 2

Решите неравенство: 

Ответ: 

Задание 3.

Решите неравенство 

Ответ: 

Задание 4.

Решите неравенство 

Ответ: 

Решите неравенство:

1)      
                                                                    Ответ:

2)      
                                                      Ответ:

3)      
                                                        Ответ:

4)      
                                                           Ответ:

5)      
                                                        Ответ:

6)      
                     Ответ:

7)      
                                                     Ответ:

      
                                              Ответ:
  

9)      
                                                          Ответ:

10)  
                                                                      Ответ:

11)  
Найти область определения функции  

             
                                                                                                                                    Ответ:
 

8.    
Примеры оценивания
экзаменационных работ

Комментарий.

Можно отметить не
самый удачный путь к «цели», но способ решения не оценивается. Ответ правильный
и получен приемлемым обоснованием.

Оценка эксперта:
2 балла.

Решите неравенство 
.     Ответ:  .      

Комментарий.

Задача практически
полностью решена. Но при решении простейшего логарифмического неравенства  допущена очень грубая и одна из
древнейших ошибок: пропало ограничение .
Крайне неприятный казус: за почти верное решение – ни одного балла.

Оценка эксперта:  0 баллов.

Комментарий. Типичный один балл. Путаница в знаках корней квадратного уравнения (у),
а потом все верно. Оценка эксперта: 1 балл.