Егэ по физике задача с воздушным шаром - Помощь в подготовке к экзаменам и поступлению

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 153 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Добавить в вариант

В сосуд налита вода, поверх которой налит не очень толстый слой масла. В сосуде плавает деревянный шар. При помощи шприца масло из сосуда аккуратно удаляют. Как в результате этого изменятся следующие физические величины: давление на дно сосуда; модуль выталкивающей силы, действующей на шар; высота части шара, выступающей над поверхностью жидкости?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины.

Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  давление на дно сосуда

Б)  модуль выталкивающей силы, действующей на шар

В)  высота части шара, выступающей над поверхностью жидкости

ИХ ИЗМЕНЕНИЕ

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

По гладкой горизонтальной поверхности движутся поступательно навстречу друг другу два одинаковых шара. Модули скоростей шаров одинаковые, сопротивление воздуха пренебрежимо мало. Между шарами происходит абсолютно неупругое лобовое соударение. Этот опыт повторяют с теми же шарами, увеличив модуль скорости каждого из них в два раза. Как для второго опыта по сравнению с первым изменились модуль суммарного импульса шаров и количество выделившейся при соударении теплоты?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Модуль суммарного

импульса шаров

Количество теплоты,

выделившейся при соударении

По гладкой горизонтальной поверхности движутся поступательно навстречу друг другу два одинаковых шара. Модули скоростей шаров одинаковые, сопротивление воздуха пренебрежимо мало. Между шарами происходит абсолютно неупругое лобовое соударение. Этот опыт повторяют с теми же шарами, уменьшив модуль скорости каждого из них в три раза.

Как для второго опыта по сравнению с первым изменились модуль суммарного импульса шаров и количество выделившейся при соударении теплоты?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Модуль суммарного

импульса шаров

Количество теплоты,

выделившейся при соударении

Мальчик решил подняться в воздух на воздушных шарах с гелием. Известно, что мальчик весит 40 кг, а на улице нормальное атмосферное давление и температура 27 °C. Учитывая, что объем одного шара составляет 10 литров, найдите, сколько потребуется шаров для такого путешествия. Массой оболочки шаров и объемом мальчика пренебречь.

Источник: ЕГЭ по физике 07.06.2017. Основная волна

Навстречу тележке массой 4,75 кг, движущейся по инерции равномерно со скоростью 2 м/с по гладким горизонтальным рельсам, летит шар массой 0,25 кг со скоростью 40 м/с. После столкновения шар застревает в песке, насыпанном на тележку. Определите, во сколько раз отличаются модули начального (до застревания в песке) и конечного импульса шара в системе отсчёта, связанной с рельсами.

Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи

В маленький шар массой M  =  230 г, висящий на нити длиной l  =  50 см, попадает и застревает в нём горизонтально летящая пуля. Минимальная скорость пули υ₀, при которой шар после этого совершит полный оборот в вертикальной плоскости, равна 120 м/c. Чему равна масса пули? Сопротивлением воздуха пренебречь. Обоснуйте применимость законов, используемых при решении задачи.

Источник: Демонстрационная версия ЕГЭ—2023 по физике

Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха а давление ? Считать, что оболочка шара не оказывает сопротивления изменению объёма шара.

Задания Д7 B13 № 4347

Металлический шар имеет заряд Если сообщить этому шару дополнительный заряд, равный то модуль потенциала поверхности шара

1)  увеличится

2)  уменьшится

3)  не изменится

4)  станет равен нулю

Задания Д7 B13 № 4382

1)  увеличится

2)  уменьшится

3)  не изменится

4)  станет равен нулю

Если потереть шерстью эбонитовую палочку, то она электризуется, приобретая отрицательный заряд, и стрелка электрометра при поднесении палки к его шару отклоняется, а при удалении палки  — возвращается к неотклонённому состоянию. Если же в момент поднесения наэлектризованной палки к электрометру коснуться рукой его металлического корпуса и сразу же убрать руку, то после удаления палки отклонение стрелки сохраняется, хотя и меньшее по величине.

Объясните, основываясь на известных физических законах и закономерностях, почему это происходит.

Электрометр (см. рис.) представляет собой металлический цилиндрический корпус, передняя и задняя стенки которого стеклянные. Корпус закреплён на изолирующей подставке. Через изолирующую втулку внутрь корпуса сверху входит металлическая трубка, заканчивающаяся внизу стержнем с установленной на нём легкоподвижной стрелкой, отклонение которой определяется величиной заряда. Стрелка может вращаться вокруг горизонтальной оси. Внутри корпуса установлена шкала электрометра, по которой определяется отклонение стрелки. Снаружи корпуса, наверху трубки прикрепляется металлический шар или тарелка, к которой подносят заряженные тела.

Если потереть стеклянную палочку шёлком, то она электризуется, приобретая положительный заряд, и стрелка электрометра при поднесении палки к его шару отклоняется, а при удалении палки  — возвращается к неотклонённому состоянию. Если же в момент поднесения наэлектризованной палки к электрометру коснуться рукой его металлического корпуса и сразу же убрать руку, то после удаления палки отклонение стрелки сохраняется, хотя и меньшее по величине. Объясните, основываясь на известных физических законах и закономерностях, почему это происходит.

Шар радиусом 10 см равномерно заряжен электрическим зарядом. В таблице представлены результаты измерений модуля напряжённости E электрического поля от расстояния r до поверхности этого шара. Чему равен модуль заряда шара? (Ответ дать в нКл.) Коэффициент k принять равным 9·10⁹ Н·м²/Кл².

r, см	10	20	30	40	50
E, В/м	900	400	225	144	100

На неподвижный бильярдный шар налетел другой такой же шар. Налетевший шар имел до удара импульс p  =  0,5 кг·м/с. После удара шары разлетелись под углом 90° так, что импульс одного p₁  =  0,4 кг·м/с (см. рисунок). Каков импульс другого шара после соударения?

Источник: Демонстрационная версия ЕГЭ—2015 по физике.

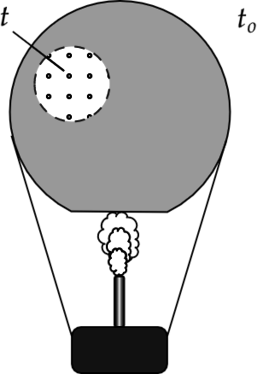
Воздушный шар, оболочка которого имеет массу M = 145 кг и объем V = 230 м³, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t₀  =  0 °С. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.

Источник: Материалы для подготовки экспертов ЕГЭ, 2015

Задания Д28 C1 № 9328

Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см². В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой T. Если нить перерезать, то шар всплывёт, а уровень воды изменится на h = 5 см. Найдите силу натяжения нити T.

Источник: Демонстрационная версия ЕГЭ—2018 по физике

Источник: Демонстрационная версия ЕГЭ−2019 по физике

Всего: 153 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …

Источник

Автор: admin. Рубрики: Всякая всячина. Опубликовано: Октябрь 1st, 2014

Задача для подготовки к ЕГЭ по физике по теме «Законы сохранения в механике». Эта задача может быть интересна учащимся 10-х классов и для подготовки к ЕГЭ и ГИА.

К корзине воздушного шара массой 240 кг привязана верёвочная лестница, на конце которой стоит человек массой 60 кг. Вся система находится в воздухе в положении равновесия. Какова будет скорость воздушного шара, если человек перемещается по лестнице со скоростью 0,15 м/с?

Задача подобного плана уже есть на сайте, но, как говориться: «Повторение — мать учения».

В основе решения задачи лежит «Закон сохранения импульса». То есть для начала, согласно алгоритму, выполняем рисунок, изображая начальное и конечное состояние системы.

В начальный момент система находилась в состоянии покоя.

Далее, человек поднимается вверх с некоторой скоростью, а воздушный шар опускается вниз. При этом, скорости человека и воздушного шара записываем в системе отсчёта, связанной с Землёй. Тогда для закона сохранения импульса имеем: где М — масса воздушного шара, m — масса человека.
Импульсы воздушного шара и человека равны по модулю и противоположны по направлению.
Из этого уравнения осталось выразить неизвестную величину — скорость воздушного шара. В итоге получаем формулу:

Остаётся подставить численные значения физических величин и получить числовой ответ. Скорость воздушного шара составит 0,03 м/с или 3 см/с.

Важно! Формулу закона сохранения импульса записываем в системе отсчёта, связанной с Землёй.

Вы можете оставить комментарий, или поставить трэкбек со своего сайта.

Нажми ЕЩЕ, чтобы получить ссылки на ШПОРЫ ПО ФИЗИКЕ, БЕСПЛАТНЫЙ КУРС, СПРАВОЧНИК, ССЫЛКИ на распродажу курсов!

ОНЛАЙН-КУРС ПО ФИЗИКЕ НА 100 БАЛЛОВ:

ОНЛАЙН-КУРС ДЛЯ ПРЕПОДАВАТЕЛЕЙ:

ТАБЛИЦА КЛЮЧЕЙ для решения задач ЕГЭ по физике:

БЕСПЛАТНЫЙ КУРС ЕГЭ ПО ФИЗИКЕ:

Скачайте расширение из Интернет-магазина Chrome, которое позволяет просмотр видео в разрешении 1080p Embedy HD

Лучший бесплатный поисковик фильмов

Вы не хотите платить за просмотр видео и для вас этот параметр является приоритетным? Embedy.cc позаботился о том, чтобы вы могли быстро найти фильмы и сериалы в хорошем качестве. Поиск производится по множеству источников. Поэтому вы стопроцентно найдёте то, что вас интересует.

Вниманию посетителей нашего сайта будет предложено:

огромная база кинолент;

удобный интерфейс;

отличное качество видео;

воспроизведение контента на любом браузере, установленном у пользователя.

При этом производится поиск видео онлайн бесплатно. Воспользоваться всем этим можно, если обратиться к нам. Благодаря работе нашего сайта вы будете смотреть фильмы и сериалы любых жанров и тематик. Желаем вам приятного просмотра. Мы уверены, что вы, однажды посетив наш портал, обязательно вернётесь к нам вновь.

Канал видеоролика: Физик Воронежский

Смотреть видео:

СМОТРЕТЬ ВИДЕОРОЛИК:

youtu.be/QI22v-3-e3U

#физика #егэфизика #огэфизика #термодинамика #репетиторпофизике #фтф #мифи #мфти #физтех

Свежая информация для ЕГЭ и ОГЭ по Физике (листай):

С этим видео ученики смотрят следующие ролики:

Физика с Герцем | Задание 23 | Физика ОГЭ

Евгений Герц

Физика. Подготовка к ЦТ. Задание А1. Пилотный выпуск.

Физика. Подготовка к ЦТ. Задание А2.

Тестирование по физике

Физика. Подготовка к ЦТ. Задание А3.

Тестирование по физике

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

18.06.2019

Решение задание 30 демоверсии ЕГЭ по физике 2019:

Воздушный шар, оболочка которого имеет массу М = 145 кг и объём V = 230 м³, наполняется при нормальном атмосферном давлении горячим воздухом, нагретым до температуры t = 265 °С. Определите максимальную температуру t0 окружающего воздуха, при которой шар начнёт подниматься. Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие (см. рисунок).

Будем благодарны, если вы поделитесь данной записью со своими друзьями в социальных сетях, оставите отзыв и посмотрите другие материалы на нашем сайте.

Вконтакте

Одноклассники

Мой мир

E-mail

Источник

Решение задание 30 демоверсии ЕГЭ по физике 2019:

Источник

Канал видеоролика: Физика ЕГЭ сотка

Смотреть видео:

#физика #егэфизика #огэфизика #термодинамика #физикаегэ #фтф #мифи #мфти #физтех

Свежая информация для ЕГЭ и ОГЭ по Физике (листай):

С этим видео ученики смотрят следующие ролики:

Электрическая мощность | Разбор задачи | ЕГЭ Физика | Николай Ньютон

Николай Ньютон

Разбор задачи по ЭЛЕКТРОСТАТИКЕ | ЕГЭ Физика | Николай Ньютон

Николай Ньютон

Правило правой и левой руки + разбор задачи| ЕГЭ Физика | Николай Ньютон

Николай Ньютон

Динамика | Разбор задачи | ЕГЭ Физика | Николай Ньютон

Николай Ньютон

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

20.07.2022

Источник

30. Молекулярная физика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Смешанные задачи

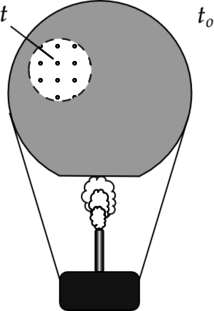
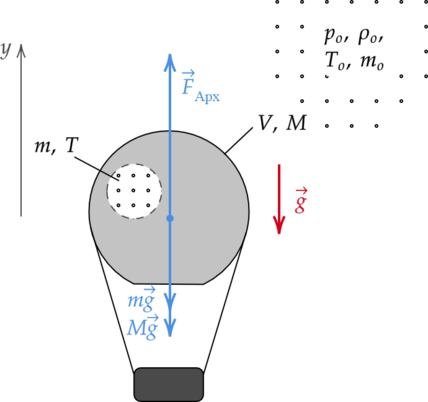
Воздушный шар, оболочка которого имеет массу (M) = 145 кг и объём (V) = 230 м(^3), наполняется при нормальном атмосферном давлении горячим воздухом, нагретым до температуры (t) = 265 (^{circ})С. Определите максимальную температуру (t_o) окружающего воздуха, при которой шар начнёт подниматься. Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие (см. рисунок).

“Демоверсия 2019”

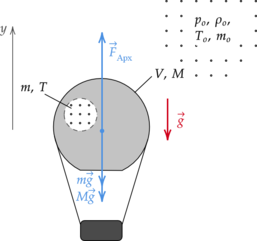
Покажем на рисунке все силы, действущие на воздушный шар и введем вертикальную ось (y):

Рассмотрим предельный случай, когда шар вот-вот оторвется от поверхности земли, и запишем для него второй закон Ньютона: [vec{F}_text{Арх} + mvec{g} +Mvec{g} = 0] где (F_text{Арх}) — выталкивающая сила, (m) — масса горячего воздуха, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на ось (y), направленную вертикально вверх: [; ; ; ; F_text{Арх} — mg-Mg = 0 ; ; ; ; (1)] Выталкивающая сила равна: [; ; ; ; F_text{Арх} = rho_o gV ; ; ; ; (2)] где (rho_o) — плотность холодного воздуха, (V) — объем шара.
Подставим (2) в (1) и разделим на (g): [; ; ; ; rho_o V — m — M = 0 ; ; ; ; (3)] Заметим, что (rho_o V = m_o), где (m_o) — масса холодного воздуха.
Тогда уравнение (3) будет иметь вид: [; ; ; ; m_o — m — M = 0 ; ; ; ; (4)] Чтобы найти массы горячей и холодного воздуха, запишем для них уравнение Менделеева – Клапейрона: [; ; ; ; p_oV = dfrac{m}{Mr}RT ; ; ; Rightarrow ; ; ; m = dfrac{p_o VMr}{RT} ; ; ; ; (5)] [; ; ; ; p_oV = dfrac{m_o}{Mr}RT_o ; ; ; Rightarrow ; ; ; m_o = dfrac{p_o VMr}{RT_o} ; ; ; ; (6)] где (p_o) — атмосферное давление, (Mr) — молярная масса воздуха, (R) — универсальная газовая постоянная, (T) (T_o) — абсолютные температуры горячего и холодного воздуха соответственно.
Подставим (5), (6) в (4) и выразим максимальную температуру окружающего воздуха, при которой шар начнет подниматься: [dfrac{p_o VMr}{RT_o} — dfrac{p_o VMr}{RT} — M = 0 ; ; ; / :dfrac{p_o VMr}{RT}] [dfrac{1}{T_o} — dfrac{1}{T} — dfrac{MR}{p_oVMr} = 0] [T_o=dfrac{mu p_oVT}{mu p_oV+MRT}] [T_o = dfrac{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3cdot(265+273)text{ К}}{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3+145text{ кг}cdot8,31text{ Дж/(моль$cdot$К)}cdot(265+273)text{ К}}approx273 text{ К}=0^{circ}text{С}]

Ответ: 0 ∘С (273 К)

В теплоизолированном сосуде в начальный момент находится одноатомный газ при температуре (T_o) = 300 К и кусочек железа массой (m) = 2 кг, нагретый до температуры (T_1) = 500 К. Начальное давление газа (p_o) = 10(^5) Па, его объем (V_o) = 10000 см(^3), удельная теплоемкость железа (c) = 0,45 кДж/(кг(cdot)К). Найдите давление газа в равновесном состоянии, считая объем газа неизменным.

Так как по условию задачи система замкнута, то внутренняя энергия ее неизменна. Поэтому равновесное состояние системы будет устанавливаться при передаче тепла газу от более горячего куска железа. По первому закону термодинамики: [Delta U=Q-A,] где (Delta U) — изменение внутренней энергии, (Q) — количество теплоты, которое подводили к телу, (A) — работа газа.
В данном случае работа газа равна нулю, так как (V=const). Уравнение теплового баланса в этом случае имеет вид: [dfrac{3}{2}nu R(T-T_o)=cm(T_1-T), hspace{7 mm} (1)] где (nu) — количество вещества газа, (R) — универсальная газовая постоянная.
Запишем уравнение Менделеева – Клапейрона: [p_oV_o=nu R T_o] Выразим отсюда: [hspace{5 mm} nu R=dfrac{p_oV_o}{T_o} hspace{7 mm} (2)] Выразим из (1) температуру газа (T): [T=dfrac{cmT_1+1,5nu RT_0}{cm+1,5nu R}hspace{5 mm} (3)] Так как объем постоянен и количество вещества газа не меняется, то по закону Шарля: [dfrac{p_1}{T_1} = dfrac{p_o}{T_o}hspace{3 mm} Rightarrow hspace{3 mm} p_1=p_ocdotdfrac{T}{T_o}hspace{5 mm} (4)] Подставим (3) в (4): [p_1=p_ocdotdfrac{cmT_1+1,5nu RT_o}{T_o(cm+1,5nu R)}hspace{5 mm} (5)] Подставим (2) в (5): [p_1=p_ocdotdfrac{cmT_1+1,5dfrac{p_oV_o}{T_o}T_o}{T_oleft(cm+1,5dfrac{p_oV_o}{T_o}right)} = p_ocdotdfrac{cmT_1+1,5p_oV_o}{T_ocm+1,5p_oV_o}] Найдем давление газа в равновесном состоянии: [p_1 = 10^5 text{ Па}cdotdfrac{450text{ Дж}/(text{кг}cdottext{К})cdot2 text{ кг} cdot500 text{ К}+1,5cdot10^5text{ Па}cdot10^{-2}text{ м$^3$}}{300text{ К}cdot450text{ Дж}/(text{кг}cdottext{К})cdot2 text{ кг}+1,5cdot10^5text{ Па}cdot10^{-2}text{ м$^3$}} approx 166 text{ кПа}]

Ответ: 166 кПа

Два литра жидкого аргона находится при температуре своего кипения -186 (^{circ})С. Какое количество теплоты нужно сообщить этому количеству аргона для того, чтобы при постоянном давлении перевести его в газ, имеющий температуру 0 (^{circ})С? Плотность жидкого аргона 1400 кг/м(^3), его удельная теплота испарения 87 кДж/кг.

Чтобы перевести аргон в газ, имеющий температуру 0 (^circ)С, сначала необходимо перевести его из жидкого состояния в газообразное, а затем нагреть до нужной температуры.
Общее количество теплоты (Q), которое необходимо для этого, будет складываться из двух составяющих: [; ; ; ; Q = Q_1 + Q_2 ; ; ; ; (1)] Количество теплоты, которое потребуется для парообразования аргона: [; ; ; ; Q_1=rm, ; ; ; ; (2)] где (m) — масса аргона, (r) — удельная теплота испарения.
Когда аргон превратится в газ, мы будем его рассматривать как идеальный одноатомный газ. Значит, для нагрева аргона до 0 (^{circ}) С запишем перове начало термодинамики: [Q_2=Delta U+A,] где (Q_2) — количество теплоты, необходимое для нагревания, (Delta U) — изменение внутренней энергии аргона, (A) — работа аргона.
[Q_2=dfrac{3}{2}nu RDelta T+p(V_2-V_1), hspace{7 mm} (3)] где (nu) — количество вещества, (Delta T) — изменение температуры, (p) — давление, (V_2) и (V_1) — конечное и начальное давлени газа, а в дальнейшнем (mu) — молярная масса газа, (rho) — плотность аргона.
По уравнению Клапейрона — Менделеева: [p(V_2-V_1)=nu R Delta T hspace{7 mm} (4)] Подставим (4) в (3): [Q_2=dfrac{3}{2}nu RDelta T+nu RDelta T] [; ; ; ; Q_2 = dfrac{5}{2}nu RDelta T ; ; ; ; (5)] Подставим (2), (5) в (1): [Q=rm+dfrac{5}{2}nu RDelta T] Количество вещества аргона можно найти по формуле: (nu = dfrac{m}{mu}), где (mu) — молярная масса аргона.
Массу аргона можно найти, зная его плотность и объем: (m = rho V).
С учетом этого: [Q=rrho V+dfrac{5}{2}cdotdfrac{rho V}{mu}RDelta T] [Q=87cdot10^3text{ кДж/кг}cdot2cdot10^{-3}text{ м$^3$}cdot1400text{ кг/м$^3$} +dfrac{5}{2}cdotdfrac{1400text{ кг/м$^3$}cdot2cdot10^{-3}text{ м$^3$}}{40cdot10^{-3}text{кг/моль}}cdot8,31cdot186^circtext{C} approx 591 text{ кДж}]

Ответ: 591 кДж

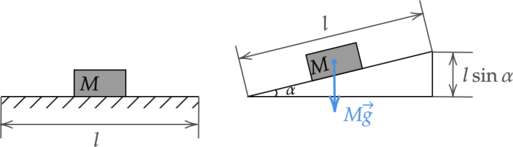
Когда легковой автомобиль едет с постоянной скоростью по горизонтальному шоссе, расход бензина составляет (mu_1) = 7 л/100 км. Каков будет расход бензина (mu_2), если этот автомобиль поедет с той же скоростью вверх по наклонному участку шоссе, образующему угол (alpha) = 0,01 рад с горизонтом? Качество дорожного покрытия на горизонтальном и наклонном участках шоссе одинаково. Масса автомобиля (M) = 1000 кг, коэффициент полезного действия двигателя (eta = 30%), удельная теплота сгорания бензина (q) = 42 МДж/кг, плотность бензина (rho) = 0,7 кг/л. При расчетах положить (sin alpha approx alpha).

По условию задачи КПД двигателя автомобиля равен 30%. Это означает, что только 30% от выделевшегося количества теплоты пойдет на совершение работы по перемещению автомомбиля: [; ; ; ; A = 0,3Q ; ; ; ; (1)] Количество теплоты, которое выделится при сгорании бензина, равно: [; ; ; ;Q = qm ; ; ; ; (2)] где (m) — масса сгоревшего бензина.
Массу бензина можно найти, зная его плотность: [; ; ; ; rho = dfrac{m}{V} ; ; ; Rightarrow ; ; ; m = rho V ; ; ; ; (3)] где (V) — объем сгоревшего бензина.
Зная расход бензина и пройденное расстояние, найдем объем израсходованного бензина: [; ; ; ;V = mu l ; ; ; ;(4)] Подставим последовательно (4), (3), (2) в (1): [; ; ; ;A = 0,3qrhomu l ; ; ; ; (5)] В то же время работа при перемещении автомобиля на расстояние (l) по определению равна: [A = Flcosalpha_o] где (F) — модуль равнодействующей всех сил, действующих на автомобиль, (alpha_o) — угол между направлением силы и направлением перемещения.
В рассматриваемых случаях и для горизонтального движения и для движения под углом к гори3 зонту (cosalpha = 1): [; ; ; ; A = Fl ; ; ; ;(6)]
Рассмотрим движение автомобиля по горизонтальному участку шоссе.
В этом случае работа, совершенная двигателем, по величине равна работе сил сопротивления.
Исходя из формул (5) и (6), получаем, что: [0,3qrhomu_1 l = Fl] Выразим отсюда силу (F): [; ; ; ; F = 0,3qrhomu_1 ; ; ; ; (7)] Рассмотрим движение автомобиля по наклонному участку шоссе той же длины.
В этом случае работа двигателя равна сумме величины работы сил сопротивления и изменения (приращения) потенциальной энергии автомобиля в поле силы тяжести: [A = Fl + Mglsinalpha] С учетом формулы (5) имеем, что: [0,3qrhomu_2 l = Fl + Mglsinalpha] Выразим отсюда силу (F): [; ; ; ; F = 0,3qrhomu_2 — Mgsinalpha ; ; ; ; (8)] Приравняем (7) и (8) с учетом того, что по условию (sinalpha approx alpha), и выразим искомый расход бензина: [0,3qrhomu_1 = 0,3qrhomu_2 — Mgsinalpha] [mu_2 = mu_1 + dfrac{Mgalpha}{0,3rho q}] [mu_2 = 7(text{ л/$100$ км}) + dfrac{1000text{ кг}cdot10text{ м/с}^2cdot0,01}{0,3cdot0,7text{ кг/л}cdot 42cdot10^6text{ Дж/кг}}cdot10^5 approx 8,13text{ л/100 км}]

Ответ: 8,13 л/100 км

Мальчик решил подняться в воздух на воздушных шарах с гелием. Известно, что мальчик весит 40 кг, а на улице нормальное атмосферное давление и температура 27 (^{circ})С. Учитывая, что объем одного шара составляет 10 литров, найдите, сколько потребуется шаров для такого путешествия. Массой оболочки шаров и объемом мальчика пренебречь.

Cила тяжести, действующая на систему, уравновешивается силой Архимеда.
Рассмотрим предельный случай, когда мальчик на воздушных шарах вот-вот оторвется от поверхности земли, и запишем второй закон Ньютона для данной системы: [vec{F}_text{Арх} + Mvec{g} + nmvec{g} = 0] где (M) — масса мальчика, (m) — масса гелия в одном шарике, (n) — количество шаров, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на вертикальную ось, направленную вверх: [F_text{Арх} — Mg — nmg = 0] [; ; ; ; F_text{Арх} = Mg + nmg ; ; ; ; (1)] Сила Архимеда равна: [F_text{Арх} = rho_o gnV] где (rho_o) — плотность воздуха, (V) — объем одного шарика.
Подставим (2) в (1): [rho_o gnV = Mg + nmg] [; ; ; ; rho_o nV = M + nm ; ; ; ; (3)] Запишем уравнение Менделеева-Клапейрона для воздуха: [; ; ; ; p_oV_o = dfrac{m_o}{mu_o} RT_o ; ; ; ; (4)] где (p_o) — атмосферное давление, (V_o) — объем, занимаемый воздухом, (m_o) — (mu_o) — масса воздуха, (R) — универсальная газовая постоянная, (T_o) — абсолютная температура воздуха.
Плотность воздуха равна: [; ; ; ; rho_o = dfrac{m_o}{V_o} ; ; ; ; (5)] Подставим (5) в (4) и выразим плотность воздуха: [; ; ; ; p_o = dfrac{rho_o}{mu_o}RT_o ; ; ; Rightarrow ; ; ; rho_o = dfrac{p_omu_o}{RT_o} ; ; ; ; (6)] Найдем массу гелия в одном шарике из уравнения Менделеева-Клапейрона: [; ; ; ; p_o V = dfrac{m}{mu}RT_o ; ; ; Rightarrow ; ; ; m = dfrac{p_o Vmu}{RT_o} ; ; ; ; (7)] где (m) — масса гелия, (mu) — молярная масса гелия.
Подставим (6), (7) в (3) и выразим количество шариков: [M + ndfrac{p_o Vmu}{RT_o} = dfrac{p_o mu_o}{RT_o}nV] [n = dfrac{MRT_o}{p_o V(mu_o — mu)}] [n = dfrac{40text{ кг}cdot8,31text{Дж/(моль$cdot$К)}cdot300text{ К}}{10^5text{ Па}cdot10^{-2}text{ м}^3cdot(29-4)cdot10^{-3} text{кг/моль}}=3989]

Ответ: 3989

Покажем на рисунке все силы, действущие на воздушный шар и введем вертикальную ось (y):

Рассмотрим предельный случай, когда шар вот-вот оторвется от поверхности земли, и запишем для него второй закон Ньютона: [vec{F}_text{Арх} + mvec{g} +Mvec{g} = 0] где (F_text{Арх}) — выталкивающая сила, (m) — масса горячего воздуха, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на ось (y), направленную вертикально вверх: [; ; ; ; F_text{Арх} — mg-Mg = 0 ; ; ; ; (1)] Выталкивающая сила равна: [; ; ; ; F_text{Арх} = rho_o gV ; ; ; ; (2)] где (rho_o) — плотность холодного воздуха, (V) — объем шара.
Подставим (2) в (1) и разделим на (g): [; ; ; ; rho_o V — m — M = 0 ; ; ; ; (3)] Заметим, что (rho_o V = m_o), где (m_o) — масса холодного воздуха.
Тогда уравнение (3) будет иметь вид: [; ; ; ; m_o — m — M = 0 ; ; ; ; (4)] Чтобы найти массы горячей и холодного воздуха, запишем для них уравнение Менделеева – Клапейрона: [; ; ; ; p_oV = dfrac{m}{Mr}RT ; ; ; Rightarrow ; ; ; m = dfrac{p_o VMr}{RT} ; ; ; ; (5)] [; ; ; ; p_oV = dfrac{m_o}{Mr}RT_o ; ; ; Rightarrow ; ; ; m_o = dfrac{p_o VMr}{RT_o} ; ; ; ; (6)] где (p_o) — атмосферное давление, (Mr) — молярная масса воздуха, (R) — универсальная газовая постоянная, (T) (T_o) — абсолютные температуры горячего и холодного воздуха соответственно.
Подставим (5), (6) в (4) и выразим максимальную температуру окружающего воздуха, при которой шар начнет подниматься: [dfrac{p_o VMr}{RT_o} — dfrac{p_o VMr}{RT} — M = 0 ; ; ; / :dfrac{p_o VMr}{RT}] [dfrac{1}{T_o} — dfrac{1}{T} — dfrac{MR}{p_oVMr} = 0] [T_o=dfrac{mu p_oVT}{mu p_oV+MRT}] [T_o = dfrac{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3cdot(265+273)text{ К}}{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3+145text{ кг}cdot8,31text{ Дж/(моль$cdot$К)}cdot(265+273)text{ К}}approx273 text{ К}=0^{circ}text{С}]

Ответ: 0 ∘С (273 К)

Сосуд объемом (V) л, содержащий (nu) моль воздуха при давлении (p) Па и температуре (T_o) К, сверху заткнут пробкой массой (m) кг с площадью (S) см(^2). Найдите на какую величину надо увеличить температуру газа, чтобы пробка вылетела из сосуда, если коэффицент трения пробки о стенки сосуда равен (mu), а атмосферное давление равно (p_o).

Запишем 2 закон Ньютона для предельного случая, когда пробка вот-вот вылетит из сосуда: [; ; ; ; F = F_text{тяж}+F_text{тр}+F_text{атм}, ; ; ; ; ; (1)] где (F) — сила, с которой газ воздействует на пробку, (F_text{тяж}) — сила тяжести, действующая на пробку , (F_text{тр}) — сила трения пробки о стенки сосуда, (F_text{атм}) — сила давления атмосферы на пробку.
Сила, с которой газ воздействует на пробку, равна: [; ; ; ; p=dfrac{F}{S} ; ; ; Rightarrow ; ; ; F=pS ; ; ; ; (2)] По уравнению Клайперона – Менделеева: [; ; ; ; pV=nu R T ; ; ; Rightarrow ; ; ; p=dfrac{nu R T}{V},; ; ; ; (3)] где (T) — абсолютная температура газа, (Delta T) — изменение температуры газа.
Подставим (3) в (2): [; ; ; ; F = dfrac{nu R T}{V}S ; ; ; ; (4)] Сила давления атмосферы на пробку равна: [; ; ; ; F_text{атм}=p_oS ; ; ; ; (5)] Силу тяжести и силу трения найдем по формулам: [; ; ; ; F_text{тяж}=mg ; ; ; (6) ; ; ; ; ; ; ; ; ; ; ; F_text{тр}=mu mg, ; ; ; (7)] где (g) — ускорение свободного падения.
Подставим (4), (5), (6), (7) в (1) и получим: [; ; ; ; S dfrac{nu R T}{V} = mg +mu m g +p_o S ; ; ; ; (8)] Конечная температура газа равна: [; ; ; ; T=T_o + Delta T ; ; ; ; (9)] Подставим (9) в (8) и выразим (Delta T), на которую нужно увеличить температуру газа, чтобы пробка вылетела: [S dfrac{nu R (T_o + Delta T)}{V} = mg +mu m g +p_o S] [Delta T =dfrac{V}{nu R}left(dfrac{mg}{S}+dfrac{mu m g }{S}+p_oright)-T_o]

Ответ: $Delta T =dfrac{V}{nu R}left(dfrac{mg}{S}+dfrac{mu m g }{S}+p_oright)-T_o$

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задача про воздушный шарик

Сложная задача про шарик с тянущейся за ним веревкой.

Задача. Наполненный гелием воздушный шарик почти идеальной сферической формы, если его отпустить в безветренную погоду, будет подниматься вверх со скоростью, постепенно достигающей величины м/с. Если привязать к нему кусок тонкой гибкой нерастяжимой однородной веревки, то шарик сможет подниматься вверх, если длина куска не превышает см. К шарику привязали кусок такой же веревки длиной м и расстелили нижний конец веревки на горизонтальной поверхности. Коэффициент трения между веревкой и поверхностью . С какой скоростью будет в установившемся режиме двигаться шарик с прикрепленной веревкой при ветре, дующем вдоль поверхности со скоростью м/с?

Задача про шарик

На какой высоте над поверхностью будет двигаться верхний конец веревки? Воздействием ветра на веревку пренебречь. Сила сопротивления воздуха, действующая на шар, пропорциональна квадрату его скорости относительно воздуха.