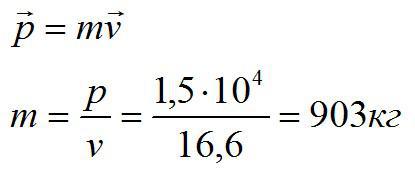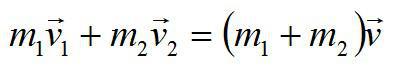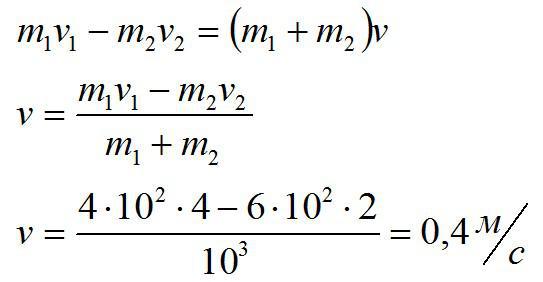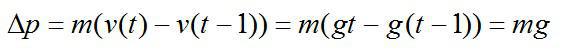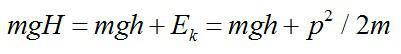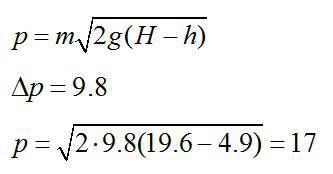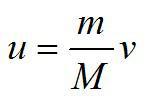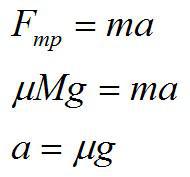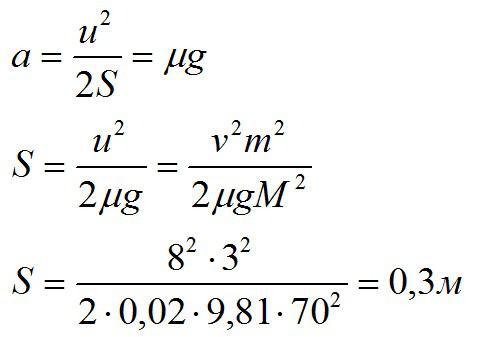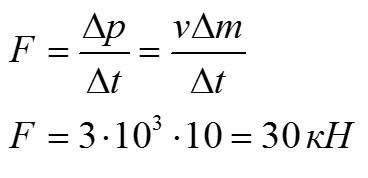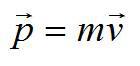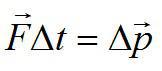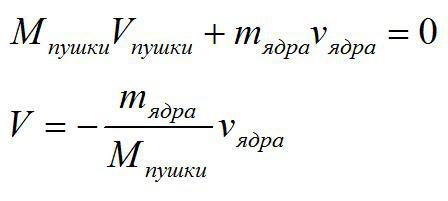Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
2
Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы этих тел. Чему по модулю равен импульс всей системы? Ответ выразите в килограммах на метр в секунду и округлите до десятых.
3
Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы этих тел. Чему по модулю равен импульс всей системы? (Ответ дайте в килограммах на метр в секунду.)
4
Система состоит из двух тел 1 и 2, массы которых равны 0,5 кг и 2 кг. На рисунке стрелками в заданном масштабе указаны скорости этих тел. Чему равен импульс всей системы по модулю? (Ответ дайте в килограммах на метр в секунду.)
5
Охотник массой 60 кг, стоящий на гладком льду, стреляет из ружья в горизонтальном направлении. Масса заряда 0,03 кг. Скорость дробинок при выстреле Какова скорость охотника после выстрела? (Ответ дайте в метрах в секунду.)
Пройти тестирование по этим заданиям
Закон сохранения импульса.
Задачи ЕГЭ с решениями
Формулы для решения задач по теме «Закон сохранения импульса. Задачи ЕГЭ».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Тело массой 2 кг свободно падает без начальной скорости с высоты 5 м на горизонтальную поверхность и отскакивает от нее со скоростью 5 м/с. Найдите абсолютную величину изменения импульса тела при ударе, g = 10 м/с2.
Задача 2.
Мячик массой 200 г летел со скоростью 20 м/с. После удара о стенку он отскочил под прямым углом к прежнему направлению со скоростью 15 м/с. Найдите модуль изменения импульса мячика при ударе.
Посмотреть РЕШЕНИЕ и ответ
Задача 3.
Стальной шарик массой 0,1 кг падает на горизонтальную плоскость с высоты 0,2 м и отскакивает после удара снова до высоты 0,2 м. Найдите среднюю силу давления шарика на плоскость при ударе, если его длительность 0,04 с. g = 10 м/с2.
Посмотреть РЕШЕНИЕ и ответ
Задача 4.
Стальной шарик массой 40 г, летящий горизонтально со скоростью 20 м/с, ударяется о наклонную плоскость, составляющую угол 30° с горизонтом. Считая удар абсолютно упругим, найдите среднюю силу взаимодействия шарика с наклонной плоскостью. Продолжительность удара 0,01 с. Действием силы тяжести за время удара пренебречь.
Посмотреть РЕШЕНИЕ и ответ
Задача 5.
Какова средняя сила давления на плечо при стрельбе из автомата, если масса пули 10 г, а скорость пули при вылете 300 м/с? Автомат делает 300 выстрелов в минуту.
Посмотреть РЕШЕНИЕ и ответ
Задача 6.
Ракета массой 2 т неподвижно висит над землей, выбрасывая вниз реактивную струю со скоростью 1250 м/с. Какая масса газов выбрасывается в струе за 1 с? g = 10 м/с2.
Посмотреть РЕШЕНИЕ и ответ
Замечание. Если ракета движется с ускорением, формула для реактивной силы имеет такой же вид. Проще всего убедиться в этом, перейдя в систему отсчета, в которой ракета в данный момент покоится.
Задача 7.
Тонкую мягкую цепочку массой 200 г удерживают за один конец так, что другой ее конец касается стола. Цепочку отпускают, и она падает на стол. Считая, что все элементы цепочки, находящиеся в воздухе, падают свободно, найдите силу давления на стол в тот момент, когда в воздухе находится половина цепочки, g = 10 м/с2.
Посмотреть РЕШЕНИЕ и ответ
Задача 8.
Конькобежец катил груженные сани по льду со скоростью 5 м/с, а затем толкнул их вперед и отпустил. С какой скоростью (в см/с) покатится конькобежец непосредственно после толчка, если скорость саней возросла до 8 м/с? Масса саней 90 кг, масса человека 60 кг. В ответе укажите модуль скорости.
Посмотреть РЕШЕНИЕ и ответ
Задача 9.
Три лодки массами 100 кг каждая идут одна за другой с одинаковыми скоростями. Из средней лодки одновременно в переднюю и заднюю бросают горизонтально со скоростью 2,2 м/с относительно лодки грузы массой 10 кг каждый. Найдите величину относительной скорости (в см/с) передней и задней лодок после попадания в них грузов.
Посмотреть РЕШЕНИЕ и ответ
Задача 10.
От поезда, идущего с постоянной скоростью 64 км/ч, отделяется пятая часть состава. Через некоторое время скорость отделившихся вагонов уменьшилась в 2 раза. Считая, что сила тяги при разрыве не изменилась, найдите скорость (км/ч) головной части поезда в этот момент. Сила трения пропорциональна весу.
Посмотреть РЕШЕНИЕ и ответ
Задача 11.
Снаряд, летящий с некоторой скоростью, распадается на два осколка. Скорость большего осколка по величине равна начальной скорости снаряда и направлена перпендикулярно к ней. Скорость другого осколка по величине в 5 раз больше первоначальной. Найдите отношение масс осколков.
Посмотреть РЕШЕНИЕ и ответ
Задача 12.
Снаряд массой 50 кг, летящий под углам 30° к вертикали со скоростью 600 м/с, попадает в платформу с пескам и застревает в ней. Найдите скорость платформы после попадания снаряда. Масса платформы 950 кг. Трением между платформой и рельсами пренебречь.
Посмотреть РЕШЕНИЕ и ответ
Задача 13.
В ящик с песком массой 9 кг, соскальзывающий с гладкой наклонной плоскости, попадает горизонтально летящее ядро массой 3 кг и застревает в нем. Найдите скорость ящика сразу же после попадания ядра, если непосредственно перед попаданием скорость ящика равнялась 6 м/с, а скорость ядра 12 м/с. Угол наклона плоскости к горизонту 60°.
Посмотреть РЕШЕНИЕ и ответ
Задача 14.
Тележка стоит на гладких рельсах. Человек переходит с одного ее конца на другой параллельно рельсам. На какое расстояние относительно земли переместится при этом тележка? Масса человека 60 кг, масса тележки 120 кг, ее длина 6 м.
Посмотреть РЕШЕНИЕ и ответ
Задача 15.
На стол поставили в вертикальном положении тонкую палочку длиной 80 см и отпустили. На сколько сантиметров сместится нижний конец палочки к тому моменту, когда она будет составлять с поверхностью стола угол 60°? Трением пренебречь.
Посмотреть РЕШЕНИЕ и ответ
Задача 16.
Веревку длиной 80 см и массой 200 г положили на гладкую горизонтальную поверхность и раскрутили вокруг одного из концов с угловой скоростью 10 рад/с. Чему равна сила натяжения веревки в середине ее длины?
Посмотреть РЕШЕНИЕ и ответ
Задача 17.
Два шарика массой 250г каждый, соединенные нитью длиной 1 м, движутся по гладкой горизонтальной поверхности. В некоторый момент один из шариков неподвижен, а скорость другого равна 4 м/с и направлена перпендикулярно нити. Чему равна сила натяжения нити?
Посмотреть РЕШЕНИЕ и ответ
Вы смотрели конспект по теме «Закон сохранения импульса. Задачи ЕГЭ». Ключевые слова конспекта: Определение импульса. Изменение импульса и средняя сила. Закон сохранения импульса. Сохранение проекции импульса. Комплексные задачи. Центр масс.
Автор задач и решений: Алексей Игоревич Черноуцан. Выберите дальнейшие действия:
- Перейти к теме:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Закон сохранения импульса на плоскости
-
Теория
-
Задачи
-
Задача 1
-
Задача 2.
-
Задача 3.
-
Задача 4.
Из кодификатора по физике, 2020.
«1.4.3. Закон сохранения импульса: в ИСО
Теория
Импульс тела — векторная физическая величина, равная произведению массы тела m на его скорость :
— Обозначается буквой , измеряется в килограмм-метр в секунду (кг∙м/с).
— Импульс тела направлен в ту же сторону, что и скорость тела, и наоборот.
Изменение импульса тела
где и
— конечный и начальный импульсы тела,
и
— конечная и начальная скорости тела, m — масса тела.
Импульс системы тел равен векторной сумме импульсов тел
входящих в эту систему
где m1, m2, … — массы тел системы, — скорости тел системы.
Изменение импульса системы тел
где — конечный импульс системы тел,
— начальный импульс системы тел, m1, m2, … — массы тел системы,
— конечные скорости тел системы,
— начальные скорости тел системы.
Импульс силы — векторная физическая величина, равная произведению силы на время t ее действия:
— Обозначается буквой , измеряется в Ньютон на секунду (Н∙с).
— Импульс силы направлен в ту же сторону, что и сила, и наоборот.
Закон сохранения импульса:
в инерциальной системе отсчета (ИСО) векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю.
Задачи на применение закона сохранения импульса тел (системы тел) решайте, придерживаясь следующего плана:
1. Сделайте схематический чертеж. Укажите направления осей координат ОX и ОY.
— Материальную точку изобразите в виде двух прямоугольников (или окружностей) и укажите над ними (если это известно) направления скорости или импульса до и после взаимодействия.
— Индексы скоростей, импульсов на рисунке должны соответствовать индексам скоростей, импульсов в условии.
2. Определите, векторная сумма внешних сил, действующих на систему тел, равна нулю или нет. Если равна нулю, то запишите закон сохранения импульса тел в векторном виде и в проекциях.
Определите значения проекций всех величин.
3. Решите полученные уравнения.
к оглавлению ▴
Задачи
Задача 1
Два тела движутся по взаимно перпендикулярным пересекающимся прямым, как показано на рисунке. Модуль импульса первого тела p1 = 4 кг⋅м/с, а второго тела p2 = 3 кг⋅м/с . Чему равен модуль импульса системы этих тел после их абсолютно неупругого удара?
Решение. Импульс тел изменяет их столкновение. До удара двигались тела отдельно друг от друга. После неупругого удара тела двигались вместе.
Внешних сил нет, поэтому запишем закон сохранения импульса
1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда импульс тел (направление которого неизвестно) будет равен (рис. 2, а)
Направление осей OХ и OY показаны на рисунке условия. Запишем уравнение (1) в проекциях на оси:
После подстановки уравнений (3) и (4) в (2) получаем:
2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 2, б). Модуль импульса p после удара найдем по теореме Пифагора
к оглавлению ▴
Задача 2.
По гладкой горизонтальной плоскости движутся вдоль осей X и Y две шайбы с импульсами, равными по модулю p10 = 5 кг·м/с и p20 = 3 кг·м/с (рис. 3). После их соударения первая шайба продолжает двигаться по оси Y в прежнем направлении. Модуль импульса первой шайбы после удара равен p1 = 2 кг·м/с. Найдите модуль импульса второй шайбы после удара. Ответ округлите до десятых.
Решение. Импульс шайб изменяет их столкновение. До удара шайбы двигались отдельно друг от друга. После удара шайбы так же двигались отдельно.
Внешних сил нет, поэтому запишем закон сохранения импульса
1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда импульс вто-рой шайбы (направление которого неизвестно) будет равен
Направление осей OХ и OY показаны на рисунке 4. Запишем уравнение (1) в проекциях на оси:
После подстановки уравнений (3) и (4) в (2) получаем:
к оглавлению ▴
Задача 3.
Лодка массой 100 кг плывет без гребца вдоль пологого берега со скоростью 1 м/с. Мальчик массой 50 кг прыгает с берега в лодку со скоростью 2 м/с так, что векторы скорости лодки и мальчика составляют прямой угол. Определите значение и направление скорости лодки (в см/с) с мальчиком. Ответ округлите до целых.
Решение. Скорость лодки изменяет прыжок мальчика. До прыжка двига-лись лодка и мальчик отдельно друг от друга. После прыжка мальчик и лодка двигались вместе.
Векторная сумма внешних сил (силы тяжести и силы реакции опоры) равна нулю, поэтому запишем закон сохранения импульса
1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда скорость лодки с мальчиком (направление которой неизвестно) будет равна
Направим ось OХ вдоль начальной скорости лодки, ось OY — вдоль начальной скорости мальчика, т.к. векторы скорости лодки и мальчика составляют прямой угол (рис. 5, а). Запишем уравнение (1) в проекциях на оси:
После подстановки уравнений (3) и (4) в (2) получаем:
Направление скорости υ определим следующим образом (рис. 5, б):
Примечание. Угол α можно было определить и через другие формулы
2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 5, в). Модуль скорости υ после прыжка найдем по теореме Пифагора
Направление скорости υ определим следующим образом (см. рис. 5, в):
к оглавлению ▴
Задача 4.
Летящий снаряд разрывается на два осколка, при этом первый осколок летит со скоростью 50 м/с под углом 90° по отношению к направлению движения снаряда, а второй — со скоростью 200 м/с под углом 30°. Найдите отношение массы первого осколка к массе второго осколка.
Скорость снаряда изменяет взрыв. До взрыва двигался только снаряд. После взрыва осколки снаряда двигались отдельно друг от друга.
Внешних сил нет, поэтому запишем закон сохранения импульса
1 способ (координатный). Направим ось OХ вдоль начальной скорости снаряда, ось OY — вдоль конечной скорости первого осколка (рис. 6, а). Запишем уравнение (1) в проекции на ось:
2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 6, б). Тогда из прямоугольного треугольника получаем
Автор Сакович А.Л.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Закон сохранения импульса на плоскости» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
|
Под действием постоянной силы, равной по модулю 6 Н, импульс тела изменился на 30 кг·м/с. Сколько времени потребовалось для этого? |
||
|
1) |
0,5 с |
|
|
2) |
5 с |
|
|
3) |
36 с |
|
|
4) |
180 с |
Навстречу друг другу летят шарики из пластилина. Модули их импульсов равны соответственно 510–2 кгм/с и 310–2 кгм/с. Столкнувшись, шарики слипаются. Импульс слипшихся шариков равен
1)
810–2 кгм/с
2)
410–2 кгм/с
3)
210–2 кгм/с
4)
10–2 кгм/с
Санки после толчка движутся по горизонтальной дорожке. Как изменится модуль импульса санок, если на них в течение 5 с действует сила трения о снег, равная 20 Н?
1)
ответить невозможно, так как неизвестна масса санок
2)
увеличится на 4 Н/с
3)
увеличится на 100 кгм/с
4)
уменьшится на 100 кгм/с
Шары одинаковой массы движутся так, как показано на рисунке, и абсолютно неупруго соударяются. Как будет направлен импульс шаров после соударения?
1)
2)
3)
4)
На неподвижный бильярдный шар налетел другой – такой же. После удара шары разлетелись под углом 90 так, что импульс одного Р1 = 0,3 кгм/с, а другого Р2 = 0,4 кгм/с (см. рисунок). Налетевший шар имел до удара импульс, равный
1)
0,1 кгм/с
2)
0,5 кгм/с
3)
0,7 кгм/с
4)
0,25 кгм/с
Ракета, состоящая из двух ступеней, двигалась со скоростью 0 = 6 км/с (рис. А). Первая ступень после отделения движется со скоростью 1 = 2 км/с (рис. Б). Масса первой ступени m1 = 1103 кг, масса второй m2 = 2103 кг. Вторая ступень после отделения первой имеет скорость
1)
2 км/с
2)
4 км/с
3)
6 км/с
4)
8 км/с
Если на вагонетку массой m, движущуюся по горизонтальным рельсам со скоростью v, сверху вертикально опустить груз, масса которого равна половине массы вагонетки, то скорость вагонетки с грузом станет равной
1)
2/3v
2)
3/2v
3)
1/2v
4)
1/4v
С балкона высотой 20 м упал на землю мяч массой 0,2 кг. Из-за сопротивления воздуха скорость мяча у земли оказалась на 20% меньше скорости тела, свободно падающего с высоты 20 м. Импульс мяча в момент падения равен
1)
4,0 кгм/с
2)
4,2 кгм/с
3)
3,2 кгм/с
4)
6,4 кгм/с
Шар массой 200 г падает с начальной скоростью 10 м/с на неподвижную, горизонтально расположенную платформу, под углом 45 к ней. Модуль изменения импульса шара в результате абсолютно упругого удара шара о платформу равен
1)
0 кгм/с
2)
2 кгм/с
3)
4 кгм/с
4)
2√2 кгм/с
На экране монитора в Центре управления полетов отображены графики скоростей двух космических аппаратов после их расстыковки (см. рис.). Масса первого из них равна 10 т, масса второго равна 15 т. С какой скоростью двигались аппараты перед их расстыковкой?

1)
2103 м/с
2)
7,4103 м/с
3)
1103 м/с
4)
7,6103 м/с
Две тележки движутся вдоль одной прямой в одном направлении. Массы тележек m и 2m, скорости – соответственно 2v и v. Какой будет их скорость после абсолютно неупругого столкновения?
1)
3/4v
2)
2/3v
3)
3v
4)
1/3v
После пережигания нити первая тележка, масса которой равна 0,6 кг, стала двигаться со скоростью 0,4 м/с (см. рисунок). С какой по модулю скоростью начала двигаться вторая тележка, масса которой равна 0,8 кг?
1)
0,2 м/с
2)
0,3 м/с
3)
0,4 м/с
4)
0,6 м/с
Тело массой 2 кг движется вдоль оси ОХ. Его координата меняется в соответствии с уравнением х = А +Bt + Ct2, где А = 2 м, В = 3 м/с, С = 5 м/с2. Чему равен импульс тела в момент времени t = 2 c?
1)
86 кгм/с
2)
48 кгм/с
3)
46 кгм/с
4)
26 кгм/с
Шар массой 200 г падает с начальной скоростью 10 м/с на неподвижную платформу под углом 45 к ней. Какой импульс будут иметь шар и платформа в результате абсолютно неупругого удара шара о платформу, если платформа может скользить по горизонтальной поверхности без трения?
1)
0 кгм/с
2)
2 кгм/с
3)
√2 кгм/с
4)
2√2 кгм/с
Два автомобиля одинаковой массы m движутся со скоростями v и 2v относительно Земли в противоположных направлениях. Чему равен модуль импульса второго автомобиля в системе отсчета, связанной с первым автомобилем?
1)
3mv
2)
2mv
3)
mv
4)
0
На сани, стоящие на гладком льду, с некоторой высоты прыгает человек массой 50 кг. Проекция скорости человека на горизонтальное направление в момент соприкосновения с санями 4 м/с. Скорость саней с человеком после прыжка составила 0,8 м/с. Какова масса саней?
1)
150 кг
2)
200 кг
3)
250 кг
4)
400 кг
На стоящие на горизонтальном льду сани массой 200 кг с разбега запрыгивает человек массой 50 кг. Скорость саней после прыжка составила 0,8 м/с. Какова проекция скорости человека на горизонтальное направление в момент касания саней?
1)
1 м/с
2)
8 м/с
3)
6 м/с
4)
4 м/с
Тело движется по прямой. Под действием постоянной силы величиной 4 Н за 2 с импульс тела увеличился и стал равен 20 кгм/с. Первоначальный импульс тела равен
1)
4 кгм/с
2)
8 кгм/с
3)
12 кгм/с
4)
28 кгм/с
На рисунке изображены графики изменения скорости двух взаимодействующих тележек разной массы (одна тележка догоняет и толкает другую). Какую информацию о тележках содержат эти графики?
1)
тележка 1 едет сзади и имеет бóльшую массу
2)
тележка 1 едет сзади и имеет меньшую массу
3)
тележка 2 едет сзади и имеет бóльшую массу
4)
тележка 2 едет впереди и имеет меньшую массу
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Закон сохранения импульса
Закон сохранения импульса
Импульс замкнутой системы, состоящей из (n), тел остается постоянным с течением времени при любых взаимодействиях тел внутри данной системы
[displaystylesum_{i=1}^{n}vec{p}_i=displaystylesum_{i=1}^{n}m_ivec{v}_i=const]
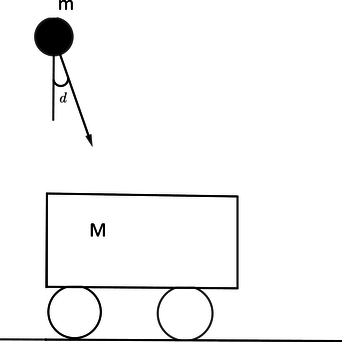
Охотник, стоящий на гладком льду, стреляет из ружья. Масса заряда (0,05 text{кг} ). Скорость снаряда (200 text{м/c}). Какова масса охотника, если его скорость после выстрела равна (0,1 text{м/c})
Так как до выстрела общий импульс системы равен нулю. По Закону Сохранения импульса: [m_1cdot upsilon_1 — m_2cdot upsilon_2 = 0] Где (m_2) – масса охотника, (m_1) – масса снаряда (v_1), (upsilon_2) – скорости снаряда и охотника соответственно [m_2 = frac {m_1 cdot upsilon_1} {upsilon_2}] [m_2= frac {0,05 text {кг} cdot 200 text{ м/с}}{0,1 text{м/c} } =100text{ кг}]
Ответ: 100
Камень массой (m =4 text { кг} ) падает под углом (alpha=30^circ) к вертикали со скоростью (10 text { м/с}) в тележку с песком общей массой ( M= 16 text { кг}), покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в неё камня.
В начале импульс тележки равен нулю. по Закону Сохранения Импульса(на горизонтальную ось): [m_1cdot upsilon_1sinalpha=(m+M)cdotupsilon’] [upsilon’=frac{m_1cdot upsilon_1sinalpha}{m+M}] [upsilon’=frac{4text{ кг}cdot 10text{ м/с} cdotdfrac 1 2 }{4text{ кг}+16text{ кг}}=1text{ м/c}]
Ответ: 1
С неподвижной лодки массой (M=50text{ кг } ) на берег прыгнул мальчик массой (m=40text{ кг } ) со скоростью (upsilon_1 = 1 text{ м/c } ) относительно берега, направленной горизонтально. Какую скорость (upsilon_2) относительно берега приобрела лодка?
Начальный импульс системы равен нулю. По закону Сохранения Импульса: [Mcdotupsilon_2-mcdotupsilon_1 = 0] [upsilon_2=frac{mcdotupsilon_1}{M}] [upsilon_2=frac{40 text{ кг }cdot 1 text{ м/с } } {50 text{ кг}} =0,8 text{ м/c }]
Ответ: 0, 8
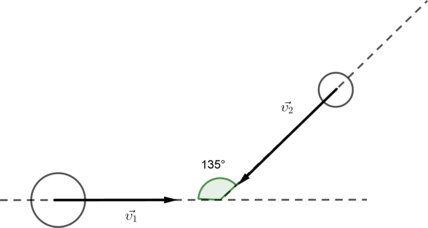
Одинаковые шары массой (m = 1 text{ кг } ) каждый движутся со скоростями, направления которых указаны на рисунке, и сталкиваются. Чему будет равен суммарный импульс шаров после столкновения, если (upsilon_1=16 text{ м/c }), а (upsilon_2=upsilon_1 cdot sqrt{2})?
Из рисунка видно, что углы между осями и вторым шаром равны (45^circ). По закону сохранения импульса суммапрный импульс системы до удара и после удара будет одинаковый. Найдем проекции суммарного импульса на каждую ось: (p_x’) – Суммарный импульс на ось Ox (p_y’) – суммарный импульс на ось Oy [p_{2x}-p_{1x}=p_x’] [p_{2y}-p_{1y} =p_y’] По рисунку (p_{1y}=0) По теореме Пифагора: [P_{text{итог}}’=sqrt{p_y’^2+p_x’^2}] Заменим (upsilon_2) на (upsilon_1 cdot sqrt{2} ). [p_y’=mcdotupsilon_1sqrt{2}cos{45^circ}] [p_x’=mcdot upsilon_1cdot (cos{45^circ} cdot sqrt{2}-1)] [p_y’= 1 text{кг} cdot 16 text{ м/c } cdot frac{sqrt2} 2cdot sqrt 2 = 16 frac{text{ кг }cdot text{ м }} {text{ c }}] [p_x’= 1 кг cdot 16 text{м/c} left(frac{sqrt2} {2} cdot sqrt2 — 1right)=0frac{text{ кг }cdot text{ м }} {text{ c }}] [P_{ итог } = sqrt{left(16frac{text{кг}cdot text{м}} { c}right)^2}=16frac{text{ кг }cdot text{ м }} { text{ c } }]
Ответ: 16
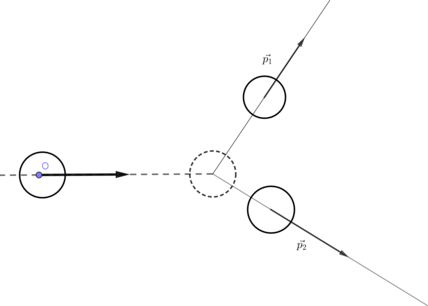
На неподвижный бильярдный шар налетел другой такой же. После удара шары разлетелись под углом (90^circ) так, что импульс одного равен (p_1=5dfrac {text{ кг }cdot text{ м }} {text{ c }} ), а другого (p_2 = 12dfrac{text{ кг }cdot text{ м }}{text{ c }}) (см.рисунок). Чему был равен импульс налетающего шара?
По закону сохранения импульса: [vec{p’}=vec{p_1}+vec{p_2}] Так как шары разлетелись под углом (90^{circ}), применим теорему Пифагора: [p’=sqrt{p_1^2 + p_2^2}] [p’=sqrt{left(5 frac {text{ кг }cdot text{ м }} {text{ c }} right)^2 + left(12frac {text{ кг }cdot text{ м }} {text{ c }} right)^2}=13frac {text{ кг }cdot text{ м }} {text{ c }}]
Ответ: 13
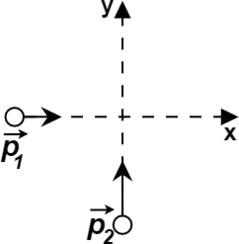
По гладкой горизонтальной плоскости по осям Оx и Оy движутся две шайбы с импульсами равными по модулю (p_1 =3 ) кг(cdot)м/с и (p_2 =6 ) кг(cdot)м/с (см.рисунок). После их соударения вторая шайба продолжает двигаться по оси y в прежнем направлении. Модуль импульса первой шайбы после удара равен (p_1’= 5 ) кг(cdot)м/с. Найдите модуль импульса второй шайбы после удара.
Запишем ЗСИ (закон сохранения импульса): [vec{p_1}+vec{p_2}=vec{p_1}’+vec{p_2}’ quad(1)] Спроецируем данное уравнение на ось Оx: [p_1=p_{1x}’ quad(2)] Спроецируем на ось Оy: [p_2=p_{1y}’+p_2′ quad(3)] После удара импульс первой шайбы стал равен [p_1’=sqrt{p_{1x}^{prime 2}+p_{1y}^{prime 2}} quad(4)] Из (2) следует, что (p_{1x}’ =3 ) кг(cdot)м/с. Из (4) следует, что [p_{1y}=sqrt{p_1^{prime 2}- p_{1x} ^{prime 2}}=sqrt{25-9} = 4 text{ кг$cdot$м/c}]
Найдем (p_2′) из (3): [p_2’=p_2-p_{1y}’= 6 — 4 = 2text{ кг·м/c}]
Ответ: 2
Снаряд, выпущенный вертикально вверх, мгновенно разрывается в высшей точке траектории на два осколка, массы которых (m) и (4m). Скорость лѐгкого осколка сразу после взрыва (upsilon_1=500) м/с. Найдите скорость (upsilon_2) второго осколка сразу после взрыва.
Суммарный импульс снаряда до взрыва равен 0 (так как взрыв происходит в наивысшей точки траектории), следовательно сразу после взрыва суммарный импульс тоже равен 0: [0=vec{p_1}+vec{p_2}] где (p_1) и (p_2) – это импульс первого и второго осколка. Найдем скорость второго осколка: [mupsilon_1=4mupsilon_2] [upsilon_2=frac{upsilon_1}{4}=frac{500}{4}=125 text{ м/с}]
Ответ: 125

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Сегодня в рубрике «Физика для чайников» занимаемся решением и разбором задач на закон сохранения импульса. И не говорите, что вы этого не ждали.
Полезные лайфхаки и новости для студентов – ежедневно на нашем телеграм-канале. Подписывайтесь!
Задачи на закон сохранения импульса с решением
Задача №1 на нахождение импульса
Условие
Небольшой автомобиль движется со скоростью 60 км/ч, его импульс равен 1,5*10^4 кг*м/с. Какова масса автомобиля?
Решение
По формуле для импульса найдем:
Ответ: 903 кг.
Задача №2 на закон сохранения импульса
Условие
Дрезина массой 400 кг движется со скоростью 4 м/с, а навстречу ей со скоростью 2 м/с едет дрезина массой 60 кг. После неупругого соударения дрезины движутся вместе. В каком направлении и с какой скоростью будут двигаться дрезины?
Решение
Общий импульс системы до и после соударения должен остаться неизменным:
Запишем закон сохранения импульса в проекции на горизонтальную ось:
Движение будет происходить в сторону первой дрезины. Именно она изначальна имела больший импульс.
Ответ: 0,4 м/с.
Задача №3 на нахождение импульса
Условие
Тело массой m=1 кг упало с высоты H=19,6 м. Определить изменение импульса тела за последнюю секунду движения и импульс тела на высоте h=4,9 м.
Решение
Изменение импульса тела за последнюю секунду движения равно:
Импульс тела на заданной высоте найдем по закону сохранения энергии, который имеет вид для двух состояний:
Отсюда получим:
Ответ: Изменение импульса равно 9,8 кг*мс2; р=17 кг*мс2.
Задача №4 на применение закона сохранения импульса и второго закона Ньютона
Условие
Хоккеист массой М = 70 кг стоит на льду и бросает в горизонтальном направлении шайбу массой m = 3 кг со скоростью v = 8 м/с относительно льда. На какое расстояние S откатится при этом конькобежец, если коэффициент трения равен 0,02.
Решение
По закону сохранения импульса найдем скорость u, с которой хоккеист откатиться назад:
По второму закону Ньютона для хоккеиста:
С другой стороны:
Ответ: 0,3 м.
Задача №5 на реактивное движение
Условие
Реактивный двигатель каждую секунду выбрасывает 10 кг продуктов сгорания топлива со скоростью 3 км/с относительно ракеты. Какую силу тяги он развивает?
Решение
Запишем второй закон Ньютона в импульсной форме и найдем силу, которая действует на выбрасываемые продукты сгорания топлива:
По третьему закону Ньютона сила тяги будет равна найденной силе.
Ответ: 30 кН.
Вопросы на закон сохранения импульса
Вопрос 1. Что такое замкнутая система?
Ответ. Замкнутая система – такая система, на которую не действуют внешние силы со стороны других тел.
Вопрос 2. Что такое импульс силы?
Ответ. Импульс силы – физическая величина, равная произведению силы на время ее действия.
Вопрос 3. Как направлен импульс тела?
Ответ. Направление импульса совпадает с направлением вектора скорости тела.
Вопрос 4. Что такое реактивное движение?
Ответ. Реактивное движение – движение, основанное на принципе отдачи. По аналогии с системой «пушка-ядро», систему «ракета-выхлопные газы» также можно считать замкнутой.
Вопрос 5. Два тела разной массы движутся с одинаковой скоростью. Импульс какого тела больше?
Ответ. Тело с большей массой обладает большим импульсом.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Импульс и закон сохранения импульса
Что такое импульс в механике
Импульс, или количество движения – векторная физическая величина, равная произведению массы тела на его скорость.
Обозначается латинской буквой p и измеряется в килограммах на метр в секунду.
Второй закон Ньютона с применением импульса можно записать следующим образом:
Здесь дельта p – изменение импульса тела за время дельта t под действием равнодействующей силы F.
Закон сохранения импульса
Этот фундаментальный закон природы и гласит:
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Закон сохранения импульса является следствием второго и третьего законов Ньютона.
Более подробную теорию по этой и другим темам вы найдете в нашем справочнике.
Пример действия закона сохранения импульса
Представим себе пушку, которая стреляет ядрами. Систему «пушка-ядро» можно считать замкнутой. При стрельбе из пушки действует закон сохранения импульса. Ядро летит в одну сторону, а пушка под действием отдачи откатывается назад. При этом скорость, приобретенная пушкой, зависит от соотношения масс орудие/ядро и скорости ядра.
Знак минус указывает на то, что пушка и ядро движутся в разные стороны.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис.
За это задание ты можешь получить 2 балла. Уровень сложности: повышенный.
Средний процент выполнения: 67.9%
Ответом к заданию 4 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
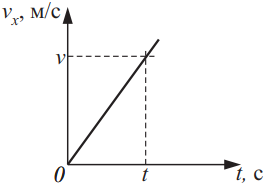
На рисунке изображён график зависимости проекции скорости тела массой m от времени (t). На основании графика выберите два верных утверждения из приведённого ниже списка для момента времени t. Укажите их номера.
- Движущаяся сила вычисляется по формуле F = m · v · t.
- Работу силы можно найти по формуле $A = {m· v}/{2t}$.
- Движущаяся сила вычисляется по формуле $F = {mv}/{t}$.
- Работу силы можно найти по формуле $A = {m·v^2}/{2}$.
- Работу силы можно найти по формуле $A = {m·v^2}/{2t^2}$.
Решение
3) Движущаяся сила $F=ma$, где $a={υ-υ_0}/{y}={υ}/{t}$, поскольку $υ_0=0$, что видно графика. Тогда $F=ma={mυ}/{t}$.
4) Работа силы равна изменению кинетической энергии, т.е. $A=∆E_к={mυ^2}/{2}-{mυ_0^2}/{2}$, поскольку $υ_0=0$, то $A={mυ^2}/{2}-0={mυ^2}/{2}$.
Ответ: 34
Задача 2
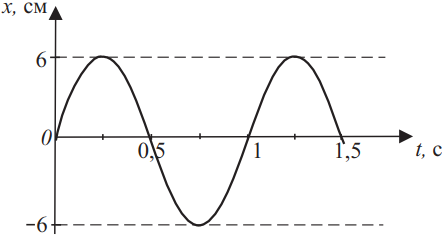
По экспериментальным данным построен график зависимости координаты колебания от времени на рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 6 см.
- Координату тела в момент времени t можно найти по формуле x = 6 sin(π · t).
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 0 см.
- Координату тела в момент времени t можно найти по формуле x = 6 cos(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 6 sin(2π · t).
Решение
1) Из графика видно, что период колебаний тела $T=1с$, амплитудное значение координаты $x_m=6$см. Значит, угловая частота тела $ω={2π}/{T}={2π}/{1}=2π$. Запишем уравнение колебаний в общем виде: $x=x_m·sin({2π}/{T}·t)$. Подставим наши данные, имеем: $x=6·sin({2πt}/{1})=6·sin(2π·t)$. Координата колебания подчиняется закону синуса, следовательно, в момент времени, равный 10 периодам колебаний, тело находится в точке с координатой $х=0$ см.
Ответ: 35
Задача 3
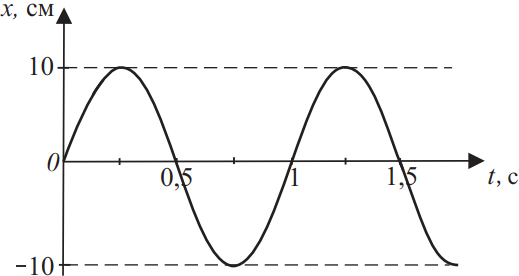
Координата колеблющегося тела меняется так, как показано на графике рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- Период колебаний тела равен 1 с.
- Координату тела в момент времени t можно найти по формуле x = 0,1 sin(π · t + π/4).
- Тело совершает колебания с периодом 0,1 с.
- Координату тела в момент времени t можно найти по формуле x = 10 sin(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 10 cos(2π · t + π/4).
Решение
1) Из графика видно, что период колебаний тела равен 1с.
4) Поскольку координата колеблющегося тела изменяется по закону синуса, $x_m=10$см — амплитудное значение координаты и начальная фаза $ϕ_0=0$, то координату тела в момент времени $t$ можно найти по формуле $x=10·sin(2π·t)$.
Ответ: 14
Задача 4
Ученик исследовал зависимость модуля силы упругости F пружины от её растяжения x. Результаты эксперимента приведены в таблице. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, м | 0 | 0,02 | 0,04 | 0,06 | 0,08 | 0,10 |
- Коэффициент упругости пружины равен 2,5 Н/м.
- При увеличении массы груза растяжение пружины уменьшается.
- Потенциальная энергия пружины пропорциональна растяжению пружины.
- Потенциальная энергия пружины при её растяжении на 0,08 м равна 0,08 Дж.
- При подвешенном к пружине грузе массой 100 г её удлинение составит 4 см.
Решение
Исходя из теории упругости и результатов опыта, определим $E_n={kx^2}/{2}={25·0.08^2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.
Ответ: 45
Задача 5
Грузик, подвешенный на нити, совершает гармонические колебания. В таблице представлены значения координаты грузика через одинаковые промежутки времени. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.
| t, c | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| x, см | 6 | 3 | 0 | 3 | 6 | 3 | 0 | 3 |
- Максимальная скорость грузика равна 0,15 м/с.
- Период колебаний шарика равен 0,4 с.
- В момент времени 0,1 с кинетическая энергия шарика максимальна.
- Полная механическая энергия шарика остаётся неизменной.
- Амплитуда колебаний шарика равна 6 мм.
Решение
Исходя из теории о гармонических колебаниях и данной таблицы, полная механическая энергия шарика остается неизменной. (4 — верно).
Период колебании — время за которое происходит одно полное колебание — 0,4 с (2 — верно)
Максимальная скорость шарика связана с амплитудой ( $υ_{max}=А ω ={А2π}/{T}= {0,03* 2*3.14}/{0,4}=0,471$м/с. (1 — неверно)
Максимальная кинетическая энергия будет в момент прохождения шариком положения равновесия x=3 см, это соответствует времени t=0,1 с (3 — верно)
Амплитуда колебания — это максимальное отклонение от положения равновесия, так как координата колеблется между значениями 6 см и 0, положению равновесия будет соответствовать координата х=3 см, значит амплитуда: А=6-3=3 см (5 — неверно)
Ответ: 234
Задача 6
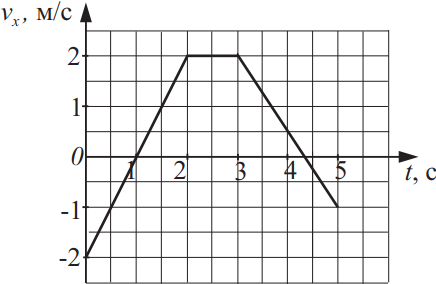
Тело массой 15 кг движется вдоль оси Ox в инерциальной системе отсчёта. График зависимости проекции скорости vx этого тела на ось Ox от времени представлен на рисунке. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленного графика и укажите их номера.
- В течение первых двух секунд перемещение тела равно 2 м.
- Модуль ускорения тела в промежутке времени от 1 с до 2 с на 25% больше модуля ускорения тела в промежутке времени от 3 с до 4 с.
- В течение первой секунды кинетическая энергия тела увеличилась на 30 Дж.
- В промежутке времени от 1 с до 2 с импульс тела увеличился в 2 раза.
- В момент времени 4 с модуль равнодействующей сил, действующих на тело, равен 22,5 Н.
Решение
Из теории кинематики и данного графика можно сказать, что модуль ускорения тела с 1 до 2 на 25% больше 3-4, т.е. $a_{1-2}=2м/с^2; a_{3-4}=1.5м/с^2$. В момент времени 4с модуль равнодействующих сил, $F=22.5H$, т.к. $a_4=1.5м/с^2$, $F_p=ma_4=15·1.5=22.5H$
Ответ: 25
Задача 7
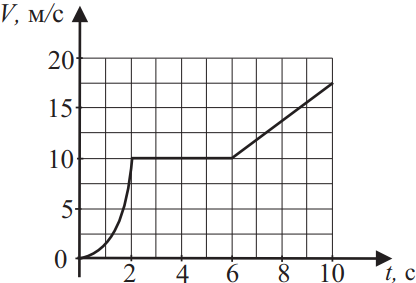
На рисунке представлен график зависимости скорости V от времени t для тела, движущегося прямолинейно. Используя данные графика, выберите из приведённого ниже списка все верные утверждения и укажите их номера.
- Первые две секунды тело двигалось равноускоренно.
- Со 2-й по 6-ю секунду тело переместилось на 40 м.
- Со 2-й по 6-ю секунду тело переместилось на меньшее расстояние, чем за первые две секунды.
- Средняя скорость тела во время движения со 2-й по 10-ю секунду равна 12,5 м/с.
- С 6-й по 10-ю секунду тело двигалось равноускоренно.
Решение
1) Неверно, так как равноускоренному движению соответствует линейный график: $v(t)=v_0+at$.
2)Верно. Из данного рисунка видно, что с 2 по 6 сек, тело прошло 40 м (площадь под графиком)
3) Неверно. Площадь под графиком со 2 по 6-ю секунды гораздо больше, чем площадь под графиком за первые две секунды.
4)Чтобы найти среднюю скорость, нужно разделить весь путь со 2-й по 10-ю секунду на всё соответствующее время, т.е. на 8 с. При этом путь определяем как площадь под графиком, так как у нас есть график в координатах v(t):
$S=S_1+S_2=8·10+{4·7,5}/2=110$ м.
Тогда $v_{ср}={110}/8=13,75$. Утверждение 4 — неверно.
5) Верно. С 6 по 10 сек, тело двигалось равноускоренно, т.к. за равные промежутки времени скорость увеличивается на одну ту же величину (линейная зависимость v(t)).
Ответ: 25
Задача 8

Математический маятник совершает незатухающие колебания между точками А и Б. Точка О соответствует положению равновесия маятника. Используя текст и рисунок, выберите из предложенного ниже списка все верные утверждения. Укажите их номера.
- За время, равное периоду колебаний, маятник проходит путь, равный длине дуги АБ.
- При перемещении маятника из положения О в положение В потенциальная энергия уменьшается, а кинетическая энергия увеличивается.
- В точке О кинетическая энергия маятника максимальна.
- Расстояние АБ соответствует амплитуде колебаний координаты.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение.
Решение
- За время, равное периоду колебаний, маятник проходит путь, равный ДВУМ длинам дуги АБ — «туда и обратно». 1 — неверно.
- При перемещении маятника из положения О в положение В потенциальная энергия УВЕЛИЧИВАЕТСЯ (т.к. высота растёт), а кинетическая энергия УМЕНЬШАЕТСЯ (т.к. маятник замедляется). 2 — неверно
- В точке О кинетическая энергия маятника максимальна, так как положение равновесия груз маятника проходит с наибольшей скоростью — верно
- Амплитуда колебаний координаты — это половина расстояния АБ — отклонение от положения равновесия. 4 — неверно.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение, так как груз находится на наибольшей высоте. 5 — верно.
В точке О кинетическая энергия максимальна. Потенциальная энергия принимает максимальное значение в точках А и Б.
Ответ: 35
Задача 9
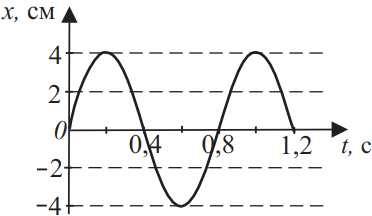
Координата колеблющегося тела меняется так, как показано на графике рисунка. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Период колебаний тела равен 1 с.
- Амплитуда колебаний равна 8 см.
- Частота колебаний равна 1,25 Гц.
- Амплитуда колебаний равна 4 см.
- Период колебаний тела равен 0,4 с.
Решение
Из данного графика очевидно, что $A=4$см (2 — неверно, 4 — верно), период колебаний T=0.8 c (1, 5 — неверно), а частота $v={1}/{T}={1}/{0.8}=1.25$Гц.(3 — верно)
Ответ: 34
Задача 10
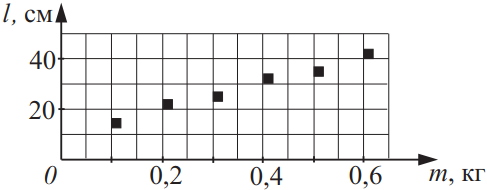
На рисунке приведён график зависимости длины пружины от величины нагрузки. Из приведённого ниже списка выберите два утверждения, соответствующих результатам этого эксперимента, и укажите их номера.
- Коэффициент упругости пружины примерно равен 20 Н/м.
- Коэффициент упругости пружины примерно равен 30 Н/м.
- Коэффициент упругости пружины примерно равен 50 Н/м.
- Коэффициент упругости пружины примерно равен 10 Н/м.
- Для данного эксперимента выполняется закон Гука.
Решение
$k=F/(l-l_0)$
Если продолжить прямую, видно, что длина недеформированной пружины 10 см
$k=2/(0.2-0.1)=20$ Н/м
Ответ: 15
Задача 11
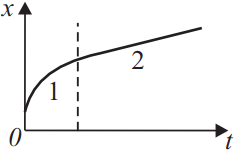
Бусинка скользит по неподвижной горизонтальной спице. На графике изображена зависимость координаты бусинки от времени. Ось Ox параллельна спице. Из приведённого ниже списка на основании графика выберите два верных утверждения о движении бусинки и укажите их номера.
- На участке 1 проекция ускорения ax бусинки отрицательна.
- На участке 1 модуль скорости остаётся неизменным, а на участке 2 — уменьшается.
- На участке 1 модуль скорости увеличивается, а на участке 2 — уменьшается.
- На участке 1 модуль скорости уменьшается, а на участке 2 — остаётся неизменным.
- В процессе движения вектор скорости бусинки менял направление на противоположное.
Решение
Скорость — это производная координаты по времени. Графически это $tgα$ наклонной графика зависимости координаты от времени. Заметим, что координата все время растет, но на участке 1 — скорость уменьшается, следовательно, проекция ускорения отрицательна. На участке 2, скорость неизменна, а координата растет, тело не меняет направление движения.
Ответ: 14
Задача 12
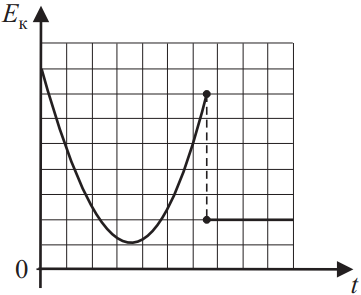
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два верных утверждения, описывающих движение в соответствии с данным графиком.
- В конце наблюдения кинетическая энергия тела равна нулю.
- Кинетическая энергия тела в течение всего времени наблюдения увеличивается.
- Кинетическая энергия тела в начальный момент времени максимальна.
- Тело брошено вертикально вверх с балкона и упало на Землю.
- В конце наблюдения скорость тела не равна нулю.
Решение
1) В конце наблюдения $E_к=0$, неверно, т.к. при $t=t_к⇒E_к≠0$, если $E_к=0$, то график должен проходить через ось ординат.
2) $E_к$, в течении всего времени увеличивается, неверно, т.к. при $t={t_к}/{2}$ $E_к=min$, в середине пути кинетическая энергия минимальна.
3) Исходя из графика $E_к$ максимальная в момент (верно) $t=0$.
4) Неверно, т.к. график вертикально брошенного тела, выглядит иначе.
5) При $t_к=t; E_к≠0$ (верно), т.к. $υ≠0⇔E_к≠0$.
Ответ: 35
Задача 13
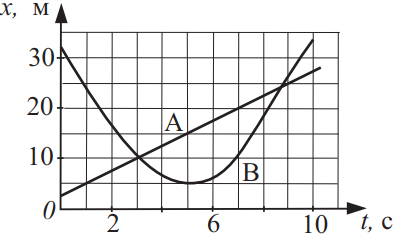
На рисунке приведены графики зависимости координаты от времени для двух тел A и B, движущихся по прямой, вдоль которой и направлена ось Ox. Из приведённого ниже списка выберите два верных утверждения о характере движения тел и укажите их номера.
- Тело A движется равномерно.
- Тело A движется с постоянным ускорением, равным 5 м/с2.
- Первый раз тела A и B встретились в момент времени, равный 3 с.
- Вторично тела A и B встретились в момент времени, равный 7 с.
- В момент времени t = 5 с тело B достигло максимальной скорости движения.
Решение
1) Тело А движется равномерно, т.к. равномерное движение — это движение, при котором тело за равные промежутки времени проходит одинаковые расстояния (подходит).
2) Ускорение тела А равно нулю, т.к. оно движется с постоянной скоростью $υ={20-10}/{7-3}=2.5м/с$ (не подходит).
3) Графики зависимости координаты от времени для двух тел А и В пересекаются в момент времени $t=3c$, значит, первый раз тела А и В встретились в момент времени, равный 3с (подходит).
Ответ: 13
Задача 14
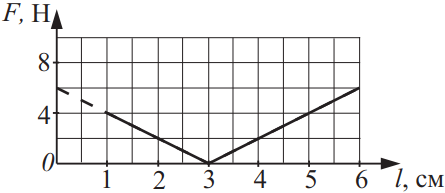
При проведении эксперимента ученик исследовал зависимость модуля силы упругости пружины, которая выражается формулой F (l) = k|l − l0|, где l0 — длина пружины в недеформированном состоянии, от её длины. График полученной зависимости приведён на рисунке. Из приведённого ниже списка выберите все верные утверждения на основании анализа графика и укажите их номера.
- Длина пружины в недеформированном состоянии равна 6 см.
- Длина пружины в недеформированном состоянии равна 3 см.
- При действии силы 2 Н деформация пружины равна 2 см.
- При действии силы 4 Н деформация пружины равна 2 см.
- Коэффициент жёсткости пружины равен 50 Н/м.
Решение
1) Из графика видно, что длина пружины в не деформированном состоянии равна 3 см, т.к. при l=3см сила упругости $F=OH$(не подходит).
2) Длина пружины в не деформированном состоянии равна 3 см (подходит).
3) При действии сила 2Н деформация пружины равна |2см-3см|=|-1см|=1см или |4см-3см|=1см (не подходит).
4) При действии сила 4Н пружина сжимается или растягивается на 2см, поскольку |1см-3см|=|-2см|=1см или |5см-3см|=2см (подходит).
Ответ: 24
Задача 15
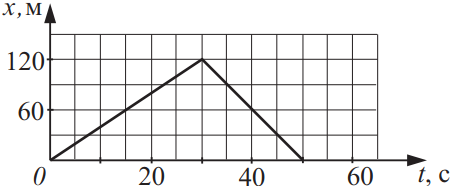
На рисунке приведена зависимость координаты движущегося тела от времени. Из приведённого ниже списка выберите два верных утверждения
- Скорость движения тела в интервале времени от 30 до 50 с на 2 м/с больше, чем скорость в интервале времени от 0 до 30 с.
- Скорость тела возрастала в интервале времени от 0 до 30 с и убывала в интервале от 30 до 50 с.
- Максимальная скорость движения на всём пути равна 2,4 м/с.
- За всё время движения тело прошло путь 120 м.
- За всё время движения тело прошло путь 240 м.
Решение
1) $υ_1[30-50c]={x_к-x_н}/{t_к-t_н}={0-120}/{50-30}=-{120}/{20}=-6м/с$. Знак «минус» говорит о том, что тело движется в обратном направлении, поэтому возьмем по модулю $υ[30-50c]=6м/с; υ_2[0-30c]={x_к-x_н}/{t_к-t_н}={120-0}/{30-0}={120}/{30}=4м/с; ∆υ=υ_1[30-50c]-υ_2[0-30c]=6-4=2м/с$(подходит).
2) Скорость тела возрастала в интервале времени от 0 до 30с и в интервале от 30 до 50с (не подходит).
3) Максимальная скорость на всем пути равна 6м/с (не подходит).
4) За все время движения тело прошло путь: $S=S_1+S_2=υ_1·∆t_1+υ_1·∆t_2=6·(50-30)+4·(30-0)=6·20+4·30=120+120=240$м (не подходит).
5) За все время движения тело прошло путь 240м (подходит).
Ответ: 15
Задача 16
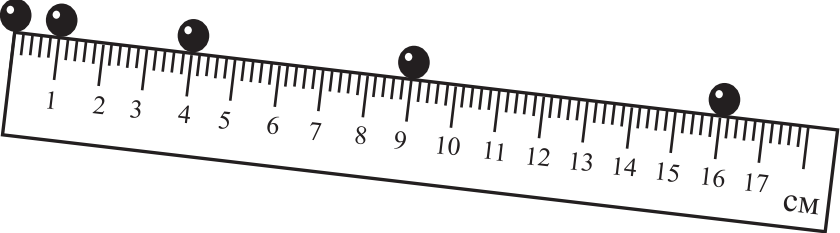
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.
- Движение шарика равномерное.
- Скорость шарика увеличивается.
- Шарик движется под действием переменной силы.
- Если промежуток времени между двумя последовательными положениями шарика равен 2 с, то его ускорение равно 0,5 см/с2.
- Импульс шарика в процессе движения остаётся постоянным.
Решение
1) Шарик за одинаковые промежутки времени проходит разные расстояния, значит, его движение неравномерное (не подходит).
2) Движение шарика равноускоренное, значит, скорость шарика увеличивается (подходит).
3) Шарик движется под действием постоянной силы $F↖{→}=ma↖{→}$ (не подходит).
4) $S=0.16м; t=4·2=8c; υ_0=0м/с; a=0.005м/с^2$. При равноускоренном движении перемещение равно: $S=υ_0е+{at^2}/{2}=0·8+{0.005·(8)^2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит).
Ответ: 24
Задача 17
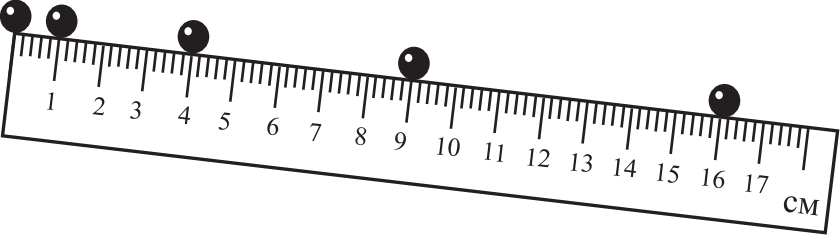
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.
- Шарик движется с переменным ускорением.
- Скорость шарика уменьшается.
- Шарик движется под действием постоянной силы.
- Если промежуток времени между двумя последовательными положениями шарика равен 2 с и он начинал движение из состояния покоя, то его скорость в точке с координатой 9 см равна 3 см/с.
- Импульс шарика в процессе движения уменьшается.
Решение
1) Шарик движется с постоянным ускорением (не подходит).
2) Скорость шарика увеличивается, т.к. за равные промежутки времени он проходит все больше расстояния (не подходит).
3) Шарик движется под действием постоянной силы $F=m·a$ (подходит).
4) $υ_k=υ_0+at$(1), т.к. $υ_0=0$м/с, поскольку начинает движение из состояния покоя, то $υ_k=at$(2). Перемещение $S={at^2}/{2}⇒a={2·S}/{t^2}$(3), где $S=0.09$м, $t=6c$ (т.к. 3 вспышки стробослота), тогда $a={2·0.09}/{36}=0.005$, тогда $υ=at=0.005·6=0.03=3$см/с (подходит).
Ответ: 34
Задача 18
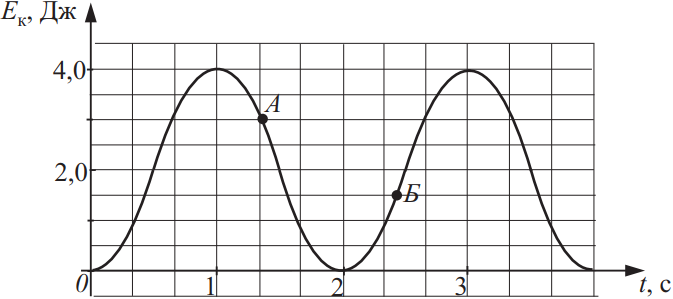
На рисунке приведён график зависимости кинетической энергии тела от времени t. Выберите все верные утверждения на основании анализа представленного графика.
- Тело движется под действием постоянной силы.
- Потенциальная энергия тела в точке Б равна 1,5 Дж.
- Период колебаний тела равен 4 с.
- Максимальное значение потенциальной энергии равно значению потенциальной энергии в точке А.
- Полная механическая энергия тела равна 4 Дж.
Решение
1. Из графика видно, что время одного полного колебания равно 4с, т.к. в течение одного полного колебания тело проходит три максимальных значения (или три минимальных значения) кинетической энергии, т.е. период колебаний тела равен 4с (верно).
2. Поскольку полная механическая энергия тела равна: $E=E_{к,max}=E_{к,max}=E_к+Е_п$(1), а максимальная кинетическая энергия тела равна 4 Дж, то полная механическая энергия тела равна 4 Дж (верно).
Ответ: 35
Задача 19
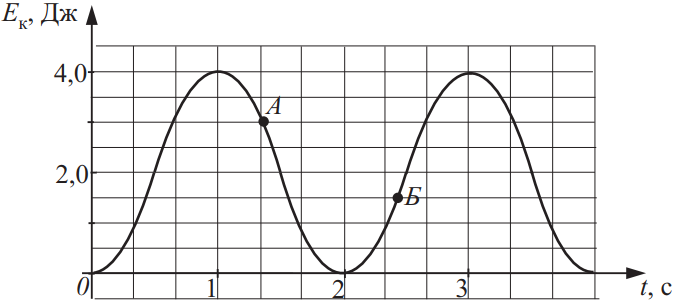
На рисунке приведён график зависимости кинетической энергии тела от времени t. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Тело совершает гармонические колебания.
- Потенциальная энергия тела в точке A равна 1 Дж.
- Период колебаний тела равен 2 с.
- Максимальное значение потенциальной энергии равно потенциальной энергии в точке Б.
- Частота колебаний тела равна 4 Гц.
Решение
1. Тело совершает гармонические колебания, т.к. гармонические колебания — это колебания, подчиняющиеся закону синуса или косинуса, а на графике мы видим синусоиду (1 — верно).
2. Поскольку полная механическая энергия тела равна: $E=E_{п,max}=E_{п,max}=E_к+Е_п$(1), где $E_к$ — кинетическая энергия тела, $E_{к,max}=4$Дж, $E_п$ — потенциальная энергия тела. В точке А $E_к=3$Дж, значит, $E_п=E-E_к=E_{к,max}-E_к=4-3=1$Дж (2 — верно)
3. За один период колебаний тела, успевает произойти два колебания кинетической энергии, поэтому период колебаний тела равен 4с, а не 2. (3 — неверно)
4. Максимальное значение потенциальной энергии будет в той точке, в которой кинетическая энергия минимальна. Точка Б под это условие не подходит (4 — неверно)
5. Частота колебания тела равна: $v=1/T=1/4=0,25$ Гц (5 — неверно)
Ответ: 12
Задача 20
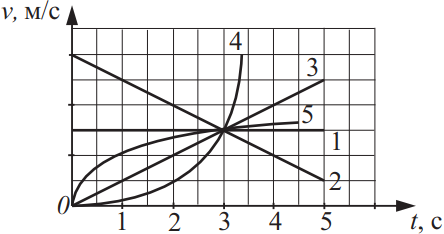
На рисунке представлены графики зависимости проекции скорости v на некоторую ось от времени t для пяти тел. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленных графиков и укажите их номера.
- Наибольшей начальной скоростью обладало второе тело.
- Первое тело покоится.
- Наименьший путь за первые три секунды прошло второе тело.
- Третье тело движется равноускоренно.
- Пятое тело совершает равнопеременное движение.
Решение
Из графика видно, что в момент времени t=0с наибольшей начальной скоростью обладает тело 2.
Третье тело движется равноускоренно, т.к. график скорости напрвлен вверх.
Ответ: 14