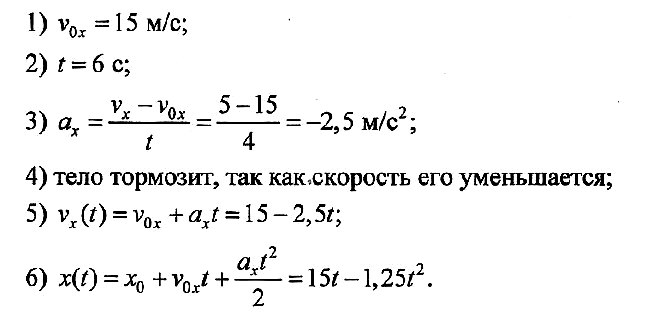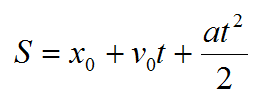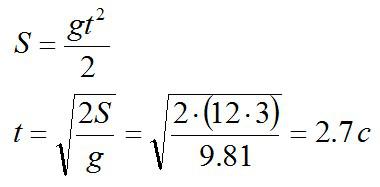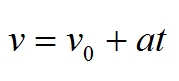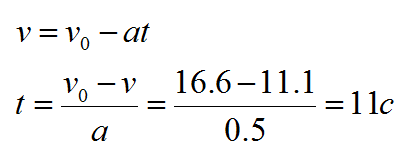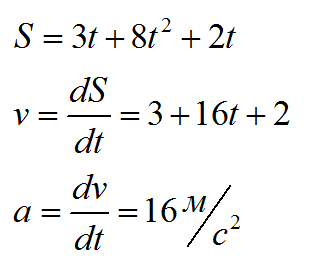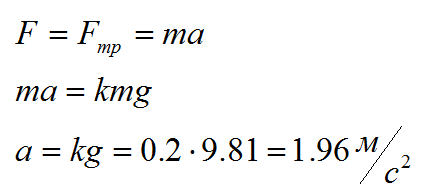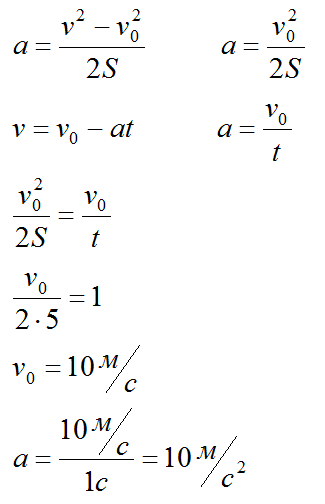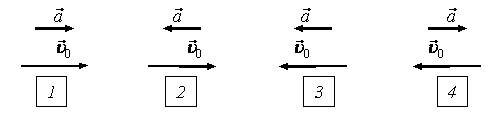Егэ по физике задачи на равноускоренное движение - Помощь в подготовке к экзаменам и поступлению

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 196 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

На рисунке приведён график зависимости модуля средней скорости V_р материальной точки от времени t при прямолинейном движении. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.

1)  Модуль ускорения точки равен 2 м/с².

2)  Модуль ускорения точки равен 4 м/с².

3)  За первые 3 с движения материальная точка проходит путь 8 м.

4)  За первые 2 с движения материальная точка проходит путь 12 м.

5)  Модуль начальной скорости материальной точки равен 2 м/с.

В лаборатории исследовали прямолинейное движение тела массой m  =  300 г из состояния покоя. В таблице приведена экспериментально полученная зависимость пути, пройденного телом, от времени. Выберите все верные утверждения, соответствующие результатам эксперимента.

t, с	0	1	2	3	4	5	6	7
L, м	0	1	4	9	16	25	36	49

1)  Тело двигалось равноускоренно.

2)  Скорость тела в момент времени 4 с равнялась 8 м/с.

3)  Кинетическая энергия тела в момент времени 5 с равна 25 Дж.

4)  Равнодействующая сил, действующих на тело, всё время возрастала.

5)  За первые 3 с работа равнодействующей сил, действующих на тело, была равна 5,4 Дж.

Источник: ЕГЭ по физике 2022. Досрочная волна

В процессе прямолинейного равноускоренного движения тело за 2 секунды прошло путь 20 м, при этом его скорость уменьшилась в 3 раза. Какой была начальная скорость тела?

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания

Грузик массой m = 100 г неподвижно висит на лёгкой абсолютно упругой гибкой резинке с коэффициентом упругости k = 100 Н/м в поле силы тяжести с ускорением свободного падения g. Грузик поднимают из этого положения вертикально вверх на высоту h = 80 см, меньшую длины резинки, и отпускают без начальной скорости. Найдите время движения грузика вниз до точки его остановки. Начальной деформацией резинки при покоящемся грузике можно пренебречь.

Какие законы Вы используете для описания движения груза на резинке? Обоснуйте их применение к данному случаю.

Тело, свободно падающее с некоторой высоты из состояния покоя, за время после начала движения проходит путь в n=5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения.

Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.

При прямолинейном движении зависимость координаты тела x от времени t имеет вид:

Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)

Материальная точка движется прямолинейно с постоянным ускорением вдоль оси Ох. График зависимости её координаты от времени изображён на рисунке. Определите проекцию а_х ускорения этого тела. Ответ дайте в метрах на секунду в квадрате.

Источник: Демонстрационная версия ЕГЭ—2021 по физике

По гладкой наклонной плоскости пускают шайбу. Максимальное удаление шайбы от линии пересечения наклонной плоскости и горизонтали 68 см. Угол плоскости с горизонталью α  =  30°. Угол между начальной скоростью и линией AB β  =  60°. Найдите начальную скорость шайбы.

Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.

Источник: ЕГЭ 20.06.2016 по физике. Основная волна волна. Вариант 52 (Часть С)

Точечное тело начинает прямолинейное движение вдоль оси OX. На рисунке показана зависимость проекции скорости V_x этого тела от времени t. Чему равен модуль изменения координаты этого тела за третью секунду движения?

Небольшое тело начинает равноускоренно двигаться вдоль оси OX без начальной скорости. На рисунке приведён график зависимости координаты x этого тела от времени t. Чему равна проекция скорости υ_x этого тела в момент времени t = 3 c? Ответ выразите в метрах в секунду.

На шероховатую наклонную плоскость положили брусок (см. рис.). Коэффициент трения бруска о плоскость равен μ = 0,35, тангенс угла α наклона плоскости к горизонту равен 0,15. В первом случае бруску ударом придали скорость vec v , направленную вдоль плоскости вверх, а во втором  — вниз. Во сколько раз путь, пройденный бруском до остановки на наклонной плоскости во втором случае, будет больше, чем в первом?

Какие законы Вы используете для описания движения бруска? Обоснуйте их применение к данному случаю.

Источник: Тренировочная работа по физике 16.02.2017, вариант ФИ10303

Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста  — 0,5 м/с². Сколько секунд длился спуск?

Точечное тело начинает прямолинейное движение вдоль оси OX. На рисунке показана зависимость координаты x этого тела от времени t. Определите проекцию скорости этого тела на ось OX в интервале времени от 6 до 10 секунд.

Точечное тело начинает движение из состояния покоя и движется равноускоренно вдоль оси Оx по гладкой горизонтальной поверхности. Используя таблицу, определите значение проекции на ось Оx ускорения этого тела. (Ответ дайте в метрах в секунду в квадрате.)

Момент времени t, c	Координата тела x, м
0	2
3	6,5
4	10

Момент времени

t, c

Координата тела

x, м

6,5

Задания Д1 B1 № 6143

Небольшое тело движется вдоль горизонтальной оси OX. В момент времени t  =  0 координата этого тела равна x₀  =  −2 м. На рисунке приведена зависимость проекции скорости v этого тела на ось OX от времени t.

На каком из следующих рисунков правильно показана зависимость координаты x этого тела от времени?

Задания Д14 B25 № 727

На рисунке представлена установка для исследования равноускоренного движения ползунка (1) массой 0,05 кг по наклонной плоскости, установленной под углом к горизонту.

В момент начала движения верхний датчик (А) включает секундомер (2), при прохождении ползунка мимо нижнего датчика (В) секундомер выключается. Числа на линейке обозначают длину в сантиметрах. Секундомер измеряет время в секундах. Скорость ползунка в любой момент времени вычисляется по формуле

3)   v =6t

4)   v =60t

Всего: 196 1–20 | 21–40 | 41–60 | 61–80 …

Источник

ЗАДАЧИ на Прямолинейное равноускоренное
движение с решениями

Формулы, используемые в 9-11 классах по теме
«ЗАДАЧИ на Прямолинейное равноускоренное движение».

Название величины	Обозначение	Единица измерения	Формула
*Время*	t	с
*Проекция начальной скорости*	v_0x	м/с
*Проекция мгновенной скорости*	v_x	м/с
*Проекция ускорения*	a_x	м/с²
*Проекция перемещения*	S_x	м
*Координата*	x	м

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

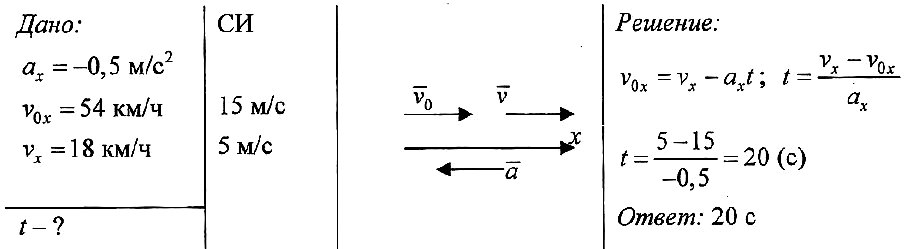
Задача № 1.
Автомобиль, двигаясь с ускорением –0,5 м/с², уменьшил свою скорость от 54 до 18 км/ч. Сколько времени ему для этого понадобилось?

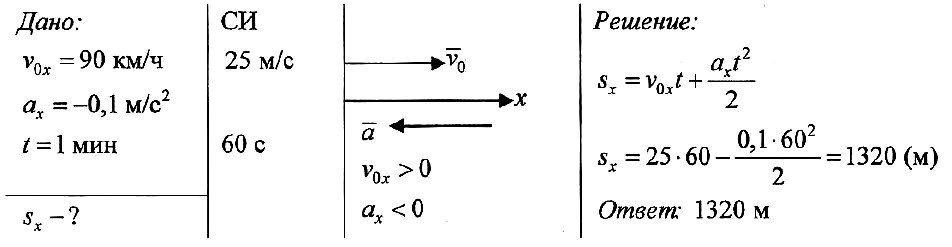
Задача № 2.
При подходе к станции поезд начал торможение с ускорением 0,1 м/с², имея начальную скорость 90 км/ч. Определите тормозной путь поезда, если торможение длилось 1 мин.

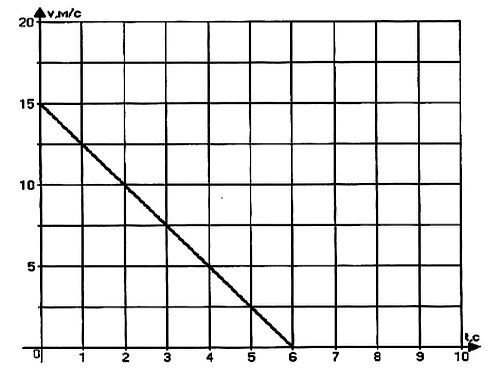
Задача № 3.
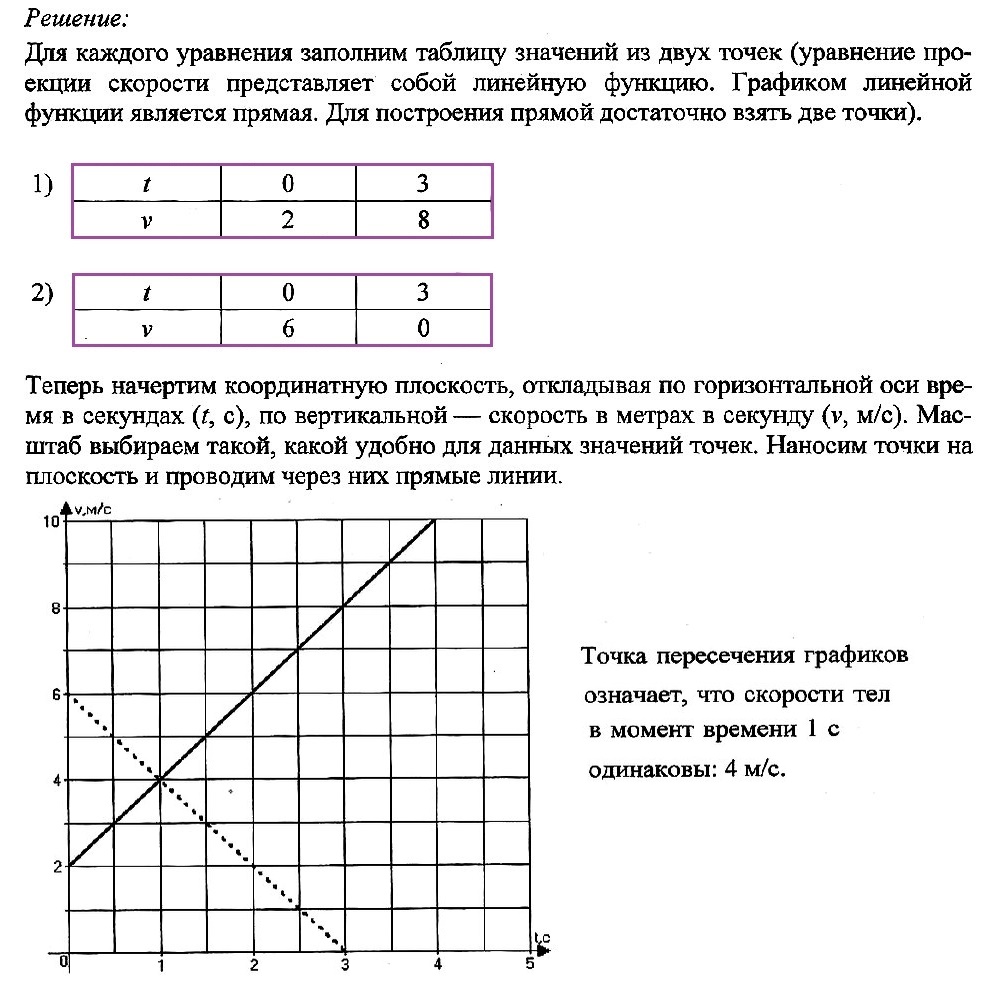
По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).

Решение:

Задача № 4.
Движение двух тел задано уравнениями проекции скорости:
v_1x(t) = 2 + 2t
v₂_x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?

Задача № 5.
Движение тела задано уравнением x(t) = 5 + 10t — 0,5t². Определите: 1) начальную координату тела; 2) проекцию скорости тела; 3) проекцию ускорения; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) определите значение координаты и скорости в момент времени t = 4 с. Сравним уравнение координаты в общем виде с данным уравнением и найдем искомые величины.

Решение:

Задача № 6.
Вагон движется равноускоренно с ускорением -0,5 м/с². Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.

Задача № 7.
Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с² в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

Задача № 8.
Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равноускоренно с ускорением 0,6 м/с². Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(t).

Задача № 9.
Тело, имея некоторую начальную скорость, движется равноускоренно. За время t = 2 с тело прошло путь S = 18 м, причём его скорость увеличилась в 5 раз. Найти ускорение и начальную скорость тела.

Задача № 10. (повышенной сложности)
Прямолинейное движение описывается формулой х = –4 + 2t – t². Опишите движение, постройте для него графики v_x(t), s_x(t), l(t).

Задача № 11.
ОГЭ
Поезд, идущий со скоростью v₀ = 36 км/ч, начинает двигаться равноускоренно и проходит путь S = 600 м, имея в конце этого участка скорость v = 45 км/ч. Определить ускорение поезда а и время t его ускоренного движения.

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).

Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.

Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на Свободное падение тел с решениями
Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике (онлайн-тесты).

Источник

Из кодификатора по физике, 2020:

«1.1.6. Равноускоренное прямолинейное движение:

$x(t)={ x }_{ 0 }+{ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ , ${ upsilon }_{ x }(t)={ upsilon }_{ 0x }+{ a }_{ x }cdot t$
${ a }_{ x }=const$ , $quad { upsilon }_{ 2x }^{ 2 }-{ { upsilon } }_{ 1x }^{ 2 }=2{ a }_{ x }cdot ({ x }_{ 2 }-{ x }_{ 1 })$ .»

Теория

В данной статье будем считать, что Вы умеете без проблем находить проекции величин и в примерах не будем подробно объяснять, чему они равны.
В задачах на равноускоренное движение применяют пять величин: проекции перемещения ${ s }_{ x }$ , проекции начальной скорости ${ upsilon }_{ 0x }$ , проекции конечной скорости ${ upsilon }_{ x }$ , проекции ускорения ${ a }_{ x }$ и времени t. Достаточно знать любые три величины, чтобы найти все остальные.

При решении задач по данной теме применяют два способа решения.

1 способ. При решении запоминаем и применяем две формулы:

${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ ,

${ s }_{ x }={ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ .

А в наиболее сложных случаях решаем систему этих двух уравнений.

2 способ. При решении запоминаем и применяем пять формул (см. таблицу 1).

Таблица 1

Почему пять формул? Каждая из этих формул использует только четыре величины из пяти. Одна из величин не используется при решении (отсутствует) (см. таблицу 1, столбец № 3). Вариантов с одной отсутствующей величиной из пяти может быть только пять.

Алгоритм решения вторым способом.

1) определите, какие величины используются (даны или надо найти), а ка-кая отсутствует;

2) по отсутствующей величину из таблицы выберите рабочую формулу.

Пример 1. Найдите перемещение ${ s }_{ x }$ , если известны ${ upsilon }_{ x }$ , ${ upsilon }_{ 0x }$ и ${ a }_{ x }$ .

Отсутствующая величина t. Согласно таблице 1 для решения нужно ис-пользовать формулу № 4:
${ s }_{ x }=frac { { upsilon }_{ x }^{ 2 }-{ upsilon }_{ 0x }^{ 2 } }{ 2{ a }_{ x } }$ .

Пример 2. Найдите перемещение ${ s }_{ x }$ если известны ${ upsilon }_{ x }$ , ${ upsilon }_{ 0x }$ и t.

Отсутствующая величина ${ a }_{ x }$ . Согласно таблице 1 для решения нужно использовать формулу № 5

${ s }_{ x }=frac { { upsilon }_{ x }+{ upsilon }_{ 0x } }{ 2 } cdot t$ .

Для сомневающихся и любопытных.

Вывод формулы №3. Из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ найдем проекцию начальной скорости:

${ upsilon }_{ 0x }={ upsilon }_{ x }-{ a }_{ x }cdot t$ .

Подставим полученное выражение в формулу № 2:

Вывод формулы №4. Из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ найдем время:

$t=frac { { upsilon }_{ x }-{ upsilon }_{ 0x } }{ { a }_{ x } }$ .

Подставим полученное выражение в формулу № 2:

Вывод формулы №5. Из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ найдем проекцию ускорения:

${ a }_{ x }=frac { { upsilon }_{ x }-{ upsilon }_{ 0x } }{ t }$ .

Подставим полученное выражение в формулу № 2:

Задачи

Задача 1. Пассажирский поезд тормозит с ускорением 0,2 м/с2. На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 15 м/с?

Решение. Скорость поезда уменьшается, поэтому ускорение направлено против начальной скорости. При прямолинейном движении (без поворотов) перемещение поезда равно расстоянию, которое он пройдет, т.е. s = s. Ось 0Х направим по направлению начальной скорости (рис. 1), поэтому

${ s }_{ x }=s,quad { upsilon }_{ x }=upsilon ,quad { upsilon }_{ 0x }={ upsilon }_{ 0 },quad { a }_{ x }=-a$

1 Способ. Из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ находим время:

$t=frac { { upsilon }_{ x }-{ upsilon }_{ 0x } }{ { a }_{ x } } =frac { upsilon -{ upsilon }_{ 0 } }{ -a } ,quad t=50c.$

Перемещение находим из уравнения ${ s }_{ x }={ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ :

$s={ upsilon }_{ 0 }cdot t-frac { acdot { t }^{ 2 } }{ 2 }$ , s = 500 м.

2 Способ. Используются υ0, υ, a и s (надо найти).

Так как отсутствующая величина t, то применяем формулу № 4:

Задача 2. Самолет при взлете за 20 с пробегает по дорожке взлетной полосы 700 м. Какую скорость самолет имеет в конце дорожки взлетной полосы? Движение самолета считайте равноускоренным.

Решение. Скорость самолета увеличивается, поэтому ускорение направлено в сторону движения. Фраза из условия «при взлете» позволяет сделать вывод, что υ0 = 0. Ось 0Х направим по направлению начальной скорости (рис. 2), поэтому

${ s }_{ x }=s,quad { upsilon }_{ x }=upsilon ,quad { upsilon }_{ 0x }=0,quad { a }_{ x }=a$

1 способ. Из уравнения ${ s }_{ x }={ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ находим ускорение:

Конечную скорость находим из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ :

м/с.

2 способ. Используются ${ upsilon }_{ 0 }$ , upsilon (надо найти), t и s.

Так как отсутствующая величина a, то применяем формулу № 5:

Тогда

Задача 3. Шарик в начале наклонного желоба толкнули вниз со скоростью 2 м/с. Определите скорость шарика в конце желоба, если шарик двигался с ускорением 1,25 м/с2, а длина желоба – 2 м.

Решение. Скорость шарика увеличивается, поэтому ускорение направлено в сторону движения. По условию длина желоба – это расстояние, которое пройдет шарик, и при прямолинейном движении s = l. Ось 0Х направим по направлению начальной скорости (рис. 3), поэтому

${ s }_{ x }=l,quad { upsilon }_{ x }=upsilon ,quad { upsilon }_{ 0x }={ upsilon }_{ 0 },quad { a }_{ x }=a.$

1 способ. Из уравнения ${ s }_{ x }={ upsilon }_{ 0x }cdot t+frac { { a }_{ x }cdot { t }^{ 2 } }{ 2 }$ находим время:

Получили квадратное уравнение относительно t. Корни этого уравнения:

находим конечную скорость из уравнения ${ upsilon }_{ x }={ upsilon }_{ 0x }+{ a }_{ x }cdot t$ :

$upsilon ={ upsilon }_{ 0 }+acdot t,quad upsilon =3$ м/с.

2 способ. Используются ${ upsilon }_{ 0 }$ , upsilon (надо найти), a и s.

Так как отсутствующая величина t, то применяем формулу № 4:

Тогда

Задача 4. Хоккейная шайба проскользила по льду 50 м за 2,5 с и остановилась. С каким ускорением двигалась шайба?

Решение. По условию длина поля – это расстояние, которое пройдет шайба, и при прямолинейном движении s = l. «Шайба … остановилась» следовательно, . Скорость шайбы уменьшается, поэтому ускорение направлено против движения. Ось 0Х направим по направлению начальной скорости (рис. 4), поэтому

${ s }_{ x }=l,quad { upsilon }_{ x }=0,quad { upsilon }_{ 0x }={ upsilon }_{ 0 },quad { a }_{ x }=-a$

1 способ. Данную задачу по действиям решить нельзя, т.к. в каждом уравнение неизвестны две величины (ускорение и начальная скорость). Необходимо решать систему уравнений:

или

В итоге получаем:

2 способ. Используются upsilon , a (надо найти), t и s.

Так как отсутствующая величина ${ upsilon }_{ 0 }$ , то применяем формулу № 3:

Тогда

Вывод.

1) Преимущество первого способа только в том, что нужно запомнить две формулы. При применении второго способа надо запомнить пять формул.

2) При применении первого способа вы можете решать, как линейное уравнение с одним неизвестным, так и квадратные уравнения или систему двух уравнений в общем виде. При применении второго способа вы решаете одно уравнение с одним неизвестным.

Сакович А.Л., 2020

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи на равноускоренное движение» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник

Задачи ЕГЭ на равноускоренное движение

Задачи для этой статьи взяты из книги «Отличник ЕГЭ. Физика. Решение сложных задач.» Задачи не сложные, но требующие внимательности, и аккуратности при составлении уравнений. И снова тот же совет: решать больше самостоятельно. Но примеры решений всегда полезны.

Задача 1.

За время с прямолинейного равноускоренного движения тело прошло путь м, увеличив свою скорость в раза. Определите конечную скорость тела.

Пусть скорость тела была , тогда через 2 с она стала равна . Зная путь, пройденный телом, можем найти ускорение:

Тогда можно записать пройденный телом путь как:

Получили квадратное уравнение относительно , решим его:

Конечная скорость тогда равна м/с.

Ответ: 15 м/с.

Задача 2.

Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с. На каком расстоянии от остановки мотоциклист догонит грузовик?

Путь, пройденный мотоциклистом, равен:

Путь, пройденный грузовиком до и за время движения мотоцикла:

Приравняем и решим квадратное уравнение относительно :

Тогда от остановки встреча произошла на расстоянии м.

Ответ: 150 м.

Задача 3.

Пассажир, стоящий на перроне, заметил, что первый вагон электропоезда, приближающегося к станции, прошел мимо него в течение с, а второй – в течение с. Определить ускорение поезда , если передний конец поезда остановился на расстоянии м от пассажира? Движение поезда считать равнозамедленным.

Обозначим длину вагона . Поезд подошел к пассажиру со скоростью . Тогда для первого вагона запишем:

Второй вагон подошел к пассажиру уже со скоростью :

Тогда для второго вагона:

Так как поезд затем полностью остановился, то

Приравняем выражения, записанные для первого и второго вагонов:

Подставим :

Разделим на обе части:

Выразим :

Чтобы найти ускорение, найдем квадрат скорости:

Тогда искомое ускорение:

Ответ: м/c.

8 комментариев

Сергей
✉️
08.11.2018 04:07:51

Здравствуйте! В первой задаче ошибка в строке после дискриминанта. В знаменателе вместо двойки должно быть 4t², в итоге получится, что v₀ в два раза меньше.

Ещё можно обойтись без квадратного уравнения: выразить ускорение вторым способом a = (v-v₀) / t и приравнять это к ускорению, полученному во втором уравнении задачи. И выражать второе уравнение лучше сразу через v, а не v₀.

Анна Валерьевна
✨
08.11.2018 12:44:33

Согласна, кривенько, кривенько. Это старая статья. Теперь бы решала графически — вообще в два счета.

иван шкинёв
✉️
19.07.2020 22:53:52

…очень,уж, легкомысленно Вы берёте ускорение=3 м/сс.
Машина отъедет 50 м.,когда поедет мотоцикл. 50 м. он «проскочит» за 4 с. За это время машина проедет ещё 40.м. Всего 90 м.
Мотоцикл проедет 90 м. за: S=att, t=5,5 сек. Скорость его будет=2at. 2*3*5,5=33 м/с — 120 км/час.

Анна Валерьевна
✨
21.07.2020 07:45:07

Задача решена верно. Легкомысленно к ней подошли Вы.

иван шкинёв
✉️
23.07.2020 21:17:46

машина : 10*5=50 м.
50 м мотоцикл проедет за: 50=3*tt. t=4 сек.
машина проедет ещё 40 м. за 4 сек. Итого 50+40=90 м.
…Если тела прошли путь S за одинаковое время-график движения НЕ имеет значения ни для СРЕДНЕЙ скорости, ни для «а».. Формула пути: S=att (без /2). S= att/2- ОШИБКА !!!

Анна Валерьевна
✨
24.07.2020 07:04:47

Задача решена верно. Вот ссылка на подобные: https://phys-ege.sdamgia.ru/test?filter=all&category_id=273
Учите физику!

иван шкинёв
✉️
16.08.2021 20:13:53

Через 15 с. скорость мотоцикла будет 2at, т.е. 2*3*15=90 м/с. Это=360 км/ч. !
Мотоцикл пройдёт: S=att. 3*15*15=675 м (!)
Представляю: …по городку с грохотом несётся мотоцикл по ухабам за грузовиком, который еле-еле тащится…
Правильный ответ: S=108 м. t=6 c.
Проверка: машина: S=108 м. t=10,8 c S=10*10,8
мотоцикл: S=att 3*6*6=108 м. V кон.=2at. 2*3*6=36 м/с. t мотоцикла=6 сек.

Самое главное (БЫ): А какова МОЩНОСТЬ мотоцикла? (условие:) m мотоцикла и седока=250 кг F=3*250=750 кг.м/с. КПД ДВС=16%. 750/75*6.25=62,5 л.с.

Анна Валерьевна
✨
17.08.2021 04:46:35

Здравствуйте, Иван. Решение третьей задачи выполнено верно. Мотоцикл догонит грузовик за 10 с. И разовьет скорость at=30 м/с. Нормально для мотоцикла. Не понимаю, о каких 15 с идет речь. Не понимаю, откуда формула 2at — это неверно. Мотоцикл пройдет 150 м — почему у вас 675? Вы неверно решаете задачу, смотрите внимательно разбор.

Источник

При решении задач на равноускоренное движение не обойтись без формул кинематики и второго закона Ньютона. Рекомендуем сначала изучить теорию по этим разделам, а уже потом приступать к практике.

Больше полезных сведений и ежедневная интересная рассылка – на нашем телеграм-канале, присоединяйтесь!

Равноускоренное движение: определение и примеры

Равноускоренное движение – это движение с меняющейся скоростью, но постоянным ускорением (a=const).

Самый простой случай такого движения – равноускоренное прямолинейное движение.

Вот типичные примеры равноускоренного движения:

рояль падает с 12-го этажа с ускоренинием свободного падения g;
автомобиль разгоняется со светофора от 0 до 60 км/ч с ускорением равным 1 метр на секунду в квадрате;
автобус плавно тормозит перед светофором. Это также равноускоренное движение, только векторы скорости и ускорения направлены в разные стороны.

Вопросы с ответами на равноускоренное движение

Вопрос 1. График движения представляет собой прямую линию. Является ли движение тела равноускоренным?

Ответ: да. Если график представляет собой кривую, то ускорение тела меняется со временем. Равномерное движение, которое также описывается прямой – частный случай равноускоренного движения с нулевым ускорением. Перемещение при равноускоренном движении численно равно площади трапеции, ограниченной осями координат и графиком.

Вопрос 2. Тело равномерно движется по окружности. Как направлено ускорение?

Ответ: перпендикулярно телу. В общем случае при криволинейном движении ускорение имеет две составляющие: нормальную (центростремительное ускорение) и тангенциальную, направленную по касательной к скорости. Тангенциальное ускорение при равномерном движении по окружности равно нулю.

Вопрос 3. Является ли ускорение свободного падения постоянным ускорением?

Ответ: да, является.

Вопрос 4. Может ли тело иметь нулевую скорость и ненулевое ускорение?

Ответ: да, может. После того, как скорость станет равна нулю, тело начнет двигаться в другом направлении.

Вопрос 5. Что такое ускорение?

Ответ: Векторная физическая величина, характеризующая изменение скорости за единицу времени. При равноускоренном движении скорость меняется одинаково за равные промежутки времени.

Задачи на равноускоренное движение

Сначала обратимся к уже приведенным примерам.

Задача №1. Равноускоренное движение

Условие

Рояль роняют с 12 этажа с нулевой начальной скоростью. За какое время он долетит до земли? Один этаж имеет высоту 3 метра, сопротивлением воздуха принебречь.

Решение

Известно, что рояль движется с ускорением свободного падения g. Применим формулу для пути из кинематики:

Начальная скорость равна нулю, а за точку отсчета примем то место, откуда рояль начал движение вниз.

Ответ: 2.7 секунды.

Скорость свободно падающих тел не зависит от их массы. Любое тело в поле силы тяжести Земли будет падать с одинаковым ускорением. Этот факт был экспериментально установлен Галилео Галилеем в его знаменитых экспериментах со сбрасыванием предметов с Пизанской башни.

Задача №2. Равноускоренное движение

Условие

Автобус ехал со скоростью 60 км/ч и начал тормозить на светофоре с ускорением 0,5 метра на секунду в квадрате. Через сколько секунд его скорость станет равной 40 км/ч?

Решение

Вспоминаем формулу для скорости:

Начальная скорость дана в условии, но автобус тормозит, а значит, векторы скорости и ускорения направлены в противоположные стороны. В проекции на горизонтальную ось ускорение будем записывать со знаком минус:

Ответ: 11 секунд.

Обязательно переводите величины в систему СИ.Чтобы перевести километры в час в метры в секунду нужно значение скорости в километрах в час сначала умножить на 1000, а потом разделить на 3600.

Задача №3. Нахождение ускорения

Условие

Тело движется по закону S(t)=3t+8t^2+2t. Каково ускорение тела?

Решение

Вспоминаем, что скорость – это производная пути по времени, а ускорение – производная скорости:

Ответ: 16 метров на секунду в квадрате.

При решении физических задач не обойтись без знания производной.

Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.

Задача №4. Нахождение ускорения при равноускоренном движении

Условие

Грузовик разгоняется на дороге, а в кузове лежит незакрепленный груз. С каким максимальным ускорением должен разгоняться грузовик, чтобы груз не начал смещаться к заднему борту? Коэффициент трения груза о дно кузова k=0.2, g=10 м/c2

Решение

Для решения этой задачи нужно использовать второй закон Ньютона. Сила трения в данном случае равна F=kmg.

Ответ: 2 метра на секунду в квадрате.

Задача №5. Нахождение ускорения и скорости при равноускоренном движении

Условие

За пятую секунду прямолинейного движения с постоянным ускорением тело проходит путь 5 м и останавливается. Найти ускорение тела.

Решение

Конечная скорость тела v равна 0, v нулевое – скорость в конце 4-й секунды.

Ответ: 10 метров на секунду в квадрате.

Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис в любое время.

Источник

Уровень А

1. Куда направлены ускорения следующих тел:

а) у поезда, который начинает тормозить;

б) у поезда, который отходит от станции?

Решение

2. Куда движутся тела и как изменяются их скорости, векторы начальных скоростей и ускорений которых показаны на рисунке 1?

Рис. 1.

Решение

3. Скорость движения автомобиля за 40 с возросла от 5 м/с до 15 м/с. Определите ускорение автомобиля.

Решение

4. С каким ускорением двигался автобус, если, трогаясь с места стоянки, он развил скорость 15 м/с за 50 с?

Решение

5. Двигаясь со скоростью 72 км/ч, мотоциклист притормозил и через 20 с достиг скорости 36 км/ч. С каким ускорением он тормозил?

Решение

6. Поезд подходит к станции со скоростью 21,6 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?

Решение

7. В начале измерения скорость тела равнялась 5 м/с и направлена была на север. Через 50 с измерения показали, что тело двигается со скоростью 15 м/с на юг. Считая движения тела равноускоренным прямолинейным, определите его ускорение.

Решение

8. Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/с². Через сколько времени он приобретет скорость 54 км/ч?

Решение

9. Через сколько времени останавливается автобус, если его начальная скорость 20 м/с, а ускорение 1,25 м/с²?

Решение

10. Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

Решение

11. Какую скорость приобретает отходящий от станции поезд через 7 с от начала движения, если его ускорение равно 0,9 м/с²?

Решение

12. Какую скорость приобретает автомобиль при торможении с ускорением 0,5 м/с² через 10 с от начала торможения, если начальная скорость его была равна 72 км/ч?

Решение

13. Определите скорость тела при торможении с ускорением 0,2 м/с² через 30 с от начала торможения, если начальная скорость его была равна 2 м/с.

Решение

14. На каком расстоянии от Земли оказался бы космический корабль через 30 мин после старта, если бы он все время двигался с ускорением 9,8 м/с²?

Решение

15. Тело движется прямолинейно равнозамедленно с начальной скоростью 10 м/с и ускорением 2 м/с². Определите перемещение тела через 5 с после начала движения.

Решение

16. Чтобы оторваться от земли, самолет должен набрать скорость 180 м/с. На каком расстоянии от места старта на взлетной полосе самолет достигает этого значения скорости, если его ускорение постоянно и равно 2,5 м/с²?

Решение

17. Пассажирский поезд тормозит с ускорением 0,2 м/с². На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 54 км/ч?

Решение

18. Автобус движется со скоростью 36 км/ч. На каком расстоянии от остановки водитель должен начать тормозить, сообщая автобусу ускорение, не превышающее 1,2 м/с²?

Решение

19. Автомобиль движется прямолинейно с постоянным ускорением 2,0 м/с², имея в данный момент скорость 10 м/с. Где он был 4,0 с назад?

Решение

20. Поезд, движущийся после начала торможения с ускорением 0,40 м/с², через 15 с имел скорость 10 м/с. Найдите пройденный путь за это время.

Решение

21. Снаряд, летящий со скоростью 1000 м/с, пробивает стенку блиндажа за 0,001 с, и после этого его скорость оказывается равной 200 м/с. Считая движение снаряда в толще стенки равноускоренным, найдите ее толщину.

Решение

22. После старта гоночный автомобиль достиг скорости 360 км/ч за 25 с. Какое расстояние он прошел за это время?

Решение

23. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найдите тормозной путь.

Решение

Уровень B

1. Шарик скатывается по желобу длиной 1,25 м с ускорением 1,6 м/с². Какова скорость шарика в конце жалоба?

Решение

2. Хоккейная шайба пересекла ледяное поле длиной 60 м за 3,0 с и остановилась. Какая скорость была сообщена шайбе клюшкой хоккеиста?

Решение

3. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с², пройдет 30 м?

Решение

4. Самолет при отрыве от земли имеет скорость 252 км/ч и пробегает по бетонированной дорожке расстояние 700 м. Сколько времени продолжает разбег самолет? Движение считайте равноускоренным.

Решение

5. Ножной тормоз грузового автомобиля считается исправным если при торможении автомобиля, движущегося со скоростью 30 км/ч по сухой и ровной дороге, тормозной путь не превышает 9,0 м. Найдите соответствующее этой норме тормозное ускорение.

Решение

6. При какой начальной скорости поезд пройдет путь 1260 м в течении 60 с, замедляя ход с ускорением 1,5 м/с²?

Решение

7. Электропоезд тормозит с ускорением 0,40 м/с². Определите, за какое время он остановится, если тормозной путь равен 50 м.

Решение

8. Лифт Останкинской телевизионной башни заканчивает свое движение после прохождения 49 м за 14 с. Найдите ускорение и начальную скорость лифта.

Решение

9. Поезд, двигаясь с горы с ускорением 0,2 м/с², прошел путь 340 м и развил скорость 19 м/с. Сколько времени двигался поезд и какой была его скорость в начале отсчета?

Решение

10. Поезд, движущийся после начала торможения с ускорением 0,40 м/с², через 25 с остановился. Найдите скорость в момент начала торможения и тормозной путь.

Решение

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Равноускоренное прямолинейное движение

Равноускоренное движение — это движение с постоянным вектором ускорения (displaystyle vec {a}=const.)

Уравнение координаты материальной точки в проекциях на ось при равноускоренном движении: [x=x_0+v_text{0x}t+dfrac{a_xt^2}{2}] Формула для скорости при равноускоренном движении: [v_x={v_text{0x}}t+a_xt]

Перемещение:

[S_x=v_text{0x}t+dfrac{a_xt^2}{2}]

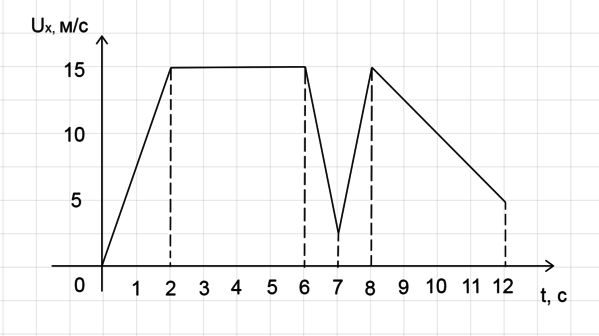
На рисунке приведён график зависимости проекции скорости тела (upsilon_{x}) от времени. Чему равна проекция ускорения этого тела ( a_{x} ) в интервале времени от 8 до 12 с? Ответ выразите в м/с(^{2}).

Ускорение можно найти по формуле: [displaystyle a=frac{upsilon_{1}-upsilon_{0}}{Delta t}] На интервале времени от (t_{1}=8) до (t_{2}= 12) (upsilon_{0}=15) м/с, а (upsilon_{1}=5) м/с. Подставив эти значения, получаем: [displaystyle a=frac{5text{ м/с}-15text{ м/с}}{4text{ с}}=-2,5 text{ м/с}^{2}]

Ответ: -2,5

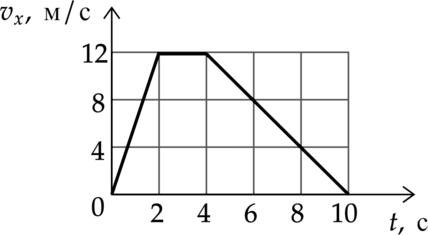
На рисунке показан график зависимости от времени для проекции (v_x) скорости тела. Какова проекция (a_x) ускорения этого тела в интервале времени от 4 до 8 c?

“Демоверсия 2018”

Ускорение тела равно: [a_x=dfrac{Delta v_x}{t}= dfrac{-8text{ м/с}}{4text{ с}}=-2text{ м/с$^2$}]

Ответ: -2

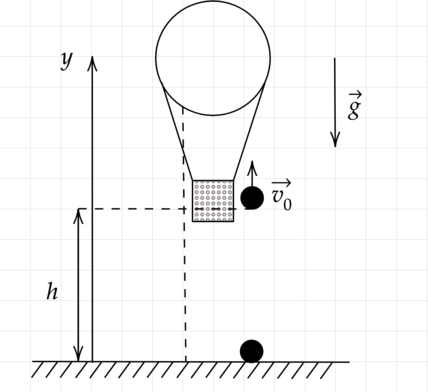
Воздушный шар поднимается с земли вертикально вверх с ускорением 2 м/с(^{2}) без начальной скорости. Через время (tau = 5) c от начала движения из него выпал предмет. Через какое время t предмет упадёт на землю? («Ответ дайте в секундах и округлите до сотых.)

Уравнения для координаты и скорости движения предмета в проекциях на ось (textit{Y}) имеют вид: [y = y_{0} + upsilon_{0y}t + dfrac{a_{y}t^{2}}{2}, quad upsilon_{y} = upsilon_{0y} + a_{y}t] [y = h + upsilon_{0y}t — dfrac{gt^{2}}{2}] Так как начальная скорость равна 0, то высота подъема шара и скорость выражаются формулами: [h = dfrac{atau^{2}}{2}] [upsilon_{0y} = atau] Эти условия соответствуют моменту начала падения предмета. В момент падения предмета на землю (y = 0), то есть:
[0 =dfrac{atau^{2}}{2} + atau t — dfrac{gt^{2}}{2} Rightarrow 0 = atau^{2} + 2atau t — gt^{2}]
Решая квадратное уравнение относительно (t), получаем:
[t = dfrac{tau}{g}( a + sqrt{a(a + g})) =dfrac{5}{10}(2 + sqrt{2(2 + 10}))= 3,45 text{ с}]

Ответ: 3,45

Тело движется равнозамедленно с ускорением (a=0,5) м/с(^2), не изменяя направления движения. За время t модуль скорости тела уменьшился от 4 м/с до 3 м/с. Какой путь прошло тело за это время? (Ответ дайте в метрах)

1 способ:
Примем, что начальная скорость тела равна (upsilon_0=4) м/с, а скорость, которую тело приобрело спустя время (t), равна (upsilon=3) м/с. Перемещение при равноускоренном движении можно выразить формулой: [S_x=frac{v_x^2-v_{0x}^2}{2a_x}] [S=frac{v^2-v^2_0}{-2a}=frac{(3 text{ м/с})^2-(4 text{ м/с})^2}{2cdot0,5 text{ м/с}^2}=7 text{ м}]
2 способ:
Примем, что начальная скорость тела равна (upsilon_0=4) м/с, а скорость, которую тело приобрело спустя время (t), равна (upsilon=3) м/с. По формуле скорости при равнозамедленном движении: [upsilon=upsilon_0-at] Отсюда выразим (t): [t=dfrac{upsilon_0-upsilon}{a}] По формуле перемещения при равнозамедленном движении: [S=upsilon_0t-dfrac{at^2}{2}] Подставив ((t)), получим: [S=upsilon_0cdotdfrac{upsilon_0-upsilon}{a}-dfrac{acdotdfrac{(upsilon_0-upsilon)^2}{a^2}}{2}=dfrac{upsilon_0(upsilon_0-upsilon)}{a}-dfrac{(upsilon_0-upsilon)^2}{2a}=dfrac{upsilon_0-upsilon}{a}cdotBigg(upsilon_0-dfrac{(upsilon_0-upsilon)}{2}Bigg)] Подставим значения: [S=dfrac{4text{ м/с}-3text{ м/с}}{0{,}5text{ м/с$^2$}}cdotBigg(4text{ м/с}-dfrac{4text{ м/с}-3text{ м/с}}{2}Bigg)=7text{ м}]

Ответ: 7

Координата тела (textit{x}) меняется с течением времени (textit{t}) согласно закону: [textit{x}= 18+32textit{t}-6textit{t}^{2}] где (textit{t}) выражено в секундах, а (textit{x}) — в метрах. Определите проекцию ускорение (a_{x}) этого тела. (Ответ дайте в м/с(^2))

Общий вид закона изменения со временем координаты тела при движении с постоянным ускорением имеет вид: [textit{x}=textit{x}_{0}+upsilon_{0x}t+frac{a_{x}t^{2}}{2}]
Приведенная в условии зависимость координаты тела от времени (textit{x}= 18+32textit{t}-6textit{t}^{2}) описывается этой квадратичной зависимостью. Приравнивая коэффициенты при t находим, что величина постоянного ускорения (a_{x}=-12) м/c(^{2})

Ответ: -12

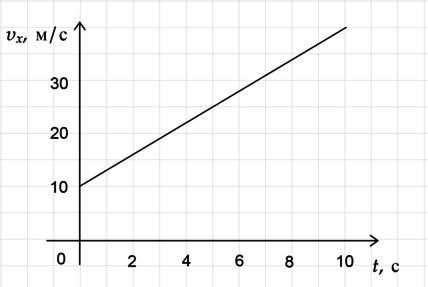
На рисунке представлен график зависимости модуля скорости (upsilon_{x}) Человека — паука от времени (t). Определите по графику путь, который пролетел Человек — паук за первые 10 секунд. (Ответ дайте в метрах)

Путь можно найти двумя способами:

1 способ:
Путь — величина строго положительная, это длина пройденного телом участка траектории. Под перемещением же тела понимается изменение его координаты, перемещение может быть отрицательным. Путь можно найти как площадь под графиком зависимости скорости от времени без учета знаков, а перемещение с их учетом. В данном случае необходимо найти площадь трапеции.
[S=dfrac{10+40}{2}cdot10=250 text{ м}]

2 способ:
Рассмотрим участок движения от 0 до 10 с, где (upsilon_{0} = 10) м/с , (upsilon_{1} = 40) м/с.
[displaystyle a = dfrac{upsilon_{1}-upsilon_{0}}{Delta t} = dfrac{40-10}{10} = 3 text{ м/с$^{2}$}] [displaystyle S = upsilon_{0}t + dfrac {at^2}{2} = 10cdot10+dfrac {3cdot10^2}{2} = 250 text{ м}]

Ответ: 250

На рисунке показан график зависимости от времени для проекции (v_x) скорости тела. Какова проекция (a_x) ускорения этого тела в интервале времени от 5 до 6 c?

“Демоверсия 2019”

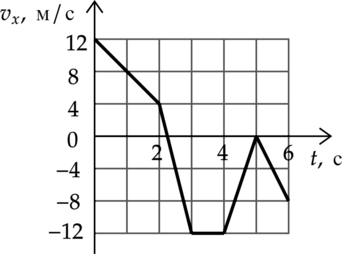
Ускорение: [a_x=dfrac{Delta v_x}{t}=dfrac{-8text{ м/с}}{1text{ с}}=-8]

Ответ: -8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями

Название величины

Обозначение

Единица измерения

Формула

t

v0x

vx

ax

Sx

x

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Краткое пояснение для решения ЗАДАЧИ на Прямолинейное равноускоренное движение.

Теория

Задачи

Задачи ЕГЭ на равноускоренное движение

8 комментариев

Равноускоренное движение: определение и примеры

Вопросы с ответами на равноускоренное движение

Задачи на равноускоренное движение

Задача №1. Равноускоренное движение

Задача №2. Равноускоренное движение

Задача №3. Нахождение ускорения

Задача №4. Нахождение ускорения при равноускоренном движении

Задача №5. Нахождение ускорения и скорости при равноускоренном движении

Уровень А

Уровень B

Равноускоренное прямолинейное движение

ЗАДАЧИ на Прямолинейное равноускоренное
движение с решениями

v_0x

v_x

a_x

S_x

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.