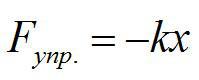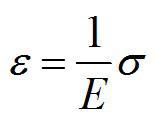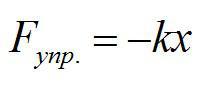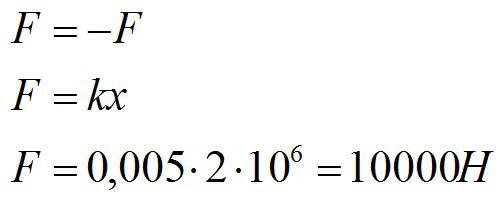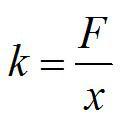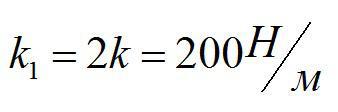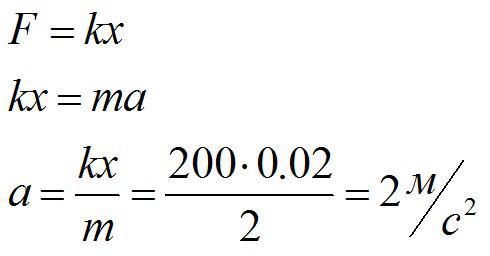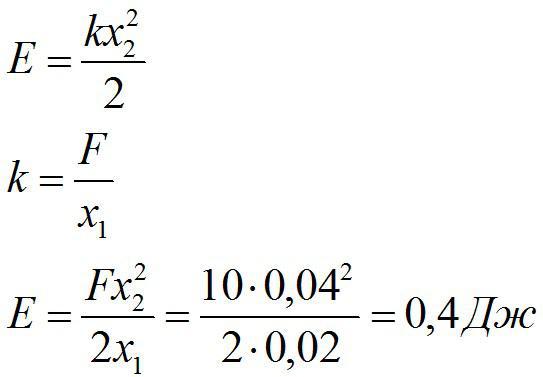Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
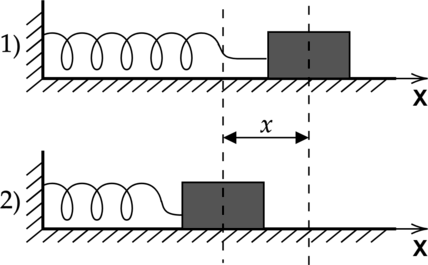
На сколько сантиметров растянется пружина, жёсткость которой под действием силы 100 H? Пружину считайте идеальной.
2
На рисунке изображен лабораторный динамометр.
Шкала проградуирована в ньютонах. Каким будет растяжение пружины динамометра, если к ней подвесить груз массой 200 г? (Ответ дайте в сантиметрах.) Ускорение свободного падения считать равным 10 м/с2.
3
Под действием силы 4,5 Н пружина удлинилась на 6 см. Чему равен модуль силы, под действием которой удлинение этой пружины составит 4 см? (Ответ дайте в ньютонах.)
5
На сколько растянется пружина жесткостью под действием силы 1000 Н? (Ответ дайте в сантиметрах.)
Пройти тестирование по этим заданиям
Пружины. Задачи части С ЕГЭ по физике и олимпиадные
В этой статье собраны задачи, в которых так или иначе присутствует сила упругости. Задачи прошлых лет ЕГЭ или из олимпиадных подборок.
Задача 1.
Две невесомые пружины прикреплены к верхнему и нижнему торцам неподвижного цилиндра. Концы пружин соединены. Жесткость верхней пружины равна Н/м, жесткость нижней
Н/м. Пружины находятся в нерастянутом состоянии. Между ними вставили тонкую платформу массой
кг. Пружины прикрепляют к платформе (см. рис.). На сколько при этом растянулась верхняя пружина?
К задаче 1
Запишем уравнение по второму закону Ньютона для груза:
Здесь — сила упругости верхней пружины, она пытается вернуться в нерастянутое состояние, поэтому будет тянуть платформу вверх.
— сила упругости нижней пружины, она пытается вернуться в нерастянутое состояние, поэтому будет толкать платформу вверх.
Тогда
При этом на сколько растянулась верхняя пружина, на столько же сжалась нижняя: . Следовательно,
Ответ: 40 см.
Задача 2.
К потолку прикреплена конструкция, состоящая из двух пружин и двух маленьких чашек A и B. Расстояние от пола до потолка равно 2 м. Жесткости пружин равны Н/м и
Н/м. Длины нерастянутых пружин одинаковы и равны 30 см. Масса чашки A равна
г, чашка B невесома. Груз какой массы надо положить в чашку A, чтобы чашка B достала до пола? Какой груз надо положить в чашку B, чтобы она достала до пола (чашка A при этом пуста)?
К задаче 2
Чтобы чашка В достала до пола, нужно, чтобы первая пружина растянулась до длины 1,7 м – тогда нерастянутая вторая пружина длиной 30 см коснется пола. Тогда удлинение пружины А должно составить 1 м 40 см. Следовательно,
Но сама чаша весит 100 г, следовательно, добавив 2 кг в чашу, мы обеспечим нужную силу.
Система из двух пружинок, соединенныx последовательно, имеет жесткость
Растягивать всю систему будем на 1,4 м – именно столько чашку В отделяет от пола.
Так как чашка А весит 100 г, то в этом случае масса дополнительного груза будет 1,3 кг.
Ответ: а) 2 кг; б)1,3 кг.
Задача 3.
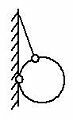
Два шарика подвешены на вертикальных тонких нитях так, что они находятся на одной высоте. Между ними находится сжатая и связанная нитью пружина. При пережигании связывающей нити пружина распрямляется, отклоняя шарики в разные стороны на одинаковые углы. Во сколько раз одна нить длиннее другой, если отношение масс ? Считать величину сжатия пружины во много раз меньше длин нитей.
К задаче 3
Когда пружина толкнет шарики, они начнут двигаться по окружностям радиусов и
соответственно. Первый поднимется при этом на высоту
, а второй – на высоту
. Определим эти высоты:
По закону сохранения импульса
Возведем в квадрат:
Или
Из равенства кинетической и потенциальной энергий следует, что
И аналогично
Поэтому
Подставим выражения, полученные вначале:
Сократим:
Ответ: .
Задача 4.
Брусок, покоящийся на горизонтальном столе, и пружинный маятник, состоящий из грузика и легкой пружины, связаны легкой нерастяжимой нитью через идеальный блок (см. рисунок). Коэффициент трения между основанием бруска и поверхностью стола равен 0,25. Груз маятника совершает колебания с периодом 0,5 с вдоль вертикали, совпадающей с вертикальным отрезком нити. Максимально возможная амплитуда этих колебаний, при которой они остаются гармоническими, равна 4 см. Чему равно отношение массы бруска к массе грузика?
К задаче 4
Координата грузика при колебаниях может быть записана как
Запишем второй закон Ньютона для грузика:
Запишем второй закон Ньютона для бруска:
Сила трения скольжения равна
Тогда, чтобы брусок не поехал под действием качаний грузика, нужно, чтобы соблюдалось условие:
Откуда отношение масс равно
Определить ускорение можно, взяв вторую производную по координате:
Максимальное ускорение равно
Подставим это ускорение в полученное отношение масс:
Ответ:
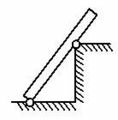
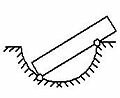
Задача 5. Пружинное ружьё наклонено под углом к горизонту. Энергия сжатой пружины равна 0,41 Дж. При выстреле шарик массой
г проходит по стволу ружья расстояние
, вылетает и падает на расстоянии
м от дула ружья в точку
, находящуюся с ним на одной высоте (см. рис.). Найдите расстояние
. Трением в стволе и сопротивлением воздуха пренебречь.
К задаче 5
Определим скорость шарика при вылете из ружья .
По горизонтали шарик полетит равномерно со скоростью :
По вертикали шарик будет иметь начальную скорость , и она станет равной нулю в максимальной точке подъема:
Тогда время полета до максимальной точки подъема
Откуда скорость равна
Определим скорость шарика вначале. Вся энергия пружины переходит в кинетическую энергию шарика:
Таким образом, в начале трубы скорость была 4,05, а в конце – 3,4 м/с. Составим закон сохранения энергии. Учтем, что конец трубы приподнят относительно начала, следовательно, часть энергии шарика превратилась в потенциальную:
Откуда
Тогда длина ствола больше вдвое, так как катет, лежащий против угла в тридцать градусов, вдвое короче гипотенузы. .
Ответ: 48 см.
9 комментариев
Элиза
✉️
29.01.2020 17:14:45
Почему в первой задаче пружина k1 будет стремится вверх? Наоборот, ее ведь сжали, чтобы разжаться, она будет давить вниз. Разве нет?
Анна Валерьевна
✨
29.01.2020 17:32:51
Первая — верхняя пружина. Она растянута висящим на ней грузом и стремится сократиться.
anton
✉️
28.02.2021 08:23:46
2 задача- во втором случае чашка a не весит НИЧЕГО! ошибка!
Анна Валерьевна
✨
28.02.2021 12:17:33
Все верно, Антон. Ошибок нет.
Евгения
✨
28.02.2021 23:23:00
Есть подозрение, что второй пункт этой задачи решается не так. Нельзя считать пружины соединенными параллельно, ведь между ними весомая чашка.
Анна Валерьевна
✨
01.03.2021 08:17:41
Я думаю, факт наличия чаши не повлияет на решение. Все равно пружины соединены последовательно. Можно, конечно, посчитать их удлинения по отдельности и сложить — но ведь это то же самое.
Евгения
✨
01.03.2021 10:01:01
В таких ситуациях я обычно говорю ученикам: не надо думать, надо формулы писать :))) У меня получился ответ 1.27 кг
Анна Валерьевна
✉️
01.03.2021 10:30:02
[latexpage]
$$Delta l_1=frac{(m_A+M)g}{k_1}$$
$$Delta l_2=frac{Mg}{k_2}$$
$$Delta l_1+Delta l_2=1,4$$
$$frac{m_Ag}{k_1}+frac{Mg}{k_1}+frac{Mg}{k_2}=1,4$$
$$Mgleft(frac{1}{k_1}+frac{1}{k_2}right)=1,4-frac{m_Ag}{k_1}=1,33$$
$$M=1,33$$
Евгения
✨
01.03.2021 11:21:48
соглашаюсь.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
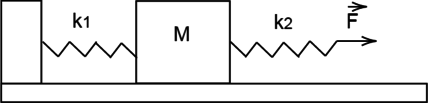
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
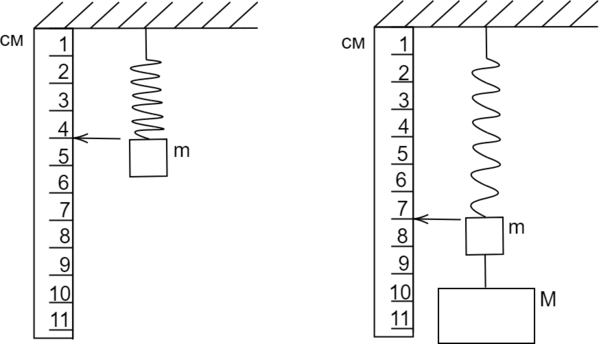
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
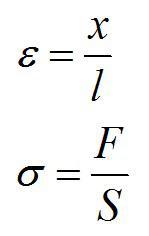
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
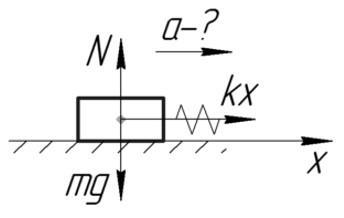
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
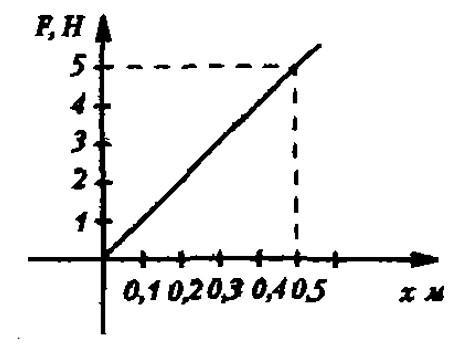
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Задачи на закон Гука
(F=kx ) .
(F)- Сила, растягивающая или сжимающая пружину
(k)- коэффициент жесткости пружины
(x)- удлинение пружины (насколько растянулась пружина)
Репетитор по физике
+7 916 478 10 32
Задача 1. ( Закон Гука )
Пружина, с коэффициентом жесткости (k=100 Н/м ), растянулась на (x=0,1 м) после приложения к свободному концу
этой пружины силы (F.)
Найти силу (F), приложенную к этой пружине.
Показать ответ
Показать решение
Видеорешение
Задача 2. ( Закон Гука )
К пружине с коэффициентом жесткости (k=100 Н/м ) была приложена сила (F) , вследствии чего она удлиннилась на 10 сантиметров.
Найти силу (F), вызвавшую это удлинение.
Показать ответ
Показать решение
Видеорешение
Задача 3. ( Закон Гука )
Сила (F=50Н ) растягивает пружину на (x=0,5 м.)
Найти коэффициент жесткости этой пружины.
Показать ответ
Показать решение
Видеорешение
Задача 4. ( Закон Гука )
Найти коэффициент жесткости пружины, если сила (F=200Н), может растянуть эту пружину на 5 сантиметров.
Показать ответ
Показать решение
Видеорешение
Задача 5. ( Закон Гука )
На сколько растянется пружина с коэффициентом жесткости ( k=25Н/м ), если к ее будет растягивать сила
(F=10Н )
Показать ответ
Показать решение
Видеорешение
Задача 6. ( Закон Гука )
Найти растяжение пружины жесткостью ( k=600Н/м ), если к ее свободному концу приложить силу (F=30Н .)
Ответ дать в сантиметрах.
Показать ответ
Показать решение
Видеорешение
Задача 7. Приведено решение для тех, кому тяжело понять
Один конец пружины жесткостью ( k=400Н/м ) прикрепляют к потолку, а к другому ее концу
подвешивают груз массой (m=1 кг .)
На сколько сантиметров удлиннится пружина?
(g=10 Н/кг )
Показать ответ
Показать решение
Видеорешение
Задача 7. Приведено решение для тех, кто хочет научиться решать сложные задачи
Один конец пружины жесткостью ( k=400Н/м ) прикрепляют к потолку, а к другому ее концу
подвешивают груз массой (m=1 кг .)
На сколько сантиметров удлиннится пружина?
(g=10 Н/кг .)
Показать ответ
Показать решение
Видеорешение
Задача 8. Приведено решение для тех, кому тяжело понять
К свободному концу пружины жесткостью ( k=800Н/м ) прикрепляют груз массой (m=4 кг .)
Найти растяжение пружины.
Дать ответ в сантиметрах. (g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 8. Приведено решение для тех, кто хочет научиться решать сложные задачи
Один конец пружины жесткостью ( k=800Н/м ) прикрепляют к потолку, а к другому ее концу
подвешивают груз массой (m=4 кг .)
На сколько сантиметров удлиннится пружина?
Дать ответ в сантиметрах. (g=10 Н/кг .)
Показать ответ
Показать решение
Видеорешение
Задача 9. Приведено решение для тех, кому тяжело понять
К пружине, закрепленной у потолка, подвешивают груз, при этом пружина растягивается на (x=0,08 м.)
Коэффициент жесткости пружины ( k=500Н/м ).
Найти массу груза, подвешенного к пружине.
(g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 9. Приведено решение для тех, кто хочет научиться решать сложные задачи
К пружине, закрепленной у потолка, подвешивают груз, при этом пружина растягивается на (x=0,08 м.)
Коэффициент жесткости пружины ( k=500Н/м ).
Найти массу груза, подвешенного к пружине.
(g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 10. Приведено решение для тех, кому тяжело понять
К пружине, закрепленной у потолка, подвешивают груз, при этом пружина растягивается на (x=0,01 м.)
Коэффициент жесткости пружины ( k=150Н/м ).
Найти массу груза, подвешенного к пружине.Дать ответ в граммах.
(g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 10. Приведено решение для тех, кто хочет научиться решать сложные задачи
К пружине, закрепленной у потолка, подвешивают груз, при этом пружина растягивается на (x=0,08 м.)
Коэффициент жесткости пружины ( k=500Н/м ).
Найти массу груза, подвешенного к пружине. Дать ответ в граммах.
(g=10 Н/кг . )
Показать ответ
Показать решение
Видеорешение
Задача 11. ( Закон Гука )
Найти коэффициент жесткости пружины, если груз массой (m=5 кг ) растягивает ее на 2 сантиметра.
Показать ответ
Показать решение
Видеорешение
Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения
В. З. Шапиро
Второе задание ЕГЭ по физике проверяет знания по разделу «Динамика». Это задание базового уровня сложности, без возможности выбора ответа. Для его решения необходимо знать законы Ньютона, формулы, которые выражают силу тяжести, силу всемирного тяготения, силу упругости, вес тела, силу трения, силу реакции опоры на горизонтальной поверхности и на наклонной плоскости. Во многих задачах применяется одна и та же формула, но в различных ситуациях. Как правило, необходимо составить и решить систему из двух уравнений.
Применение закона всемирного тяготения
Необходимая теория: Сила тяготения
1. Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Во сколько раз больше будет модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами в два раза больше, а массы звёзд равны 2m и 3m?
Ответ: в _________________________ раз(а).
В этой задаче необходимо записать формулу закона всемирного тяготения для двух случаев:
(1).
(2).
Разделив (2) на (1), получим:
Ответ: в 1,5 раза.
Подобные задачи проверяют знания основных физических формул. Их необходимо записать в общем виде и в случае, когда происходит изменение какой-либо физической величины. Полученную систему уравнений решаем любым удобным способом. Задания такого типа часто встречаются в различных разделах курса физики.
Применение II закона Ньютона
Необходимая теория: Второй и третий законы Ньютона
2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей сил, приложенных к телу.
Равнодействующая сила равна геометрической сумме сил, приложенных к телу.
Следующий шаг – найти сумму проекций сил на оси OX и OY.
Сумма проекций сил на ось OX равна:
Сумма проекций сил на вертикальную ось равна:
По теореме Пифагора, модуль равнодействующей силы определяется:
Ответ: 2 Н.
Секрет решения: Многие задачи по динамике требует прочных знаний по геометрии. Теорема Пифагора, а также соотношения в прямоугольном треугольнике являются обязательными инструментами для тех, кто собирается сдавать экзамен по физике.
Применение формулы силы упругости (закон Гука)
Необходимая теория: Сила упругости
3. Подвешенная к потолку пружина под действием силы 5 Н удлинилась на 10 см. Чему равно удлинение этой пружины под действием силы 8 Н?
Ответ: ___________________________ см.
Запишем формулу закона Гука для двух случаев:
(1)
(2)
Разделим (2) на (1).
(м).
Ответ: 16 см.
Задача решается стандартным применением физической формулы для двух случаев. Обратите внимание на единицы измерения, которые требуются в ответе.
Применение формул для силы реакции опоры и силы трения
Необходимая теория: Сила трения
4. Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.
Ответ: ___________________________.
Общая формула для силы трения имеет вид:
где N — сила реакции опоры.
Отсюда коэффициент трения можно выразить
Проведем расчет:
Ответ: 0,25.
Секрет решения: Помним, что коэффициент трения находится в интервале от 0 до 1. Это поможет вам более уверенно решать задачи на расчет коэффициента трения.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 2 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Уровень А
1. Какого вида деформации испытывают при нагрузке:
а) ножка скамейки;
б) сиденье скамейки;
в) натянутая струна гитары;
г) винт мясорубки;
д) сверло;
е) зубья пилы?
Решение
2. С какой деформацией (упругой или пластической) имеют дело при лепки фигур с глины, пластилина?
Решение
3. Проволока длиной 5,40 м под действием нагрузки удлинилась до 5,42 м. Определите абсолютное удлинение проволоки.
Решение
4. При абсолютном удлинении на 3 см длина пружины стала равной 27 см. Определите ее начальную длину, если пружину:
а) растянули;
б) сжали.
Решение
5. Абсолютное удлинение проволоки длиной 40 см равно 2,0 мм. Определите относительное удлинение проволоки.
Решение
6. Абсолютное и относительное удлинение стержня равны 1 мм и 0,1% соответственно. Определите длину недеформированного стержня?
Решение
7. При деформации стержня сечением 4,0 см2 сила упругости равна 20 кН. Определите механическое напряжение материала.
Решение
8. Определите модуль силы упругости в деформированном стержне площадью 4,0 см2, если при этом возникает механическое напряжение 1,5·108 Па.
Решение
9. Найдите механическое напряжение, возникающее в стальном тросе при его относительном удлинении 0,001.
Решение
10. При растяжении алюминиевой проволоки в ней возникло механическое напряжение 35 МПа. Найдите относительное удлинение.
Решение
11. Чему равен коэффициент жесткость пружины, которая удлиняется на 10 см при силе упругости 5,0 H?
Решение
12. На сколько удлинилась пружина жесткостью 100 Н/м, если сила упругости при этом равна 20 Н?
Решение
13. Определите максимальную силу, которую может выдержать стальная проволока, площадь поперечного сечения которой 5,0 мм2.
Решение
14. Берцовая кость человека выдерживает силу сжатия 50 кН. Считая предел прочности кости человека равным 170 МПа, оцените среднюю площадь поперечного сечения берцовой кости.
Решение
Уровень B
1. Какая колба выдержит большее давление снаружи – круглая или плоскодонная?
Решение
2. Для чего рама велосипеда делается из полых трубок, а не сплошных стержней?
Решение
3. При штамповке детали иногда предварительно нагревают (горячая штамповка). Для чего это делают?
Решение
4. Укажите направление сил упругости, действующих на тела в указанных точках (рис. 1).
-
а
-
б
-
в
-
г
-
д
Рис. 1
Решение
5. Почему нет таблиц для коэффициента жесткости тела k, вроде таблиц для плотности вещества?
Решение
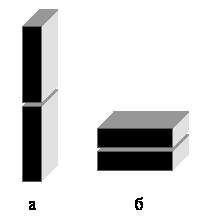
6. При какой кладке кирпичей (рис. 2) нижний из кирпичей окажется под большим напряжением?
Рис. 2
Решение
7. Сила упругости – сила переменная: она изменяется от точки к точке по мере удлинения. А как ведет себя ускорение, вызванное этой силой?
Решение
8. К закрепленной одним концом проволоке диаметром 2,0 мм подвешен груз массой 10 кг. Найдите механическое напряжение в проволоке.
Решение
9. На две вертикальные проволоки, диаметры которых отличаются в 3 раза, прикрепили одинаковые грузики. Сравните возникающие в них напряжения.
Решение
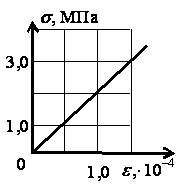
10. На рис. 3 дан график зависимости напряжения, возникающего в бетонной свае, от ее относительного сжатия. Найдите модуль упругости бетона.
Рис. 3
Решение
11. Проволока длиной 10 м с площадью сечения 0,75 мм2 при растяжении силой 100 Н удлинилась на 1,0 см. Определите модуль Юнга для материала проволоки.
Решение
12. С какой силой нужно растягивать закрепленную стальную проволоку длиной 1 м с площадью сечения 0,5 мм2, чтобы удлинить ее на 3 мм?
Решение
13. Определите диаметр стальной проволоки длиной 4,2 м, чтобы при действии продольной растягивающей силы, равной 10 кН, ее абсолютное удлинение было равно 0,6 см?
Решение
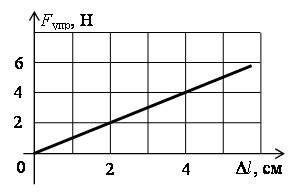
14. Определите по графику (рис. 4) коэффициент жесткости тела.
Рис. 4
Решение
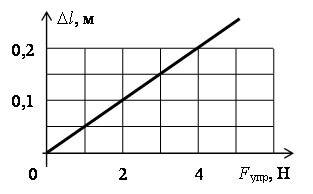
15. По графику зависимости изменения длины резинового жгута от приложенной к нему силы найдите жесткость жгута (рис. 5).
Рис. 5
Решение
16. Постройте график зависимости силы упругости, возникающей в деформированной пружине Fупр = f(Δl), от ее удлинения, если жесткость пружины 200 Н/м.
Решение
17. Постройте график зависимости удлинения пружины от приложенной силы Δl = f(F), если коэффициент жесткости пружины 400 Н/м.
Решение
18. Закон Гука для проекции силы упругости пружины имеет вид Fx = –200 х. Чему равна проекция силы упругости, если при удлинении пружины из недеформированного состояния проекция перемещения конца пружины на ось Х составляет 10 см?
Решение
19. Два мальчика растягивают резиновый жгут, прикрепив к его концам динамометры. Когда жгут удлинился на 2 см, динамометры показывали силы по 20 Н каждый. Что показывают динамометры при растяжении жгута на 6 см?
Решение
20. Две пружины равной длины, соединенные последовательно, растягивают за свободные концы руками. Пружина жесткостью 100 Н/м удлинилась на 5 см. Какова жесткость второй пружины, если ее удлинение равно 1 см?
Решение
21. Пружина изменила свою длину на 6 см, когда к ней подвесили груз массой 4 кг. На сколько бы она изменила свою длину под действием груза массой 6 кг?
Решение
22. На двух проволоках, одинаковой жесткости, длиной 1 и 2 м подвешены одинаковые грузы. Сравните абсолютные удлинения проволок.
Решение
23. Диаметр капроновой рыболовной лески 0,12 мм, а разрывная нагрузка 7,5 Н. Найдите предел прочности на разрыв данного сорта капрона.
Решение
24. При каком наибольшем диаметре поперечного сечения стальная проволока под действием силы в 7850 Н разорвется?
Решение
25. Люстру массой 10 кг нужно подвесить на проволоке сечением не более 5,0 мм2. Из какого материала следует взять проволоку, если необходимо обеспечить пятикратный запас прочности?
Решение
Уровень С
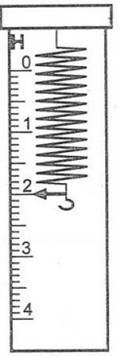
1. Если к вертикально расположенному динамометру прикрепить деревянный брусок массой 200 г, то показание динамометра окажется таким, как показано на рисунке 1. Определите ускорение, с которым начнет двигаться тот же брусок, если его оттянуть так, что пружина удлинится еще на 2 см, а затем брусок отпустить.
Рис. 1
Решение