Задания
Версия для печати и копирования в MS Word
Тип 2 № 27112
От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Спрятать решение
Решение.
Объем призмы больше объема пирамиды с такой же площадью основания и высотой в 3 раза. Объем оставшейся части составляет тогда две трети исходного, он равен 4.
Ответ: 4.
Аналоги к заданию № 27112: 74915 74959 74917 74919 74921 74923 74925 74927 74929 74931 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Дата: 2020-07-03
1389
Категория: Стерео Призма
Метка: ЕГЭ-№2
27112. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Устная задача. Строим призму, отсекаем указанную часть: 
То есть он составляет одну треть от объёма призмы и равен 2. Таким образом, объём оставшейся части равен 4.
Ответ: 4
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
B11 № 27043. В куб вписан шар радиуса 1.
Найдите объем куба.
Ответ: 8
B11 № 27055. Площадь поверхности куба равна
18. Найдите его диагональ.
Ответ: 3
B11 № 27056. Объем куба равен 8. Найдите
площадь его поверхности.
Ответ: 24

№ 27061. Если каждое ребро куба увеличить на 1, то его площадь
поверхности увеличится на 54. Найдите ребро куба.
Ответ: 4
B11 № 27080. Три ребра прямоугольного
параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро
равновеликого ему куба.
Ответ: 6
B11 № 27081. Во сколько раз увеличится
объем куба, если его ребра увеличить в три раза?
Ответ: 27
B11 № 27098. Диагональ куба равна .
Найдите его объем.
Ответ: 8
B11 № 27099. Объем куба равен .
Найдите его диагональ.
Ответ: 6
B11 № 27102. Если каждое ребро куба
увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Ответ: 2
B11 № 27130. Во сколько раз увеличится
площадь поверхности куба, если его ребро увеличить в три раза?
Ответ: 9

№ 27139. Диагональ куба равна 1. Найдите площадь его поверхности.
Ответ: 2
B11 № 27141. Площадь поверхности куба равна
24. Найдите его объем.
Ответ: 8
B11 № 27168. Объем одного куба в 8 раз
больше объема другого куба. Во сколько раз площадь поверхности первого куба
больше площади поверхности второго куба?
Ответ: 4
B11 № 72007. В куб вписан шар радиуса 3.
Найдите объем куба.
Ответ: 216
B11 № 72585. Площадь поверхности куба равна
2592. Найдите его диагональ.
Ответ: 36
B11 № 74429. Диагональ куба равна .
Найдите его объем.
Ответ: 729
B11 № 27047. Сосуд, имеющий форму
правильной треугольной призмы, налили 2300 воды и погрузили в воду деталь. При этом
уровень воды поднялся с отметки 25 см до отметки 27
см. Найдите объем детали. Ответ выразите в .
Ответ: 184
B11 № 27048. В сосуд, имеющий форму
правильной треугольной призмы, налили воду. Уровень воды достигает 80
см. На какой высоте будет находиться уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого?
Ответ выразите в см.
Ответ: 5
B11 № 27057. Найдите площадь боковой
поверхности правильной шестиугольной призмы, сторона основания которой равна
5, а высота – 10.
Ответ: 300

прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и
боковым ребром, равным 10.
Ответ: 248
B11 № 27063. Найдите боковое ребро
правильной четырехугольной призмы, если сторона ее основания равна 20, а
площадь поверхности равна 1760.
Ответ: 12
B11 № 27064. Правильная четырехугольная
призма описана около цилиндра, радиус основания и высота которого равны 1.
Найдите площадь боковой поверхности призмы.
Ответ: 8
B11 № 27065. Найдите площадь боковой
поверхности правильной треугольной призмы, описанной около цилиндра, радиус
основания которого равен ,
а высота равна 2.
Ответ: 36
B11 № 27066. Найдите площадь боковой
поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус
основания которого равен ,
а высота равна 2.
Ответ: 24
B11 № 27068. Через среднюю линию основания
треугольной призмы, площадь боковой поверхности которой равна 24, проведена
плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности
отсеченной треугольной призмы.
Ответ: 12
B11 № 27082. Основанием прямой треугольной
призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно
5. Найдите объем призмы.
Ответ: 120
B11 № 27083. Основанием прямой треугольной
призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен
30. Найдите ее боковое ребро.
Ответ: 4

шестиугольной призмы, стороны основания которой равны 1, а боковые ребра
равны .
Ответ: 4,
B11 № 27106. Через среднюю линию основания
треугольной призмы, объем которой равен 32, проведена плоскость, параллельная
боковому ребру. Найдите объем отсеченной треугольной призмы.
Ответ: 8

треугольной призмы проведена плоскость, параллельная боковому ребру. Объем
отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Ответ: 20
B11 № 27108. Найдите объем призмы, в
основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые
ребра равны и наклонены
к плоскости основания под углом 30.
Ответ: 18
B11 № 27132. Основанием прямой треугольной
призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна
10. Найдите площадь ее поверхности.
Ответ: 288
B11 № 27148. В основании прямой призмы
лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248.
Найдите боковое ребро этой призмы.
Ответ: 10

боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других
боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Ответ: 240
B11 № 27151. Основанием прямой треугольной
призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее
поверхности равна 288. Найдите высоту призмы.
Ответ: 10
B11 № 27153. Через среднюю линию основания
треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь
боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь
боковой поверхности исходной призмы.
Ответ: 16
B11 № 27170. Найдите площадь боковой
поверхности правильной треугольной призмы, вписанной в цилиндр, радиус
основания которого равен ,
а высота равна 2.
Ответ: 36
B11 № 27183. Объем куба равен 12. Найдите
объем треугольной призмы, отсекаемой от него плоскостью, проходящей через
середины двух ребер, выходящих из одной вершины и параллельной третьему
ребру, выходящему из этой же вершины.
Ответ: 1,5
B11 № 245335. Найдите объем многогранника,
вершинами которого являются точки ,
,
,
,
,
прямоугольного параллелепипеда
, у которого
,
,
.
Ответ: 3
B11 № 245344.
Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы
, площадь основания которой равна 6,
а боковое ребро равно 3.
Ответ: 3
B11 № 245345. Найдите объем многогранника,
вершинами которого являются точки ,
,
,
,
,
,
,
правильной шестиугольной призмы
, площадь основания которой равна 6,
а боковое ребро равно 2.
Ответ: 8

вершинами которого являются точки ,
,
,
,
,
,
,
правильной шестиугольной призмы
, площадь основания которой равна 6,
а боковое ребро равно 2.
Ответ: 6
B11 № 245347. Найдите объем многогранника,
вершинами которого являются точки ,
,
,
правильной шестиугольной призмы
, площадь основания которой равна 6,
а боковое ребро равно 3.
Ответ: 1
B11 № 245356.
Площадь поверхности правильной треугольной призмы равна 6. Какой будет
площадь поверхности призмы, если все ее ребра увеличить в три раза?
Ответ: 54
B11 № 245357.
Найдите объем правильной шестиугольной призмы, все ребра которой равны .
Ответ: 13,5
B11 № 27069. Стороны основания правильной
четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь
поверхности этой пирамиды.
Ответ: 340
B11 № 27070. Стороны основания правильной
шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь
боковой поверхности этой пирамиды.
Ответ: 360
B11 № 27074. Объем параллелепипеда равен 9. Найдите объем
треугольной пирамиды .
Ответ: 1,5
B11 № 27085. Во сколько раз увеличится
объем правильного тетраэдра, если все его ребра увеличить в два раза?
Ответ: 8
B11 № 27086. Основанием пирамиды является
прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой
пирамиды.
Ответ: 4
B11 № 27087. Найдите объем правильной
треугольной пирамиды, стороны основания которой равны 1, а высота равна .
Ответ: 0,25
B11 № 27088. Найдите высоту правильной
треугольной пирамиды, стороны основания которой равны 2, а объем равен .
Ответ: 3
B11 № 27089. Во сколько раз увеличится
объем пирамиды, если ее высоту увеличить в четыре раза?
Ответ: 4
B11 № 27109. В правильной четырехугольной
пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Ответ: 256
B11 № 27110. Основанием пирамиды служит
прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три
другие боковые грани наклонены к плоскости основания под углом 60. Высота пирамиды равна 6.
Найдите объем пирамиды.
Ответ: 48
B11 № 27111. Боковые ребра треугольной
пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем
пирамиды.
Ответ: 4,5
B11 № 27112. От треугольной призмы, объем
которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через
сторону одного основания и противоположную вершину другого основания. Найдите
объем оставшейся части.
Ответ: 4
B11 № 27113. Объем треугольной пирамиды , являющейся частью
правильной шестиугольной пирамиды , равен 1. Найдите объем шестиугольной
пирамиды.
Ответ: 6
B11 № 27114. Объем правильной
четырехугольной пирамиды равен
12. Точка – середина
ребра . Найдите объем
треугольной пирамиды .
Ответ: 3
B11 № 27115. От треугольной пирамиды, объем
которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через
вершину пирамиды и среднюю линию основания. Найдите объем отсеченной
треугольной пирамиды.
Ответ: 3
B11 № 27116. Объем треугольной пирамиды
равен 15. Плоскость проходит через сторону основания этой пирамиды и
пересекает противоположное боковое ребро в точке, делящей его в отношении 1 :
2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые
плоскость разбивает исходную пирамиду.
Ответ: 10

площадь поверхности правильного тетраэдра, если все его ребра увеличить в два
раза?
Ответ: 4
B11 № 27155. Найдите площадь поверхности
правильной четырехугольной пирамиды, стороны основания которой равны 6 и
высота равна 4.
Ответ: 96
B11 № 27171. Найдите площадь боковой
поверхности правильной четырехугольной пирамиды, сторона основания которой
равна 6 и высота равна 4.
Ответ: 60
B11 № 27172. Во сколько раз увеличится
площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Ответ: 4

Найдите площадь сечения, проходящего через середины четырех его ребер.
Ответ: 0,25

которой равна 6, а основание – прямоугольник со сторонами 3 и 4.
Ответ: 24
B11 № 27178. В правильной четырехугольной
пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой
пирамиды.
Ответ: 13
B11 № 27179. Сторона основания правильной
шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем
пирамиды.
Ответ: 12
B11 № 27180. Объем правильной шестиугольной
пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Ответ: 7
B11 № 27181. Сторона основания правильной
шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием
равен 45. Найдите объем
пирамиды.
Ответ: 48
B11 № 27182. Объем параллелепипеда равен 12. Найдите объем
треугольной пирамиды .
Ответ: 2
B11 № 27184. Объем куба равен 12. Найдите
объем четырехугольной пирамиды, основанием которой является грань куба, а
вершиной — центр куба.
Ответ: 2
B11 № 27209. Объем параллелепипеда равен 4,5. Найдите объем
треугольной пирамиды .
Ответ: 1,5
B11 № 245336. Найдите объем многогранника,
вершинами которого являются точки ,
,
,
прямоугольного параллелепипеда
, у которого
,
, АА1.
Ответ: 8
B11 № 245337.
Найдите объем многогранника, вершинами которого являются точки ,
,
,
,
прямоугольного параллелепипеда
, у которого
,
,
.
Ответ: 16
B11 № 245338. Найдите объем многогранника,
вершинами которого являются точки ,
,
,
прямоугольного параллелепипеда
, у которого
,
,
.
Ответ: 6
B11 № 245339. Найдите объем многогранника,
вершинами которого являются точки ,
,
,
прямоугольного параллелепипеда
, у которого
,
,
.
Ответ: 10
B11 № 245340. Найдите объем многогранника,
вершинами которого являются точки ,
,
,
правильной треугольной призмы
, площадь основания которой равна 2,
а боковое ребро равно 3.
Ответ: 2

вершинами которого являются точки ,
,
,
правильной треугольной призмы
, площадь основания которой равна 4,
а боковое ребро равно 3.
Ответ: 4
B11 № 245343. Найдите объем многогранника,
вершинами которого являются точки ,
,
,
,
,
,
правильной шестиугольной призмы
, площадь основания которой равна 4,
а боковое ребро равно 3.
Ответ: 4
B11 № 245353.
Найдите объем пирамиды, изображенной на рисунке. Ее основанием является
многоугольник, соседние стороны которого перпендикулярны, а одно из боковых
ребер перпендикулярно плоскости основания и равно 3.
B11 № 318146. В правильной четырёхугольной
пирамиде с основанием
боковое ребро
равно 5, сторона основания равна
. Найдите объём пирамиды.
Ответ: 24
B11 № 501211. Площадь боковой поверхности
пятиугольной пирамиды равна 13. Чему будет равна площадь боковой поверхности
пирамиды, если все ее ребра уменьшить в 2 раза?
Ответ: 3,25
B11 № 501544. В правильной четырёхугольной
пирамиде с основанием
боковое ребро
равно 5, сторона основания равна
. Найдите объём пирамиды.
Ответ: 32
B11 № 25541. Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 18
B11 № 25561. Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 76

многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 92
B11 № 25601. Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 110

многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 94

многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 132
B11 № 25661. Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 114

многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 48
B11 № 25701. Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 84

многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 96
B11 № 25881. Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 124
B11 № 27071. Найдите площадь поверхности
многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ: 14
B11 № 27075. Из единичного куба вырезана
правильная четырехугольная призма со стороной основания 0,5 и боковым ребром
1. Найдите площадь поверхности оставшейся части куба.
Ответ: 7,5
B11 № 27157. Во сколько раз увеличится
площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Ответ: 9
B11 № 27158. Найдите площадь поверхности
пространственного креста, изображенного на рисунке и составленного из
единичных кубов.
Ответ: 30
B11 № 27215. Площадь поверхности тетраэдра
равна 1,2. Найдите площадь поверхности многогранника, вершинами которого
являются середины сторон данного тетраэдра.
Ответ: 0,6

многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 162
B11 № 77156. Найдите площадь поверхности
многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 140

многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 152
B11 № 27044. Найдите объем многогранника,
изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ: 8
B11 № 27117. Найдите объем
пространственного креста, изображенного на рисунке и составленного из
единичных кубов.
Ответ: 7
B11 № 27187. Найдите объем многогранника,
изображенного на рисунке (все двугранные углы прямые).
Ответ: 56
B11 № 27188. Найдите объем многогранника,
изображенного на рисунке (все двугранные углы прямые).
Ответ: 7
B11 № 27189. Найдите объем многогранника,
изображенного на рисунке (все двугранные углы прямые).
Ответ: 40
B11 № 27190. Найдите объем многогранника,
изображенного на рисунке (все двугранные углы прямые).
Ответ: 34
B11 № 27042. Прямоугольный параллелепипед
описан около цилиндра, радиус основания которого равен 4. Объем
параллелепипеда равен 16. Найдите высоту цилиндра.
Ответ: 0,25
B11 № 27045. В цилиндрический сосуд налили
2000 воды. Уровень воды
при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При
этом уровень жидкости в сосуде поднялся на 9
см. Чему равен объем детали? Ответ выразите в .
Ответ: 1500
B11 № 27046. В цилиндрическом сосуде
уровень жидкости достигает 16 см. На какой высоте будет находиться уровень
жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в
см.
Ответ: 4
B11 № 27049. В основании прямой призмы
лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра,
описанного около этой призмы.
Ответ: 125
B11 № 27050. В основании прямой призмы
лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой
призмы.
Ответ: 4
B11 № 27051. Цилиндр и конус имеют общее
основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен
25.
Ответ: 75
B11 № 27053. Объем первого цилиндра равен 12
м3. У второго цилиндра высота в три раза больше, а радиус
основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра.
Ответ дайте в кубических метрах.
Ответ: 9
B11 № 27058. Радиус основания цилиндра
равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра,
деленную на .
Ответ: 12
B11 № 27091. В цилиндрический сосуд, в
котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в
сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
Ответ: 3
B11 № 27118. Одна цилиндрическая кружка
вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема
второй кружки к объему первой.
Ответ: 1,125
B11 № 27133. Длина окружности основания
цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности
цилиндра.
Ответ: 6
B11 № 27173. Площадь осевого сечения
цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на .
Ответ: 4
B11 № 27196. Найдите объем V части
цилиндра, изображенной на рисунке. В ответе укажите .
Ответ: 45
B11 № 27197. Найдите объем части цилиндра, изображенной на
рисунке. В ответе укажите .
Ответ: 3,75
B11 № 27198. Найдите объем части цилиндра, изображенной на
рисунке. В ответе укажите .
Ответ: 144
B11 № 27199. Найдите объем части цилиндра, изображенной на
рисунке. В ответе укажите .
Ответ: 937,5
B11 № 27200. Найдите объем части цилиндра, изображенной на
рисунке. В ответе укажите .
Ответ: 14
B11 № 27201. Найдите объем части цилиндра, изображенной на
рисунке. В ответе укажите .
Ответ: 105
B11 № 245350.
Конус вписан в цилиндр. Объем конуса равен 5. Найдите объем цилиндра.
Ответ: 15
B11 № 245354.
Правильная четырехугольная призма описана около цилиндра, радиус основания
которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту
цилиндра.
Ответ: 3
B11 № 245358.
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна
6. Найдите высоту цилиндра.
Ответ: 2
B11 № 500147. В цилиндрическом сосуде
уровень жидкости достигает 405 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в
9 раз больше диаметра первого? Ответ выразите в сантиметрах.
Ответ: 5
B11 № 500167. В цилиндрическом сосуде
уровень жидкости достигает 28 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в
2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Ответ: 7
B11 № 500251. Объём первого цилиндра равен 12
м3. У второго цилиндра высота в три раза больше, а радиус
основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в
м3).
Ответ: 9
B11 № 27052. Объем конуса равен 16. Через
середину высоты параллельно основанию конуса проведено сечение, которое
является основанием меньшего конуса с той же вершиной. Найдите объем меньшего
конуса.
Ответ: 2
B11 № 27093. Найдите объем V конуса,
образующая которого равна 2 и наклонена к плоскости основания под углом 30. В ответе укажите
.
Ответ: 1
B11 № 27094. Во сколько раз уменьшится
объем конуса, если его высоту уменьшить в 3 раза?
Ответ: 3

объем конуса, если его радиус основания увеличить в 1,5 раза?
Ответ: 2,25
B11 № 27096. Цилиндр и конус имеют общие
основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Ответ: 50
B11 № 27120. Высота конуса равна 6,
образующая равна 10. Найдите его объем, деленный на .
Ответ: 128
B11 № 27121. Диаметр основания конуса равен
6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса,
деленный на .
Ответ: 9
B11 № 27122. Конус получается при вращении
равнобедренного прямоугольного треугольника вокруг катета, равного 6. Найдите его объем,
деленный на .
Ответ: 72
B11 № 27123. Конус описан около правильной
четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его
объем, деленный на .
Ответ: 16
B11 № 27124. Во сколько раз объем конуса,
описанного около правильной четырехугольной пирамиды, больше объема конуса,
вписанного в эту пирамиду?
Ответ: 2
B11 № 27135. Длина окружности основания
конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности
конуса.
Ответ: 3
B11 № 27136. Во сколько раз увеличится
площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
Ответ: 3
B11 № 27159. Высота конуса равна 6,
образующая равна 10. Найдите площадь его полной поверхности, деленную на .
Ответ: 144
B11 № 27160. Площадь боковой поверхности
конуса в два раза больше площади основания. Найдите угол между образующей
конуса и плоскостью основания. Ответ дайте в градусах.
Ответ: 60
B11 № 27161. Площадь полной поверхности
конуса равна 12. Параллельно основанию конуса проведено сечение, делящее
высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Ответ: 3
B11 № 27167. Радиус основания конуса равен
3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на .
Ответ: 24
B11 № 27202. Найдите объем части конуса, изображенной на
рисунке. В ответе укажите .
Ответ: 87,75
B11 № 245351.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара
равен 28. Найдите объем конуса.
Ответ: 7

конуса, уровень жидкости достигает высоты. Объём жидкости равен 70 мл. Сколько
миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Ответ: 490
B11 № 27059. Площадь большого круга шара
равна 3. Найдите площадь поверхности шара.
Ответ: 12

площадь поверхности шара, если радиус шара увеличить в 2 раза?
Ответ: 4
B11 № 27073. Около шара описан цилиндр,
площадь поверхности которого равна 18. Найдите площадь поверхности шара.
Ответ: 12
B11 № 27097. Во сколько раз увеличится
объем шара, если его радиус увеличить в три раза?
Ответ: 27
B11 № 27105. Объем прямоугольного
параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
Ответ: 3
B11 № 27125. Радиусы трех шаров равны 6, 8
и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ: 12
B11 № 27126. В куб с ребром 3 вписан шар.
Найдите объем этого шара, деленный на .
Ответ: 4,5
B11 № 27127. Около куба с ребром описан шар. Найдите объем
этого шара, деленный на .
Ответ: 4,5
B11 № 27162. Объем одного шара в 27 раз
больше объема второго. Во сколько раз площадь поверхности первого шара больше
площади поверхности второго?
Ответ: 9
B11 № 27163. Радиусы двух шаров равны 6, 8.
Найдите радиус шара, площадь поверхности которого равна сумме площадей их
поверхностей.
Ответ: 10
B11 № 27174. Объем шара равен 288 . Найдите площадь его
поверхности, деленную на .
Ответ: 144
B11 № 27206. Вершина куба
со стороной 1,6 является центром сферы,
проходящей через точку .
Найдите площадь части
сферы, содержащейся внутри куба. В ответе запишите величину .
Ответ: 1,28
B11 № 27207. Середина ребра куба со
стороной 1,9 является центром шара радиуса 0,95. Найдите площадь части поверхности шара,
лежащей внутри куба. В ответе запишите .
Ответ: 0,9025
B11 № 245348.
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
Ответ: 22
B11 № 245349.
Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Ответ: 36

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса
равен 6. Найдите объем шара.
Ответ: 24
B11 № 245355. Куб вписан в шар радиуса . Найдите объем куба.
Ответ: 8
-
ЕГЭ по математике (база) 2023
- /
-
Задание 10
- /
- Задача 26
- /
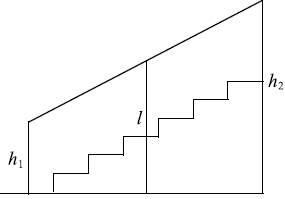
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным с…
Разбор сложных заданий в тг-канале:
Сложность:
Среднее время решения: 47 сек.
ЕГЭ по математике (база) 2023 задание 10: номер 26 | 71pac | Перила лестницы дачного дома …
25
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту $l$ этого столба, если наименьшая высота $h_1$ перил равна 40 см, а наибольшая высота $h_2$ равна 90 см. Ответ дайте в сантиметрах.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Диагональ прямоугольного экрана равна 20 см, а ширина экрана — 12 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 2:00?
Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 4:00?
Диагональ прямоугольного экрана равна 20 см, а ширина экрана — 12 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №421
|
||||
|
https://alexlarin.net/ege/2023/trvar421.html |
|||
  |
||||
|
|
||||
|
OlegTheMath |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Спасибо за интересный вариант! Подробности: надеюсь, правильно. |
|||
  |
||||
|
hpbhpb |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
OlegTheMath писал(а): Спасибо за интересный вариант! Подробности: надеюсь, правильно. Да, правильно. |
|||
  |
||||
|
Владимiръ |
Заголовок сообщения: Re: Тренировочный вариант №421
|
|||
|
Задача 18 Подробности: |
|||
  |
||||
| Показать сообщения за: Сортировать по: |