Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
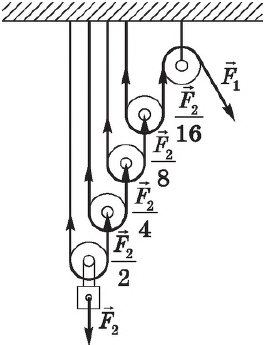
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода? (Ответ дайте в ньютонах.) Трение в осях блоков мало. Блоки и нити считайте невесомыми.
Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.
2
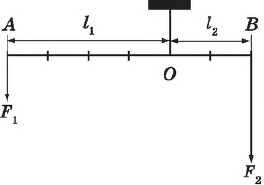
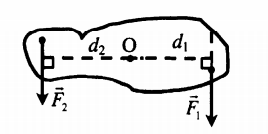
К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рис.).
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии? (Ответ дайте в килограммах.)
3
На рычаг действуют две силы. Момент первой силы относительно оси вращения рычага равен 50 Н · м. Какова величина второй силы, если её плечо относительно этой же оси равно 0,5 м и рычаг при этом находится в равновесии?
Ответ дайте в Ньютонах.
Источник: Демонстрационная версия ЕГЭ—2022 по физике
4
Под действием веса груза mg и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, а груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 240 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)
5
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.).
Чему равна масса груза, который надо подвесить ко второму делению левого плеча рычага для достижения равновесия? (Ответ дайте в килограммах.)
Пройти тестирование по этим заданиям
Равновесие механической системы (абсолютно твердого тела)
Равновесие механической системы — это состояние, при котором все точки механической системы находятся в покое по отношению к рассматриваемой системе отсчета. Если система отсчета инерциальна, равновесие называется абсолютным, если неинерциальна — относительным.
Для нахождения условий равновесия абсолютно твердого тела необходимо мысленно разбить его на большое число достаточно малых элементов, каждый из которых можно представить материальной точкой. Все эти элементы взаимодействуют между собой — эти силы взаимодействия называются внутренними. Помимо этого на ряд точек тела могут действовать внешние силы.
Согласно второму закону Ньютона, чтобы ускорение точки равнялось нулю (а ускорение покоящейся точки равно нулю), геометрическая сумма сил, действующих на эту точку, должна быть равна нулю. Если тело находится в покое, значит, все его точки (элементы) также находятся в покое. Следовательно, для любой точки тела можно записать:
${F_i}↖{→}+{F’i}↖{→}=0$,
где ${F_i}↖{→}+{F’i}↖{→}$ — геометрическая сумма всех внешних и внутренних сил, действующих на $i$-й элемент тела.
Уравнение означает, что для равновесия тела необходимо и достаточно, чтобы геометрическая сумма всех сил, действующих на любой элемент этого тела, была равна нулю.
Из уравнения легко получить первое условие равновесия тела (системы тел). Для этого достаточно просуммировать уравнение по всем элементам тела:
$∑{F_i}↖{→}+∑{F’i}↖{→}=0$.
Вторая сумма равна нулю согласно третьему закону Ньютона: векторная сумма всех внутренних сил системы равна нулю, т. к. любой внутренней силе соответствует сила, равная по модулю и противоположная по направлению.
Следовательно,
$∑{F_i}↖{→}=0$
Первым условием равновесия твердого тела (системы тел) является равенство нулю геометрической суммы всех внешних сил, приложенных к телу.
Это условие является необходимым, но не достаточным. В этом легко убедиться, вспомнив о вращающем действии пары сил, геометрическая сумма которых тоже равна нулю.
Вторым условием равновесия твердого тела является равенство нулю суммы моментов всех внешних сил, действующих на тело, относительно любой оси.
Таким образом, условия равновесия твердого тела в случае произвольного числа внешних сил выглядят так:
$∑{F_i}↖{→}=0;∑M_k=0$
Простые механизмы. КПД механизмов
Простыми механизмами называются приспособления, изменяющие величину или направление приложенных к телу сил.
Они применяются для перемещения или подъема больших грузов с помощью небольших усилий. К ним относятся рычаг и его разновидности — блоки (подвижный и неподвижный), ворот, наклонная плоскость и ее разновидности — клин, винт и др.
Рычаг. Правило рычага
Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.
Правило рычага гласит:
Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:
${F_2}/{F_1}={l_1}/{l_2}$
Из формулы ${F_2}/{F_1}={l_1}/{l_2}$, применив к ней свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), можно получить такую формулу:
$F_1l_1=F_2l_2$
Но $F_1l_1=M_1$ — момент силы, стремящейся повернуть рычаг по часовой стрелке, а $F_2l_2=M_2$ — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, $M_1=M_2$, что и требовалось доказать.
Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту $147$ м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу $2.5$ тонн!
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).
Неподвижный блок
Действие неподвижного блока аналогично действию рычага с равными плечами: $l_1=l_2=r$. Приложенная сила $F_1$ равна нагрузке $F_2$, и условие равновесия имеет вид:
$F_1=F_2$
Неподвижный блок применяют, когда нужно изменить направление силы, не меняя ее величину.
Подвижный блок
Подвижный блок действует аналогично рычагу, плечи которого составляют: $l_2={l_1}/{2}=r$. При этом условие равновесия имеет вид:
$F_1={F_2}/{2}$
где $F_1$ — приложенная сила, $F_2$ — нагрузка. Применение подвижного блока дает выигрыш в силе в два раза.
Полиспаст (система блоков)
Обычный полиспаст состоит из $n$ подвижных и $n$ неподвижных блоков. Его применив дает выигрыш в силе в $2n$ раз:
$F_1={F_2}/{2n}$
Степенной полиспаст состоит из п подвижных и одного неподвижного блока. Применение степенного полиспаста дает выигрыш в силе в $2^n$ раз:
$F_1={F_2}/{2^n}$
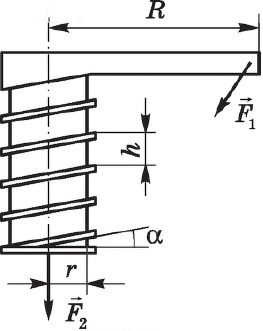
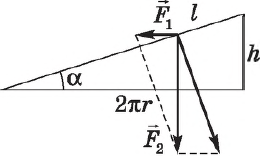
Винт
Винт представляет собой наклонную плоскость, навитую на ось.
Условие равновесия сил, действующих на винт, имеет вид:
$F_1={F_2h}/{2πr}=F_2tgα, F_1={F_2h}/{2πR}$
где $F_1$ — внешняя сила, приложенная к винту и действующая на расстоянии $R$ от его оси; $F_2$ — сила, действующая в направлении оси винта; $h$ — шаг винта; $r$ — средний радиус резьбы; $α$ — угол наклона резьбы. $R$ — длина рычага (гаечного ключа), вращающего винт с силой $F_1$.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) — отношение полезной работы ко всей затраченной работе.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой $η$ («эта»):
$η={A_п}/{A_3}·100%$
где $А_п$ — полезная работа, $А_3$ — вся затраченная работа.
Полезная работа всегда составляет лишь часть полной работы, которую затрачивает человек, используя тот или иной механизм.
Часть совершенной работы тратится на преодоление сил трения. Поскольку $А_3 > А_п$, КПД всегда меньше $1$ (или $< 100%$).
Когда КПД немного меньше $1$, можно считать, что затраченная работа примерно равна полезной: $А_3 ≈ А_п$.
Поскольку каждую из работ в этом равенстве можно выразить в виде произведения соответствующей силы на пройденный путь, то его можно переписать так: $F_1s_1≈F_2s_2$.
Отсюда следует, что, выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот. Этот закон называют золотым правилом механики.
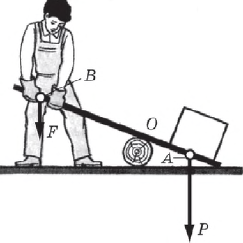
Золотое правило механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
Так, например, благодаря этому правилу сразу можно сказать, что рабочему, изображенному на рисунке, при двукратном выигрыше в силе подъема груза на $10$ см придется опустить противоположный конец рычага на $20$ см.
Статика твёрдого тела.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: момент силы, условия равновесия твёрдого тела.
Статика изучает равновесие тел под действием приложенных к ним сил. Равновесие — это состояние тела, при котором каждая его точка остаётся всё время неподвижной в некоторой инерциальной системе отсчёта.
Условием равновесия материальной точки является равенство нулю равнодействующей (т. е. векторной суммы) всех сил, приложенных к точке. В этом случае наша точка будет двигаться равномерно и прямолинейно в произвольной инерциальной системе отсчёта. Значит, система отсчёта, связанная с точкой, также будет инерциальной, и в ней точка будет покоиться.
В случае твёрдого тела ситуация сложнее. Прежде всего, важно учитывать точку приложения каждой силы.
-Сила тяжести приложена в центре тяжести тела. Для тела простой формы центр тяжести совпадает с центром симметрии.
-Силы упругости и трения приложены в точке или в плоскости контакта тела с соприкасающимся телом.
Прямая линия, проходящая через точку приложения вдоль вектора силы, называется линией действия силы. Оказывается, точку приложения силы можно переносить вдоль линии её действия — от этого механическое состояние тела не изменится (в частности, равновесие не нарушится).
Для равновесия твёрдого тела недостаточно потребовать равенства нулю векторной суммы всех приложенных к телу сил.
В качестве примера рассмотрим пару сил — так называются две равные по модулю противоположно направленные силы, линии действия которых не совпадают. Пусть пара сил и
приложена к твёрдому стержню (рис. 1).
 |
| Рис. 1. Пара сил |
Векторная сумма этих сил равна нулю. Но стержень покоиться не будет: он начнёт вращаться. В данном случае не выполнено второе условие равновесия твёрдого тела. Чтобы его сформулировать, нужно ввести понятие момента силы.
Как должна быть направлена линия действия силы, чтобы тело стало вращаться вокруг неподвижной оси? Для начала заметим следующее.
— Если линия действия силы параллельна данной оси, то вращения не будет.
— Если линия действия силы пересекает данную ось, то вращения не будет.
В каждом из этих случаев действие силы вызывает лишь деформацию твёрдого тела.
Чтобы началось вращение, линия действия силы и ось вращения должны быть скрещивающимися прямыми.
Без ограничения общности можно считать эти прямые перпендикулярными друг другу. Мы всегда можем этого добиться, разложив силу на две составляющие — параллельную и перпендикулярную оси вращения — и отбросив параллельную составляющую как не вызывающую вращения. Поэтому везде далее мы считаем, что все силы, действующие на тело, перпендикулярны оси вращения.
Момент силы.
Плечо силы — это расстояние от оси вращения до линия действия силы (т. е. длина общего перпендикуляра к двум этим прямым).
В качестве примера на рис. 2 изображён диск, к которому приложена сила . Ось вращения перпендикулярна плоскости чертежа и проходит через точку
. Плечом силы является величина
, где
— основание перпендикуляра, опущенного из точки
на линию действия
силы.
 |
| Рис. 2. Плечо силы |
Момент силы относительно оси вращения — это произведение силы на плечо:
.
Чтобы учесть также направление вращения, вызываемого действием силы, моменту силы приписывают знак. Именно, момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.
Условия равновесия.
Если тело имеет неподвижную ось вращения и если алгебраическая сумма моментов всех сил относительно этой оси обращается в нуль, то тело будет находиться в равновесии. Это так называемое правило моментов . Оказывается, что в этом случае обращается в нуль алгебраическая сумма моментов всех сил относительно любой другой оси, параллельной оси вращения.
В общем случае, когда твёрдое тело может совершать как поступательное, так и вращательное движение, мы имеем два условия равновесия.
1. Равна нулю векторная сумма всех сил, приложенных к телу.
2. Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.
Так, в примере на рис. 1 алгебраическая сумма моментов пары сил не обращается нуль (оба момента положительны). Поэтому стержень не находится в равновесии.
При решении задач удобно использовать сформулированные выше условия равновесия в следующем виде.
1′. Силы уравновешены вдоль любой оси.
2′. Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.
Сейчас мы разберём одну достаточно содержательную задачу по статике и посмотрим, как работают наши условия равновесия.
Задача. Однородная лестница опирается на гладкую вертикальную стену, образуя с ней угол . При каком максимальном значении
лестница будет покоиться? Коэффициент трения между лестницей и полом равен
.
Решение. Пусть лестница опирается о пол и стену в точках и
соответственно (рис. 3). Расставим силы, действующие на лестницу.
 |
| Рис. 3. К задаче |
Поскольку лестница однородная, сила тяжести приложена в середине лестницы. Сила упругости пола
и сила трения
приложены в точке
. На рис. 3 точка приложения этих сил немного смещена от точки
внутрь лестницы; тем самым мы однозначно указываем, что силы приложены именно к лестнице (а не к полу).
Точно так же сила упругости стены приложена в точке
. Поскольку стена гладкая, сила трения между стеной и лестницей отсутствует.
Воспользуемся условием 1′. Вдоль горизонтальной оси силы уравновешены:
. (1)
Вдоль вертикальной оси силы также уравновешены:
. (2)
Теперь переходим к правилу моментов — условию 2′. Какую ось вращения выбрать? Удобнее всего взять ось, проходящую через точку (перпендикулярно плоскости рисунка). В таком случае моменты сразу двух сил
и
обратятся в нуль — ведь плечи этих сил относительно точки
равны нулю (поскольку линии действия сил проходят через эту точку). Ненулевые моменты относительно точки
имеют силы
и
, которые стремятся вращать лестницу в разные стороны; стало быть, моменты данных сил должны быть равны друг другу.
Плечо силы — это длина перпендикуляра
, опущенного из точки
на линию
действия силы
. Плечо силы
— это длина перпендикуляра
, опущенного из точки
на линию действия силы
. Согласно правилу моментов имеем:
Пусть длина лестницы равна . Тогда
. Подставляем эти соотношения в равенство моментов:
откуда
(3)
С учётом равенства (1) имеем вместо (3):
(4)
Вспомним теперь, что в условии спрашивается максимальное значение . При максимальном угле
лестница пока ещё стоит, но уже находится на грани проскальзывания. Это означает, что сила трения
достигла своего максимального значения, равного силе трения скольжения:
.
Теперь из (4) получаем:
,
а с учётом равенства (2):
.
Отсюда получаем искомую максимальную величину :
.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Статика твёрдого тела.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Статика — раздел механики, изучающий условия равновесия тел.
Виды равновесия
Устойчивое равновесие |
|
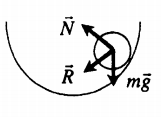 |
Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min). |
Неустойчивое равновесие |
|
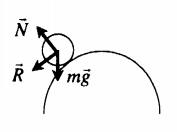 |
Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max). |
Безразличное равновесие |
|
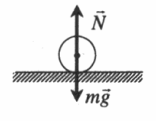 |
При выведении тела из положения безразличного равновесия дополнительных сил не возникает. |
Момент силы
Определение
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M = Fd
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
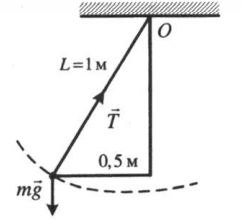
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)
Момент силы может быть положительным и отрицательным.
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
M1 = F1d1
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
M2 = F2d2
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
∑Mi=0
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑Mпо час. стр.=∑Mпр. час. стр.
Условия равновесия тел
| Тело не участвует в поступательном движении: |
∑→Fi=0; →vo=0 |
| Тело не участвует во вращательном движении: |
∑Mi=0; ω0=0 |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) |
∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0 |
Простые механизмы
Определение
Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
Наклонная плоскость |
|
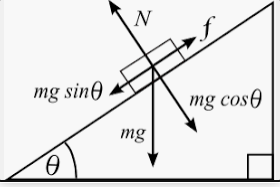 |
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg |
Рычаг |
|
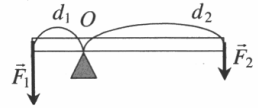 |
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1 |
Неподвижный блок |
|
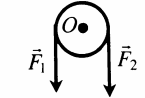 |
Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2 |
Подвижный блок |
|
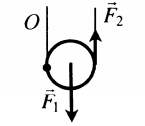 |
Дает выигрыш в силе в 2 раза:
d1 = R d2 = 2R F1 = 2F2 |
Клин |
|
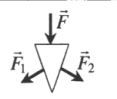 |
Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2 |
Золотое правило механики
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
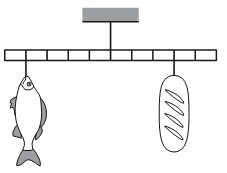
Задание EF22660
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов и выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2=0,8·0,30,4=0,6 (кг)
Ответ: 0,6
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18706
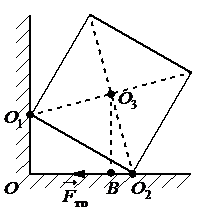
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Решение
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 8.9k
Статика. Правило моментов
В задачах, связанных с равновесием тел, нужно, как правило, найти две силы (или больше) которые стремятся это тело повернуть по и против часовой стрелки. Если моменты этих сил равны, тело будет находиться в равновесии. А чтобы рассчитать момент, нужно также правильно определить плечо силы: это расстояние от оси вращения до линии действия силы.
Задача 1. К концу стержня длиной 2 м, укрепленного шарнирно одним концом к стене, а с другого конца поддерживаемого тросом
длиной 2,5 м, подвешен груз массой 120 кг. Найдите силы, действующие на трос и стержень.
К задаче 1
Введем оси координат и напишем по каждой из осей уравнение по второму закону Ньютона. Удобно выбрать такое расположение координатных осей, как показано на рисунке. Тогда по оси :
Здесь угол .
По оси :
Из первого уравнения можем найти силу натяжения троса:
Тогда
Где
Подставим:
Теперь подставим численные данные:
Также нужно определить силу :
Ответ: Н,
Н
Задача 2.
Тяжелый однородный шар подвешен на нити, конец которой закреплен на вертикальной стене. Точка прикрепления шара к нити находится на одной вертикали с центром шара. Каков должен быть коэффициент трения между шаром и стенкой, чтобы шар находился в равновесии?
К задаче 2
Понятно, что из положения 1, как показано на рисунке, шар стремится повернуться в положение 2 — повернуться относительно своего центра масс. Не дает этого сделать сила трения, направленная вверх вдоль стенки. Введем систему координат и распишем уравнения по второму закону по координатным осям, а кроме того, добавим уравнение равновесия моментов. Ось направим вверх, а ось
— вправо. Тогда по горизонтальной оси:
По вертикальной оси:
Правило моментов ( — плечо обеих сил относительно центра масс шара):
Чтобы шар не проворачивался, нужно, чтобы сила трения была больше чем , тогда
Или
Ответ: .
Задача 3.
Какую силу надо приложить к рукоятке молотка, чтобы вырвать гвоздь, если сила сопротивления гвоздя 160 Н? Длина рукоятки 32 см. Расстояние от конца молотка до гвоздя 8 см.
К задаче 3. Вырываем гвоздь
Сила сопротивления гвоздя направлена внутрь дерева, в которое он вбит. То есть по отношению к точке упора молотка пытается этот молоток вращать против часовой стрелке. Сила, с которой мы давим на рукоять, наоборот, вращает рукоять по часовой стрелке. Тогда составим правило моментов относительно точки упора:
Ответ: 40 Н
Задача 4.
Между двумя одинаковыми ящиками, стоящими на полу, вставлена палка, немного не доходящая до пола. К верхнему концу палки приложена горизонтальная сила. Какой из ящиков сдвинется быстрее? Рассмотреть два случая: трение между ящиком и полом отсутствует; трение между ящиками и полом есть.
К задаче 4. Исходное положение палки
Первый случай: трения нет. Тогда, как только мы начнем воздействовать на ящики с силой любой величины, они сразу сдвинутся с места, одновременно, потому что нет никакого противодействия этой силе.
Второй случай: трение есть. Тогда сила трения одинакова для обоих ящиков, ведь по условию они идентичны. Следовательно, сдвинется быстрее тот ящик, для которого мы эту силу трения преодолеем быстрее, то есть тот, на который палка давит с большей силой.
К задаче 4. Плечи сил, действующих на ящики
Палка упрется в правый ящик, точкой опоры для нее будет его верхний левый угол, значит, плечо силы будет равно
, как показано на рисунке. В левый ящик палка упрется своим нижним концом, следовательно, плечом будет расстояние
. Тогда
Так как , то
— быстрее сдвинется правый ящик.
«Рычаг. Равновесие рычага.
Момент силы. Правило моментов»
Рычагом называют твердое тело, которое может вращаться вокруг неподвижной точки. Неподвижную точку называют точкой опоры. Расстояние от точки опоры до линии действия силы называют плечом этой силы.
Условие равновесия рычага: рычаг находится в равновесии, если приложенные к рычагу силы F1 и F2 стремятся вращать его в противоположных направлениях, причем модули сил обратно пропорциональны плечам этих сил: F1/F2 = l2/l1 Это правило было установлено Архимедом. По легенде он воскликнул: Дайте мне точку опоры и я подниму Землю.
Для рычага выполняется «золотое правило» механики (если можно пренебречь трением и массой рычага).
Прикладывая к длинному рычагу некоторую силу, можно другим концом рычага поднимать груз, вес которого намного превышает эту силу. Это означает, что, используя рычаг, можно получить выигрыш в силе. При использовании рычага выигрыш в силе обязательно сопровождается таким же проигрышем в пути.
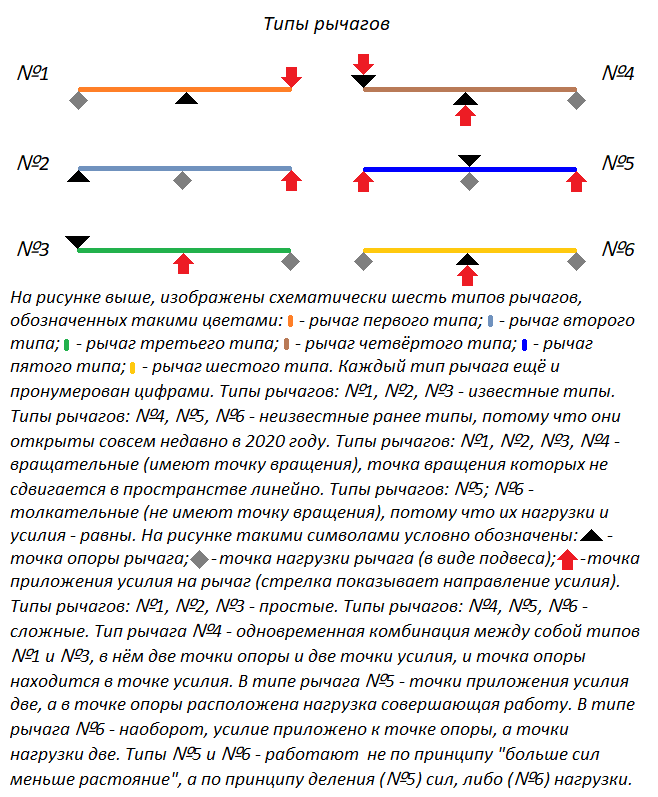
Все типы рычагов:
Момент силы. Правило моментов
Произведение модуля силы на ее плечо называют моментом силы. M = Fl, где М — момент силы, F — сила, l — плечо силы.
Правило моментов: рычаг находится в равновесии, если сумма моментов сил, стремящихся вращать рычаг в одном направлении, равна сумме моментов сил, стремящихся вращать его в противоположном направлении. Это правило справедливо для любого твердого тела, способного вращаться вокруг закрепленной оси.
Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от ее плеча. Именно поэтому, например, желая открыть дверь, стараются приложить силу как можно дальше от оси вращения. С помощью небольшой силы при этом создают значительный момент, и дверь открывается. Открыть ее, оказывая давление около петель, значительно труднее. По той же причине гайку легче отворачивать более длинным гаечным ключом, шуруп легче вывернуть с помощью отвертки с более широкой ручкой и т. д.
Единицей момента силы в СИ является ньютон-метр (1 Н*м). Это момент силы 1 Н, имеющей плечо 1 м.
Конспект урока «Рычаги. Равновесие рычага. Момент силы».
Следующая тема: «Механическая энергия. Закон сохранения энергии».
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Момент силы
Мы уже изучили правило рычага, которое гласит: F1/F2 = l2/l1. Используя свойство пропорции (произведение крайних членов пропорции равно произведению её средних членов), можно сформулировать это правило так:
F1l1 = F2l2.
В левой части равенства у нас оказывается произведение силы F1 на её плечо l1, а в правой, соответственно, произведение силы F2 на её плечо l2. Из частей равенства мы можем вывести формулу момента силы – произведения модуля силы, которая вращает тело, на её плечо:
M = Fl.
Если момент силы вращения рычага по часовой стрелке равен моменту силы вращения против часовой стрелки, то можно считать, что рычаг находится в равновесии под действием этих двух сил. Это правило называется правилом моментов и записывается в виде формулы так:
М1 = М2.
Момент силы можно измерить. Единица момента силы называется ньютон-метр (Н × м) и рассчитывается из момента силы, равного 1 Н, с плечом 1 метр. Момент силы выступает характеристикой действия силы и демонстрирует, что оно находится в зависимости от модуля силы и её плеча одновременно. В жизни этому существует множество примеров. Так, намного проще открутить гайку, вооружившись более длинным ключом, а ведро легче вытащить из колодца, если у него длинная ручка ворота.
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.