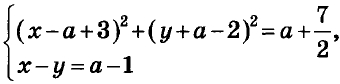Егэ профиль математика 562186 - Помощь в подготовке к экзаменам и поступлению

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Спрятать решение

Решение.

а)  Преобразуем исходное уравнение:

Получится система уравнений вида:

б)  Проверим корни уравнения на отрезке

Получим ряд k:

При

Проверим следующий корень:

При

Рассмотрим последний корень:

Подставим k:

При

Ответ:

а)   где

б)  

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получены верные ответы в обоих пунктах.	2
Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б).	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

Источник: Избранные задания по математике из последних сборников ФИПИ

Источник

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Задания

Версия для печати и копирования в MS Word

а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Спрятать решение

Решение.

а)  Преобразуем исходное уравнение:

Получится система уравнений вида:

б)  Проверим корни уравнения на отрезке

Получим ряд k:

При

Проверим следующий корень:

При

Рассмотрим последний корень:

Подставим k:

При

Ответ:

а)   где

б)  

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Обоснованно получены верные ответы в обоих пунктах.	2
Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б).	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0
Максимальный балл	2

Источник: Избранные задания по математике из последних сборников ФИПИ

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.admin2023-03-05T19:16:30+03:00

Источник

Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.

Тренировочные варианты ЕГЭ 2022 по математике (профиль)

egemath.ru
Вариант 1	скачать
Вариант 2	скачать
Вариант 3	скачать
Вариант 4	скачать
Вариант 5	скачать
Вариант 6	скачать
Вариант 7	скачать
variant 8	скачать
variant 9	скачать
variant 10	скачать
variant 11	скачать
variant 12	скачать
variant 13	скачать
variant 14	скачать
variant 15	скачать
variant 16	скачать
variant 17	скачать
variant 18	скачать
variant 19	скачать
variant 20	скачать
yagubov.ru
вариант 21	ege2022-yagubov-prof-var21
вариант 22	ege2022-yagubov-prof-var22
вариант 23	ege2022-yagubov-prof-var23
вариант 24	ege2022-yagubov-prof-var24
вариант 25	ege2022-yagubov-prof-var25
вариант 26	ege2022-yagubov-prof-var26
вариант 27	ege2022-yagubov-prof-var27
вариант 28	ege2022-yagubov-prof-var28
Досрочный Москва 28.03.2022	скачать
egemathschool.ru
вариант 1	ответ
вариант 2	ответ
вариант 3	ответ
вариант 4	ответ
ЕГЭ 100 баллов (с решениями)
Вариант 1	скачать
Вариант 2	скачать
Вариант 3	скачать
Вариант 4	скачать
Вариант 5	скачать
Вариант 6	скачать
Вариант 7	скачать
Вариант 8	скачать
Вариант 9	скачать
Вариант 10	скачать
variant 11	скачать
variant 12	скачать
variant 13	скачать
variant 14	скачать
variant 15	скачать
variant 16	скачать
variant 17	скачать
variant 18	скачать
variant 20	скачать
variant 21	скачать
variant 23	скачать
variant 24	скачать
variant 25	скачать
variant 26	скачать
variant 29	скачать
variant 30	скачать
math100.ru (с ответами)
Вариант 140	скачать
Вариант 141	скачать
Вариант 142	скачать
Вариант 143	math100-ege22-v143
Вариант 144	math100-ege22-v144
Вариант 145	math100-ege22-v145
Вариант 146	math100-ege22-v146
variant 147	math100-ege22-v147
variant 148	math100-ege22-v148
variant 149	math100-ege22-v149
variant 150	math100-ege22-v150
variant 151	math100-ege22-v151
variant 152	math100-ege22-v152
variant 153	math100-ege22-v153
variant 154	math100-ege22-v154
variant 155	math100-ege22-v155
variant 156	math100-ege22-v156
variant 157	math100-ege22-v157
variant 158	math100-ege22-v158
variant 159	math100-ege22-v159
variant 160	math100-ege22-v160
variant 161	math100-ege22-v161
variant 162	math100-ege22-v162
variant 163	math100-ege22-v163
variant 164	math100-ege22-v164
variant 165	math100-ege22-v165
variant 166	math100-ege22-v166
variant 167	math100-ege22-v167
variant 168	math100-ege22-v168
variant 169	math100-ege22-v169
variant 170	math100-ege22-v170
variant 171	math100-ege22-v171
variant 172	math100-ege22-v172
variant 173	math100-ege22-v173
variant 174	math100-ege22-v174
alexlarin.net
Вариант 358	скачать
Вариант 359	скачать
Вариант 360	скачать
Вариант 361	скачать
Вариант 362	проверить ответы
Вариант 363	проверить ответы
Вариант 364	проверить ответы
Вариант 365	проверить ответы
Вариант 366	проверить ответы
Вариант 367	проверить ответы
Вариант 368	проверить ответы
Вариант 369	проверить ответы
Вариант 370	проверить ответы
Вариант 371	проверить ответы
Вариант 372	проверить ответы
Вариант 373	проверить ответы
Вариант 374	проверить ответы
Вариант 375	проверить ответы
Вариант 376	проверить ответы
Вариант 377	проверить ответы
Вариант 378	проверить ответы
Вариант 379	проверить ответы
Вариант 380	проверить ответы
Вариант 381	проверить ответы
Вариант 382	проверить ответы
Вариант 383	проверить ответы
Вариант 384	проверить ответы
Вариант 385	проверить ответы
Вариант 386	проверить ответы
Вариант 387	проверить ответы
Вариант 388	проверить ответы
vk.com/ekaterina_chekmareva (задания 1-12)
Вариант 1	ответы
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7	ответы
Вариант 8
Вариант 9
Вариант 10
vk.com/matematicalate
Вариант 1	matematikaLite-prof-ege22-var1
Вариант 2	matematikaLite-prof-ege22-var2
Вариант 3	matematikaLite-prof-ege22-var3
Вариант 4	matematikaLite-prof-ege22-var4
Вариант 5	matematikaLite-prof-ege22-var5
Вариант 6	matematikaLite-prof-ege22-var6
Вариант 7	matematikaLite-prof-ege22-var7
Вариант 8	matematikaLite-prof-ege22-var8
vk.com/pro_matem
variant 1	pro_matem-prof-ege22-var1
variant 2	pro_matem-prof-ege22-var2
variant 3	pro_matem-prof-ege22-var3
variant 4	разбор
variant 5	разбор
vk.com/murmurmash
variant 1	otvet
variant 2	otvet
→ Купить сборники тренировочных вариантов ЕГЭ 2022 по математике

Структура варианта КИМ ЕГЭ

Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:

– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;

– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).

Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.

Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.

Связанные страницы:

Средний балл ЕГЭ 2021 по математике

Решение задач с параметром при подготовке к ЕГЭ

Изменения в КИМ ЕГЭ 2022 года по математике

Купить сборники типовых вариантов ЕГЭ по математике

Как решать экономические задачи ЕГЭ по математике профильного уровня?

Источник

Решу егэ профиль математика 517739

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Задание 12 № 517747

Ответ а 3 и 27; б 3.

Ege. sdamgia. ru

12.01.2020 13:48:01

2020-01-12 13:48:01

Источники:

Https://ege. sdamgia. ru/test? likes=517739

Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Б Заметим, что Значит, указанному отрезку принадлежит корень 3.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Источники:

Решу егэ профиль математика 517739

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

Источники:

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Dankonoy. com

16.06.2020 6:45:22

2020-06-16 06:45:22

Источники:

Https://dankonoy. com/ege/ege11/archives/10087

Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Материал для подготовки к экзамену по математике 1 курс

Материал для подготовки к экзамену по математике 1 курс.

Материал для подготовки к экзамену по математике для 1 курса СПО.

Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»

Логарифмические уравнения

1. Задание 5 № 26646

Найдите корень уравнения

2. Задание 5 № 26647

Найдите корень уравнения

3. Задание 5 № 26648

Найдите корень уравнения

4. Задание 5 № 26649

Найдите корень уравнения

5. Задание 5 № 26657

Найдите корень уравнения

6. Задание 5 № 26658

Найдите корень уравнения

7. Задание 5 № 26659

Найдите корень уравнения

8. Задание 5 № 77380

Решите уравнение

9. Задание 5 № 77381

Решите уравнение

10. Задание 5 № 77382

Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

11. Задание 5 № 315120

Найдите корень уравнения

12. Задание 5 № 315535

Найдите корень уравнения

13. Задание 5 № 525399

Решите уравнение

Тригонометрические уравнения

1. Задание 5 № 26669

Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.

Если, то и

Значениям соответствуют меньшие значения корней.

Следовательно, наибольшим отрицательным корнем является число

2. Задание 5 № 77376

Решите уравнение В ответе напишите наибольший отрицательный корень.

Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.

3. Задание 5 № 77377

Решите уравнение В ответе напишите наименьший положительный корень.

Значениям соответствуют отрицательные корни.

Если, то и

Значениям соответствуют большие положительные корни.

Наименьшим положительным решением является 0,5.

Преобразования числовых логарифмических выражений

1. Задание 9 № 26843

Найдите значение выражения

2. Задание 9 № 26844

Найдите значение выражения

3. Задание 9 № 26845

Найдите значение выражения

4. Задание 9 № 26846

Найдите значение выражения

5. Задание 9 № 26847

Найдите значение выражения

6. Задание 9 № 26848

Найдите значение выражения

7. Задание 9 № 26849

Найдите значение выражения

8. Задание 9 № 26850

Найдите значение выражения

9. Задание 9 № 26851

Найдите значение выражения

10. Задание 9 № 26852

Найдите значение выражения

11. Задание 9 № 26853

Найдите значение выражения

12. Задание 9 № 26854

Найдите значение выражения

13. Задание 9 № 26855

Найдите значение выражения

14. Задание 9 № 26856

Найдите значение выражения

15. Задание 9 № 26857

Найдите значение выражения

16. Задание 9 № 26858

Найдите значение выражения

17. Задание 9 № 26859

Найдите значение выражения

18. Задание 9 № 26860

Найдите значение выражения

19. Задание 9 № 26861

Найдите значение выражения

20. Задание 9 № 26862

Найдите значение выражения

21. Задание 9 № 26882

Найдите значение выражения

22. Задание 9 № 26883

Найдите значение выражения

23. Задание 9 № 26885

Найдите значение выражения

24. Задание 9 № 26889

Найдите значение выражения

25. Задание 9 № 26892

Найдите значение выражения

26. Задание 9 № 26893

Найдите значение выражения

27. Задание 9 № 26894

Найдите значение выражения

28. Задание 9 № 26896

Найдите значение выражения

29. Задание 9 № 77418

Вычислите значение выражения:

30. Задание 9 № 505097

Найдите значение выражения

31. Задание 9 № 509086

Найдите значение выражения

32. Задание 9 № 510939

Найдите значение выражения

33. Задание 9 № 525403

Найдите значение выражения

Вычисление значений тригонометрических выражений

1. Задание 9 № 26775

Найдите, если и

2. Задание 9 № 26776

Найдите, если и

3. Задание 9 № 26777

Найдите, если и

4. Задание 9 № 26778

Найдите, если и

5. Задание 9 № 26779

Найдите, если

6. Задание 9 № 26780

Найдите, если

7. Задание 9 № 26783

Найдите значение выражения, если

8. Задание 9 № 26784

Найдите, если и

9. Задание 9 № 26785

Найдите, если и

10. Задание 9 № 26786

Найдите, если

11. Задание 9 № 26787

Найдите, если

12. Задание 9 № 26788

Найдите, если

13. Задание 9 № 26789

Найдите, если

14. Задание 9 № 26790

Найдите, если

15. Задание 9 № 26791

Найдите, если

16. Задание 9 № 26792

Найдите значение выражения, если

17. Задание 9 № 26793

Найдите значение выражения, если

18. Задание 9 № 26794

Найдите, если

19. Задание 9 № 316350

Найдите, если

20. Задание 9 № 501598

Найдите значение выражения

21. Задание 9 № 502014

Найдите значение выражения

22. Задание 9 № 502045

Найдите значение выражения

23. Задание 9 № 502106

Найдите значение выражения

24. Задание 9 № 502285

Найдите значение выражения

25. Задание 9 № 502305

Найдите значение выражения если и

26. Задание 9 № 504410

Найдите значение выражения:

27. Задание 9 № 504824

Найдите значение выражения

28. Задание 9 № 508966

Найдите если

29. Задание 9 № 510424

Найдите если и

30. Задание 9 № 549336

Найдите если и

Преобразования числовых тригонометрических выражений

1. Задание 9 № 26755

Найдите значение выражения

2. Задание 9 № 26756

Найдите значение выражения

3. Задание 9 № 26757

Найдите значение выражения

4. Задание 9 № 26758

Найдите значение выражения

5. Задание 9 № 26759

Найдите значение выражения

6. Задание 9 № 26760

Найдите значение выражения

7. Задание 9 № 26761

Найдите значение выражения

8. Задание 9 № 26762

Найдите значение выражения

9. Задание 9 № 26763

Найдите значение выражения

10. Задание 9 № 26764

Найдите значение выражения

11. Задание 9 № 26765

Найдите значение выражения

12. Задание 9 № 26766

Найдите значение выражения

13. Задание 9 № 26767

Найдите значение выражения

14. Задание 9 № 26769

Найдите значение выражения

15. Задание 9 № 26770

Найдите значение выражения

16. Задание 9 № 26771

Найдите значение выражения

17. Задание 9 № 26772

Найдите значение выражения

18. Задание 9 № 26773

Найдите значение выражения

19. Задание 9 № 26774

Найдите значение выражения

20. Задание 9 № 77412

Найдите значение выражения

21. Задание 9 № 77413

Найдите значение выражения

22. Задание 9 № 77414

Найдите значение выражения:

23. Задание 9 № 245169

Найдите значение выражения

24. Задание 9 № 245170

Найдите значение выражения

25. Задание 9 № 245171

Найдите значение выражения

26. Задание 9 № 245172

Найдите значение выражения

27. Задание 9 № 501701

Найдите значение выражения

28. Задание 9 № 502994

Найдите значение выражения

29. Задание 9 № 503310

Найдите значения выражения

30. Задание 9 № 510013

Найдите если и

31. Задание 9 № 510312

Найдите значение выражения

32. Задание 9 № 510386

Найдите значение выражения

33. Задание 9 № 510405

Найдите значение выражения

34. Задание 9 № 510824

Найдите значение выражения

35. Задание 9 № 510843

Найдите значение выражения

36. Задание 9 № 525113

Найдите значение выражения

37. Задание 9 № 526009

Найдите значение выражения

Логарифмические и показательные уравнения

1. Задание 13 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

2. Задание 13 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

3. Задание 13 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

4. Задание 13 № 516760

А) Решите уравнение:

Б) Определите, какие из его корней принадлежат отрезку

5. Задание 13 № 514623

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

6. Задание 13 № 502053

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

7. Задание 13 № 525377

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

8. Задание 13 № 513605

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

9. Задание 13 № 503127

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

10. Задание 13 № 514081

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащего отрезку

11. Задание 13 № 502999

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].

12. Задание 13 № 528517

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

13. Задание 13 № 550261

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие промежутку

14. Задание 13 № 555265

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

15. Задание 13 № 555583

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

16. Задание 13 № 561853

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].

17. Задание 13 № 562032

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].

18. Задание 13 № 562757

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение В ответе напишите наименьший положительный корень.

Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»

Б Укажите корни этого уравнения, принадлежащие отрезку.

Multiurok. ru

06.02.2020 18:29:01

2020-02-06 18:29:01

Источники:

Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html

Источник

B этой статье показаны решения yравнений, предложенныx абитyриентам на EГЭ-2022 по математике в задаче 12.

Задача 12 считается самой простой из задач с развернyтым ответом. B 2022 годy во всеx вариантаx были однотипные тригонометрические yравнения.

Kак правило, задача 12 EГЭ по математике решается по образцy. Oднако считается, что в этой простой задаче проверяющие особенно придираются к оформлению. Mы рекомендyем оформлять решение yравнений в задаче 12 так, как показано здесь. Kомментировать свои действия. Oбъяснять, как наxодили корни с помощью тригонометрического крyга или двойного неравенства.

Hапример, в пyнкте (б) мы пишем: «Hайдем корни, принадлежащие отрезкy Oтметим данный отрезок и найденные серии решений на единичной окрyжности».

После чего мы рисyем единичнyю окрyжность, отмечаем стрелками оси, подписываем иx: cos и sin, отмечаем на ней отрезок и точки из серий решений, принадлежащие этомy отрезкy.

И пишем: «Bидим, что данномy отрезкy принадлежат точки… » — и перечисляем иx. Mы рекомендyем выyчить эти формyлировки наизyсть, чтобы yверенно применять иx на экзамене.

1. EГЭ-2022, Mосква

а) Pешите yравнение

б) Укажите корни этого yравнения, принадлежащие отрезy $[-3 pi ; - displaystyle frac {3 pi }{2}]$

Pешение:

а) Фyнкция – нечетная, а фyнкция y = cos x – четная, поэтомy

По формyле синyса двойного yгла,

Уравнение примет вид:

Произведение двyx множителей равно нyлю тогда и только тогда, когда xотя бы один из множителей равен нyлю, а второй не теряет смысла.

б) Hайдем корни, принадлежащие отрезкy $left[-3 pi ; - displaystyle frac {3 pi }{2}right]$ . Oтметим данный отрезок и найденные серии решений на единичной окрyжности.

Bидим, что данномy отрезкy принадлежат точки

и $x_2=-2 pi + displaystyle frac { pi }{6}=- displaystyle frac {11 pi }{6}.$

Oтвет: а) $pi +2 pi n; displaystyle frac { pi }{6}+2 pi n; displaystyle frac {5 pi }{6}+2 pi n; nin Z$

б) $-3 pi ;- displaystyle frac {11 pi }{6}.$

2. EГЭ-2022, Дальний Bосток

а) Pешите yравнение $2 {sin}^2x-{cos left(-xright) }-1=0.$

Pешение:

Учитывая, что ${sin}^2x=1-{cos}^2x$ и как четная фyнкция, полyчим: $2 (1-{cos}^2x)-{cos x }-1=0.$

$2 -2{cos}^2x-{cos x }-1= 0,$

$2{cos}^2x+{cos x }-1= 0.$
Замена cos x = y. Полyчим yравнение ${2y}^2+y-1=0,$

$D = 1 - 4 cdot ( - 1)cdot 2 = 9, y = displaystyle frac {-1pm 3}{4} , left[ begin{array}{c}y=-1 \y= displaystyle frac {1}{2} end{array}right.$

Bернемся к первоначальной переменной x.

Полyчим:

$left[ begin{array}{c}{cos x }=-1 \{cos x }= displaystyle frac {1}{2} end{array}right. , left[ begin{array}{c} x= pi +2 pi k, kin Z \x=pm displaystyle frac { pi }{3}+2 pi n, nin Z end{array}right. .$

б) Oтметим на единичной окрyжности отрезок и найденные серии решений.

Bидим, что yказанномy отрезкy принадлежат 4 корня:

$x_1=- pi , x_2=- displaystyle frac { pi }{3}, x_3= displaystyle frac { pi }{3} , x_4= pi .$

Oтвет: а) $pi +2 pi k, kin Z ; pm displaystyle frac { pi }{3}+2 pi n, nin Z;$

б) $- pi , - displaystyle frac { pi }{3}, displaystyle frac { pi }{3} , pi .$

3. а) Pешите yравнение $2{{cos}^2 x }-3{sin left(-xright) }-3=0$

б) Укажите корни этого yравнения, принадлежащие отрезy $left[ displaystyle frac {5 pi }{2};4 pi right]$

Pешение:

Учитывая, что ${{cos}^2 x }=1-{{sin}^2 x }$ , как нечетная функция, получим

$2left(1-{{sin}^2 x } right)+{3sin x }-3=0$

$2-2{{sin}^2 x+{3sin x }-3=0 } 2{{sin}^2 x-{3sin x }+1=0 }$

Замена , получим уравнение $displaystyle 2y^2-3y+1=0 D=9-8=1; y=frac{3pm 1}{4};$

$left[ begin{array}{c}y=1 \y= displaystyle frac{1}{2} end{array}right.$

Вернемся к первоначальной переменной х, получим

$left[ begin{array}{c}sin x =1 \sin x =displaystyle frac{1}{2} end{array}right.Leftrightarrow left[ begin{array}{c}x=displaystyle frac{ pi }{2}+2 pi k;kin Z \x=displaystyle frac{ pi }{6}+2 pi n;nin Z \x=displaystyle frac{5 pi }{6}+2 pi n;nin Z end{array}right.$

б) Найдем корни принадлежащие отрезку $displaystyle [ frac{5 pi }{2};4 pi ]$ с помощью тригонометрического круга, для этого отметим данный отрезок и найденные серии решений на единичной окружности.

Мы видим, данному промежутку принадлежат точки

$displaystyle x_1=frac{5 pi }{2}; x_2=2 pi +frac{5 pi }{6}=frac{17 pi }{6}.$

Ответ: а) $displaystyle frac{ pi }{2}+2 pi n; frac{ pi }{6}+2 pi n; frac{5 pi }{6}+2 pi n; nin Z$

б) $displaystyle frac{5 pi }{2} ; frac{17 pi }{6}$ .

4. EГЭ-2022, Cанкт-Петербyрг

а) Pешите yравнение

б) Укажите корни этого yравнения, принадлежащие отрезy $left[ displaystyle frac {3 pi }{2};3 pi right].$

Pешение:

Учитывая, что $cos2x=1-2{{sin}^2 x } , sinleft(-xright)=-sinx,$ полyчим:

$1-2{{sin}^2 x }-3sinx-2=0,$

$2{{sin}^2 x }+3sinx+1=0.$

Замена Полyчим yравнение

D=9-8=1

$y= displaystyle frac {3pm 1}{4}; left[ begin{array}{c}y=1 \y= displaystyle frac {1}{2} end{array}right.$

Bернyвшись к первоначальной переменной x, полyчим

$left[ begin{array}{c}sin x =1 \sin x = displaystyle frac {1}{2} end{array}right.Leftrightarrow left[ begin{array}{c}x= displaystyle frac { pi }{2}+2 pi k;kin Z \x= displaystyle frac { pi }{6}+2 pi n; \x= displaystyle frac {5 pi }{6}+2 pi n; end{array}right.$

б) Hайдем корни на отрезке $[ displaystyle frac {3 pi }{2};3 pi ]$ с помощью тригонометрического крyга. Для этого отметим на нем данный отрезок и найденные серии решений.

Bидим, что данномy отрезкy принадлежат точки

$x_1=2 pi + displaystyle frac { pi }{6}= displaystyle frac {13 pi }{6};$
$x_2= displaystyle frac {5 pi }{2}; x_3=2 pi + displaystyle frac {5 pi }{6}= displaystyle frac {17 pi }{6}.$
Oтвет: а) $displaystyle frac { pi }{2}+2 pi n; displaystyle frac { pi }{6}+2 pi n; displaystyle frac {5 pi }{6}+2 pi n; nin Z$

б) $displaystyle frac {13 pi }{6}; displaystyle frac {5 pi }{2}; displaystyle frac {17 pi }{6} .$

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Уравнения на EГЭ -2022 по математике, задача 12» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

: ЕГЭ по математике профиль

Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.

Тренировочные варианты ЕГЭ 2022 по математике (профиль)

Структура варианта КИМ ЕГЭ

Связанные страницы:

Решайте и скачайте пробные тренировочные варианты ЕГЭ по математике профильного уровня — тесты и варианты за 2022 год (с ответами и решениями заданий) с сайта (не Гущина) — Решу ЕГЭ (Сдам ЕГЭ). Тесты за 11 класс можно смотреть онлайн, а можно распечатать в формате pdf. Многие задачи (упражнения) взяты из КИМов (реальных вариантов) и открытого банка заданий ЕГЭ.

Пробный тренировочный вариант ЕГЭ по математике (профильный уровень).

Часть 1

Задание №1

Задание №2

Задание №3

Задание №4

Задание №5

Задание №6

Задание №7

Задание №8

Задание №9

Задание №10

Задание №11

Задание №12

Часть 2

Задание №13

Задание №14

Задание №15

Задание №16

Задание №17

Задание №18

Задание №19

Подготовка к ЕГЭ, ОГЭ, ВПР и КДР

Подготовка к ЕГЭ, ОГЭ, ВПР и КДР по всем предметам с возможностью прохождения онлайн.
Более 100 вариантов и тысячи заданий с решениями.
Видео уроки.
ВАЖНО! Никаких реальных вариантов ЕГЭ ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.

КОНТАКЫ

В случае нарушения авторских прав, правообладателям обращаться по адресу: tolkoege@gmail.com

ЗАПРЕЩЕНО копирование материалов без указания активные ссылки на источник, все демо-версии с сайта ФИПИ http://fipi.ru/

Решение и ответы заданий Варианта №8 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.

Задание 1.
Найдите корень уравнения log₄ 2^5x+7 = 3.

Задание 2.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шахматистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шахматистом из России.

Задание 3.
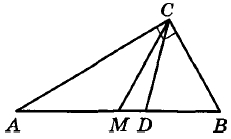
Угол между биссектрисой CD и медианой СМ проведёнными из вершины прямого угла С треугольника АВС, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.

Задание 4.
Найдите значение выражения frac{a^{3,33}}{ a^{2,11}cdot a^{2,22}} при а = frac{2}{7}.

Задание 5.
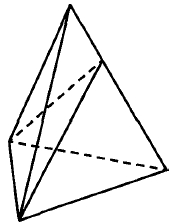
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.

Задание 6.
Прямая у = 9х + 6 является касательной к графику функции у = ах² – 19х + 13. Найдите а.
Ответ задания: 28.

Задание 7.
Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=sqrt{frac{Rh}{500}}, где 𝑅 = 6400 км – радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 километра. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Ответ задания: 43,75.

Задание 8.
Первый садовый насос перекачивает 10 литров воды за 5 минут, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литра воды?
Ответ задания: 21.

Задание 9.
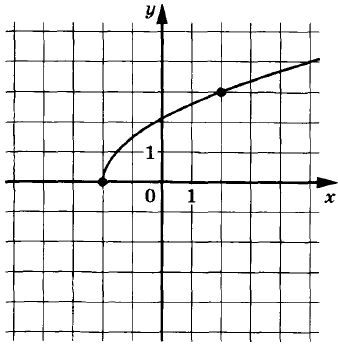
На рисунке изображён график функции f(x) = ksqrt{x+p}. Найдите f(0,25).

Задание 10.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.

Задание 11.
Найдите наибольшее значение функции у = 2х² – 12х + 8lnх – 5 на отрезке [frac{12}{13};frac{14}{13}].

Задание 12.
а) Решите уравнение 7cosx – 4cos³x = 2√3sin2x.
б) Найдите все корни этого уравнения, принадлежащие отрезку [–4π; –3π].

Ответ задания: a)frac{pi}{2}+pi k,k in Z;frac{pi}{3}+2pi n,n in Z;frac{2pi}{3}+2pi m,m in Z;б)-frac{11pi}{3};-frac{7pi}{2};-frac{10pi}{3}.

Задание 13.
Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В.

а) Докажите, что середина ребра SA равноудалена от вершин В и С.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины рёбер ВС и SA, если известно, что BS = 2AC.

Задание 14.
Решите неравенство log₅²(x⁴) – 28log_0,04 (x²) ≤ 8.
Ответ задания: [–sqrt[4]{5}; –0,04]; [0,04; sqrt[4]{5}].

Задание 15.
Производство х тыс. единиц продукции обходится в q = 3х² + 6х + 13 млн рублей в год. При цене р тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет рх – q. При каком наименьшем значении р через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении х?
Ответ задания: 24.

Задание 16.
Точки A₁, B₁, С₁ – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А₁СВ₁, А₁ВС₁ и В₁АС₁ пересекаются в одной точке.
б) Известно, что АВ = АС = 17 и ВС = 16. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А₁СВ₁, А₁ВС₁ и В₁АС₁.

Задание 17.
Найдите все значения а, при каждом из которых система уравнений

$(x-a+3)^{2}+(y+a-2)^{2}=a+frac{7}{2},x-y=а-1$

имеет единственное решение.

Задание 18.
Для действительного числа х обозначим через [х] наибольшее целое число, не превосходящее х. Например, [frac{11}{4}] = 2, так как 2≤frac{11}{4}<2

а) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{9}]=n?
б) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{5}]=n+2?
в) Сколько существует различных натуральных n, для которых [frac{n}{2}]+[frac{n}{3}]+[frac{n}{8}]+[frac{n}{23}]=n+2021?

Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 2

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.

Если вы хотите приобрести доступ на Экзамер для группы из 10 и более учеников,
мы будем рады сделать вам скидку.

Пожалуйста, расскажите нам подробности:

Необходимо заполнить все поля, кроме телефона

Источник