Поиск
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 61 1–20 | 21–40 | 41–60 | 61–61
Добавить в вариант
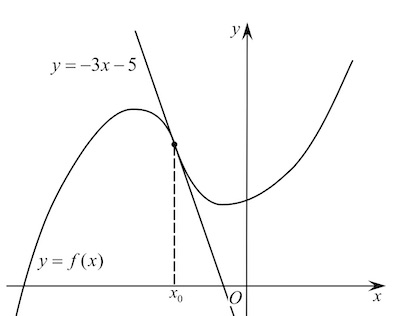
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
Прямая является касательной к графику функции
Найдите a.
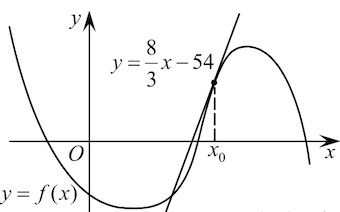
Прямая является касательной к графику функции
Найдите a.
Прямая является касательной к графику функции
Найдите b, учитывая, что абсцисса точки касания больше 0.
Прямая является касательной к графику функции
Найдите ординату точки касания.
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 2.
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1.
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Прямая является касательной к графику функции
Найдите b, учитывая, что абсцисса точки касания меньше 0.
Прямая является касательной к графику функции
Найдите b, учитывая, что абсцисса точки касания больше 0.
Прямая является касательной к графику функции
Найдите b, учитывая, что абсцисса точки касания больше 0.
Прямая является касательной к графику функции
Найдите c.
Прямая является касательной к графику функции
Найдите c.
Прямая является касательной к графику функции
Найдите с.
Прямая является касательной к графику функции
Найдите с.
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Прямая y = −4x − 8 является касательной к графику функции y = x3 − 3x2 − x − 9. Найдите абсциссу точки касания.
На стороне BC треугольника ABC отмечена K точка так, что AK = 4, ВК = 9, КС = 3. Около треугольника ABK описана окружность. Через точку C и середину D стороны AB проведена прямая, которая пересекает окружность в точке P, причем CP > CD и
а) Докажите подобие треугольников АВС и АКС;
б) Найдите DP.
Источник: А. Ларин: Тренировочный вариант № 219.
Всего: 61 1–20 | 21–40 | 41–60 | 61–61
Прямая у = 9х + 6 является касательной к графику функции у = ах2 – 19х + 13. Найдите а.
Источник: Ященко ЕГЭ 2023 (36 вар)
Решение:
В точке касания функции и прямой значения у равны:
ах2 – 19х + 13 = 9х + 6
ах2 – 19х + 13 – 9х – 6 = 0
ax2 – 28x + 7 = 0
Точка касания единственная, уравнение должно иметь 1 решение, значит D = 0.
D = (–28)2 – 4·a·7 = 0
784 – 28a = 0
–28a = –784
a=frac{–784}{–28}=28
Ответ: 28.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.6 / 5. Количество оценок: 11
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
ЕГЭ Профиль №7. Геометрический смысл производной, касательная
Скачать файл в формате pdf.
Решение задач
| Задача 1 | Задача 2 | Задача 3 |
| Задача 4 | Задача 5 | Задача 6 |
| Задача 7 | Задача 8 | Задача 9 |
| Задача 10 | Задача 11 | Задача 12 |
| Задача 13 | Задача 14 |
ЕГЭ Профиль №7. Геометрический смысл производной, касательная
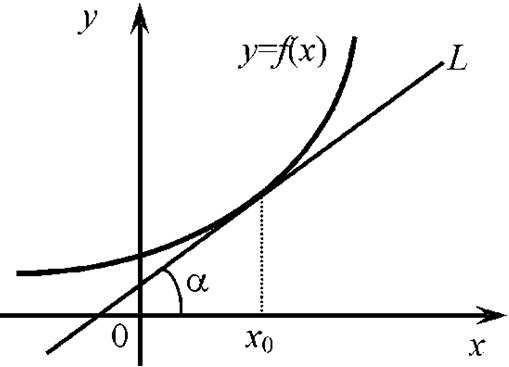
Из курса алгебры известно, что уравнение прямой имеет вид: (y = k,x + b). Производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. Это и есть геометрический смысл производной. А угловой коэффициент в свою очередь равен тангенсу угла наклона касательной:
Если (alpha = 0) (касательная параллельна оси абсцисс), то (f’left( {{x_0}} right) = 0). Если (0 < alpha < {90^ circ }) (касательная возрастает), то (f’left( {{x_0}} right) > 0.) Если ({90^ circ } < alpha < {180^ circ }) (касательная убывает), то (f’left( {{x_0}} right) < 0).
Уравнение касательной к графику функции (fleft( x right)) в точке с абсциссой x0 имеет вид:
(y = f’left( {{x_0}} right),left( {x — {x_0}} right) + fleft( {{x_0}} right))
Комментарии для сайта Cackle
Необходимая теория:
Производная функции
Таблица производных
Первообразная функции
Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции в точке
равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
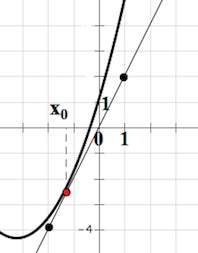
1. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции
в точке
Производная функции в точке
равна тангенсу угла наклона касательной, проведенной в точке
.
Достроив до прямоугольного треугольника АВС, получим:
Ответ: 0,25.
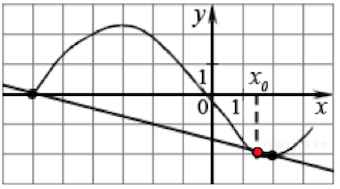
2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке
Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке
образует тупой угол
с положительным направлением оси
. Поэтому из прямоугольного треугольника мы найдём тангенс угла
, смежного с углом
.
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку
, имеем:
Ответ: −0, 25.
Касательная к графику функции
3. Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Запишем условие касания функции и прямой
в точке
При значения выражений
и
равны.
При этом производная функции равна угловому коэффициенту касательной, то есть
.
Из второго уравнения находим или
Первому уравнению удовлетворяет только
.
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону , где
— расстояние от точки отсчета в метрах,
— время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени
с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени
получим:
.
Ответ: 3.
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если , то функция
возрастает.
Если , то функция
убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| 0 | 0 |
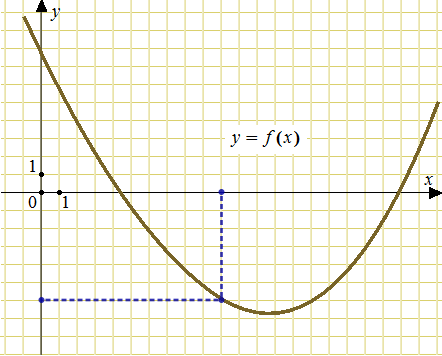
5. На рисунке изображен график функции , определенной на интервале
Найдите количество точек, в которых производная функции
равна 0.
Производная функции в точках максимума и минимума функции
Таких точек на графике 5.
Ответ: 5.
6. На рисунке изображён график — производной функции
, определённой на интервале
. В какой точке отрезка
функция
принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.
На отрезке производная функции
положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение
Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
Ответ: 3.
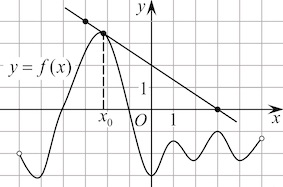
7. На рисунке изображён график функции , определённой на интервале
. Найдите количество точек, в которых касательная к графику функции параллельна прямой
Прямая параллельна оси абсцисс. Найдем на графике функции
точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
Ответ: 7.
8. На рисунке изображен график производной функции , определенной на интервале
Найдите количество точек максимума функции
на отрезке
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это
Ответ: 1.
9. На рисунке изображен график производной функции , определенной на интервале
Найдите точку экстремума функции
на отрезке
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке
В этой точке производная меняет знак с минуса на плюс.
Значит, является точкой экстремума.
Первообразная и формула Ньютона-Лейбница
Функция , для которой
является производной, называется первообразной функции
Функции вида
образуют множество первообразных функции
10. На рисунке изображён график — одной из первообразных некоторой функции
, определённой на интервале
Пользуясь рисунком, определите количество решений уравнения
на отрезке
Функция для которой
является производной, называется первообразной функции
Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции
равна нулю. Это точки максимума и минимума функции
На отрезке
таких точек 4.
Ответ: 4.
Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье
Первообразная функции. Формула Ньютона-Лейбница.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №7. Производная. Поведение функции. Первообразная u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
09
Авг 2013
Категория: 07 Производная, ПО
07. Геометрический смысл производной. Касательная
2013-08-09
2022-09-11
Задача 1. Прямая параллельна касательной к графику функции
. Найдите абсциссу точки касания.
Решение: + показать
Задача 2. Прямая является касательной к графику функции
. Найдите абсциссу точки касания.
Решение: + показать
 Замечание.
Замечание.
Немного облечим себе задачу на будущее. Хотя вполне можно решать задачи способом, показанным выше (задача 2).
Сформулируем условие касания графика функции и прямой
в точке (точках)
.
+ показать
Задача 3. Прямая является касательной к графику функции
Найдите
Решение: + показать
Задача 4. Прямая является касательной к графику функции
. Найдите
, учитывая, что абсцисса точки касания больше
.
Решение: + показать
Задача 5. На рисунке изображён график функции и касательная к нему в точке с абсциссой
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 6. На рисунке изображён график функции и касательная к нему в точке с абсциссой
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 7. На рисунке изображен график функции . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке
.
Решение: + показать
Задача 8. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 9. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 10. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Уравнение касательной показано на рисунке. Найдите значение функции
в точке
.
Решение: + показать
Вы можете пройти тест по задачам, аналогичным разобранным, здесь.
Автор: egeMax |
комментариев 14
20
Янв 2012
06 Задание (2022)ПРОИЗВОДНАЯ
Касательная к графику функции. Задача с параметром.
Задание 7 (№ 119973) из Открытого банка заданий для подготовки к ЕГЭ по математике.
Прямая 

Решение.
Для начала, как обычно, вспомним теорию, и «вытащим» из условия задачи все факты, которые помогут ее решению.
1. Так как прямая 

а) Производная функции 

То есть y’=-5
Найдем производную функции 
y’=56x+b
Получаем: 
Так как на значение абсциссы точки касания накладывается дополнительное условие (абсцисса точки касания больше 0), выразим переменную х через параметр

б) Прямая является касательной к параболе, если имеет с ней одну общую точку.
Чтобы найти точку пересечения прямой 

В конечном итоге, нам нужно определить, при каком значении параметра 
Приравняем правые части уравнений системы:
Перенесем все слагаемые влево и сгруппируем:
Мы получили квадратное уравнение, которое имеет единственный корень, если дискриминант равен нулю. Приравняем дискриминант к нулю:
Решим квадратное уравнение:
Отсюда 

По условию задачи абсцисса точки касания больше 0.
Вспомним, как мы выразили абсциссу точки касания через параметр 
Подставим значения параметра 
а) 
б) 

Нас устраивает случай б)
Ответ:
Вероятно, Ваш браузер не поддерживается. Попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.














 Замечание.
Замечание.