Егэ резерв математика профиль

Решение заданий №1-11 варианта Дальнего Востока ЕГЭ от 27 июня 2022 года по математике (профильный уровень). Резервная волна КИМ, ДВ, Дальневосточный, Владивосток, профиль. 

Задание 1.
Решите уравнение frac{1}{2x-6}=5.

Задание 2.
Конкурс исполнителей проводится в 4 дня. Всего заявлено 75 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день 21 выступление, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в четвёртый день конкурса?

Задание 3.
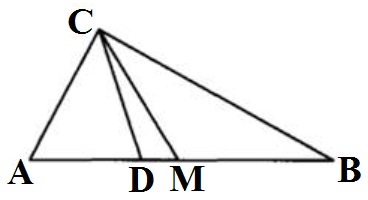
Острый угол В прямоугольного треугольника АВС равен 28°. Найдите угол между биссектрисой СD и медианой СМ, проведёнными из вершины прямого угла С. Ответ дайте в градусах.

Острый угол В прямоугольного треугольника АВС равен 28°.

Задание 4.
Найдите значение выражения (sqrt{48}-sqrt{27})cdot sqrt{3}.

Задание 5.
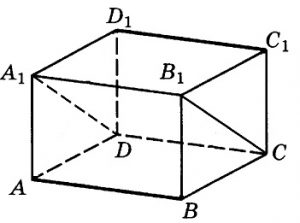
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB = 6, BC = 5, AA1 = 4. Найдите объём многогранника, вершинами которого являются точки A, B, C, D, A1, B1.

В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB = 6, BC = 5, AA1 = 4.

Задание 6.
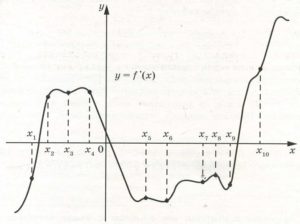
На рисунке изображён график у = f′(х) – производной функции f(х). На оси абсцисс отмечены 10 точек: х1, х2, x3, x4, x5, х6, х7, х8, х9‚ х10. Сколько из этих точек лежит на промежутках убывания функции f(х)?

На рисунке изображён график у = f′(х) – производной функции f(х).

Задание 7.
Груз массой 0,5 кг колеблется на пружине. Его скорость v меняется по закону v=v_{0}cos frac{2pi t}{T}, где t – время с момента начала колебаний, Т = 27 с – период колебаний, v0 = 0,8 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E=frac{mv^{2}}{2}, где m – масса груза в килограммах, v – скорость груза в м/с2. Найдите кинетическую энергию груза через 9 секунд после начала колебаний. Ответ дайте в джоулях.

Задание 8.
Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?

Задание 9.
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A. Найдите абсциссу точки A.

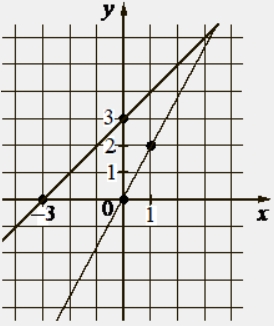
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A. Найдите абсциссу точки A.

Задание 10.
Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,4 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,6?

Задание 11.
Найдите точку максимума функции y = (x2 − 13x + 13)∙e5–x.

Источник варианта: Резервная волна ЕГЭп 2022.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.5 / 5. Количество оценок: 13

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 401

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

1

Призерами олимпиады стали 18 человек, что составило 10% от участвующих. Сколько всего человек участвовало в олимпиаде?

Ответ:

2

На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали  — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.

Ответ:

3

На клетчатой бумаге с размером клетки 1times1 изображён параллелограмм. Найдите длину его большей высоты.

Ответ:

4

В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Г., входящий в состав группы, пойдёт в магазин?

Ответ:

5

Найдите корень уравнения левая круглая скобка x плюс 4 правая круглая скобка в кубе = минус 125.

Ответ:

6

В треугольнике ABC угол B равен 45°, угол BAD равен 30°, AD  — биссектриса. Найдите угол C.

Ответ:

7

На рисунке изображен график функции y  =  f(x), определенной на интервале (−3; 9) . Найдите количество точек, в которых производная функции f(x) равна 0.

Ответ:

8

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Ответ:

9

Найдите значение выражения: 4 корень из 2 косинус в квадрате дробь: числитель: 15 Пи , знаменатель: 8 конец дроби минус 2 корень из 2.

Ответ:

10

11

Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 104 км. На следующий день он отправился обратно со скоростью на 5 км/ч больше прежней. По дороге он сделал остановку на 5 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.

Ответ:

12

Найдите точку минимума функции y=2x минус ln левая круглая скобка x минус 3 правая круглая скобка плюс 5.

Ответ:

13

a)  Решите уравнение 7 синус левая круглая скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс x правая круглая скобка плюс 4 корень из 3 синус x косинус x = 4 косинус в кубе x.

б)  Укажите корни этого уравнения, принадлежащие отрезку левая квадратная скобка минус дробь: числитель: 5 Пи , знаменатель: 2 конец дроби ; минус Пи правая квадратная скобка .

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

14

В основании правильной треугольной призмы ABCA1B1C1 лежит треугольник ABC. На прямой AA1 отмечена точка D так, что A1  — середина AD. На прямой B1C1 отмечена точка E так, что C1  — середина B1E.

а)  Докажите, что прямые A1B1 и DE перпендикулярны.

б)  Найдите расстояние между прямыми AB и DE, если AB = 4, а AA1 = 1.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

15

Решите неравенство дробь: числитель: 1, знаменатель: конец дроби 2 в степени x минус 1 плюс дробь: числитель: 4 в степени левая круглая скобка x плюс дробь: числитель: 1, знаменатель: 2 конец дроби правая круглая скобка минус 2 в степени левая круглая скобка x плюс 5 правая круглая скобка плюс 4, знаменатель: 2 в степени x минус 16 конец дроби geqslant2 в степени левая круглая скобка x плюс 1 правая круглая скобка .

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

16

Окружность с центром О, построенная на катете AC прямоугольного треугольника ABC как на диаметре, пересекает гипотенузу AB в точках A и D. Касательная проведенная к этой окружности в точке D, пересекает катет BC в точке M.

а)  Докажите, что BM  =  CM.

б)  Прямая DM пересекает прямую AC в точке P, прямая OM пересекает прямую BP в точке K. Найдите BK : KP, если косинус angle BAC = дробь: числитель: 4, знаменатель: 5 конец дроби .

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

17

15 декабря 2024 года планируется взять кредит в банке на 31 месяц. Условия возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 30-й (с января 2025 года по июнь 2027 года включительно) долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;

— 15 июня 2027 года долг составит 100 тысяч рублей;

— 15 июля 2027 года долг должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 555 тысяч рублей?

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

18

Найдите все значения параметра a, при каждом из которых уравнение

|a минус 2|x в степени 4 минус 2ax в квадрате плюс |a минус 12| = 0

имеет хотя бы два различных корня.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

19

Первый член конечной геометрической прогрессии, состоящей из трехзначных натуральных чисел равен 128. Известно, что в прогрессии не меньше трех чисел.

а)  Может ли число 686 являться членом такой прогрессии?

б)  Может ли число 496 являться членом такой прогрессии?

в)  Какое наибольшее число может являться членом такой прогрессии?

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

Завершить тестирование, свериться с ответами, увидеть решения.

Источник
Skip to content

Вариант резервного ЕГЭ Профиль 2021 с ответами 29.06.2021

Вариант резервного ЕГЭ Профиль 2021 с ответами 29.06.2021admin2021-07-24T14:09:20+03:00

Источник

Шкалирование

Первичный Тестовый Оценка
5-6 27-34 3
7-8 40-46 4
9-10 52-58
11-12-13 64-66-68 5
14-15-16 70-72-74
17-18-19 76-78-80
20-21-22 82-84-86
23-24-25 88-90-92
26-27-28 94-96-98
29-30-31 100
Первичный балл
/
Тестовый балл		 5/27 6/34 7/40 8/46 9/52 10/58 11/64 12/66 13/68 14/70
15/72 16/74 17/76 18/78 19/80 20/82 X / 2X+42 29+ / 100
Источник
3398 В правильной треугольной призме ABCA1B1C1 точка M — середина ребра CC1, точки K и N отмечены на рёбрах AB и A1B1 соответственно, так что AK : KB = B1N : NA1.
а) Докажите, что плоскость MKN перпендикулярна плоскости AA1B1.
б) Найдите площадь сечения плоскостью MKN, если AB=BB1=42, AK:KB = 1:41
Решение		 В правильной треугольной призме ABCA1B1C1 точка M — середина ребра CC1, точки K и N отмечены на рёбрах AB и A1B1 соответственно ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 13 ...X
3396 Две окружности пересекаются в точках A и B. Общая касательная к этим окружностям касается в точках C и D. Прямая AB пересекает отрезок CD в точке M. Центры окружностей лежат в разных полуплоскостях относительно прямой AB, точка B лежит между точками A и M.
а) Докажите, что CM=MD.
б) Найдите расстояние между центрами данных окружностей, если их радиусы равны 1 и 3 соответственно, а точка B является серединой отрезка AM
Решение		 Две окружности пересекаются в точках A и B. Общая касательная к этим окружностям касается в точках C и D ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 16 ...X
3395 Точка D лежит на основании AC равнобедренного треугольника ABC. точки I и J  — центры окружностей, описанных около треугольников ABD и CBD соответственно.
а) Докажите, что прямые BI и DJ параллельны.
б) Найдите IJ, если AC=12, cos/_BDC=2/7
Решение		 Точка D лежит на основании AC равнобедренного треугольника ABC. точки I и J  — центры окружностей ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 16 ...X
3394 Точка M — середина ребра AA1 треугольной призмы ABCA1B1C1, в основании которой треугольник ABC. Плоскость альфа проходит через точки B и B1 перпендикулярно прямой C1M.
а) Докажите, что одна из диагоналей грани ACC1A1 равна одному из рёбер этой грани.
б) Найдите расстояние от точки C до плоскости альфа, если плоскость альфа делит ребро AC в отношении 1:5, считая от вершины A, AC=20, AA1=32
Решение		 Точка M — середина ребра AA1 треугольной призмы ABCA1B1C1, в основании которой треугольник ABC ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 13 ...X
3393 а) Решите уравнение log_{11}(2sin^2(x)+7sqrt(3)sin(x)-11)=0 б) Укажите корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi].
Решение     График		 а) Решите уравнение log 11 (2sin2 x +7 sqrt3 sinx -11 ) =0 ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 12 ...X
3392 Решите неравенство (3-4^x)/(2-2^x) >= 3/2
Решение     График		 Решите неравенство 3 — 4^x / 2- 2^x >= 3/2 ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 14 ...X
3391 Найдите все значения параметра a, при каждом из которых уравнение sqrt(15x^2+6ax+9)=x^2+ax+3 имеет три различных решения
Решение     График		 Найдите все значения параметра a, при каждом из которых уравнение корень из 15×2 +6ax+9 =x2 +ax+3 имеет три различных решения ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 17 ...X
3221 Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,4?
Решение		 Стрелок в тире стреляет по мишени до тех пор, пока не поразит её ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 10 ...X
813 Окружности с центрами O1 и O2 разных радиусов пересекаются в точках A и B. Хорда AC большей окружности пересекает меньшую окружность в точке M и делится этой точкой пополам. а) Докажите, что проекция отрезка O1O2 на прямую AC в четыре раза меньше AC. б) Найдите O1O2, если известно, что радиусы окружностей равны 5 и 17, а AC=16
Решение		 Окружности с центрами O1 и O2 разных радиусов пересекаются в точках A и B ! ЕГЭ по математике 27-06-2022 резервный день Задание 16 #Ященко ЕГЭ 2017 30 вариантов Вариант 16 задача 16 ...X
Show filter builder dialog   Clear

||||Hide

Источник

Сроки: конец марта – начало апреля.

Досрочный период сдачи ЕГЭ проводится примерно за пару месяцев до начала основной волны. Сдать ЕГЭ в этот период имеют возможность только те ученики, которые могут отсутствовать в основном периоде сдачи экзамена по определённым причинам.

Кто может сдать:

  • выпускники школ прошлых лет, учащиеся техникумов и колледжей;
  • выпускники 11 классов, которые учатся за пределами страны;
  • выпускники 11 классов, находящиеся на лечении в медицинских учреждениях на момент проведения основного этапа ЕГЭ;
  • выпускники 11 классов, принимающие участие в международных или общероссийских олимпиадах/соревнованиях, дата проведения которых совпадает с основным этапом проведения ЕГЭ;
  • выпускники 11 классов, готовящиеся к переезду на ПМЖ в другую страну;
  • выпускники 11 классов вечерних школ, которым предстоит нести военную службу (весенний призыв).

    • Расписание досрочного периода

    Март 2023

    Пн Вт Ср Чт Пт Сб Вс
    1 2 3 4 5
    6 7 8 9 10 11 12
    13 14 15 16 17 18 19
    20

    Досрочный ЕГЭ география, литература

    		 21 22 23

    Досрочный ЕГЭ русский язык

    		 24 25 26
    27

    Досрочный ЕГЭ математика профиль/база

    		 28 29 30

    Досрочный ЕГЭ биология, физика, иностранные языки (за исключением раздела «Говорение»),

    		 31

    Апрель 2023

    Пн Вт Ср Чт Пт Сб Вс
    1 2
    3

    Досрочный ЕГЭ иностранные языки (раздел «Говорение»)

    		 4 5 6

    Досрочный ЕГЭ обществознание, информатика (ИКТ)

    		 7 8 9
    10

    Досрочный ЕГЭ химия, история

    		 11 12

    Досрочный ЕГЭ Резерв география, химия, информатика (ИКТ), иностранные языки (раздел «Говорение»), история

    		 13 14

    Досрочный ЕГЭ Резерв иностранные языки (за исключением раздела «Говорение»), литература, физика, обществознание, биология

    		 15

    Досрочный ЕГЭ Резерв русский язык

    		 16
    17 18

    Досрочный ЕГЭ Резерв математика профиль

    		 19 20 21 22 23
    24 25 26 27 28 29 30

    Сроки: конец мая – начало июля.

    Большинство выпускников 11-х классов сдают ЕГЭ в основной период.

    Кто может сдать:

  • выпускники 11-х классов, допущенные к ГИА;
  • выпускники 10-х классов, досрочно завершившие освоение программы по математике или русскому языку за курс 11-го класса и имеющие годовую оценку;
  • выпускники прошлых лет (при подаче заявления по желанию);
  • учащиеся, находящиеся на семейном обучении, завершившие освоение программы за курс 11-го класса.

    • Расписание основного периода

    Май 2023

    Пн Вт Ср Чт Пт Сб Вс
    1 2 3 4 5 6 7
    8 9 10 11 12 13 14
    15 16 17 18 19 20 21
    22 23 24 25 26

    ЕГЭ география, литература, химия

    		 27 28
    29

    ЕГЭ русский язык

    		 30 31

    Июнь 2023

    Пн Вт Ср Чт Пт Сб Вс
    1

    ЕГЭ математика профиль/база

    		 2 3 4
    5

    ЕГЭ история, физика

    		 6 7 8

    ЕГЭ обществознание

    		 9 10 11
    12 13

    ЕГЭ иностранные языки (за исключением раздела «Говорение»), биология

    		 14 15 16

    ЕГЭ иностранные языки (раздел «Говорение»)

    		 17

    ЕГЭ иностранные языки (раздел «Говорение»)

    		 18
    19

    ЕГЭ информатика (ИКТ)

    		 20

    ЕГЭ информатика (ИКТ)

    		 21 22

    ЕГЭ Резерв русский язык

    		 23

    ЕГЭ Резерв география, литература, иностранные языки (раздел «Говорение»)

    		 24 25
    26

    ЕГЭ Резерв математика профиль

    		 27

    ЕГЭ Резерв иностранные языки (за исключением раздела «Говорение»), биология, информатика (ИКТ)

    		 28

    ЕГЭ Резерв обществознание, химия

    		 29

    ЕГЭ Резерв история, физика

    		 30

    Июль 2023

    Пн Вт Ср Чт Пт Сб Вс
    1

    ЕГЭ Резерв по всем учебным предметам

    		 2
    3 4 5 6 7 8 9
    10 11 12 13 14 15 16
    17 18 19 20 21 22 23
    24 25 26 27 28 29 30
    31

    Сроки: начало сентября.

    Дополнительный период предназначен для тех учеников, кто в основную волну набрал менее минимального аттестационного порога, «вторая пересдача». Сдача экзаменов в этот период нужна исключительно для получения аттестата.

    Расписание дополнительного периода

    Сентябрь 2023

    Пн Вт Ср Чт Пт Сб Вс
    1 2 3
    4 5 6

    Дополнительный ЕГЭ русский язык

    		 7 8 9 10
    11 12

    Дополнительный ЕГЭ математика база

    		 13 14 15 16 17
    18 19 20 21 22 23 24
    25 26 27 28 29 30
    Источник

    29.03.2022

    Начинаем собирать реальные варианты ЕГЭ 2022 года по профильной математике. Все варианты собираются и публикуются после проведения экзамена.

    • Смотреть реальные варианты ЕГЭ 2022 по всем предметам

    ОБНОВЛЕНО 05.06.2022

    Все возможные варианты с досрочного ЕГЭ 2022 по математике и с основной волны, которая прошла 02.06.2022. Смотрим, разбираем. Все варианты будут сопровождаться видеоуроками, на которых будут разобраны примеры решения, правильные ответы и т.д.

    • Другие варианты ЕГЭ по профильной математике (включая Статград)

    Есть вопросы? Пишите их ниже! Обсудим, решим, ответим.

    • Вариант досрочного ЕГЭ 2022 по профильной математике от 28.03.2022
    • Открытый вариант от ФИПИ ЕГЭ 2022 по профильной математике (аналог досрочного варианта) от 28.04.2022

    Один из вариантов досрочного реального ЕГЭ 2022 по математике

    Варианты с основной волны от 2 июня 2022

    Вариант в формате PDF

    Смотреть в PDF:

    Или прямо сейчас: cкачать в pdf файле.

    Видеоразборы заданий ЕГЭ 2022 по профилю с основной волны

    Источник

    Понравилась статья? Поделить с друзьями:
  • Егэ расшифровка по буквам
  • Егэ расшифровка мем
  • Егэ после какого класса сдают в россии
  • Егэ после какого класса сдавать
  • Егэ после домашнего обучения