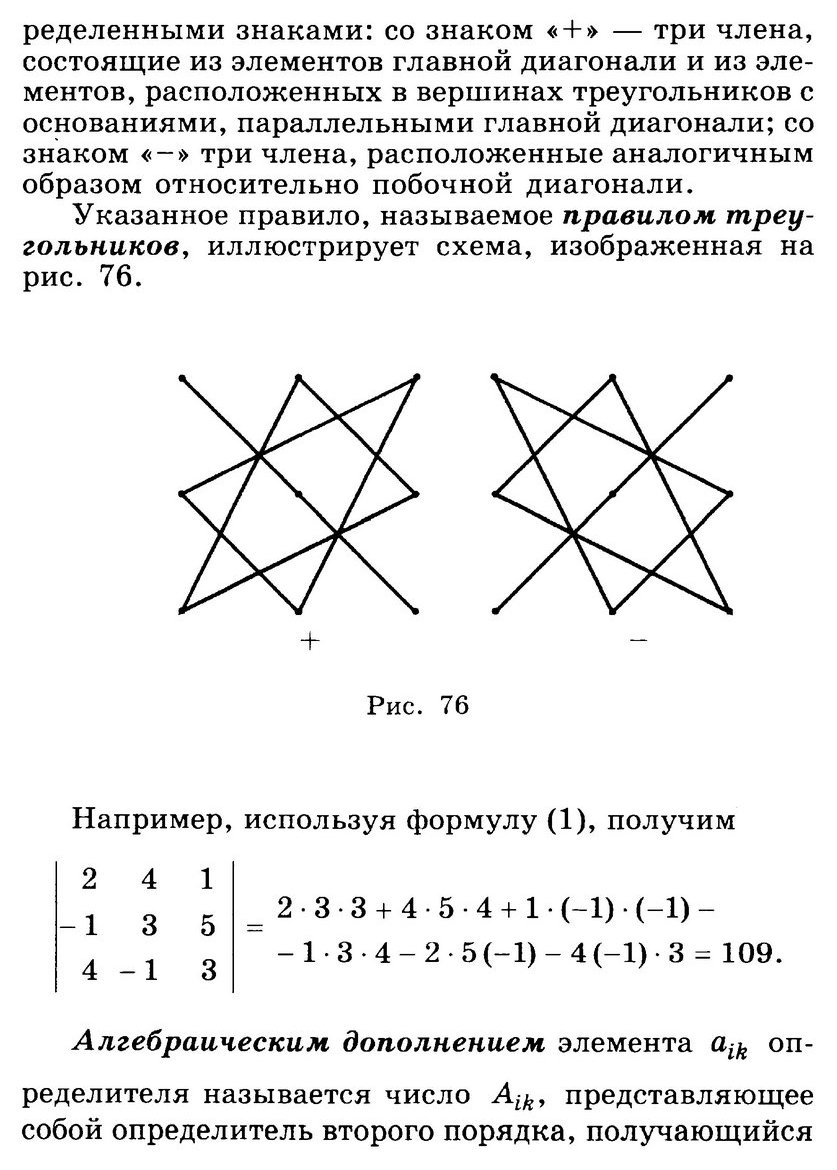
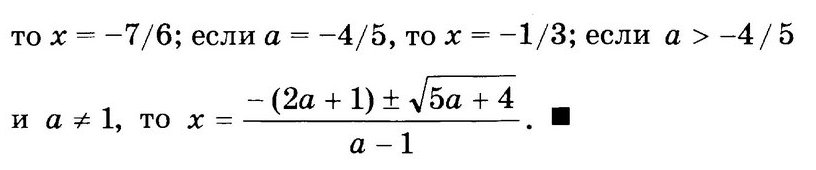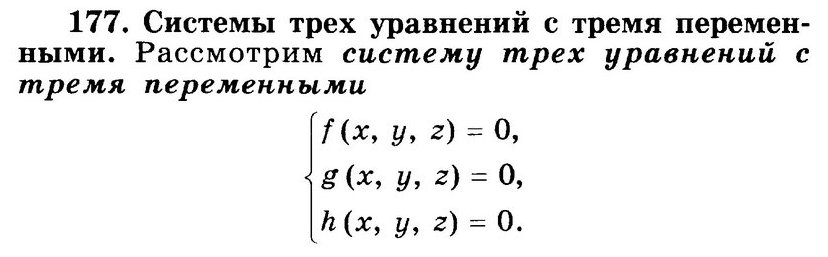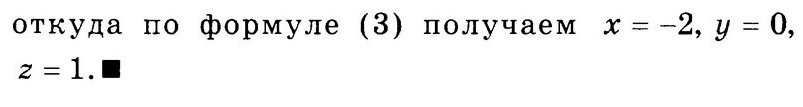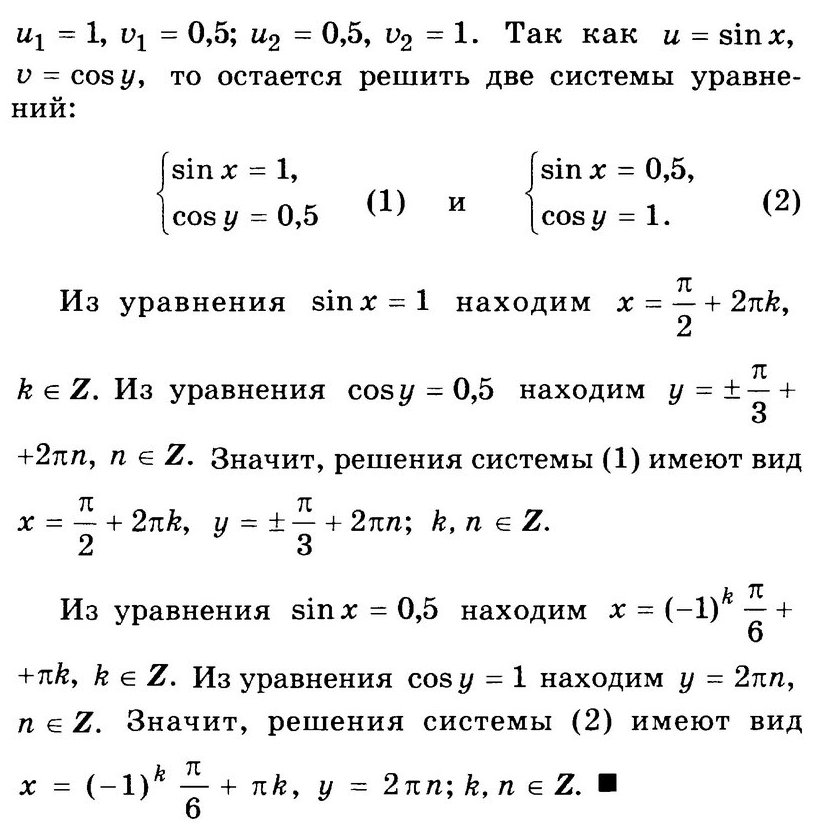в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 94 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
При каких значениях параметра а система имеет четыре решения?
Известно, что значение параметра а таково, что система уравнений
имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
Источник: ЕГЭ по математике 2021 года. Досрочная волна., Задания 18 ЕГЭ–2021
Источник/автор: Некрасов В. Б., Гущин Д. Д. «Просвещение», 2010; Гущин Д. Д. «Учительская газета», 2013; ЕГЭ по математике − 2021
При каких значениях параметра а система имеет единственное решение?
Найти все значения a, при каждом из которых система
имеет единственное решение.
При каждом значении а решите систему
При каких p данная система имеет решения:
Найдите все значения параметра a, при каждом из которых система уравнений
имеет единственное решение.
Источник: РЕШУ ЕГЭ
Найдите все значения параметра a, при каждом из которых система уравнений
имеет единственное решение.
Источник: РЕШУ ЕГЭ
Найдите все значения параметра a, при каждом из которых система уравнений
имеет единственное решение.
Источник: А. Ларин. Тренировочный вариант № 361.
При каких значениях параметра а система имеет четыре решения?
При каких p данная система имеет решения:
Решите систему неравенств:
Источник: А. Ларин: Тренировочный вариант № 71.
Решите систему уравнений
При каждом значении а решите систему
Решите систему неравенств
Источник: А. Ларин: Тренировочный вариант № 4.
Решите систему:
Решите систему уравнений
Решите систему уравнений:
Решите систему уравнений:
Решите систему уравнений:
Всего: 94 1–20 | 21–40 | 41–60 | 61–80 …
Системы алгебраических уравнений
Систему уравнений можно решать методом подстановки – выражать переменную из одного уравнения и подставлять в другое.
Уравнения в системе можно также складывать друг с другом и вычитать одно из другого. Например, левую часть одного уравнения складываем с левой частью другого, правую – с правой.
Можно умножать и даже делить одно уравнение на другое! Конечно, при этом надо следить, чтобы не умножить или не поделить на ноль.
Обратите внимание – когда мы решаем систему уравнений, она не распадается на «кусочки», на отдельные уравнения. Каждый раз мы переходим от системы уравнений к равносильной ей системе.
1. Решите систему уравнений:
Раскроем скобки в каждом уравнении:
Вычтем из первого уравнения системы второе: . И подставим во второе уравнение.
2. Решите систему уравнений:
Мы разложили левую часть первого уравнения на множители по формуле суммы кубов.
Поделим первое уравнение системы на второе
Подставим в уравнение
3. Решите систему уравнений:
Дальше – цепочка равносильных переходов.
Решения первой системы:
Решим квадратное уравнение . Его корни:
и .
Это полезно
Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.
Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
Как решать системы уравнений с двумя переменными
Что такое система уравнений с двумя переменными
Системой уравнений в алгебре называется некое условие, смысл которого заключается в одновременном выполнении нескольких уравнений относительно нескольких (либо одной) переменных.
Это значит, что система представляет собой комплекс уравнений. Данные равенства могут содержать одну, две или более переменных. Основным условием понятия «система уравнений» является то, что все эти уравнения выполняются в одно время.
Объединить уравнения в систему можно с помощью фигурной скобки:
У р а в н е н и е 1 У р а в н е н и е 2 У р а в н е н и е 3 …
Графический метод решения
Принцип решения систем уравнений графическим способом заключается в построении графиков для каждого уравнения в общей системе координат. Тогда решения системы соответствуют точкам, в которых данные графики пересекаются. После объяснения решения ответ принято записывать, как координаты этих точек.
Разберем наглядный пример. Предположим, что дана некая система уравнений, решать которую нужно графическим способом. Выполним работу последовательно:
- Запишем систему.
- Выразим одну из переменных (пусть это будет у).
- Построим на координатной прямой графики функций.
- Найдем точки пересечения графиков.
2 x + 3 y = 12 3 x — y = 7 ⇔ y = 4 — 2 3 x y = 3 x — 7
Заметим, что точка пересечения графиков имеет следующие координаты:
Графический метод решения систем уравнений уступает в точности другим способам. Использовать график целесообразно в том случае, когда в задаче записана система линейных уравнений. Подобные задачи встречаются в средних классах школы. Такие уравнения имеют вид y = a x + b без квадратных членов, а их графики являются прямыми.
Метод подстановки
Алгоритм решения системы уравнений с помощью метода подстановки:
- выражение одной переменной через другие;
- подстановка выражения, которое получилось, в начальные уравнения на место выраженной переменной;
- повторение второго шага до тех пор, пока не будут определены другие переменные.
Рассмотрим последовательность действий на практике. Предположим, что имеется некая система уравнений, которую требуется решить:
2 x + 3 y = 12 3 x — y = 7
Выразим у из второго уравнения:
Выполним подстановку полученного выражения в первое равенство:
2 x + 3 3 x — 7 = 12
Для полученного уравнения с одной переменной несложно найти корни:
2 x + 3 3 x — 7 = 12
2 x + 3 · 3 x — 3 · 7 = 12
2 x + 9 x — 21 = 12
Зная х, выполним подстановку и найдем у:
y = 3 x — 7 = 3 · 3 — 7 = 2 .
Запишем в ответ значения двух переменных.
Ответ: x = 3 ; y = 2 , либо (3;2).
Метод сложения
При сложении левых частей пары (или более) уравнений выражение, полученное в результате, равно сложенным правым частям этих же равенств, согласно формуле:
a = b c = d ⇒ a + c = b + d
В обратную сторону записанное свойство не работает:
a + c = b + d ◃ ≠ ▹ a = b c = d
Таким образом, при решении систем уравнений можно увеличивать обе части уравнения на одинаковое число. Например, сложим первое уравнение с числом с:
a = b c = d ⇒ a + c = b + c
Исходя из того что c=d, можно выполнить замену c на d справа:
a = b c = d ⇒ a + c = b + c ⇒ a + c = b + d .
В качестве примера попробуем решить систему уравнений:
2 x + y = 12 3 x — y = 3
Следуя правилу, суммируем уравнения. В процессе левые части складываем друг с другом. Аналогичным образом поступим с правыми частями равенств. В результате:
2 x + y = 12 3 x — y = 3 ⇒ 2 x ¯ ¯ + y ¯ + 3 x ¯ ¯ — y ¯ = 15 ⇔ 5 x = 15 ⇔ x = 3 .
Получилось избавиться от переменной у. В итоге задача значительно упростилась. Подставим число 3 на место слагаемого с х:
2 x + y = 12 x = 3 ⇔ 2 · 3 + y = 12 x = 3 ⇔ y = 6 x = 3
В следующем примере система уравнений имеет следующий вид:
2 x + 3 y = 13 4 x + 5 y = 23
Заметим, что с помощью сложения задание не получится упростить. В этом случае можно воспользоваться умножением уравнения на какое-либо число, отличное от нуля. Важно выбрать такой множитель, который позволит избавиться от одной из переменных. В этом случае лучше использовать (-2):
2 x + 3 y = 13 · — 2 4 x + 5 y = 23 ⇔ — 4 x — 6 y = — 26 4 x + 5 y = 23
Приступим к сложению:
— 4 x — 6 y = — 26 4 x + 5 y = 23 ⇒ — 4 x — 6 y + 4 x + 5 y = — 26 + 23 ⇔ — y = — 3 ⇔
Выполним подстановку у=3 в первое уравнение:
2 x + 3 y = 13 y = 3 ⇔ 2 x + 9 = 13 y = 3 ⇔ x = 2 y = 3
Задания для самостоятельного решения
Нужно решить систему уравнений:
13 x + 6 y = 7 2 x — 4 y = 6
Выразим х с помощью второго уравнения:
Найти значения переменных:
2 x + 5 y = 10 8 y — 5 x = 57
Из первого равенства выразим х:
2 x + 5 y = 10 2 x = 10 — 5 y
Подставим полученное значение во второе уравнение и запишем ответ.
Дана система уравнений, которую требуется решить:
2 x + 5 y = 10 3 x — 2 y = 1
В данном случае следует умножить первое уравнение на число 2, а второе равенство умножить на число 5:
2 x + 5 y = 10 · 2 3 x — 2 y = 1 · 5 ⇔ 4 x + 10 y = 20 15 x — 10 y = 5
После сложения уравнений остается лишь определить х:
19 x = 25 ⇔ x = 25 19
При подстановке х в какое-либо из двух уравнений можно вычислить у и записать ответ.
Ответ: ( 25 19 ; 28 19 ) .
Требуется найти переменные:
3 y — 4 x = — 13 3 x + 7 y = 56
Здесь следует в первую очередь найти произведение первого уравнения и числа 3, умножить второе уравнение на множитель 4. Далее остается суммировать уравнения и записать ответ.
Нужно решить систему уравнений:
7 x + 3 y = 21 4 y — 5 x = — 15
Множителем для первого уравнения является число 4. Второе уравнение нужно умножить на -3. Полученные равенства следует сложить и записать ответ.
Решить систему уравнений:
6 x — 8 y = — 2 9 x + 10 y = 8
В данном случае предполагается умножение уравнений на дробные числа. Множителем для первого уравнения является дробь 1 4 . Второе уравнение следует умножить на 1 5 :
6 x — 8 y = — 2 · 1 4 9 x + 10 y = 8 · 1 5 ⇔ 6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5
Далее выполним сложение:
6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5 ⇔ 3 2 x + 9 5 x =-0,5+1,6 ⇔ ⇔ 15 10 x + 18 10 x = 1,1 ⇔ 33 10 x = 1 , 1 ⇔ ⇔ 33 = 11 x x = 3
Путем подстановки определим y:
6 3 — 8 y = — 2 x = 3 ⇔ — 8 y = — 4 x = 3 ⇔ y = 2 x = 3
Найти корни следующих систем уравнений:
2 x + 3 y = 11 3 x + 2 y = 9
3 x — y = 85 5 x + 2 y = 17
x — 3 y = 6 2 y — 5 x = — 4
y 4 — x 5 = 6 x 15 + y 12 = 0
y — x = 5 x + 3 y = 3
Ответ: (1; 3), (17; -34), (0; -2), (-15; 12), (-3; 2).
источники:
http://skysmart.ru/articles/mathematic/reshenie-sistem-uravnenij
http://wika.tutoronline.ru/algebra/class/9/kak-reshat-sistemy-uravnenij-s-dvumya-peremennymi
Материалы для подготовки к ЕГЭ. Онлайн-Справочник по математике.
Раздел 4 «Уравнения и системы уравнений» (§§ 14-16). Уравнения с одной переменной. Уравнения с двумя переменными. Система уравнений.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Раздел IV. Уравнения и системы уравнений
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
§ 14. Уравнения с одной переменной.
138. Определение уравнения. Корни уравнения.
139. Равносильность уравнений.
140. Линейные уравнения.
141. Квадратные уравнения.
142. Неполные квадратные уравнения.
143. Теорема Виета.
144. Системы и совокупности уравнений.
145. Уравнения, содержащие переменную под знаком модуля.
146. Понятие следствия уравнения. Посторонние корни.
147. Уравнения с переменной в знаменателе.
148. Область определения уравнения.
149. Рациональные уравнения.
150. Решение уравнения р(х) = 0 методом разложения его левой части на множители.
151. Решение уравнений методом введения новой переменной.
152. Биквадратные уравнения.
153. Уравнения высших степеней.
154. Решение задач с помощью уравнений.
155. Иррациональные уравнения.
156. Показательные уравнения.
157. Логарифмические уравнения.
158. Показательно-логарифмические уравнения.
159. Простейшие тригонометрические уравнения.
160. Решение тригонометрических уравнений методом разложения на множители.
161. Решение тригонометрических уравнений методом введения новой переменной.
162. Однородные тригонометрические уравнения.
163. Универсальная подстановка.
164. Метод введения вспомогательного аргумента.
165. Графическое решение уравнений.
166. Уравнения с параметром.
§ 15. Уравнения с двумя переменными.
167. Решение уравнения с двумя переменными.
168. График уравнения с двумя переменными.
169. Линейное уравнение с двумя переменными и его график.
§ 16. Системы уравнений.
170. Системы двух уравнений с двумя переменными. Равносильные системы.
171. Решение систем двух уравнений с двумя переменными методом подстановки.
172. Решение систем двух уравнений с двумя переменными методом сложения.
173. Решение систем двух уравнений с двумя переменными методом введения новых переменных.
174. Определители второго порядка. Исследование систем двух линейных уравнений с двумя переменными.
175. Симметрические системы.
176. Графическое решение систем двух уравнений с двумя переменными.
177. Системы трех уравнений с тремя переменными.
178. Определители третьего порядка. Исследование систем трех линейных уравнений с тремя переменными.
179. Системы показательных и логарифмических уравнений.
180. Системы тригонометрических уравнений.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Материалы для подготовки к ЕГЭ. Онлайн справочник по математике.
Раздел 4 «Уравнения и системы уравнений» (§§ 14-16). Уравнения с одной переменной. Уравнения с двумя переменными. Система уравнений.
Просмотров:
4 558
Системы алгебраических уравнений
Систему уравнений можно решать методом подстановки – выражать переменную из одного уравнения и подставлять в другое.
Уравнения в системе можно также складывать друг с другом и вычитать одно из другого. Например, левую часть одного уравнения складываем с левой частью другого, правую – с правой.
Можно умножать и даже делить одно уравнение на другое! Конечно, при этом надо следить, чтобы не умножить или не поделить на ноль.
Обратите внимание – когда мы решаем систему уравнений, она не распадается на «кусочки», на отдельные уравнения. Каждый раз мы переходим от системы уравнений к равносильной ей системе.
1. Решите систему уравнений:
Раскроем скобки в каждом уравнении:
Вычтем из первого уравнения системы второе: . И подставим во второе уравнение.
Ответ: .
2. Решите систему уравнений:
Мы разложили левую часть первого уравнения на множители по формуле суммы кубов.
Поделим первое уравнение системы на второе
Подставим в уравнение
Ответ: (1;1)
3. Решите систему уравнений:
Сделаем замену
Дальше – цепочка равносильных переходов.
Решения первой системы:
Получим:
Вторая система:
Решим квадратное уравнение . Его корни:
и
.
<
, и уравнение
в этом случае решений не имеет.
>
, тогда
<
и уравнение
не имеет решений. Значит, у второй системы решений нет.
Ответ: (2; 2), (2; –2), (–2; –2),(–2; –2)
4. Решите систему уравнений:
Замена:
;
;
.
Ответ: 1, 2, 3.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Системы алгебраических уравнений» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
09
Окт 2015
Категория: Справочные материалы
Способы решения систем уравнений с двумя неизвестными
2015-10-09
2019-08-08
Линейные системы уравнений
Системы линейных уравнений. Метод подстановки
+ показать
Решить систему уравнений:
Решение: + показать
Системы линейных уравнений. Метод сложения
+ показать
1. Решить систему уравнений:
Решение: + показать
2. Решить систему уравнений:
Решение: + показать
Нелинейные системы уравнений
Системы уравнений, сводящихся к линейным
1. Решить систему уравнений:
Решение: + показать
2. Решить систему уравнений:
Решение: + показать
Нелинейные системы уравнений. Метод подстановки
Решить систему уравнений:
Решение: + показать
Нелинейные системы уравнений. Метод сложения
Решить систему уравнений:
Решение: + показать
Нелинейные системы уравнений. Метод почленного умножения (деления)
1. Решить систему уравнений:
Решение: + показать
Симметрические системы. Метод введения переменной
Симметрическая система – система, все уравнения которой симметрические. Симметрическое уравнение от двух переменных и
– уравнение, которое не изменяется при замене
на
и
на
.
Для таких систем удобно использовать замену
Решить систему уравнений:
Решение: + показать
Системы однородных уравнений и приводящиеся к ним системы
Однородным уравнением с двумя неизвестными будем называть уравнение вида
1. Решить систему уравнений:
Решение: + показать
2. Решить систему уравнений:
Решение: + показать
Графический метод решения систем уравнений
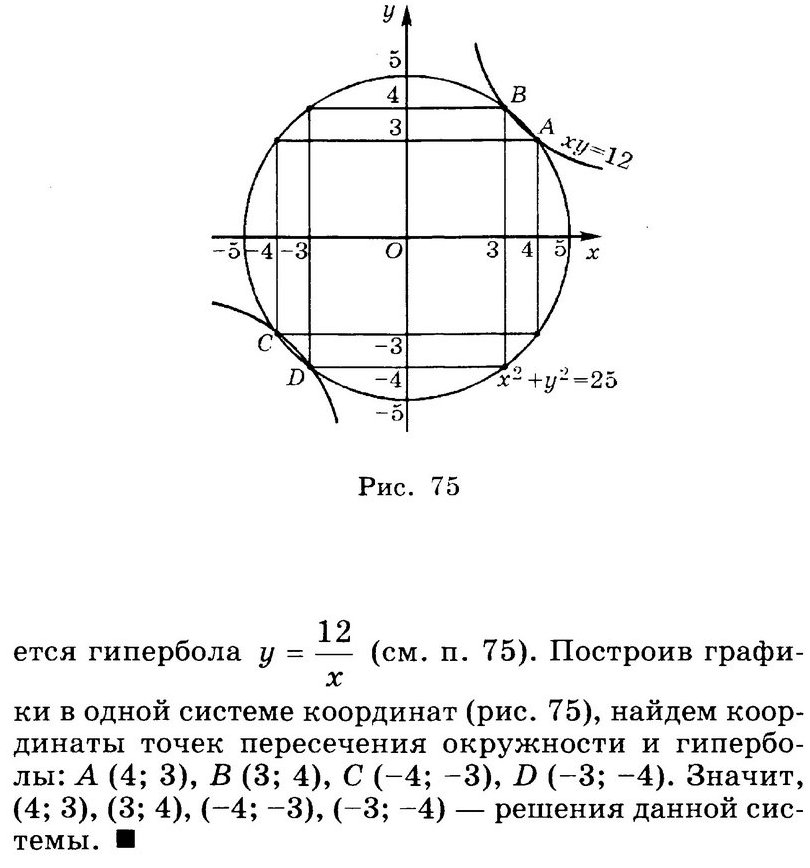
1. Решите графически систему уравнений:
Решение: + показать
2. Решите графически систему уравнений:
Решение: + показать
3. Решите графически систему уравнений:
Решение: + показать
Задания для самостоятельной работы
+ показать
Автор: egeMax |
комментариев 10
ЕГЭ Профиль №18. Линейные уравнения, неравенства и системы уравнений с параметрами