Егэ сложное неравенство - Помощь в подготовке к экзаменам и поступлению

Теория

1.	Ещё раз про ОДЗ
2.	Решение неравенств с помощью систем
3.	Системы неравенств
4.	Метод интервалов
5.	Метод рационализации
6.	Как решать задание ЕГЭ

Задания

1.	Метод введения новой переменной Сложность: среднее	2
2.	Дробное рациональное неравенство (теорема Виета) Сложность: среднее	2
3.	Дробное рациональное неравенство (разность квадратов) Сложность: среднее	2
4.	Квадратный трёхчлен в знаменателе Сложность: среднее	2
5.	Дробно-рациональный показатель степени Сложность: среднее	2
6.	Неизвестное основание Сложность: сложное	2
7.	Неравенство третьей степени в ОДЗ Сложность: сложное	2
8.	Логарифм произведения Сложность: сложное	2
9.	Дробно-рациональное выражение под логарифмом Сложность: сложное	2
10.	Неравенства с отрицательными степенями Сложность: сложное	2
11.	Показательное с модулем Сложность: сложное	2
12.	Монотонность логарифмической функции Сложность: сложное	2
13.	Трёхчлен в основании логарифма Сложность: сложное	2
14.	Монотонность квадратного корня Сложность: сложное	2
15.	Показательное с переменным основанием Сложность: сложное	2

Экзаменационные задания (подписка)

1.	Как на ЕГЭ (1). Сложное неравенство Сложность: сложное	2
2.	Как на ЕГЭ (2). Сложное неравенство Сложность: сложное	2
3.	Как на ЕГЭ (3). Сложное неравенство Сложность: сложное	2
4.	Как на ЕГЭ (4). Сложное неравенство Сложность: сложное	2

Тесты

Тренировка по теме Сложное неравенство

Сложность: сложное

Материалы для учителей

Методическое описание

Источник

Неравенства. Метод замены множителя (метод рационализации)

Полезный прием для решения сложных неравенств на ЕГЭ по математике – метод рационализации неравенства. Другое название — метод замены множителя. Это один из тех секретов, о которых ученику рассказывает репетитор. В учебниках о таком не написано.

Суть метода в том, чтобы от неравенства, содержащего в качестве множителей сложные показательные или логарифмические выражения, перейти к равносильному ему более простому рациональному неравенству.

Давайте для начала вспомним, что такое равносильные уравнения (или неравенства). В школьной программе этот важный вопрос почти не обсуждается. Поэтому запишем определение.

Равносильными называются уравнения, множества решений которых совпадают.

Заметим, что внешне уравнения могут быть и не похожи друг на друга.

Например, уравнения (x − 3)² = 0 и x − 3 = 0 равносильны. Число 3 является единственным решением и того, и другого.

Уравнения $x^{2}=-1$ и также равносильны. Оба они не имеют решений. Другими словами, множество решений каждого из них – пусто.

Уравнения и $2x-1=(x-2)^{2}$ не являются равносильными. Решением первого уравнения является только x = 5. Решения второго – два числа: x = 5 и x = 1. Получается, что возведение обеих частей уравнения в квадрат в общем случае приводит к уравнению, неравносильному исходному.

Аналогичное определение – для неравенств.

Равносильными называются неравенства, множества решений которых совпадают.

Например, неравенства и $frac{x-1}{x-3}>0$ равносильны – ведь множества их решений совпадают. В этом легко убедиться с помощью метода интервалов.

Неравенства $log_{2}x>log_{2}5$ и x> 5 также равносильны при x> 0 . Заметим, что внешне эти неравенства не похожи – одно из них логарифмическое, другое алгебраическое.

Другими словами, при x > 0 неравенства $log_{2}x-log_{2}5>0$ и x-5>0 имеют одинаковые решения. Если какое-либо число x > 0 является решением одного из них, то оно будет и решением второго.

А это значит, что при любом x > 0 выражение $log_{2}x-log_{2}5$ будет иметь такой же знак, как и выражение x − 5. Следовательно, если в какое-либо сложное неравенство входит в качестве множителя выражение $log_{2}x-log_{2}5$ , то при выполнении условия x > 0 его можно заменить на более простое x − 5 и получить неравенство, равносильное исходному.

Вот ключевой момент. На этом и основан метод рационализации – замены множителей, содержащих сложные логарифмические или показательные выражения, на более простые алгебраические множители.

Например, выражение вида $log_{a}f-log_{a}g$ , где f и g – функции от x, a – число, можно заменить на более простое (f − g) (a − 1) – конечно, при условии, что f(x) > 0 и g(x) > 0. Доказательство легко провести самостоятельно.

А сейчас – самое главное: волшебная таблица, позволяющая заменять сложные логарифмические (или показательные) множители в неравенствах на более простые. Эта таблица является ключом к задаче С3. Вот увидите, она выручит вас на ЕГЭ по математике:

Сложный множитель	На что заменить
log_h f − log_h g	(h − 1) (f − g)
log_h f − 1	(h − 1) (f − h)
log_h f	(h − 1) (f − 1)
h^f − h^g	(h − 1) (f − g)
h^f − 1	(h − 1) · f
f^h − g^h	(f − g) · h
f, g — функции от x. h — функция или число.

Конечно же, все выражения, которые содержат логарифмы, существуют при f, g, h > 0 и h ≠ 1.

Когда на ЕГЭ по математике вы применяете метод рационализации (замены множителя), – обязательно поясните, что вы им воспользовались. И не забудьте доказать соответствующую формулу. Иначе можно потерять балл.

Обратите внимание, что мы говорим о замене множителя в неравенствах вида Знак здесь может быть любой: >, ≥, ≤. Правая часть обязательно должна быть равна нулю. И заменяем мы именно множитель (а не слагаемое, например). Иначе ничего не получится.

Перейдем к практике – к решению задач из вариантов ЕГЭ по математике Профильного уровня.

1. $log_{2-x}(x+2)cdot log_{x+3}(3-x)leq 0$ .

ОДЗ неравенства: .

Применим метод рационализации. В соответствии с нашей таблицей, множитель $log_{2-x}(x+2)$ заменим на (2 − x − 1)(x + 2 − 1). Множитель вида $log_{x+3}(3-x)$ заменим на (x + 3 − 1)(3 − x − 1). Таким образом, от логарифмического неравенства мы перешли к рациональному:

(1 − x) (x + 1) (x + 2) (2 − x) ≤ 0.

Решим его методом интервалов:

Ответ: .

2. $frac{10^{x}}{2cdot log^{2}_{2}(x+1)^{2}cdot log_{3}(x+2)}leq frac{(15cdot 3^{x})^{x}}{9cdot log^{2}_{2}(x+1)^{2}cdot log_{3}(x+2)}.$

Начнем с ОДЗ.

$left{begin{matrix} xneq 0;\ x>-2;\ xneq -1. end{matrix}right.$

Заметим, что выражение $log^{2}_{2}(x+1)^{2}$ положительно при x ∈ ОДЗ. Умножим обе части неравенства на это выражение.
Упростим числитель правой части неравенства:

$(15cdot 3^{x})^{x}=5^{x}cdot 3^{x}cdot 3^{x^{2}}=5^{x}cdot 3^{x^{2}+x}$
Поделим обе части неравенства на 5^x > 0:

$frac{2^{x}}{2log_{3}(x+2)}leq frac{3^{x^{2}+x}}{9log_{3}(x+2)}: : Leftrightarrow \ , , \ : : \ Leftrightarrow frac{2^{x-1}-3^{x^{2}+x-2}}{log_{3}(x+2)}leq 0: : Leftrightarrow \ , , \ : : \ Leftrightarrow frac{2^{x-1}-3^{(x-1)(x+2)}}{log_{3}(x+2)}leq 0.$ Неравенство уже намного проще, чем исходное. Но основания степеней разные! Чтобы применить метод рационализации, нам придется представить 2^{x − 1} в виде степени с основанием 3.

$2^{x-1}=3^{log_{3}2^{x-1}}=3^{(x-1)log_{3}2}.$ Неравенство примет вид:

$frac{3^{(x-1)log_{3}2}-3^{(x-1)(x+2)}}{log_{3}(x+2)}leq 0.$ Воспользуемся методом замены множителя. Множитель вида h^f −h^g можно заменить на (h − 1) (f − g). Да и логарифм в знаменателе можно заменить на выражение x + 1.

$frac{(x-1)(x-(log_{3}2-2))}{x+1}geq 0.$ Оценим $log_{3}2-2$ . Это необходимо сделать, чтобы правильно расставить точки на числовой прямой.

$log_{3}1<log_{3}2<log_{3}3;$ $0<log_{3}2<1$ $-2<log_{3}2-2<-1$ Ответ:

3. $frac{10^{log_{2}x}}{2x^{2}(x+1)}leq frac{(15cdot 3^{log_{2}x})^{log_{2}x}}{9x^{2}(x+1)}$ .

Постараемся упростить это неравенство. Область допустимых значений

$left{begin{matrix} x>0;\ x+1neq 0. end{matrix}right.$ Отсюда следует, что x > 0. Это хорошо, потому что при данных значениях x выражение x + 1 строго положительно, следовательно, мы можем умножить на него обе части неравенства. Да и на x² тоже можно умножить обе части неравенства, и тогда оно станет проще:

$frac{10^{log_{2}x}}{2}leq frac{15^{log_{2}x}cdot 3^{log^{2}_{2}x}}{9}$ Преобразуем числители выражений в левой и правой части и сделаем замену log₂x = t:

$frac{2^{t}cdot 5^{t}}{2}leq frac{3^{t}cdot 5^{t}cdot 3^{t^{2}}}{9}$ Теперь обе части неравенства можно сократить на 5^t > 0:

$2^{t-1}leq 3^{t^{2}+t-2};$
$2^{t-1}-3^{(t+2)(t-1)}leq 0.$

Поскольку $2=3^{log_{3}2}$ , выражение 2^t−1 можно записать как 3^{(t−1)·log₃2}:

$3^{(t-1)cdot log_{3}2}leq 3^{(t+2)(t-1)};$ $(t-1)cdot log_{3}2leq (t-1)(t+2);$ $(t-1)cdot log_{3}2-(t-1)(t+2)leq 0.$ $(t-1)(log_{3}2-t-2)leq 0;$ $(t-1)(t-(log_{3}2-2))leq 0.$ Заметим, что log₃2 − 2 < 0.

Мы получили квадратичное неравенство относительно t. Решим его:

Итак, t ≥ 1 или t ≤ log₃2 − 2.

Вернемся к переменной x:

$: \ log_{2}xgeq 1\ xgeq 2;$ или $: \ log_{2}xleq log_{3}2-2;\ 0<xleq 2^{log_{3}2-2}.$

Ответ: $x in (0;2^{log_3 2-2}]cup[2;+infty).$

4. Еще одна задача из той же серии:

$frac{14^{log_{2}(4x)}}{7cdot log^{2}_{2}(32x)cdot log_{2}(0,25x)}geq frac{(4cdot 2^{log_{2}(4x)})^{log_{2}(4x)}}{4cdot log^{2}_{2}(32x)cdot log_{2}(0,25x)}.$ Запишем ОДЗ:

$left{begin{matrix} x>0;\ 32xneq 1;\ 0,25xneq 1. end{matrix}right.$

$xin left ( 0;frac{1}{32} right )cup left ( frac{1}{32};4 right )cup left (4;+infty right ) .$

Умножим обе части неравенства на $log^{2}_{2}32x>0$ . Постараемся упростить числители выражений в левой и правой части:

$frac{7^{log_{2}(4x)}cdot 2^{log_{2}(4x)}}{7cdot log_{2}(0,25x)}geq frac{4^{log_{2}(4x)}cdot 2^{(log_{2}(4x))^{2}}}{4cdot log_{2}(0,25x)}$
Поделим обе части неравенства на $2^{log_{2}(4x)}>0.$

$frac{7^{log_{2}(4x)}}{7cdot log_{2}(0,25x)}geq frac{2^{(log_{2}(4x))^{2}+log_{2}(4x)}}{4cdot log_{2}(0,25x)};$

$frac{7^{log_{2}(4x)-1}-2^{left ((log_{2}(4x))^{2}+log_{2}(4x)-2 right )}}{ log_{2}(0,25x)} geq 0$
Хорошо бы сделать замену. Пусть log₂(4x) = t. Тогда:

$log_{2}x=t-2;$

$log_{2}(0,25x)=log_{2}left ( frac{1}{4} right )+log_{2}x=log_{2}x-2=t-4.$ Неравенство примет вид:

$frac{7^{t-1}-2^{t^{2}+t-2}}{t-4}geq 0.$
Мы уже знаем, как представить число 7 в виде степени числа 2: $7=2^{log_{2}7}.$

$frac{2^{(t-1)cdot log_{2}7}-2^{(t-1)(t+2)}}{t-4}geq 0.$ Применим метод рационализации:

$frac{(t-1)cdot log_{2}7-(t-1)(t+2)}{t-4}geq 0;$

$frac{(t-1) (log_{2}7-t-2)}{t-4}geq 0;$

Оценим $log_{2}7-2:$

4 < 7 < 8;

$log_{2}4<log_{2}7<log_{2}8;$

$2<log_{2}7<3$

$0<log_{2}7-2<1$

$tleq log_{2}7-2\ , \ log_{2}(4x)leq log_{2}7-2;\ , \ log_{2}(4x)leq log_{2}frac{7}{4};\ , \ 0<xleq frac{7}{16};$ или $1leq t<4;\ , \ 1leq log_{2}(4x)<4;\ , \ log_{2}2leq log_{2}(4x)<log_{2}16;\ , \ frac{1}{2}leq x<4;$

Ответ: $xin left ( 0;frac{1}{32} right )cup left ( frac{1}{32};frac{7}{16} right ]cup left [ frac{1}{2};4 right ).$

5. Еще одна задача-страшилка из того же сборника:

$frac{log_{2^{left ( left ( x-1 right )^{2}-1 right )}}left ( log_{(2x^{2}+10x+15)}(x^{2}+2x) right )}{log_{2^{left ( left ( x-1 right )^{2}-1 right )}}left ( x^{2}+10x+26 right )}geq 0.$ Начнем с ОДЗ. Условий будет много – все выражения под логарифмами должны быть положительны, все основания логарифмов положительны и не равны единице, и еще знаменатель не равен нулю

$left{begin{matrix} (x-1)^{2}-1neq 0;\ x(x+2)>0;\ xneq -5. end{matrix}right.$

Применим в левой части неравенства формулу перехода к другому основанию:

$frac{log_{c}b}{log_{c}a}=log_{a}b;$

$log_{x^{2}+10x+26}left ( log_{2x^{2}+10x+15} left ( x^{2}+2x right )right )geq 0.$

Последовательно применим метод замены множителя, то есть метод рационализации.

Напомним, что множитель log_h f можно заменить на (h-1)( f-1), а множитель (log_h f — 1) — на (h — 1)( f — h):

$(x^{2}+10x+25)(log_{2x^{2}+10x+15}(x^{2}+2x)-1)geq 0;$

Поскольку $(x+5)^{2}>0$ при x ∈ ОДЗ, а $2x^{2}+10x+14>0$ при всех x, получим:

С учетом ОДЗ:

Ответ: x ∈ (-5; -3].

Посмотрим, чем поможет метод замены множителя в решении сложного показательного неравенства.

6. Решите неравенство: $displaystyle frac{{rm 2}cdot {{rm 3}}^{{rm 2x+1}}{rm -}{{rm 6}}^{{rm x}}{rm -}{{rm 4}}^{{rm x+1}}{rm -}{rm 9}}{{{rm 9}}^{{rm x}}{rm -}{rm 3}}le {rm 3.}$

$displaystyle frac{{rm 2}cdot {{rm 3}cdot {rm 3}}^{{rm 2x}}{rm -}{{rm 6}}^{{rm x}}{rm -}{rm 4}cdot {{rm 2}}^{{rm 2x}}{rm -}{rm 3}cdot {{rm 3}}^{{rm 2x}}{rm -}{rm 9+9}}{{{rm 3}}^{{rm 2x}}{rm -}{rm 3}}le {rm 0}.$

$displaystyle frac{{{rm 3}cdot {rm 3}}^{{rm 2x}}{rm -}{{rm 3}}^{{rm x}}cdot {{rm 2}}^{{rm x}}{rm -}{rm 4}cdot {{rm 2}}^{{rm 2x}}}{{{rm 3}}^{{rm 2x}}{rm -}{rm 3}}le {rm 0}.$

Числитель дроби в левой части — однородное выражение, где каждое слагаемое имеет степень 2х. Поделим обе части неравенства на ${{rm 2}}^{{rm 2}{rm x}}{rm textgreater 0.}$

Получим:

$displaystyle newline frac{3 cdot left (frac{3}{2} right )^{2x}-left (frac{3}{2} right )^{x}-4}{3^{2x}-3}leq 0;$

$displaystyle newline , newline 3 cdot left (frac{3}{2} right )^{2x}-left (frac{3}{2} right )^{x}-4=0;$

$displaystyle newline , newline frac{3left ( left ( frac{3}{2} right )^x+1 right )left ( left ( frac{3}{2} right )^x-frac{4}{3} right )}{3^{2x}-3}leq 0.$

Разложим числитель на множители.

Сделаем замену:

$displaystyle newline left ( frac{3}{2} right )^x=t; , ,3t^2-t-4=0;$

$displaystyle newline , newline t=frac{1pm 7}{6}; , t_1=-1; , t_2=frac{4}{3};$

$displaystyle newline , newline 3t^2-t-4=3left ( t+1 right )left ( t-frac{4}{3} right ).$

Вернемся к неравенству:

$displaystyle frac{3left ( left ( frac{3}{2} right )^x+1 right )left ( left ( frac{3}{2} right )^x-frac{4}{3} right )}{3^{2x}-3}leq 0.$

Поскольку $displaystyle {left(frac{3}{2}right)}^x textgreater 0$ , поделим обе части неравенства на $displaystyle {left(frac{3}{2}right)}^x+1 textgreater 0.$

$displaystyle frac{{left(frac{3}{2}right)}^x-frac{4}{3}}{3^{2x}-3}le 0.$

Применяя метод рационализации, множитель вида h^f-h^g заменяем на

Получим: $displaystyle newline frac{left ( frac{3}{2} -1right )left ( x-log_{frac{3}{2}}frac{4}{3} right )}{left ( 3-1 right )left ( 2x-1 right )} leq 0;$

$displaystyle newline , newline frac{x-log_{frac{3}{2}}frac{4}{3}}{x-frac{1}{2}}leq 0.$

Остается решить неравенство методом интервалов. Но как сравнить $displaystyle frac{1}{2}$ и ${{log}_{frac{3}{2}} frac{4}{3} }$ ?

Что больше? Давайте представим $displaystyle frac{1}{2}$ как логарифм с основанием $displaystyle frac{3}{2}:$

$displaystyle frac{1}{2}={{log}_{frac{3}{2}} {left(frac{3}{2}right)}^{frac{1}{2}} }={{log}_{frac{3}{2}} sqrt{frac{3}{2}} };$

$displaystyle frac{4}{3} vee sqrt{frac{3}{2}};$

$displaystyle frac{16}{9} vee frac{3}{2};$

Значит, $displaystyle {{log}_{frac{3}{2}} frac{4}{3} } textgreater frac{1}{2}.$

Ответ: $displaystyle xin left(frac{1}{2}; {{log}_{frac{3}{2}} frac{4}{3} }right].$

7. Теперь логарифмическое неравенство. Обратите внимание, что здесь лучше всего записывать решение в виде цепочки равносильных переходов. И само неравенство, которое мы упрощаем, и область его допустимых значений мы записываем в одну систему. И решаем ее.

Решите неравенство: $displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }ge -2.$

$displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }ge -2 textless = textgreater left{ begin{array}{c}3-x textgreater 0 \3-xne 1 \displaystyle frac{x+4}{{left(x-3right)}^2} textgreater 0 \displaystyle {{log}_{3-x} frac{x+4}{{left(x-3right)}^2} }+2ge 0 end{array}right. .$

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что ${left(a-bright)}^2={left(b-aright)}^2 .$

Используем также условия

$left{ begin{array}{c}x textless 3 \xne 2 \x+4 textgreater 0 \{log}_{3-x}left(x+4right)-{log}_{3-x}{left(3-xright)}^2+2ge 0 end{array}right. textless = textgreater left{ begin{array}{c}x textless 3 \xne 2 \x textgreater -4 \{log}_{3-x}left(x+4right)ge 0 end{array}right. .$

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, ${{log}_a {left(bleft(xright)right)}^2=2{{log}_a left|bleft(xright)right| } }.$

Поскольку $3-x textgreater 0, { log}_{3-x}{left(3-xright)}^2=2{{log}_{3-x} left|3-xright|= }2{{log}_{3-x} left(3-xright)=2. }$

Согласно методу замены множителя, выражение ${log}_{3-x}left(x+4right)$ заменим на

Получим систему:

$left{ begin{array}{c}xne 2 \-4 textless x textless 3 \left(2-xright)left(x+3right)ge 0 end{array}right. .$

Решить ее легко.

Ответ:

8. А теперь неравенство с ловушкой. Мы надеемся, что вы помните — нельзя извлекать корень из неравенства.

Решите неравенство: $displaystyle {{lg}^2 frac{{left(x+2right)}^2left(x+5right)}{5} textless {lg}^2frac{x+5}{20} }.$

Извлекать корень из неравенства нельзя! Можно перенести все в левую часть неравенства и разложить на множители как разность квадратов:

$displaystyle left ( lgfrac{left ( x+2 right )^2left ( x+5 right )}{5}-lgfrac{x+5}{20} right )left ( lgfrac{left ( x+2 right )^2left ( x+5 right )}{5}+lgfrac{x+5}{20} right ) textless 0.$

Применим формулы разности и суммы логарифмов, следя за областью допустимых значений. Все выражения под логарифмами в исходном неравенстве должны быть положительны.

$left{ begin{array}{c}displaystyle lgfrac{{left(x+2right)}^2left(x+5right)cdot 20}{5cdot left(x+5right)}cdot {lg left(frac{{left(x+2right)}^2cdot {left(x+5right)}^2}{100}right) } textless 0 \displaystyle {left(x+2right)}^2left(x+5right) textgreater 0 \x+5 textgreater 0 end{array}right. .$

Посмотрим на второе и третье неравенства системы. Поскольку х+5 положительно, то и выражение (x+2)^2 должно быть положительно.

Заметим, что решения неравенства — это все числа, кроме x= - 2.

Получим:

$left{ begin{array}{c}displaystyle lgleft ( 4cdotleft ( x+2 right )^2 right ) cdot lg left ( frac{left ( x+2 right )^2 cdot left ( x+5 right )^2}{100} right ) textless 0\x textgreater -5 \xne -2 end{array}right..$

По методу рационализации, каждый из множителей вида ${{log}_h f }$ заменяем на

$newline left{ begin{array}{c}displaystyle left(10-1right)cdot left(4{left(x+2right)}^2-1right)cdot left(10-1right)left(frac{{left(x+2right)}^2cdot {left(x+5right)}^2}{100}-1right) textless 0 \x textgreater -5 \xne -2 end{array}right.newline textless = textgreater left{ begin{array}{c}left(2x+4-1right)left(2x+4+1right)left(left(x+2right)left(x+5right)-10right)left(left(x+2right)left(x+5right)+10right) textless 0 \x textgreater -5 \xne -2 end{array}right.newlinetextless = textgreater left{ begin{array}{c}left(2x+3right)left(2x+5right)cdot xcdot left(x+7right)cdot left(x^2+7x+20right) textless 0 \x textgreater -5 \xne -2 end{array}right.newline textless = textgreater left{ begin{array}{c}left(2x+3right)left(2x+5right)cdot xcdot left(x+7right) textless 0 \x textgreater -5 \xne -2 end{array}right. .$

Просто равносильные преобразования. Выражение положительно всегда — так как в уравнении дискриминант отрицателен. Осталось применить метод интервалов.

Ответ: $displaystyle xin left(-5;-frac{5}{2}right)cup left(-frac{3}{2};0right).$

Больше неравенств: Задание 15 Профильного ЕГЭ по математике

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Неравенства. Метод замены множителя (метод рационализации)» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Решение неравенств

Задание
1

#2500

Уровень задания: Легче ЕГЭ

Решите неравенство [x+10<3x^2]

Перенесем слагаемые в левую часть: [-3x^2+x+10<0] Разложим на множители выражение (-3x^2+x+10): [-3x^2+x+10=0 quad Rightarrow quad x_1=2quadtext{и}quad x_2=-dfrac53] Следовательно, (-3x^2+x+10=-3(x-2)left(x-frac53right)=-(x-2)(3x+5)).
Тогда неравенство примет вид [-(x-2)(3x+5)< 0quad Rightarrow
quad (x-2)(3x+5)>0] Решим его методом интервалов:

Таким образом, подходят (xin
left(-infty;-frac53right)cup(2;+infty)).

Ответ:

(left(-infty;-frac53right)cup(2;+infty))

Задание
2

#2501

Уровень задания: Легче ЕГЭ

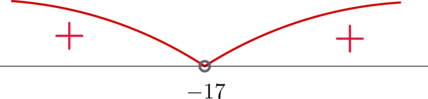
Решите неравенство [x^2+34x+289>0]

Заметим, что по формуле квадрата суммы (x^2+34x+289=(x+17)^2), следовательно, неравенство принимает вид: [(x+17)^2>0] Решим его методом интервалов:

Таким образом, нам подходят (xin(-infty;-17)cup(-17;+infty)).

Ответ:

((-infty;-17)cup(-17;+infty))

Задание
3

#2502

Уровень задания: Легче ЕГЭ

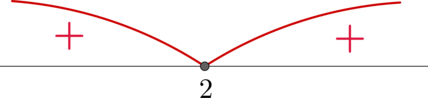
Решите неравенство [x^2-4x+4leqslant 0]

Заметим, что по формуле квадрата разности (x^2-4x+4=(x-2)^2), следовательно, неравенство принимает вид: [(x-2)^2leqslant 0] Решим его методом интервалов:

Таким образом, нам подходят (xin{2}).

Ответ:

({2})

Задание
4

#2503

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2+3x+3geqslant 0]

Разложим на множители выражение (x^2+3x+3), для этого решим уравнение (x^2+3x+3=0). Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех (x). Проверить его знак можно, подставив вместо (x) любое число, например, (x=0): получим (3), следовательно, выражение всегда (>0).

Таким образом, нам подходят (xin mathbb{R}).

Ответ:

(mathbb{R})

Задание
5

#2412

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x — 1)(x + 2)}{(x — 3)(x + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x — 1)(x + 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = 1,qquadqquad x = -2]

2) Найдём нули знаменателя: [(x — 3)(x + 4) = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 3\
x = -4
end{gathered}
right.]

По методу интервалов:

откуда [xin(-4; -2]cup[1; 3),.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-4; -2]cup[1; 3))

Задание
6

#3762

Уровень задания: Легче ЕГЭ

Решить неравенство [dfrac 6{xsqrt3-3}+dfrac{xsqrt3-6}{xsqrt3-9}geqslant 2]

(Задача от подписчиков)

Пусть (xsqrt3-3=t). Тогда [dfrac 6t+dfrac{t-3}{t-6}geqslant 2quadLeftrightarrowquad
dfrac{t^2-15t+36}{t(t-6)}leqslant 0quadLeftrightarrowquad
dfrac{(t-3)(t-12)}{t(t-6)}leqslant 0] Решая данное неравенство методом интервалов, получим (0<tleqslant 3) или (6<tleqslant 12). Следовательно, [left[begin{gathered}begin{aligned}
&0<xsqrt3-3leqslant 3\
&6<xsqrt3-3leqslant
12end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sqrt3<xleqslant 2sqrt3\
&3sqrt3<xleqslant 5sqrt3
end{aligned}end{gathered}right.]

Ответ:

((sqrt3;2sqrt3]cup(3sqrt3;5sqrt3])

Задание
7

#2413

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x + 1)(x — 2)}{(x + 3)(x^2 + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x^2 + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x + 1)(x — 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = -1,qquadqquad x = 2]

2) Найдём нули знаменателя: [(x + 3)(x^2 + 4) = 0] так как (x^2geqslant 0), то (x^2 + 4geqslant 4), следовательно, нули знаменателя: [x = -3]

По методу интервалов:

откуда [xin(-infty; -3)cup[-1; 2],.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-infty; -3)cup[-1; 2])

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Простые неравенства
Cложные неравенства
Иррациональные неравенства
Неравенства с модулем

Простые неравенства

С простыми неравенствами проблем, как правило, не бывает: решаем уравнение относительно нуля, расставляем точки, соответствующие корням, рисуем интервалы, определяем знаки.

Например: (х — 1)² (х + 3)⁶ (х — 5)⁹ ≥ 0 . Корнями этого выражения будут точки: х₁ = 1; х₂ = -3; х₃ = 5. Но точки х₁ и х₂ на знак не влияют,так как первые два множителя заведомо положительные, они возводятся в четную степень. Или, другими словами, в первой скобке два одинаковых корня, во второй — четыре. Определяем, какой знак будет иметь выражение, скажем, в точке 10. Положительное. Рисуем числовую ось и расставляем знаки. Ответ: х ∈ { -3 } ∪ { 1} ∪ [ 5; +∞ )

Почему -3 и 1 появились? Потому что они не меняют знак, но являются частью уравнения, так как у нас стоит знак «больше и равно». Если бы было строгое неравенство, то подобные точки, соответствующие четным корням, необходимо было бы выколоть.

Рассмотрим еще одно неравенство:

Ищем нули функции. Это корни числителя: х_1,2= ±4, х₃ = 3, три корня х₄ = -1; корни знаменателя: х₅ ≠ -4, х₆ ≠ 2. Считаем, какой знак получится у выражения, когда, скажем, х=0. В нуле функция отрицательна. Строим интервалы. Учитываем, что корней х = -4 два, а значит, в этой точке знак не меняется:

Пишем ответ: x ∈ [ -1; 2 ) ∪ [ 3; 4 ]

Сложные неравенства

Решаем сложное неравенство, в котором присутствуют две различные функции в числителе и знаменателе:

Решить это неравенство — значит определить промежутки, где функция положительная. Чтобы расставить все точки над «i», посмотрим, как выглядит график функции. Положительные значения функции находятся выше оси 0х, то есть выше точек пересечения графика с осью. А эти точки — не что иное, как корни уравнения, проще говоря. нас интересуют нули функции. Нули знаменателя, конечно, не совсем корни, делить на ноль нельзя, но в этих точках функция все равно меняет знак. Нас-то интересует знак!!! А корни знаменателя, меняющие знак, «выкалываются». На графике видно, что в точках, где х = 2 и х = -2, функция стремится к бесконечности, но при этом меняет зак с «плюса» на «минус» и с «минуса» на «плюс».

Для наглядности посмотрите, как ведут себя графики числителя (зеленый пунктир), точки «нулей » знаменателя (синие точки) и график нашей функции. Все корни совпали, а точки (-2; 0) и (2;0) изменили знак функции.

Отсюда вывод:

Для того, чтобы решить любое неравенство, достаточно определиться с так называемыми нулями функции, не забывая «выколоть» нули знаменателя, определить знак любого промежутка из получившихся и чередовать знаки.
Если появились одинаковые корни, количество которых кратно двум, то в них знак не меняется.

Иррациональные неравенства

• Решим неравенство : $(x^2-9)sqrt{x-2}$ ≥ 0 . Неравенство несложное, но есть некоторые тонкости, которые следует учитывать, решая выражения с корнем:

Квадратный корень всегда число неотрицательное по определению, на знак нашего выражения не влияет.
Квадратный корень можно извлечь только из неотрицательного числа.
Решать такие выражения очень часто приходится возведением обеих частей неравенства в квадрат, а это — не всегда равносильные выражения.

При решении уравнений все вышесказанное приводит к обязательной проверке корней, что невозможно сделать в неравенстве. Поэтому такие неравенства превращаются в систему неравенств.

Так как в конкретном нашем выражении корень не влияет на знак, мы на него делим. Напомню, что неравенства можно делить или умножать на выражения или числа только, если известен знак этого выражения или числа, так как в противном случае такое деление может изменить знак всего неравенства.

Решаем систему: $begin{Bmatrix}{x^2-9 ge 0}\{x-2ge 0}end{matrix}$ Первое неравенство имеет решение при х ≤ -3 и х ≥ 3. Второе — при х ≥ 2. Выводим общие для обоих неравенств интервалы.

Ответ: х ∈ [ 3; +∞ )

• Рассмотрим еще одно неравенство: .

Функция ограниченная из-за двух корней, поэтому сначала найдем область определения функции (ООП):

$begin{Bmatrix}{16 - 2x ge 0}\{x +1 ge 0}end{matrix}$ Решение этого неравенства: х ∈ [ -1; 8 ].

Теперь решаем само неравенство. Можно решить стандартно, возводя в квадрат обе части, при этом желательно перенести второй корень в правую часть, а единицу влево, и возвести в квадрат: $(sqrt{16-2x} +1)^2< (sqrt{x+1})^2$ . Обращаю ваше внимание, что придется возводить в квадрат два раза, так как слева после возведения останется корень от удвоенного произведения первого слагаемого на второе.

Но можно несколько облегчить себе задачу, введя новую переменную . Тогда х+1 = t² , х = t² — 1, а

$sqrt{16-2x} =sqrt{16-2(t^2-1)}=sqrt{18-2t^2}$

а все выражение превратится в выражение с одним корнем:

$sqrt{18-2t^2}$ — t < -1 ⇒ $sqrt{18-2t^2}$ < t — 1

Возводим в квадрат,…….и т.д. Дальше решать не буду, Думаю, все понятно. Корни будут иррациональными, и это — нормально.

Неравенства с модулем

Отдельная история — неравенства с модулем. Вспомним,что такое модуль числа

Очевидно, что решать уравнения или неравенства с модулем можно только, раскрыв модуль. Модуль раскрывается по правилу в зависимости от знака выражения, стоящего под модулем. Давайте разбираться на конкретных примерах:

а).

Если построить числовую ось, то все значения, удовлетворяющие этому неравенству, окажутся внутри интервала х ∈ ( -3; 3) Неравенство у нас строгое, значит скобки будут круглые.

в). ⇒ $begin{bmatrix}{x > 3}\{x< -3}end{matrix}$

Ответ: х ∈ ( — ∞; -3) ∪ ( 3; +∞ ), то есть больше большего корня и меньше меньшего корня.

Если же у нас под знаком модуля будут какие-нибудь функции, модуль будет раскрываться аналогично вышеизложенному, только уже не получится сразу интервалов, а будет системы или объединенные множества неравенств.

1. Решаем следующее неравенство:

I 2x — 7 I ≤ 5

Открываем модуль:

-5 ≤ 2x -7 ≤ 5

Внутри модуля функция линейная, которую можно решить двойным неравенством. Сначала прибавим ко всем трем частям 7, получим :

2 ≤ 2x ≤ 12,

затем разделим все неравенство на 2 :

1 ≤ x ≤ 6

Ответ: х ∈ [ 1; 6 ].

2. Еще одно неравенство:

Сначала найдем область определения функции, т.к. наша функция — ограниченная. ООП: х > -2.

Убираем модуль. Наше неравенство превращается в объединенное множество:Учитывая ООП, получаем ответ: х ∈ ( -2; -17/9 ) ∪ ( 7; +∞)

3. Ну, и наконец, неравенство с двумя модулями: В этом неравенстве две точки смены знака под модулем, это точки 3 и 5, следовательно, модули будем открывать на трех промежутках:

Ответ: х∈ ( — ∞; 2 ] ∪ [4; +∞)

Это неравенство можно представить графически. Для этого достаточно построить графики функции (зеленой) с модулями

y = Ix — 3I + Ix — 5I (в неравенстве слева) и (красной) линейной функции

y =6 — x, находящейся на правой стороне неравенства. По условию неравенства нас интересует та часть графиков, где зеленая функция находится выше красной. Как видите, ответ тот же самый!

NB: Кстати, решение уравнений и неравенств при помощи графиков часто очень помогает разобраться с задачами с параметрами — с задачами №18 профильного ЕГЭ. Но это уже тема для другой статьи.

Источник

Павел Бердов
уроки математики

Глава 1.: Логарифмические неравенства
§ 1.: Пример решения задачи 15
§ 2.: Задача 15: системы логарифмических неравенств
Глава 2.: Показательные неравенства
§ 1.: Показательные неравенства в задаче 15
§ 2.: Что делать, если в показателе стоит логарифм
§ 3.: Задача 15: тонкости решения систем неравенств
§ 4.: Особенности сравнения корней в логарифмических неравенствах
§ 5.: Пример из настоящего ЕГЭ: решение нестандартной системы неравенств
§ 6.: Задача 15 из пробного ЕГЭ 2016 от 3 марта — решаем неравенство
§ 7.: Как монотонность логарифма помогает упростить решение неравенства в несколько раз? (абсолютно легальный приём)
§ 8.: Задание 15: метод интервалов для логарифмов

Источник

Неравенства. Метод замены множителя (метод рационализации)