Поиск
Всего: 117 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Прямая является касательной к графику функции
Найдите a.
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
На рисунке изображён график функции y = f(x), определённой на интервале (−4; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 18.
На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
На рисунке изображен график функции f(x) и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции f(x) в точке x0.
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 19.03.2019. Вариант 2
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
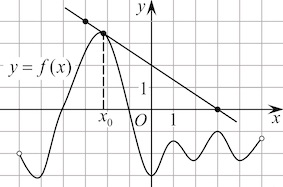
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
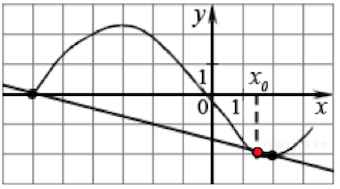
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
На рисунке изображён график функции
и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
Всего: 117 1–20 | 21–40 | 41–60 | 61–80 …
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на нахождение касательной
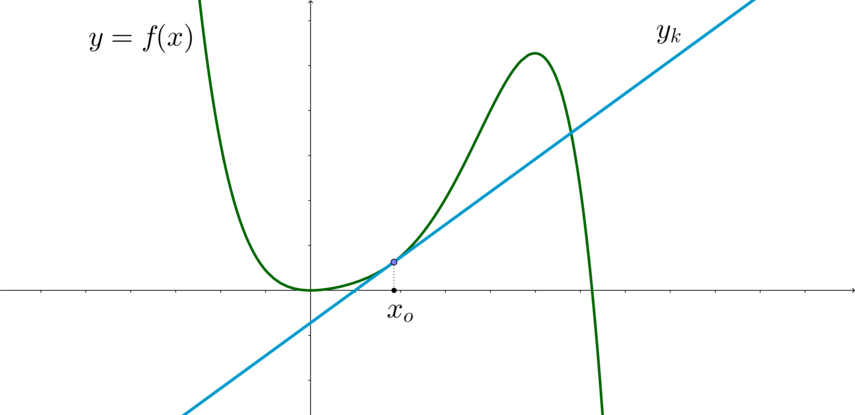
(blacktriangleright) Если к функции (y=f(x)) в точке (x_o) проведена касательная, то уравнение касательной имеет вид [{Large{y_k=f(x_o)+f'(x_o)(x-x_o)}}] Таким образом, угловой коэффициент касательной (k=f'(x_o)).
(blacktriangleright) Для того, чтобы определить, при каких (k) и (b) прямая (y_k=kx+b) является касательной к функции (y=f(x)), необходимо решить одну из двух систем: [{Large{begin{cases} k=f'(x_o)\ b=f(x_o)-f'(x_o)cdot
x_oend{cases}}} quad text{ или } quad {Large{begin{cases} k=f'(x_o)\
f(x_o)=y_k(x_o)end{cases}}}]
Задание
1
#1238
Уровень задания: Легче ЕГЭ
Найдите все значения параметра (a), при каждом из которых графики функций
[f(x)=x^2+2x-3 quad и quad ay+5x+6a=0]
имеют ровно одну точку пересечения.
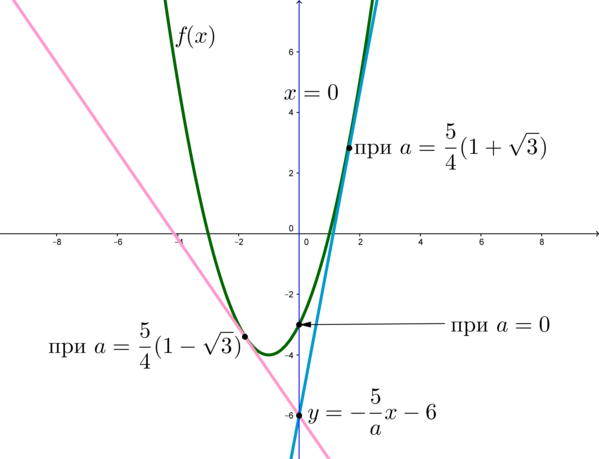
Графиком (f(x)) является парабола, пересекающая ось (Ox) в точках (x=-3) и (x=1), а ось (Oy) в точке (y=-3).
Графиком (ay+5x+6a=0) при каждом фиксированном (a) является прямая:
1) При (a=0) это прямая (x=0). Она имеет ровно одну точку пересечения с (f(x)), а именно, точку ((0;-3)).
2) При (ane 0) это пучок прямых (y=-dfrac{5}{a}x-6), проходящих через точку ((0;-6)).
Графики будут иметь ровно 1 точку пересечения при тех значениях (a), при которых прямая (y) будет касаться параболы.
Условия касания в точке (x_o): [begin{cases}
f'(x_o)=-dfrac{5}{a}\
f(x_o)=y(x_o)
end{cases} Rightarrow
begin{cases}
x_o=-dfrac{5}{2a}-1\
8a^2-20a-25=0
end{cases} Rightarrow a=dfrac{5}{4}(1 pm sqrt3)]
Ответ:
(ain Big{ dfrac{5}{4}(1-sqrt3); 0;
dfrac{5}{4}(1+sqrt3)Big}).
Задание
2
#1239
Уровень задания: Равен ЕГЭ
Найдите все возможные значения параметра (a), при каждом из которых уравнение [dfrac{1}{3}x^3+2x^2-dfrac{88}{3}=a(x+8)]
имеет ровно одно решение.
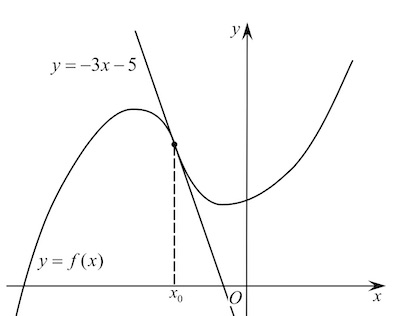
Рассмотрим функцию (f(x)=dfrac{1}{3}x^3+2x^2-dfrac{88}{3}) и пучок прямых (y=a(x+8)).
(f'(x)=x^2+4x Rightarrow x=-4=x_{max}) – точка максимума, (x=0=x_{min}) – точка минимума.
(f(x_{max})=-dfrac{56}{3}, f(x_{min})=-dfrac{88}{3}).
Все прямые (y=ax+8a) проходят через точку ((-8;0)).
Найдем случаи, когда прямая (y) касается графика функции (f(x)) ((x_o) – точка касания). Найдем соответствующие этому значения параметра: [begin{cases}
f'(x_o)=a\
f(x_o)=y(x_o)
end{cases} Rightarrow
begin{cases}
x_o^2+4x_o=a\
2x_o^3+30x_o^2+96x_o+88=0
end{cases}Rightarrow
begin{cases}
x_o^2+4x_o=a\
(x_o+2)^2(x_o+11)=0
end{cases} Rightarrow
left[
begin{gathered}
begin{aligned}
&begin{cases}
x_o=-2\
a=-4
end{cases}\
&begin{cases}
x_o=-11\
a=77
end{cases}
end{aligned}
end{gathered}
right.]
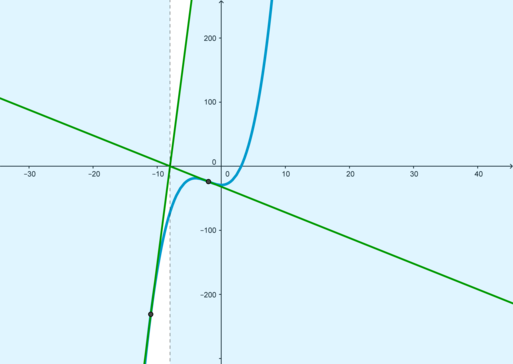
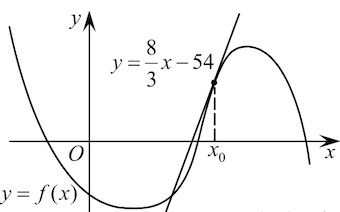
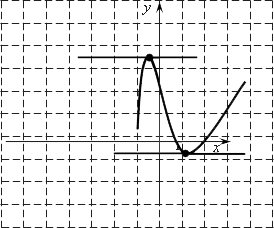
Таким образом, уравнение (f(x)=y) будет иметь единственное значение при тех значениях (a), при которых прямые (y) будут располагаться в закрашенных областях: (причем граничный случай (a=77) не подходит)
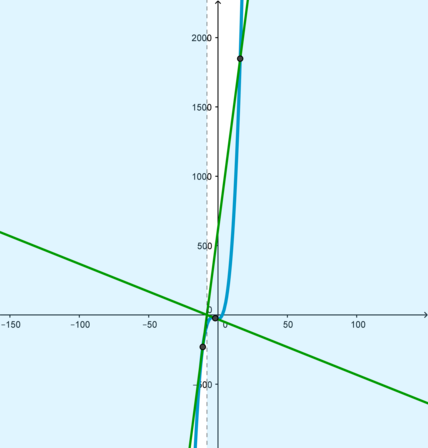
В уменьшенном масштабе это выглядит так:
Следовательно, (ain (-infty; 77)).
Ответ:
(ain (-infty; 77)).
Задание
3
#3160
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых система [begin{cases}
sqrt{(x-a)^2+y^2}+sqrt{x^2+(y+a)^2}=|asqrt2|\
x^2+y^2leqslant 18 end{cases}]
будет иметь единственное решение.
Задача от подписчиков.
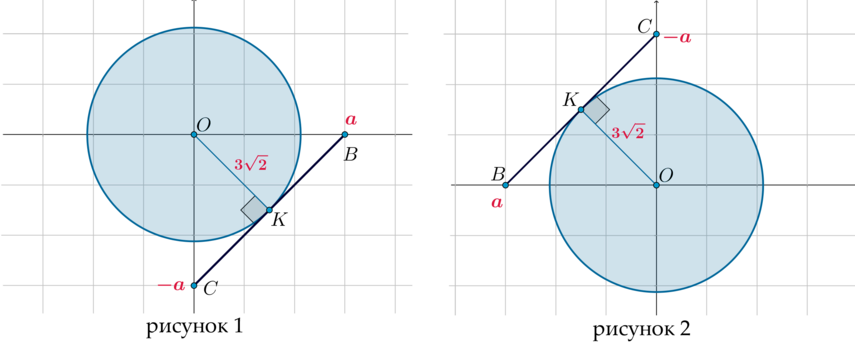
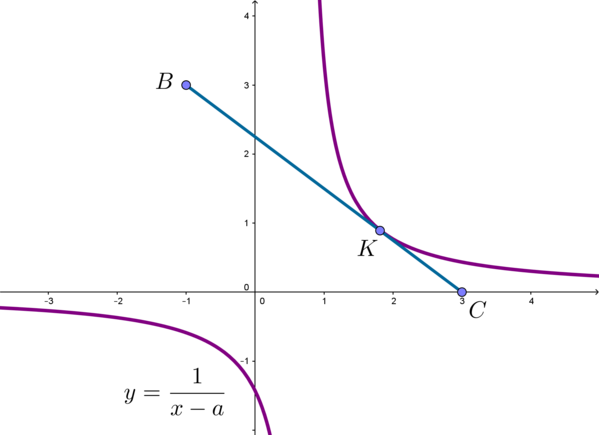
1) Первое уравнение системы при (ane 0) задает отрезок (BC), где (B(a;0)), (C(0;-a)).
Действительно, пусть (A(x;y)). Тогда [begin{aligned}
&BA=sqrt{(x-a)^2+y^2}\[1ex]
&AC=sqrt{x^2+(y+a)^2}\[1ex]
&BC=sqrt{(a-0)^2+(0+a)^2}=|asqrt2| end{aligned}] Таким образом, первое уравнение можно записать в виде [BA+AC=BC] То есть данное уравнение задает множество точек (A), лежащих на отрезке (BC).
При (a=0) данное уравнение задает единственную точку (O(0;0)).
2) Второе неравенство задает круг с центром в точке (O(0;0)) и радиусом (R=3sqrt2).
3) Для того, чтобы данная система имела единственное решение при (ane 0), нужно, чтобы отрезок касался круга: при (a>0) отрезок (BC) будет находиться в четвертой четверти (рисунок 1), при (a<0) – во второй (рисунок 2).
Случай, когда (a=0), нам также подходит (так как точка (O) принадлежит кругу).
При (a>0): (BO=CO=|a|=a, OK=3sqrt2) – радиус, проведенный в точку касания. Тогда [dfrac12cdot OBcdot OC=S_{triangle OBC}=dfrac12cdot OKcdot BC
quadRightarrowquad acdot a=3sqrt2cdot asqrt2
quadRightarrowquad a=6.] При (a<0): (BO=CO=|a|=-a). Тогда [dfrac12cdot OBcdot OC=S_{triangle OBC}=dfrac12cdot OKcdot BC
quadRightarrowquad -acdot (-a)=3sqrt2cdot (-asqrt2)
quadRightarrowquad a=-6.]
Ответ:
(ain {-6;0;6})
Задание
4
#1237
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение (3x^3+ax+5=0) имеет единственное решение.
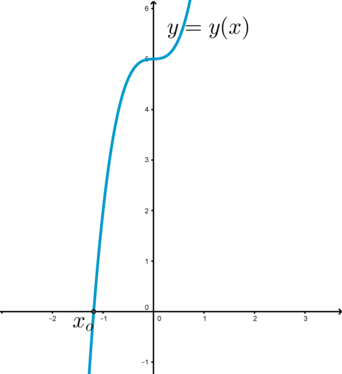
Пусть (y=3x^3+ax+5). Рассмотрим несколько случаев:
1) (a=0). Тогда уравнение имеет единственное решение (x=-sqrt[3]{dfrac{5}{3}}).
2) (a>0). Найдем производную (y’=9x^2+a). Т.к. (a>0), то (y’>0) при любых (x). Следовательно, функция (y) монотонно возрастает на всем (mathbb{R}). Значит, имеет не более одной точки пересечения с осью (Ox).
Заметим, что (yleft(-dfrac{5}{a}right)=-dfrac{375}{a^3}<0;
y(0)=5>0), следовательно, на промежутке (left(-dfrac{5}{a};0right)) есть точка (x_o), в которой (y(x_o)=0). Значит, (x_o) и есть единственное решение данного уравнения.
3) (a<0). Обозначим (-a=b>0).
Рассмотрим уравнение в виде (3x^3=bx-5). Обозначим (f(x)=3x^3,
g(x)=bx-5). Найдем положительные значения (b), при которых функции (f(x)) и (g(x)) имеют ровно одну точку пересечения.
Найдем значения (b), при которых (g(x)) касается (f(x)):
(f'(x)=9x^2). Пусть (x_o) – точка касания. Тогда: [begin{cases}
b>0\
f'(x_o)=b\
f(x_o)=g(x_o)
end{cases} Rightarrow b=9sqrt[3]{dfrac{25}{36}}]
Значит, при (b=9sqrt[3]{dfrac{25}{36}}) функции (f(x)) и (g(x)) имеют 2 точки пересечения, а при (0<b<9sqrt[3]{dfrac{25}{36}}) функции (f(x)) и (g(x)) имеют ровно одну точку пересечения (например, прямая, обозначенная пунктиром).
Тогда (-9sqrt[3]{dfrac{25}{36}}<a<0).
Значит, уравнение будет иметь единственный корень при (ain
left(-9sqrt[3]{dfrac{25}{36}}; +inftyright)).
Ответ:
(ain left( -9sqrt[3]{dfrac{25}{36}}; +infty right)).
Задание
5
#2945
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых наименьшее значение функции [f(x)=4ax+|x^2-6x+5|]
больше, чем (-24).
(Задача от подписчиков)
Вопрос можно переформулировать следующим образом: неравенство [4ax+|x^2-6x+5|>-24] должно выполняться при всех (x) из ОДЗ (а ОДЗ: (xin
mathbb{R})).
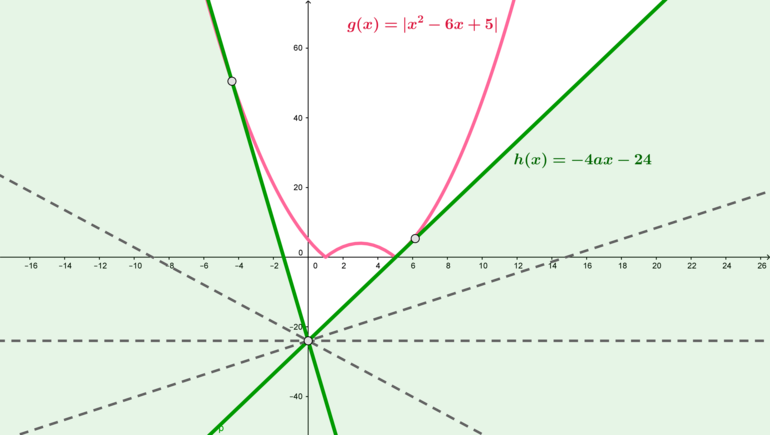
Перепишем неравенство в виде [|x^2-6x+5|>-4ax-24qquad (*)] и рассмотрим функции (g(x)=|x^2-6x+5|) и (h(x)=-4ax-24). Тогда для того, чтобы неравенство ((*)) было выполнено при всех (x), нужно, чтобы прямая (h) находилась ниже графика функции (g).
1) Рассмотрим случай, когда (b=-4a>0). Пусть прямая (h) касается правой ветви параболы (y=x^2-6x+5) (при (xgeqslant 5)).
(y’=2x-6). Следовательно, если они касаются в точке с абсциссой (x_0), то [2x_0-6=b quad {small{text{и}}} quad x_0^2-6x_0+5=bx_0-24] Из этих двух уравнений находим, учитывая (xgeqslant 5), что (x_0=sqrt{29}).
Следовательно, при (x_0=sqrt{29}) имеем (b=2(sqrt{29}-3)).
Тогда при всех (0<b<2(sqrt{29}-3)) прямая будет находиться ниже графика (g), следовательно, для всех (x) будет выполнено неравенство ((*)).
2) Рассмотрим случай, когда (b=0). Тогда прямая (h(x)=-24) параллельна оси абсцисс и находится ниже графика (g) при всех (x). Следовательно, это значение (b) нам подходит.
3) Рассмотрим случай, когда (b<0). Пусть прямая (h) касается левой ветви параболы (y=x^2-6x+5) (при (xleqslant
1)).
(y’=2x-6). Следовательно, если они касаются в точке с абсциссой (x_0), то [2x_0-6=b quad {small{text{и}}} quad
x_0^2-6x_0+5=bx_0-24] Из этих двух уравнений находим, учитывая (xleqslant 1), что (x=-sqrt{29}). Отсюда находим, что (b=-2(sqrt{29}-3)).
Следовательно, при всех (-2(sqrt{29}+3)<b<0) прямая (h) будет находиться ниже графика (g) и неравенство будет выполнено при всех (x).
Итого заключаем, что нам подходят значения: [-2(sqrt{29}+3)<b<2(sqrt{29}-3) quadRightarrowquad
-dfrac{sqrt{29}-3}2<a<dfrac{sqrt{29}+3}2]
Прямые (h) должны находиться в зеленой области.
Ответ:
(-dfrac{sqrt{29}-3}2<a<dfrac{sqrt{29}+3}2)
Задание
6
#2433
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых неравенство [x^2+2|x-a|-4xleqslant -a] имеет единственное целочисленное решение. Для найденных значений (a) выпишите это решение.
Перепишем неравенство в виде: [2|x-a|+aleqslant -x^2+4x]
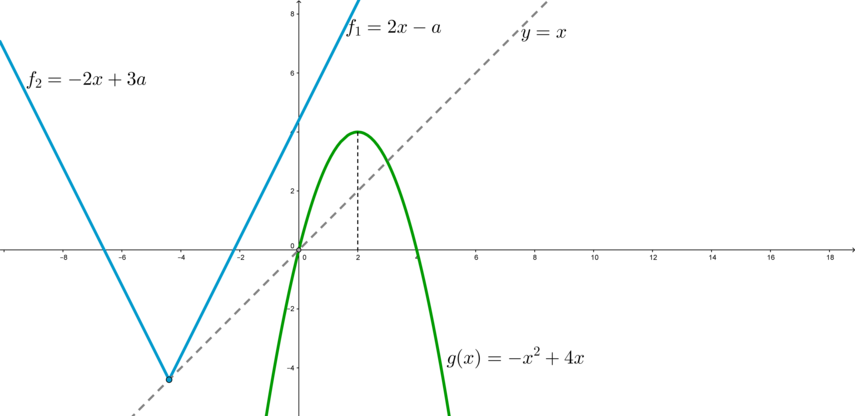
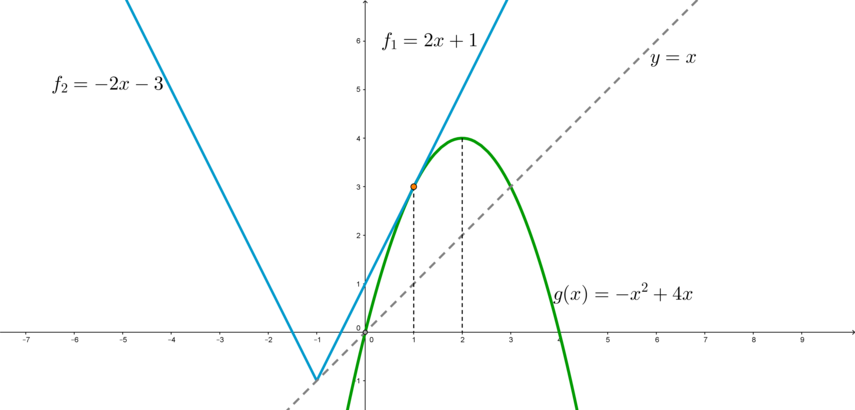
Пусть (f(x)=2|x-a|+a), (g(x)=-x^2+4x) – функции. Тогда по условию задачи необходимо, чтобы промежуток, для которого график (f) лежит не выше графика (g), содержал ровно одну целую точку.
Заметим, что графиком функции (f) является уголок, вершина которого скользит по прямой (y=x). Правая ветвь уголка задается уравнением (f_1(x)=2(x-a)+a=2x-a) при (xgeqslant a); левая ветвь — (f_2(x)=-2(x-a)+a=-2x+3a) при (x<a).
1) Найдем значение параметра, при котором правая ветвь уголка касается параболы (т.к. если уголок находится левее этого положения, то неравенство не имеет решений).
(g’=-2x+4). Если (f_1) касается (g) в точке (x_0), то (g'(x_0)) равно коэффициенту при (x) в уравнении (f_1), то есть:
[-2x_0+4=2 quad Rightarrow quad x_0=1]
Т.к. (f_1) касается (g), то (f_1(x_0)=g(x_0)), откуда находим значение параметра (a=-1).
Таким образом, при (a=-1) правая ветвь (f_1) касается параболы:
Заметим, что при (a=-1) существует ровно одно решение для неравенства, и это (x=1), что является целочисленным значением. Следовательно, (a=-1) нам подходит.
2) Заметим, что при (a=0) вершина уголка находится в точке ((0;0)) и уголок имеет две точки пересечения с параболой: (x=0) и (x=2). Следовательно, решением неравенства является отрезок ([0;2]) (т.к. на этом отрезке уголок находится не выше параболы), содержащий три целых точки ((0,1) и (2)). А вот при (a<0) (но (ageqslant -1)) левая ветвь уголка не пересекает параболу, а правая ветвь пересекает параболу в двух точках, причем одна находится между (0) и (1), а вторая между (1) и (2). То есть в промежуток, удовлетворяющий неравенству, будет входить ровно одна целая точка (x=1). Следовательно, все (-1leqslant a<0) нам подходят.
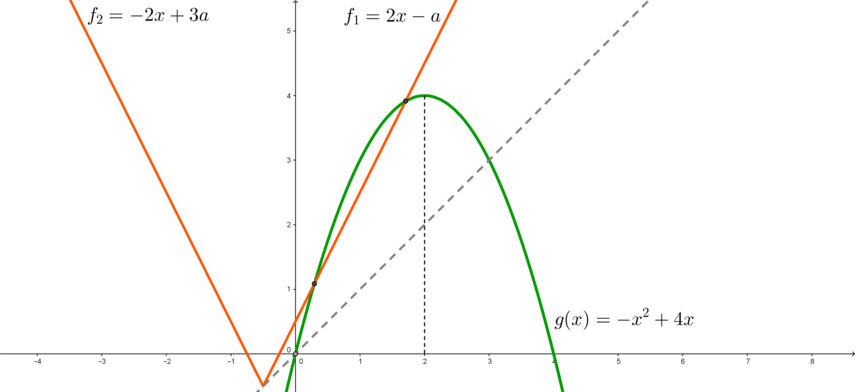
3) Заметим, что если вершина уголка находится в точке ((3;3)) (то есть (a=3)), то левая ветвь уголка касается параболы (в этой точке). Действительно, это можно проверить, поступив так же, как мы поступили в первом пункте: (g’=-2x+4). Если (f_2) касается (g) в точке (x_0), то (g'(x_0)) равно коэффициенту при (x) в уравнении (f_2), то есть:
[-2x_0+4=-2 quad Rightarrow quad x_0=3]
Следовательно, при (a=3) решением неравенства является единственная точка (a=3), которая является целой, то есть (a=3) нам подходит.
Заметим также, что при (a>3) уголок будет находится всегда выше параболы, то есть неравенство не будет иметь решений.
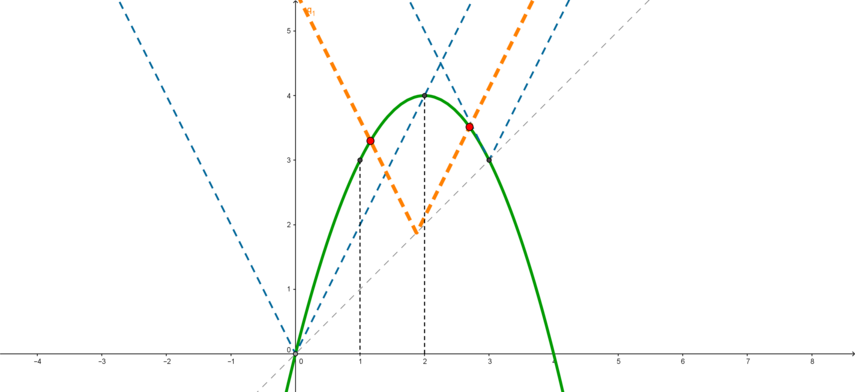
4) Рассмотрим ситуацию, когда (0<a<3). При этих (a) правая ветвь уголка пересекает параболу в точке (xin(2;3)), а вот левая ветвь пересекает параболу в какой-то точке (xin(0;3)). Следовательно, чтобы неравенство имело единственное целочисленное решение, этим решением должно быть (x=2) и точка (x’), в которой левая ветвь пересекает параболу, должна удовлетворять: (1<x’leqslant 2)(оранжевый уголок).
Поэтому найдем значение (a), при котором левая ветвь уголка пересекает параболу в точке (x=1): [f_2(1)=g(1) quad Rightarrow
quad -2+3a=-1+4 quad Rightarrow quad a=dfrac53]
Теперь найдем значение (a), при котором левая ветвь уголка пересекает параболу в точке (x=2):[f_2(2)=g(2) quad Rightarrow
quad -4+3a=-4+8 quad Rightarrow quad a=dfrac83]
То есть при (a=frac53) решением неравенства является отрезок ([1;2,…]), содержащий 2 целые точки ((x=1;2)); при (a=frac83) решением неравенства является отрезок ([2;2,…]), содержащий одну целую точку ((x=2)).
Следовательно, при (frac52<aleqslant frac83) решением будет отрезок ([1,…;2,…]), который содержит одну целую точку (x=2). Такие значения (a) нам подходят.
Таким образом, итоговый ответ:
при (-1leqslant a<0) целочисленное решение (x=1);
при (frac53<aleqslant frac83) целочисленное решение (x=2);
при (a=3) целочисленное решение (x=3).
Ответ:
(ain [-1;0)cupleft(frac53;frac83right]cup{3})
Задание
7
#3071
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых система [begin{cases}
sqrt{x^2+2x+y^2-6y+10}+sqrt{x^2-6x+y^2+9}=5\
xy=1+ay end{cases}]
имеет ровно 2 решения.
(Задача от подписчиков)
Рассмотрим первое уравнение системы. Перепишем его в виде: [sqrt{(x+1)^2+(y-3)^2}+sqrt{(x-3)^2+y^2}=5] Пусть (A(x;y)), (B(-1;3)), (C(3;0)) – точки. Тогда [begin{aligned}
&BA=sqrt{(x+1)^2+(y-3)^2} \[2ex]
&AC=sqrt{(x-3)^2+y^2}\[2ex]
&BC=sqrt{(-1-3)^2+(3-0)^2}=5 end{aligned}] Следовательно, первое уравнение равносильно: [BA+AC=BC] Значит, (A) – точка, принадлежащая отрезку (BC). То есть уравнение задает множество точек отрезка (BC).
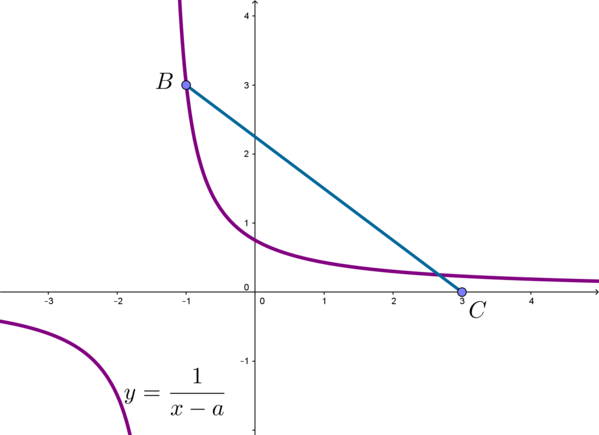
Рассмотрим второе уравнение. Заметим, что (xne a), так как в этом случае уравнение принимает вид (0=1), что не является верным равенством. Тогда можно переписать уравнение в виде: [y=dfrac1{x-a}] Графиком данной функции при каждом фиксированном (a) является гипербола (сдвинутая на (|a|) единиц влево/вправо, если (a<0)/(a>0)).
Заметим, что отрезок (BC) находится в верхней полуплоскости, следовательно, только правая ветка гиперболы может его пересекать.
Найдем значения (a), при которых гипербола проходит через точку (B).
Тогда [3=dfrac1{-1-a} quadLeftrightarrowquad a=-dfrac43.] Найдем значения (a), при которых гипербола касается отрезка (BC) в точке (K(x_0;y_0)).
Для этого нужно написать уравнение прямой, проходящей через точки (B, C). Пусть (y=kx+b) – уравнение этой прямой. Тогда [begin{cases}
3=-k+b\
0=3k+b end{cases} quadLeftrightarrowquad begin{cases}
k=-dfrac34\[2ex]
b=dfrac94 end{cases} quadRightarrowquad y=-dfrac34x+dfrac94] Производная функции, задающей гиперболу, равна [y’=-dfrac1{(x-a)^2}] Тогда условие касания задается [begin{cases}
-dfrac1{(x_0-a)^2}=-dfrac34\[2ex]
dfrac1{x_0-a}=-dfrac34x_0+dfrac94 end{cases}
quadLeftrightarrowquad begin{cases} x_0=3-dfrac2{sqrt3}\[2ex]
a=3-dfrac4{sqrt3} end{cases}] Следовательно, при [ain
left[-dfrac43;3-dfrac4{sqrt3}right)] гипербола будет иметь с отрезком (BC) равно две точки пересечения.
Ответ:
(ain left[-frac43;3-frac4{sqrt3}right))
Нахождение касательной к графику — одно из обязательных для решения заданий, включенных в итоговое тестирование по математике. Как показывает практика последних лет, подобные задачи с вычислением углового коэффициента и нахождением точки пересечения вызвали сложности у многих выпускников. Их выполнение осложняется тем, что системы могут иметь более 1 решения.
Готовьтесь к итоговому тестированию по математике вместе с сайтом «Школково»!
Для нахождения касательной необходимо в первую очередь вспомнить формулы и понять алгоритм решения. Портал «Школково» предлагает все необходимые материалы. Перед решением задач с уравнениями касательной ученики могут повторить правила, выучить самые сложные и только потом приступать к выполнению упражнений, начиная с самых простых. Благодаря такому подходу к обучению школьники сразу выделяют трудные для себя задания и начинают занятия именно с них.
На нашем сайте собрана обширная база упражнений на нахождение касательной. Преподаватели «Школково» подготовили все необходимые материалы и изложили их в наиболее доступной форме. Список задач постоянно пополняется и обновляется, благодаря чему ученики могут выбирать новые задания каждый день.
Чтобы начать нахождение углового коэффициента касательной, повторите правила решения подобных уравнений. После этого приступайте к выполнению самых простых задач с графиками функции. Если они не вызвали трудностей, пропустите несколько упражнений и переходите к более сложным примерам.
Для успешной сдачи Единого государственного экзамена советуем ежедневно заниматься на нашем портале. Занятия доступны не только старшеклассникам из Москвы, но и учащимся из других городов России. Уже через пару недель вы заметите значительное улучшение знаний по конкретным тематикам, которые ранее вызывали трудности. Начните обучение вместе со «Школково» уже сегодня!

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
09
Авг 2013
Категория: 07 Производная, ПО
07. Геометрический смысл производной. Касательная
2013-08-09
2022-09-11
Задача 1. Прямая параллельна касательной к графику функции
. Найдите абсциссу точки касания.
Решение: + показать
Задача 2. Прямая является касательной к графику функции
. Найдите абсциссу точки касания.
Решение: + показать
 Замечание.
Замечание.
Немного облечим себе задачу на будущее. Хотя вполне можно решать задачи способом, показанным выше (задача 2).
Сформулируем условие касания графика функции и прямой
в точке (точках)
.
+ показать
Задача 3. Прямая является касательной к графику функции
Найдите
Решение: + показать
Задача 4. Прямая является касательной к графику функции
. Найдите
, учитывая, что абсцисса точки касания больше
.
Решение: + показать
Задача 5. На рисунке изображён график функции и касательная к нему в точке с абсциссой
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 6. На рисунке изображён график функции и касательная к нему в точке с абсциссой
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 7. На рисунке изображен график функции . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке
.
Решение: + показать
Задача 8. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 9. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 10. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Уравнение касательной показано на рисунке. Найдите значение функции
в точке
.
Решение: + показать
Вы можете пройти тест по задачам, аналогичным разобранным, здесь.
Автор: egeMax |
комментариев 14
Геометрический
смысл производной
1.
На рисунке изображены график
функции y = f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение производной
функции f(x) в точке x0.
2. 
функции y = f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение производной
функции f(x) в точке x0.
3.
На рисунке изображён график
функции y=f(x) и касательная к нему в точке с абсциссой x0.
Найдите значение производной функции f(x) в точке x0.
4.
На рисунке изображён график
функции и касательная к нему в точке с
абсциссой Найдите значение производной
функции в точке
5.
На рисунке изображён график функции y=f(x) и
касательная к нему в точке с абсциссой x0. Найдите
значение производной функции f(x) в точке x0.
6.
На рисунке изображён график
функции и касательная к нему
в точке с абсциссой Найдите значение производной
функции
в точке
7.
На рисунке изображён график
функции и касательная к нему
в точке с абсциссой Найдите значение производной
функции
в точке
8.
На рисунке изображён график
функции y=f(x) и касательная к нему в точке с абсциссой x0.
Найдите значение производной функции f(x) в точке x0.
9.
На рисунке изображён график
функции и касательная к нему в точке с
абсциссой Найдите значение производной
функции в точке
10.
На рисунке изображены график
функции y = f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение производной
функции f(x) в точке x0.
11.
На рисунке изображён график
функции и касательная к нему
в точке с абсциссой Найдите значение производной
функции
в точке
12.
На рисунке изображён график
функции и касательная к нему
в точке с абсциссой Найдите значение производной
функции
в точке
13.
На рисунке изображён график
функции и касательная к нему в точке с
абсциссой x0. Найдите значение производной функции f(x) в
точке x0.
14.
На рисунке изображены график
функции y = f (x) и касательная к нему
в точке с абсциссой x0. Найдите значение производной функции f (x)
в точке x0.
15.
На рисунке изображён график
функции и касательная к нему
в точке с абсциссой Найдите значение производной
функции
в точке
16.
На рисунке изображён график
функции и касательная к нему
в точке с абсциссой Найдите значение производной
функции
в точке
17. На рисунке изображен график
функции y = f(x). Прямая, проходящая через начало
координат, касается графика этой функции в точке с абсциссой 8. Найдите
18.
На рисунке изображен график функции Прямая,
проходящая через начало координат, касается графика этой функции в точке с
абсциссой 10. Найдите
19.
На рисунке изображён график
функции и восемь точек на оси
абсцисс:
В
скольких из этих точек производная функции положительна?
20.
На рисунке изображён график
функции y = f(x) и семь точек на оси
абсцисс: x1, x2, x3,
…, x7. В скольких из этих точек производная
функции положительна?
23.
На рисунке изображён график
функции y = f(x) и восемь точек на оси
абсцисс: x1, x2, x3,
…, x8. В скольких из этих точек производная
функции f(x) положительна?
24.
На рисунке изображён график
функции и двенадцать точек на оси
абсцисс:
В
скольких из этих точек производная функции отрицательна?
25.
На рисунке изображён график
функции y = f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8.
В скольких из этих точек производная функции f(x) отрицательна?
26.На рисунке изображён график
функции и десять точек на оси
абсцисс:
В
скольких из этих точек производная функции отрицательна?
27.
На рисунке изображен график
функции и отмечены точки −2, −1, 1, 2.
В какой из этих точек значение производной наибольшее? В ответе укажите эту
точку.
28.На рисунке изображен график функции и
отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной
наибольшее? В ответе укажите эту точку.
29.
На рисунке изображен график
функции и отмечены точки -2, -1, 1, 2.
В какой из этих точек значение производной наибольшее? В ответе укажите эту
точку.
30.
На рисунке изображен график
функции и отмечены точки -2, 1, 2, 4.
В какой из этих точек значение производной наибольшее? В ответе укажите эту
точку.
31.
На рисунке изображен график
производной функции Найдите абсциссу точки, в
которой касательная к графику параллельна прямой
или совпадает с ней.
32.
На рисунке изображен график
производной функции Найдите абсциссу точки, в
которой касательная к графику параллельна оси абсцисс или
совпадает с ней.
33.
На рисунке изображён график — производной
функции Найдите абсциссу точки, в
которой касательная к графику параллельна прямой y = 3x − 6
или совпадает с ней.
34. Прямая параллельна
касательной к графику функции Найдите
абсциссу точки касания.
35. Прямая параллельна
касательной к графику функции Найдите
абсциссу точки касания.
36.Прямая параллельна
касательной к графику функции Найдите
абсциссу точки касания.
37.Прямая параллельна
касательной к графику функции Найдите
абсциссу точки касания.
38.Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
39. Прямая является касательной к графику функции
Найдите
абсциссу точки касания.
40. Прямая является касательной к графику функции
Найдите
абсциссу точки касания.
41.Прямая является касательной к графику функции
Найдите
абсциссу точки касания.
42. Прямая y = 3x +
1 является касательной к графику функции ax2 +
2x + 3. Найдите a.
43. Прямая является касательной к графику функции
Найдите a.
44.Прямая является
касательной к графику функции Найдите b,
учитывая, что абсцисса точки касания больше 0.
45. Прямая является касательной к графику функции
Найдите
учитывая,
что абсцисса точки касания больше 0.
16 января 2014
Существует целый класс задач 6 из профильного ЕГЭ, в которых вообще не дается график функции. Все, что известно — это уравнение функции и касательной. И сегодня мы будем учиться решать именно такие задачи.
В этой короткой серии уроков мы разберем непростые задачи, которые не так часто встречаются в настоящем ЕГЭ по математике. Однако если встречаются, то у многих учеников вызывают серьезные затруднения. Речь идет о касательных, заданных уравнением, функция которого также задана своим уравнением. Никаких графиков в этих задачах нет. Более того, отдельные два видеоурока будут посвящены примерам, содержащие параметры. И хотя, на первый взгляд, может показаться, что параметры — это очень сложно, на самом деле, такие задания решаются буквально в несколько строчек.
Решаем реальный пример
Итак, первая задача:
Прямая[y˜=16x-38]является касательной к графику функции:
[y={{x}^{3}}-3{{x}^{2}}+7x-11]
Найдите абсциссу точки касания.
Прежде всего, давайте вообще вспомним, что такое касательная к графику функции. Итак, у нас есть некий график, а также прямая, которая касается этого графика, т. е. пересекает график только в одной точке, причем угол ее пересечения с осью $Ox$, точнее, тангенс этого угла равен значению производной в этой точке:
[tglambda ={f}’left( {{x}_{0}} right)]
Теперь переведем формальное определение на понятный человеку язык. Во-первых, поскольку наша прямая, заданная уравнением, является касательной, то эти уравнения обязательно имеют общую точку, т. е. они имеют общее решение. Следовательно, мы можем приравнять их правые части, т. е.:
[16x-38={{x}^{3}}-3{{x}^{2}}+7x-11]
С другой стороны, поскольку речь идет о касательной к графику, а не о произвольной секущей, мы вправе потребовать, чтобы равны были не только сами функции, но еще и их производные, т. е.:
[{{left( 16x-38 right)}^{prime }}={{left( {{x}^{3}}-3{{x}^{2}}-11 right)}^{prime }}]
Давайте займемся первым выражением:
[16x-38={{x}^{3}}-3{{x}^{2}}+7x-11]
[{{x}^{3}}-3{{x}^{2}}+7x-11-16x+38=0]
[{{x}^{3}}-3{{x}^{2}}+9x+27=0]
Вот мы получили первую конструкцию. Это уравнение третьей степени. Для его решения можно попробовать разложить этот многочлен на множители, и, действительно, после определенных преобразований и нескольких строчек вычислений мы получим несколько кандидатов на ответ. Однако вспомним, что речь идет о простой задаче из ЕГЭ по математике, причем задача из части В. Следовательно, она должна решаться гораздо проще без всяких разложений. И именно для этого нам дано второе уравнение. Мы уже приравняли производные, а теперь давайте посчитаем их:
[{{left( 16x-38 right)}^{prime }}={{left( {{x}^{3}}-3{{x}^{2}}=7x-11 right)}^{prime }}]
[16=3{{x}^{2}}-6x+7]
[3{{x}^{2}}-6x+7-16=0]
[3{{x}^{2}}-6x-9=0]
[{{x}^{2}}-2x-3=0]
Мы получили уравнение второй степени. Данное тождество легко решается и через дискриминант, и по формулам Виета. Давайте решим его по формуле Виета:
[left( -3 right)left( +1 right)=0]
[{{}_{1}}=3]
[{{}_{2}}=-1]
Вот мы и получили два корня, это два кандидата на ответ, т. е. те абсциссы, в которых производная нашей касательной к графику функции равна производной. Теперь возвращаемся к нашей исходной конструкции и вспоминаем, что помимо производных сами функции тоже должны быть равны, т. е. из полученных нами иксов нужно выбрать те, которые удовлетворяют уравнению. Давайте подставим[=3]:
[27-27-27+27=0]
[0=0]
Очевидно, что[=3]является корней обоих выражений — и нашего исходного, и производной. На этом можно было бы закончить решение, но давайте для надежности мы подставим и[=-1]:
[-1-3cdot 1-9cdot left( -1 right)+27=0]
[-text{ }4+9+27=0]
[32ne 0]
Очевидно, что данное выражение не является равенством. Следовательно,[=-1]не является корнем нашего тождества. Отсюда заключаем, что единственным корнем, удовлетворяющим все требования, является[=3]. Это и является ответом к задаче. Мы нашли абсциссу точки касания к графику.
Ключевые моменты
В заключении давайте еще раз пробежимся по ключевым шагам решения.
В первую очередь, что значит, что прямая является касательной графику функции? Это значит, что данная прямая и $fleft( x right)$ имеют общее решение. Следовательно, мы можем приравнять $y$ из выражений. Мы получим первое тождество.
Однако после его преобразования, мы получим уравнение третьей степени, а поскольку такая конструкция вообще решается довольно сложно и к тому же имеет несколько корней, мы записываем вспомогательное равенство, вспоминая о том, что речь идет именно о касательных к графику функции, т. е. помимо самих $fleft( x right)$ равными должны быть еще и их производные. В нашем случае производные легко считаются. Итого у нас получилось простое квадратное равенство, которое затем легко решается, и получается два корня.
Возникает вопрос: какой из этих корней является правильным ответом? Чтобы найти правильный ответ, достаточно каждое из этих чисел подставить в наше уравнение, которое мы получили в самом начале. Здесь мы и получим, что один из корней нас полностью устраивает, а второй корень — нет, т. е. он точно не является решением.
С точки зрения геометрии происходит следующее. Допустим, что у нас есть вот такая функция:
У нее есть точка максимума и точка минимума. В обоих случаях производная равна нулю, и, следовательно, касательная, проведенная через каждую из этих точек, тоже имеет производную, равную 0, т. е. она горизонтальна. Однако, как мы видим, не существует такой касательной к графику функции. Если касательная проходит сверху, то она никак не сможет пересечь кривую в нижнем значении. И, наоборот, если мы рассматриваем касательную в нижней точке, то она никак не сможет пересечь нашу кривую в верхнем значении. Этим и объясняется, что хотя производная функции равна производной касательной в двух точках, в итоге в нашем уравнении нас удовлетворяет лишь одна из них.
Задачи B9 такого типа действительно встречаются на ЕГЭ. Как правило, в процессе решения таких задач возникают целые системы уравнений, которые надо уметь решать. В этом и следующих видеоуроках мы последовательно рассмотрим такие «нестандартные» задачи — от самых простых (как сегодня) до действительно серьезных — с параметром и квадратичной функцией.
Смотрите также:
- ЕГЭ 2022, задание 6. Касательная к графику функции
- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
- Сложение и вычитание дробей
- Сводный тест по задачам B15 (1 вариант)
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: тарифы на сотовую связь
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Геометрический смысл производной. Касательная к графику функции»
Открытый банк заданий по теме геометрический смысл производной. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1165
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
Прямая y=3x+2 является касательной к графику функции y=-12x^2+bx-10. Найдите b, учитывая, что абсцисса точки касания меньше нуля.
Показать решение
Решение
Пусть x_0 — абсцисса точки на графике функции y=-12x^2+bx-10, через которую проходит касательная к этому графику.
Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=-24x_0+b=3. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть -12x_0^2+bx_0-10=3x_0+2. Получаем систему уравнений begin{cases} -24x_0+b=3,\-12x_0^2+bx_0-10=3x_0+2. end{cases}
Решая эту систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания меньше нуля, поэтому x_0=-1, тогда b=3+24x_0=-21.
Ответ
-21
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1160
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
Прямая y=-3x+4 параллельна касательной к графику функции y=-x^2+5x-7. Найдите абсциссу точки касания.
Показать решение
Решение
Угловой коэффициент прямой к графику функции y=-x^2+5x-7 в произвольной точке x_0 равен y'(x_0). Но y’=-2x+5, значит, y'(x_0)=-2x_0+5. Угловой коэффициент прямой y=-3x+4, указанной в условии, равен -3. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что =-2x_0 +5=-3.
Получаем: x_0 = 4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1157
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
Показать решение
Решение
По рисунку определяем, что касательная проходит через точки A(-6; 2) и B(-1; 1). Обозначим через C(-6; 1) точку пересечения прямых x=-6 и y=1, а через alpha угол ABC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол pi -alpha, который является тупым.
Как известно, tg(pi -alpha) и будет значением производной функции f(x) в точке x_0. Заметим, что tg alpha =frac{AC}{CB}=frac{2-1}{-1-(-6)}=frac15. Отсюда по формулам приведения получаем: tg(pi -alpha ) =-tg alpha =-frac15=-0,2.
Ответ
-0,2
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1156
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
Прямая y=-2x-4 является касательной к графику функции y=16x^2+bx+12. Найдите b, учитывая, что абсцисса точки касания больше нуля.
Показать решение
Решение
Пусть x_0 — абсцисса точки на графике функции y=16x^2+bx+12, через которую
проходит касательная к этому графику.
Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=32x_0+b=-2. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть 16x_0^2+bx_0+12=-2x_0-4. Получаем систему уравнений begin{cases} 32x_0+b=-2,\16x_0^2+bx_0+12=-2x_0-4. end{cases}
Решая систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания больше нуля, поэтому x_0=1, тогда b=-2-32x_0=-34.
Ответ
-34
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1152
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
На рисунке изображён график функции y=f(x), определённой на интервале (-2; 8). Определите количество точек, в которых касательная к графику функции параллельна прямой y=6.
Показать решение
Решение
Прямая y=6 параллельна оси Ox. Поэтому находим такие точки, в которых касательная к графику функции параллельна оси Ox. На данном графике такими точками являются точки экстремума (точки максимума или минимума). Как видим, точек экстремума 4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1151
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
Прямая y=4x-6 параллельна касательной к графику функции y=x^2-4x+9. Найдите абсциссу точки касания.
Показать решение
Решение
Угловой коэффициент касательной к графику функции y=x^2-4x+9 в произвольной точке x_0 равен y'(x_0). Но y’=2x-4, значит, y'(x_0)=2x_0-4. Угловой коэффициент касательной y=4x-7, указанной в условии, равен 4. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что 2x_0-4=4. Получаем: x_0=4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1147
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
Показать решение
Решение
По рисунку определяем, что касательная проходит через точки A(1; 1) и B(5; 4). Обозначим через C(5; 1) точку пересечения прямых x=5 и y=1, а через alpha угол BAC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол alpha.
Как известно, tg alpha и будет значением производной функции f(x) в точке x_0.
Заметим, что tg alpha =frac{BC}{AC}=frac34=0,75.
Ответ
0,75
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1145
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
Прямая y=-2x-8 является касательной к графику функции y=x^3+3x^2-11x-3. Найдите абсциссу точки касания.
Показать решение
Решение
Угловой коэффициент касательной к графику функции y=x^3+3x^2-11x-3 в произвольной точке x_0 равен y'(x_0). Но y’=3x^2+6x-11, значит y'(x_0)=3x_0^2+6x_0-11. Угловой коэффициент касательной y=-2x-8, указанной в условии равен -2. Поэтому находим такое значение x_0, что 3x_0^2+6x_0-11=-2, 3x_0^2+6x_0-9=0. По формулам корней квадратного уравнения получаем, что либо x_0=-3, либо x_0=1.
Заметим, что y(-3)= (-3)^3+3cdot (-3)^2-11cdot (-3)-3= 30, а y(1)= 1^3+3cdot 1^2-11cdot 1-3= -10. Получаем две возможные точки касания: (-3; 30); (1; -10). Выясним, через какую из них проходит касательная y=2x-8. Координаты точки (-3; 30) не удовлетворяют уравнению касательной, так как равенство 30=-2cdot (-3)-8 не является верным. Но равенство -10=(-2)cdot 1-8 является верным. Поэтому касательная проходит через точку (1, -10) с абсциссой, равной 1.
Ответ
1
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1144
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
Прямая y=-2x+5 является касательной к графику функции y=ax^2+2x+7. Найдите a.
Показать решение
Решение
Пусть (x_0; y_0) — точка, в которой прямая y=-2x+5 касается графика функции y=ax^2+2x+7. Тогда угловой коэффициент касательной к графику функции y=ax^2+2x+7 в точке x_0 равен y'(x_0). Но y’=2ax+2, значит y'(x_0)=2ax_0+2.
Угловой коэффициент касательной y=-2x+5, указанной в условии, равен -2. Поэтому 2ax_0+2=-2. Отсюда, a neq 0.
Кроме того точка (x_0; y_0) лежит на прямой y=-2x+5 и на графике функции y=ax^2+2x+7. Значит, выполняется равенство y_0=-2x_0+5=ax_0^2+2x_0+7. Получаем систему:
begin{cases} 2ax_0+2=-2, \ -2x_0+5=ax_0^2+2x_0+7; end{cases}
begin{cases} x_0=-frac2a, \ ax_0^2+4x_0+2=0; end{cases}
aleft(-frac2aright)^2+4left(-frac2aright)+2=0,
frac4a-frac8a+2=0,
frac4a=2,
a=2;
Ответ
2
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1141
Тип задания: 7
Тема:
Геометрический смысл производной. Касательная к графику функции
Условие
На рисунке изображён график y=f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.
Показать решение
Решение
Пусть x_0 — абсцисса точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней. Тогда значение производной y=f'(x) в точке x_0 равно 0, так как угловой коэффициент оси абсцисс y=0 равен 0.
Но из графика видно, что f'(x)=0 в единственной точке x_0=-5.
Действительно, прямая y=0 пересекает график функции y=f'(x) в единственной точке (-5; 0), абсцисса которой равна -5.
Ответ
-5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
ЕГЭ Профиль №7. Геометрический смысл производной, касательная


 Замечание.
Замечание.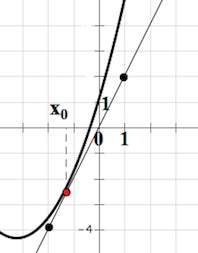


































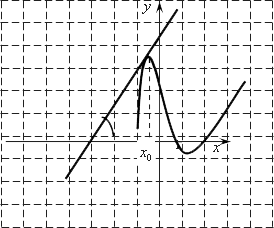
.png)




.png)