Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
2
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.
3
В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.
4
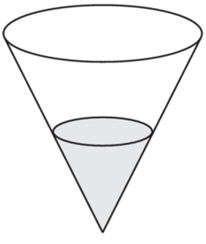
В сосуде, имеющем форму конуса, уровень жидкости достигает
высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Источник: Пробный экзамен Санкт-Петербург 2014. Вариант 1.
5
Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 120911., ЕГЭ по базовой математике 26.03.2015. Досрочная волна
Пройти тестирование по этим заданиям
10
Сен 2013
Категория: 02 Стереометрия
02. Цилиндр.
2013-09-10
2022-09-11
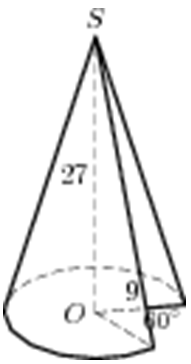
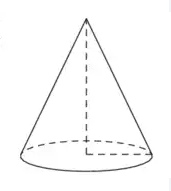
Задача 1. Радиус основания цилиндра равен высота равна
Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 2. Площадь боковой поверхности цилиндра равна а диаметр основания равен
Найдите высоту цилиндра.
Решение: + показать
Задача 3. Длина окружности основания цилиндра равна высота равна
Найдите площадь боковой поверхности цилиндра.
Решение: + показать
Задача 4. Площадь осевого сечения цилиндра равна Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 5. Объём первого цилиндра равен 48 м У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м
).
Решение: + показать
Задача 6. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Решение: + показать
Задача 7. В цилиндрический сосуд налили см
воды. Уровень воды при этом достигает высоты
см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на
см. Чему равен объем детали? Ответ выразите в см
Решение: + показать
Задача 8. В цилиндрический сосуд налили см
воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в
раза. Найдите объем детали.
Ответ выразите в см
Решение: + показать
Задача 9. В цилиндрическом сосуде уровень жидкости достигает см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в
раза больше первого? Ответ выразите в сантиметрах.
Решение: + показать
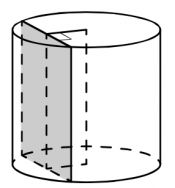
Задача 10. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 11. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 12. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 13. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Вы можете пройти тест “Цилиндр”
Автор: egeMax |
комментария 3
Печать страницы
20 февраля 2022
В закладки
Обсудить
Жалоба
Объёмы тел вращения
В данной методической разработке приведены формулы и разобраны примеры решения традиционных задач на вычисление объёмов тел вращения.
obemy-tel-vraschenija.docx
obemy-tel-vraschenija.pdf
Задача №1
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 36 см3.
Задача №2
Высота одного цилиндра вдвое больше высоты второго цилиндра, но его радиус в два раза меньше радиуса второго цилиндра. Найти отношение их объёмов
Задача №3
Найти объем 25м цилиндрической трубы (полого цилиндра), если внешний радиус равен 50см, диаметр стенок равен 10см.
Задача №4
Объём конуса равен 36, а его высота равна 12. Найдите радиус основания конуса.
Задача №5
Объём конуса равен 24 см3. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объём меньшего конуса.
Задача №6
Диаметр основания конуса равен 16, а длина образующей — 17. Найдите объем конуса.
Задача №7
Радиусы оснований усечённого конуса равны 4 и 12, а образующая равна 10. Вычислить объем усечённого конуса.
Задача №8
Внутренний диаметр полого шара равен 8 см, а толщина стенок равна 2 см. Найдите объем материала, из которого сделан шар.
Задача №9
Прямоугольная трапеция с основаниями 11см и 17 см и высотой 12 см вращается около прямой, проходящей через вершину острого угла перпендикулярно основаниям. Hайдите объем полученного тела вращения.
Задача №10
Прямоугольный треугольник с катетами 20 см и 15 см вращается вокруг гипотенузы . Найти объём полученного тела вращения.
Задания для самостоятельного решения.
1. Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?
2. Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
3. Осевое сечение конуса равносторонний треугольник, сторона которого равна 12 см. Найдите объём конуса.
4. Найти объем тела, полученного в результате вращения прямоугольного треугольника вокруг гипотенузы, если катеты равны 3см и 4 см.
5. Прямоугольная трапеция с основанием 5 см и 8 см и высотой 4 см вращается около большего основания. Найдите объем тела вращения.
Автор: Барсукова Наталья Александровна.
ЦИЛИНДР
1. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
2. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 6. Объем параллелепипеда равен 36. Найдите высоту цилиндра.
3. В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 15 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 12 см. Чему равен объем детали? Ответ выразите в
.
4. В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше диаметра первого? Ответ выразите в сантиметрах.
5. В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра призмы равны . Найдите объём цилиндра, описанного около этой призмы.


6. В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра призмы равны . Найдите объём цилиндра, описанного около этой призмы.
7. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 40. Найдите объём цилиндра.
8. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
9. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
10. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
11. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2,5. Найдите объем параллелепипеда.
12. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 2. Найдите высоту цилиндра.
13. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 18,5. Объем параллелепипеда равен 5476. Найдите высоту цилиндра.
14. В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 24 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 6 см. Чему равен объем детали? Ответ выразите в
.
15. В цилиндрическом сосуде уровень жидкости достигает 405 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
16. В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые ребра призмы равны . Найдите объём цилиндра, описанного около этой призмы.
17. Дано два цилиндра. Объём первого цилиндра равен 86. У второго цилиндра высота в 3 раза больше, а радиус основания в 2 раза меньше, чем у первого. Найдите объём второго цилиндра.
18. Радиус основания цилиндра равен 7, высота равна 8. Найдите площадь боковой поверхности цилиндра, деленную на .
19. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 7. Найдите площадь боковой поверхности призмы.
20. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 1.
21. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 111. Найдите площадь поверхности шара.
22. Длина окружности основания цилиндра равна 4, высота равна 4. Найдите площадь боковой поверхности цилиндра.
23. В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
24. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.
25. Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
26. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
27. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
28. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
29. Площадь боковой поверхности цилиндра равна , а диаметр основания — 1. Найдите высоту цилиндра.
30. В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые рёбра призмы равны 2π. Найдите объём цилиндра, описанного около этой призмы.
31. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объём параллелепипеда равен 36. Найдите высоту цилиндра.
32. Площадь боковой поверхности цилиндра равна 12 π, а диаметр основания равен 6. Найдите высоту цилиндра.
33. В цилиндрическом сосуде уровень жидкости достигает 64 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
34. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объём параллелепипеда.
35. В цилиндрический сосуд налили 500 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился
в 1,2 раза. Найдите объём детали. Ответ выразите в куб. см.
36. Площадь боковой поверхности цилиндра равна 24 π,
а диаметр основания равен 8. Найдите высоту цилиндра.
37. В цилиндрическом сосуде уровень жидкости достигает 80 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
38. В цилиндрический сосуд, в котором находится 6 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в дм3.
39. В цилиндрическом сосуде уровень жидкости достигает 32 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
40. Шар вписан в цилиндр. 
41. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). 
42. Цилиндр описан около шара. Объём шара равен 50. 
43. Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
44. В цилиндрический сосуд налили 2800 см3 воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Найдите объём детали. Ответ выразите
в куб. см.
45. Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте
в сантиметрах.
46.
|
Радиус основания цилиндра равен 15, а его образующая |
|
47. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
48. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго — 7 и 3.
Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности вт
49.
|
Радиус основания цилиндра равен 15, а его образующая |
|
50. В бак цилиндрической формы, площадь основания которого 60 квадратных сантиметров, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
51. Даны две кружки цилиндрической формы. Первая кружка в четыре раза ниже второй,
а вторая в полтора раза шире первой.
Во сколько раз объём первой кружки меньше объёма второй?
52. Высота бака цилиндрической формы равна 40 см, а площадь его основания 150 квадратных сантиметров. Чему равен объём этого бака (в литрах)?
В одном литре 1000 кубических сантиметров.
53.
|
54. Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 3, а второго — 3 и 6.
Во сколько раз объём первого цилиндра больше объёма второго?
55. Высота бака цилиндрической формы равна 50 см, а площадь его основания 160 квадратных сантиметров. Чему равен объём этого бака (в литрах)?
В одном литре 1000 кубических сантиметров.
56.
ЕГЭ Профиль №5. Цилиндр, конус, шар
Скачать файл в формате pdf.
ЕГЭ Профиль №5. Цилиндр, конус, шар
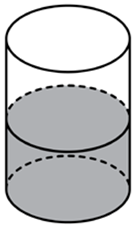
| Задача 1. В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
Ответ
ОТВЕТ: 1500. |
 |
| Задача 2. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Ответ
ОТВЕТ: 4. |
|
| Задача 3. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на (pi ).
Ответ
ОТВЕТ: 12. |
|
| Задача 4. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
Ответ
ОТВЕТ: 3. |
|
| Задача 5. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Ответ
ОТВЕТ: 1,125. |
|
| Задача 6. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Ответ
ОТВЕТ: 6. |
|
| Задача 7. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Ответ
ОТВЕТ: 2. |
|
| Задача 8. Площадь боковой поверхности цилиндра равна (72pi ), а диаметр основания — 9. Найдите высоту цилиндра.
Ответ
ОТВЕТ: 8. |
|
| Задача 9. Площадь боковой поверхности цилиндра равна (2pi ), а высота — 1. Найдите диаметр основания.
Ответ
ОТВЕТ: 2. |
|
| Задача 10. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на (pi ).
Ответ
ОТВЕТ: 4. |
|
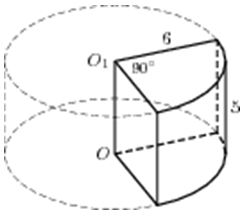
| Задача 11. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 45. |
 |
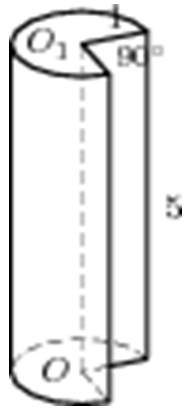
| Задача 12. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 3,75. |
 |
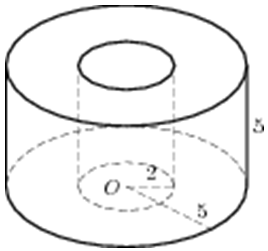
| Задача 13. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 144. |
 |
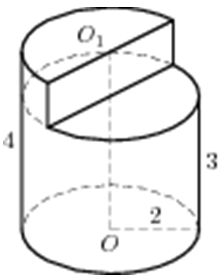
| Задача 14. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 937,5. |
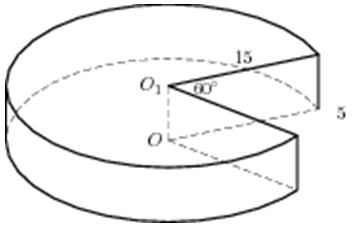 |
| Задача 15. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 14. |
 |
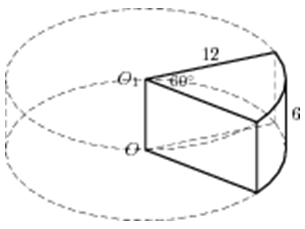
| Задача 16. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 105. |
 |
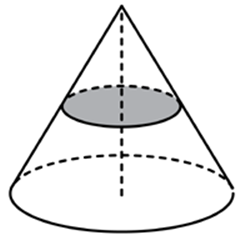
| Задача 17. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ
ОТВЕТ: 2. |
 |
| Задача 18. Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30o. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 1. |
|
| Задача 19. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза, а радиус основания останется прежним?
Ответ
ОТВЕТ: 3. |
|
| Задача 20. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза, а высота останется прежней?
Ответ
ОТВЕТ: 2,25. |
|
| Задача 21. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на (pi )
Ответ
ОТВЕТ: 128. |
|
| Задача 22. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на (pi ).
Ответ
ОТВЕТ: 9. |
|
| Задача 23. Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 6. Найдите его объем, деленный на (pi ).
Ответ
ОТВЕТ: 72. |
|
| Задача 24. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на (pi )
Ответ
ОТВЕТ: 16. |
|
| Задача 25. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
Ответ
ОТВЕТ: 3. |
| Задача 26. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза, а радиус основания останется прежним?
Ответ
ОТВЕТ: 3. |
|
| Задача 27. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза, а образующая останется прежней?
Ответ
ОТВЕТ: 1,5. |
|
| Задача 28. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Ответ
ОТВЕТ: 60. |
|
| Задача 29. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Ответ
ОТВЕТ: 3. |
|
| Задача 30. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на (pi )
Ответ
ОТВЕТ: 24. |
|
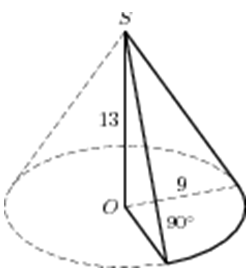
| Задача 31. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 87,75. |
 |
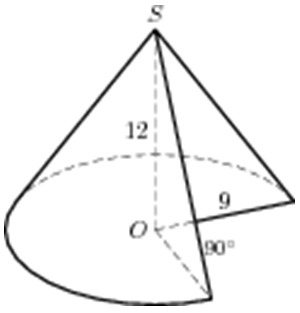
| Задача 32. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 243. |
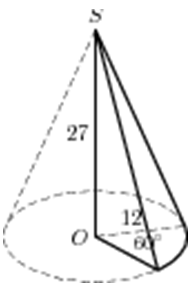
 |
| Задача 33. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 216. |
 |
| Задача 34. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 607,5. |
 |
| Задача 35. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Ответ
ОТВЕТ: 5. |
|
| Задача 36. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Ответ
ОТВЕТ: 6. |
|
| Задача 37. Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
Ответ
ОТВЕТ: 4. |
|
| Задача 38. В сосуде, имеющем форму конуса, уровень жидкости достигает (frac{1}{2}) высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Ответ
ОТВЕТ: 490. |
 |
| Задача 39. Площадь основания конуса равна (16pi ), высота – 6. Найдите площадь осевого сечения конуса.
Ответ
ОТВЕТ: 24. |
|
| Задача 40. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Ответ
ОТВЕТ: 2. |
|
| Задача 41. Высота конуса равна 8, а длина образующей – 10. Найдите площадь осевого сечения этого конуса.
Ответ
ОТВЕТ: 48. |
|
| Задача 42. Диаметр основания конуса равен 12, а длина образующей – 10. Найдите площадь осевого сечения этого конуса.
Ответ
ОТВЕТ: 48. |
|
| Задача 43. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Ответ
ОТВЕТ: 4. |
|
| Задача 44. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Ответ
ОТВЕТ: 27. |
|
| Задача 45. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ
ОТВЕТ: 12. |
|
| Задача 46. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Ответ
ОТВЕТ: 9. |
|
| Задача 47. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Ответ
ОТВЕТ: 10. |
|
| Задача 48. Объем шара равен (288pi ). Найдите площадь его поверхности, деленную на (pi ).
Ответ
ОТВЕТ: 144. |
|
| Задача 49. Площадь поверхности шара равна 12. Найдите площадь большого круга шара.
Ответ
ОТВЕТ: 3. |
Задачи ЕГЭ база
Даны два цилиндра.Радиус основания и высота первого равны 2 и 3 соответственно, а второго 5 и 12. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?
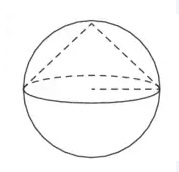
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен (10sqrt{2}). Найдите образующую конуса.
Даны два конуса. Радиус основания и высота первого конуса равны соответственно 4 и 9, а второго – 6 и 8. Во сколько раз объём второго конуса больше объёма первого?
Две кружки имеют форму цилиндра. Первая кружка в полтора раза ниже второй, а вторая втрое уже первой. Во сколько раз объём первой кружки больше объёма второй?
Объём конуса равен (9pi), а радиус его основания равен 3. Найдите высоту конуса.
Вода в сосуде цилиндрической формы находится на уровне (h=80 см). На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у данного? Ответ дайте в сантиметрах.
Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
Конус имеет высоту, равную 16 см, и образующую, равную 20 см. Найдите объем конуса в (см^3), в ответе укажите объем, деленный на (pi).
Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объём второй кружки больше объёма первой?
В сосуд цилиндрической формы налили воду до уровня 80 см. Какого уровня достигнет вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у первого? Ответ дайте в см.
Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
Источники: fipi, os.fipi.
Решение:
Объём цилиндра находится по формуле:
V = πR2h
Высота 2-й кружки h, высота 1-й кружки в 2 раза больше, т.е. 2·h. Радиус 1-й кружки R, радиус 2-й кружки в 3 раза больше, т.е. 3·R.
Подставим значения в формулу и найдём отношение объёмов:
frac{V_{2}}{V_{1}}=frac{picdot (3cdot R)^{2}cdot h}{picdot R^{2}cdot 2cdot h}=frac{9cdot R^{2}}{R^{2}cdot 2}=frac{9}{2}=4,5
Ответ: 4,5.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 12
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.