Всего: 37 1–20 | 21–37
Добавить в вариант
Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 25. Найдите периметр ромба.
Сумма двух углов ромба равна 120°, а его периметр равен 68. Найдите длину меньшей диагонали ромба.
Источник: Досрочная волна ЕГЭ−2020 по математике. Вариант 2
Сумма двух углов ромба равна 120°, а его периметр равен 84. Найдите длину меньшей диагонали ромба.
Источник: Досрочная волна ЕГЭ−2020 по математике. Вариант 1
Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 30. Найдите периметр ромба.
Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 8. Найдите периметр ромба.
Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 27. Найдите периметр ромба.
Найдите площадь ромба, если его высота равна 2, а острый угол 30°.
Ромб и квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 64.
Номер в банке ФИПИ: 4720CB
Ромб и квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 36.
Номер в банке ФИПИ: 04CFC3
Найдите меньшую диагональ ромба, стороны которого равны 2, а острый угол равен
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 153692.
Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Острый угол ромба равен
Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.
Сторона ромба равна 1, острый угол равен
Найдите радиус вписанной окружности этого ромба.
В параллелограмме диагонали являются биссектрисами его углов и равны 16 и 30. Найдите периметр параллелограмма.
В параллелограмме диагонали являются биссектрисами его углов и равны 22 и 120. Найдите периметр параллелограмма.
Всего: 37 1–20 | 21–37
26
Июл 2013
Категория: 01 Геометрия
01. Ромб. Прямоугольник
2013-07-26
2022-09-11
Задача 1. В ромбе угол
равен
. Найдите угол
. Ответ дайте в градусах.
Решение: + показать
Задача 2. Найдите меньшую диагональ ромба, стороны которого равны а острый угол равен
.
Решение: + показать
Задача 3. Найдите высоту ромба, сторона которого равна , а острый угол равен
.
Решение: + показать
Задача 4. Диагонали ромба равны и
см. Найти сторону ромба.
Решение: + показать
Задача 5. Найдите площадь ромба, если его диагонали равны и
Решение: + показать
Задача 6. Площадь ромба равна Одна из его диагоналей равна
Найдите другую диагональ.
Решение: + показать
Задача 7. Площадь ромба равна Одна из его диагоналей в
раза больше другой. Найдите меньшую диагональ.
Решение: + показать
Ответ:
Задача 8. Диагонали ромба относятся как Периметр ромба равен
Найдите высоту ромба.
Решение: + показать
Задача 9. Периметр прямоугольника равен а площадь
Найдите большую сторону прямоугольника.
Решение: + показать
Задача 10. Периметр прямоугольника равен а диагональ равна
Найдите площадь этого прямоугольника.
Решение: + показать
Задача 11. Периметр прямоугольника равен а площадь равна
Найдите диагональ этого прямоугольника.
Решение: + показать
Задача 12. Найдите площадь квадрата, если его диагональ равна
Решение: + показать
Задача 13. Меньшая сторона прямоугольника равна диагонали пересекаются под углом
. Найдите диагонали прямоугольника.
Решение: + показать
Задача 14. В прямоугольнике диагональ делит угол в отношении меньшая его сторона равна
Найдите диагональ данного прямоугольника.
Решение: + показать
Задача 15. Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, которые образует диагональ со сторонами прямоугольника? Ответ выразите в градусах.
Решение: + показать
Вы можете пройти тест по теме «Ромб. Прямоугольник»
Автор: egeMax |
комментария 3
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Ромб и его свойства
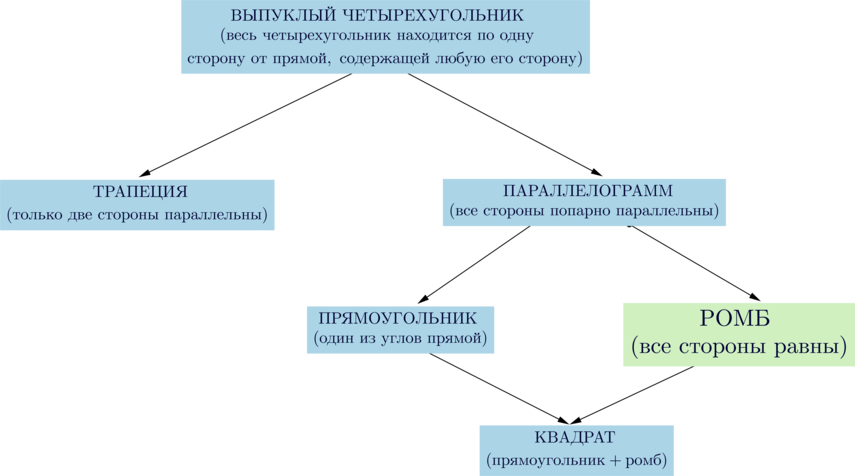
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
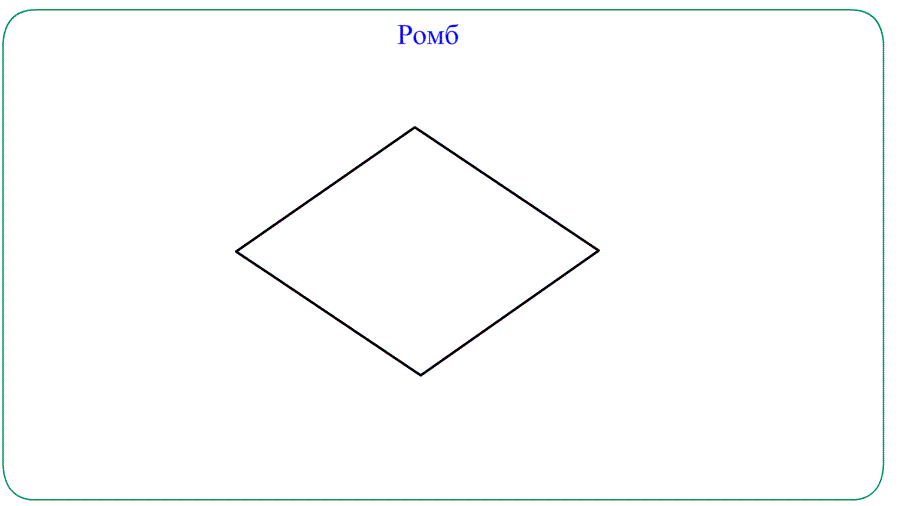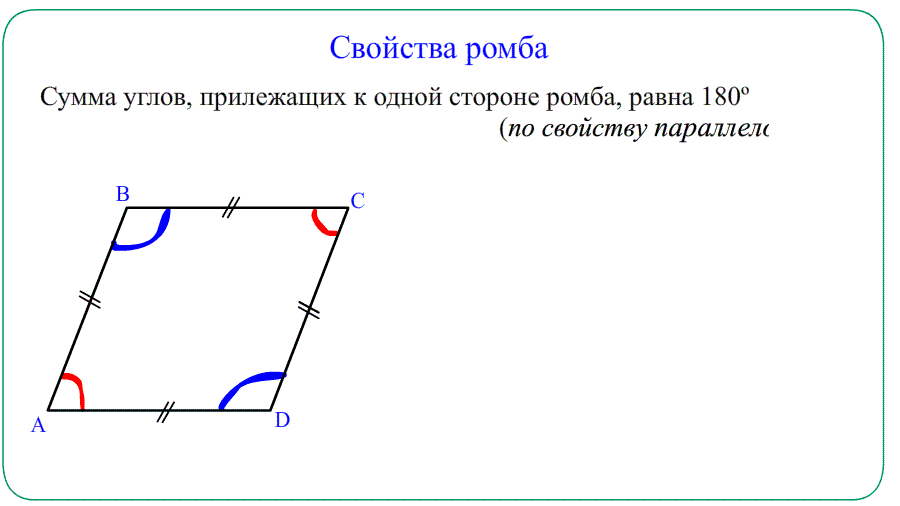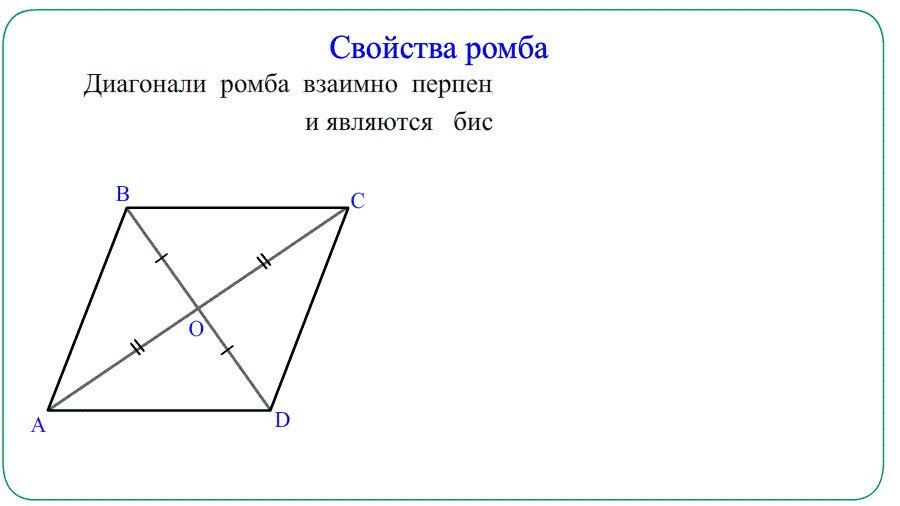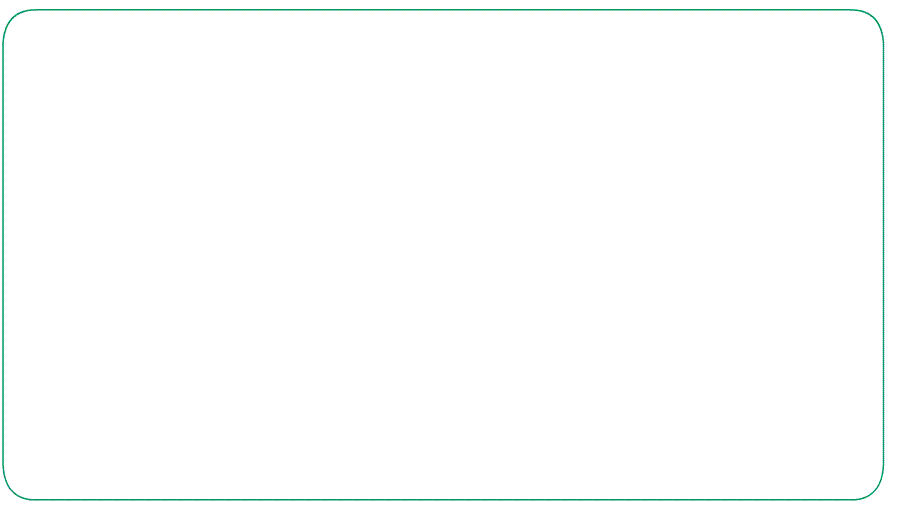
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
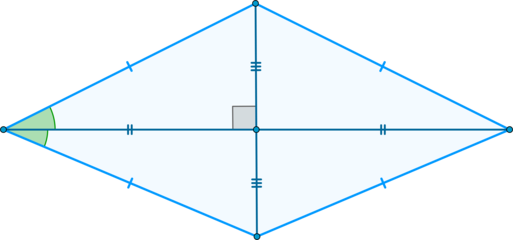
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.
2. Площадь ромба равна половине произведения его диагоналей.
Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.
В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} — angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
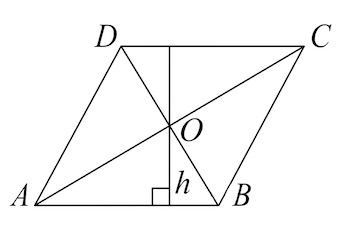
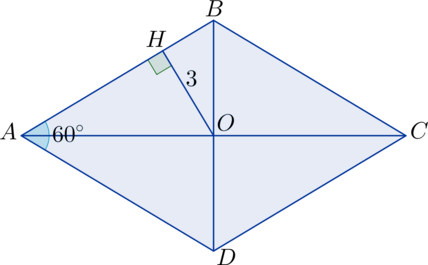
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
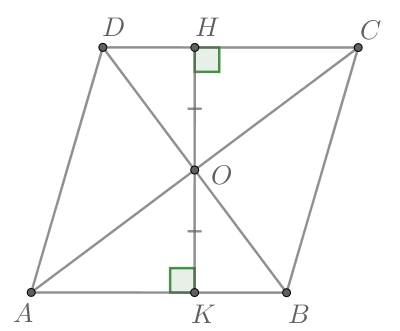
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
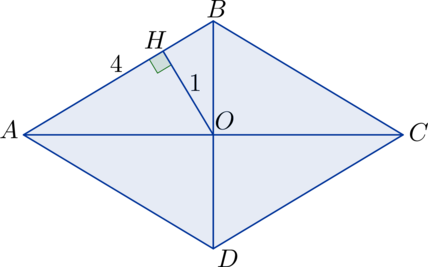
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = 
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
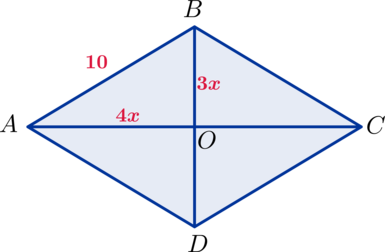
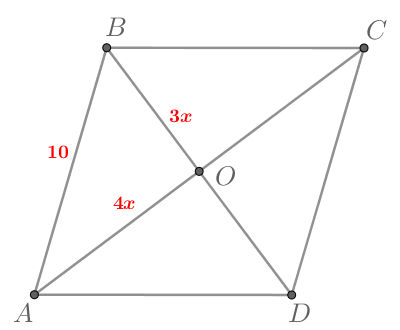
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ
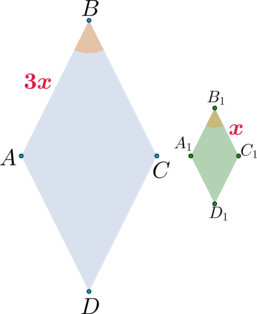
Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Учебник
Геометрия, 11 класс
Ромб: Свойства, Формулы. Задачи
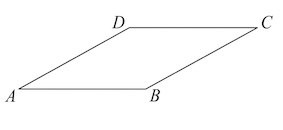
Ромб — это параллелограмм, у которого все стороны равны.
- «Чтоб Выучить, распознать нечто стоящее — узнать его в движении, при изменениях»
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей — ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали — новый ромб совпадет с прежним. Симметрия.
Замечание: Если «зряче видим» центральную и осевые симметрии ромба, то все его свойства у нас «в кармане».
Свойства ромба:
- Ромб симметричен относительно точки O — пересечения диагоналей. O — центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ — ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов — делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая — $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
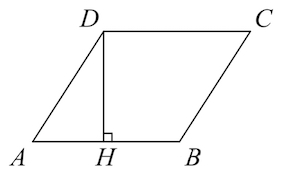
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . — половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали — суть биссектрисы углов.
Задача 1: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: «Односторонние углы»: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 2: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 3: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ — пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.
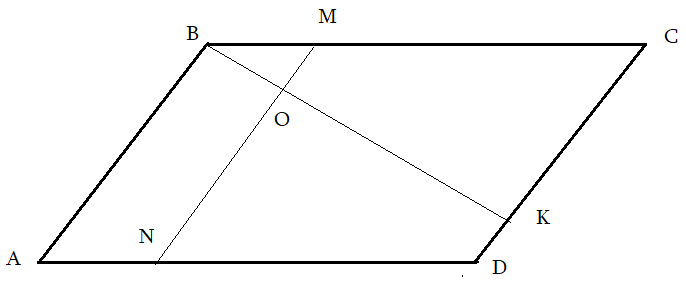
Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ — параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ — квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб — это параллелограмм, у которого все стороны равны.
- «Чтоб Выучить, распознать нечто стоящее — узнать его в движении, при изменениях»
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей — ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали — новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали — ромб совпадает с самим собой. Симметрия.
Замечание: Если «зряче видим» центральную и осевые симметрии ромба, то все его свойства у нас «в кармане».
Свойства ромба:
- Ромб симметричен относительно точки O — пересечения диагоналей. O — центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ — ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов — делят углы пополам.
- Диагонали ромба со сторанами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая — $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . — половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали — суть биссектрисы углов.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершине $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: «Односторонние углы»: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 3: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 4: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ — пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.

Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ — параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ — квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб — это параллелограмм, у которого все стороны равны.
- «Чтоб Выучить, распознать нечто неподвижное — узнать его в движении, при изменениях»
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей — ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали — новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали — ромб совпадает с самим собой. Симметрия.
Замечание: Если «зряче видим» центральную и осевые симметрии ромба, то все его свойства у нас «в кармане».
Свойства ромба:
- Ромб симметричен относительно точки O — пересечения диагоналей. O — центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ — ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов — делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

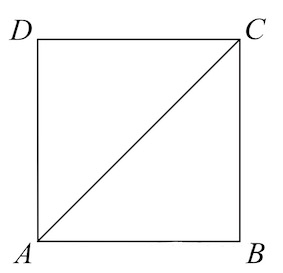
Квадрат — одновременно прямоугольник, ромб, параллелограмм. Диагонали квадрата равны между собой и делятся пополам.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершины $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: «Односторонние углы»: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


- Полезные напоминания: «В равностороннем треугольнике все углы равны 60 градусов.
- Если в равнобренном треугольнике один из углов 60, то это равносторонный треугольник — стороны равны, углы тоже.
- В прямоугольном треугольнике катет напротив угла 30 градусов равен половине гипотенузы.
Упражнения:
Задачи из сайта https://resh.edu.ru :
Задача 11: В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO.
Задача 12: В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC.
Задача 13: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Задача 14: ???? В любом ромбе равны… Противолежащие углы равны, сумма соседних углов равна 180 градусов:(?) Ромб, у которого все углы равны, это… (?) Диагонали пересекаются и точкой пересечения делятся пополам. (?) Диагонали взаимно перпендикулярны. (?)
Задача 15: Отрезки AB и CD пересекаются в их общей середине. В образовавшемся четырёхугольнике ∠CAD = ∠ADB. Найдите ∠BCA.
Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
Задача 17: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Тема 1.
Геометрия на плоскости (планиметрия)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
геометрия на плоскости (планиметрия)
1.01Треугольник: внутренние и внешние углы
1.02Треугольник: высота, биссектриса, медиана
1.03Треугольник: задачи на подобие
1.04Прямоугольный треугольник и теорема Пифагора
1.05Треугольник: площадь и периметр
1.06Параллелограмм и его свойства
1.07Параллелограмм и свойство его биссектрисы
1.08Прямоугольник и его свойства
1.09Ромб и его свойства
1.10Квадрат и его свойства
1.11Трапеция и ее свойства
1.12Равнобедренная трапеция
1.13Окружность: центральный и вписанный углы
1.14Окружность: углы, образованные хордами, секущими, касательными
1.15Окружность: отрезки хорд, секущих, касательных
1.16Окружность: описанная около многоугольника
1.17Окружность: вписанная в многоугольник или угол
1.18Длина окружности или дуги и площадь круга или сектора
1.19Правильный шестиугольник и его свойства
1.20Площадь многоугольника: различные формулы
1.21Внешние углы многоугольника и тригонометрия
1.22Решение треугольника и других фигур с помощью тригонометрии
1.23Теорема синусов и теорема косинусов
1.24Координатная плоскость
1.25Векторы: сложение, вычитание, координаты
1.26Задачи на клетчатой бумаге
Решаем задачи
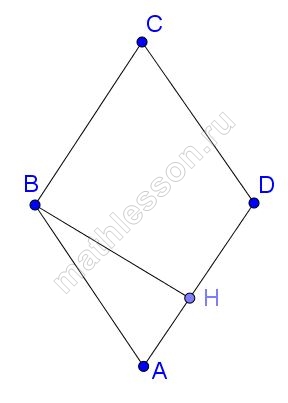
Высота ромба
делит сторону
на отрезки
и
Найдите высоту ромба.
Показать ответ и решение
Стороны ромба равны между собой, то есть
Треугольник — прямоугольный, по теореме Пифагора
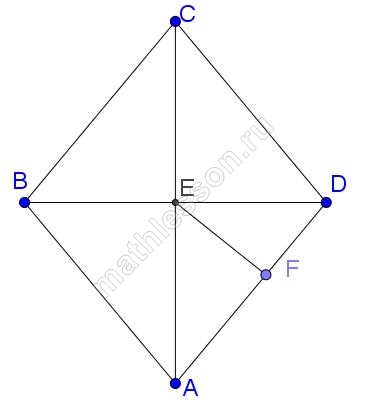
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40.
Найдите острый угол ромба. Ответ дайте в градусах.
Показать ответ и решение
Пусть диагональ Так как диагонали ромба точкой пересечения делятся пополам,
Тогда в прямоугольном треугольнике катет
равен половине гипотенузы
то есть
В ромбе диагонали являются биссектрисами, то есть
Тогда острый угол ромба равен
Сторона ромба равна 4, а один из углов этого ромба равен Найдите высоту этого ромба.
Показать ответ и решение
Так как один из углов ромба равен то другой равен
Треугольник — прямоугольный, угол
Тогда катет, противолежащий этому углу, равен половине
гипотенузы. Таким образом,
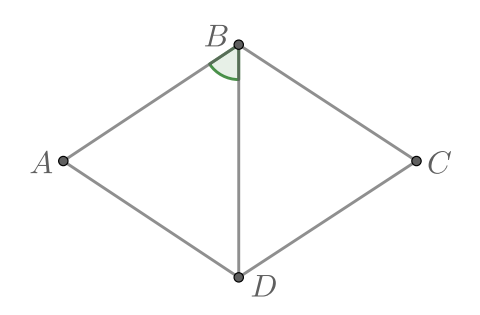
В ромбе угол
равен
Найдите угол
Ответ дайте в градусах.
Показать ответ и решение
Так как — ромб,
т.е. треугольник
— равнобедренный.
а значит
Так как в ромбе диагонали являются биссектрисами,
Угол между стороной и диагональю ромба равен Найдите острый угол ромба. Ответ выразите в градусах.
Показать ответ и решение
Диагональ ромба является его биссектрисой. Тогда
Ромб является параллелограммом, поэтому сумма его углов, прилегающих к одной стороне, равна
Отсюда острый угол ромба равен
Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
Показать ответ и решение
Обозначим меньшую диагональ ромба через тогда большая равна
Диагонали ромба перпендикулярны, площадь
выпуклого четырехугольника с перпендикулярными диагоналями равна половине произведения диагоналей, следовательно,
площадь ромба равна
должен быть положителен, ответ 2.
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
Показать ответ и решение
Обозначим неизвестную диагональ ромба через Диагонали ромба перпендикулярны, площадь выпуклого четырехугольника
с перпендикулярными диагоналями равна половине произведения диагоналей, следовательно, площадь ромба
равна
Площадь ромба равна Одна из его диагоналей в три раза больше другой. Найдите меньшую диагональ.
Показать ответ и решение
Пусть меньшая диагональ равна тогда большая равна
Так как площадь ромба равна половине произведения диагоналей,
то
Найдите площадь ромба, если его диагонали равны 4 и 12.
Показать ответ и решение
Так как площадь ромба равна половине произведения диагоналей, то
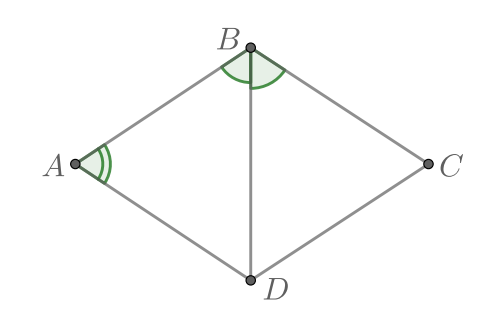
В ромбе угол
равен
Найдите угол
Ответ дайте в градусах.
Показать ответ и решение
Так как в ромбе диагонали являются биссектрисами углов, то Так как у ромба все стороны равны, то
следовательно, Тогда
В ромбе угол
равен
Найдите угол
Ответ дайте в градусах.
Показать ответ и решение
Так как в ромбе диагонали являются биссектрисами углов, то Так как у ромба все стороны равны, то
следовательно, Тогда
Диагонали ромба относятся как Периметр ромба равен 200. Найдите высоту ромба.
Показать ответ и решение
Отрезок — высота ромба. Так как
и
то
Способ 1.
Так как диагонали ромба делят его на 4 равных прямоугольных треугольника, а у равных треугольников высоты, опущенные к
равным сторонам, равны, то
Рассмотрим Так как
то также
Пусть
Следовательно,
Так как у ромба все стороны равны, то его сторона равна следовательно,
и
Высота прямоугольного треугольника опущенная из вершины прямого угла
равна
следовательно,
Способ 2.
Так как у ромба все стороны равны, то его сторона равна Следовательно, площадь ромба равна
(произведение стороны на высоту, проведенную к этой стороне).
Так как то можно принять
Так как площадь ромба равна полупроизведению диагоналей,
то
Cледовательно,
Так как диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, то по теореме Пифагора из
Следовательно,
Найдите высоту ромба, сторона которого равна а острый угол равен
Показать ответ и решение
Пусть — высота ромба
из условия. Тогда в прямоугольном треугольнике
имеем:
Поскольку катет напротив угла равен половине гипотенузы, то
Отсюда по теореме Пифагора в треугольнике :
Периметр ромба равен 40, а его диагонали относятся как Найдите площадь ромба.
Показать ответ и решение
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении Зная периметр,
найдем сторону ромба: Сторона и половины диагоналей образуют прямоугольный треугольник
Пусть
Тогда по теореме Пифагора:
Диагонали ромба равны
Тогда искомая площадь равна
В ромбе
Найдите
Ответ дайте в градусах.
Показать ответ и решение
В ромбе диагонали перпендикулярны, тогда
тогда
Так как диагонали ромба делят его углы пополам, то
Острый угол ромба равен
одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно а острый угол ромба равен
Найдите
большую диагональ ромба.
Площадь ромба равна Одна из его диагоналей равна
Найдите другую диагональ.
Показать ответ и решение
Пусть — диагональ ромба, которую нужно найти. Так как площадь ромба равна половине произведения диагоналей,
то
Найдите площадь ромба, если его высота равна а острый угол равен
Показать ответ и решение
Проведем .
Так как а катет, лежащий против угла
равен половине гипотенузы, то
, так как в ромбе по определению все стороны равны. Площадь ромба равна произведению высоты на сторону, к
которой проведена высота, следовательно,
Найдите большую диагональ ромба, сторона которого равна а острый угол равен
Показать ответ и решение
Проведем диагональ
Пусть
Докажем, что
— большая диагональ.
Так как в ромбе, как и в параллелограмме, диагонали точкой пересечения делятся пополам, то
Так как в ромбе диагонали являются биссектрисами углов и взаимно перпендикулярны, то
и
соответственно
В треугольнике против большего угла лежит большая сторона, следовательно, значит,
— большая
диагональ.
Катет, лежащий против угла , равен половине гипотенузы, следовательно,
. Тогда по теореме
Пифагора:
Задание 1027
|
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. |
|
Ответ: 3
Задание 1028
|
Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ. |
|
Ответ: 2
Задание 1037
|
Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба. |
|
Ответ: 48
Задание 1038
В ромбе ABCD угол ABC равен 122°. Найдите угол ACD. Ответ дайте в градусах.
Ответ: 29
Задание 1039
В ромбе ABCD угол ACD равен 43°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 94
Задание 1854
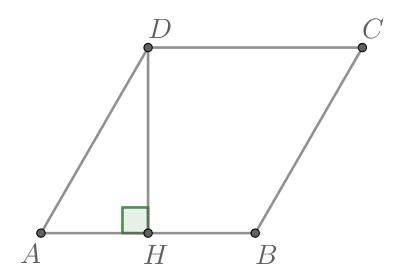
Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе через точку с запятой в порядке возрастания.
Ответ: 17; 17
Скрыть
Пусть BH — высота ромба, тогда треугльник BHA — прямоугольный и $$AH=AB*cos A=34*frac{1}{2}=17$$, тогда HD=AD-AH=34-17=17
Задание 1855
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Ответ: 3
Скрыть
Сторона ромба равна $$frac{36}{4}=9$$, из формулы площади ромба:$$h=frac{S}{a}=frac{36}{9}=4$$, где h — высота, a — сторона ромба.
Задание 1856
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
В ответе запишите величины различных углов в порядке возрастания через точку с запятой.
Ответ: 60; 120
Скрыть
По свойству диагоналей ромба: $$AE=frac{1}{2}AC$$, пусть AC=76, тогда AE=38. Треугольник AEF — прямоугольный, тогда $$sin EAF=frac{EF}{EA}=frac{19}{38}=0,5Rightarrow$$$$angle EAF=30^{circ}$$, тогда по свойству диагоналей ромба $$angle A=60^{circ}$$ и по свойству углов ромба $$angle B=180-angle A=120^{circ}$$
Задание 1857
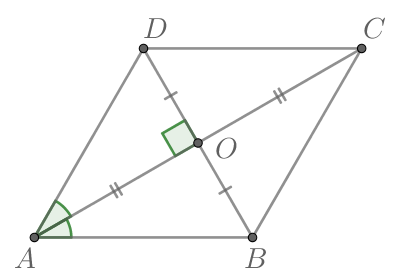
Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах.
Ответ: 60
Скрыть
OP=OR=PQ=QR ( по свойству ромба ), тогда, так как PR — общая, то треугольники POR И PQR равны, следовательно, $$angle O=angle Q$$. Пусть $$angle Q=x$$, тогда большая дуга PR=2x (по свойству вписанного угла), тогда меньшая дуга RP=360-2x и $$angle O=360-2x$$ ( по свойству центрального угла ), тогда $$x=360-2xLeftrightarrow$$$$x=120$$, то есть $$angle O=120^{circ}$$, тогда по свойству углов ромба $$angle P=180-angle O=60^{circ}$$
Задание 2968
| Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? |
Ответ: 13
Скрыть
|
$$AB=AD$$ $$Rightarrow$$ $$bigtriangleup ABD$$ — равнобедренный; $$angle B=angle D=frac{180-angle A}{2}=60^{circ}$$ $$Rightarrow$$ $$bigtriangleup ABD$$ — равносторонний $$Rightarrow$$ ВН — медиана, биссектриса, высота $$Rightarrow$$ $$AH=HD=frac{26}{2}=13$$ |
Задание 5218
Площадь ромба равна 60, а периметр равен 30. Найдите высоту ромба.
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Раз периметр равен 30, то одна сторона ромба: $$a=frac{30}{4}=7,5$$. Высоту ромба можно найти через его площадь: $$h=frac{S}{a}=frac{60}{7,5}=8$$
Задание 5690
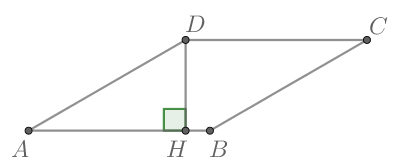
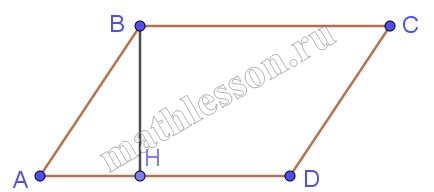
Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.
Ответ:
Задание 6064
Сторона ромба равна 14, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Ответ: 7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$AH=AB*cos A=14*cos 60=7$$. Тогда $$HD=AD-AH=14-7=7.$$
Задание 7465
Площадь ромба равна 15, а периметр равен 20. Найдите высоту ромба.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем сторону ромба: $$a=frac{P}{4}=5$$ Найдем высоту ромба: $$h=frac{S}{a}=3$$
Задание 9215
Сторона ромба равна 14, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Ответ: 7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до нее равно 1. Найдите площадь этого ромба.
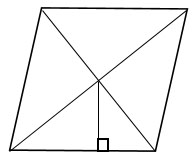
#481
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
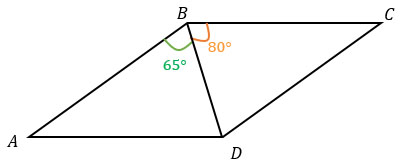
#479
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла А образует со стороной ВС угол, равный 21°. Ответ дайте в градусах.
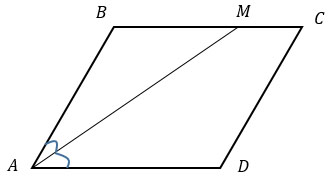
#478
Найдите площадь ромба, если его диагонали равны 32 и 4.
#474
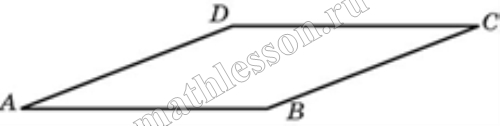
Найдите площадь параллелограмма, изображенного на рисунке.
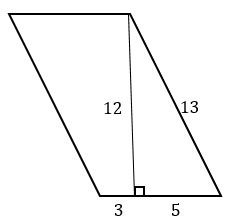
#468
Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите его высоты. В ответе укажите бо́льшую высоту.
#356
Докажите, что диагональ параллелограмма разбивает его на два равных треугольника.
#265
Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке, лежащей на стороне ВС. Найдите АВ, если ВС = 40.
#375
В параллелограмме ABCD диагональ АС является биссектрисой угла А. Найдите сторону ВС, если периметр ABCD равен 36.
#374
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 12.
#370