Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Новосибирск & (Красноярск & Хабаровск | Норильск) | 570 |
| Новосибирск & Красноярск & Хабаровск | 436 |
| Новосибирск & Красноярск & Хабаровск & Норильск | 68 |
Какое количество страниц (в тысячах) будет найдено по запросу
Новосибирск & Норильск
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц, тыс. |
|---|---|
| Новосибирск & (Красноярск & Хабаровск | Норильск) | 570 |
| Новосибирск & Норильск | 214 |
| Новосибирск & Красноярск & Хабаровск & Норильск | 68 |
Какое количество страниц (в тыс.) будет найдено по запросу
Новосибирск & Красноярск & Хабаровск?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц, тыс. |
|---|---|
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Ирландия | 304 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тыс.) будет найдено по запросу
Англия & Уэльс & Шотландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Руда | 64 |
| Железо | 41 |
| Витамины | 36 |
| Руда | Железо | Витамины | 105 |
| Железо & Витамины | 27 |
| Руда & Витамины | 0 |
Сколько страниц (в тысячах) будет найдено по запросу Железо & Руда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Источник: ЕГЭ по информатике 03.07.2020. Основная волна
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу Аврора & Крейсер?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Источник: ЕГЭ по информатике 03.07.2020. Основная волна
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Чаплин | 272 |
| Малыш | 620 |
| Чаплин | Малыш | Карлсон | 980 |
| Чаплин & Карлсон | 0 |
| Чаплин & Малыш | 94 |
| Малыш & Карлсон | 314 |
Сколько страниц (в тысячах) будет найдено по запросу Карлсон?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Карлсон | 428 |
| Малыш | 704 |
| Чаплин | Малыш | Карлсон | 1030 |
| Чаплин & Карлсон | 0 |
| Чаплин & Малыш | 114 |
| Малыш & Карлсон | 382 |
Сколько страниц (в тысячах) будет найдено по запросу Чаплин?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| куб | шар | луза | 144 |
| куб & луза | 0 |
| куб | 70 |
| луза | 45 |
| шар | 89 |
| куб & шар | 32 |
Сколько страниц (в тысячах) будет найдено по запросу шар & луза?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| куб | шар | луза | 159 |
| куб & луза | 0 |
| куб | 58 |
| луза | 39 |
| шар | 92 |
| луза & шар | 14 |
Сколько страниц (в тысячах) будет найдено по запросу шар & куб?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Парабола | 125 |
| Гипербола | 161 |
| Литота | 75 |
| Парабола | Литота | 200 |
| Парабола & Гипербола | 23 |
| Парабола | Гипербола | Литота | 278 |
Сколько страниц (в тысячах) будет найдено по запросу Гипербола & Литота?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Парабола | 149 |
| Гипербола | 189 |
| Литота | 88 |
| Парабола | Литота | 237 |
| Литота & Гипербола | 69 |
| Парабола | Гипербола | Литота | 323 |
Сколько страниц (в тысячах) будет найдено по запросу Гипербола & Парабола?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Смешарики | 289 |
| Дикобраз | 114 |
| Ёжик & Дикобраз | 43 |
| Смешарики | Дикобраз | 403 |
| Смешарики | Ёжик | 415 |
Сколько страниц (в тысячах) будет найдено по запросу Ёжик | Смешарики | Дикобраз?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Смешарики | 271 |
| Дикобраз | 141 |
| Ёжик & Смешарики | 192 |
| Смешарики | Дикобраз | 412 |
| Дикобраз | Ёжик | 512 |
Сколько страниц (в тысячах) будет найдено по запросу Ёжик | Смешарики | Дикобраз?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Семёновский | 136 |
| Преображенский | 318 |
| Борменталь | 93 |
| Преображенский | Борменталь | 331 |
| Преображенский & Семёновский | 92 |
| Семёновский | Борменталь | 229 |
Сколько страниц (в тысячах) будет найдено по запросу Семёновский | Преображенский | Борменталь?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество
страниц (тыс.) |
|---|---|
| Семёновский | 86 |
| Преображенский | 294 |
| Борменталь | 70 |
| Преображенский | Семёновский | 320 |
| Преображенский & Борменталь | 66 |
| Семёновский | Борменталь | 156 |
Сколько страниц (в тысячах) будет найдено по запросу Семёновский | Преображенский | Борменталь?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Бейсик | Паскаль | Ньютон | 953 |
| Бейсик & Паскаль & Ньютон | 1 |
| Бейсик | 355 |
| Паскаль | 618 |
| Ньютон | 319 |
| Бейсик | Ньютон | 673 |
| Бейсик & Паскаль | 223 |
Какое количество страниц (в тысячах) будет найдено по запросу
Паскаль & Ньютон?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Бейсик | Паскаль | Ньютон | 914 |
| Бейсик & Паскаль & Ньютон | 1 |
| Бейсик | 343 |
| Паскаль | 585 |
| Ньютон | 311 |
| Бейсик | Ньютон | 653 |
| Ньютон & Паскаль | 110 |
Какое количество страниц (в тысячах) будет найдено по запросу
Паскаль & Бейсик?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Лондон & Манчестер | 270 |
| Лондон & (Ливерпуль | Манчестер) | 470 |
| Лондон & Ливерпуль | 355 |
Какое количество страниц (в тысячах) будет найдено по запросу Лондон & Ливерпуль & Манчестер?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Париж & Лион | 320 |
| (Париж & Лион) | (Париж & Марсель) | 455 |
| Париж & Марсель | 355 |
Какое количество страниц (в тысячах) будет найдено по запросу Париж & Лион & Марсель?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Инфоурок
›
Информатика
›Презентации›Презентация на тему «Запросы для поисковых систем с использованием логических выражений (Задание 17 ЕГЭ)»
Скачать материал

Скачать материал


- Сейчас обучается 29 человек из 17 регионов


- Сейчас обучается 31 человек из 21 региона


- Сейчас обучается 629 человек из 77 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Г.Саратов
Запросы для поисковых систем с использованием логических выражений
(Задание 17 ЕГЭ)Автор: Чурсаева Н. И.
МОУ «СОШ № 84»
Информатика и ИКТ -
2 слайд
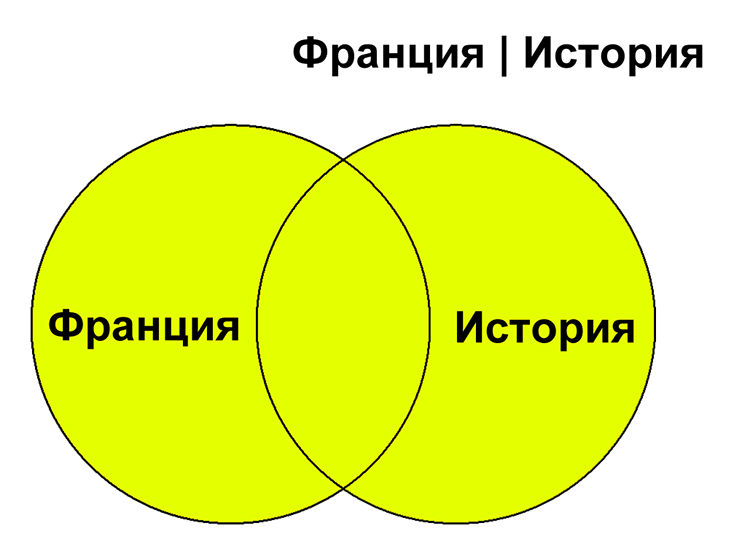
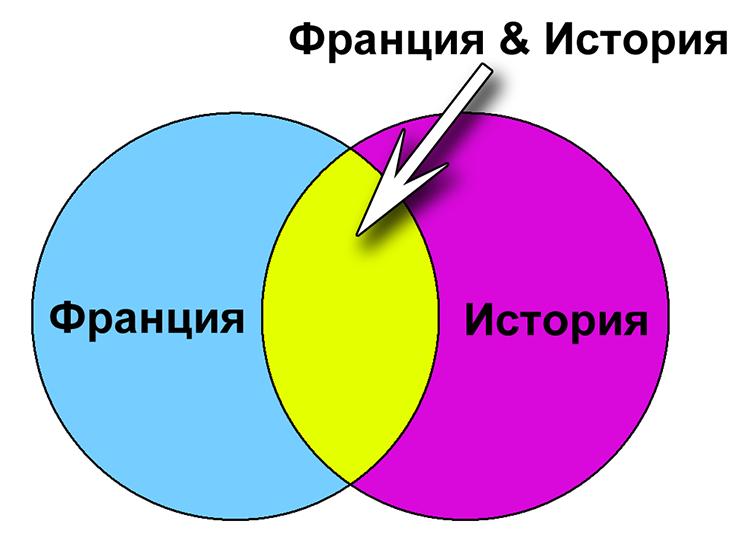
Для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены логические выражения соответствующие множествам .Какое количество множества будет найдено по выражению
Реал& (Атлетико|Барселона) -
3 слайд
Основные правила:
Большинство задач, связанных с поисковыми запросами, проще
решать, используя круги Эйлера.1. Инверсия ¬ A 2. Конъюнкция A B
3. Дизъюнкция A B4. Импликация A → B
5. Эквивалентность A B
Круги Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. -
4 слайд
Для двух областей справедлива формула включений и исключений, которая позволяет легко решать все задачи с двумя областями:
A
B
A | B
NA | B = NA + NB – NA & B
A & B
(1)
Пусть A – множество страниц, на которых встречается слово A, а B – множество страниц, на которых встречается слово B; тогда
запрос A & B соответствует пересечению множеств A B
запрос A|B соответствует объединению множеств A B
будем обозначать через NX количество страниц, которые выдаёт поисковая система по запросу X -
5 слайд
Задача1 на два множества
Сколько страниц (в тысячах) будет найдено по запросу
торты
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета: -
6 слайд
Запишем условие задачи в наших обозначениях
N1
N3
N2
Пироги
Торты
N1+ N2 +N3 =12000
N2 =6500
N2 +N3 = 7700
Дано:
Найти: N1+ N2
Решение:
N3 =7700 – 6500=1200
N1+ N2 = 12000 – 1200 = 10800 -
7 слайд
Три множества
A
B
(A | B) & С
N(A | B) & C = NA & C + NB & C – NA & B & C
(A & B) & C
C
A & С
A
B
C
B & С -
8 слайд
Задача 2 на три множества
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:Сколько страниц (в тысячах) будет найдено по запросу
Рубин & Динамо & Спартак -
9 слайд
Запишем условие задачи в наших обозначениях
N1
N3
N2
Р
Д
N6
N4
N5
N7
С
Дано:
N2 + N4 = 320
N4 + N6 = 280
N2+ N4 +N6 = 430Найти: N4
Решение:
N6 = 430 – 320 = 110
N4 = 280 – 110 = 170 -
10 слайд
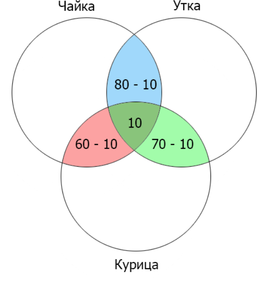
Запишем условие задачи в наших обозначениях
N1
N3
N2
У
Ч
N6
N4
N5
N7
К
Дано:
N1 + N2+ N4 +N5 = 200
N2 + N3+ N4 +N6 = 150
N4 + N5+ N6 +N7 = 120
N2+ N4 = 80
N4+ N6 = 70
N4+ N5 = 60
N4 = 10
Найти: N1 + N2 + N3 + N4+ N5 +N6
Решение:
N2 = 80 – 10 = 70
N3= 150 -70 — 70 = 10
N6 = 70 – 10 = 60
N1 + N2 + N3 + N4+ N5 +N6 = 200+10+60=270 -
11 слайд
Задача 3 на три множества
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:Сколько страниц будет найдено по запросу чайка | утка ?
-
12 слайд
Задача 4 c пустым множеством
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько страниц будет найдено по запросу линейка | ручка | карандаш ? -
13 слайд
Запишем условие задачи в наших обозначениях, учитывая, что множества линейка и карандаш не пересекаются.
N1
N3
N2
Л
Р
N4
N5
К
Дано:
N1 + N2 = 300
N4 + N5 = 200
N2 + N3+ N4 = 280
N4 = 80
N2 = 70
Найти: N1 + N2 + N3 + N4+ N5Решение:
N1 = 300 – 70 = 230
N5= 200 -80 = 120
N1 + N2 + N3 + N4+ N5 = 230+280+120=630 -
14 слайд
Задача 5 c пустым неявным множеством
Сколько страниц будет найдено по запросу: конверт | книга | журнал?В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Внимание!
Запросы: Конверт=100, Книга = 200, а запрос Конверт | Книга = 300. Это говорит о том, что множества Конверт и Книга
не пересекаются, а значит решение будет как в примере 4. -
15 слайд
Запишем условие задачи в наших обозначениях, учитывая, что множества Конверт и Книга не пересекаются.
N1
N3
N2
Книга
Журнал
N4
N5
Конверт
Дано:N1 + N2 = 100
N4 + N5 = 200
N2 + N3+ N4 = 400
N4 = 60
N2 = 50
Найти: N1 + N2 + N3 + N4+ N5Решение:
N1 = 100 – 50 = 50
N5= 200 — 60 = 140
N1 + N2 + N3 + N4+ N5 = 50 + 400+140 = 590 -
16 слайд
Задача 6 c четырьмя множествами
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:Сколько страниц (в тысячах) будет найдено по запросу
Ростов & Орёл & Курск -
17 слайд
Заметим, что во всех четырёх запросах есть «сомножитель» «Ростов &», поэтому эта задача равносильна такой:
Сколько страниц (в тысячах) будет найдено по запросу
Орёл & КурскПоэтому решаем как пример 2 или пример 3.
-
18 слайд
Запишем условие задачи в наших обозначениях
N1
N3
N2
К
О
N6
N4
N5
N7
Б
Дано:N2 + N4+ N5 +N6 + N7 = 370
N4 + N5+ N6 +N7 = 204
N4 = 68Найти: N2 + N4
Решение:
N2 = 370 – 204 = 166
N2 + N4 = 166 + 68 = 234 -
19 слайд
Задача 7 из сборника Крылова 2020
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Какое максимальное количество страниц (в тысячах) может быть найдено по запросу
Школа | Вуз | Подготовка? -
20 слайд
Запишем условие задачи в наших обозначениях
N1
N3
N2
В
Ш
N6
N4
N5
N7
П
Дано:N1 + N2+ N4 +N5 = 68
N2 + N3+ N4 +N6 = 100
N4 + N5+ N6 +N7 = 65
N2 + N4= 19
N4 = 11Найти: N1 +N2 + N3 + N4 + N5+ N6 +N7
Решение:
N2 = 19 – 11 = 8
N1 + N5 = 68 — 19 = 49
N3 + N6 = 100 — 19 = 81
N1 +N2 + N3 + N4 +N5+N6=19+49+81=149
Оценим N7 из 3 уравнения. Пусть N5=0
N6=0. N7=65-11=54. тогда
N1 +N2 + N3 + N4 + N5+ N6 +N7=149+54=203 -
21 слайд
Источники
Все решения, составлены автором.
http://kpolyakov – сайт Полякова Ю. К.
http://www.fipi.ru – федеральный институт педагогических изменений
http://metodist.lbz.ru/authors/informatika/3/ — методические разработки Босовой Л.Л. на официальном сайте издательства Бином
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 651 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
-
Скачать материал
-
08.06.2020
2715
-
PPTX
1.7 мбайт -
214
скачиваний -
Рейтинг:
5 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Чурсаева Наталья Ивановна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 9 лет
- Подписчики: 0
- Всего просмотров: 11746
-
Всего материалов:
5
Файлы
Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….
Информатика (Запросы для поисковых систем с использованием логических выражений)
- 1
- 2
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| лук | арбалет | 426 |
| лук | чеснок | 414 |
| арбалет & чеснок | 0 |
| лук | арбалет | чеснок | 480 |
Какое количество страниц (в тысячах) будет найдено по запросу лук?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Заметили ошибку в тексте?
Выделите её и нажмите Ctrl + Enter

Запросы для поисковых систем с использованием логических выражений
Расположение запросов в порядке убывания/возрастания
№1. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке возрастания количества
страниц, которые найдет поисковый сервер по каждому запросу. Для
обозначения логической операции «ИЛИ» в запросе используется символ
|, а для логической операции «И» – &.
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
Пояснение.
(вариант 1, рассуждение с использованием свойств
операций «И» и «ИЛИ»):
1) меньше всего результатов выдаст запрос с наибольшими
ограничениями — первый (нужны одновременно принтеры, сканеры и
продажа)
2) на втором месте – второй запрос (одновременно принтеры
и продажа)
3) далее – третий запрос (принтеры или продажа)
4) четвертый запрос дает наибольшее количество результатов
(принтеры или сканеры или продажа)
№2. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке возрастания количества
страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” в запросе
используется символ |, а для логической операции “И” – &.
№ Запрос
1 канарейки | щеглы | содержание
2 канарейки & содержание
3 канарейки & щеглы & содержание
4 разведение & содержание & канарейки &
щеглы
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Следовательно ответ 4321
№3. Используя данные таблицы, расположите
номера запросов в порядке возрастания количества страниц, которые
найдет поисковый сервер по каждому запросу.
1) Модемы & факсы & продажа
2) Модемы & продажа
3) Модемы | продажа
4) Модемы | факсы | продажа
Пояснение.
Ответ: 1234
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
№4. Ниже приведены запросы к поисковому
серверу. Расположите номера запросов в порядке убывания количества
страниц, которые найдет поисковый сервер по каждому запросу.
1) спорт & футбол & чемпионат
2) спорт | футбол & чемпионат
3) cпорт | футбол | чемпионат & 2006
4) спорт | футбол | чемпионат
Пояснение.
Логическая операция «И» истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции «ИЛИ» достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Следовательно, на этом примере можно понять, как располагать
по убыванию количества страниц варианты в данной задаче.
Правильный ответ: 4321.
№5. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке возрастания количества
страниц, которые найдет -поисковый сервер по каждому запросу. Для
обозначения логической операции «ИЛИ» в запросе используется символ
|, а для логической операции «И» — &.
1) живопись & литература
2) живопись | литература
3) живопись | литература | графика
4) живопись & литература & графика
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Ответ:4123.
№6. Расположите номера запросов в порядке
убывания количества страниц, которые найдет поисковый сервер по
каждому запросу.Для обозначения логической операции «ИЛИ» в запросе
используется символ а для логической операции «И» — &.
1) барокко | классицизм
2) барокко | (классицизм & модерн)
3) (барокко & ампир) | (классицизм & модерн)
4) барокко | ампир | классицизм | модерн
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Ответ: 4123.
№7. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке возрастания количества
страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения
логической операции «ИЛИ» в запросе используется символ |, а для логической
операции «И» — &.
1) живопись & литература & графика
2) живопись | литература | графика
3) живопись | литература
4) живопись & литература
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Ответ: 1432.
№8 в порядке возрастания количества страниц,
которые найдет поисковый сервер по каждому запросу. Для обозначения
логической операции «ИЛИ» в запросе используется символ |, а для логической
операции «И» — &.
1) графика | литература
2) живопись | литература | графика
3) живопись & литература & графика
4) живопись & графика
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
№9. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке убывания количества
страниц, которые найдёт поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» в запросе
используется символ а для логической операции «И» — &.
1) зайцы & кролики
2) зайцы & (кролики | лисицы)
3) зайцы & кролики & лисицы
4) кролики | лисицы
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
№10. Приведены запросы к поисковому серверу.
Расположите номера запросов в порядке возрастания количества
страниц, которые найдёт поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» в запросе
используется символ а для логической операции «И» — &.
1) яблоки & груши
2) яблоки | сливы
3) яблоки
4) яблоки & сливы & груши
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «яблоки &
груши» необходимо, чтобы в тексте содержалось и слово «груши» и слово
«яблоки».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
« яблоки ∨ груши» необходимо, чтобы в тексте содержалось
или слово
«груши» или слово «яблоки».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Сложные запросы
№1. Некоторый сегмент сети Интернет состоит
из 5000 сайтов. Поисковый сервер в автоматическом режиме составил
таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Количество сайтов,для которых |
|
принтеры |
400 |
|
сканеры |
300 |
|
мониторы |
500 |
Сколько сайтов будет найдено по запросу (принтеры
| мониторы) & сканеры
если по запросу принтеры | сканеры было
найдено 600 сайтов,
по запросу принтеры | мониторы –
900,
а по запросу сканеры | мониторы –
750.
Пояснение.
Для сокращения записи обозначим через C, П, М высказывания
«ключевое слово на сайте – сканер» (соответственно принтер, монитор)
и нарисуем эти области виде диаграммы (кругов Эйлера). Заметим, что
поскольку по запросу принтеры | мониторы было найдено 900 страниц,
по запросам принтеры — 400, мониторы — 500, а
900 = 500 + 400, области П и М не пересекаются. Интересующему
нас запросу (П | M) & C соответствует объединение областей 4 и 2
(«зеленая зона» на рисунке). Количество сайтов, удовлетворяющих запросу
в области i, будем обозначать через Ni.
Из условия:
N1 + N4 + N7
+ N2= 750,
N1 +
N4 + N2 + N3= 600,
N2 +
N3 = 400,
N1 +
N2 + N4 = 300,
N4 +
N7 = 500.
Тогда из первого и пятого уравнений получаем, что N1 +
N2 = 250, а из четвёртого:
N4 = 300 − 250 = 50.
Из второго и четвёртого уравнений получаем, что N3 =
300, а из третьего:
N2 = 400 − 300 = 100.
Следовательно ответ N2 + N4 =
150.
№2. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
Спартак |
45000 |
|
Красс |
2000 |
|
Динамо |
49000 |
|
Спартак & Красс |
1700 |
|
Спартак & Динамо |
36000 |
По запросу Динамо & Красс ни одной
страницы найдено не было.
Какое количество страниц (в тысячах) будет найдено
по запросу Спартак | Динамо | Красс ?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Наша цель — N1 + N4 + N2 +
N5 + N3.
Количество запросов в данной области будем обозначать
Ni.
Тогда из таблицы находим, что:
N1 + N4 = 49 000
N5 + N3 = 2 000
N2 + N4 + N5 =
45 000
N5 = 1 700
N4 = 36 000
Из первого и последнего уравнения: N1 =
13 000.
Из второго и предпоследнего уравнения: N3 =
300
Таким образом:
N1 + N4 + N2 +
N5 + N3 = 45 000 + 13 000 + 300 = 58300.
№3. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
Гоголь |
6000 |
|
Башмачкин |
40 |
|
Кряква |
600 |
|
Гоголь & Кряква |
200 |
|
Гоголь & Башмачкин |
30 |
По запросу Башмачкин & Кряква ни
одной страницы найдено не было.
Какое количество страниц (в тысячах) будет найдено
по запросу Гоголь | Башмачкин | Кряква? Считается, что все
запросы выполнялись практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за время выполнения запросов.
Пояснение.
Наша цель — N1 + N4 + N2 +
N5 + N3.
Количество запросов в данной области будем обозначать
Ni.
Тогда из таблицы находим, что:
N1 + N4 = 40
N5 + N3 = 600
N2 + N4 + N5 =
6 000
N5 = 200
N4 = 30
Из первого и последнего уравнения: N1 =
10.
Из второго и предпоследнего уравнения: N3 =
400
Таким образом:
N1 + N4 + N2 +
N5 + N3 = 6000 + 400 + 10 = 6410.
№4. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
(Суворов & Альпы) | (Суворов & Варшава) |
1100 |
|
Суворов & Варшава |
600 |
|
Суворов & Варшава & Альпы |
50 |
Какое количество страниц (в тыс.) будет найдено по запросу Суворов
& Альпы?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni.
Наша цель — N5 + N6.
Тогда из таблицы находим, что:
N4 + N5 = 600,
N5 = 50,
N4 + N5 + N6 =
1100.
Из первого и второго уравнения: N4 =
550.
Из последнего уравнения: N5 + N6 =
550.
№5. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
(Испания & Америка) | (Испания & Индия) |
800 |
|
Испания & Америка |
600 |
|
Испания & Индия & Америка |
50 |
Какое количество страниц (в тыс.) будет найдено по запросу Испания
& Индия?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni.
Наша цель — N5 + N6.
Тогда из таблицы находим, что:
N2 + N5 = 600,
N5 = 50,
N2 + N5 + N6 =
800.
Из первого и второго уравнения: N2 =
550.
Из последнего уравнения: N5 + N6 =
250.
№6. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет:
|
Запрос |
Найдено страниц |
|
Леннон & Маккартни & Старр |
1100 |
|
Леннон & Маккартни & Харрисон |
1300 |
|
Леннон & Маккартни & Старр & Харрисон |
1000 |
Какое количество страниц (в тыс.) будет найдено по запросу
(Леннон & Маккартни & Старр) | (Леннон &
Маккартни & Харрисон)?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — найти
N9 + N13 + N10.
Тогда из таблицы находим, что:
N9 + N13 = 1100,
N13 + N10 = 1300,
N13 = 1000.
Сложим первое и второе уравнение: N9 +
2N13 + N10 = 2400. Для того, чтобы найти количество
страниц по запросу «(Леннон & Маккартни & Старр) | (Леннон
& Маккартни & Харрисон)», вычтем из правой и левой частей
уравнения N13. Получим: N9 + N13 +
N10 = 1400.
№7. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет:
|
Запрос |
Найдено страниц |
|
Ильф & Петров & Остап |
800 |
|
Ильф & Петров & Бендер |
600 |
|
Ильф & Петров & Бендер & Остап |
500 |
Какое количество страниц (в тыс.) будет найдено по запросу
(Ильф & Петров & Остап)|(Ильф & Петров
& Бендер)?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — найти
N9 + N13 + N10.
Тогда из таблицы находим, что:
N9 + N13 = 600,
N13 + N10 = 800,
N13 = 500.
Сложим первое и второе уравнение: N9 +
2N13 + N10 = 1400. Для того, чтобы найти количество
страниц по запросу «(Ильф & Петров & Остап)|(Ильф & Петров
& Бендер)», вычтем из правой и левой частей уравнения N13.
Получим: N9 + N13 + N10 =
900.
Ответ: 900.
№8. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» – символ «&». В таблице приведены
запросы и количество найденных по ним страниц некоторого сегмента
сети Интернет:
|
Запрос |
Найдено страниц |
|
Толстой & Гоголь & Чехов |
110 |
|
Гоголь & Чехов |
275 |
|
Толстой & Чехов |
215 |
Компьютер печатает количество страниц (в тысячах),
которое будет найдено по следующему запросу: (Толстой|Гоголь)
& Чехов Укажите целое число, которое напечатает компьютер.
Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за
время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — N2 + N5 + N4.
Тогда из таблицы находим, что:
N4 + N5 = 275,
N2 + N5 = 215,
N5 = 110.
Из первого и второго уравнения: N4 +
2N5 + N2 = 490.
Из последнего уравнения: N4 + N5 +
N2 = 380
Ответ: 380.
№9. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» – символ «&». В таблице приведены
запросы и количество найденных по ним страниц некоторого сегмента
сети Интернет:
|
Запрос |
Найдено страниц |
|
протон & бозон |
165 |
|
фотон & протон & бозон |
80 |
|
фотон & бозон |
125 |
Компьютер печатает количество страниц (в тысячах),
которое будет найдено по следующему запросу: (протон|фотон)
& бозон Укажите целое число, которое напечатает компьютер.
Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за
время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — N4 + N5 + N6.
Тогда из таблицы находим, что:
N5 + N6 = 165,
N4 + N5 = 125,
N5 = 80.
Из первого и второго уравнения: N4 +
2N5 + N6 = 290.
Из последнего уравнения: N4 + N5 +
N2 = 210.
Ответ: 210.
№10. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» – символ «&». В таблице приведены
запросы и количество найденных по ним страниц некоторого сегмента
сети Интернет:
|
Запрос |
Найдено страниц |
|
Чацкий & Молчалин & Фамусов |
150 |
|
Чацкий & Фамусов |
350 |
|
Чацкий & Молчалин |
270 |
Компьютер печатает количество страниц (в тысячах),
которое будет найдено по следующему запросу: Чацкий &
(Молчалин|Фамусов) Укажите целое число, которое напечатает
компьютер. Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за
время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — N2 + N5 + N4.
Тогда из таблицы находим, что:
N5 = 150,
N2 + N5 = 350,
N4 + N5 = 270.
Из второго и третьего уравнения: N2 +
2N5 + N4 = 620.
Из последнего уравнения: N2 + N5 + N4 =
470.
Ответ: 470.
Формула включений и исключений
№1. Некоторый сегмент сети Интернет состоит
из 1000 сайтов. Поисковый сервер в автоматическом режиме составил
таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Найдено страниц |
|
сканер |
200 |
|
принтер |
250 |
|
монитор |
450 |
Сколько сайтов будет найдено по запросу «(принтер |
сканер) & монитор», если по запросу «принтер | сканер» было найдено
450 сайтов, по запросу «принтер & монитор» — 40, а по запросу
«сканер & монитор» — 50.
Пояснение.
сканер 200
принтер 250
принтер | сканер 450
поскольку последнее число равно сумме двух предыдущих,
можно сразу же придти к выводу, что в этом сегменте сети нет сайтов, для
которых ключевыми словами являются одновременно принтер и сканер:
принтер & сканер 0
Следовательно, для того, чтобы определить, сколько
сайтов удовлетворяют заданному условию
достаточно просто сложить числа, соответствующие
запросам «принтер & монитор» и
«сканер & монитор»
40 + 50 = 90
№2. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
крейсер | линкор |
7000 |
|
крейсер |
4800 |
|
линкор |
4500 |
Сколько страниц (в тыс.) будет найдено по запросу крейсер
& линкор
Пояснение.
По формуле включений и исключений имеем:
m(крейсер | линкор) = m(крейсер) + m(линкор) — m(крейсер
& линкор) = 4800 + 4500 — m(крейсер & линкор) = 7000.
=> m(крейсер & линкор) = 2300.
№3. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
шахматы | теннис |
7770 |
|
теннис |
5500 |
|
шахматы & теннис |
1000 |
Сколько страниц (в тысячах) будет найдено
по запросу шахматы
Пояснение.
По формуле включений и исключений имеем:
m(шахматы | теннис) = m(теннис) + m(шахматы) — m(шахматы
& теннис) = 5500 + m(шахматы) — 1000 = 7770. => m(шахматы) = 3270.
№4. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
фрегат | эсминец |
3000 |
|
фрегат |
2000 |
|
эсминец |
2500 |
Сколько страниц будет найдено по запросу фрегат
& эсминец
Пояснение.
По формуле включений и исключений имеем:
m(фрегат | эсминец) = m(фрегат) + m(эсминец) — m(фрегат
& эсминец) = 2000 + 2500 — m(фрегат & эсминец) = 3000. => m(фрегат
& эсминец) = 1500.
№5. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
пирожное | выпечка |
14200 |
|
пирожное |
9700 |
|
пирожное & выпечка |
5100 |
Сколько страниц (в тысячах) будет найдено
по запросу
выпечка
Пояснение.
По формуле включений и исключений имеем:
m(пирожное | выпечка) = m(пирожное) + m(выпечка) —
m(пирожное & выпечка) = 9700 + m(выпечка) — 5100 = 14200. => m(выпечка)
= 9600.
№6. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
фрегат & эсминец |
500 |
|
фрегат | эсминец |
4500 |
|
эсминец |
2500 |
Сколько страниц (в тысячах) будет найдено
по запросу фрегат
Пояснение.
По формуле включений и исключений имеем:
m(фрегат | эсминец) = m(фрегат) + m(эсминец) − m(фрегат
& эсминец) = m(фрегат) + 2500 − 500 = 4500.
Откуда получаем, что m(фрегат) = 4500 − 2500 + 500 =
2500.
Ответ: 2500.
№7. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
торты | пироги |
12000 |
|
торты & пироги |
6500 |
|
пироги |
7700 |
Сколько страниц (в тысячах) будет найдено
по запросу торты
Пояснение.
По формуле включений и исключений имеем:
m(торты | пироги) = m(торты) + m(пироги) — m(торты &
пироги) = m(торты) + 7700 — 6500 = 12000. => m(торты) = 10800.
№8. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
фрегат & эсминец |
500 |
|
фрегат |
2000 |
|
эсминец |
2500 |
Сколько страниц (в тысячах) будет найдено
по запросу фрегат | эсминец
Пояснение.
По формуле включений и исключений имеем:
m(фрегат | эсминец) = m(фрегат) + m(эсминец) − m(фрегат
& эсминец) = 2000 + 2500 − 500 = 4000.
№9. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&». В таблице приведены
запросы и количество найденных по ним страниц некоторого сегмента
сети Интернет.
|
Запрос |
Найдено страниц |
|
Пушкин |
3500 |
|
Лермонтов |
2000 |
|
Пушкин |Лермонтов |
4500 |
Какое количество страниц (в тысячах) будет найдено
по запросу Пушкин & Лермонтов? Считается, что все запросы
выполнялись практически одновременно, так что набор страниц, содержащих
все искомые слова, не изменялся за время выполнения запросов.
Пояснение.
По формуле включений и исключений имеем:
m(Пушкин | Лермонтов) = m(Пушкин) + m(Лермонтов) —
m(Пушкин & Лермонтов) = 3500 + 2000 — m(Пушкин & Лермонтов) =
4500. => m(Пушкин & Лермонтов) = 1000.
№10. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ
|
Запрос |
Количество страниц |
|
Сербия & Хорватия |
500 |
|
Сербия|Хорватия |
3000 |
|
Сербия |
2000 |
Какое количество страниц (в тысячах) будет найдено
по запросу Хорватия? Считается, что все запросы выполнялись
практически одновременно, так что набор страниц, содержащих все искомые
слова, не изменялся за время выполнения запросов.
Пояснение.
По формуле включений и исключений имеем:
m(Сербия|Хорватия) = m(Сербия) + m(Хорватия) — m(Сербия&Хорватия).
Тогда 3000 = 2000 + m(Хорватия) — 500, откуда m(Хорватия)
= 1500.
Задачи типа 18 ГИА по информатике призваны проверить умение осуществлять поиск информации в Интернете. Как правило от ученика требуется расставить количество найденных
поисковой системой страниц в порядке убывания или возрастания. Обычно начинаются такие задачи со слов
В таблице приведены запросы к поисковому серверу
Рассмотрим решение подобной задачи
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества
страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции ИЛИ в запросе используется символ |, а для
логической операции И – символ &.
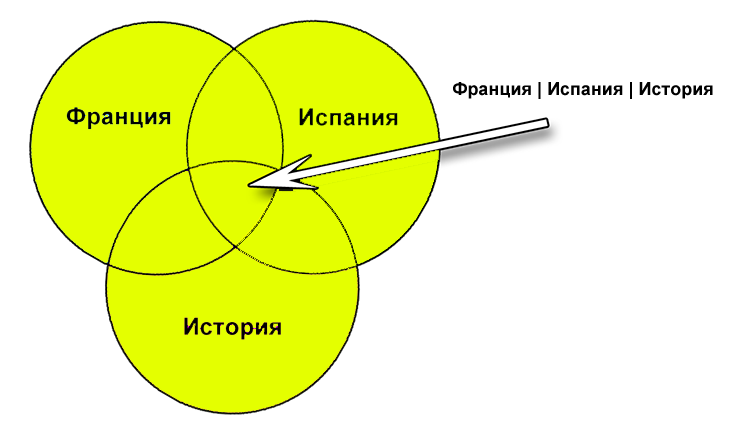
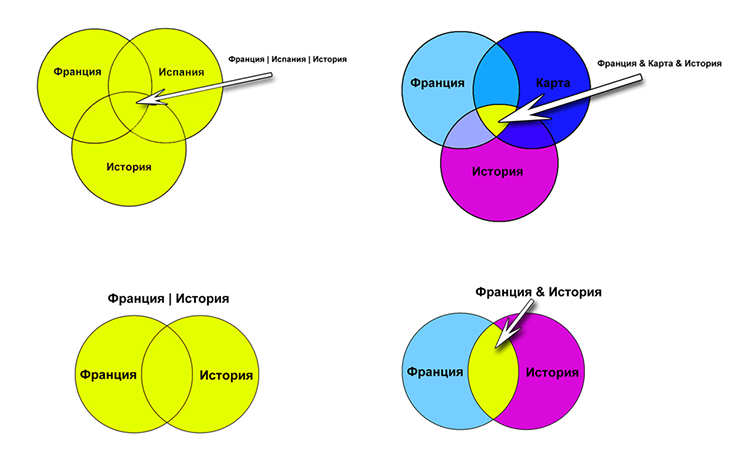
| 1 | Франция | Испания | История |
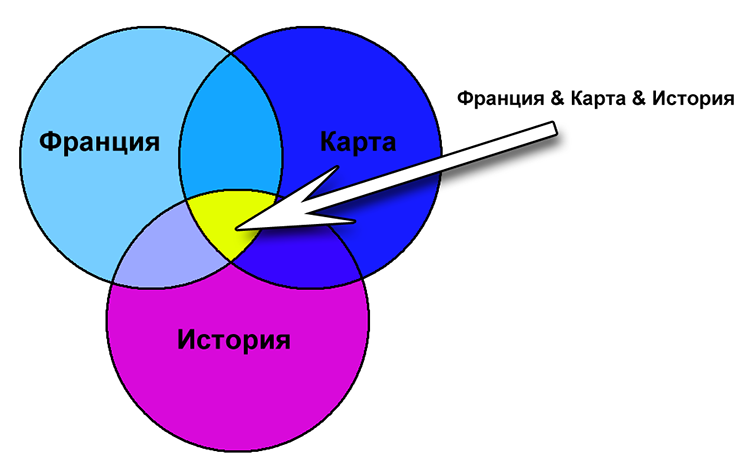
| 2 | Франция & Карта & История |
| 3 | Франция | История |
| 4 | Франция & История |
Решение:
В запросах у нас встречается 4 разных с слова — Франция, Испания, История и Карта. Для решения мы будем использовать очень наглядный инструмент — круги Эйлера. Итак, каждое слово из запросов мы
представим в виде круга.
Решение задач типа 18 ГИА по информатике
При этом, если у нас два слова в запросе объединяются логической операцией ИЛИ (кстати, эту операцию называют дизъюнкция), то в результате получается новая фигура, объединяющая две исходных. Давайте посмотрим это на
примере:
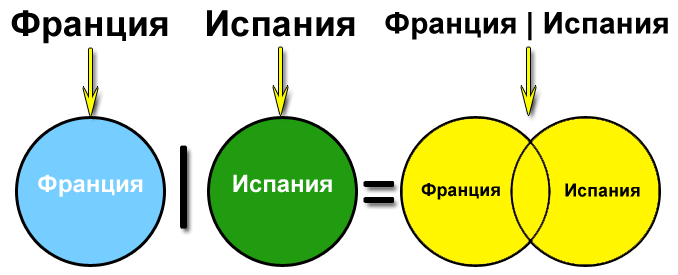
Возьмем такой запрос — Франция | Испания и построим его графический эквивалент
Подготовка к ГИА по информатике — задача 18
Полученная фигура закрашена желтым цветом. Сразу видно, что ее площадь больше, чем площадь отдельных запросов Франция или Испания. Делаем вывод, что объединение слов в запросе логической
операцией ИЛИ увеличивает количество найденных страниц.
Теперь рассмотрим, что произойдет, если слова объединить логической операцией И (эту операцию называют конъюнкция)
В таблице приведены запросы к поисковому серверу
Как мы видим, в данном случае полученная фигура (она выделена желтым цветом) имеет площадь меньше, чем площади исходных слов. Значит, количество страниц, найденных по запросу с
использованием логической операции И будет меньше, чем для отдельных слов.
Вот теперь мы готовы к окончательному решению задачи. Для этого построим графический эквивалент для каждого запроса. Мы получим 4 фигуры, потом нам нужно будет просто сравнить их площади, а затем
расставить их в требуемом порядке. Желтым цветом выделены фигуры, соответствующие запросу.
1) Франция | Испания | История
Франция | Испания | История
2) Франция & Карта & История
Франция & Карта & История
3) Франция | История
Франция | История
4) Франция & История
Франция & История
Если теперь посмотреть на полученные фигуры и сравнить площади желтых участков, то довольно просто расположить их в порядке возрастания:
Задача 18 ГИА по информатике
Франция & Карта & История
Франция & История
Франция | История
Франция | Испания | История.
А значит правильный ответ будет 2431
Для подготовки к ГИА рассмотрим еще один пример из демоверсии 2013 года
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г.
Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдёт поисковый сервер по каждому запросу. Для
обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Решение:
Подробно решение подобных задач рассмотрено выше, поэтому здесь я приведу только итоговые фигуры:
Решение ГИА 2013
Осталось сравнить площади фигур и расставить их в порядке убывания:
Муха | Денежка | Самовар
(Муха & Денежка) | Самовар
Муха & Денежка & Самовар
Муха & Денежка & Базар & Самовар
В итоге правильный ответ ВАГБ
(Старый формат ЕГЭ) 17. Запросы в поисковых системах
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
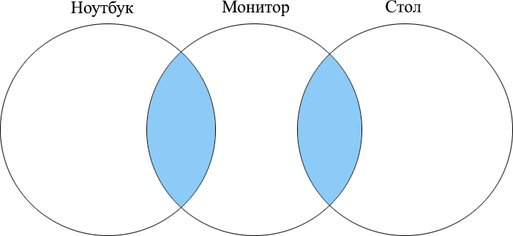
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{ноутбук}&100\
hline
text{монитор}&200\
hline
text{стол}&350\
hline
text{ноутбук | стол}&450\
hline
text{ноутбук} & text{монитор}&50\
hline
text{стол} & text{монитор}&40\
hline
end{array}]
Сколько страниц будет найдено по запросу (ноутбук | стол) & монитор?
Если сложить количество страниц, найденных отдельно по запросам ”ноутбук” и ”монитор”, получим 450. Можно заметить, что (ноутбук | стол) так же равно 450. Это значит, что эти два множества не пересекаются, то есть (text{(ноутбук} & text{монитор)}=0).
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Исходя из рисунка, нам нужно найти сумму (text{(ноутбук} & text{монитор)}+text{(стол} & text{монитор)}). Все данные приведены в таблице, значит, наш ответ (50+40=90).
Ответ: 90
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
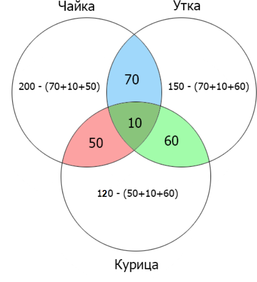
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{чайка}&200\
hline
text{утка}&150\
hline
text{курица}&120\
hline
text{чайка} & text{утка}&80\
hline
text{утка} & text{курица}&70\
hline
text{чайка} & text{курица}&60\
hline
text{чайка} & text{курица} & text{утка}&10\
hline
end{array}]
Сколько страниц будет найдено по запросу (чайка | утка)?
Первый способ решения
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Посчитаем количество найденных страниц для каждого пересечения:
Посчитаем оставшиеся данные:
Затем складываем все данные, входящие в круги ”чайка” и ”утка”: (70+70+50+10+60+10=270)
Второй способ решения
Чтобы найти объединение (операция «ИЛИ») множеств, необходимо сложить отдельно количество страниц, найденных по каждому запросу, а затем вычесть их пересечение (операция «И»): (200+150-80=270)
Ответ: 270
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{карандаш}&300\
hline
text{линейка}&200\
hline
text{ручка}&280\
hline
text{ручка} & text{линейка}&80\
hline
text{ручка} & text{карандаш}&70\
hline
text{линейка} & text{карандаш}&0\
hline
end{array}]
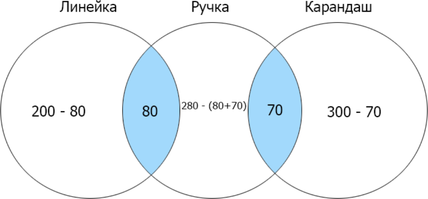
Сколько страниц будет найдено по запросу (линейка | ручка | карандаш)?
Первый способ решения
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Отметим известные данные и посчитаем недостающее:
Затем складываем все данные, входящие в искомую область: (120+130+230+80+70=630).
Второй способ решения
Заметим, что по условию нам необходимо найти сумму всех найденных страниц по введенным запросам. Если мы сложим все отдельные значения найденных страниц, мы учтем по 2 раза каждое из двух пересечений. Таким образом, можем посчитать искомое по формуле: (линейка) + (ручка) + (карандаш) — (ручка & линейка) — (ручка & карандаш) (=300+200+280-80-70=630).
Ответ: 630
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{конверт}&100\
hline
text{книга}&200\
hline
text{журнал}&400\
hline
text{конверт | книга}&300\
hline
text{конверт} & text{журнал}&50\
hline
text{журнал} & text{книга}&60\
hline
end{array}]
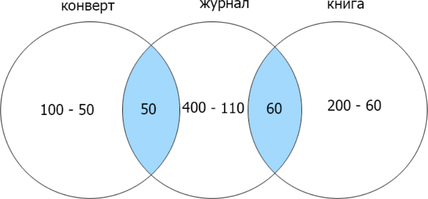
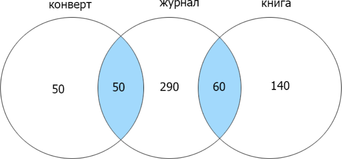
Сколько страниц будет найдено по запросу (конверт | книга | журнал)?
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к. сумма количества страниц, найденных по запросам конверт и книга = 300, а (конверт | книга) = 300, (конверт & книга) = 0. Теперь отобразим известные данные:
Отметим найденные данные и сложим каждую отдельную область для нахождения объедиения трех множеств:
(50+50+290+60+140=590).
Ответ: 590
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{шкаф} & text{стул}&50\
hline
text{стул} & text{стол}&60\
hline
text{стол} & text{шкаф}&70\
hline
text{(шкаф} & text{стул) | (стул} & text{стол) | (стол} & text{шкаф)}&120\
hline
end{array}]
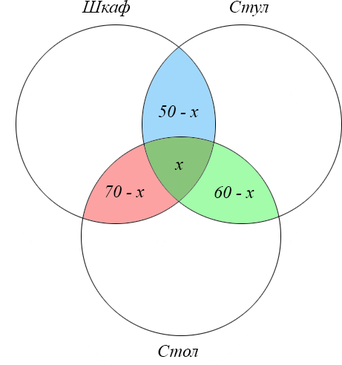
Сколько страниц будет найдено по запросу (шкаф & стул & стол)?
Обозначим искомую область за (x) и выразим данные через (x):
Из последней строки таблицы нам известно, что сумма всех отмеченных элементов равна 120. Значит, можем найти (x) через следующее уравнение:
((50-x)+(70-x)+(60-x)+x=120)
(180-2x=120)
(2x=60)
(x=30)
Ответ: 30
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
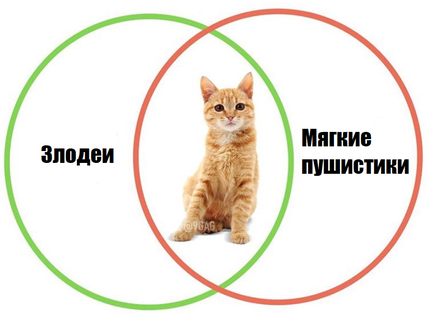
text{злодеи}&150\
hline
text{мягкие пушистики}&210\
hline
text{злодеи | мягкие пушистики}&300\
hline
end{array}]
Сколько страниц будет найдено по запросу кот, если известно, что коты находятся на пересечении множеств злодеев и мягких пушистиков?
Отметим искомую область:
Заметим, что кот = (злодеи & мягкие пушистики) = злодеи + пушистики — (злодеи | мягкие пушистики) = (150+210-300=60).
Ответ: 60
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
textbf{Запрос} & textbf{Найдено страниц (в тысячах)}\
hline
text{сок}&100\
hline
text{фрукты}&100\
hline
text{сахар | фрукты | сок}&300\
hline
text{сок | фрукты}&200\
hline
text{сок} ; & ; text{сахар}&20\
hline
text{сахар} ; & ; text{фрукты}&30\
hline
end{array}]
Сколько страниц будет найдено по запросу сахар?
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к.сумма количества страниц, найденных по запросам сок и фрукты = 200, а (сок | фрукты) = 200, (сок & фрукты) = 0. Теперь отобразим известные данные: 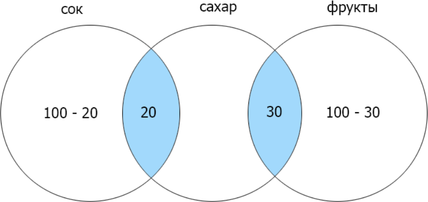
Ответ: 150

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
СОСТАВЛЕНИЕ ЗАПРОСОВ ДЛЯ ПОИСКОВЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
Задача 1: В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.
1) цветы & розы & ромашки
2) цветы & ромашки
3) ромашки | розы
4) цветы | ромашки | розы
Решение (вариант 1, рассуждение с использованием свойств операций «И» и «ИЛИ»):
- меньше всего результатов выдаст запрос с наибольшими ограничениями – первый (нужны одновременно цветы & розы & ромашки)
- на втором месте – второй запрос (одновременно цветы & ромашки)
- далее – третий запрос (ромашки | розы)
- четвертый запрос дает наибольшее количество результатов (цветы | ромашки | розы)
- таким образом, верный ответ – 1234 .
Решение (вариант 2, через диаграммы Эйлера-Венна):
- покажем области, определяемые этими выражениями, на диаграмме с тремя областями
- сравнивая диаграммы, находим последовательность областей в порядке увеличения: (1,2,3,4), причем каждая следующая область в этом ряду охватывает целиком предыдущую
- таким образом, верный ответ – 1234 .
|
1) цветы & розы & ромашки |
2) цветы & ромашки |
3) ромашки | розы |
4) цветы | ромашки | розы |
Задача 2:В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц (тыс.) |
||
|
пирожное & конфеты |
2500 |
||
|
пирожное |
7500 |
||
|
конфеты |
6100 |
Сколько страниц (в тысячах) будет найдено по запросу пирожное | выпечка.
Для обозначения логической операции «ИЛИ» в запросе используется символ | , а для логической операции «И» – &.
Решение (вариант 1, решение системы уравнений):
- количество сайтов, удовлетворяющих запросу, будем обозначать через Ni
- составляем уравнения, которые определяют запросы, заданные в условии:
- пирожное & конфеты N2 = 2500
- пирожное N1 + N2 = 7500
- конфеты N2 + N3 = 6100
- подставляя значение N2 из первого уравнения в остальные, получаем
- N1 = 7500 — N2 = 7500 – 2500 = 5000
- N3 = 6100 — N2 = 6100 – 2500 = 3600
- количество сайтов по запросу пирожное | выпечка равно
- N1 + N2 + N3 = 5000 + 2500 + 3600 = 11100
- таким образом, ответ – 11100.
Решение (вариант 2, рассуждения по диаграмме):
- построим диаграмму Эйлера-Венна:
- число сайтов в интересующей нас области равно N1 + N2 + N3 = (N1 + N2) + (N3 + N2) – N2
- поскольку нам известно, что по условию
пирожное N1 + N2 = 7500
пирожное & конфеты N2 = 2500
конфеты N2 + N3 = 6100
- Получаем N1 + N2 + N3 = 7500 + 6100 — 2500 = 11100
- таким образом, ответ – 11100.
Задачи для самостоятельного решения:
- В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.
a) Америка | путешественники | Колумб
b) Америка | путешественники | Колумб | открытие
c) Америка | Колумб
d) Америка & путешественники & Колумб
- В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.
а ) Информатика & уроки & Excel
b ) Информатика | уроки | Excel | диаграмма
с) Информатика | уроки | Excel
d) Информатика | Excel
- В таблице приведены запросы к поисковому серверу, условно обозначенные буквами от А до Г. Расположите запросы в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.
А) Тенерифе & Климат & Флора & Фауна
Б) Тенерифе & Флора
В) (Тенерифе & Флора) | Фауна
Г) Тенерифе | Флора | Фауна
- В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
а) Зенит & футбол
b) спорт | футбол | Петербург | Зенит
с) Зенит | футбол | Петербург
d) спорт & футбол & Петербург & Зенит
- В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц |
|
корабль | лодка |
3500 |
|
корабль |
2000 |
|
лодка |
2500 |
Сколько страниц (в тысячах) будет найдено по запросу корабль& лодка
- В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц |
|
яблоки & груши |
1500 |
|
яблоки |
2000 |
|
груши |
3000 |
Сколько страниц (в тысячах) будет найдено по запросу яблоки | груши
- В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц |
|
мальчики & девочки |
2500 |
|
мальчики | девочки |
6500 |
|
девочки |
4500 |
Сколько страниц (в тысячах) будет найдено по запросу мальчики
- В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц (тыс.) |
|
яхта | паром |
8000 |
|
яхта |
6800 |
|
паром |
4500 |
Сколько страниц (в тысячах) будет найдено по запросу яхта & паром
* — Использованные источники:
1. Материалы сайта http://kpolyakov.narod.ru/
2. О.Ю.Заславская, И.В.Левченко Информатика. Весь курс для подготовки к ЕГЭ – М.: Эксмо, 2009
3. Зорина Е.М. ЕГЭ 2010: Информатика. Сборник заданий – М.: Эксмо, 2009
4. Н.Д.Угринович Информатика и ИКТ. Учебник для 10-11 классов (профильный).- М.: БИНОМ. Лаборатория знаний, 2010