Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
по теме:
«Экономические задачи ЕГЭ и способы их решения»
Выполнил:
Учащийся 11 класса «А»
Задонский Ярослав Владимирович
Подпись
Научный руководитель:
Сухненко Ирина Александровна
учитель математики
Тамбов, 2018
Содержание:
Введение…………………………………………………………………. С. 3
РАЗДЕЛ ПЕРВЫЙ. Теоретический аспект изучения экономических задач ЕГЭ ………………………………………………………………………. С. 5
Раздел второй. Типы экономических задач на аннуитетный и дифференцированный платежи ………………………………………..
Раздел третий. Особые экономические задачи
Заключение ……………………………………………………………….
Список литературы ………………………………………………………
Введение
В настоящее время общее образование находится на этапе модернизации и обновления системы и содержания в условиях введения новых федеральных государственных стандартов. Приоритетом общества и системы образования является способность вступающих в жизнь людей самостоятельно решать встающие перед ними новые, еще неизвестные задачи. На первый план наряду с общей грамотностью выступает умение выпускников, например, разрабатывать и проверять гипотезы, умение работать в проектном режиме, проявлять инициативу в принятии решений. Это и становится одним из значимых ожидаемых результатов образования и предметом стандартизации.
Русский математик и механик, основоположник Петербургской математической школы, академик Петербургской академии наук П.Л. Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды». С такими задачами в наше время приходится иметь дело представителям самых разных специальностей. Технологи – стараются так организовать производство, чтобы выпускалось как можно больше продукции. Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д.
Актуальность данной темы исследования определяется тем, что начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая практико-ориентированная задача №17, так называемая «банковская» задача. Важным видом учебной деятельности, в процессе которой усваиваются математические знания, умения и навыки, является решение задач и одними из наиболее востребованных типов задач в рамках государственного экзамена являются задачи на проценты, в частности экономические задачи.
Объектом данного исследования являются экономические задача единого государственного экзамена.
Предметом исследования выступают способы решения экономических задач единого государственного экзамена.
Гипотеза исследования — общего способа решения экономических задач быть не может, не существует единого алгоритма, позволяющего за конечное число шагов решать эти задачи.
Продукт проекта — методические рекомендации по решению банковских задач
В связи с объектом и предметом, цель проекта заключается в нахождении решения экономических задач.
Достижение поставленной цели осуществлялось через постановку и решение следующих исследовательских задач:
— проанализировать учебную и научную литературу по теме исследования, с целью определения базовых понятий и степени изученности проблемы;
— рассмотреть теоретические аспекты изучения экономических задач;
— выделить типы экономических задач;
— рассмотреть особые способы решения экономических задач на аннуитетный и дифференцированный платежи
Все вышесказанное, подчеркивает востребованность и необходимость рассмотрения экономических задач в едином государственном экзамене.
РАЗДЕЛ ПЕРВЫЙ. Теоретический аспект изучения экономических задач
При чтении условий любой задачи можно встретить такие величины как вклады, проценты и кредиты. Потому что именно задачи с процентами с недавних пор добавлены во вторую часть единого государственного экзамена по математике. За решение этой задачи согласно спецификациям ЕГЭ предлагается сразу три первичных балла, т. е. экзаменаторы считают эту задачу одной из самых сложных.
Вместе с тем, для решения любой из указанных задач из ЕГЭ по математике необходимо знать всего лишь две формулы, каждая из которых вполне доступна любому школьному выпускнику.
Вкладываем деньги в банк
Прежде всего, хотелось бы сделать небольшое лирическое отступление, связанное с финансами, банками, кредитами и вкладами, на основании которых мы и получим те формулы, которые будем использовать для решения данной задачи. Итак, давайте немного отвлечемся от экзаменов, от предстоящих школьных проблем, и посмотрим в будущее.
Допустим, вы выросли и собираетесь покупать квартиру. Допустим, вы собираетесь покупать не какую-то плохую квартиру на окраине, а хорошую качественную квартиру за 20 миллионов рублей. При этом также предположим, что вы устроились на более-менее нормальную работу и зарабатываете по 300 тысяч рублей в месяц. В этом случае за год вы сможете отложить примерно три миллиона рублей. Разумеется, зарабатывая по 300 тысяч рублей в месяц, за год у вас получится чуть большая сумма — 3600000 — но эти 600000 пусть будут потрачены на еду, на одежду и на прочие ежедневные бытовые радости. Итого вводные данные таковы: необходимо заработать двадцать миллионов рублей, у нас же в распоряжении имеется лишь три миллиона рублей в год. Возникает естественный вопрос: сколько лет нам необходимо откладывать по три миллиона, чтобы получить эти самые двадцать миллионов. Считается это так:
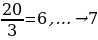
Однако как мы уже отмечали, вы зарабатываете 300 тысяч рублей в месяц, это значит, что вы умные люди и не будете откладывать деньги «под подушку», а отнесете их в банк. И, следовательно, ежегодно на те вклады, которые вы принесете в банк, будут начисляться проценты. Допустим, вы выберете надежный, но при этом более-менее прибыльный банк, и поэтому ваши вклады ежегодно будут расти на 15% годовых. Другими словами можно сказать, что сумма на ваших счетах ежегодно будет увеличиваться в 1,15 раза. Формула:
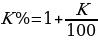
Посчитаем, сколько денег будет на ваших счетах после каждого года:
В первый год, когда вы только начнете откладывать деньги, никакие проценты не накопятся, т. е. в конце года вы отложите три миллиона рублей:
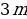
В конце второго года на те три миллиона рублей, которые остались с первого года, уже будут начислены проценты, т.е. нам нужно умножить на 1,15. Однако в течение второго года вы также доложили еще три миллиона рублей. Разумеется, на эти три миллиона еще не были начислены проценты, потому что к концу второго года эти три миллиона только появились на счету:
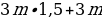
Итак, третий год. В конце третьего года на эту сумму будут начислены проценты, т. е. необходимо всю эту сумму умножить на 1,15. И опять же, в течение всего года вы усердно работали и еще отложили три миллиона рублей:
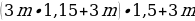
Рассчитаем еще четвертый год. Опять же, вся сумма, которая оказалась у нас к концу третьего года, умножается на 1,15, т.е. на всю сумму будут начислены проценты. В том числе, будут начислены проценты на проценты. И к этой сумме добавляется еще три миллиона, потому что в течение четвертого года вы также работали и также откладывали деньги:

А теперь раскроем скобки и посмотрим, какая у нас будет сумма к концу четвертого года откладывания денег:
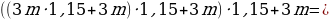
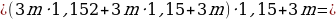
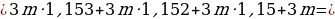
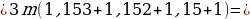
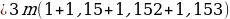
Как видим, в скобках у нас стоят элементы геометрической прогрессии, т. е. у нас стоит сумма элементов геометрической прогрессии.
Если геометрическая прогрессия задана элементом b1, а также знаменателем q, то сумма элементов будет считаться по следующей формуле:
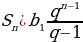
Эту формулу обязательно нужно знать и четко применять.
Обратим внимание: формула n-го элемента звучит следующим образом:
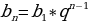
Из-за этой степени многие ученики путаются. В сумме у нас стоит просто n для суммы n-элементов, а сам n-й элемент имеет степень n−1. Другими словами, если мы сейчас попытаемся посчитать сумму геометрической прогрессии, то нужно учитывать следующее:
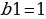
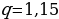
Теперь мы можем посчитать сумму:
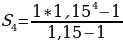
Посчитаем числитель отдельно:
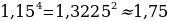
Итого, возвращаясь к сумме геометрической прогрессии, мы получим:
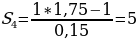
В итоге мы получаем, что за четыре года накоплений наша исходная сумма увеличится не в четыре раза, как если бы мы не клали деньги в банк, а в пять раз, т. е. пятнадцать миллионов. Давайте запишем это отдельно:
4 года → 5 раз
Забегая вперед, отмечу, что если бы мы копили не четыре года, а пять лет, то в итоге наша сумма накоплений увеличилась бы в 6,7 раза:
5 лет → 6,7 раз
Другими словами, к концу пятого года мы бы получили на счету следующую сумму:
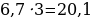
Т. е. к концу пятого года накоплений с учетом процентов по вкладу мы бы уже получили свыше двадцати миллионов рублей. Таким образом, общий счет накоплений за счет банковских процентов снизился бы с почти семи лет до пяти лет, т. е. почти на два года.
Таким образом, даже, несмотря на то, что банк начисляет достаточно низкий процент на наши вклады (15%), уже через пять лет эти самые 15% дают прибавку, существенно превышающую наш ежегодный заработок. При этом основной мультипликационный эффект приходится на последние годы и даже, скорее, на последний год накоплений.
Если мы действительно хотим приумножить свои сбережения, то вкладывать их нужно не в банк, а в реально действующий бизнес, где эти самые проценты, т. е. рентабельность в условиях российской экономики редко опускается ниже 30%, т. е. вдвое больше банковских вкладов.
А вот что действительно полезно во всех этих рассуждениях, так это формула, которая позволяет нам найти итоговую сумму вклада через размер ежегодных платежей, а также через проценты, которые начисляет банк. Так и запишем:
Сам по себе % считается по следующей формуле:
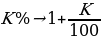
Эту формулу также необходимо знать, как и основную формулу суммы вклада. А, в свою очередь, основная формула способна значительно сократить вычисления в тех задачах с процентами, где требуется посчитать именно вклад.
Почему стоит пользоваться формулами, а не таблицами?
У многих наверняка возникнет вопрос, а к чему вообще все эти сложности, нельзя ли просто расписать каждый год в табличке, как это делают во многих учебниках, посчитать отдельно каждый год, а затем посчитать общую сумму вклада? Конечно, можно вообще забыть про сумму геометрической прогрессии и все считать с помощью классических табличек — так сделано в большинстве сборников для подготовки к ЕГЭ. Однако, во-первых, резко увеличивается объем вычислений, а во-вторых, как следствие, увеличивается вероятность допустить ошибку.
Да и вообще, использовать таблицы вместо этой замечательной формулы — это то же самое, что на стройке копать траншеи руками вместо того, чтобы использовать стоящий рядом и полностью работающий экскаватор.
Ну, или то же самое, что умножить пятерку на десятку не с помощью таблицы умножения, а складывать пятерку с самой собой десять раз подряд. Впрочем, это я уже отвлекся, поэтому еще раз повторю самую главную мысль: если есть какой-то способ упростить и сократить вычисления, то именно этим способом и надо воспользоваться.
Проценты по кредитам
Далее рассмотрим следующий вопрос, а именно — к процентам по кредитам.
Итак, пока вы копите деньги, скрупулезно планируете свой бюджет, думаете о своей будущей квартире, ваш одноклассник, а нынче простой безработный, решил жить сегодняшним днем и просто взял кредит. При этом он еще будет подкалывать и смеяться над вами, мол, у него кредитный телефон и подержанный автомобиль, взятый в кредит, а вы до сих пор ездите на метро и пользуетесь старым кнопочным телефоном. Разумеется, за все эти дешевые вещи вашему бывшему однокласснику придется дорого расплатится. Насколько дорого — вот это именно сейчас мы и посчитаем.
Для начала краткая вводная информация. Допустим, ваш бывший одноклассник взял два миллиона рублей в кредит. При этом согласно договору он должен платить x рублей в месяц. Допустим, что кредит он взял по ставке 20% годовых, что в нынешних условиях выглядит вполне прилично. Кроме того, предположим, что срок кредита составляет всего три месяца. Давайте попробуем связать все эти величины в одну формулу.
Итак, в самом начале, как только ваш бывший одноклассник вышел из банка у него в кармане два миллиона, и это и есть его долг. При этом не год прошел, и не месяц, а это только самое начало:
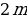
Затем спустя один месяц на сумму задолженности будут начислены проценты. Как мы уже знаем для вычисления процентов достаточно умножить исходную задолженность на коэффициент, который считается по следующей формуле:
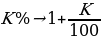
В нашем случае речь идет о ставке 20% годовых, т. е. мы можем записать:
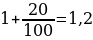
Это коэффициент суммы, которая будет начисляться в год. Однако наш одноклассник не очень умный и он не читал договор, и на деле кредит ему выдали не под 20% в год, а под 20% в месяц. И уже к концу первого месяца на эту сумму будут начислены проценты, и она увеличится в 1,2 раза. Сразу после этого человеку будет необходимо оплатить оговоренную сумму, т. е. x рублей в месяц:
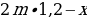
Далее к концу второго месяца уже на эту сумму будут вновь начислены проценты:
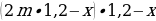
И вновь наш паренек вносит платеж в размере x рублей.
Затем к концу третьего месяца сумма его задолженности еще раз увеличивается на 20%:
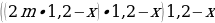
И по условию за три месяца он должен полностью расплатиться, т. е. после внесения последнего третьего платежа его объем задолженности должен быть равен нулю. Мы можем записать такое уравнение:
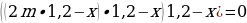
Давайте решать:

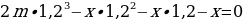
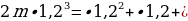
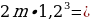
Перед нами вновь геометрическая прогрессия, а точнее, сумма трех элементов геометрической прогрессии. Давайте перепишем ее в порядке возрастания элементов:
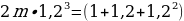
Теперь нам нужно найти сумму трех элементов геометрической прогрессии. Давайте запишем:
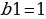
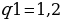
Теперь найдем сумму геометрической прогрессии:
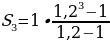
Следует напомнить, что сумма геометрической прогрессии с такими параметрами(b1;q) считается по формуле:
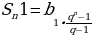
Вот этой формулой мы только что и воспользовались. Подставляем эту формулу в наше выражение:
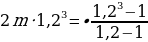
Для дальнейших вычислений нам следует узнать, чему равна 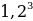
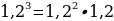
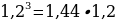
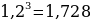
Переписываем наше выражение:
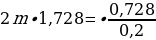
Это классическое линейное выражение. Давайте вернемся к следующей формуле:
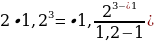
По сути, если обобщить ее, то мы получим формулу, связывающую проценты, кредиты, платежи и сроки. Формула звучит следующим образом:
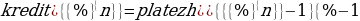
Вот она, самая главная формула, с помощью которой считается не менее 80% всех экономических задач из ЕГЭ по математике во второй части. Знать эту формулу, связывающую кредиты платежи и проценты, также необходимо как и сумму геометрической прогрессии. Именно с помощью этих формул решаются реальные экономические задачи из ЕГЭ по математике
Кредитные инструменты очень полезны и крайне необходимы нашей экономике, но только при условии, что кредит берется на развитие бизнеса. В крайнем случае, можно взять кредит на покупку жилья, т. е. ипотеку либо на неотложное медицинское лечение — все, других причин взять кредит просто не существует.
Помимо ставки вознаграждения по кредиту (проценты по кредиту), клиенту необходимо обратить внимание на такой важный показатель, как метод погашения кредита — аннуитетный и дифференцированный, или еще его называют «равными долями».
Отметим, что в то время как в России существовал только один вид платежа – дифференцированный, на западе практиковался другой – аннуитетный. Оба вида выполняют одну и ту же функцию, помогая гражданам соблюдать свои обязательства по кредиту, говоря простыми словами – выплачивать долги.
Дифференцированный платеж
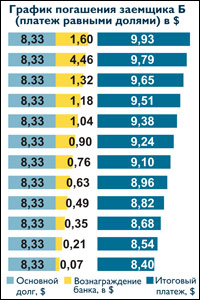
При дифференцированных платежах вся сумма кредита (основного долга) делится на равные части с учетом срока и периодичности погашения платежа по кредиту (ежемесячно, ежедневно, ежеквартально).
В даты платежа по графику клиент выплачивает часть суммы кредита (основного долга) плюс начисленные проценты.
Проценты начисляются на остаток основного долга, соответственно, сумма начисленного вознаграждения по мере погашения кредита уменьшается.
Наиболее распространенной периодичностью погашения является ежемесячный график.
Например, сумма кредита — 100 000 тенге, срок кредита — 1 год, периодичность погашения – ежемесячно (100 000:12 месяцев = 8 333,33 тенге), дополнительно к полученной сумме прибавляется сумма начисленного вознаграждения, которая производится в первый месяц от 100 000 тенге, во второй месяц — от 91 666,66 тенге (100 000 – 8 333,33 = 91 666,66) и т.д.
Недостатком дифференцированного платежа является то, что клиенту необходимо или помнить, или постоянно уточнять, сколько денег ему нужно платить в очередной раз.
При дифференцированном графике в первую половину срока кредита заемщик направляет на погашение кредита гораздо большую сумму из своего дохода, чем во второй ее половине. При таком методе слова «деньги сейчас дороже, чем потом» не работают на клиента, т.к. на деньги, которые заемщик направляет на погашение в первой половине, можно купить гораздо больше, чем через 5, 10 или 20 лет, ведь инфляция велика, и объективных признаков ее снижения в обозримом будущем нет.
Данный вид платежа приемлем для клиентов, у которых нефиксированный доход, который ежемесячно варьируется (больше или меньше). Во-вторых, по кредиту с дифференцированным платежом требования к платежеспособности выше, ведь банк оценивает максимальную сумму кредита, исходя из способности клиента «потянуть» первые платежи по кредиту. Однако учитывая возможность изменения и улучшения условий в будущем (возможное уменьшение % по кредиту, инфляцию, повышение доходов), в последующем выплаты по кредиту становятся все менее обременительными, и к концу срока фактически снижаются.
Плюсы и минусы дифференцированного платежа
Особенности дифференцированного платежа таят в себе как плюсы, так и минусы. Основным плюсом является факт более выгодного способа оплачивать кредит, поскольку данный вид платежа существенно снижает переплаты по кредиту.
Минусом являются большие размеры первоначальных платежей, поэтому дифференцированный платеж называют платежом для обеспеченных людей. Еще одним минусом является отсутствие популярности платежа у банков – большинство банков используют аннуитетную платежную систему, как более выгодную. Несмотря на то, что в России имеется порядка 6-9 банков, где предусмотрена подобная система платежа, среди населения не наблюдается особого ажиотажа – сказывается необходимость выплачивать большие суммы на первоначальном этапе.
Если кредит, к примеру, ипотечный и берется на долгие годы, то имеет смысл перераспределить «тяжесть» платежей таким образом, чтобы основная кредитная нагрузка пришлась на молодые годы, когда человек еще не обременен множеством обязательств, а поиск работы не сопряжен с возрастными ограничениями.
Аннуитетный платеж
Аннуитетный платеж остается неизменным в течение всего срока действия кредитного договора.
Это значит, что каждый месяц клиент платит за кредит одинаковую сумму, которая состоит из начисленных процентов за кредит и части суммы, списывающейся в счет основного долга.
Преимущество аннуитетных платежей заключается в их неизменности. Клиенту известна сумма, которую он должен платить каждый месяц в установленный срок. Больше никаких цифр держать в своей голове ему не надо. Это очень удобно для клиентов, имеющих фиксированный доход.
Таким образом, при выборе графика погашения необходимо выбирать наиболее подходящий для себя метод платежа с учетом текущих ежемесячных расходов, особенно это важно при оформлении кредита на длинные сроки.
К примеру, при оформлении ипотеки на 15-20 лет клиентам, имеющим доход в виде ежемесячной заработной платы, наиболее удобным при планировании семейного бюджета будет аннуитетный вид платежа.
В случае, если вы решите выбрать кредит с дифференцированными платежами, необходимо также учитывать, что максимально возможная сумма кредита может оказаться меньше в отличие от варианта с аннуитетным платежом, так как банк при расчете вашей платежеспособности будет учитывать максимально возможную сумму кредита с учетом первого платежа, который в сравнении с аннуитетом будет больше.
Исходить нужно исключительно из своих возможностей и не забывать, что независимо от вида выбранного платежа, у вас всегда есть право досрочного погашения кредита.
Пример:
-
Клиент А получил кредит 100 долларов сроком на 12 месяцев по ставке 10% (ГЭСВ 10,62 %). Выбрал аннуитетный график платежа по кредиту.
Отличительной особенностью данного вида платежа является фиксированный размер платежа на всем сроке кредита, что позволяет клиенту ежемесячно выделять из бюджета равную сумму денежных средств для погашения кредита. -
Клиент Б получил кредит на аналогичных условиях, но выбрал график с дифференцированными платежами (погашение основного долга равными долями).
Отличительной особенностью данного графика является то, что в течение всего срока кредита размер платежа изменяется от наибольшего к наименьшему.
Подводя итог, отметим, что выбирая кредитную программу, потенциальные заемщики ориентируются на процентную ставку по кредиту. Но не только ставка влияет на сумму выплачиваемых процентов, а также способ их начисления и метод погашения кредита. Таких методов существует два: аннуитетные платежи и дифференцированные платежи.
На наш взгляд, наиболее выгодная схема погашения ипотечного кредита — дифференцированные платежи. Так, общая сумма выплаченных банку денег, взятых под 12 % годовых и погашенных дифференцированными платежами — намного меньше, чем взятых под 12 % годовых, но погашенных аннуитетными платежами.
Дифференцированные платежи характерны тем, что задолженность по кредиту погашается равномерно начиная с самых первых выплат, а проценты начисляются по фактическому остатку. Таким образом, каждый последующий платеж меньше предыдущего. Досрочное погашение не ограничено ни по времени, ни по сумме и позволяет существенно сэкономить на выплачиваемых процентах.
Аннуитет — начисление равных платежей на весь срок погашения кредита. При этом в первой половине срока погашения задолженность по кредиту практически не гасится — выплачиваются в большей части проценты. Эта особенность делает платежи относительно небольшими, но значительно увеличивает общую сумму начисляемых процентов.
Раздел второй. Типы экономических задач на аннуитетный и дифференцированный платежи
Приведем примеры решения задач формата ЕГЭ на аннуитетный платеж
№ 1. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Решение. Пусть сумма кредита равна a, ежегодный платеж равен x рублей, а годовые составляют k %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент 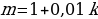
После первой выплаты сумма долга составит: 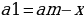
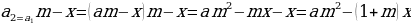
После третьей выплаты сумма оставшегося долга:
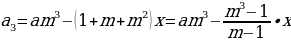
По условию тремя выплатами Сергей должен погасить кредит полностью, поэтому откуда при 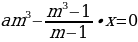
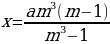
Ответ: 3 993 000 рублей.
№ 2. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69690821 рубль.
Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?
Решение.
Если искомая сумма составляет S рублей, то при коэффициенте ежегодной процентной ставки q, равной 1,31, фиксированная сумма Ф, которую клиент ежегодно должен возвращать в банк в течение 3 лет, составляет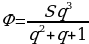
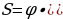
Заметим, что 69690821 кратно 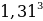
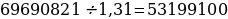
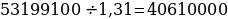
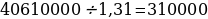
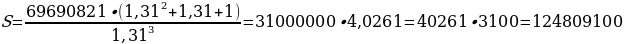
Ответ: 124 809 100 рублей.
№ 3. 31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк x рублей. Какой должна быть сумма x, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Пусть сумма кредита равна S, а годовые составляют a%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a. После первой выплаты сумма долга составит S1 = Sb − x. После второй выплаты сумма долга составит:
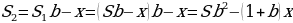
После третьей выплаты сумма оставшегося долга равна:
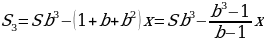
После четвёртой выплаты сумма оставшегося долга равна
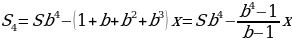
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому
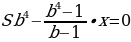
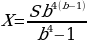
При S = 6 902 000 и a = 12,5, получаем: b = 1,125 и
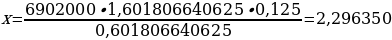
рублей
Ответ: 2 296 350.
№ 4. 31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение.
Пусть сумма кредита равна S, а годовые составляют 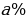
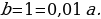
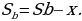
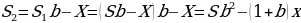
После третей выплаты сумма оставшегося долга равна
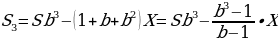
По условию тремя выплатами Тимофей погасил кредит полностью, поэтому
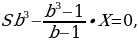
откуда 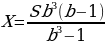
Рассуждая аналогично, находим, что если бы Тимофей гасил долг двумя равными выплатами, то каждый год он должен был бы выплачивать 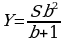
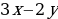
При 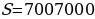
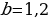
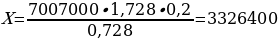
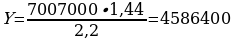
Значит, 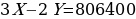
Ответ: 806400.
№ 5. 31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк X рублей. Какой должна быть сумма X, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?
Решение.
Пусть сумма кредита равна S, а годовые составляют а%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01а. После первой выплаты сумма долга составит S1 = Sb − X. После второй выплаты сумма долга составит 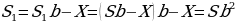
По условию двумя выплатами Дмитрий должен погасить кредит полностью, поэтому откуда 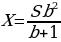
При S = 4 290 000 и а = 14,5, получаем: b = 1,145 и 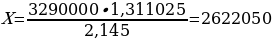
Ответ: 2 622 050.
Приведем примеры решения задач формата ЕГЭ на дифференцированный платеж
№
Решение.
Пусть сумма кредита S у.е., процентная ставка банка x %.
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет: 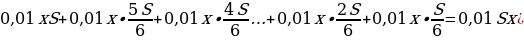
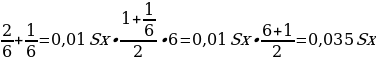
Общая сумма, выплаченная Антоном за 6 месяцев: 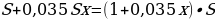
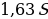
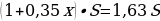
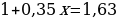
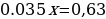
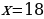
Ответ: 18.
№2. Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
Решение.
Пусть Bi — размер долга Жанны на конец месяца i, Xi — платеж Жанны в конце месяца i. Мы знаем, что имеет место соотношение Bi = 1,02Bi − 1 − Xi. Кроме того, мы знаем, что последовательность (Bi) является арифметической прогрессией. При этом B0 = 1200 тыс. руб., а B24 = 0, так как в конце срока кредитования долг Жанны должен быть равен нулю. Этих двух точек достаточно, чтобы узнать всю последовательность Bi: 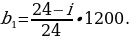
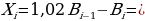
Поскольку Xi линейно зависит от i, последовательность Xi также является арифметической прогрессией. Значит,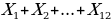
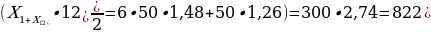
Ответ: 822 тыс. рублей.
№3 Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Сергеем банку (сверх кредита)?
Решение.
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Сергей взятую сумму, без учета процентов, возвращал равными долями.
Общая сумма, уплаченная Сергеем банку сверх кредита, обусловлена только применением процентной ставки.
В первом месяце эта часть заплаченной суммы составляла 0,12S, во втором — 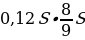
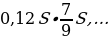
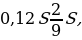
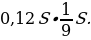
Всего за 9 месяцев:
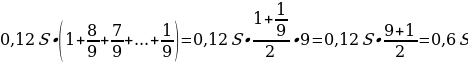
Искомое процентное отношение есть 60 
Ответ: 60.
№4. Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.
Решение.
Пусть сумма кредита равна 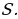
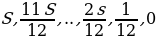
К концу каждого месяца к сумме долга добавляется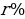
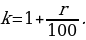
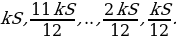
Следовательно, выплаты должны быть следующими:
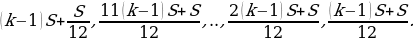
Всего следует выплатить:
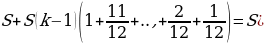
Общая сумма выплат оказалась на 13% больше суммы, взятой в кредит, поэтому:
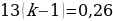
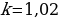
Откуда получаем, что 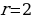
Ответ: 2.
№ 5.15-го января планируется взять кредит в банке на девять месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.
Решение.
По формуле для переплаты П при выплате суммы кредита S дифференцированными платежами имеем: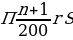
где n = 9 — число месяцев, а r — искомая величина платежной ставки в процентах. По условию, переплата П равна 0,25S, тогда: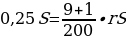
откуда r = 5.
Приведем другое решение.
Долг уменьшается на 15-е число равномерно: 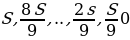
Первого числа долг возрастает на r%, значит, долг на первое число:
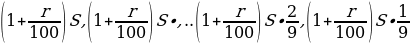
Выплаты:
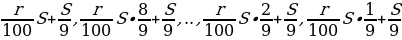
Тогда 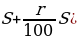
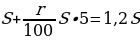
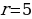
Ответ: 5.
Раздел третий. Особые экономические задачи
№ 1. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом 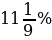
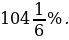
Решение.
Известно:
1. Проценты на вклад начислялись ежемесячно.
2. Каждая последующая процентная надбавка по истечении календарного месяца начислялась с учетом вновь образованной суммы вклада и с учетом предыдущих надбавок.
Если первоначальная сумма вклада при ежемесячной 5%-ной ставке начисления процентов продержалась k месяцев, то вклад ежемесячно увеличивался в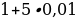
При изменении процентной надбавки с 5% на 12% (ставка 12% продержалась m месяцев) первоначальная сумма вклада за 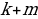

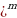
Предположим, что процентная ставка 11 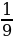


Таким образом, коэффициент повышения суммы вклада в целом за весь период хранения вклада в банке составит:

Это — с одной стороны. Но с другой стороны, согласно условию задачи первоначальная сумма вклада за это же время увеличилась на 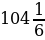
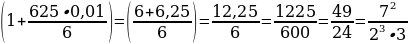
Значит,
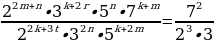
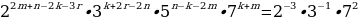
Согласно основной теореме арифметики каждое натуральное число, большее 1, можно представить в виде произведения простых множителей, и это представление единственное с точностью до порядка их следования. В таком случае:
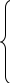
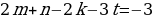
k+2t-2n=-1
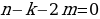
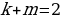
Решим эту систему относительно натуральных k,m,n и t. И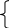

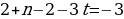
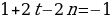
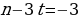
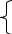
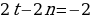
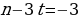
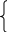
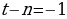
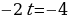
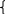
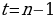
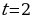
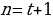
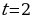
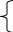
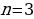
Итак, 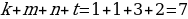
Ответ: 7.
№ 2. В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
− каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
|
Месяц и год |
Июль 2016 |
Июль 2017 |
Июль 2018 |
Июль 2019 |
|
Долг (в млн рублей) |
S |
0,7S |
0,4S |
0 |
Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн рублей.
Решение.
Долг перед банком (в млн рублей) на июль каждого года должен уменьшаться до нуля следующим образом:
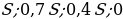
По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен:
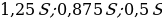
Следовательно, выплаты с февраля по июнь каждого года составляют:
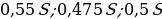
По условию, каждая из выплат должна быть больше 5 млн рублей. Это будет верно, если минимальная из выплат больше 5 млн рублей то есть если0,475S
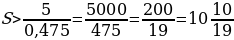
Наименьшее целое решение этого неравенства — число 11. Значит, искомый размер кредита — 11 млн рублей.
Ответ: 11.
№ 3. В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
|
Месяц и год |
Июль 2016 |
Июль 2017 |
Июль 2018 |
Июль 2019 |
Июль 2020 |
|
Долг (в млн рублей) |
S |
0,8S |
0,5S |
0,1S |
0 |
Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.
Решение.
Долг перед банком (в млн рублей) на июль каждого года должен уменьшаться до нуля следующим образом:
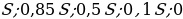
По условию, в январе каждого года долг увеличивается на 15%, значит, долг в январе каждого года равен:
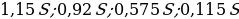
Следовательно, выплаты с февраля по июнь каждого года составляют:
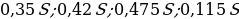
По условию, сумма выплат должна быть меньше 50 млн рублей.
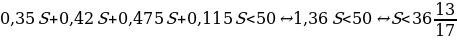
Наибольшее целое решение этого неравенства — число 36. Значит, искомый размер кредита — 36 млн рублей.
Ответ: 36.
№4. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик пополняет вклад на х млн рублей, где х — целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 6 млн рублей.
Решение.
Составим неравенство согласно условию задачи:
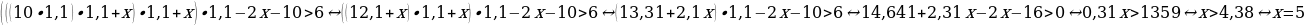
Ответ: 5.
Подводя итог, отметим, что необходимо знать для решения задания №17 на ЕГЭ
-
1% — это сотая часть чего-либо
-
За 100% принимает ту величину, с которой сравниваем
-
Основные формулы для подсчета процентов
Если величину S увеличить на а%, то получим S(1+0,1а)
Если величину S уменьшить на а%, то получим S(1-0,1а)
Если величину S дважды увеличить на а%, то получим S(1+0,1а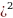
Если величину S уменьшить на а%, то получим S(1-0,01а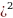
Заключение
В связи с преобразованием России из системы централизованного планирования в экономику рыночной ориентации экономические знания стали необходимыми как в профессиональной сфере, так и в повседневной жизни. Экономические знания позволяют понимать роль и права человека в обществе, готовят учеников к адекватному восприятию общества и производства, помогают им определить для себя сферу деятельности, профессию в будущем.
Эффективному постижению азов экономики поможет решение задач, в содержании которых идет речь о процентах. Понятие «проценты» буквально вошло в нашу жизнь, оно атакует нас в пору утверждения рыночных отношений в экономике, в пору банкротств, инфляций, финансовых кризисов. Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
Задачи с экономическим содержанием являются практическими задачами. А их решение, бесспорно, способствует более качественному усвоению содержания курса математики средней школы, позволяет осуществлять перенос полученных знаний и умений в экономику, что в свою очередь, активизирует интерес к задачам прикладного характера и изучению математики в целом. Такие задачи позволяют наиболее полно реализовывать прикладную направленность в обучении и способствуют более качественному усвоению самого учебного материала и формированию умения решать задачи данного типа.
На основе проанализированных задач, мы считаем, что введение такого рода заданий важно в современное время. Данные виды заданий чрезвычайно полезны так как, работая над моделями, сформулированными в условиях, они заставляют задумываться о реальной жизни. О том, что кредиты, отношения с банками, игра на бирже, колебания курсов ценных бумаг, начисление процентов дело сложное и требует больших знаний. К этому нельзя относиться легкомысленно. С чего начинать решать экономические задачи – очень внимательно читать условия задачи и по шагам распределить действия, затем постараться математически выразить их и постараться прийти к ответу.
ЛИТЕРАТУРА
1. Акимов Д.В. Решение задач по экономике: от простых до олимпиадных.М.,2016
2.Бондаренко М. Краткий курс лекций и рекомендаций по решению экономических задач. Чебоксары, 2016.
3. Гришаева Л.С. Основы экономики: задачи с решениями. М., 2016
4.Демонстрационный вариант контрольно-измерительных материалов единого государственного экзамена 2015 года по математике. Профильный уровень. Сайт http://www.ege.edu.ru/Ященко И. В. и др.
5. Колесникова С.И. Экономические задачи ЕГЭ. М., 2016
6. Малыхин В. Финансовая математика. СПб., 2014
7.Подготовка к ЕГЭ по математике в 2016 году. Базовый и профильный уровни. Методические указания / И. В. Ященко, С. А. Шестаков, А. С. Трепалин. – М.: МЦНМО, 2015.
8.Пучков Н.П. Математика в экономике. М., 2015
9.Спецификация контрольно-измерительных материалов для проведения в 2015 году единого государственного экзамена по математике. Профильный уровень. Сайт http://www.ege.edu.ru/
10. Хачатрян С. Методы и модели решения экономических задач. М., 2015
Научно-образовательный форум школьников Республики Мордовия
Лицей федерального государственного бюджетного образовательного учреждения высшего образования «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва»
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
ГОТОВИМСЯ К ЕГЭ. ЭКОНОМИЧЕСКИЕ ЗАДАЧИ В ПРОФИЛЬНОЙ МАТЕМАТИКЕ
Секция: Математический калейдоскоп
|
Автор работы: |
Душутина К. A. |
|
10 класс Лицей МГУ им. Н. П. Огарева |
|
|
Руководитель работы: |
Кубанцева А. В. |
|
учитель математики Лицей МГУ им Н. П. Огарева |
Саранск
2021
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 5
1.1 Содержательный смысл определения экономической науки 5
1.2 Взаимосвязь двух наук: экономики и математики 5
1.3 Основные определения и понятия 6
1.3.1 Понятие процента и процентной ставки 7
1.3.2 Понятие арифметической и геометрической прогрессий 8
1.3.3 Понятия фиксированных, аннуитетных и дифференцируемых платежей 10
2 ПРАКТИЧЕСКАЯ ЧАСТЬ 12
2.1 Типы экономических задач и способы их решения 12
2.1.1 Кредиты 12
2.1.2 Вклады 21
2.1.3 Задачи на оптимальный выбор 23
2.1.4 Нестандартные задачи 24
ЗАКЛЮЧЕНИЕ 26
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 27
ВВЕДЕНИЕ
Современная экономическая обстановка актуализирует проблему экономического воспитания подрастающего поколения. Экономические знания современной молодежи носят сугубо теоретический характер, оторванный от реальной действительности. Причем все больше осознается необходимость в формировании экономической грамотности у старшеклассников, тех, кто стоит на пороге самостоятельной жизни и которым в ближайшем будущем предстоит занять активную позицию в обществе. От экономической грамотности выпускников школы во многом будет зависеть их успешная адаптация к социально – экономическим условиям общества. Проблема обучения старшеклассников решению задач с экономическим содержанием складывается из нескольких составляющих: наличие в таких задачах большого количества терминов, неизвестных учащимся; старшеклассники плохо ориентируются в материале, изученном в 5-9 классах и необходимом для решения задач с экономическим содержанием: темы процентов, арифметической, геометрической прогрессий вызывают затруднения.
Задачи о вкладах и кредитовании, а также задачи оптимизации производства товаров и услуг сравнительно недавно включены во вторую часть ЕГЭ по математике профильного уровня и вызывают значительные затруднения у большинства выпускников.
Актуальность данной темы обусловлена тем, что в курсе математики, изучаемой в школе, решению задач с экономическим содержанием не уделено достаточно времени. Жизнь настоятельно требует, чтобы выпускник имел развитое экономическое мышление и был готов к жизни в условиях рыночных отношений. Однако основные практические навыки и умения у большинства учеников сформированы на уровне, не удовлетворяющем требованиям подготовки к ЕГЭ и повседневной жизни.
Гипотеза исследования – в современном мире необходимы знания об экономике и в этом может помочь математика.
Объект исследования – процесс подготовки к единому государственному экзамену по математике профильного уровня.
Предмет исследования – экономические задачи №17, встречающиеся в ЕГЭ по математике профильного уровня.
Цель исследования – исследование методов решения задач с экономическим содержанием.
Для достижения поставленной цели необходимо решить следующие задачи:
1. Изучить теоретико-методологические основы экономики.
2. Провести классификацию и систематизацию типов экономических задач, включенных во вторую часть ЕГЭ по математике профильного уровня, и методов их решений.
Методы исследования – теоретический анализ и синтез научной и учебной литературы по теме исследования, сравнение, систематизация информации, обобщение, вывод, подбор и решение задач.
Научная новизна работы заключается в обобщении, систематизация, анализе экономических задач, входящих в ЕГЭ по математике профильного уровня.
Практическое значимость – возможность использования обобщенных данных при подготовке выпускников к сдаче единого государственного экзамена по математике профильного уровня, отработке решения задач экономического содержания.
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
-
Содержательный смысл определения экономической науки
У всякой науки свой предмет, т.е. своя главная тема исследований. В центре внимания экономической теории – хозяйственная деятельность людей, которая осуществляется при определенных условиях, в определенной обстановке, экономической среде. [2]. В зависимости от условий, обстановки и экономической среды, термин «экономика» имеет различные определения. Приведем одно из определений экономики (экономической теории) как науки:
Экономика – это наука, изучающая типичные мотивы и модели поведения людей в процессах производства, обмена и потребления жизненных благ. [6].
Другими словами, экономика – наука об оптимальном, т.е. наилучшем в конкретных условиях, использовании ограниченных ресурсов [8].
-
Взаимосвязь двух наук: экономики и математики
Математика настолько практична, что немногое из окружающего мира может без нее функционировать. От банков и магазинов, бирж и страховых компаний до штрихкодов, прослушивания дисков и разговоров по мобильному телефону – все это и многое другое работает благодаря процессорам и математическим моделям, задача которых – постоянное выполнение математических операций.
Особенности математики, как отличительной области знаний, которые делают ее неповторимой, заключаются в следующем:
- недопустимость расхождения в определении правил и создании математических формул;
- математические формулы составляются из ряда аксиом, на основе строгих условий;
- возможность владеть теми или иными понятиями, не раскрывая их смысла.
Именно благодаря всем вышеперечисленным особенностям математический аппарат является многофункциональным аналитическим инструментом для всех отраслей знаний. [4].
Экономика представляет собой науку, которая изучает объективные причины и условия ведения в обществе хозяйственной деятельности. В этой связи экономике изначально были присущи различные количественные характеристики, исследование и описание которых потребовало использование большого числа математических методов. Экономические объекты, процессы и явления изучаются математически формализованным образом. Роль математики в экономике заключается в том, что ее язык позволяет сформулировать содержательные и проверяемые гипотезы о многих сложных экономических явлениях. Причем большая часть этих явлений вообще не может быть изучена без привлечения математического аппарата. В частности, его использование привело к созданию математических моделей, в которых нашли отражение некоторые теоретические экономические взаимосвязи.
На сегодняшний день обширное использование математического аппарата в своих исследованиях способствует достижению наибольших успехов в разных областях. Поэтому применение математики на практике позволяет достичь более значительных результатов в изучении явлений природы и общества.
-
Основные определения и понятия
Решение финансовых задач основывается на использовании различных математических моделей: уравнений, неравенств, их систем с привлечением процентов, арифметической и геометрической прогрессий, производной. Прежде чем рассмотреть способы решения экономических задач, целесообразно привести основные определения, понятия, таблицы и формулы.
-
Понятие процента и процентной ставки
Процентом называют одну сотую часть числа. С точки зрения экономики, процент – это абсолютная часть дохода, получаемая в результате финансовой операции за определенный период времени при наращении.
При решении экономических задач часто используется определение процентной ставки за определенный период времени – величины, характеризующей относительное изменение денежной суммы F за этот период:
где 
Определенная таким образом процентная ставка измеряется в процентах (%). Если относительное изменение денежной суммы не умножать на 100, то ставка будет измеряться в долях единицы (дробях).
Отрезок времени, к которому приурочена процентная ставка, называют периодом начисления. В качестве такого периода принимают год, полугодие, квартал, месяц или даже день. Чаще всего на практике имеют дело с годовыми ставками.
В зависимости от того, какая из сумм дана и какую нужно найти, выделяют два направления финансовых расчетов: наращение и дисконтирование.
Наращение – определение величины итоговой стоимости по заданной текущей стоимости. Дисконтирование – определение текущей стоимости по ожидаемой итоговой сумме в будущем. [3].
Различают простые и сложные процентные ставки, или проценты.
Для начисления простых процентов применяют постоянную базу начисления. В этом случае начисленные за весь срок проценты I составят:
где P – первоначальная денежная сумма, n – период начисления процентов, i – ставка наращения процентов в виде десятичной дроби.
Наращенная сумма представляет собой сумму первоначальной денежной суммы и наращенных процентов:
Когда за базу принимается сумма, полученная на предыдущем этапе наращения (дисконтирования), используют сложные процентные ставки. В этом случае база начисления последовательно изменяется, то есть проценты начисляются на проценты.
В конце первого года проценты будут равны величине I = Р * i, а наращенная сумма составит S = Р + Р * i = Р * (1 + i). К концу второго года она достигнет величины Р * (1 + i) + Р * (1 + i) * i = Р * (1 + i)2 и т.д. В конце n-го года наращенная сумма будет равна:
где P – первоначальная денежная сумма, n – период начисления процентов, i – ставка наращения процентов в виде десятичной дроби.
Проценты за этот срок составят:

-
Понятие арифметической и геометрической прогрессий
Арифметическая прогрессия – это числовая последовательность, в которой каждый член равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d. [7].

Очевидно, что арифметическая прогрессия представляется возрастающей последовательностью, если d > 0, и убывающей, если d < 0.
Формула n-ого члена арифметической прогрессии:
Формула суммы первых n членов арифметической прогрессии:
Каждый член арифметической прогрессии, кроме первого (и последнего – в случае конечной прогрессии), равен среднему арифметическому предыдущего и последующего членов. Верно и обратное: если последовательность (an) такова, что для любого n > 1 выполняется равенство:

то (аn) – арифметическая прогрессия. [5].
Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число q, называют геометрической прогрессией. При этом число q называют знаменателем прогрессии. [1].
Формула n-ого члена геометрической прогрессии:
Формула суммы первых n членов арифметической прогрессии:
Квадрат каждого члена геометрической прогрессии, первого (и последнего – в случае конечной последовательности), равен произведению предшествующего и последующего членов. Верно и обратное: если последовательность (bn) такова, что для любого n > 1 выполняется равенство:
то (bn) – геометрическая прогрессия. [1].
-
Понятия фиксированных, аннуитетных и дифференцируемых платежей
Фиксированные платежи – платежи, которые четко оговариваются в условии задачи. Аннуитетный платеж – это платеж, который устанавливается в равной сумме через равные промежутки времени. Месячный аннуитетный платеж находится по формуле:
где X – месячный платеж, S – сумма кредита, P – 1/12 процентной ставки, N – количество месяцев.
Дифференцируемый платеж – это платеж, который представляет собой неравные ежемесячные транши, пропорционально уменьшающиеся в течение срока кредитования. Если при аннуитетной схеме неизменным является сам аннуитетный платеж, то при дифференцируемой – не меняется именно взнос, идущий на погашение тела кредита. Рассчитывается он по формуле:
где St – сумма, которая идет на погашение тела кредита, S – сумма кредита, N – количество месяцев. Для расчёта доли процентов в дифференцированных платежах пользуются следующей формулой:
где In – сумма, которая идёт на погашение процентов по кредиту в данный расчётный период, Sn — остаток задолженности по кредиту, P – годовая процентная ставка. Зная долю тела кредита и долю процентов, мы можем рассчитать дифференцированный платёж, используя формулу:
где X — размер дифференцированного платежа по кредиту, St – сумма, которая идёт на погашение тела кредита, In – сумма уплачиваемых процентов. [3].
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Экономические задачи были введены в задания ЕГЭ по математике профильного уровня (№17) в 2015 году. По своей сложности задачи с экономическим содержанием находятся на одном уровне с заданиями, содержащие параметры и теорию чисел.
Низкий процент успешной сдачи решения задания №17 (за 2015 – 2020 годы – 2, 5) объясняется как трудностью самих задач, так и их отсутствием в школьном курсе математики.
Основными ошибками, которыми допускали учащиеся при решении задач финансовой математики, являются:
- неверное составление модели;
- вычислительными, или арифметические;
- прекращение решения на промежуточном шаге, то есть без доведения ответа до числового значения;
- решение методом перебора без обоснования единственности;
- решение без вывода формул. В ряде случаев трактуется как неумение строить математическую модель.
С целью подготовки учащихся к успешной ЕГЭ имеет смысл подробно рассмотреть типы экономических задач и методы их решения.
-
Типы экономических задач и способы их решения
Условно выделяют несколько типов задач экономического содержания.
Далее приведем подробные разборы примеров задания №17 каждого типа.
-
Кредиты
ПРИМЕР №1 (Подтип 1: Нахождение количества лет (месяцев) выплаты кредита). 1 января 2015 года Павел Витальевич взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк платёж. На какое минимальное количество месяцев Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не более 125 тыс. рублей? [10].
РЕШЕНИЕ:
СПОСОБ №1. Сначала найдем минимальное количество месяцев, за которое Павел Витальевич сможет погасить основную сумму долга, если его ежемесячный платеж будет составлять 125 тыс. рублей: 1 000 000 : 125 000 = 8 (месяцев).
Но банк ежемесячно начисляет 1% на оставшуюся сумму долга. Тем самым получаем, что общая сумма долга будет превышать 1 млн рублей.
Составим таблицу, наглядно показывающую схему кредита, и найдем № месяца, когда задолженность будет меньше, чем ежемесячная выплата:
|
Месяц, № |
Задолженность в начале месяца, руб. |
Задолженность после погашения, руб. |
|
1 |
1 000 000 + 1% = 1 010 000 |
1 010 000 – 125 000 = 885 000 |
|
2 |
885 000 + 1% =893 850 |
893 850 – 125 000 = 768 850 |
|
3 |
768 850 + 1% = 776 538, 5 |
776 538, 5 – 125 000 = 651 538,5 |
|
4 |
651 538,5 + 1% = 658 054 |
658 054 – 125 000 = 533 054 |
|
5 |
533 054 + 1% = 538 385 |
538 385 – 125 000 = 413 385 |
|
6 |
413 385 + 1% = 417 519 |
417 519 – 125 000 = 292 519 |
|
7 |
292 519 + 1% = 295 445 |
295 445 – 125 000 = 170 445 |
|
8 |
170 445 + 1% = 172 150 |
172 150 – 125 000 = 47 150 |
|
9 |
47 150 + 1% = 47 622 |
0 |
СПОСОБ №2. За 8 месяцев Павел Витальевич сможет оплатить за кредит не более, чем 125 000 * 8 = 1 000 000 рублей, но с учетом начисляемых процентов общая сумма долга будет превышать 1 млн рублей.
За 9 месяцев банк начислит не более, чем 9 сумм процентов за первый месяц (максимально начисленные проценты будут составлять 10 000 рублей), то есть 10 000 * 9 = 90 000, что составляет меньше, чем ежемесячный платеж. Таким образом, Павел Витальевич полностью погасит кредит за 9 месяцев.
ОТВЕТ: на 9 месяцев.
ПРИМЕР №2 (Подтип 1: Нахождение количества лет (месяцев) выплаты кредита). В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок. Условия его возврата таковы:
- каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 1, 4 млн руб.? [11].
РЕШЕНИЕ: Чтобы найти минимальное количество лет, надо обозначить размер максимального первого платежа – 1,4 млн рублей.
|
Дата |
Долг до выплаты, млн руб. |
Выплата, млн руб. |
Долг после выплаты, млн руб. |
|
Июль 0-ого года |
5 |
||
|
Январь 1-ого года |
5 + 15% = 5,75 |
||
|
Февраль 1-ого года |
1,4 |
5,75 — 1,4 = 4,35 |
|
|
Июль 1-ого года |
4,35 (разница 0,65) |
||
|
Июль 2-ого года |
4,35 – 0,65 = 3,7 |
||
|
Июль 3-его года |
3, 7 – 0,65 = 3,05 |
||
|
Июль 4-ого года |
3,05 – 0,65 = 2,4 |
||
|
Июль 5-ого года |
2,4 – 0,65 = 1,75 |
||
|
Июль 6-ого года |
1,75 – 0,65 = 1,1 |
||
|
Июль 7-ого года |
1,1 – 0,65 = 0,45 |
||
|
Июль 8-ого года |
0 |
Мы можем найти оставшуюся сумму долга на июль данного года, найдя фиксированную разницу между 1-ым и 2-ым годами выплаты кредита. Как только, оставшаяся сумма долга будет меньше, чем разница, кредит будет считаться полностью оплаченным в этот год.
ОТВЕТ: 8 лет.
ПРИМЕР №3 (Подтип 2: Вычисление процентной ставки по кредиту). В июле 2019 планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга.
Найдите число r, если известно, что кредит был полностью погашен за два года, причём в первый год было переведено 52 500 рублей, а во второй год – 67 500 рублей? [11].
РЕШЕНИЕ: Пусть банк начисляет r процентов, умножая сумму долгу на x = (1 + 
|
Дата |
Долг до выплаты, тыс. руб. |
Выплата, тыс. руб. |
Долг после выплаты, тыс. руб. |
|
1.7.2019 |
100 |
||
|
1.1.2020 |
100x |
||
|
1.2.2020 |
52,5 |
||
|
1.7.2020 |
100x – 52,5 |
||
|
1.1.2021 |
(100x – 52,5) * x = 100x2 – 52,5x |
||
|
1.2.2021 |
67,5 |
||
|
1.7.2021 |
100x2 – 52, 5x – 67,5 = 0 |
Решив квадратное уравнение: 100x2 – 52, 5x – 67,5 = 0, получаем, что x1= = — 0,6 (не подходит, т. к. процентная ставка не может быть отрицательным числом) и x2 = 1, 125. Отсюда получаем: x = 1 + 
ОТВЕТ: 12,5
ПРИМЕР №4 (Подтип 3: Нахождение суммы кредита). Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 10 млн. [10].
РЕШЕНИЕ:
СПОСОБ №1. Обозначим за S полную сумму кредита. Составим схему погашения кредита:
|
Дата |
Долг до выплаты, млн руб. |
Выплата, млн руб. |
Долг после выплаты, млн руб. |
|
Начало 1/2/3-ого годов |
S |
||
|
Середина 1/2/3-ого годов |
S + 20%=1,2S |
||
|
Конец 1/2/3-ого годов |
0,2S |
S |
|
|
Начало 4-ого года |
S |
||
|
Середина 4-ого года |
S + 20%=1,2S |
||
|
Конец 4-ого года |
X |
1,2S — X |
|
|
Начало 5-ого года |
1,2S — X |
||
|
Середина 5-ого года |
(1,2S– X)+20% =1,44S-1,2X |
||
|
Конец 5-ого года |
X |
1,44S — 1,2X – X = 0 |
Решаем уравнение 1,44S — 1,2X – X = 0. Получаем, что X = 
Общая сумма выплат составляет 0,6S + 2X = 0,6S + 


СПОСОБ №2. Обозначим за S полную сумму кредита. Каждый год заёмщик выплачивает по 0,2S млн. Всего 0,6S за три года.
Рассмотрим погашение кредита за следующие два года. В середине 4-го года долг возрастёт до 1,2S млн. Обозначим через X размер выплаты в конце 4-го и 5-го годов. После выплаты в конце 4-го года долг равен (1,2S — X), а в середине 5-го года он равен 1,2(1,2S — X). В конце 5-го года весь долг должен быть погашен. Отсюда следует, что последняя выплата равна 1,2(1,2S- X), а по условию равна X. Получаем, что X = 
Общая сумма выплат составляет 0,6S + 2X = 0,6S + 


ОТВЕТ: 6 млн рублей.
ПРИМЕР №5 (Подтип 4: Нахождение ежегодного (ежемесячного) транша). 31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк X рублей. Какой должна быть сумма X, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)? [10].
РЕШЕНИЕ: Составим схему погашения кредита:
|
Дата |
Долг до выплаты, руб. |
Выплата, руб. |
Долг после выплаты, руб. |
|
31.12.2014 |
4 290 000 |
||
|
31.12. 2015 |
4 290 000 + 14,5% = 4 912 050 |
X |
4 912 050 — X |
|
31.12. 2016 |
(4 912 050 – X) + 14,5% = 5 624 298 – 1,145X |
X |
5 624 298 – 2,145X = 0 |
Решаем уравнение 5 624 298 – 2,145X = 0. Получаем, что X = 2 622 050.
ОТВЕТ: 2 622 050 рублей.
ПРИМЕР №6 (Подтип 4: Нахождение ежегодного (ежемесячного) транша). Клиент взял в банке кредит 18000 рублей на год под 18 %. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно? [10].
РЕШЕНИЕ: Через год банк начисляет 18% годовых, то есть долг увеличивается в 1,18 раз. Получится, что клиент должен банку 18 000 * 1,18 = 21 240 рублей. Соответственно ежемесячная выплата составит:
21 240 / 12 = 1 770 рублей.
ОТВЕТ: 1 770 рублей.
ПРИМЕР №7 (Подтип 5: Нахождение разницы). 31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа? [10].
РЕШЕНИЕ: Построим схему выплаты кредита:
|
Дата |
Долг до выплаты, руб. |
Выплата, руб. |
Долг после выплаты, руб. |
|
31.12.2014 |
7 007 000 |
||
|
31.12.2015 |
7 007 000 + 20% = 8 408 400 |
X |
8 408 400 – X |
|
31.12.2016 |
(8 408 400 – X) + 20% = 10 090 080 – 1,2X |
X |
10 090 080 – 2,2X |
|
31.12.2017 |
(10 090 080 – 2,2X) + 20% = 12 108 096 – 2,64X |
X |
12 108 096 – 3,64X |
Схема №1 (3 равных платежа). Последним платежом Тимофей полностью погасит кредит. Решим уравнение 12 108 096 – 3,64X1 = 0. Получаем, что X1 = 3 326 400.
Схема №2 (2 равных платежа). Решим уравнение 10 090 080 – 2,2X2 = 0. Получаем, что X2 = 4 586 400.
Находим разницу: 3X1 – 2X2 = 9 979 200 – 9 172 800 = 806 400 рублей.
ОТВЕТ: на 806 400 рублей.
ПРИМЕР №8 (Подтип 6: Задачи, связанные с известным остатком). В январе 2020 года планируется взять кредит в банке на три года в размере 800 тыс. рублей. Условия его возврата таковы:
- каждый ноябрь долг увеличивается на 20% по сравнению с концом предыдущего года;
- в декабре каждого года необходимо выплатить одним платежом часть долга;
- в январе каждого года долг (в тыс. рублей) должен соответствовать следующей таблице:
|
Месяц и год |
Январь 2020 |
Январь 2021 |
Январь 2022 |
Январь 2023 |
|
Долг, тыс. руб. |
800 |
600 |
300 |
0 |
Сколько тыс. рублей нужно заплатить по кредиту в декабре 2021 года? [11].
РЕШЕНИЕ:
СПОСОБ №1. Составим схему погашения кредита:
|
Дата |
Долг до выплаты, тыс. руб. |
Выплата, тыс. руб. |
Долг после выплаты, тыс. руб. |
|
Январь 2020 |
800 |
||
|
Ноябрь 2020 |
800 + 20% = 960 |
||
|
Декабря 2020 |
X1 = 960 – 600 = 360 |
||
|
Январь 2021 |
960 – X1 = 600 |
||
|
Ноябрь 2021 |
600 + 20% = 720 |
||
|
Декабрь 2021 |
X2 =720 – 300 = 420 |
||
|
Январь 2022 |
720 – X2 = 300 |
||
|
Ноябрь 2022 |
300 + 20% = 360 |
||
|
Декабрь 2022 |
X3 = 360 |
||
|
Январь 2023 |
360 – X3 = 0 |
По таблице видим, что в декабре 2021 года клиент должен будет заплатить банку 420 тыс. рублей.
СПОСОБ №2. В ноябре 2021 года долг в размере 600 тыс. руб., который остался в 2021 году, увеличится на 20% и будет составлять 600 *1,2 = 720 тыс. руб. В январе 2022 года долг должен стать равным 300 тысячам рублей, так что в декабре 2021 года должно быть выплачено 720 – 300 = 420 тыс. руб.
ОТВЕТ: 420 руб. тыс.
ПРИМЕР №9 (Подтип 7: Задачи, связанные с дифференцированными платежами). 15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования? [11].
РЕШЕНИЕ: Обозначим за S размер кредита, взятого в банке 15 января. 1-го февраля он уже вырастет на 3% и будет составлять 1,03S. После этого происходит выплата так, чтобы долг менялся каждый месяц на одну и ту же величину, то есть выплата в первый месяц составит: 
|
Дата |
Долг до выплаты, тыс. руб. |
Выплата, тыс. руб. |
Долг после выплаты, тыс. руб. |
|
15.01 |
S |
||
|
01.02 |
1,03S |
||
|
14.02 |
|
||
|
15.02 |
|
||
|
1.03 |
|
||
|
14.03 |
|
||
|
15.03 |
|
||
|
15.04 |
|
||
|
15.05 |
|
||
|
15.06 |
|
|
|
Решим уравнение: 
Рассчитаем всю сумму, выплаченную банку за 9 месяцев:

ОТВЕТ: 517,5 тыс. руб.
ПРИМЕР №10 (Подтип 7: Задачи, связанные с дифференцированными платежами). Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r. [9]
РЕШЕНИЕ: Обозначим за S полную сумму кредита. По условию долг должен уменьшатся до нуля равномерно. Составим геометрическую прогрессию: S; 


К концу каждого месяца долг увеличивается на r%, то есть умножается на коэффициент k, равный 



Отсюда следует, что ежемесячные выплаты должны быть представлены в следующем виде: 



Всего следует заплатить: 
Общая сумма выплат оказалась на 13% больше суммы, взятой в кредит. Получаем: 

ОТВЕТ: 2%.
-
Вклады
ПРИМЕР №11. В банк был положен вклад под 10% годовых. Через год, после начисления процентов, вкладчик снял со счета 2000 рублей, а еще через год (опять после начисления процентов) снова внес 2000 рублей. Вследствие этих действий через три года со времени открытия вклада вкладчик получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы он получил? [10].
РЕШЕНИЕ: Обозначим за S общую сумму вклада. Составим схему начисления процентов по вкладу:
|
Год, № |
Реальная сумма, руб. |
Запланированная сумма, руб. |
|
0 |
S |
S |
|
1 |
1,1S |
1,1S |
|
2 |
1,1(1,1S – 2000) |
1,1 * 1,1S |
|
3 |
1,1(1,1(1,1S – 2000) + 2000) = 1,1 * (1,21S – 200) = 1, 331S -220 |
1,1 * 1,1 * 1,1S = 1, 331S |
Найдем разницу:
1,1(1,1(1,1S – 2000) + 2000) — 1,1 * 1,1 * 1,1S = 1, 331S – 220 – 1,331S = — 220. Таким образом, вкладчик получил на 220 рублей меньше запланированной суммы.
ОТВЕТ: на 220 рублей.
ПРИМЕР №12. По бизнес-плану предполагается изначально вложить в четырёхлетний проект 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по целому числу n млн рублей в первый и второй годы, а также по целому числу m млн рублей в третий и четвёртый годы.
Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся. [11].
РЕШЕНИЕ: Составим схему увеличения вклада:
|
Год |
Сумма вклада |
Год |
Сумма вклада |
|
0 |
10 |
3 |
((1,15 * 10 + 4) * 1,15 +4) *1,15 + m = 21,825 * 1, 15 + m = 25,099 + m |
|
1 |
1,15 * 10 + n |
4 |
(25,099 + m) * 1, 15 + m |
|
2 |
(1,15 * 10 + n) * 1,15 + n |
В условии задачи сказано, что за два года первоначальные вложения как минимум удвоятся, значит, можно составить неравенство:
(1,15 * 10 + n) * 1,15 + n ≥ 20. Получаем, что n ≥ 3,5. (Минимальное целочисленное решение n = 4).
За четыре года первоначальные вложения утроятся. Составим неравенство: (25,099 + m) * 1, 15 + m ≥ 30. Получаем, что m ≥ 0,528. (Минимальное целочисленное решение m = 1).
ОТВЕТ: 4 и 1 млн рублей.
-
Задачи на оптимальный выбор
ПРИМЕР №13. В январе 2000 года ставка по депозитам в банке «Возрождение» составляла х% годовых, тогда как в январе 2001 года она составила у% годовых, причем известно, что x + y = 30. В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение х при котором сумма на счету вкладчика в январе 2002 года станет максимально возможной. [10].
РЕШЕНИЕ: Обозначим за S сумму вклада, которую положили в банк в январе 2000 года. В январе 2001 года вклад будет уже составлять S(1+0,01x), но вкладчик снял 0,2S. Поэтому на январь 2021 на вклад приходится: S(1+0,01x) – 0,2S = 0,8S +0,01Sx. В январе 2002 года вклад увеличится на y%, то есть умножится на (1 + 0,01y) = (1 + 0,01(30 – x), и будет составлять (0,8S +0,01Sx) * (1 + 0,01(30 — x)) = — 0,0001Sx2 + 0,005Sx + 1, 04S.
Функция f(x) = — 0,0001Sx2 + 0,005Sx + 1, 04S является убывающей. Найдем ее максимальное значение x0 = 
ОТВЕТ: 25.
-
Нестандартные задачи
ПРИМЕР №14. В одной стране в обращении находилось 1 000 000 долларов, 20% из которых были фальшивыми. Некая криминальная структура стала ввозить в страну по 100 000 долларов в месяц, 10% из которых были фальшивыми. В это же время другая структура стала вывозить из страны 50 000 долларов ежемесячно, из которых 30% оказались фальшивыми. Через сколько месяцев содержание фальшивых долларов в стране составит 5% от общего количества долларов? [10].
РЕШЕНИЕ: Найдем ежемесячное увеличение валютной массы, находящейся в обращении: 100 – 50 = 50 тыс. долларов. Через n месяцев в стране будет – (1 000 + 50n) тыс. долларов.
Ежемесячно количество фальшивых купюр уменьшается на 50 * 0,3 – 100 * 0, 1 = 5 тыс. долларов. Изначально их было 1 000 000 * 0, 2 = 200 000. Тогда, через n месяцев их будет – (200 – 5n) тыс. долларов, что составляет 5% от общего количества долларов. Получаем: (1 000 + 50n) * 0, 05 = 200 – 5n.
n = 20.
ОТВЕТ: через 20 месяцев.
ПРИМЕР №15. При рытье колодца глубиной свыше 10 м за первый метр заплатили 1000 руб., а за каждый следующий на 500 руб. больше, чем за предыдущий. Сверх того, за весь колодец дополнительно было уплачено 10 000 руб. Средняя стоимость 1 м оказалась равной 6250 руб. Определите глубину колодца. [10].
РЕШЕНИЕ: Обозначим за Х м глубину колодца. Тогда, часть выплат, зависящая от глубины колодца, представляет собой арифметическую прогрессию, где a1 = 1000, а d = 500. Последний член прогрессии имеет вид: 1000 + 500(X –1).
Найдем сумму всех выплат по формуле суммы n – членов арифметической прогрессии: 
Поскольку сверх этого было выплачено еще 10 000 руб., а средняя стоимость 1 м при этом составила 6250 руб., то имеет место уравнение вида: 250X2 + 750X + 10 000 = 6250X. Решим, получаем: Х1 = 2 (не подходит, т. к. Х> 10 м) и Х2 = 20.
ОТВЕТ: 20 м.
ЗАКЛЮЧЕНИЕ
В результате проведенной работы по классификации и систематизации типов задач финансовой математики, включенных во вторую часть ЕГЭ по математике профильного уровня, и методов их решений были получены следующие выводы и результаты:
1. Было дано определение экономики как науки, изучающей типичные мотивы и модели поведения людей в процессах производства, обмена и потребления жизненных благ, а также установлена ее связь с математикой, заключающаяся в построении теоретических моделей математическим методом при анализе экономических явлений и процессов.
2. Были выделены четыре типа, один из которых содержит в себе семь подтипов, экономических задач ЕГЭ по математике профильного уровня и приведены различные способы их решений.
В ходе исследования было замечено, что наиболее наглядным и понятным методом решения задач с экономических содержанием оказался табличный метод. Именно этот способ решения рекомендуется использовать учащимся для построения точной теоретической модели экономической задачи.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
- Алимов, Ш. А. Алгебра: учебник для учащихся 9 кл. средней школы / Ш.А. Алимов. – М.: Просвещение, 2012. – 287 с.
- Ермаков, С. Л. Экономика: учебное пособие (Бакалавриат) / С.Л. Ермаков, С.В. Устинов, Ю.Н. Юденков. – Москва: КНОРУС, 2020. – 270 с.
- Копнова, Е. Д. Финансовая математика: учебник и практикум для бакалавриата и магистратуры / Е. Д. Копнова. — М.: Издательство Юрайт, 2016. — 413 с.
- Лагошина Ю.С. Взаимосвязь математики с экономическими отраслями / Ю.С. Лагошина // Международный студенческий научный вестник. – 2017. – № 4 – С. 4.
- Мордкович, А.Г. Алгебра: Учебник. 9 класс / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2010. – 224 с.
- Носова, С.С. Основы экономики: учебник (Среднее профессиональное образование) /С. С. Носова. – Москва: КНОРУС, 2020. – 312 с.
- Пичурин Л.Ф. За страницами учебника алгебры: Кн. Для учащихся 7-9 кл. средн. Шк. / Л.Ф. Пичурин. – М.: Просвещение, 1990. – 224 с.
- Шимко, П. Д. Основы экономики: учебник (Среднее профессиональное образование) / П.Д. Шимко. – Москва: КНОРУС, 2021. – 292 с.
- fipi.ru: сайт. – 2009. – URL: https://fipi.ru/
- ege.sdamgia.ru: образовательный портал: сайт. – 2011. — URL: https://ege.sdamgia.ru/
- yandex.ru/tutor: образовательный портал: сайт. – 2018. – URL: https://yandex.ru/tutor/
Автор работы:
Оганесян Сусанна Гагиковна
Руководитель проекта:
Поликарпова Галина Павловна
Учреждение:
ГБОУ СОШ лицей №150 Калининского района Санкт-Петербурга
В процессе работы над индивидуальным исследовательским проектом по математике на тему «Экономическая задача в ЕГЭ по математике» автором была поставлена цель, создать методическое пособие к декабрю 2019 года, содержащее много разных типов экономических задач и необходимых теоретических знаний, позволяющих ученикам научиться решать 17 задачу из ЕГЭ по профильной математике, что приведет к успешным результатам сдачи экзамена.
Подробнее о работе:
В ученическом проекте по математике «Экономическая задача в ЕГЭ по математике» автором был изучен принцип работы банков, рассмотрены правила осуществления банковских вкладов и получения кредитов. В работе рассматриваются примеры решения экономических задач на вклады и на кредиты, а также производственно-бытовых задач. В работе предложены экономические задачи для самоподготовки к ЕГЭ.
Учебная исследовательская работа по математике на тему «Экономическая задача в ЕГЭ по математике» будет интересна учащимся 10 и 11 класса, рассматривает теоретическую базу финансовой и математической грамотности. В работе представлен разбор основных типов задач с примерами их решений, автор анализирует ошибки, часто совершаемые учениками при решении экономических задач.
В работе автор приводит информацию, найденную в различных исторических, научных, энциклопедических источниках, и примеры решения текстовой задачи социально-экономической тематики. Это задача на применение математических методов для решения содержательных задач из различных областей науки и практики и интерпретацию результата с учётом реальных ограничений. Автор разрабатывает методические рекомендации, в которых содержится необходимый теоретический материал, примеры решения финансовых задач разных типов, задания для самопроверки, разбор наиболее сложных задач, которые были на ЕГЭ прошлых годов.
Оглавление
Введение
1. Принцип работы банков.
1.1. Вклады.
1.2. Кредиты.
2. Примеры решения экономических задач.
2.1. Задача на вклады.
2.2. Задачи на кредиты.
2.3. Производственно-бытовые задачи.
3. Экономические задачи для самоподготовки.
Заключение
Литература
Введение
Новым типом задач повышенного уровня сложности, впервые введённым в структуру Единого государственного экзамена в 2015 году, является текстовая задача социально-экономической тематики. Это задача на применение математических методов для решения содержательных задач из различных областей науки и практики и интерпретацию результата с учётом реальных ограничений.
Использование подобных задач предполагает проверку следующих умений учащихся:
- переходить от текста задачи к построению соответствующей математической модели степенями с натуральным показателем обращаться с процентами;
- обращаться с целыми числами, то есть уметь использовать при решении задач элементы теории делимости целых чисел;
- производить действия со сложными процентами и долями.
Как показывает анализ содержания подобных задач, сюжеты, описанные в них, являются некоторыми текстовыми упрощениями, моделями реально возникающих в окружающей жизни ситуации. Кроме того, сами сюжеты условно можно разделить на два типа, использующие соответственно дискретные модели (проценты, погашения кредитов и так далее) и непрерывные модели (различные производства, протяжённый во времени объема продукции и так далее).
За правильное выполнение задания выставляются три балла. Пособие поможет обучающимся сдать Единый государственный экзамен по математике на высокий балл, а также послужит учителям для организации имя эффективной подготовки школьников.
Цель проекта: создать методическое пособие к декабрю 2019 года, содержащее много разных типов экономических задач и необходимых теоретических знаний, позволяющих ученикам научиться решать 17 задачу из ЕГЭ по профильной математике, что приведет к успешным результатам.
Задачи проекта:
- Изучить теоретическую базу финансовой и математической грамотности
- Разобрать основные типы задач с примерами решений
- Проанализировать ошибки совершаемые учениками
- Создать продукт
Вопросы проекта:
- Какие темы по математике следует повторить ученикам для успешного решения экономических задач?
- Какие типы экономических задач вызывают наибольшую трудность у учеников?
- Как повысить процент учащихся, которые успешно справляются с решением экономических задач?
Актуальность: решение экономических задач очень полезно, так как жизнь современного человека тесно связана с финансовыми операциями
В соответствии с указом «О национальных целях и стратегических задачах развития Российской Федерации на период до 2024 года» получение качественного образования необходимо ученикам, чтобы быть конкурентоспособными в будущем на рынке труда, а также для обеспечения вхождения России в число 10 ведущих стран мира по качеству среднего образования приближается ЕГЭ, а большинство школьников еще не приступили к решению экономической задачи за решение этого задания на экзамене можно получить 3 первичных балла, что говорит о важности выполнения этого задания несмотря на то, что экономическая задача большинству школьников кажется несложной, в ней ученики чаще всего совершают ошибки.
Продукт проекта: методические рекомендации.
Новым типом задач повышенного уровня сложности, впервые введённым в структуру Единого государственного экзамена в 2015 году, является текстовая задача социально-экономической тематики. Это задача на применение математических методов для решения содержательных задач из различных областей науки и практики и интерпретацию результата с учётом реальных ограничений.
Методические рекомендации будут содержать необходимый теоретический материал, примеры решения финансовых задач разных типов, задания для самопроверки, разбор наиболее сложных задач, которые были на ЕГЭ прошлых годов. Пособие поможет обучающимся сдать Единый государственный экзамен по математике на высокий балл, а также послужит учителям для организации ими эффективной подготовки школьников.
Аналоговый анализ:
Недостатки других методических пособи
- наличие только типовых заданий,
- слабая теоретическая база,
- краткое пояснение к задачам.
Достоинства моего продукта:
- комплексный подход к решению задач,
- решение самых разнообразных заданий,
- грамотно составленная теоретическая база,
- представление подробных решений задач,
Этапы работы над проектом:
| Название этапа | Дата | Содержание работы | Отметка о выполнении | Коррективы |
|---|---|---|---|---|
| Подготовительный | сентябрь 2018 года | Выбор темы, формы представления проекта, типа проекта, формулирование проблемы, цели, задач | Выполнено | Проблема должна быть более точной и лаконичной. Цель проекта следует расширить, сформулировать более глобально |
| Организационный | Октябрь 2018 года | Составление аннотации и актуальности работы | Выполнено | Указать актуальность проекта как для себя лично, так и более масштабно (например, значение для государства) |
| Аналитический | ноябрь 2018 года | Поиск статистики | Выполнено | Следует вставить ссылку на статистику |
| Аналитический | декабрь 2018 года | Аналоговый анализ | Выполнено | Помимо достоинств моего продукта следует также указать недостатки других аналогичных работ |
| Практический | Январь-сентябрь 2019 года | Работа над исследовательской частью (составление решения разных типов задач) | Частично | В решении задач лучше объяснять значение некоторых математических символов, не часто использующихся на курсе базовой математики |
| Практический | Август-сентябрь 2019 года | Работа над дизайном методички | Частично | Дизайн должен быть современным, но не слишком броским, чтобы не отвлекать внимание читателей |
Принцип работы банков
Итак, 17 задача бывает банковской, то есть на вклады и кредиты, и производственно-бытовой. Второй тип задач интуитивно понятен большинству школьников и требует просто много практики. Для банковских же задач изложим немного теории.
Смоделируем ситуацию. Есть предприимчивый Андрей, который решает открыть банк, имея 100 рублей. Он объявляет, что будет выдавать кредиты под 20 % годовых. Это означает, что если Андрей даст кому-нибудь некую сумму на год, то через год он получит на 20 % больше денег. К Андрею приходит первый клиент, который хочет взять 100 рублей.
Он их получает, и Андрей целый год сидит и ждет, пока пройдет год и он получит уже 120 рублей. Но проблема в том, что прошел целый год, а у Андрея всего 120 рублей, хотя было 100. Разница небольшая. Значит, Андрею нужно действовать по-другому. Тогда он объявляет, что будет принимать вклады и процентная ставка будет составлять 10 % годовых.
Получается, если кто-то вложит в банк некую сумму, то через год получит в 1,1 раз больше денег от банка (на 10 % больше изначальной суммы). К Андрею приходит некий богач и вкладывает в банк 10 000 рублей. Через год банк должен вернуть богачу 11 000. Это достаточно проблематично, так как у Андрея нет 11 000 рублей.
Есть только 10 000 + 120=10120 рублей. С другой стороны целый год деньги богача будут в распоряжении банка, а значит, можно будет выдавать кредиты, увеличивая имеющиеся деньги. Таким образом, при удачном стечении обстоятельств Андрей получит от заемщиков через год сумму, превышающую 11000 рублей. Богач получает деньги от вклада, заемщики возвращают взятые суммы с процентами, а Андрей в плюсе и счастлив.
Вклады
В случае банковского вклада банк выступает в роли заёмщика (получает деньги, обязуясь их вернуть, а вкладчик в роли кредитора (предоставляет деньги).При внесении вкладчиком банка денег отношения между вкладчиком и банком закрепляются договором, в котором банк, принявший поступившую от вкладчика денежную сумму, обязуется возвратить ему сумму вклада и выплатить на неё проценты на условиях и в порядке, предусмотренных договором. Как правило, вкладчик имеет возможность распоряжаться начисленными процентами.
Кредиты
Кредит-это финансовая сделка, в результате которой кредитор (банк или другой финансовое учреждение) предоставляет на определенный срок деньги заемщику. За пользование деньгами заемщик кроме погашения основного долга (называемого в финансовой литературе телом кредита) выплачивает кредитору также проценты.
Разделение повышающих платежей на две части — погашение долга (тела кредита) и погашение процентных денег — принципиально важно, поскольку от этого зависят выплачиваемые налоги. Разберем и сравним две важные схема выплаты кредитов: дифференцированными и аннуитетными платежами. При дифференцированной схеме каждой платёж состоит из двух частей. Первая часть — основной платёж, его размер не изменяется на всём сроке кредитования.
Скажем, если в кредит взяли 1 млн рублей на 5 месяцев, а платежи ежемесячные, то тело кредита делится на пять равных частей по 200000 руб. — это и будет ежемесячный основной платеж. Вторую часть платежа составляют проценты на текущую часть долга. Долг постепенно уменьшается, потому и платежи в счет процентов тоже уменьшаются.
Первый платёж самый большой, последний — самый маленький. На практике платежи обычно ежемесячные, а банки учитывают каждый день кредитования: важно, сколько дней в месяце, високосный год или нет. А в экзаменационных задачах обычно упрощённая схема: за каждый платежный период проценты начисляются один раз.
Иначе говоря, если проценты начисляются ежегодно, то и выплаты по кредиту раз в год. Если проценты начисляются ежемесячно, то и выплаты ежемесячные. При аннуитетных платежах сумма кредита и сумма процентов за всё время пользования кредитом суммируются и делятся на число платежей, все платежи получаются равными.
Примеры решения экономических задач можно посмотреть в полном тексте проекта, прикрепленном внизу этой странице в формате *doc
Задачи для самоподготовки
1)
В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
- в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в млн рублей) | S | 0,7S | 0,4S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн рублей.
2) Взяли кредит в банке на сумму 250 000 рублей под r% процентов годовых и выплатили за 2 года платежами 150 000 рублей в первый год и 180 000 рублей — во второй.
Найдите r.
3) В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
- в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
- с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, на какую сумму взяли кредита банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 78 030 рублей больше суммы взятого кредита.
4) Георгий взял кредит в банке на сумму 804 000 рублей. Схема выплата кредита такова: в конце каждого года банк увеличивает на 10 процентов оставшуюся сумму долга, а затем Георгий переводит в банк свой очередной платеж. Известно, что Георгий погасил кредит за три года, причем каждый его следующий платеж был ровно вдвое меньше предыдущего. Какую сумму Георгий заплатил в третий раз? Ответ дайте в рублях.
5) 15-го декабря планируется взять кредит в банке на 26 месяцев. Условия возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по 25-й долг должен быть на 20 тысяч рублей меньше долга на 15-е число предыдущего месяца;
- к 15-му числу 26-го месяца кредит должен быть полностью погашен.
- Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 1407 тысяч рублей?
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
- Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 1,5 млн рублей?
- Софья Колесникова: ЕГЭ. Математика. Экономические задачи
- ЕГЭ 2019. Математика. Профильный уровень. Типовые тестовые задания. 36 вариантов заданий. Под редакцией И.В.Ященко.
- С.А. Шестаков: ЕГЭ 2018. Математика. Задачи с экономическим содержанием. Задача 17 (профильный уровень).
- Прокофьев, Корянов: ЕГЭ. Математика. 10-11 классы. Социально-экономические задачи. Задание 17.
- Дремов, Дерезин, Кривенко: ЕГЭ. Математика. Задача с экономическим содержанием.
6) В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы::
7) 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
8)15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
9 )Три сестры пришли на рынок и продавали поштучно цыплят. Первая принесла 16 цыплят, вторая — 25, третья — 30 цыпленка. Каждая из них часть товара продала утром, а часть — вечером. Утренняя цена одного цыпленка была у всех сестер одинаковая, и вечерняя цена тоже одинаковая, но более низкая (положительная). К вечеру весь товар был распродан, и дневная выручка (за утро и вечер) у всех сестер оказалась одинаковой: 7 руб 75 коп. Найдите общую утреннюю выручку (в рублях).
10) В банк был положен вклад под 10% годовых. Через год, после начисления процентов, вкладчик снял со счета 2000 рублей, а еще через год снова внес 2000 рублей. Вследствие этих действий через три года со времени открытия вклада вкладчик получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы он получил?
Ответы:
1) 11
2) 20
3) 119700
4) 133100
5) 400 000
6) 16,2
7) 22,5

9) 11
10) 220
Заключение
Представленные в данной работе теория и решения задач позволят ученикам успешно справиться с экономической задачей в ЕГЭ, так как не дают им готовые модели, а предлагают методы и средства для самостоятельного составления математических моделей в задачах, что способствует развитию интеллекта школьников. Ведь решение экономических задач нужно не только для сдачи экзамена, а также для повышения финансовой грамотности молодёжи.
Даже достаточно сложные задачи на ЕГЭ можно подать школьникам в доступной и красочной форме. Главное – подавать информацию кратко, структурировано, но с другой стороны стараться охватить как можно более разнообразные типы задач. Именно этот редкий баланс я пыталась соблюдать при разработке своей методички.
Список использованной литературы
Если страница Вам понравилась, поделитесь в социальных сетях:
ПРОЕКТ ПО МАТЕМАТИКЕ
«50 ЭКОНОМИЧЕСКИХ ЗАДАЧ»
Выполнила: Позднякова Полина,
ученица 11 «А» класса
МБОУ Щёлковский лицей №7.
Руководитель: Позднякова Ольга Вячеславовна.
2018 год
2
Оглавление
1. Введение ……………………………………………………………………………………….. 3
2. Теория
2.1 Проценты ………………………………………………………………………………… 5
2.2 Платежи ………………………………………………………………………………….. 5
2.3 Таблицы …………………………………………………………………………………. 5
2.4 Арифметическая и геометрическая прогрессии ………………………… 7
2.5 Производная ……………………………………………………………………………. 8
3. Практическое решение экономических задач
3.1 Кредиты
1 тип: Нахождение количества лет (месяцев) выплаты кредита.
(Аннуитетные платежи) ………………………………………………………………. 10
2 тип: Вычисление процентной ставки по кредиту. (Фиксированные
платежи) ……………………………………………………………………………………… 13
3 тип: Нахождение суммы кредита. (Аннуитетные платежи) ………… 16
4 тип: Нахождение ежегодного ( ежемесячного)
транша.(Аннуитетные платежи) …………………………………………………… 19
5 тип: Нахождение разницы. (Аннуитетные платежи) ………………….. 22
6 тип: Задачи, связанные с известным остатком. (Фиксированные
платежи) ……………………………………………………………………………………… 25
7 тип: Задачи, связанные с дифференцированными платежами …….. 28
8 тип: Нестандартные задачи, связанные с кредитом ……………………. 32
3.2 Вклады …………………………..………………………………………………………. 36
3.3 Задачи на оптимизацию ………………………………………………………….. 44
3.4 Нестандартные задачи ……………………………………………………………. 56
4.Заключение ……………………………………………………….…………………………. 61
5.Список литературы ……………………………………………………………………….. 61
3
1. Введение
Экономическую задачу ввели в экзамен ЕГЭ «Профиль по математике» только
с 2015 года. Она стала называться заданием номер 17 и по своей сложности
находится на одном уровне с заданиями на параметры и теорию чисел.
Приведу примеры статистики сдачи ЕГЭ по математике (профильный
уровень) за 2016 и 2017 годы (использовала данные с сайта ФИПИ)
Набрали
ненулевой
балл (от
сдавших
экзамен
учащихся)
Набрали
ненулевой
балл (от
всех
учащихся)
Набрали
максимальный
балл (от
сдавших
экзамен
учащихся)
Набрали
максимальный
балл (от всех
учащихся)
Такая статистика решения экономической задачи объясняется и сложностью
задания и просто тем, что такой темы просто нет в наших учебниках по алгебре.
Поэтому у меня и появилась идея написать методичку «50 экономических задач для
подготовки к сдаче ЕГЭ «Профиль по математике»», целью которой является
подготовка учащихся к ЕГЭ.
Конечно, на различных сайтах и в математической литературе можно найти
решения таких задач, но зачастую либо они содержат много лишней информации,
либо они решены непонятным для меня способом. Я же использовала табличный
метод, так как считаю его самым наглядным и простым.
4
Из необходимых знаний и умений мне понадобились:
1) Определение понятия «Процент»
2) Определение понятий «Фиксированные платежи», «Аннуитетные платежи» и
«Дифференцируемые платежи».
3) Виды мною созданных таблиц
4) Определение, формулы n-ого члена и суммы n первых членов арифметической
и геометрической прогрессий
5) Знание алгоритмов нахождения промежутков возрастания (убывания)
функций и точек экстремума.
Каждую неделю, начиная с сентября 2016 года, я решала по две
экономических задачи. Условия таких задач я брала:
1. ЕГЭ 2018 под редакцией А. Л. Семенова, И.В. Ященко
2. Открытый банк заданий ЕГЭ fipi.ru
3. Сайт «Решу ЕГЭ»
4. И мой любимый сайт «Алекс Ларин»
Всего я решила примерно 152 задачи, выбрала из них 50 задач, разделив их
условно на типы:
Кредиты.
1 тип: Нахождение количества лет (месяцев) выплаты кредита.
(Аннуитетные платежи) — 3 задачи
2 тип: Вычисление процентной ставки по кредиту. (Фиксированные платежи)
– 3 задачи
3 тип: Нахождение суммы кредита. (Аннуитетные платежи)— 3 задачи
4 тип: Нахождение ежегодного (ежемесячного) транша. (Аннуитетные
платежи)— 3 задачи
5 тип: Нахождение разницы. (Аннуитетные платежи) – 3 задачи
6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)— 3
задачи
7 тип: Задачи, связанные с дифференцированными платежами.— 3 задачи
8 тип: Нестандартные задачи, связанные с кредитом.— 4 задачи
Вклады. – 8 задач
Задачи на оптимизацию. —12 задач
Нестандартные задачи.-5 задач
Конечно, наиболее трудными среди экономических задач считаются задачи на тему
«Оптимизация» и нестандартные задачи с сайта «Алекс Ларин».
5
2.Теория.
Решение финансовых задач основывается на использовании различных
математических моделей: уравнений, неравенств, их систем с привлечением
процентов, арифметической и геометрической прогрессий и производной.
Приведу основные определения, понятия, таблицы и формулы.
2.1 Проценты.
Определение: один процент – это одна сотая доля. Чтобы найти данное число
процентов от числа, нужно проценты записать десятичной дробью, а затем число
умножить на эту десятичную дробь.
Пример: 5% от 80 это будет 0,05
r% от 14 это будет 0,01r
При решении задач необходимо понимать механизм начисления процентов по
вкладам или кредитам. Например, если банк выдаёт кредит (S) клиенту, то через год
клиент должен банку не только сумму кредита, но и некий процент (r). Возникает
необходимость введения нового коэффициента b, b=1+0,01r. С учётом этого , долг
клиента банку через год можно записать следующим образом:
S + r% от S = S + 0,01r = S (1 + 0,01r) = bS
2.2 Платежи.
В задачах по теме «Кредит» используют о три основных вида платежа:
1. Фиксированные платежи (платежи, которые чётко оговариваются в
условии задачи)
2. Аннуитетные платежи (постоянные ежемесячные или ежегодные
платежи, которые не меняются на протяжении всего периода кредитования)
3. Дифференцируемые платежи (ежемесячные или ежегодные платежи,
уменьшающиеся к концу срока кредитования и обеспечивающие
уменьшение суммы долга на одну и ту же величину)
2.3 Таблицы.
При решении задач, связанных с аннуитетными платежами мне было очень
удобно заполнять следующую таблицу:
S – сумма кредита
r% — годовые (ежемесячные) проценты
6
b=1+0,01r – коэффициент
х – ежегодная (ежемесячная) выплата
(Sb
3
-x b
2
-xb-x)b= Sb
4
-xb
3
—
xb
2
-xb
(Sb
4
-xb
3
-xb
2
-xb-x)b= Sb
5
—
xb
4-
xb
3
-xb
2
-xb
(Sb
5
-xb
4-
xb
3
-xb
2
-xb-x)b=
Sb
6
-xb
5
-xb
4-
xb-
3
xb
2
-xb
Полная выплата, долг
равен 0
При решении задач, связанных с дифференцированными платежами я
использовала следующую таблицу:
7
При решении задач по теме «Вклады»:
При решении задач, в которых осуществлялись какие—либо действия
(пополнение или снятие денег с вклада):
х – действие
2.4 Арифметическая и геометрическая прогрессии.
Арифметическая прогрессия
Определение. Последовательность чисел, в которой каждое следующее отличается
от предыдущего ровно на одну и ту же величину, называется арифметической
прогрессией.
Любой член арифметической прогрессии вычисляется по формуле:
=
+ (n-1)d
Формула суммы n—первых членов арифметической прогрессии
S
n
=
С учётом этой формулы : (n-1) + (n-2) +…+3+2+1 =
=
=
=
=
=
8
Геометрическая прогрессия
Определение. Геометрической прогрессией называется последовательность
отличных от нуля чисел, каждый член которой, начиная со второго, равен
предыдущему члену, умноженному на одно и то же число.
Любой член геометрической прогрессии вычисляется по формуле:
b
n
=b
1
· q
n-1
Формула суммы n—первых членов геометрической прогрессии
S
n
=
Из этой формулы следует: b
n-1
+b
n-2
+…+b
2
+b+1=
2.5 Производная.
Достаточные признаки возрастания и убывания функции:
Если производная данной функции положительна для всех значений х в интервале
(а; в), т.е. f'(x) > 0, то функция в этом интервале возрастает.
Если производная данной функции отрицательна для всех значений х в интервале (а;
в), т.е. f'(x) < 0, то функция в этом интервале убывает
Порядок нахождения промежутков монотонности:
Найти область определения функции.
1. Найти производную функции.
2. Найти критические точки (точки, в которых производная не существует) и
стационарные (точки, в которых производная равна нулю). Исследовать знак
производной в промежутках, на которые найденные точки делят область
определения функции.
Достаточное условие существования максимума состоит в смене знака производной
при переходе через критическую точку с «+» на «—«, а для минимума с «—» на «+».
Если при переходе через критическую точку смены знака производной не
происходит, то в данной точке экстремума нет
Пример:
f(x) =
Найдём производную.
9
=(
)
,
=
=
=
=
Критические точки
= 1,
= -1
Стационарные точки
=
= —
,
= 0
Ответ: возрастает (—
;+
убывает
; —
=
;
=
.
10
3.Практическое решение экономических задач.
3.1 Кредиты.
1 тип: Нахождение количества лет ( месяцев) выплаты кредита.
n-? (Аннуитетные платежи)
Задача №1
Максим хочет взять кредит 1,5 млн рублей. Погашение кредита происходит раз
в год равными суммами ( кроме, может быть, последней) после начисления
процентов. Ставка процента 10% годовых. На какое минимальное количество
лет может Максим взять кредит, чтобы ежегодные выплаты были не более
350 тысяч рублей?
Решение:
Кредит (S) 1500000 руб.
Ставка (r) 10% годовых. Введём коэффициент b=1+0,01r
Ежегодная выплата (х) ≤350000 руб.
Сколько лет (n)-?
11
Задача №2
1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит.
Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк
начисляет 3% на оставшуюся сумму долга (то есть увеличивает долг на 3%),
затем Андрей Владимирович переводит в банк платеж. На какое минимальное
количество месяцев Андрей Владимирович может взять кредит, чтобы
ежемесячные выплаты были не более 220 тыс. рублей?
Решение.
Кредит (S) 1100000 руб.
Ставка (r) 3% годовых. Введём коэффициент b=1+0,01r
Ежемесячная выплата (х) ≤220000 руб.
Сколько месяцев (n)-?
12
Задача №3.
1 января 2015 года Павел Витальевич взял в банке 1 млн. рублей в кредит. Схема
выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет
1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел
Витальевич переводит в банк платеж. На какое минимальное количество месяцев
Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не
более 125 тыс. рублей?
Решение.
Кредит (S) 1000000 руб.
Ставка (r) 1% годовых. Введём коэффициент b=1+0,01r
Ежемесячная выплата (х) ≤125000 руб.
Сколько лет –(n)-?
13
2 тип: Вычисление процентной ставки по кредиту.
r-? (Фиксированные платежи)
Задача №1
31 декабря 2014 года Борис взял в банке 1 млн. рублей в кредит. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга ( то есть увеличивает долг на
определенное количество процентов), затем Борис переводит очередной транш.
Борис выплатил кредит за два транша, переводя в первый раз 560 тыс. рублей,
во второй – 661,1 тыс. рублей. Под какой процент банк выдал кредит Борису?
Решение Кредит (S) 1000000 руб.
Введём коэффициент b=1+0,01r
1 год выплата – x
1
=560000руб.
2 год выплата – x
2=
644100 руб.
r-?
Sb
2
-x
1
b=x
2
1000000b
2
-560000b-644100=0
10000b
2
-5600b-6441=0
D=5600
2
+4•10000•6441=31360000+257640000=289000000
b
1
= =1,13
b
2
= =-0,57 не подходит по условию задачи.
b=1+0,01r
r=13
Ответ: 13
14
Задача №2.
31 декабря 2014 года Антон взял в банке 1 млн. рублей в кредит. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга ( то есть увеличивает долг на определенное
количество процентов), затем Антон переводит очередной транш. Антон
выплатил кредит за два транша, переводя в первый раз 510 тыс. рублей, во второй
– 649 тыс. рублей. Под какой процент банк выдал кредит Антону?
Решение:
Кредит (S) 1000000 руб.
Введём коэффициент b=1+0,01r
1 год выплата – x
1
=510000руб.
2 год выплата – x
2=
649000 руб.
r-?
Sb
2
-x
1
b=x
2
1000000b
2
—510000b-649000=0
10000b
2
—5100b-649=0
D=5100
2
+4•10000•649=260100+2596000=2856100
b
1
= =1,1
b
2
= =-0,59 не подходит по условию задачи.
Ответ: r =10
15
Задача№3.
31 декабря 2014 года Арсений взял в банке 1 млн. рублей в кредит. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга ( то есть увеличивает долг на определённое
количество процентов), затем Арсений переводит очередной транш. Арсентий
выплатил кредит за два транша, переводя в первый раз 550 тыс. рублей, во второй
– 638,4 тыс. рублей. Под какой процент банк выдал кредит Арсению?
Решение:
Кредит (S) 1000000 руб.
Введём коэффициент b=1+0,01r
1 год выплата – x
1
=550000руб.
2 год выплата – x
2=
638400 руб.
r-?
Sb
2
-x
1
b=x
2
1000000b
2
-550000b-638400=0
10000b
2
-5500b-6384=0
D=5500
2
+4•10000•6384=30250000+255360000=285610000
b
1
= =1,12
b
2
= =-0,57 не подходит по условию задачи.
Ответ: r=12.
16
3 тип: Нахождение суммы кредита.
S-? (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Сергей взял в банке некоторую сумму в кредит под 12%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего
года банк начисляет проценты на оставшуюся сумму долга ( то есть
увеличивает долг на 12%), затем Сергей переводит в банк 3512320 рублей. Какую
сумму взял Сергей в банке, если он выплатил долг тремя равными платежами (
то есть за три года)?
Решение:
Ставка (r) — 12% , b=1,12
Ежегодная выплата (х) — 3512320 рублей
Количество лет (n) 3 года
Сумма кредита (S) —?
Sb
3_
хb
2
—xb =x
Sb
3
-(1+b+b
2
)x=0
S=
Ответ: 8436000рублей.
рублей
b
xbb
8436000
404928,1
3744,33512320
404928,1
)2544,112,11(3512320)1(
3
2
=
•
=
++•
=
++
17
Задача №2.
31 декабря 2014 года Игорь взял в банке некоторую сумму в кредит под 13%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг
на 13%), затем Игорь переводит в банк 5107600 рублей. Какую сумму взял Игорь в
банке, если он выплатил долг двумя равными платежами ( то есть за два года)?
Решение:
Ставка (r) — 13%, b=1,13
Ежегодная выплата (х) — 5107600 рублей
Количество лет (n) 2 года
Сумма кредита (S) —?
Sb
2
-xb=x
Sb
2
-(1+b)x=0
S=
Ответ: 8520000 рублей.
рублей
b
bx
8520000
2769,1
13,25107600
13,1
)13,11(5107600)1(
22
=
•
=
+•
=
+
18
Задача№3.
31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего
года банк начисляет проценты на оставшуюся сумму долга ( то есть
увеличивает долг на 10%), затем Михаил переводит в банк 2928200 рублей.
Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными
платежами ( то есть за четыре года)?
Решение:
Ставка (r) — 10%
b=1,1
Ежегодная выплата (х) — 2928200 рублей
Количество лет (n) 4 года
Сумма кредита (S) -?
(Sb
3
-x b
2
-xb-x)b= Sb
4
-xb
3
—
xb
2
-xb
Полная выплата —
остаток 0
Sb
4
-xb
3
-xb
2
-xb =x
Sb
4
-(1+b+b
2+
b
3
)x=0
S=
Ответ: 9282000 рублей.
9282000
1,1
)1,11,11,11(*2928200)1(
4
32
4
32
=
+++
=
+++
b
bbbx
19
4 тип: Нахождение ежегодного ( ежемесячного) транша.
х-? (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Алексей взял в банке 9282000рублей в кредит по 10% годовых.
Схема выплат кредита следующая: 31 декабря каждого следующего года банк
начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х,
чтобы Алексей выплатил долг четырьмя равными платежами ( то есть за четыре
года)?
Решение:
Сумма кредита (S)- 9282000рубля
Ставка (а)=10%, b=1,1
Количество лет (n) 4 года
Ежегодная выплата ( транш) Х -?
(Sb
3
-x b
2
—xb-x)b= Sb
4
—xb
3
—
xb
2
—xb
Полная выплата —
остаток 0
Sb
4
—xb
3
—xb
2
-xb =x
Sb
4
-(b+b
2
+b
3
)x=x
Sb
4
-(1+b+b
2
+b
3
)x=0
X=
X=
Ответ: 2928200 рублей.
рублей2928200
641,4
4641,19282000
331,121,11,11
4641,19282000
1,11,11,11
1,19282000
32
4
=
•
=
+++
•
=
+++
•
20
Задача №2.
31 декабря 2014 года Иван взял в банке 4230000 рублей в кредит по 11,5% годовых.
Схема выплат кредита следующая: 31 декабря каждого следующего года банк
начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
11,5%), затем Иван переводит в банк Х рублей. Какой должна быть сумма Х,
чтобы Иван выплатил долг двумя равными платежами ( то есть за два года)?
Сумма кредита (S)- 4230000рубля
Ставка (а)=11,5%, b=1,115
Количество лет (n) 2 года
Ежегодная выплата ( транш) Х -?
Sb
2
-xb=x
Sb
2
-(1+b)x=0
X=
X=
Ответ: 2486450рублей.
рублей2486450
115,2
243225,14230000
115,11
115,14230000
2
=
•
=
+
•
21
Задача №3.
31 декабря 2014 года Павел взял в банке 6327000 рублей в кредит по 12%
годовых. Схема выплат кредита следующая: 31 декабря каждого следующего
года банк начисляет проценты на оставшуюся сумму долга (то есть
увеличивает долг на 12%), затем Павел переводит в банк Х рублей. Какой
должна быть сумма Х, чтобы Павел выплатил долг тремя равными платежами
( то есть за три года)?
Решение:
Сумма кредита (S)- 6327000 рубля
Ставка (а)=12%,b=1,12
Количество лет (n) 3 года
Ежегодная выплата ( транш) Х -?
Sb
3_
хb
2
—xb =x
Sb
3
—(b
2
-b)x=x
Sb
3
-(1+b+b
2
)x=0
X= =
Ответ: 2634240 рублей.
2634240
112,112,1
12,1*632700
2
3
=
++
22
5 тип: Нахождение разницы. (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Федор взял в банке 6951000рублей в кредит под 10% годовых.
Схема выплат кредита следующая: 31 декабря каждого следующего года банк
начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
10%), затем Федор переводит в банк платеж. Весь долг Федор выплатил за 3
равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог
выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 6951000 рублей
Ставка (r) —10%, b=1,1
3 равных платежа
Sb
3
— хb
2
—xb=x
Sb
3
-(b
2
+b+1)x=0
X=
2 равных платежа
Sb
2
-xb=x
Sb
2
-(1+b)x=0
X=
За три года: 2795100 3=8385300
За два года:4005100 2=8010200
Разница: 8385300-8010200=375100
Ответ: на 375100 рублей.
2795100
31,3
331,16951000
11,11,1
331,16951000
1
22
3
=
•
=
++
•
=
++ bb
Sb
4005100
1,2
21,16951000
1,11
1,16951000
1
22
=
•
=
+
•
=
+ b
Sb
23
Задача №2.
31 декабря 2014 года Степан взял в банке 4004000 рублей в кредит под 20%
годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг
на 20%), затем Степан переводит в банк платеж. Весь долг Степан выплатил за 3
равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог
выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 4004000 рублей
Ставка (r) —20%, b=1,2
3 равных платежа
Sb
3
—хb
2
—xb=x
Sb
3
-(b
2
+b+1)x=0
X=
2 равных платежа
Sb
2
-xb=x
Sb
2
-(1+b)x=0
X=
За 3 года выплатил: 3*1900800=5702400
За два года: 2*2620800=5241600
Разница: 5702400-5241600=460800
Ответ: 460800 рублей.
1900800
12,144,1
728,1*4004000
12,12,1
2,1*4004000
1
2
3
2
3
=
++
=
++
=
++ bb
Sb
2620800
12,1
2,1*4004000
1
22
=
+
=
+b
Sb
24
Задача №3.
31 декабря 2014 года Алексей взял в банке 3689000 рублей в кредит под 12,5%
годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг
на 12,5%), затем Алексей переводит в банк платеж. Весь долг Алексей выплатил за
3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог
выплатить долг за 2 равных платежа?
Решение: Сумма кредита (S) – 3689000 рублей
Ставка (r) -12,5%, b=1,125
3 равных платежа
Sb
3
—хb
2
—xb=x
Sb
3
-(b
2
+b+1)x=0
X=
2 равных платежа
Sb
2
-xb=x
Sb
2
-(1+b)x=0
X=
За три года: 1549125 3=4647375
За два года:2197125 2=4394250
Разница: 4647375-4394250=253125
Ответ: 253125 рублей.
1549125
1125,1125,1
125,1*3689000
2
3
=
++
2197125
1
8
1
1
)
8
1
1(*3689000
1
2
2
=
+
=
+b
Sb
25
6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)
Задача №1.
15—го января был выдан полугодовой кредит на развитие бизнеса. В таблице
представлен график его погашения.
Долг (в процентах от кредита)
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а
выплаты по погашению кредита происходили в первой половине каждого месяца,
начиная с февраля. На сколько процентов общая сумма выплат при таких условиях
больше суммы самого кредита?
Решение: S – сумма кредита
r% — годовые (ежемесячные) проценты (5%)
b=1+0,01r – коэффициент (1,05)
Полная выплата —
остаток 0
Общая сумма выплат:
(Sb+0,9Sb+0,8Sb+0,7Sb+0,6Sb+0,5Sb)-(0,9S+0,8S+0,7S+0,6S+0,5S)=
4,5Sb-3,5S=S(4,5b-3,5)=S(4,5*1,05-3,5)=1,225S
Ответ: 22,5 процента.
26
Задача №2.
15—го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев.
Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на целое число r процентов по
сравнению с концом предыдущего месяца;
− со 2—го по 14—е число каждого месяца необходимо выплатить часть долга;
− 15—го числа каждого месяца долг должен составлять некоторую сумму в
соответствии со следующей таблицей
Найдите наибольшее значение r, при котором общая сумма выплат будет
составлять менее 1,2 млн рублей.
Решение: S – сумма кредита (1000000рублей)
Найти : r% — годовые (ежемесячные) проценты
b=1+0,01r – коэффициент
Полная выплата —
остаток 0
Общая сумма выплат:
(Sb+0,6Sb+0,4Sb+0,3Sb+0,2Sb+0,1Sb)-(0,6S+0,4S+0,3S+0,2S+0,1S)=
2,6Sb-1,6S=S(2,6b-1,6)=1*(2,6b-1,6)=2,6b-1,6
2,6b-1,6<1,2 ; 2,6b<2,8 ; b<1,076 ; b=1,07 ; r=7
Ответ: 7 процентов.
27
Задача №3.
В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей,
где S — натуральное число, на 3 года. Условия его возврата таковы
− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего
года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть
долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со
следующей таблицей.
Найдите наименьшее значение S, при котором каждая из выплат будет
составлять целое число тысяч рублей.
Решение: S – сумма кредита
r% — годовые (ежемесячные) проценты (15%)
b=1+0,01r – коэффициент (1,15)
Полная выплата —
остаток 0
1 выплата 1,15S-0,7S= 0,45S=
2 выплата 0,7*1,15S-0,4S= 0,405S=
3 выплата 0,4*1,15S= 0,46S=
По условию, все выплаты должны быть целыми. Значит, число S должно делиться
на 20, 200 и 50. Наименьшее общее кратное этих чисел равно 200.
Ответ: 200 тысяч.
28
7 тип: Задачи, связанные с дифференцированными платежами.
Задача №1.
Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен
вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся
сумме долга добавляется r % этой суммы и своим ежемесячным платежом
Алексей погашает эти добавленные проценты и уменьшает сумму долга.
Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же
величину каждый месяц (на практике такая схема называется «схемой с
дифференцированными платежами»). Известно, что общая сумма, выплаченная
Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма,
взятая им в кредит. Найдите r.
Решение: Сумма кредита (S), ставка (r) —? %, b=1+0,01r
29
Sb(1+
)-S
)=1,13S
—
=1,13S /S
—
=1,13
78b=1,13*12+66
b=1,02
r=2%
Ответ:2%.
Задача 2.
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата
таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом
предыдущего месяца;
— со 2—го по 14—е число каждого месяца необходимо выплатить часть долга;
— 15—го числа каждого месяца долг должен быть на одну и ту же величину меньше
долга на 15—е число предыдущего месяца.
Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей.
Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение: Сумма кредита (S)
Ставка (r) -3 %, b=1,03 n=9 Сумма всех выплат =?
=57,5
5Sb-4S=517,5
S(5b-4)=517,5
S(5*1,03-4)=517,5
S=450
Sb(1+
)-S
)=5Sb-4S=
450*(5*1,03-4)=450*1,15=517,5
Ответ:517,5 тысяч.
Задача 3.
15—го января планируется взять кредит в банке на несколько месяцев. Условия его
возврата таковы:
— 1-го числа каждого месяца долг возврастает на 5% по сравнению с концом
предыдущего месяца;
— со 2—го по 14—е число месяца необходимо выплатить часть долга;
— 15—го числа каждого месяца долг должен быть на одну и ту же сумму меньше
долга на 15—е число предыдущего месяца.
На сколько месяцев можно взять кредит, если известно, что общая сумма выплат
после полного погашения кредита на 25% больше суммы, взятой в кредит. (решение
с помощью формулы суммы арифметической прогрессии)
Решение: Сумма кредита (S) , ставка (r) -5 %, b=1,05 n=?
Sb(
)-S
)=1,25S
По формуле суммы арифметической прогрессии получаем
Sb*
— S*
=1,25S /S
b*
—
=1,25
1,05*(n+1)-(n-1)=2,5
1,05n+1,05-n+1=2,5
0,05n=0,45
n=9
Ответ: 9 месяцев.
32
8 тип: Нестандартные задачи, связанные с кредитом.
Задача 1.
В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия
возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года.
— с февраля по июнь необходимо выплатить часть долга.
— в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.
— суммы выплат 2020 и 2021 годов равны.
Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты
составят 12,6 млн. рублей.
Решение: S=6,6
r% =? b=1+0,01r
1)Sb
2
—xb=x
2)3Sb-3S+2x=12,6
19,8b-19,8+2x=12,6
x=16,2-9.9b
1)6,6 b
2
–(16,2-9,9b)b=16,2-9,9b
6,6 b
2
-16,2b+9,9 b
2
=16,2-9,9b
16,5 b
2
-6,3b-16,2=0
165 b
2
—63b-162=0
D=63
2
+4•162•165=110889
b
1
=1,2
b
2
= —0,81не подходит по условию задачи.
Ответ: r=20.
33
Задача №2.
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты
кредита следующая: 1 марта каждого следующего года банк начисляет проценты
на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий
переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем
второй платеж оказался в два раза больше первого, а третий – в три раза больше
первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку
2 395 800 рублей?
Решение:
Сумма кредита (S)-?
Ставка (а)=10%, b=1,1
Количество лет (n) 3 года
Полная выплата —
остаток 0
x+2x+3x=2395800
6x=2395800
x=399300
Sb
3_
хb
2
-2xb =3x
Sb
3
-(3+2b+b
2
)x=0
S=
Ответ: 1923000рублей.
Задача №3.
Анатолий решил взять кредит в банке 331000 рублей на 3 месяца под 10% в месяц.
Существуют две схемы выплаты кредита.
По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся
сумму долга (то есть увеличивает долг на 10%), затем Анатолий переводит в банк
фиксированную сумму и в результате выплачивает весь долг тремя равными
платежами (аннуитетные платежи).
рублей
b
xbb
1923000
331,1
41,6399300
331,1
)21,12,23(399300)23(
3
2
=
•
=
++•
=
++
34
По второй схеме тоже сумма долга в конце каждого месяца увеличивается на 10%,
а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в
конце каждого месяца, подбираются так, чтобы в результате сумма долга
каждый месяц уменьшалась равномерно, то есть на одну и ту же величину
(дифференцированные платежи). Какую схему выгоднее выбрать Анатолию?
Сколько рублей будет составлять эта выгода?
Решение: Сумма кредита (S) – 331000 рублей
Ставка (r) —10%, b=1,1
Аннуитетные платежи.
Sb
3_
хb
2
—xb=x
Sb
3
-(b
2
+b+1)x=0
3х=399300
Дифференцированные платежи.
Sb(1+
)-S
)=2Sb-S
2*331000*1,1- 331000=331000*1,2=397200
399300 – 397200= 2100
Ответ: дифференцированные платежи, выгода 2100 рублей.
133100
11,11,1
1,1*331000
2
3
=
++
=x
35
Задача №4.
Петр Иванович взял кредит на несколько лет и выплатил его равными ежегодными
платежами по 200000 руб. При этом в начале каждого
года сумма текущего долга увеличивалась на 10 %, а в конце года производился пла
тёж. Если бы Петр Иванович не делал платежей, то за это время вследствие начи
сления процентов сумма кредита составила бы 928200 руб. На сколько лет был взя
т кредит?
Решение:
Кредит (S)
Введём коэффициент b=1+0,01r
Sb
n
=928200,
ставка (r) —10%, b=1,1
х= 200000рублей, аннуитетные платежи.
Полная выплата,
долг равен 0
Sb
n
—xb
n-1
—xb
n-2-
…—xb
2
—xb-x=0
Sb
n
-x(b
n-1
+b
n-2
+…+b
2
+b+1)=0
По формуле суммы геометрической прогрессии
b
n-1
+b
n-2
+…+b
2
+b+1=
Sb
n
— x
=0
928200- 200000
=0
2000000
-1)=928200
=1+0,4641,
=1,4641
n=4
Ответ:4 года.
36
3.2 Вклады.
Задача №1.
Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из
первых двух лет хранения после начисления процентов он дополнительно вносил на
счет одну и ту же фиксированную сумму. К концу третьего года после начисления
процентов оказалось, что размер вклада увеличился по сравнению с первоначальным
на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?
Решение:
S=3600 тысяч – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=3 года, х =? – действие
Sb
3
+хb
2
+xb = 1,485S
х(b
2
+b) = 1,485S — Sb
3
х(1,21+1,1) = 1,485S – 1,331S
2,31х = 0,154*3600
2,31х = 554,4
х = 240
Ответ: 240000.
37
Задача №2.
Василий кладет в банк 1 000 000 рублей под 10% годовых на 4 года (проценты
начисляются один раз после истечения года) с правом докладывать три раза (в
конце каждого года) на счет фиксированную сумму 133 000 рублей. Какая сумма
будет на счете у Василия через 4 года? (Решение с помощью формулы суммы
геометрической прогрессии)
Решение:
S=1000000 – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=4 года, х =133000 – действие
b(Sb
3_
+хb
2
+xb+х)=
Sb
4_
+хb
3
+xb
2
+хb
Sb
4_
+хb
3
+xb
2
+хb=Sb
4_
+хb(b
2
+b+1)=
Ответ: 1948353 рублей.
рублей
b
b
xbSb 1948353
11,1
)1331,1(1,1133000
10000004641,1
1
)1(
3
4
=
−
−••
+•=
−
−
+=
38
Задача №3.
Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10%
годовых Однако через год и Саша, и Паша сняли со своих счетов соответственно
10% и 20% имеющихся денег. Еще через год каждый из них снял со своего счета
соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего
года на счету окажется большая сумма денег? На сколько рублей?
Решение:
S=50000 – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=3 года, х – действие
Саша
(0,9Sb
2
— 20000)*b =
0,9Sb
3_
20000b
0,9Sb
3_
20000b = 0,9*50000*1,331–20000*1,1 = 59895–22000 = 37895рублей
Паша
(0,8Sb2— 15000)*b =
0,8Sb3_ 15000b
0,8Sb
3_
15000b = 0,8*50000*1,331–15000*1,1 = 53240–16500 = 36740рублей
37895 – 36740 = 1155 рублей
Ответ: у Саши на 1155 рублей.
39
Задача №4.
Миша и Маша положили в один и тот же банк одинаковые суммы под 10%
годовых. Через год сразу после начисления процентов Миша снял со своего счета
5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год
доложила на свой счет 5000 рублей, а еще через год сразу после начисления
процентов сняла со счета 5000 рублей. Кто через три года со времени
первоначального вложения получит большую сумму и на сколько рублей?
Решение:
S – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=3 года, х – действие
Миша
(Sb2-5000b+5000)*b =
Sb3-5000b2+5000b
Sb
3
-5000b
2
+5000b = 1,331S-5000*1,21+5000*1,1=1,331S-6050+5500=1,331S-550
Маша
(Sb2+5000b-5000)*b =
Sb3+5000b2-5000b
Sb
3
+5000b
2
-5000b = 1,331S+5000*1,21-5000*1,1=1,331S+6050-5500=1,331S+550
Ответ: у Маши на 1100 рублей.
40
Задача №5.
Гражданка Васильева вложила 44 млрд. рублей в два оффшорных банка на 3 года:
часть денег в банк А, остальное в банк Б. Известно, что банк А ежегодно
начисляет 10% годовых; банк Б в первый год начисляет 5% годовых, во второй –
10%, а в третий – 15%. Сколько рублей было вложено в каждый из банков, если
через три года доход гражданки Васильевой от вложения денег составил 14 520
млн. рублей.
Решение:
S=44000млн – сумма вклада
r% — годовые (ежемесячные) проценты,
b=1+0,01r – коэффициент,
n=3 года
1 банк
1,05*1,1*1,15S=1,32825(44000-S)
1,331S+1,32825(44000-S)-44000=14520
1,331S-1,32825S=14520-58443+44000
0,00275S=77
S=28000 млн=28 млрд положила в 1 банк
44—28=16 положила во 2 банк
Ответ: 28 млрд и 16 млрд рублей.
41
Задача №6.
1 ноября 2017 года Николай открыл в банке счёт «Управляй», вложив S тысяч
рублей (S – целое число) сроком на 4 года под 10% годовых. По договору с банком
проценты по вкладу должны начисляться 31 октября каждого последующего года.
1 ноября 2019 года и 1 ноября 2020 года Николай планирует снять со счёта 100
тысяч и 50 тысяч рублей соответственно. 1 ноября 2021 года Николай собирается
закрыть счёт в банке и забрать все причитающиеся ему деньги.
Найдите наименьшее значение S, при котором доход Николая от вложений в банк з
а эти 4 года окажется более 70 тысяч рублей.
Решение:
S – сумма вклада
r% — годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=4 года, х – действие
b(Sb3_100b-50)=
Sb4_100b2-50b
Sb
4_
100b
2
-50b –S+150
70
S(b
4_
1)-100b
2
-50b +150
70
S(1,1
4_
1)
70-150+55+121
0,4641S
96
S
206,9
S=207
Ответ: 207тысяч рублей.
42
Задача №7.
За время хранения вклада в банке проценты по нему начислялись ежемесячно
сначала в размере 5%, затем 12%, потом 11
и, наконец, 12,5% в месяц. Известно,
что под действием каждой новой процентной ставки вклад находился целое число
месяцев, а по истечении срока хранения первоначальная сумма увеличилась на
104
%. Определите срок хранения вклада.
Решение:
S – сумма вклада
1,125p×
k 1,12m 1,05nS
Пусть n месяцев лежал вклад под 5%, m месяцев – под 12%, k месяцев – под 11
,
p месяцев – под 12,5 %.
1,125
p
k
1,12
m
1,05
n
S =
S
1,125
p
=
p
=
p
=
=
k
=
=
1,12
m
=
m
=
m
=
=
1,05
n
=
n
=
n
=
=
=
=
=
—2n+2m+k-3p=-3 n=1
=
n-2k+2p = -1 m=1
=
-n+k-2m = 0 k=3
=
m+ n = 2 p=2
1+1+3+2 = 7
Ответ: 7 месяцев.
43
Задача №8
Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год
возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и
положить вырученные деньги на банковский счёт. Каждый год сумма на счёте
будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен
продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги
сумма на банковском счёте была наибольшей?
Решение:
Чтобы сумма на банковском счёте была наибольшей необходимо, чтобы процент (r)
от стоимости ценной бумаги в n-ом году был больше, чем 2000 рублей
r(7000+(n-1)2000)2000
0,1(7000+2000n-2000)2000
500+200n2000
200n
n
n=8
Ответ: 8 года.
44
3.3 Задачи на оптимизацию.
Задача №1.
У фермера есть два поля, каждое площадью 100 гектаров. На каждом поле можно
выращивать картофель и свёклу, поля можно делить между этими культурами в
любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а
на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а
на втором — 400 ц/га. Фермер может продавать картофель по цене 10 000 руб. за
центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход
может получить фермер?
Решение:
Вся площадь: 100 га
Составим функцию полного дохода:
∑(x,k) = 4000000x+3300000kx→наиб
Заметим, что x+kx=100, т.е. x=
где k
∑(k) =
+
→наиб
∑(k) =
→наиб
Возьмём производную этой функции
=
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить
картофелем, при этом доход будет 4000000 рублей
Из второй таблицы видно, что свекла имеет, как большую урожайность, так и
большую цену за центнер, следовательно, второе поле нужно засадить свеклой. При
этом доход будет 40011000 рублей
Полный доход составляет 400 млн + 440 млн = 840 млн рублей.
Ответ: 840 млн рублей.
45
Задача №2.
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно
выращивать картофель и свёклу, поля можно делить между этими культурами в
любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а
на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а
на втором – 500 ц/га. Фермер может продать картофель по цене 5000 руб. за
центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может
получить фермер?
Вся площадь: 10 га
Составим функцию полного дохода:
∑(x,k) = 2500000x+2400000kx→наиб
Заметим, что x+kx=10, т.е. x=
где k
∑(k) =
+
→наиб
∑(k) =
→наиб
Возьмём производную этой функции
=
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить
картофелем, при этом доход будет 2500000 рублей
Из второй таблицы видно, что свекла имеет, как большую урожайность, так и
большую цену за центнер, следовательно, второе поле нужно засадить свеклой. При
этом доход будет 5008000 рублей
Полный доход составляет 25 млн + 40 млн = 65 млн рублей.
Ответ: 65 млн рублей.
46
Задача №3.
Предприниматель купил здание и собирается открыть в нём отель. В отеле могут
быть стандартные номера площадью 27 квадратных метров и номера «люкс»
площадью 45 квадратных метров. Общая площадь, которую можно отвести под
номера, составляет 981 квадратный метр. Предприниматель может поделить
эту площадь между номерами различных типов, как хочет. Обычный номер будет
приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки.
Какую наибольшую сумму денег сможет заработать в сутки на своём отеле
предприниматель?
Решение:
Общая площадь: 981
Составим функцию полного дохода:
∑(x,y) = 2000x+4000y→наиб
Заметим, что 27x+45y981, т.е. x
где y
, т.е. y
∑(y) =
+4000y→наиб
∑(y) =
→наиб
Возьмём производную этой функции
=
Значит функция возрастает во всей области определения, т.е. принимает своё
наибольшее значение при y=21. Это означает, что номеров люкс будет 21. Проверим
общую площадь: 45
ер. При этом полный доход
будет рублей.
Ответ: 86000 рублей.
47
Задача №4.
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут
быть стандартные номера площадью 30 квадратных метров и номера «люкс»
площадью 40 квадратных метров. Общая площадь, которую можно отвести под
номера, составляет 940 квадратных метров. Предприниматель может
определить эту площадь между номерами различных типов, как хочет. Обычный
номер будет приносить отелю 4000 рублей в стуки, а номер «люкс» — 5000 рублей
в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем
отеле предприниматель?
Решение: Общая площадь : 940
Составим функцию полного дохода:
∑(x,y) = 4000x+5000y→наиб
Заметим, что 30x+40y940, т.е. x
где y
, т.е. y
∑(y) =
+5000y→наиб
∑(y) =
→наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при y=0. Это означает, что стандартных номеров будет 940
. Проверим общую площадь: 30
ер на номер люкс.
При этом полный доход будет рублей.
Ответ: 125000 рублей.
48
Задача №5.
Антон является владельцем двух заводов в разных городах. На заводах
производится абсолютно одинаковые товары при использовании одинаковых
технологий. Если рабочие на одном из заводов трудятся суммарно t
2
часов в
неделю, то за эту неделю они производят t единиц товара. За каждый час работы
на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а
на заводе, расположенном во втором городе, — 200 рублей. Антон готов выделять
900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество
единиц товара можно произвести за неделю на этих двух заводах?
Решение: Оплата труда в неделю : 900000рублей
Составим функцию количества единиц товара:
∑(x,y) = x+y→наиб
Заметим, что 250
+200
900000, т.е. x
где y
∑(y) =
+y→наиб
Возьмём производную этой функции
=
+1 =
Найдём нули производной:
=0
=0
0,64
=(3600—
)
1,44
=3600
y=50
Функция принимает своё наибольшее значение при y=50 (точка максимума).
x
=
=40
Найдём количество единиц товара : +50 = 90
Ответ: 90 единиц товара.
49
Задача №6.
Григорий является владельцем двух заводов в разных городах. На заводах
производятся абсолютно одинаковые товары, но на заводе, расположенном во
втором городе, используется более совершенное оборудование. В результате, если
рабочие на заводе, расположенном в первом городе, трудятся суммарно t
2
часов в
неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе,
расположенном во втором городе, трудятся суммарно t
2
часов в неделю, то за эту
неделю они производят 4t единиц товара. За каждый час работы (на каждом из
заводов) Григорий платит рабочему 500 рублей. Готов выделять 5 000 000 рублей в
неделю на оплату труда рабочих. Какое наибольшее количество единиц товара
можно произвести за неделю на этих двух заводах?
Решение: Оплата труда в неделю: 5000000рублей
Составим функцию количества единиц товара:
∑(x,y) = 3x+4y→наиб
Заметим, что 500
+500
5000000, т.е. x
где y
∑(y) =3
+4y→наиб
Возьмём производную этой функции
= 3
+4 =
Найдём нули производной:
=0
=0
9
=16(10000-
)
25
=1600000
y=80
Функция принимает своё наибольшее значение при y=80 (точка максимума).
x
=
=60
Найдём количество единиц товара: 3 +480 = 180+320 = 500
Ответ: 500 единиц товара.
50
Задача №7.
Борис является владельцем двух заводов в разных городах. На заводах производятся
абсолютно одинаковые товары при использовании одинаковых технологий. Если
рабочие на одном из заводов трудятся суммарно t
2
часов в неделю, то за эту
неделю они производят t единиц товара. За каждый час работы на заводе,
расположенном в первом городе, Борис платит рабочему 500 рублей, а на заводе,
расположенном во втором городе, — 200 рублей. Борису нужно каждую неделю
производить 70 единиц товара. Какую наименьшую сумму придётся тратить
еженедельно на оплату труда рабочих?
Решение: 70 единиц товара
Составим функцию еженедельной оплаты труда:
∑(x,y) = 500
→наим
Заметим, что x+y70, т.е. x где y
∑(y) =500
→ наим
∑(y) =500
=700
-70000y+2450000
Возьмём производную этой функции
= 1400y-70000
Найдём нули производной: 1400y-70000=0
y=50
Функция принимает своё наименьшее значение при y=50 (точка минимума).
x
Найдём еженедельную оплату труда:
+200
= 500 +200
500000=700000
Ответ: 700 тысяч рублей .
51
Задача №8.
Фёдор является владельцем двух заводов в разных городах. На заводах
производятся абсолютно одинаковые приборы, но на заводе,
расположенном в первом городе, используется более совершенное оборудование. В р
езультате, если рабочие на заводе, расположенном в первом городе, трудятся
суммарно 3t
2
часов в неделю, то за эту неделю они производят t приборов; если
рабочие на заводе, расположенном во втором городе, трудятся суммарно 4t
2
часов в неделю, они производят t приборов.
За каждый час работы (на каждом из заводов) Фёдор платит рабочему 1 тысячу
руб. Необходимо, чтобы за неделю суммарно производилось 30 приборов. Какую
наименьшую сумму придется тратить владельцу
заводов еженедельно на оплату труда рабочих?
Решение: 30 единиц товара
Составим функцию еженедельной оплаты труда:
∑(x,y) = 3000
→наим
Заметим, что x+y30, т.е. x где y
∑(y) =3000
→наим
∑(y) =3000
=7000
—180000y+2700000
Возьмём производную этой функции
= 14000y—180000
Найдём нули производной: 14000y-180000=0
y =
=12
Функция принимает своё наименьшее значение при y=12
(точка минимума).
Пусть y=12, тогда x=18
Найдём еженедельную оплату труда:
+400
= 3000 +4000
000=1548000
Пусть y=13, тогда x=17
Найдём еженедельную оплату труда:
+400
= 3000 4000
000=1543000
Ответ: 1543000 рублей .
52
Задача №9.
В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5
часов в сутки на добыче алюминия или никеля. В первой области один рабочий за
час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг
алюминия в день требуется x
2
человеко—часов труда, а для добычи у кг никеля в день
требуется у
2
человеко—часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём
1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов
можно за сутки суммарно добыть в двух областях?
Решение:
Из таблицы видно, что в первой области совершенно одинаковые условия
добывания алюминия и никеля. Это означает, что в первой области алюминия и
никеля будут добывать поровну по
= 40 кг. Всего 80 кг.
Во второй области: x
2
+y
2
=160
x
2
+y
2
=800
x=20, y=20. Всего 40 кг.
Ответ: 120кг.
Задача №10.
В двух шахтах добывают алюминий и никель. В первой шахте имеется 60 рабочих,
каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час
добывает 2 кг алюминия или 3 кг никеля. Во второй шахте имеется 260 рабочих,
каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час
добывает 3 кг алюминия или 2 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности
производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1
кг никеля. При этом шахты договариваются между собой вести добычу металлов
так, чтобы завод мог произвести наибольшее количество сплава. Сколько
килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение: 60 человек по 5 часов в день
260 человек по 5 часов в день
Получаем, что всего алюминия производят 10x+15y
никеля: 15(60-x)+ 10(260-y)=3500-15x-10y
Так как для сплава необходимо , чтобы на2 кг алюминия приходился 1 кг никеля,
то: 10x+15y=2(3500-15x-10y)
10x+15y=7000-30x-20y
40x=7000-35y
x =
=
Составим функцию массы сплава:
∑(x,y) = 10x+15y +3500-15x-10y →наиб
∑(x,y) = 3500-5x+5y →наиб
∑(y) = 3500-5
+5y →наиб
∑(y) = 3500-5
+5y →наиб
∑(y) =
→наиб
Возьмём производную этой функции
=
Значит функция возрастает во всей области определения, т.е. принимает своё
наибольшее значение при наибольшем значении y.
Так как x =
то 1400-7y0 , y.
Проверим значение у=200, тогда x=0.
Масса сплава: 3500-5 +5 =4500
Ответ: 4500 кг.
54
Задача №11.
Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со
следующими видами начинки: ягодная и творожная. В данной ниже таблице
приведены себестоимость и отпускная цена, а также производственные
возможности фабрики по каждому виду продукта при полной загрузке всех
мощностей только данным видом продукта.
Себестоимость
(за 1 тонну)
Отпускная цена
(за 1 тонну)
Производственные
возможности
Для выполнения условий ассортиментности, которые предъявляются торговыми
сетями, продукции каждого вида должно быть выпущено не менее 15 тонн.
Предполагая, что вся продукция фабрики находит спрос (реализуется без
остатка), найдите максимально возможную прибыль, которую может получить
фабрика от производства блинчиков за 1 месяц
Решение
Пусть x тонн выпускает фабрика блинчиков с ягодами, а y тонн – с творогом. Тогда
по условию имеем : x
Составим функцию прибыли:
∑(x,y) = 30x+35y→наиб
Пусть производственная возможность равна 1, тогда
+
= 1
75x + 90y = 6750
x = 90 – 1,2y
∑(y) = 30(90 – 1,2y)+35y→наиб
∑(y) = 2700 — y→наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при y=15. Тогда x = 90-1,2
При этом максимальная прибыль будет рублей.
Ответ: 2685000 рублей.
55
Задача №12.
Консервный завод выпускает фруктовые компоты в двух видах тары — стеклянной
и жестяной. Производственные мощности завода позволяют выпускать в день 90
центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для
выполнения условий ассортиментности, которые предъявляются торговыми
сетями, продукции в каждом из видов тары должно быть выпущено не менее 20
центнеров. В таблице приведены себестоимость и отпускная цена завода за 1
центнер продукции для обоих видов тары.
Предполагая, что вся продукция завода находит спрос (реализуется без остатка),
найдите максимально возможную прибыль завода за один день (прибылью
называется разница между отпускной стоимостью всей продукции и её
себестоимостью).
Решение
Пусть x центнеров выпускает фабрика в стеклянной таре, а y центнеров – в
жестяной. Тогда по условию имеем : x
Составим функцию прибыли:
∑(x,y) = 600x+650y→наиб
Пусть производственная возможность равна 1, тогда
+
= 1
80x + 90y = 7200
x = 90 – 1,125y
∑(y) = 600(90 – 1,125y)+650y→наиб
∑(y) = 54000 — 25y→наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё
наибольшее значение при y=20. Тогда x = 90-1,12
При этом максимальная прибыль будет рублей.
Ответ: 53500 рублей.
56
3.4 Нестандартные задачи
Задача №1.
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по
направлению к перекрестку этих дорог. Один из них движется со скоростью 40
км/ч и находится на расстоянии 5 км от перекрестка, второй движется со
скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько
минут расстояние между велосипедистами станет наименьшим? Каково будет
это наименьшее расстояние?
Решение:
Составим функцию квадрата расстояния между велосипедистами:
∑(t) =
→наим, где t
∑(t) = 25-400t+1600
→наим
∑(t) = 2500
→наим
Возьмём производную этой функции
= 5000t-580
Найдём нули производной: 5000t-580=0
t =
=
=
Функция принимает своё наименьшее значение при t=
ч = 60
(точка минимума).
Найдём расстояние между велосипедистами:
=
=
=
=
= 0,6
Ответ: 0,6км, 6,96 минут .
57
Задача №2 .
Бриллиант массой 20 карат был разбит на две части после чего его стоимость
уменьшилась на 25,5%.а) Найдите массы частей на которые был разбит
бриллиант если известно, что цена бриллианта пропорциональна квадрату его
массы.б) На какое максимальное число процентов может уменьшиться цена
бриллианта разбитого на две части.
Решение:
M=20 карат, S- стоимость бриллианта
S=km ,S
1
=km
1
,S
2
=km
2
Пусть m =x, тогда m =20-x
1) S1+S2=0,745S
kx
2
+k(20-x)
2
=0,745k20
2
x
2
+(20-x)
2
=298
x
2
+400-40x+102=0
x
2
-20x+51=0
x
1
=17, x
2
=3
Ответ: массы частей 17 и 3 карат.
2) Цена бриллианта максимально снизится, если обе части будут по 10 карат
S
1
+S
2
=aS
k10
2
+k10
2
=a20
2
k
100+100=a400
a=200/400=0,5
Ответ: на 50%
58
Задача №3
В одной стране в обращении находились 1000000 долларов, 20% из которых были
фальшивыми. Некая нехорошая структура стала ввозить в страну по 100000
долларов в месяц, 10% из которых были фальшивыми. В это время другая
структура стала вывозить из страны 50000 долларов ежемесячно, из которых
30% оказались фальшивыми. Через сколько месяцев содержания фальшивых
долларов в стране составит 5%?
Решение:
n — количество месяцев
200000-5000n =0,05(1000000+50000n )
200000-5000n =50000+2500n
-7500n = -150000
n=20
Ответ: 20 месяцев
59
Задача №4
Два брокера купили акции одного достоинства на сумму 3640 рублей. Когда цена
на эти акции возросла, они продали часть акций на сумму 3927 рублей. Первый
брокер продал 75% своих акций, а второй – 80%. При этом сумма от продажи
акций, полученная вторым брокером, на 140% больше суммы первого. На сколько
процентов возросла цена одной акции?
Решение:
k- первоначальная цена 1 акции
x – штук купил первый брокер
y – штук купил второй
z – конечная цена 1 акции
Составим систему уравнений:
3)
y =
= 2,25x
1) k(x+y)=3640
k(x+2.25x)=3640
k =
=
=
2) z(0,75x+0,8y)=3927
z(0,75х+1,8x)=3927
z2,55x=3927
z=
=
=
4) Найдём, на сколько процентов возросла цена одной акции
k =
— 100%
z =
— a%
a=
137,5%
Ответ: на 37,5%
60
Задача №5.
Строительство нового завода стоит 115 млн рублей. Затраты на
производство x тыс. единиц продукции на таком заводе равны 0,5 x
2
+x+9 млн
рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то
прибыль фирмы (в млн рублей) за один год составит
px-(0,5 x
2
+x+9). Когда завод будет построен, фирма будет выпускать продукцию
в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем
значении p строительство завода окупится не более чем за 5 лет?
Решение
Составим функцию прибыли:
∑(x,p) = px-(0,5 x
2
+x+9)→наиб
∑(x,p) = px-0,5 x
2
-x-9
Возьмём производную этой функции
= p-x-1
Найдём нули производной: p-x-1=0
x = p-1
Функция принимает своё наибольшее значение при x = p-1
(точка минимума).
Найдём прибыль:
∑(p) = p(p-1)-0,5 (p-1)
2
-(p-1)—9 = 0,5p
2
-p-8,5
По условию строительство завода должно окупиться не более, чем за 5 лет. То есть
за 5 лет прибыль должна быть не меньше 115 млн рублей.
5(0,5p
2
-p-8,5115
0,5p
2
-p-8,5-23=0
p
2
-2p-63=0
p
1
=9, p
2
=-7
Ответ: 9 тысяч рублей.
61
4.Заключение
В данной работе рассмотрены основные методы решения задач на кредит, вклады и
оптимизацию. Тема работы очень актуальна, так как все рассматриваемые задачи взяты
из материалов по подготовке к ЕГЭ по математике «Профиль». Надеюсь, что данная
работа будет полезна учащимся 10—11 класса, а также преподавателям математики.
5.Список использованной литературы:
1. ЕГЭ 2018 под редакцией А. Л. Семенова, И.В. Ященко
2. Открытый банк заданий ЕГЭ fipi.ru
3. Сайт «Решу ЕГЭ»
4. Сайт «Алекс Ларин»
Автор: Фролов Глеб Романович
Место работы/учебы (аффилиация): ГБОУ «Брянский городской лицей №1 имени А.С.Пушкина», 10 класс
Актуальность исследовательской работы определяется необходимостью уметь решать экономические задачи при сдаче ЕГЭ. Решение экономических задач очень полезно, так как жизнь современного человека тесно связана с финансовыми операциями.
Проблема заключается в отсутствии навыков применения математических и экономических знаний на практике в расчетах платежей банковских кредитов и прочих операций, а также неумение и боязнь решать экономические задачи на ЕГЭ.
Предмет исследования: различные подходы к решению задач о кредитах, в зависимости от условия задачи.
Гипотеза: в современном мире необходимы знания об экономике и в этом может помочь математика.
Цель исследования – исследование методов решения задач с экономическим содержанием.
Задачи исследования:
- изучить теоретический материал по выбранной теме;
- научиться решать задачи с процентами разных видов сложности;
- разобрать основные типы задач с примерами решений;
- создать таблицы для различных видов платежей;
- показать на примерах поиск решения реальной практической задачи (кредит с разными видами платежей – аннуитетные, фиксированные и дифференцированные);
- провести анкетирование среди обучающихся 11-х профильных классов с целью выяснения трудностей, которые возникают у них при решении экономической задачи №17.
Департамент образования мэрии города Новосибирска
Дворец творчества детей и учащейся молодежи «Юниор»
XXXVIII городская открытая научно-практическая
конференция НОУ «Сибирь»
Секция: математика
Тема: Экономические задачи на ЕГЭ
Авторы:
Галахова Анастасия Александровна,
Прокопенко Анна Павловна
10 класс МБОУ СОШ № 141 с углублённым изучением математики
Первомайского района
города Новосибирска
Научные руководители:
Туленкова Елена Сергеевна,
учитель математики в.к.к.
МБОУ СОШ № 141 с углублённым изучением математики
конт. тел. 8-913-749-25-03,
Петрунина Вера Андреевна,
учитель математики в.к.к.
МБОУ СОШ № 141 с углублённым изучением математики
конт. тел. 8-913-482-02-86
Новосибирск 2018
Содержание
-
Введение…………………………………………………………………….3
-
Об экономических задачах…………………………………………………4
-
Решение экономических задач……………………………………………11
-
Заключение………………………………………………………………..18
-
Список литературы……………………………………………………….19
-
Приложение……………………………………………………………….20
Введение
В экзаменационных заданиях по математике (профильный уровень) во II части содержится задание № 17 – задача с экономическим содержанием. Она относится к повышенному уровню сложности и оценивается максимально в 3 балла.
По статистике это задание на 3 балла выполняют только 7,8% учащихся, на 2 балла – 2,4%, на 1 балл – 2,7%.
В следующем году и нам предстоит сдавать экзамен по математике. Чтобы попасть в эти 7,8 %, мы решили уже в 10 классе разобраться, что необходимо знать и уметь для решения экономических задач.
Более того, мы уверены, что умение решать такие задачи поможет нам и в повседневной жизни, например, в управлении личными финансами. Любому человеку необходимо повышать свою финансовую грамотность и разбираться в таких вопросах, как начисление заработной платы, налоговые отчисления, инфляция, потребительские и ипотечные кредиты, кредиты на образование и др. Часто финансово грамотное решение в реальной жизни вырабатывается не методом проб и ошибок, а путём аккуратных расчётов.
Цель нашей работы: выяснить, какие задачи называют экономическими, выявить основные типы задач на ЕГЭ и научиться их решать.
Задачи:
-
Изучить теоретический материал;
-
Проанализировать виды экономических задач;
-
Научиться применять полученные знания на практике.
Объект исследования:
Экономические задачи повышенного уровня сложности.
Методы:
-
поисковый метод с использованием научной и учебной литературы, интернета;
-
исследовательский метод при определении видов задач;
-
практический метод решения задач;
-
анализ полученных в ходе исследования данных.
План работы:
-
Работа с литературой
-
Анкетирование учащихся
-
Изучение видов задач на проценты
-
Изучение способов решения задач
-
Выводы
Об экономических задачах
Начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая экономическая задача №17.
Экономические задачи — задачи, решаемые в процессе экономического анализа, планирования, проектирования, связанные с определением искомых неизвестных величин на основе исходных данных. Их решение сопровождается поиском недостающих данных, экспертными оценками, обсуждением, принятием решений.
Мы изучили теоретический материал и выяснили, что эти задачи условно разделяют на два типа: непрерывные модели (производство товаров, протяжённое во времени, оптимизация производства, и т.п.) и дискретные модели (налоги, банковские проценты, вклады, погашение кредитов, и т.п.).
Непрерывные модели
-
Использование свойств функции
Решение различных экономических задач в формате ЕГЭ часто сводится к отысканию экстремальных (минимальных или максимальных) значений некоторой функции на заданном или получаемом из условия промежутке.
Нередко такими функциями являются линейная функция y=px+q(p ≠ 0) или квадратичная функция y= ax2+bx+c (a≠0). Линейная функция принимает экстремальное значение на одном из концов промежутка, которому принадлежат значения х.
Если линейная функция рассматривается только на множестве целых чисел, то число из этого промежутка, при котором функция принимает наибольшее или наименьшее значение, будет ближайшим целым числом к тому концу промежутка, на котором она принимает соответствующее экстремальное значение. Это следует из того, что линейная функция при ненулевом значении углового коэффициента является монотонно возрастающей или убывающей.
Пример. Подрядчику выделили 30000 рублей на уборку микрорайона к приезду губернатора. Из этих денег нужно выдать 2000 рублей бригадиру и по 450 рублей зарплаты каждому рабочему. Какую наибольшую сумму может потратить подрядчик на зарплату?
Решение. Пусть всего х рабочих. Зарплата рабочих и бригадира равна 2000+450х, по условию она не должна превышать 30000, т.е. 2000+450х≤30000
x ≤ 62 
Линейная функция y = 2000+450х возрастающая, поэтому наибольшее значение она примет на правом конце промежутка. По условию х – число натуральное, значит, наибольшее значение будет достигаться при х = 62, тогда наибольшее значение равно 2000+450×62 = 29900 рублей.
Ответ: 29900 рублей.
Квадратичная функция y=ax2+bx+c принимает экстремальное значение при х0= —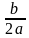
Пример. Производительность отдела в зависимости от количества сотрудников х, находящихся в офисе, описывается формулой y = -2х2+25х-8. Найдите, при каком числе сотрудников, находящихся в офисе, производительность отдела наибольшая.
Решение. Графиком функции y = -2х2+25х-8 является парабола, ветви которой направлены вниз. Значит, наибольшее значение она принимает в вершине параболы. Найдём абсциссу вершины
х0 =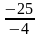
Количество сотрудников – число натуральное, значит наибольшее значение функция будет принимать при натуральном значении х, ближайшем к вершине, в данном случае х = 6.
Ответ:6
-
Применение производной
Для исследования свойств функции используют производную.
Дискретные модели
Некоторые задачи удобно решать с помощью дискретных математических моделей, то есть моделей, переменные в которых могут принимать некоторое, практически всегда конечное число наперед известных значений.
-
Простые экономические задачи. Проценты, доли и соотношения.
Часто такие задачи требуют умения обращаться с процентами — находить процент от числа, число по его процентам, а также величину и изменение величины в процентах. Это объясняется тем, что проценты широко распространены в реальной жизни при проведении различных операций, где возникают банковские проценты, проценты от зарплаты в качестве налога и т.д.
При решении задач на анализ динамики экономических показателей всегда устанавливается взаимно однозначное соответствие между процентами и коэффициентами. Выражение «величина увеличилась (уменьшилась) на x процентов» нужно воспринимать в виде «величина умножилась на коэффициент k» и наоборот. В общем виде это можно представить так:
-
увеличился на х% — умножился на коэффициент k =
;
-
уменьшился на х% — умножился на коэффициент k =
.
Пример. Налог на доходы составляет 13% от заработной платы. Заработная плата Николая Ивановича равна 22 500 рублей. Какую сумму он получит после вычета налога на доходы?
Решение. После вычета налога на доходы Николай получит 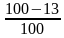
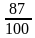
22 500×0,87 = 19 575 рублей.
Ответ: 19 575 рублей.
Но следует помнить, что если происходит последовательное изменение какой-либо величины, то каждый раз проценты берутся от ее последнего (перед очередным изменением) значения, и на соответствующий коэффициент каждый раз умножается последнее (перед очередным изменением) значение величины.
-
Вклады
Вкладом является денежная сумма или другие ценности, которые человек отдает в банк на определенных условиях, подразумевающих начисление процентов за определенный период на вложенную сумму.
Например, если в банк вложена сумма А под p% на некоторый период времени t, то по истечении этого времени вложенная сумма увеличится на р% от числа А, значит, станет равной:
А + А × 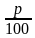
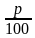
Другими словами, вклад увеличится в 1 + 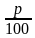
Ставка по вкладу с учетом капитализации.
Часто банк применяет ставку по вкладу с учетом капитализации, то есть если в банк была вложена сумма А под р% годовых, то каждый месяц банк увеличивает сумму, находящуюся к этому моменту на счете клиента на 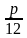
Формула расчета суммы вклада, размещенного с учетом ежемесячной капитализации под р% годовых: 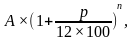
Пример. Ольга Викторовна поместила 250 000 рублей в банк на 3 месяца под 24% годовых с учетом капитализации процентов, то есть по истечении каждого месяца к ее вкладу были добавлены деньги, начисленные в качестве процентов. Какая сумма будет на счете Ольги Викторовны через 3 месяца? На сколько рублей увеличился ее первоначальный вклад?
Решение. На счете Ольги через 3 месяца будет
250000 × (1 + 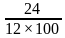
Её первоначальный вклад увеличился на 265302 – 250000 = 15302 рубля.
Ответ: 265302 рубля, на 15302 рубля.
-
Кредиты
Кредит – это финансовая сделка, в результате которой кредитор (банк или другое финансовое учреждение) предоставляет на определенный срок деньги заемщику. За пользование деньгами заемщик, кроме погашения основного долга (называемого в финансовой литературе телом кредита), выплачивает также кредитору проценты. Разделение погашающих платежей на две части, отвечающие за погашение долга (тела кредита) и погашение процентных денег, принципиально важно, поскольку от этого зависят уплачиваемые налоги.
Пример. Клиент взял в банке 135000 рублей на год под 12%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Решение. Через год долг увеличится в 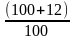
Клиент будет должен банку 135000×1,12 = 151200 рублей.
Ежемесячно он будет вносить 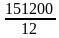
Ответ: 12600 рублей.
Дифференцированная схема
При дифференцированной (или регрессивной) схеме процент и периодичность обязательных платежей фиксируются (например, ежегодные, ежеквартальные или ежемесячные платежи), а фиксированный процент начисляется на ещё не выплаченную к моменту очередного обязательного платежа часть кредита (долг). В этом случае каждый платёжный период сумма выплат уменьшается, поскольку она состоит из фиксированной части и процентов, начисляемых на остаток долга по кредиту, величина которого каждый платёжный период уменьшается. Таким образом, при схеме с дифференцированными платежами клиент возвращает банку до истечения каждого платёжного периода 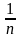
Пусть S0 – сумма кредита, который был взят на n лет под k% годовых.
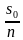
(фиксированная часть)
Процент на остаток долга
(изменяющаяся часть)
Платеж = +
|
Года |
1 |
2 |
3 |
4 |
… |
n |
|
Фиксированная часть (выплаты) |
|
|
|
|
… |
|
|
Сумма на которую начисляется процент |
|
|
|
|
… |
|
|
Начисленные проценты |
|
|
|
|
… |
|
Общая сумма начисленных процентов:
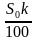
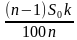
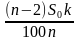
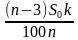
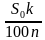
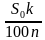
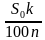
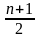
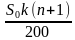
Общая сумма S всех выплат по кредиту: S = S0 + 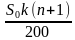
Пример. Величина предоставленного потребительского кредита – 12000руб. Процентная ставка – 12% годовых, срок погашения – 6 месяцев, схема погашения – рецессивная (т.е. в конце каждого месяца заемщик выплачивает процент на оставшуюся часть долга и одну шестую часть основного долга). Какую сумму выплатит заемщик в итоге банку?
Решение. Воспользуемся формулой, где К=12000, р=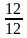
Х=12000 + 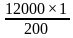
Ответ: 12420 рублей.
Но следует заметить, что чтобы использовать данную формулу на экзамене, ее нужно будет вывести самостоятельно, используя приведенные в условии данные. Но вывод формулы довольно сложный и не каждый ученик сможет его воспроизвести, поэтому существует ещё один способ решения таких задач – таблица
|
Месяц |
Долг |
Процентный платеж |
Выплата долга |
Месячный взнос |
|
Д |
П=0,01Д |
В |
П+В |
|
|
1 |
12000 |
120 |
2000 |
2120 |
|
2 |
10000 |
100 |
2000 |
2100 |
|
3 |
8000 |
80 |
2000 |
2080 |
|
4 |
6000 |
60 |
2000 |
2060 |
|
5 |
4000 |
40 |
2000 |
2040 |
|
6 |
2000 |
20 |
2000 |
2020 |
|
Всего |
420 |
12000 |
12420 |
Ответ:12420 рублей.
Аннуитетная схема
На сегодняшний день большим спросом среди заёмщиков пользуется аннуитетная схема: заёмщику удобно, когда сумма ежемесячного (ежеквартального, ежегодного) платежа фиксируется на весь срок кредитования.
Пусть кредит в размере S0 рублей выдан на n лет под k% годовых и пусть х рублей – ежегодный платеж. Тогда полная выплата по кредиту составит Х = nx рублей. Ежегодное начисление р% на остаток долга соответствует умножению этого остатка на коэффициент m=1+0,01k. Тогда
S1 = S0m – x;
S2 = mS1 – x = m2S0 – mx – x;
S3 = mS2 – x = m3S0 – m2x – mx – x;
Sn = mSn — 1 – x = mnS0 – mn — 1x – mx – x.
Поскольку по истечении платёжного периода долг равен 0, то Sn = 0, т.е.
mnS0 – mn — 1x – …–mx – x = 0.
Отсюда mn — 1x + …+ mx + x = mnS0, а после вынесения общего множителя
x(mn — 1 + …+ m + 1) = mnS0. Сумма mn — 1 + …+ m + 1 вычисляется формуле суммы s первых n членов геометрической прогрессии {bn}: S = b1×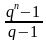
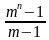
= mnS0, откуда х =
S0. (1)
m=1+0,01k, 0,01k часто обозначают буквой p. Тогда m = 1+p, формула (1) примет вид х = S0.
Пример. Клиент взял 15960000рублей в кредит под 30% годовых. По истечению каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 30%), затем клиент переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы клиент выплатил долг тремя равными ежегодными платежами?
Решение. Используем формулу
S=15960000, n=3, q=1+ =
x= = 8788000
Ответ: 8788000 рублей.
2-й способ. Эту задачу также можно решить без использования формулы.
Пусть ежегодный платеж составляет х рублей. Тогда
1-й год: 1,3×15960000-х=20748000-х
2-й год: 1,3(20748000-х)-х=26972400-2,3х
3-й год: 1,3(26972400-2,3х) –х= 35064120-3,99х.
По условию клиент должен выплатить кредит тремя равными платежами, т.е. в конце третьего года его долг составит 0 рублей. Тогда 35064120-3,99х=0. Решим уравнение и получим х=8788000.
Ответ: 8788000 рублей.
Решение экономических задач
Дискретные модели
Задача №1. Взяли кредит в банке на сумму 250000 рублей под р% годовых и выплатили за 2 года платежами 150000 рублей в первый год и 180000 рублей- во второй. Найдите р.
Решение. 1-й год: 250000 + 250000×0,01р – 150000 =100000+2500р.
2-й год: 100000+2500р + (100000+2500р)0,01р – 180000 = 25р2+3500р-80000.
Решим уравнение 25р2 + 3500р – 80000 = 0 и получим р1=20%
р2= -160% — п.к., т.к. р≥0.
Ответ: 20
Задача №2. 31 декабря 2014 года Евгений взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на а%), затем Евгений переводит очередной транш. Евгений выплатил кредит за два транша, переведя в первый раз 540 тыс. рублей, во второй 649,6 тыс. рублей. Найдите а.
Решение. Евгений выплатил кредит за два транша, т.е. за два года. Тогда
31.12.15. 1000000 + 1000000×0,01а – 540000 = 460000+10000а
31.12.16. 460000+1000а+(460000+1000а)0,01а– 649600 = 100а2+14600а -18900.
Решим уравнение 100а2+14600а-18900=0 и получим а1=12%
а2= -158%, п.к., т.к. а≥0.
Ответ: 12
Задача №3. Банк выдал заемщику кредит в размере 30000 рублей, ежегодная выплата по кредиту составляет 10000 рублей (последний платеж может отличаться от стальных в меньшую сторону), процентная ставка – 20% годовых. Через сколько лет кредит будет погашен? Сколько составит переплата?
Решение. Решим с помощь таблицы
|
Сумма по кредиту А |
Процент по кредиту 0,2А |
Ежегодная выплата |
Погашение тела кредита В=1000-0,2А |
Тело кредита на начало след.года А-В |
|
30000 |
6000 |
10000 |
4000 |
26000 |
|
26000 |
5200 |
10000 |
4800 |
21200 |
|
21200 |
4240 |
10000 |
5760 |
15440 |
|
15440 |
3088 |
10000 |
6912 |
8528 |
|
8528 |
1705,6 |
10000 |
8294,4 |
233,6 |
|
233,6 |
46,72 |
280, 32 |
233,6 |
0 |
|
Итого |
50280,32 |
30000 |
Кредит будет погашен через 6 лет. Переплата составит 50280,32-30000=20280,32 рублей.
Ответ: 6 лет; 20280,32 рублей.
Задача №4. 31 декабря 2014 года Дмитрий взял в банке 4290000 рублей в кредит по 14,5% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года в банк начисляется проценты на оставшуюся сумму долга, затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Дмитрий выплатил долг двумя равными платежами (т.е. за два года)?
Решение. 31.12.15 — 4290000×1,145 – х=4912050 – х.
31.12.16 – (4912050 – х)1,145 – х= 5624297,25 – 2,145х.
Т.к. долг погашен за два года то 5624297,25 – 2,145х=0
х=2622050 рублей.
Ответ: 2622050 рублей.
Задача №5. 15-го января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 108 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение. Пусть S0 – сумма кредита. Составим схему выплат:
1-й месяц: + 0,01S0
2-й месяц: + 0,01(S0 —
) =
+ 0,01
S0
3-й месяц: + 0,01
S0
…
8-й месяц: + 0,01
S0
Известно, что восьмая выплата составила 108 тыс. рублей, значит
+ 0,01
S0 = 108
(1 + 0,08) = 108
1,08 = 108
S0 = = 1500 тыс. рублей – сумма кредита. По выведенной нами формуле:
S = S0 + 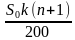
S = 1500 + = 1500 + = 1500 + 120 = 1620 тыс. рублей = 1620000рублей.
Ответ: 1620000 рублей.
Задача №6. 15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?
Решение. Пусть S – сумма, которую планируется взять в кредит, Х — сумма на которую уменьшается основной долг, Х = 30 (тысяч рублей). После каждого начисления процентов сумма долга увеличивается в 1,03 раза, т.е. k = 1,03.
Рассмотрим схему
После первого начисления процентов сумма долга равна kS. Затем, после первой выплаты, сумма долга равна S – X, где Х = 30 (тысяч рублей).
Значит, первая выплата равна kS – (S – X)
Вторая выплата: k (S – X ) – ( S – 2X).
…
Последняя выплата: k ( S – 20 X).
Найдём общую сумму выплат: kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – 20X) =
= k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X).
Упростим выражения в скобках:
k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20))
Используя сумму арифметической прогрессии найдём ;
Получим:
k (21 S – 210X ) – 20 S + 210 Х = 1604
Осталось подставить числовые значения.
1,03(21S – 210×30) – 20S + 210×30 = 1604
1,63S = 1793
S = 1100 тысяч рублей = 1 100 000 рублей.
Ответ: 1100000 рублей.
Непрерывные модели
Задача №7. По бизнес-плану предполагается вложить в четырехлетний проект 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 13% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей в третий и четвертый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.
Решение. 1-й год: 20×1,13 + n = 22,6 + n.
2-й год: (22,6+n)1,13+n = 25,538+2,13n.
По условию 25,538+2,13n ≥ 2×20
25,538+2,13n ≥ 40
n 6,78…
Наименьшее целое решение n=7.
3-й год (25,538+2,13n)1,13 + m=(25,538+2,13×7)1,13 + m=45,70624 + m
4-й год (конец проекта): (45,70624 + m)1,13 + m=51,6480512 + 2,13m
По условию 51,6480512 + 2,13m≥3×20
51,6480512 + 2,13m≥60
m≥3,92…
Наименьшее целое решение m=4.
Ответ: 7 млн рублей; 4 млн рублей.
Задача №8. По бизнес-плану предполагается вложить в четырехлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начисления процентов нужна дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвертый годы. Найдите наименьший размер первоначальных вложений, при котором они за два года станут больше 125 миллионов, а за четыре года станут больше 200 миллионов рублей.
Решение. Пусть х млн рублей – первоначальные вложения. Тогда
1-й год: 1,2х + 20.
2-й год: (1,2х + 20)1,2 + 20=1,44х + 44.
По условию 1,44х + 44˃125
х˃56,25
Наименьшее целое решение х=57.
3-й год: (1,44х + 44)1,2+10=1,728х+62,8
4-й год (конец проекта): (1,728х+62,8)1,2+10=2,0736х+85,36
По условию 2,0736х+85,36˃200
х˃55,28…
Наименьшее целое число (также удовлетворяющее условию на два года) х=57.
Ответ: 57 млн рублей.
Задача №9. Зависимость объема спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задается формулой q=280-2p. Выручка предприятия за меся r ( в тыс. руб.) вычисляется по формуле r(p)=qp. Определите цену, при которой месячная выручка r(p) будет наибольшей. Найдите наибольшую возможную выручку.
Решение. r = qp = (280-2p)p = 280p — p2. Графиком полученной функции является парабола, ветви которой направлены вниз. Значит, наибольшее значение она принимает при p0 = = 70.
При цене 70 тыс. рублей выручка будет наибольшей и будет равна
(280-2×70)70=140×70=9800 тыс. рублей.
Ответ: 70тыс. рублей; 9800 тыс. рублей.
Задача №10. Вклад в размере 6 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвертого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 15 млн рублей.
Решение. Пусть искомая сумма равна х рублей.
1-й год: 1,1×6=6,6 млн рублей.
2-й год: 1,1×6,6=7,26млн рублей.
3-й год: 1,1×7,26+х=7,986+х
4-й год: 1,1(7,986+х)+х=8,7846+2,1х.
По условию 8,7846+2,1х≥15
х≥2,95…
Наименьшее целое число х=3.
Ответ: 3 млн рублей.
Задача №11. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Решение: Пусть I объект — х рабочих, суточная зарплата: f1(x) = 4x2.
Тогда II объект 24 – x рабочих — суточная заработная плата: f2(24 – x)2 = 576 – 48x + x2.
В день начальник будет должен платить рабочим
f(x) = f1(x) + f2(x) = 4x2 + 576 – 48x + x2 = 5x2— 48x + 576, 0 є N.
Квадратичная функция f(x) принимает наименьшее значение при
х0 = =
= 4,8. Число х является натуральным числом, поэтому функция достигает наименьшего значения в точках 4 или 5. Найдем и сравним эти значения:
f(4) = 5×16 – 48×4 +576 = 80 – 192 + 576 = 464
f(5) = 5×25 – 48×5 + 576 = 125 – 240 + 576 = 461
Наименьшее значение функции достигается в точке 5. Поэтому необходимо направить 5 рабочих на первый объект, 24 – 5 = 19 рабочих — на второй объект. Зарплата рабочих составит 461 у. е.
Ответ: I объект – 5 рабочих, II объект – 19 рабочих, 461 у.е.
Задача №12. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 500 ц/га.
Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?
Решение. Продавать свеклу более выгодно, поэтому второе поле, где ее урожайность выше, следует засадить только свеклой. Она принесет доход 10 га · 500 ц/га · 8000 руб/ц = 40 млн руб.
Пусть на первом поле – х га свеклы, тогда картофеля 10 – х га, составим функцию: f(x) = x×300×8000 + (10 – x)500×5000 = 2400000x + 25000000 – 2500000x = -100000x + 25000000 = -x + 250, х є [0; 10].
Линейная функция убывающая, значит, наибольшее значение она будет принимать на левом конце промежутка, т.е. при х = 0, значит, первое поле нужно засадить только картофелем.
Тогда доход составит: 10×500×500 = 25 млн руб.
Общий доход: 40 + 25 = 65 млн. рублей.
Ответ: 65 млн руб.
Задача №13. Подрядчику выделили 30000 рублей на уборку микрорайона к приезду губернатора. Из этих денег нужно выдать 2000 рублей бригадиру и по 450 рублей зарплаты каждому рабочему. Какую наибольшую сумму может потратить подрядчик на зарплату?
Решение. Пусть всего х рабочих. Зарплата рабочих и бригадира равна 2000+450х, по условию она не должна превышать 30000, т.е. 2000+450х≤30000
x ≤ 62 
Линейная функция y = 2000+450х возрастающая, поэтому наибольшее значение она примет на правом конце промежутка. По условию х – число натуральное, значит, наибольшее значение будет достигаться при х = 62, тогда наибольшее значение равно 2000+450×62 = 29900 рублей.
Ответ: 29900 рублей.
Задача №14. Производительность отдела в зависимости от количества сотрудников х, находящихся в офисе, описывается формулой y = -2х2+25х-8. Найдите, при каком числе сотрудников, находящихся в офисе, производительность отдела наибольшая.
Решение. Графиком функции y = -2х2+25х-8 является парабола, ветви которой направлены вниз. Значит, наибольшее значение она принимает в вершине параболы. Найдём абсциссу вершины
х0 =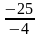
Количество сотрудников – число натуральное, значит наибольшее значение функция будет принимать при натуральном значении х, ближайшем к вершине, в данном случае х = 6.
Ответ:6
Заключение
В процессе нашей работы мы узнали, какие задачи относятся к экономическим, каких типов они бывают. В результате решения таких задач, мы поняли, что главное — это ориентироваться в базовых экономических понятиях и уметь составить математическую модель задачи. Таким образом своей цели мы достигли.
Результатами нашей работы мы планируем поделиться с учащимися 10 классов. Надеемся, что наш опыт поможет им в освоении экономических задач.
Список литературы
-
ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36 вариантов / под ред. И.В.Ященко. – М. : Издательство «Национальное образование», 2019.
-
ЕГЭ 2017. Математика. Профильный уровень. 50 вариантов типовых тестовых заданий/ И. В. Ященко, М. А. Волчкевич, И. Р. Высоцкий, Р. К. Гордин, П. В. Семёнов, О. Н. Косухин, Д. А. Фёдоровых, А. И. Суздальцев, А. Р. Рязановский, И. Н. Сергеев, В. А. Смирнов, А. В. Хачатурян, С. А. Шестаков, Д. Э. Шноль; под ред. И. В. Ященко. – М. : издательство «Экзамен», 2017.
-
Математика. ЕГЭ. Алгебра; задания с развернутым ответом: учебно – методическое пособие/ Под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова. – Ростов-на-Дону: Легион, 2016.
-
Математика. ЕГЭ. Задача с экономическим содержанием: учебно – методическое пособие/ Под. ред. Ф. Ф. Лысенко и С. Ю. Кулабухова. – Изд. 2 – е., перераб. и доп. – Ростов н/Д: Легион, 2016.
-
Ященко И. В. Я сдам ЕГЭ! Математика. Курс самоподготовки. Технология решения заданий. Учеб. пособие для общеобразоват. организаций. Проф. Уровень. В 3 ч. Ч. 2. Алгебра и начала математического анализа/ И. В. Ященко, С. А. Шестаков. – М. : Просвещение, 2018.
-
http://www.fipi.ru
-
https://ege.sdamgia.ru
-
https://dic.academic.ru/dic.nsf/dic_economic_law/
22
Методы решения экономических задач
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Платонова Д.И. 1
1МБОУ «ПСОШ №1 с УИОП им. И.М. Яковлева»
Иванова С.С. 1
1МБОУ «ПСОШ №1 с УИОП им. И.М. Яковлева»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая практико-ориентированная задача №17, так называемая «банковская» задача. На уроках математики мы готовимся к сдаче экзамена. А общаясь с выпускниками прошлых лет, мы выяснили, что одними из самых трудных заданий по математике на экзамене являются экономические задачи. Анализ результатов ЕГЭ в последние годы показал, что с задачами по экономике справляются очень малое количество выпускников. При этом высветился ряд существенных недостатков в подготовке выпускников: теоретическое содержание курса математики усваивается формально, поэтому ученики не могут использовать изученный материал в ситуации, которая даже незначительно отличается от стандартной. Нами были рассмотрены варианты ЕГЭ последних трех лет. Результаты нашей работы мы представляем в данном проекте.
Цели:
Классифицировать и систематизировать виды экономических задач.
Научиться решать экономические задачи.
Создать методическое пособие для учащихся 10-11 классов при подготовке к ЕГЭ.
Задачи:
Изучить теоретический материал в рамках подготовки ЕГЭ.
Проанализировать виды экономических задач, которые встречаются в ЕГЭ.
Развить умение применять полученные знания при решении экономических задач
Объект исследования: КИМы из сборников для подготовки к ЕГЭ 2015-2020 учебные года.
Предмет исследования: экономические задачи
Методы исследования: анализ литературы, анкетирование, обобщение, синтез.
Актуальность работы заключается в том, что благодаря грамотной классификации и знаниям основных формул и приемов практически каждый выпускник сможет решить экономическую задачу на ЕГЭ.
Новизна исследования: поиск математических представлений у учеников о решении экономических задач практической направленности.
Практическая значимость работы заключается в том, что изучение способов применения математических знаний на практике способствует повышению интереса к изучению математики у учеников, родителей. Возможно использования материала для подготовки к ЕГЭ по математике (профильный уровень).
План работы:
Работа с литературой
Провести анкетирование
Изучение видов задач на проценты
Изучение способов решения задач
Составить сборник экономических задач и задач на оптимизацию по математике
Выводы
Я провела анкетирование среди выпускников для выяснения причин малой решаемости экономических задач. Вот такие результаты мы получили.
1.Плохое знание теоретического материала — 7 человек
2. Недостаточность навыка решения экономических задач — 6 человек
3. Большая затрата времени на решение экономических задач -12 человек
4. Малое количество часов на изучение этой темы в школе — 5 человек
5.Трудность задач — 15 человек
Гипотеза: Результаты анкетирования позволяют мне предположить, что если мне удастся изложить теоретический и практический материал, необходимый для решения экономических задач, в доступной для каждого выпускника форме, количество учащихся справившихся с этим видом задач возрастет. Поэтому мы решили выполнить работу, которая поможет нам самим разобраться с экономическими задачами, которые перед нами ставит жизнь. Мы понимаем, что вряд ли содержание задач соответствует конкретным жизненным ситуациям, но желание получить три балла на экзамене за решение №17 побудило нас к созданию данного пособия. Очень надеемся, что наши труды принесут пользу не только нам, но и всем, кто ознакомится с нашим пособием.
Основные ошибки, которые допускают выпускники при решении экономической задачи
неверное составление модели;
вычислительные (арифметические);
прекращение решения без доведения ответа
до числового значения;
не доведение решения до конца из-за невнимательного прочтения вопроса;
решение методом подбора без обоснования;
применение готовых формул для задач о кредитовании, отсутствующих в учебниках
Для решения экономических задач советуем применить следующие правила упрощения решения
Для упрощения записей и вычислений при решении задач о вкладах, кредитах и оптимизацию производства переходить от «языка процентов» к десятичным дробям. Например, «увеличение величины на 15%» равносильно её умножению на число 1,15 (так как 100% + 15% = 115% = 1,15); «уменьшение величины на 24%» равносильно её умножению на число 0,76 (так как 100% — 24% = 76% = 0,76).
Для правильного выбора способа решения необходимо уметь выделять основные типы задач:
задачи о вкладах;
задачи о кредитах с аннуитетными (равными) платежами;
задачи о кредитах с дифференцированными (уменьшающимися) платежами;
задачи на оптимизацию
Большинство задач следует сначала решать «в общем виде», вводя следующие обозначения:
S – сумма вклада или кредита;
x – ежемесячный вклад или ежемесячная выплата;
n– срок (количество месяцев или лет);
r% — процентная ставка;
к=1+ – множитель для вычисления процентных начислений;
числовые данные подставлять только по окончании всех преобразований
Основные виды экономических задач
Кредит – это ссуда, предоставленная банком заемщику под определенные проценты за пользование деньгами. Как известно, существует два вида платежей по кредиту: дифференцированный и аннуитетный.
Дифференцированные платежи рассчитываются исходя из того, что сумма погашения основного долга из месяца в месяц одинаковая, а сумма погашения процентов зависит от того, сколько насчитал банк за последний месяц.
При аннуитетных платежах размер ежемесячного платежа остается постоянным на всем периоде кредитования. Ежемесячный платеж рассчитывается как сумма процентов, начисленных на текущий период и суммы идущей на погашения суммы кредита.
1.1 Задачи на кредиты с дифференцированными платежами
Задача 1
Рассмотрим задачу, которая раскрывает суть понятия «дифференцированный платеж» на простом примере. Допустим, что в банке взят кредит 1200 рублей на 12 месяцев. Причем, каждый платежный период долг сначала возрастает на 10% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же величину меньше долга на конец предыдущего платежного периода. Необходимо ответить на вопросы: Какую сумму нужно вернуть банку за весь платежный период? Какова сумма переплаты?
Рассуждаем. Долг перед банком по состоянию на конец года должен уменьшаться до нуля равномерно, то есть последовательность долгов перед банком такова:
1200;1100; 1000; 900;800; 700; 600; 500; 400; 300; 200;100.
Первого числа каждого месяца долг возрастает на 10%. Тогда последовательность долгов будет такова:
1200∙1.1; 1100∙1.1; 1000∙1.1; 900∙1.1; 800∙1.1; 700∙1.1; 600∙1.1; 500∙1.1; 400∙1.1; 300∙1.1; 200∙1.1;100∙1.1. или 1320; 1210; 1100;990; 880; …110.
Обращаем внимание на то, разница между долговыми суммами равна 110 рублей. Теперь найдем ежемесячные выплаты:
1 месяц- 1320-1100=220; 2 месяц- 1210-1000=210; 3 месяц- 1100- 900=200; 4 месяц- 990- 800=190; 5 месяц – 880-700=180 и так далее. И последняя наименьшая выплата равна 110 рублей. Замечаем, что выплаты уменьшаются ежемесячно на 10 рублей. Такова схема дифференцированного платежа. Далее можно найти сумму всех выплат. Она равна: 220+210+200+…+110 = 1980 (рублей). Таким образом, переплата составляет 65%.
Задача 2
15-го января 2015 года планируется взять кредит в банке на сумму 1.5 млн рублей на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно вернуть банку в течение всего срока кредитования? Какова сумма переплаты?
Решение. Построим математическую модель этой задачи и исследуем ее. Пусть S— сумма кредита. Долг перед банком по состоянию на конец второго года должен уменьшаться до нуля равномерно. Тогда последовательность размеров долга будет иметь вид:
; ; ; …; . Занесем эти данные в таблицу:
|
Месяц и год |
15 января 2015 г |
15 февраля 2015 г |
15 марта 2015г |
15 апреля 2015г |
… |
15 декабря 2016 года |
15 января 2017 года |
|
Долг перед банком |
… |
0 |
Найдем теперь размеры выплат:
1 месяц: — = (24∙1.03 – 23).
2 месяц: — (23∙1.03 – 22).
3 месяц:: — (22∙1.03 – 21).
……………………………………………
24 месяц: — (1∙1.03 – 0).
Найдем сумму всех выплат:
(24∙1.03+23∙1.03+22∙1.03+…+1∙1.03-23-22-21-…-1) =
= (1.03(24+23+22+…+1) –(23+22+21+…+1)) = (1.03∙300–276) = ∙33 =
Чтобы найти численное значение суммы всех выплат, надо подставить S=1,5. Получим, что сумма всех выплат равна 2,0625 миллионов рублей, или 2062500 рублей. Найдем сумму переплаты: 2062500-1500000=562500 (рублей).
Ответ: 2062500 рублей; 562500 рублей.
1.2 Задачи на кредиты с равными платежами.
Рассмотрим задачу, которая раскрывает суть понятия «аннуитетный платеж».
Задача 3
В июле 2016 года планируется взять кредит на 4 года в размере S млн рублей, где S – целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года
— с февраля по июнь каждого года необходимо выплатить часть долга
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
|
Месяц, год |
Июль 2016 |
Июль 2017 |
Июль 2018 |
Июль 2019 |
Июль 2020 |
|
долг |
S |
0.9S |
0.7S |
0.4S |
0 |
Найдите наименьшее S, при котором общая сумма выплат будет больше 20 млн рублей.
Решение.
Долг перед банком ( в млн рублей) должен уменьшаться до нуля на июль каждого года в соответствии с данной таблицей:
S; 0.9S; 0.7S; 0.4S; 0.
По условию, в январе каждого года долг увеличивается на 30%. Значит, долг в январе каждого года равен:
|
Месяц, год |
Январь 2017 |
Январь 2018 |
Январь 2019 |
Январь 2020 |
Январь 2021 |
|
Долг |
1.3S |
1.3∙0.9∙S=1.17S |
1.3∙0.7∙S=0.91S |
1.3∙0.4∙S=0.52S |
0 |
Найдем теперь выплаты с февраля по июнь каждого года:
1) 1.3∙S – 0.9∙S = 0.4∙S.
2) 1.17∙S – 0.7∙S = 0.47∙S
3) 0.91∙S – 0.4S = 0.51∙S
4) 0.52∙S – 0 = 0.52∙S
Найдем сумму всех выплат: 0.4∙S+0.47∙S+0.51∙S+0.52∙S=1.9∙S
Общая сумма выплат должна быть больше 20 млн рублей:
1.9∙S 20; S10
Наименьшее целое решение этого неравенства – число 11. Значит, искомый размер кредита – 11 млн рублей. Ответ: 11 млн рублей
Задача 4
15-го января планируется взять кредит в банке на четыре месяца в размере 2 млн руб. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r % по сравнению с концом предыдущего месяца, где r – целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
|
Долг (в млн р.) |
2 |
1.6 |
1 |
0.5 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 2,5 млн р.
Решение.
Долг перед банком ( в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:
2; 1.6; 1; 0.5; 0.
Обозначим k = 1+ Тогда долг на 1-е число каждого месяца равен:
2k; 1.6 k; 1k; 0.5k; 0.
Найдем теперь выплаты со 2-е по 14-е число каждого месяца:
2k-1.6; 1.6k-1; k-0.5; 0.5k.
Общая сумма выплат составляет:
(2k-1.6) +( 1.6k-1) + ( k-0.5) + 0.5k = 5.1k – 3.1
По условию, общая сумма выплат будет меньше 2.5 млн руб. Значит, составляем неравенство:
5.1k – 3.1≤ 2.5.Подставляя вместо k выражение 1+ и решая неравенство, получим, что r ≤ 9 . Наибольшее целое решение этого неравенства – число 9. Значит, искомое число процентов — 9%.
Ответ: 9%
1.3 Задачи на вклады
Задача 5
Производство x тыс. единиц продукции обходится в q = 0,5 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px – q). При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?
Решение. Прибыль (в млн рублей) за один год выражается величиной
px – (0,5 + x + 7) = -0,5 +(p-1)x -7
Это выражение является квадратным трехчленом, оно достигает своего наибольшего значения при x = p-1. Прибыль за три года составит не менее 75 млн рублей, если Решая это неравенство, получим, что p ≥ 9 и p ≤ -7. Так как цена продукции не может быть отрицательной, то p ≥ 9. Таким образом, искомая наименьшая цена составляет 9 тыс. р.
Ответ: 9 тыс. рублей.
1.4 Задачи на оптимальный выбор
Задача 6
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Решение:
1-й способ – с помощью логики и арифметических действий.
Найдем стоимость 1 номера стандартного: 2000:21=95 (рублей).
Найдем стоимость 1 номера «люкс»: 4500: 49 =91 (рублей).
Так как стоимость 1 стандартного номера дороже, то выгоднее разместить на этой площади больше номеров стандартных, и как можно меньше номеров «люкс». Начнем перебор количества номеров «люкс» с наименьшей цифры. Пусть номеров «люкс» будет 0. Тогда число 1099 не делится нацело на 21. Далее. Допустим, что номеров «люкс» будет 1. Тогда: 1099- 49=1050 ;
1050: 21 = 50 (номеров стандартных). Значит, на площади 1050 можно разместить 50 стандартных номеров. Тогда в сутки отель может заработать: 50∙ 2000 + 1∙ 4500=104500 (р.). Ответ: 104500 рублей.
2-й способ – с помощью составления опорной линейной функции.
Пусть х – количество стандартных номеров, у- количество номеров «люкс». Они занимают площадь 21х+49у. Составим равенство: 21х+49у = 1099. Выразим из этого равенства у = .
Составим функцию заработанных денег: S(x, y) =2000∙x + 4500∙y. Далее подставим в эту функцию выражение для у. Получим S(x) =71 ∙х + 4500∙22 . Это возрастающая линейная функция. Свое наибольшее значение она принимает при наибольшем значении х и наименьшем значении у. По условию х и у – натуральные числа. Значит, у=1 (это наименьшее натуральное число) и х=50. Значит, S (50, 1) = 2000∙50 + 4500∙ 1=104500.
Ответ: 104500 рублей.
Задачи для самостоятельного решения
Экономические задачи ЕГЭ
1. (Статград, январь 2015). В банк помещена сумма 3 900 000 рублей под 50% годовых. В конце каждого из первых четырёх лет хранения, после начисления процентов вкладчик дополнительно вносил на счёт одну и ту же сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%.. Какую сумму вкладчик добавлял к вкладу?
Ответ: 210 000.
2. (Статград, январь 2015). Банк под определённый процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счёта. Банк увеличил процент годовых на 40%. К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков новый процент годовых?
Ответ: 60%.
3. (Подготовка к ЕГЭ по математике 2016г. И.В. Семёнов, С.А. Шестаков, А.С. Трепалин.)
31 декабря Сергей взял в банке 4 382 000 рублей в кредит под 16% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 16%), затем Сергей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Сергей выплатил долг двумя тремя равными платежами (то есть за 3 года)?
Ответ: 1 951 120.
4. (Статград, январь 2015). 31 декабря Ваня взял в банке 5 005 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Ваня переводит в банк платёж. Весь долг Ваня выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Ответ: 576 000.
5. (И.В.Ященко. ЕГЭ 2015 МАТЕМАТИКА типовые экзаменационные варианты.)
1 января 2015 года Павел Витальевич взял в банке 1000000 рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк платёж. На какое минимальное количество месяцев Павел Виталье-вич может взять кредит, чтобы ежемесячные выплаты были не более 125000 рублей?
Ответ. 9
6. (Статград, март 2015). Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит.
Найдите r .
Ответ: 2.
7. (Статград, апрель 2015). Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
Ответ: 822 тыс. рублей.
8. (Экзамен 2016г.)
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
Ответ:7
9. (Статград Февраль 2015).
Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Ответ: 8.
10. (Высшая школа экономики. Задачи экономических олимпиад. Рациональная аренда.)
Молодой преподаватель экономики снимает квартиру в городе М. и в начале каждого месяца платит за аренду 26 000 руб. Деньги он снимает со своего счета в банке. Ежемесячно на сумму остатка на счете банк начисляет процент по ставке r %. Придя в начале очередного месяца за деньгами, хозяин квартиры предложил молодому экономисту следующую сделку: если он оплатит аренду сразу за два месяца вперед, то арендная плата за каждый из этих двух месяцев будет снижена до 25 500 руб. Если предложение будет принято, то в следующий раз хозяин придет за деньгами через два месяца и вновь потребует 26 000 руб. При каких значениях r арендатору стоит принимать это предложение?
Ответ: при ставке менее 4% предложение стоит принять.
11.(ЕГЭ 2016. Математика. 50 вариантов типовых тестовых заданий / И.В. Ященко, и др.) Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Ответ: 104 500 рублей в сутки
ЗАКЛЮЧЕНИЕ
В результате данной работы я:
– смогла все экономические задачи разбить на четыре основных группы;
–решила ряд экономических задач;
– создала методическое пособие для учащихся 10-11 классов при подготовке к ЕГЭ.
Исследование и решение мною заданий ЕГЭ показало, что отлично зная теоретический материал и умея оперировать этими знаниями, можно с лёгкостью решить задачи любой сложности из экзамена по теме «Экономические задачи» даже ученикам 10 класса. Проводя проектную работу, я смогла повторить прошлый материал и извлечь новую информацию, которая в будущем поможет мне на ЕГЭ. Для успешной сдачи надо помнить, что все экономические задачи в вариантах ЕГЭ вычислительные, поэтому для их успешного решения должен быть отработан аппарат стандартных вычислений. Благодаря полученным знаниям в процессе моей работы, экономические задачи стали для меня не проблемой. Теперь я с легкостью смогу решить экономическую задачу на ЕГЭ и получить 3 балла, ведь для математики 3 балла – это очень много.
Я надеюсь, что данная работа будет полезна не только мне, но и всем выпускникам, учителям математики.
Экономические задачи – это не просто задачи из математики, это часть нашей жизни в современном мире. Умение их решать будет полезно как для проверки банковских операций, так и в простых жизненных ситуациях.
Список используемой литературы.
Демонстрационный вариант контрольных измерительных материалов Единого государственного экзамена 2017 года по математике. Профильный уровень. – www.fipi.ru
ЕГЭ 2017. Математика. 30 вариантов типовых тестовых заданий и 800 заданий части 2/ И.В. Ященко, М.А. Волчкевич и др.; под ред. И.В. Ященко. – М.: Издательство «Экзамен», издательство МЦНМО, 2016.
Математика. Подготовка к ЕГЭ-2017. Профильный уровень. 40 тренировочных вариантов по демоверсии на 2017 год: учебно-методическое пособие /Под редакцией Ф.Ф.Лысенко, С..Кулабухова.- Ростов-на-Дону:Легион, 2016
ЕГЭ 2016. Математика. 30 вариантов типовых тестовых заданий
/ И.В. Ященко, М.А. Волчкевич и др.; под ред. И.В. Ященко. – М.: Издательство «Экзамен», издательство МЦНМО, 2015.
Математика. Подготовка к ЕГЭ-2015. Профильный уровень. 40 тренировочных вариантов по демоверсии на 2015 год: учебно-методическое пособие /Под редакцией Ф.Ф.Лысенко, С.Ю.Кулабухова.- Ростов-на-Дону:Легион, 2014
https://ege.sdamgia.ru
15
Просмотров работы: 1199

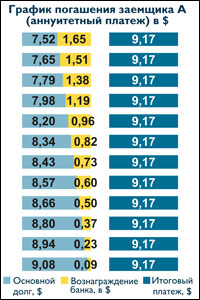

























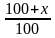 ;
;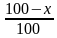 .
.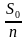
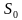
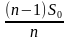
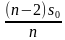
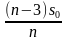
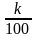 =
=