Экономические задачи егэ сборник - Помощь в подготовке к экзаменам и поступлению

Министерства спорта РС(Я)

ГБОУ РС(Я) «Чурапчинская республиканская спортивная средняя

школа- интернат олимпийского резерва им.Д.П.Коркина»

Экономические задачи в заданиях ЕГЭ по математике

Сборник

экономических задач и задач на оптимизацию

по математике

Учитель математики: Слепцова А.Н.

Чурапча

2017

«Особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды».

П. Л. Чебышев

Вступление

Начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая экономическая задача №17. В данных задачах предлагается ознакомиться с разными схемами выплаты кредита банку со стороны заемщика.

Кредит – это ссуда, предоставленная банком заемщику под определенные проценты за пользование деньгами. Существует два вида платежей по кредиту: дифференцированный и аннуитетный.

Кроме задач о кредитах есть задачи на выбор оптимального решения. Эти задачи тесно связаны с практической деятельностью человека. Как добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени.

Решение задач о кредитах в настоящее время очень актуально, так как жизнь современного человека тесно связана с экономическими отношениями, в частности, с операциями в банке.

Задачи на нахождение ежегодной платы (транша).

Задача 1 (Тренировочная работа 1). 31 декабря 2016 года Василий взял в банке 5460000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Василий переводит в банк х рублей. Какой должна быть сумма х, чтобы Василий выплатил долг тремя равными платежами (то есть за три года)?

Решение: S=5460000 — сумма кредита, х — ежегодная плата, r=20%

При начислении процентов оставшаяся сумма долга умножается на коэффициент 1+0,2=1,2.

Год	Долг банку	Остаток после ежегодной выплаты
0	S	—
1	1,2S	1,2S — x
2	1,2(1,2S — x) = 1,44S — 1,2x	1,44S — 1,2x — x= 1,44S — 2,2x
3	1,2(1,44S — 2,2x)=1,728S — 2,64x	1,728S — 2,64x — x= 1,728S — 3,64x

После третьего взноса кредит погашен полностью, значит, остаток равен нулю. Решаем полученное уравнение.

1,728S — 3,64x=0

3,64x=1,728∙5460000

x=2592000 Ответ: 2592000 рублей

Задача 2. (Тренировочная работа 42). 31 декабря 2014 года Дмитрий взял в банке 4290000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?

Решение : S = 4290000 — сумма кредита, r = 14,5%, х — ежегодная выплата

При начислении процентов оставшаяся сумма долга умножается на коэффициент 1+0,145=1,145.

Год	Долг банку	Остаток после ежегодной выплаты
0	S	—
1	1,145S	1,145S — x
2	1,145(1,145S — x) = 1,14522S — 1,145x	1,14522S — 1,145x — х = 1,14522S — 2,145x

После второго взноса кредит погашен полностью, значит, остаток равен нулю. Решаем полученное уравнение: 1,14522S — 2,145x = 0

Ответ: 2622050 рублей

При решении этих задач можно увидеть закономерность и, оформив решение в общем виде, получаем формулу.

S-сумма кредита,

р=, где a — процентная ставка,

х – сумма ежегодных выплат;

I год: S·p-х

II год:

III год:

IV год:

и т.д.

Задача 3. (Тренировочная работа 11) 31 декабря 2014 года Алексей взял в банке 6902000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк х рублей. Какой должна быть сумма х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре месяца)?

Решение. S = 6902000 — сумма кредита, r=12,5%, х — ежегодная выплата

Применяем формулу: , где

S-сумма кредита,

р=, где a— процентная ставка,

х – сумма ежемесячных выплат;

Ответ: 2 296 350 рублей.

Задачи на нахождение суммы кредита.

Задача 1. (Тренировочный вариант 6) 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15 числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что за первые 12 месяцев нужно выплатить банку 1370тыс. рублей. Какую сумму планируется взять в кредит?

Решение: Пусть начальная сумма кредита равна S. По условию, ежемесячный долг перед банком должен уменьшаться равномерно. Этот долг состоит из двух частей: постоянной ежемесячной выплаты и ежемесячной равномерно уменьшающейся выплаты процентов.

; ; ; …; . — размеры долгов (остаток по кредиту на конец месяца), тогда ежемесячная выплата процентов выглядит следующим образом:

; ; ; ; …; — ежемесячный %

Находим размеры выплат:

1-й месяц: + =

2-й месяц: + ∙ =

3-й месяц: + ∙ = и.т.д . Замечаем, что выходит последовательность, которая уменьшается на 2. Тогда используя формулу n-го члена арифметической прогрессии аn = а1 + d(n — 1) при а1=148, d= -2

находим 12-й месяц: а12 = 148 — 2(11 — 1) = 126, т.е. .

Так как нам известна сумма первых двенадцати месяцев составляем уравнение:

+ = 1370000

Вынесем за скобки общий множитель и воспользуемся формулой суммы членов арифметической прогрессии Sn =

S = = 2000000 Ответ: 2000000

Задача 2. (Тренировочная работа 18). 31 декабря 2014 года Василий взял в банке некоторую сумму кредит под 11% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 11%), затем переводит в банк 3696300 рублей. Какую сумму взял Василий в банке, если он выплатил долг двумя равными платежами (то есть за два года)?

Решение: Воспользуемся формулой: = 0, которую вывели при решении задач на нахождение ежегодной (ежемесячной) выплаты,

где p= 1+0,11=1,11, х = 3696300

0 → S = = = 6330000.

Ответ: 6330000рублей

Задача 3. (Тренировочная работа 15)15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что восьмая выплата составила 99,2 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования.

Решение: S — сумма кредита, r = 3%

Сперва нужно вычислить сумму кредита. Известно, что восьмая выплата = 99,2тыс. Находим размеры выплат:

1-й месяц: + =

2-й месяц: + ∙ =

3-й месяц: + ∙ =

….

8-й месяц: → = 99200 → S = 99200∙ = 1200000, то есть планируется взять в кредит 1200000рублей.

Теперь, чтобы найти сумму которую нужно вернуть банку в течение всего срока кредитования воспользуемся формулой суммы членов арифметической прогрессии Sn = . Для этого сперва найдем пятнадцатую выплату:

а15 = 145 — 3∙14 = 103, т.е.

Общая сумма равна: ++…S

S15 = = 1860, т.е. = = 1488000

Ответ: 1488000

Задачи на вычисление процентной ставки.

Задача 1. (Тренировочная работа 19) 15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 15% больше, чем сумма, взятая в кредит. Найдите r?

Решение. Пусть S сумма кредита равна. Долг перед банком должен уменьшаться до нуля равномерно. Тогда последовательность размеров долга будет иметь вид:

; ;…. — остаток по кредиту на конец месяца

Найдем выплаты:

1 месяц: + S=

2 месяц: +

……………………………………………

9 месяц:

Найдем сумму всех выплат. По условию общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит, значит: → 900 + 45r = 1035 → r = 3. Ответ: 3%

Задача 2. (Тренировочная работа 49). 31 декабря 2014 года Евгений взял в банке 1млн рублей в кредит. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Евгений переводит очередной транш. Евгений выплатил кредит за два транша, переведя в первый раз 540тыс. рублей, во второй 649,6 тыс. рублей. Найдите а?

Решение: S = 1000000, а — процентная ставка по кредиту.

В конце 1-го года долг составит:

∙ 1000000 — 540000 = 460000 + 10000а

В конце 2-го года:

∙(460000 + 10000а) — 649600 = 100а2 + 14600а — 189600

По условию, кредит будет погашен за два года, составляем уравнение:

100а2 + 14600а — 189600 = 0, сокращая на 100 получим

а2 + 146а — 1896 = 0. Решаем квадратное уравнение, находим дискриминант

Д = 1462 + 4∙1896 = 21316 + 7584 = 28900= 1702

а1 = , а2 = .

Ответ: 12%

Задача 3. (Тренировочная работа 26). 15 января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

Решение: S — сумма кредита r =5%

выплата за 1-й месяц: +

2-й: +

3-й: ; 4-й: ; 5-й: .

Таким образом, за все 5 месяцев сумма выплат составит:

Из выражения видно, что первоначальная сумма кредита увеличилась на 1,15 раз, т.е. на 115%.

Ответ: 115%

Задача 4. (Демонстрационный вариант ЕГЭ 2018 ). 15 января планируется взять кредит в банке на шесть месяцев в размере 1млн. рублей. Условия его возврата таковы:

— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число.

-со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в млн рублей)	1	0,6	0,4	0,3	0,2	0,1	0

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2млн рублей.

Решение: Составим ежемесячные выплаты

01.02. — (1 + )∙1 — 0,6

01.03. — (1 + )∙0,6 — 0,4

01.04 — (1 + )∙0,4 — 0,3

01.05 — (1 + )∙0,3 — 0,2

01.06 — (1 + )∙0,2 — 0,1

01.07 — (1 + )∙0,1 — 0.

Найдем общую сумму выплат:

(1 + )∙(1 + 0,6 + 0,4 + 0,3 + 0,2 + 0,1) — (0,6 + 0,4 + 0,3 + 0,2 + 0,1) =

= (1 + )∙2,6 — 1,6 = + 1

По условию: + 1 < 1,2

< 0,2, r < r < , т.е. ежемесячно долг возрастал на 7%

Ответ: 7%

Задача 5. (досрочное ЕГЭ, 16.04.16) В июле 2016 года планируется взять кредит в размере 4,2 млн рублей. Условия его возврата таковы:

— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;

— с февраля по июнь необходимо выплатить часть долга;

— в июле 2017,2018,2019 годов долг остается равным 4,2 млн рубле

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если долг выплачен полностью и общие выплаты равны 6,1 млн рублей.

Решение. Сумма выплат за первые три года равна:

4,2∙0,01∙r∙3 =0,126∙r

Сумма выплат за последние два года равна 2∙Х.

Так как общие выплаты равны 6,1 млн рублей, то составляем уравнение:

0,126∙r + 2Х= 6,1 (1).

В январе 2020 года долг составит: 4,2 +4,2∙0,01r= 4,2 (1+0,01r). После выплаты суммы Х долг станет равным:

4,2 (1+0,01r) – Х= 4,2t –Х, где t=1+ 0,01r.

В январе 2021 года долг составит (4,2t –Х)∙t. После выплаты суммы Х долг станет равным нулю:

(4,2t –Х)∙t – Х= 0 (2).

Из уравнения (2) выразим Х:

Х= и подставим в равенство (1):

12,6∙(t -1) + 2 = 6,1;

t =1, 1. Значит, r = 10%

Ответ: 10%

Задача 6. (Вариант 6. Лаппо Л.Д. ЕГЭ 2018) Лев взял кредит в банке на срок 40 месяцев. По договору Лев должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется р% этой суммы, затем следует платеж Льва.

а) Ежемесячные выплаты подбираются, таким образом, чтобы долг уменьшался равномерно.

б) Известно, что наибольший платеж Льва был в 25 раз меньше первоначальной суммы долга. Найдите р.

Решение: S — сумма кредита, р — процентная ставка.

Ежемесячный долг перед банком должен уменьшаться равномерно. Этот долг состоит из двух частей: постоянной ежемесячной выплаты и ежемесячной равномерно уменьшающейся выплаты процентов.

Выплата в 1-й месяц: + ∙S и так как он будет наибольшим составим уравнение: ( + ∙S)∙25 = S → + p = 1, p = 1,5

Ответ: 1,5%

Задачи на нахождение количества лет выплаты кредита.

Задача 1. (Тренировочная работа 21) В июле Федор планирует взять в кредит 1,1 млн. рублей. Условия его возврата таковы:

— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года Федор должен выплатить некоторую часть долга.

На какое минимальное минимальное количество лет Федор может взять кредит, чтобы ежегодные выплаты были не более 300тысяч рублей?

Решение:

1) В конце первого года долг составит:

1100000∙1,1 — 300000 = 910000

2) В конце второго года долг составит:

910000∙1,1 — 300000 = 701000

3) В конце третьего года долг составит:

701000∙1,1 — 300000 = 471000

4) В конце четвертого года долг составит:

471000∙1,1 — 300000 = 218210

5) В конце пятого года долг составит:

218210∙1,1 — 300000 0 , т.е. кредит будет погашен за 5 лет.

Ответ: 5 лет

Задачи на оптимизацию.

Задача 1. (Тренировочная работа 16). У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свеклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400ц/га, а на втором — 300ц/га. Урожайность свеклы на первом поле составляет 300ц/га, а на втором — 400ц/га.

Фермер может продавать картофель по цене 5000руб. за центнер, а свеклу — по цене 6000руб. за центнер. Какой наибольший доход может получить фермер?

Решение: Посчитаем доход фермера с 1-го поля:

1) если засеет на нем картофель, урожайность — 400ц/га, 1ц = 5000рублей

с 10 га он соберет 400ц/га∙10га = 4000ц тогда доход:

4000∙5000= 20000000рб = 20млн.

2) если засеет свеклу, урожайность — 300ц/га, 1ц = 6000 рублей

с 10 га он соберет 300∙10=3000ц, тогда доход:

3000∙6000 = 18000000рублей = 18млн.

Теперь посчитаем доход фермера со 2-го поля:

1) если засеет картофель, урожайность — 300ц/га

с 10 га он соберет 300∙10 = 3000 ц, тогда доход

3000∙5000 = 15000000 рублей = 15млн

2) если засеет свеклу, урожайность свеклы — 400ц/га

с 10 га он соберет 400∙10 = 4000ц, доход будет равен:

4000∙6000 = 24000000рублей = 24млн

Отсюда видно, что максимально возможный доход:

20млн + 24млн = 44млн. Ответ: 44млн.

Задача 2 (Тренировочная работа 34). Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег может заработать в сутки на своем отеле предприниматель?

Решение:

Найдем стоимость 1м² стандартного номера = 2000:27=74руб.

Найдем стоимость 1м² номера «люкс» =4000:45=88=88руб.

Так как стоимость 1м2 номера «люкс» дороже, то выгоднее разместить на этой площади больше номеров «люкс», и как можно меньше номеров стандартных. Начнем перебор количества номеров стандартных с наименьшей цифры.

Пусть стандартных номеров будет:

— 0, тогда 981:45≠ (нацело не делится), далее

— 1, тогда 981 — 27 = 954, 954:45≠ также нацело не делится, далее

— 2,тогда 981 — 54 = 927, 927:45≠ также не делится, идем далее

— 3,тогда 981 — 81 = 900, 900:45=20 — номеров «люкс»

Тогда в сутки отель может заработать:

20∙4000+3∙2000=80000+6000=86000 Ответ:86000

Задача 3. (Тренировочная работа 14) В двух областях есть по 250 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0.2 кг. алюминия или 0.1 кг. никеля. Во второй области для добычи х кг. алюминия в день требуется у² человеко-часов труда. Для нужд промышленности можно использовать или алюминий или никель, причем 1 кг. алюминия можно заменить 1 кг. никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?

Решение: 1). В 1 области работают 250 рабочих, каждый работает по 5ч в сутки. За один час один рабочий добывает 0,2кг алюминия, или 0,1кг никеля, т.е в сутки могут добыть:

250∙5∙0.2= 250 кг. алюминия или

250∙5∙0,1=125 кг. никеля. Отсюда видно, что выгоднее будет, если все будут добывать алюминий.

2) Во второй области также работают 250 человек, также работают по 5ч в сутки. Для добычи х кг алюминия требуется х2 человеко-часов, а для добычи у кг никеля требуется у2 человеко-часов, т.е 250 рабочих нужно разделить таким способом, чтобы извлекался корень

==25 кг.(никель) ==25 кг.(алюминий)

250+25+25=300 кг.

Ответ: 300кг

Задача 4. (Тренировочная работа 20) В двух областях есть по 100 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3кг алюминия или 0,1кг никеля. Во второй области для добычи х кг алюминия в день требуется х2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда. Обе области поставляют добытый метал на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Решение: Решение начнем со второй области

100 рабочих нужно разбить так, чтобы извлекался корень, т.е

= = 10кг алюминия

= = 30кг никеля

Теперь 1 область: пусть х — число рабочих добывающих алюминий,

тогда 100-х число рабочих добывающих никель.

х∙10∙0,3 = 3х — кг алюминия

(100 — х)∙10∙0,1 = 100 — х -кг никеля.

Составим уравнение учитывая, что на 2 кг алюминия приходится 1 кг никеля: 10 + 3х = 2(30+100 — х),

10 + 3х = 260 — 2х

5х = 250, х = 50 — рабочих на добычу алюминия, следовательно 50 рабочих на добычу никеля

50∙10∙0,3 = 150 кг алюминия

50∙10∙0,1 = 50 кг никеля.

Тогда 150 + 50 + 10 + 30 = 240кг

Ответ: 240кг.

Задача 5. (Тренировочная работа 47). В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3кг алюминия или 1 кг никеля.

Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Решение: Так как в 1-й шахте добывают больше никеля, то для наибольшей выгоды нужно, чтобы все рабочие добывали никель. Тогда

100∙5∙3 = 1500кг никеля будет добыто в 1-й шахте.

Пусть все 300 рабочих второй вахты добывают алюминий, тогда

300∙5∙3 = 4500кг алюминия будет добыто.

Так как для сплава нужно 2 раза больше алюминия, то рабочих второй шахты нужно распределить на добычу алюминия и никеля с учетом пропорции сплава.

Пусть х — число рабочих добывающих алюминий,

300 — х — число рабочих добывающих никель.

х∙5∙3 = 15х (кг) — алюминий

(300 — х)∙5∙1 = 1500 — 5х (кг) — никель

Составляем уравнение: 15х = 2(1500 — 5х + 1500)

15х = 6000 — 10х

25х = 6000, х = 240 — количество рабочих добывающих алюминий, следовательно 60 рабочих добывают никель.

240∙5∙3 = 3600кг — алюминий

60∙5∙1 = 300кг — никель

Тогда 3600 + 300 + 1500 = 5400 кг. Ответ: 5400кг.

Задача 6. (ЕГЭ — 2017. Резервный день 28.06.2017г). Борис является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.

За каждый час работы на заводе, расположенном в первом городе, Борис платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 200 рублей.

Борису нужно каждую неделю производить 70 единиц товара. Какую наименьшую сумму придется тратить еженедельно на оплату труда рабочих?

Решение: Пусть х — единиц товара 1-го завода,

у — единиц товара 2-го завода.

Тогда, х + у = 70, → х = 70 — у

500х2 + 200у2 = S

500(700 — у)2 + 200у2 = S

700у2 — 70000у + 2450000 = S

700у2 — 70000у + 2450000 — квадратный трехчлен примет наименьшее значение при у = = 50

Тогда S = 700∙502 — 70000∙50 + 2450000 = 700000

Ответ: 700000

Задача 7. (ЕГЭ — 2017. Резервный день). Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.

За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.

Антон готов выделять 900000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Решение: пусть х — на оплату труда рабочих 1-го завода, следовательно,

900000 — х — на оплату труда рабочих 2-го завода.

— часов работы 1-го завода

— часов работы 2-го завода

Количество произведенного товара за неделю = + и нужно найти наибольшее значение этого выражения, для этого найдем производную и найдем нули.

+ ∙(-) =

Решаем уравнение = 0

= 0, , возводив в квадрат с двух сторон получим: 40(900000-х) = 50х, х = 400000.

= = 40 — единиц товара 1 завод

= = 50 — единиц товара 2 завод

40+50=90 единиц. Ответ: 90.

Разные задачи

Задача 1. (Тренировочная работа 13) 15 января планируется взять в кредит в банке на сумму 2,4млн рублей на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно выплатить банку за последние 12 месяцев?

Решение: S = 2400000. По условию, ежемесячный долг перед банком должен уменьшаться равномерно. Этот долг состоит из двух частей: постоянной ежемесячной выплаты и ежемесячной равномерно уменьшающейся выплаты процентов.

; ; ; ; …; — ежемесячный %

Находим размеры выплат:

1-й месяц: + =

2-й месяц: + ∙ =

находим 13-й месяц: а13 = 148 — 2(13 — 1) = 126, т.е. и

24-й месяц: а24 = 148 — 2(24 — 1) = 102S, т.е.

Выплата за последние 12 месяцев: + …+

Вынесем за скобки общий множитель и воспользуемся формулой суммы членов арифметической прогрессии Sn = ∙n

S12= = 1356.

= = 1356000

Ответ: 1356000рублей

Задача 2. (Тренировочная работа 12). В начале 2001 года Алексей приобрел ценную бумагу за 19000руб. В конце каждого года цена бумаги возрастает на 3000 руб. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?

Решение: Продать ценную бумагу нужно в тот момент, когда 10% от стоимости станут составлять не меньше 3000 рублей, что возможно при стоимости бумаги не менее 30000 рублей. это произойдет через (19+3+3+3+3=31) четыре года. И в этот момент 10% от стоимости этой бумаги будут равны 3100 рублей, т.е. больше чем, 3000 рублей. Т.е. надо продать бумагу и положить счет в банке. 2001 + 4 = 2005.

Ответ: 2005 году

2 способ решения: аn =а1+(n-1)d, а=19000

d=3000

Ему будет выгодно отдать деньги в банк в том случае, если 10% от аn превышает d , т.е :

0,1 аn›3000

0,1(19000+3000(n-1))›3000 :0,1

19000+3000n-3000›30000

3000n›14000

n›=4

n=5 т.е бумагу можно продать в течении пятого года(сразу после 4-х лет)

Ответ:2005

Задача 3. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн. рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 20 млн. рублей.

Решение:

Пусть первоначальный вклад составляет S млн. руб., тогда:

В конце первого года на вкладе будет 1,1 S млн. руб.,

В конце второго года на вкладе будет 1,1 S∙1,1=1,21 S млн .руб.,

В конце третьего года на вкладе будет (1,21 S+3)∙1,1=1,331 S+3,3 млн. руб.,

В конце четвертого года на вкладе будет (1,331 S+3,3+3)∙1,1=1,4641S+6,93 млн. руб.,

Далее необходимо решить неравенство:

1,4641S+6,93 > 20

1,4641S > 20-6,93

1,4641S > 13,07

S > 13,07:1,4641

S > 8,93

S = 9 млн.руб. так как по условию S — целое число.

Сделаем проверку:

В конце первого года на вкладе будет 1,1∙9 = 9,9млн. руб.,

В конце второго года на вкладе будет 9,9∙1,1 = 10,89 млн. руб.,

В конце третьего года на вкладе будет (10,89+3)∙1,1 = 15,279 млн. руб.,

В конце четвертого года на вкладе будет (15,279+3)∙1,1 = 20,1069 млн. руб.

Задача 4. (Вариант 19. Лаппо Л.Д. ЕГЭ 2018) В мае 2017 года планируется взять кредит в банке на 6 лет в размере S млн. рублей. Условия его возврата таковы:

— каждый декабрь каждого года долг возрастает на 10%;

— с января по апрель каждого года необходимо выплатить часть долга;

— в мае 2018, 2019 и 2020 годов долг остается равным S млн. рублей;

— выплаты в 2021, 2022 и 2023 годах равны между собой;

— к маю 2023 года долг будет выплачен полностью.

Найдите наибольшее целое S, при котором общая сумма выплат не превысит 13млн. рублей.

Решение: Сумма выплат за первые три года: 0,1S∙3 = 0,3S

Сумма выплат за последние три года: 3∙х = 3х

По условию сумма выплат не превысит 13 млн: 0,3S + 3х ≤ 13 (1)

За последние три года долг станет равным нулю, т.е.

Sp3 — p2x — px — x = 0, p=1,1

S∙1,13 — 1,12x — 1,1x — x = 0

1,331S — 1,21x — 1,1x — x = 0

x = Полученное выражение подставим в (1)

0,3S + 3∙ ≤ 13

S(0,3 + ) ≤ 13, S ≤ 8,63 Ответ: 8 млн.

Источник

25 декабря 2016

В закладки

Обсудить

Жалоба

Сборник экономических задач и задач на оптимизацию по математике

В данном учебном пособии представлен материал по решению практико-ориентированных задач, экономических задач которые были включены на ЕГЭ по математике профильного уровня с 2015 года.

→ Задачи о кредитах.
→ Экономические задачи на оптимизацию.

→ econim-z.doc
→ Другое пособие к этому номеру

Источник

МБОУ Покровская средняя общеобразовательная школа № 1

с УИОП имени И.М. Яковлева

Сборник

экономических задач

и задач на оптимизацию

по математике

Покровск 2019

Начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая практико-ориентированная задача №17, так называемая «банковская» задача. В данных задачах учащимся предлагается ознакомиться с разными схемами выплаты кредита банку со стороны заемщика.

Кредит – это ссуда, предоставленная банком заемщику под определенные проценты за пользование деньгами. Как известно, существует два вида платежей по кредиту: дифференцированный и аннуитетный.

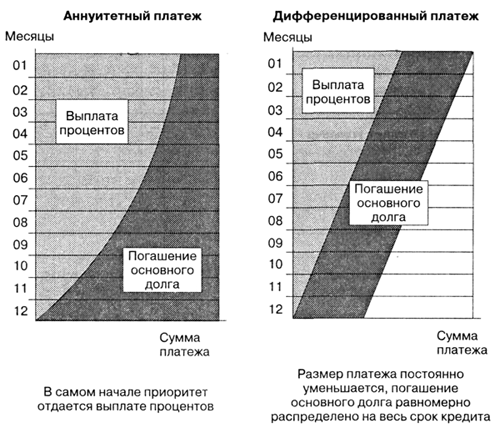
Дифференцированные платежи рассчитываются исходя из того, что сумма погашения основного долга из месяца в месяц одинаковая, а сумма погашения процентов зависит от того, сколько насчитал банк за последний месяц.

При аннуитетных платежах размер ежемесячного платежа остается постоянным на всем периоде кредитования. Ежемесячный платеж рассчитывается как сумма процентов, начисленных на текущий период и суммы идущей на погашения суммы кредита.

Такие виды платежей рассматривались в КИМах по математике ЕГЭ 2015 года. Но кроме этих известных схем выплаты платежей по кредиту существуют и индивидуальные схемы расчета платежей по кредиту. Эти схемы представлены в задании №17 по математике профильного уровня ЕГЭ 2016 года. Кроме задач о кредитах учащимся предлагается в сборниках тренировочных вариантов познакомиться с задачами на выбор оптимального решения.

правила, упрощающие решение

Для упрощения записей и вычислений при решении задач о вкладах, кредитах и оптимизацию производства переходить от «языка процентов» к десятичным дробям. Например, «увеличение величины на 15%» равносильно её умножению на число 1,15 (так как 100% + 15% = 115% = 1,15); «уменьшение величины на 24%» равносильно её умножению на число 0,76 (так как 100% — 24% = 76% = 0,76).
Для правильного выбора способа решения необходимо уметь выделять основные типы задач:

задачи о вкладах;
задачи о кредитах (дифференцированные и аннуитетные)
задачи на оптимизацию

Большинство задач следует сначала решать «в общем виде», вводя следующие обозначения:

S – сумма вклада или кредита;

x – ежемесячный вклад или ежемесячная выплата;

n – срок (количество месяцев или лет);

r% — процентная ставка;

к=(1+ множитель для вычисления процентных начислений ;

числовые данные подставлять только по окончании всех преобразований

ЗАДАЧИ О КРЕДИТАХ

Задача 1

Рассмотрим задачу, которая раскрывает суть понятия «дифференцированный платеж» на простом примере. Допустим, что в банке взят кредит 1200 рублей на 12 месяцев. Причем, каждый платежный период долг сначала возрастает на 10% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же величину меньше долга на конец предыдущего платежного периода. Необходимо ответить на вопросы: Какую сумму нужно вернуть банку за весь платежный период? Какова сумма переплаты?

Рассуждаем. Долг перед банком по состоянию на конец года должен уменьшаться до нуля равномерно, то есть последовательность долгов перед банком такова:

1200;1100; 1000; 900;800; 700; 600; 500; 400; 300; 200;100.

Первого числа каждого месяца долг возрастает на 10%. Тогда последовательность долгов будет такова:

1200∙1.1; 1100∙1.1; 1000∙1.1; 900∙1.1; 800∙1.1; 700∙1.1; 600∙1.1; 500∙1.1; 400∙1.1; 300∙1.1; 200∙1.1;100∙1.1. или 1320; 1210; 1100;990; 880; …110.

Обращаем внимание на то, разница между долговыми суммами равна 110 рублей. Теперь найдем ежемесячные выплаты:

1 месяц- 1320-1100=220

2 месяц- 1210-1000=210

3 месяц- 1100- 900=200

4 месяц- 990- 800=190

5 месяц – 880-700=180 и так далее. И последняя наименьшая выплата равна 110 рублей. Замечаем, что выплаты уменьшаются ежемесячно на 10 рублей.

Такова схема дифференцированного платежа. Далее можно найти сумму всех выплат. Она равна: 220+210+200+…+110 = 1980 (рублей). Таким образом, переплата составляет 65%.

Задача 2

15-го января 2015 года планируется взять кредит в банке на сумму 1.5 млн рублей на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

Какую сумму нужно вернуть банку в течение всего срока кредитования? Какова сумма переплаты?

Решение. Построим математическую модель этой задачи и исследуем ее. Пусть S- сумма кредита. Долг перед банком по состоянию на конец второго года должен уменьшаться до нуля равномерно. Тогда последовательность размеров долга будет иметь вид:

; ; ; …; . Занесем эти данные в таблицу:

Месяц и год

января 2015 г

февраля 2015 г

марта 2015г

апреля 2015г

…

декабря 2016 года

января 2017 года

Долг перед банком

…

Найдем теперь размеры выплат:

1 месяц: — = (24∙1.03 – 23).

2 месяц: — (23∙1.03 – 22).

3 месяц:: — (22∙1.03 – 21).

……………………………………………

24 месяц: — (1∙1.03 – 0).

Найдем сумму всех выплат:

(24∙1.03+23∙1.03+22∙1.03+…+1∙1.03-23-22-21-…-1) =

= (1.03(24+23+22+…+1) –(23+22+21+…+1)) = (1.03∙300–276) = ∙33 =

Чтобы найти численное значение суммы всех выплат, надо подставить S=1,5. Получим, что сумма всех выплат равна 2,0625 миллионов рублей, или 2062500 рублей. Найдем сумму переплаты: 2062500-1500000=562500 (рублей).

Ответ: 2062500 рублей; 562500 рублей.

Задача 3

В июле планируется взять кредит 13 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: каждый январь долг возрастет на 20% по сравнению с концом предыдущего года; в июле каждого года необходимо выплатить часть долга; в конце июля каждого года долг должен быть на одну и ту же сумму меньше долга по сравнению с концом предыдущего года. Чему равна общая сумма выплат после полного погашения кредита , если наименьший годовой платеж равен 1,56 млн рублей?

Решение.

Заметим, что наименьшая выплата в условиях дифференцированного платежа – последняя. Она равна ∙1,2. Составим уравнение: ∙1,2.= 1,56. Отсюда находим, что n = 10. Значит, кредит взят на 10 лет.

Найдем теперь размеры выплат:

1 год: — = (1.2∙10 – 9).

2 год: – (1.2∙9 – 8).

…………….

10 год: (1.2∙1– 0).

Найдем сумму всех выплат: (1,2∙(10+9+…+1) – (9+8+…+1)) =27,3.

Значит, сумма всех выплат равна 27,3 млн рублей.

Задача 4

15-го января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы: 1-го числа каждого месяца долг возрастет на r% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 24% больше суммы, взятой в кредит. Найдите r.

Решение. Пусть S сумма кредита равна , a= 1+0,01r. Долг перед банком должен уменьшаться до нуля равномерно. Тогда последовательность размеров долга будет иметь вид:

; ;….

Найдем выплаты:

1 месяц: — = (15∙а – 14).

2 месяц: — (14∙а – 13).

……………………………………………

15 месяц:

Найдем сумму всех выплат:

(а(15+14+13+…+1) –(14+13+12+…+1)) = (а∙120–105) = S(8a -7).

По условию общая сумма выплат после полного погашения кредита на 24% больше суммы, взятой в кредит. Значит, S(8a -7) =1,24 S. Решая это уравнение, находим а=1,03. Так как a= 1+0,01r, то r = 3%.

Ответ: 3%

Рассмотрим задачу, которая раскрывает суть понятия «аннуитетный платеж».

В общем виде задача формулируется так: 31 декабря 2014 года Андрей взял в банке S рублей в кредит под a процентов годовых. Схема выплаты кредита следующая: 1 числа каждого следующего года банк начисляет a процентов на оставшуюся сумму долга. Затем Андрей переводит в банк сумму X ежегодного платежа (транш). Весь долг Андрей должен выплатить за n лет, то есть за n равных платежей. Необходимо найти одну из неизвестных величин: S, a, X, или n.

Решим одну из таких задач.

Задача 5. Нахождение количества лет выплаты кредита

Максим хочет взять в банке кредит 1,5 миллиона рублей. Погашение кредита происходит раз в год равными платежами (кроме, может быть, последней) после начисления процентов. Процентная ставка 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были не более 350 тысяч рублей?

Решение.

В конце первого года долг составит:

1500000 ∙ 1,1 – 350000 =1300000 (р.)

2) В конце второго года долг составит:

1300000 ∙ 1,1 – 350000 = 1080000 (р.)

В конце третьего года долг составит:

1080000 ∙ 1,1 – 350000 = 838000 (р.)

4)В конце четвертого года долг составит:

838000 ∙ 1,1 – 350000 = 571800 (р.)

5)В конце пятого года долг составит:

571800 ∙ 1,1 – 350000 = 278980 (р.)

6) В конце шестого года долг составит:

278900 ∙ 1,1 =306878 (р.)

Эта сумма менее 350000 руб. Значит, кредит будет погашен за 6 лет.

Ответ: 6 лет

Задача 6. Вычисление процентной ставки по кредиту.

31 декабря 2014 года Валерий взял в банке 1000000 рублей в кредит. Схема выплаты кредита следующая. 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Валерий переводит в банк очередной транш. Валерий выплатил кредит за два транша, то есть за два года. В первый раз Валерий перевел в банк 660000 рублей, во второй раз – 484000 рублей. Под какой процент банк выдал кредит Валерию?

Решение. Пусть а — процентная ставка по кредиту.

1)В конце первого года долг составит:

1000000 ∙ (1 + 0,01∙ а) – 660000 = 340000 + 10000∙а

2) В конце второго года долг составит:

(340000 + 10000∙а) ∙ (1 + 0,01∙а) – 484000.

По условию задачи кредит будет погашен за два года. Составляем уравнение: (340000 + 10000∙а) ∙ (1 + 0,01∙а) – 484000 = 0;

+ 134∙а – 1440 = 0

Решая уравнение, получаем, что а = 10.

Ответ: 10%

Задача 7. Нахождение суммы кредита

31 декабря 2014 года Максим взял в банке некоторую сумму денег в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами, то есть за 4 года?

Решение. Пусть S – сумма кредита.

1)В конце первого года долг составит: (1,1х – 2928200) рублей

2) В конце второго года долг (в рублях) составит:

(1,1х – 2928200)∙1,1 – 2928200 = 1,21х – 3221020 – 2928200 = 1,21х – 6149220

3) В конце третьего года долг (в рублях) составит:

(1,21х – 6149220)∙1,1 – 2928200 = 1,331х – 6764142 – 2928200 =

=1,331х – 9692342

4) В конце четвертого года долг (в рублях) составит 2928200 рублей:

(1,331х – 9692342)∙1,1 = 2928200;

1,4641х – 10661576 = 2928200;

1,4641х = 13589776;

х = 9281999,8.

Значит, сумма кредита равна 9282000 рублей.

Ответ: 9282000 рублей.

Задача 8. Нахождение ежегодного транша

31 декабря 2014 года Роман взял в банке 8599000 рублей в кредит под 14% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга(то есть увеличивает долг на 14%), затем Роман переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Роман выплатил долг тремя равными платежами (то есть за 3 года)?

Решение.

1)В конце первого года долг составит:

8599000∙1,14 – Х = 9802860 – Х

2) В конце второго года долг составит:

(9802860 — Х)∙1,14 – Х=11175260 – 2,14∙Х

3) В конце третьего года долг (в рублях) составит:

(11175260 – 2,14∙Х) ∙1,14 – Х=12739796 – 3,4396∙Х.

Составим уравнение:

12739796 – 3,4396∙Х= 0

Х=3703860 рублей

Ответ: ежегодный транш составит 3703860 рублей.

Задача 9

В июле 2016 года планируется взять кредит на 4 года в размере S млн рублей, где S – целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года

— с февраля по июнь каждого года необходимо выплатить часть долга

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:

Месяц, год

Июль

2016

Июль

2017

Июль

2018

Июль

2019

Июль 2020

долг

0.9S

0.7S

0.4S

Найдите наименьшее S, при котором общая сумма выплат будет больше 20 млн рублей.

Решение.

Долг перед банком ( в млн рублей) должен уменьшаться до нуля на июль каждого года в соответствии с данной таблицей:

S; 0.9S; 0.7S; 0.4S; 0.

По условию, в январе каждого года долг увеличивается на 30%. Значит, долг в январе каждого года равен:

Месяц, год	Январь 2017	Январь 2018	Январь 2019	Январь 2020	Январь 2021
Долг	1.3S	1.3∙0.9∙S=1.17S	1.3∙0.7∙S=0.91S	1.3∙0.4∙S=0.52S	0

Найдем теперь выплаты с февраля по июнь каждого года:

1) 1.3∙S – 0.9∙S = 0.4∙S.

2) 1.17∙S – 0.7∙S = 0.47∙S

3) 0.91∙S – 0.4S = 0.51∙S

4) 0.52∙S – 0 = 0.52∙S

Найдем сумму всех выплат: 0.4∙S+0.47∙S+0.51∙S+0.52∙S=1.9∙S

Общая сумма выплат должна быть больше 20 млн рублей:

1.9∙S 20; S10

Наименьшее целое решение этого неравенства – число 11. Значит, искомый размер кредита – 11 млн рублей. Ответ: 11 млн рублей

Задача 10 (основная волна, 06.06.16)

15-го января планируется взять кредит в банке на четыре месяца в размере 2 млн руб. Условия его возврата таковы:

— 1-го числа каждого месяца долг увеличивается на r % по сравнению с концом предыдущего месяца, где r – целое число;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:

Дата

15.01

15.02

15.03

15.04

15.05

Долг

(в млн р.)

1.6

0.5

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 2,5 млн р.

Решение.

Долг перед банком ( в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:

2; 1.6; 1; 0.5; 0.

Обозначим k = 1+ Тогда долг на 1-е число каждого месяца равен:

2k; 1.6 k; 1k; 0.5k; 0.

Найдем теперь выплаты со 2-е по 14-е число каждого месяца:

2k-1.6; 1.6k-1; k-0.5; 0.5k.

Общая сумма выплат составляет:

(2k-1.6) +( 1.6k-1) + ( k-0.5) + 0.5k = 5.1k – 3.1

По условию, общая сумма выплат будет меньше 2.5 млн руб. Значит, составляем неравенство:

5.1k – 3.1≤ 2.5.Подставляя вместо k выражение 1+ и решая неравенство, получим, что r ≤ 9. Наибольшее целое решение этого неравенства – число 9. Значит, искомое число процентов — 9%.

Ответ: 9%

Задача 11

В июле 2016 года планируется взять кредит в банке на 5 лет в размере S тысяч рублей. Условия его возврата таковы:

— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле 2017, 2018 и 2019 годов долг остается неизменно равным S тысяч рублей;

— выплаты в 2020 и 2021 годах равны по 360 тыс рублей;

— к июлю 2021 года долг будет выплачен полностью.

Найдите общую сумму выплат за 5 лет.

Решение.

Так как в июле 2017, 2018, и 2019 годов долг перед банком не меняется, то ежегодные выплаты равны по 0,2S тысяч рублей.

В январе 2020 года долг равен 1,2S, а в июле – (1,2S – 360) тысяч рублей.

В январе 2021 года долг равен 1,2(1,2S – 360) = 1,44S – 432;

а в июле – (1,44S – 792).

Так как к июлю 2021 года долг будет выплачен полностью, то составим уравнение:

1,44S – 792 = 0; S = 550.

Найдем первые три выплаты: 0,2∙550 = 110 (тыс руб).

Общая сумма выплат составляет: 3∙ 110 + 2∙360 = 1050 (тыс руб)

Ответ: 1050 тысяч рублей

Задача 12 (из тренировочных работ СТАТГРАД)

Планируется выдать льготный кредит (целое число млн р.) на 5 лет. В середине каждого года долг заемщика возрастает на 20% по сравнению с началом года. В конце первого, второго и третьего годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заемщик выплачивает одинаковые суммы, погашая долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат превысит 10 млн р.?

Решение.

Пусть S – сумма кредита, Х – сумма выплат в конце 4-го и 5-го годов. В конце первого, второго и третьего годов заемщик выплачивает только проценты по кредиту. Значит, ежегодные выплаты равны по 0,2∙S тысяч рублей. А выплаты за три первых года равны 3∙0,2S=0,6∙ S. Выплаты за 5 лет равны (0,6∙ S +2∙Х). По условию задачи составляем неравенство: 0,6∙ S +2∙Х≥10 (1).

Рассуждаем далее. В начале 4 года долг составит 1,2∙ S. После выплаты в конце 4 года долг составит

(1,2∙ S- Х). В начале 5-го года долг составит (1,2∙ S- Х)∙1,2, а после выплаты долг станет равным нулю, то есть (1,2∙ S- Х)∙1,2 – Х=0.

Выразим из этого уравнения Х= и подставим в неравенство (1):

0,6∙ S +2∙ ≥10;

S ≥ 5.

Наименьшее целое решение этого неравенства – число 6. Значит, наименьший размер кредита равен 6 млн рублей.

Ответ: 6 млн р.

Задача 13

В июле 2016 года планируется взять кредит в размере 4,2 млн рублей. Условия его возврата таковы:

— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;

— с февраля по июнь необходимо выплатить часть долга;

— в июле 2017,2018,2019 годов долг остается равным 4,2 млн рубле

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если долг выплачен полностью и общие выплаты равны 6,1 млн рублей.

Решение.

Сумма выплат за первые три года равна:

4,2∙0,01∙r∙3 =0,126∙r

Сумма выплат за последние два года равна 2∙Х.

Так как общие выплаты равны 6,1 млн рублей, то составляем уравнение:

0,126∙r + 2Х= 6,1 (1).

В январе 2020 года долг составит: 4,2 +4,2∙0,01r= 4,2 (1+0,01r). После выплаты суммы Х долг станет равным:

4,2 (1+0,01r) – Х= 4,2t –Х, где t=1+ 0,01r.

В январе 2021 года долг составит (4,2t –Х)∙t

После выплаты суммы Х долг станет равным нулю:

(4,2t –Х)∙t – Х= 0 (2).

Из уравнения (2) выразим Х:

Х= и подставим в равенство (1):

12,6∙(t -1) + 2 = 6,1;

t =1, 1. Значит, r = 10%

Ответ: 10%

Задача 14

Алексей приобрел ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?

Решение.

Продать ценную бумагу нужно в том момент, когда 10% от стоимости станут составлять не меньше 2 тыс. рублей, что возможно при стоимости бумаги не менее 20 тыс. рублей. Это произойдет через семь лет после покупки ценной бумаги, когда ее стоимость будет равна 21 тыс рублей. И в этот момент 10% от стоимости этой бумаги будут равны 2100 рублей, то есть больше, чем 2000 р. Значит, надо продать бумагу, а вырученные деньги положить на счет в банке.

Таким образом, ценную бумагу нужно продать в течение восьмого года. Ответ: В течение 8 года

Задача 15

Производство x тыс. единиц продукции обходится в q = 0,5 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px – q). При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?

Решение. Прибыль (в млн рублей) за один год выражается величиной

px – (0,5 + x + 7) = -0,5+(p-1)x -7

Это выражение является квадратным трехчленом, оно достигает своего наибольшего значения при x = p-1. Прибыль за три года составит не менее 75 млн рублей, если Решая это неравенство, получим, что p ≥ 9 и p ≤ -7. Так как цена продукции не может быть отрицательной, то p ≥ 9. Таким образом, искомая наименьшая цена составляет 9 тыс. р.

Ответ: 9 тыс. рублей.

ЭКОНОМИЧЕСКИЕ ЗАДАЧИ НА ОПТИМИЗАЦИЮ

Задача 1

В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Решение: 1-й способ – с помощью составления опорной линейной функции.

Ознакомимся с решением экстремальных задач по теме «Линейная функция». Решение этих задач сводится к нахождению экстремума линейной функции

у = кх + в, где к и в – постоянные. Если эту функцию рассматривать на отрезке

[; ], то она будет иметь на нем наибольшее и наименьшее значение. При к 0 наименьшее значение у принимает в точке х = , а наибольшее – в точке х = , при к 0 функция у в точке х = принимает наибольшее значение, а в точке х = — наименьшее. Решим задачу.

Пусть х рабочих в 1 шахте добывают алюминий ежедневно, тогда (100-х) рабочих добывают никель. Тогда количество добытого алюминия равно (5х) кг, количество добытого никеля – 15(100-х) кг.

Пусть у рабочих во 2 шахте добывают алюминий ежедневно, (300-у) рабочих добывают никель. Тогда количество добытого алюминия равно (15у) кг, количество добытого никеля – 5(300-у) кг.

Всего количество добытого алюминия (5х+15у);а количество добытого никеля — 15(100-х)+ 5(300-у)=1500-15х+1500-5у=3000-15х-5у.

Функция сплава: F(x) = (5х+15у) + (3000-15х-5у); F(x) = -10х+10у + 3000;

Учтем условие, при котором производится сплав алюминия и никеля: 2 кг алюминия и 1 кг никеля. Тогда 5х+15у=2(3000-15х-5у). Отсюда у = -1,4х+600. Поставим это выражение в функцию сплава: F(x) = -10х+10(-1,4х+600) + 3000;

F(x) = -24х +5400. Эта линейная функция является убывающей. Наибольшее значение она принимает при х=0. Значит, F(100)=5400.

Ответ:5400

2-й способ – с помощью логических рассуждений и составления уравнения.

Так как в 1 шахте добывают больше никеля, то для наибольшей выгоды логично допустить, чтобы все рабочие в этой шахте добывали никель. Тогда в 1 шахте будет добыто 1500 кг никеля. Во 2 шахте больше добывают алюминия. Пусть все 300 рабочих добывают алюминий. Тогда алюминия будет добыто 4500 кг. Для сплава нужно алюминия в 2 раза больше, чем никеля. Значит, на 1500 кг никеля нужно 3000 кг алюминия. А у нас алюминия больше. Рассуждаем дальше. Значит, рабочих 2-й шахты нужно перераспределить на добычу не только алюминия, но и на добычу никеля с учетом пропорции сплава. Пусть х рабочих 2 шахты добывают алюминий, тогда (300-х) рабочих добывают никель. Составим уравнение: 5 ∙3∙ х =2∙(5∙ (300-х) + 1500); 15х = 6000-10х; х = 240.

Найдем у: у=300-240=60.Значит, 240 рабочих 2-й шахты должны добывать алюминий, 60 рабочих добывать никель. Тогда алюминия будет добыто

240∙ 5∙3 = 3600 (кг), никеля 1500 + 60∙5=1800(кг). Всего 3600+1800=5400 (кг). Ответ: 5400 кг

3-й способ – методом перебора. Так как в 1 шахте добывают больше никеля, то пусть все рабочие добывают никель. Тогда в 1 шахте будет добыто 1500 кг никеля. Во 2 шахте больше добывают алюминия. Пусть все 300 рабочих добывают алюминий. Тогда алюминия будет добыто 4500 кг. Для сплава нужно алюминия в 2 раза больше, чем никеля. Значит, на 1500 кг никеля нужно 3000 кг алюминия. А у нас алюминия больше. Что делать? Значит, рабочих 2 шахты нужно перераспределить на добычу не только алюминия, но и на добычу никеля. Применим метод перебора.

Допустим, что 10 рабочих 2 шахты добывают никель, а 290 рабочих – алюминий. Тогда алюминия будет добыто всего 290∙5∙3= 4350 (кг), а никеля – 1500 + 10∙5= 1550 (кг). Замечаем, что данные не удовлетворяют пропорции 1: 2. Значит, необходимо увеличить количество рабочих, добывающих никель. Допустим, что 20 рабочих 2 шахты добывают никель, а 280 рабочих – алюминий. Тогда алюминия будет добыто всего 280∙5∙3= 4200 (кг), а никеля – 1500 + 20∙5= 1600 (кг). Замечаем, что данные не удовлетворяют пропорции 1: 2. Значит, необходимо опять увеличить количество рабочих, добывающих никель. Допустим, что 40 рабочих 2 шахты добывают никель, а 260 рабочих – алюминий. Тогда алюминия будет добыто всего 260∙5∙3= 3900 (кг), а никеля – 1500 + 40∙5= 1700 (кг). Замечаем, что данные не удовлетворяют пропорции 1: 2. Значит, необходимо опять увеличить количество рабочих, добывающих никель. Допустим, что 60 рабочих 2 шахты добывают никель, а 240 рабочих – алюминий. Тогда алюминия будет добыто всего 240∙5∙3= 3600 (кг), а никеля – 1500 + 60∙5= 1800 (кг). Замечаем, что данные удовлетворяют пропорции 1: 2, то есть на 1 часть никеля приходится 2 части алюминия: 1800: 3600. Итак, всего будет добыто 3600+1800=5400 (кг) алюминия и никеля. А количество изделий из сплава тогда будет равно 1800 штук.

Ответ: 5400 кг.

Задача 2

Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

Решение:

1-й способ – с помощью логики и арифметических действий.

Найдем стоимость 1номера стандартного: 2000:21=95 (рублей).

Найдем стоимость 1номера «люкс»: 4500: 49 =91 (рублей).

Так как стоимость 1 стандартного номера дороже, то выгоднее разместить на этой площади больше номеров стандартных, и как можно меньше номеров «люкс». Начнем перебор количества номеров «люкс» с наименьшей цифры. Пусть номеров «люкс» будет 0. Тогда число 1099 не делится нацело на 21. Далее. Допустим, что номеров «люкс» будет 1. Тогда: 1099- 49=1050;

1050: 21 = 50 (номеров стандартных). Значит, на площади 1050можно разместить 50 стандартных номеров. Тогда в сутки отель может заработать: 50∙ 2000 + 1∙ 4500=104500 (р.). Ответ: 104500 рублей.

2-й способ – с помощью составления опорной линейной функции.

Пусть х – количество стандартных номеров, у- количество номеров «люкс». Они занимают площадь 21х+49у. Составим равенство: 21х+49у = 1099. Выразим из этого равенства у = .

Составим функцию заработанных денег: S(x, y) =2000∙x + 4500∙y. Далее подставим в эту функцию выражение для у. Получим S(x) =71 ∙х + 4500∙22. Это возрастающая линейная функция. Свое наибольшее значение она принимает при наибольшем значении х и наименьшем значении у. По условию х и у – натуральные числа. Значит, у=1 (это наименьшее натуральное число) и х=50. Значит, S (50, 1) = 2000∙50 + 4500∙ 1=104500.

Ответ: 104500 рублей.

Задача 3

На каждом из двух комбинатов работают по 100 человек. На первом комбинате один рабочий изготавливает за смену 3 детали А или 1 деталь В.На втором комбинате для изготовления t деталей ( и А, и В) требуется t²человеко-смен. Оба эти комбината поставляют детали на комбинат , из которых собирают изделие , для изготовления которого нужна 1 деталь А и 3 детали В. При этом комбинаты договариваются изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий может собрать комбинат при таких условиях?

Решение. Пусть на первом комбинате х человек изготавливают деталь А, по 3 штуки за смену. Значит, всего 3х деталей А. Тогда (100 –х) человек изготавливают деталь В, по 1 штуке за смену. Всего (100-х) деталей В.

Пусть на втором комбинате изготавливают a деталей А и b деталей В. Тогда на изготовление деталей А требуется a² человеко-смен, а для изготовления детали В b² человеко-смен. По условию a² + b²=100, так как в одну смену трудятся все 100 рабочих второго комбината. Сведем все данные в таблицу:

Комбинат	Количество деталей А	Количество деталей В
1-й комбинат	3х	100-х
2-й комбинат	a	b
Всего	3х +a	100 – х +b

Чтобы собрать наибольшее количество изделий, нужно соблюдать условие:

1 деталь А и 3 детали В. В противном случае лишние детали будут залеживаться, из них нельзя будет собрать изделие, пока не будет готова другая деталь. Значит, 3(3х +a) = 100 – х +b; 10х= 100 + b – 3a. (1)

В каждом изделии содержится 1 деталь А и 3 детали В. Значит, общее количество изделий равно числу изделий А.

Так как a и b – целые числа и a² + b²=100, то возможны следующие случаи:

a=0, b=10. Тогда из равенства (1) х=11 и 3х +a=3∙11 +0=33.
a=10, b=0. Тогда из равенства (1) х=7 и 3х +a=3∙7 +10=31.
a=6, b=8. Тогда х=9 и 3х +a=33.
a=8, b=6. Тогда х=8,2 – не является целым числом.

Значит, наибольшее количество изделий равно 33. Ответ: 33

Самостоятельная работа

Экономические задачи ЕГЭ

1. (Статград, январь 2015). В банк помещена сумма 3 900 000 рублей под 50% годовых. В конце каждого из первых четырёх лет хранения, после начисления процентов вкладчик дополнительно вносил на счёт одну и ту же сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%.. Какую сумму вкладчик добавлял к вкладу?

Ответ: 210 000.

2. (Статград, январь 2015). Банк под определённый процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счёта. Банк увеличил процент годовых на 40%. К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков новый процент годовых?

Ответ: 60%.

3. (Подготовка к ЕГЭ по математике 2016г. И.В. Семёнов, С.А. Шестаков, А.С. Трепалин.)

31 декабря Сергей взял в банке 4 382 000 рублей в кредит под 16% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 16%), затем Сергей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Сергей выплатил долг двумя тремя равными платежами (то есть за 3 года)?

Ответ: 1 951 120.

4. (Статград, январь 2015). 31 декабря Ваня взял в банке 5 005 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Ваня переводит в банк платёж. Весь долг Ваня выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

Ответ: 576 000.

5. (И.В.Ященко. ЕГЭ 2015 МАТЕМАТИКА типовые экзаменационные варианты.)

1 января 2015 года Павел Витальевич взял в банке 1000000 рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк платёж. На какое минимальное количество месяцев Павел Виталье-вич может взять кредит, чтобы ежемесячные выплаты были не более 125000 рублей?

Ответ. 9

6. (Статград, март 2015). Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит.

Найдите r .

Ответ: 2.

7. (Статград, апрель 2015). Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

Ответ: 822 тыс. рублей.

8. (Экзамен 2016г.)

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:

— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.

Ответ:7

9. (Статград Февраль 2015).

Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Ответ: 8.

10. (Высшая школа экономики. Задачи экономических олимпиад. Рациональная аренда.)

Молодой преподаватель экономики снимает квартиру в городе М. и в начале каждого месяца платит за аренду 26 000 руб. Деньги он снимает со своего счета в банке. Ежемесячно на сумму остатка на счете банк начисляет процент по ставке r %. Придя в начале очередного месяца за деньгами, хозяин квартиры предложил молодому экономисту следующую сделку: если он оплатит аренду сразу за два месяца вперед, то арендная плата за каждый из этих двух месяцев будет снижена до 25 500 руб. Если предложение будет принято, то в следующий раз хозяин придет за деньгами через два месяца и вновь потребует 26 000 руб. При каких значениях r арендатору стоит принимать это предложение?

Ответ: при ставке менее 4% предложение стоит принять.

11.(ЕГЭ 2016. Математика. 50 вариантов типовых тестовых заданий / И.В. Ященко, и др.) Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

Ответ: 104 500 рублей в сутки

Большую часть своих усилий человек тратит на поиск наилучшего, т.е. оптимального решения поставленной задачи. Задачи подобного рода носят общее название – экономические задачи на оптимизацию или экстремальные задачи. Эти задачи тесно связаны с практической деятельностью человека. Как добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставятся вопросы, над которыми приходится думать каждому члену общества. Экстремальные задачи с достаточной полнотой закладывают в сознание учащихся понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучшими. Решая задачи указанного типа, учащиеся видят, с одной стороны, абстрактный характер математических понятий, с другой – большую и эффективную их применимость к решению практических, жизненных задач. Такая постановка экстремальных задач способствует расширению сферы приложений учебного материала, повышает роль этих задач в осуществлении глубокой цели математического образования школьников – обучать приложению математики в различных областях человеческой деятельности. Экстремальные задачи помогают школьнику ознакомиться с некоторыми идеями и прикладными методами курса математики, которые часто применяются в трудовой деятельности, в познании окружающей действительности. Решение экстремальных задач способствует углублению и обогащению математических знаний учащихся. Через задачи они знакомятся с экстремальными свойствами изучаемых функций.

Источник

Муниципальное автономное образовательное учреждение

«Средняя образовательная школа № 37»

Ассоциация учителей математики Республики Бурятия

Байкальский образовательный центр «Эврика»

ПРАКТИКО-ОРИЕНТИРОВАННЫЕ ЗАДАЧИ

В ЗАДАНИЯХ ЕГЭ ПО МАТЕМАТИКЕ

Сборник

экономических задач и задач на оптимизацию

по математике

Улан-Удэ

Издательство Бурятского госуниверситета

017

УДК 371.275:51 (075.3)

ББК 74.202.812.24

П 691

Рецензент

Н. Н. Алексеева

канд. пед. наук, зав. кафедрой

«Развитие образовательных систем» ГАУ ДПО РБ БРИОП

Автор-составитель

Г.М. Конева

Учитель высшей категории, «Отличник просвещения РФ»,

Победитель Конкурса лучших учителей России.

П 691 Практико-ориентированные задачи в заданиях ЕГЭ по математике: сборник экономических задач и задач на оптимизацию по математике / сост. Г. М. Конева. – Улан-Удэ: Издательство Бурятского государственного университета, 2017. – 26 с.

Пособие ориентировано на подготовку учащихся старшей школы к успешной сдаче ЕГЭ по математике профильного уровня. В данном учебном пособии представлен материал по решению практико-ориентированных задач, экономических задач которые были включены на ЕГЭ по математике профильного уровня с 2015 года. Задачи ориентированы на развитие у учащихся умений строить математические модели экономических ситуаций, исследовать эти модели, получать и интерпретировать выводы.

Пособие предназначено для учащихся старшей школы и учителей математики.

УДК 371.275:51 (075.3)

ББК 74.202.812.24

П. Л. Чебышев

ВСТУПЛЕНИЕ

ЗАДАЧИ О КРЕДИТАХ

Задача 1

1200;1100; 1000; 900;800; 700; 600; 500; 400; 300; 200;100.

Первого числа каждого месяца долг возрастает на 10%. Тогда последовательность долгов будет такова:

1200∙1.1; 1100∙1.1; 1000∙1.1; 900∙1.1; 800∙1.1; 700∙1.1; 600∙1.1; 500∙1.1; 400∙1.1; 300∙1.1; 200∙1.1;100∙1.1. или 1320; 1210; 1100;990; 880; …110.

Обращаем внимание на то, разница между долговыми суммами равна 110 рублей. Теперь найдем ежемесячные выплаты:

1 месяц- 1320-1100=220

2 месяц- 1210-1000=210

3 месяц- 1100- 900=200

4 месяц- 990- 800=190

Задача 2

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

Какую сумму нужно вернуть банку в течение всего срока кредитования? Какова сумма переплаты?

Решение. Построим математическую модель этой задачи и исследуем ее. Пусть S— сумма кредита. Долг перед банком по состоянию на конец второго года должен уменьшаться до нуля равномерно. Тогда последовательность размеров долга будет иметь вид:

; ; ; …; . Занесем эти данные в таблицу:

Месяц и год

января 2015 г

февраля 2015 г

марта 2015г

апреля 2015г

…

декабря 2016 года

января 2017 года

Долг перед банком

…

Найдем теперь размеры выплат:

1 месяц: — = (24∙1.03 – 23).

2 месяц: — (23∙1.03 – 22).

3 месяц:: — (22∙1.03 – 21).

……………………………………………

24 месяц: — (1∙1.03 – 0).

Найдем сумму всех выплат:

(24∙1.03+23∙1.03+22∙1.03+…+1∙1.03-23-22-21-…-1) =

= (1.03(24+23+22+…+1) –(23+22+21+…+1)) = (1.03∙300–276) = ∙33 =

Ответ: 2062500 рублей; 562500 рублей.

Задача 3

Решение.

Найдем теперь размеры выплат:

1 год: — = (1.2∙10 – 9).

2 год: – (1.2∙9 – 8).

…………….

10 год: (1.2∙1– 0).

Найдем сумму всех выплат: (1,2∙(10+9+…+1) – (9+8+…+1)) =27,3.

Значит, сумма всех выплат равна 27,3 млн рублей.

Задача 4

; ;….

Найдем выплаты:

1 месяц: — = (15∙а – 14).

2 месяц: — (14∙а – 13).

……………………………………………

15 месяц:

Найдем сумму всех выплат:

(а(15+14+13+…+1) –(14+13+12+…+1)) = (а∙120–105) = S(8a -7).

Ответ: 3%

Рассмотрим задачу, которая раскрывает суть понятия «аннуитетный платеж».

Решим одну из таких задач.

Задача 5. Нахождение количества лет выплаты кредита

Решение.

В конце первого года долг составит:

1500000 ∙ 1,1 – 350000 =1300000 (р.)

2) В конце второго года долг составит:

1300000 ∙ 1,1 – 350000 = 1080000 (р.)

В конце третьего года долг составит:

1080000 ∙ 1,1 – 350000 = 838000 (р.)

4)В конце четвертого года долг составит:

838000 ∙ 1,1 – 350000 = 571800 (р.)

5)В конце пятого года долг составит:

571800 ∙ 1,1 – 350000 = 278980 (р.)

6) В конце шестого года долг составит:

278900 ∙ 1,1 =306878 (р.)

Эта сумма менее 350000 руб. Значит, кредит будет погашен за 6 лет.

Ответ: 6 лет

Задача 6. Вычисление процентной ставки по кредиту.

Решение. Пусть а — процентная ставка по кредиту.

1)В конце первого года долг составит:

1000000 ∙ (1 + 0,01∙ а) – 660000 = 340000 + 10000∙а

2) В конце второго года долг составит:

(340000 + 10000∙а) ∙ (1 + 0,01∙а) – 484000.

По условию задачи кредит будет погашен за два года. Составляем уравнение: (340000 + 10000∙а) ∙ (1 + 0,01∙а) – 484000 = 0;

+ 134∙а – 1440 = 0

Решая уравнение, получаем, что а = 10.

Ответ: 10%

Задача 7. Нахождение суммы кредита

Решение. Пусть S – сумма кредита.

1)В конце первого года долг составит: (1,1х – 2928200) рублей

2) В конце второго года долг (в рублях) составит:

(1,1х – 2928200)∙1,1 – 2928200 = 1,21х – 3221020 – 2928200 = 1,21х – 6149220

3) В конце третьего года долг (в рублях) составит:

(1,21х – 6149220)∙1,1 – 2928200 = 1,331х – 6764142 – 2928200 =

=1,331х – 9692342

4) В конце четвертого года долг (в рублях) составит 2928200 рублей:

(1,331х – 9692342)∙1,1 = 2928200;

1,4641х – 10661576 = 2928200;

1,4641х = 13589776;

х = 9281999,8.

Значит, сумма кредита равна 9282000 рублей.

Ответ: 9282000 рублей.

Задача 8. Нахождение ежегодного транша

Решение.

1)В конце первого года долг составит:

8599000∙1,14 – Х = 9802860 – Х

2) В конце второго года долг составит:

(9802860 — Х)∙1,14 – Х=11175260 – 2,14∙Х

3) В конце третьего года долг (в рублях) составит:

(11175260 – 2,14∙Х) ∙1,14 – Х=12739796 – 3,4396∙Х.

Составим уравнение:

12739796 – 3,4396∙Х= 0

Х=3703860 рублей

Ответ: ежегодный транш составит 3703860 рублей.

Задача 9 (основная волна, 06.06.16, вариант 446)

— каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года

— с февраля по июнь каждого года необходимо выплатить часть долга

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:

Месяц, год

Июль

2016

Июль

2017

Июль

2018

Июль

2019

Июль 2020

долг

0.9S

0.7S

0.4S

Найдите наименьшее S, при котором общая сумма выплат будет больше 20 млн рублей.

Решение.

S; 0.9S; 0.7S; 0.4S; 0.

По условию, в январе каждого года долг увеличивается на 30%. Значит, долг в январе каждого года равен:

Месяц, год	Январь 2017	Январь 2018	Январь 2019	Январь 2020	Январь 2021
Долг	1.3S	1.3∙0.9∙S=1.17S	1.3∙0.7∙S=0.91S	1.3∙0.4∙S=0.52S	0

Найдем теперь выплаты с февраля по июнь каждого года:

1) 1.3∙S – 0.9∙S = 0.4∙S.

2) 1.17∙S – 0.7∙S = 0.47∙S

3) 0.91∙S – 0.4S = 0.51∙S

4) 0.52∙S – 0 = 0.52∙S

Найдем сумму всех выплат: 0.4∙S+0.47∙S+0.51∙S+0.52∙S=1.9∙S

Общая сумма выплат должна быть больше 20 млн рублей:

1.9∙S 20; S10

Задача 10 (основная волна, 06.06.16)

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:

Дата

15.01

15.02

15.03

15.04

15.05

Долг

(в млн р.)

1.6

0.5

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 2,5 млн р.

Решение.

Долг перед банком ( в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:

2; 1.6; 1; 0.5; 0.

Обозначим k = 1+ Тогда долг на 1-е число каждого месяца равен:

2k; 1.6 k; 1k; 0.5k; 0.

Найдем теперь выплаты со 2-е по 14-е число каждого месяца:

2k-1.6; 1.6k-1; k-0.5; 0.5k.

Общая сумма выплат составляет:

(2k-1.6) +( 1.6k-1) + ( k-0.5) + 0.5k = 5.1k – 3.1

По условию, общая сумма выплат будет меньше 2.5 млн руб. Значит, составляем неравенство:

Ответ: 9%

Задача 11 (основная волна, 06.06.16)

— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле 2017, 2018 и 2019 годов долг остается неизменно равным S тысяч рублей;

— выплаты в 2020 и 2021 годах равны по 360 тыс рублей;

— к июлю 2021 года долг будет выплачен полностью.

Найдите общую сумму выплат за 5 лет.

Решение.

Так как в июле 2017, 2018, и 2019 годов долг перед банком не меняется, то ежегодные выплаты равны по 0,2S тысяч рублей.

В январе 2020 года долг равен 1,2S, а в июле – (1,2S – 360) тысяч рублей.

В январе 2021 года долг равен 1,2(1,2S – 360) = 1,44S – 432;

а в июле – (1,44S – 792).

Так как к июлю 2021 года долг будет выплачен полностью, то составим уравнение:

1,44S – 792 = 0; S = 550.

Найдем первые три выплаты: 0,2∙550 = 110 (тыс руб).

Общая сумма выплат составляет: 3∙ 110 + 2∙360 = 1050 (тыс руб)

Ответ: 1050 тысяч рублей

Задача 12 (из тренировочных работ СТАТГРАД, апрель 2016)

Решение.

Рассуждаем далее. В начале 4 года долг составит 1,2∙ S. После выплаты в конце 4 года долг составит

(1,2∙ S— Х). В начале 5-го года долг составит (1,2∙ S— Х)∙1,2, а после выплаты долг станет равным нулю, то есть (1,2∙ S— Х)∙1,2 – Х=0.

Выразим из этого уравнения Х= и подставим в неравенство (1):

0,6∙ S +2∙ ≥10;

S ≥ 5.

Наименьшее целое решение этого неравенства – число 6. Значит, наименьший размер кредита равен 6 млн рублей.

Ответ: 6 млн р.

Задача 13 (досрочное ЕГЭ, 16.04.16)

В июле 2016 года планируется взять кредит в размере 4,2 млн рублей. Условия его возврата таковы:

— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;

— с февраля по июнь необходимо выплатить часть долга;

— в июле 2017,2018,2019 годов долг остается равным 4,2 млн рубле

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если долг выплачен полностью и общие выплаты равны 6,1 млн рублей.

Решение.

Сумма выплат за первые три года равна:

4,2∙0,01∙r∙3 =0,126∙r

Сумма выплат за последние два года равна 2∙Х.

Так как общие выплаты равны 6,1 млн рублей, то составляем уравнение:

0,126∙r + 2Х= 6,1 (1).

В январе 2020 года долг составит: 4,2 +4,2∙0,01r= 4,2 (1+0,01r). После выплаты суммы Х долг станет равным:

4,2 (1+0,01r) – Х= 4,2t –Х, где t=1+ 0,01r.

В январе 2021 года долг составит (4,2t –Х)∙t

После выплаты суммы Х долг станет равным нулю:

(4,2t –Х)∙t – Х= 0 (2).

Из уравнения (2) выразим Х:

Х= и подставим в равенство (1):

12,6∙(t -1) + 2 = 6,1;

t =1, 1. Значит, r = 10%

Ответ: 10%

Задача 14

Решение.

Таким образом, ценную бумагу нужно продать в течение восьмого года.

Ответ: В течение 8 года

Задача 15

Решение. Прибыль (в млн рублей) за один год выражается величиной

px – (0,5 + x + 7) = -0,5+(p-1)x -7

Ответ: 9 тыс. рублей.

ЭКОНОМИЧЕСКИЕ ЗАДАЧИ НА ОПТИМИЗАЦИЮ

Задача 1

Решение: 1-й способ – с помощью составления опорной линейной функции.

у = кх + в, где к и в – постоянные. Если эту функцию рассматривать на отрезке

[; ], то она будет иметь на нем наибольшее и наименьшее значение. При к0 наименьшее значение у принимает в точке х = , а наибольшее – в точке х = , при к0 функция у в точке х = принимает наибольшее значение, а в точке х = — наименьшее. Решим задачу.

Всего количество добытого алюминия (5х+15у);а количество добытого никеля — 15(100-х)+ 5(300-у)=1500-15х+1500-5у=3000-15х-5у.

Функция сплава: F(x) = (5х+15у) + (3000-15х-5у); F(x) = -10х+10у + 3000;

F(x) = -24х +5400. Эта линейная функция является убывающей. Наибольшее значение она принимает при х=0. Значит, F(100)=5400.

Ответ:5400

2-й способ – с помощью логических рассуждений и составления уравнения.

240∙ 5∙3 = 3600 (кг), никеля 1500 + 60∙5=1800(кг). Всего 3600+1800=5400 (кг). Ответ: 5400 кг

Ответ: 5400 кг.

Задача 2

Решение:

1-й способ – с помощью логики и арифметических действий.

Найдем стоимость 1номера стандартного: 2000:21=95 (рублей).

Найдем стоимость 1номера «люкс»: 4500: 49 =91 (рублей).

2-й способ – с помощью составления опорной линейной функции.

Ответ: 104500 рублей.

Задача 3

Комбинат	Количество деталей А	Количество деталей В
1-й комбинат	3х	100-х
2-й комбинат	a	b
Всего	3х +a	100 – х +b

Чтобы собрать наибольшее количество изделий, нужно соблюдать условие:

В каждом изделии содержится 1 деталь А и 3 детали В. Значит, общее количество изделий равно числу изделий А.

Так как a и b – целые числа и a² + b²=100, то возможны следующие случаи:

a=0, b=10. Тогда из равенства (1) х=11 и 3х +a=3∙11 +0=33.
a=10, b=0. Тогда из равенства (1) х=7 и 3х +a=3∙7 +10=31.
a=6, b=8. Тогда х=9 и 3х +a=33.
a=8, b=6. Тогда х=8,2 – не является целым числом.

Значит, наибольшее количество изделий равно 33. Ответ: 33

ЗАКЛЮЧЕНИЕ

Рецензия

на сборник экономических задач и задач на оптимизацию

по математике для учащихся 10-11 классов

«Практико-ориентированные задачи в заданиях ЕГЭ

по математике» учителя математики МАОУ СОШ № 37

Коневой Галины Михайловны

В настоящее время общее образование находится на этапе модернизации и обновления системы и содержания в условиях введения новых федеральных государственных стандартов. Приоритетом общества и системы образования является способность вступающих в жизнь людей самостоятельно решать встающие перед ними новые, еще неизвестные задачи. На первый план наряду с общей грамотностью выступает умение выпускников, например, разрабатывать и проверять гипотезы, умение работать в проектном режиме, проявлять инициативу в принятии решений. Это и становится одним из значимых ожидаемых результатов образования и предметом стандартизации.

Практико-ориентированные задачи тесно связаны с практической деятельностью человека. Решение и анализ таких задач способствует формированию навыков и умений у выпускников самостоятельно решать жизненные задачи.

Данная работа содержит 18 задач, собранных и решенных учителем математики МАОУ СОШ №37 города Улан-Удэ Коневой Г.М. Брошюра состоит из четырех частей:

1) Вступление

2) Задачи о кредитах

3) Экономические задачи на оптимизацию

4) Заключение.

Данные задачи были включены на ЕГЭ по математике профильного уровня с 2015 года. Задачи ориентированы на развитие у учащихся умений строить математические модели экономических ситуаций, исследовать эти модели, получать и интерпретировать выводы.

Сборник задач может быть использован учащимися и учителями при подготовке к ЕГЭ по математике профильного уровня.

Н. Н. Алексеева

канд. пед. наук, зав. кафедрой

«Развитие образовательных систем» ГАУ ДПО РБ БРИОП

Аннотация

на учебное пособие «Практико-ориентированные задачи

в заданиях ЕГЭ по математике» учителя МАОУ СОШ № 37 г. Улан-Удэ
Коневой Галины Михайловны.

«Книги — это корабли мысли,

странствующие по волнам времени

и бережно несущие свой драгоценный груз

от поколения к поколению»

Френсис Бэкон

В данном учебном пособии представлен материал по решению экономических задач и задач на выбор оптимального решения. Эти задачи были включены на ЕГЭ по математике профильного уровня с 2015 года. Задачи ориентированы на развитие у учащихся умений строить математические модели экономических ситуаций, исследовать эти модели, получать и интерпретировать выводы.

Главное внимание в статье уделено решению задач о кредитах. Именно такие задачи были включены на ЕГЭ в 2015 и 2016 году. Кроме этих задач, учитель предлагает рассмотреть и задачи на выбор оптимального решения. Неоценимую важность таких экстремальных задач в школьном курсе математики я вижу в воспитании исследовательской культуры учащихся. Ведь все решения таких задач предлагаются на уровне исследования математической модели и на уровне исследования реальной ситуации с использованием оптимизационных средств. Экстремальные задачи помогают школьнику ознакомиться с некоторыми идеями и прикладными методами школьного курса математики, которые часто применяются в трудовой деятельности, в познании окружающей действительности. Решение экстремальных задач способствует углублению и обогащению математических знаний учащихся.

В данной работе учитель рассмотрел такие экстремальные задачи, которые решаются средствами элементарной математики: с помощью линейной функции, с помощью методов перебора и логических рассуждений, с помощью составления уравнения.

Данный сборник задач – это результат плодотворной работы в рядах РОО БОЦ «Эврика» на курсах усовершенствования учителей при ГАУ ДПО РБ БРИОП. Учебное пособие создано с целью оказания помощи учителям и учащимся при подготовке к ЕГЭ по математике.

К. Т. Латкина

президент Ассоциации учителей математики РБ

«Байкальский образовательный центр «Эврика»,

«Заслуженный учитель России», «Отличник просвещения РФ»,

победитель Конкурса лучших учителей России

Содержание

Вступление…………………………………………………	3
Задачи о кредитах………………………………………….	5
Экономические задачи на оптимизацию…………………	17
Заключение…………………………………………………	22

Учебное издание

ПРАКТИКО-ОРИЕНТИРОВАННЫЕ ЗАДАЧИ

В ЗАДАНИЯХ ЕГЭ ПО МАТЕМАТИКЕ

Сборник

экономических задач и задач на оптимизацию

по математике

Составитель

Галина Михайловна Конева

Св-во о государственной аккредитации

№ 1289 от 23 декабря 2011 г.

Подписано в печать 12.12.16. Формат 60 х 84 1/16.

Усл. печ. л. 1,51. Уч.-изд. л. 0,88. Тираж . Заказ .

Цена договорная.

Издательство Бурятского госуниверситета

670000, г. Улан-Удэ, ул. Смолина, 24а

E-mail: riobsu@gmail.com

Отпечатано в типографии Бурятского госуниверситета

70000, г. Улан-Удэ, ул. Сухэ-Батора, 3а

Источник

Экономические задачи ЕГЭ, Колесникова С.И., 2019.

Это краткое методическое пособие содержит решения новых текстовых задач, так называемых «экономических». Это задачи на сложные проценты: кредиты, вклады; на исследование максимума прибыли и т.д. Большинство задач, по мнению автора, требует от учащегося умения сначала вывести необходимые формулы, а затем правильно провести арифметические операции. Часто оказывается, что гораздо проще работать с простыми дробями, а не с десятичными. Для лучшего усвоения темы приводим в тексте полные решения, а в ответах — более короткие. Условия задач взяты из Интернета.

Одинаковые выплаты.
В задачах этого пункта клиент ежегодно выплачивает одну и ту же сумму, которую мы обозначим буквой Ъ.
Пример 2. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы:
1) каждый январь долг возрастает на 20% по сравнению с концом предыдущего года,
2) с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (т.е. за 4 года)?

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу Экономические задачи ЕГЭ, Колесникова С.И., 2019 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать
— pdf — Яндекс.Диск.

Дата публикации: 27.03.2020 13:38 UTC

Теги:

Колесникова :: тренировочный вариант ЕГЭ :: ЕГЭ по математике :: 11 класс :: математика :: подготовка к ЕГЭ :: ответы :: решения :: экономические задачи

Следующие учебники и книги:

Я сдам ЕГЭ, Математика, Типовые задания, Базовый уровень, Часть 1, Алгебра, Ященко И.В., Шестаков С.А., 2018
Я сдам ЕГЭ, Математика, Типовые задания, Профильный уровень, Часть 3, Геометрия, Ященко И.В., Шестаков С.А., 2019
Я сдам ЕГЭ, Математика, Типовые задания, Профильный уровень, Часть 2, Алгебра и начала математического анализа, Ященко И.В., Шестаков С.А., 2019
ЕГЭ, 4000 задач с ответами по математике, все задания «Закрытый сегмент», базовый и профильный уровни, Ященко И.В., 2020

Предыдущие статьи:

ЕГЭ 2020, 100 баллов, математика, профильный уровень, практическое руководство, Ерина Т.М., 2020
Математика, ЕГЭ, Задачи на целые числа (типовое задание 19), Учебно-методическое пособие, Прокофьев А.А., Корянов А.Г., 2018
Математика, ЕГЭ, Задача с экономическим содержанием, Учебно-методическое пособие, Лысенко Ф.Ф., Кулабухова С.Ю., 2018
Математика, 9-й класс, Подготовка к ЕГЭ-2019, Базовый уровень, 40 тренировочных вариантов по демоверсии 2019 года, Учебно-методическое пособие, Лысенко Ф.Ф., Иванова С.О., 2018

Источник