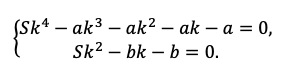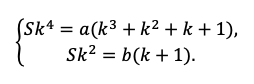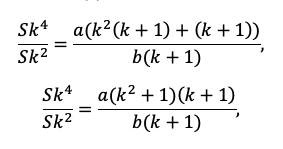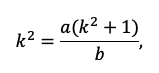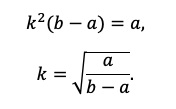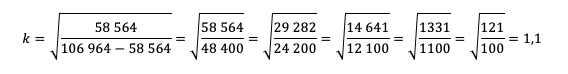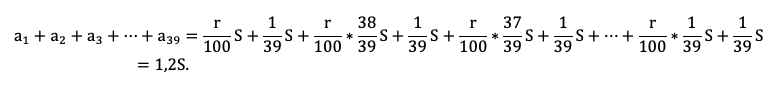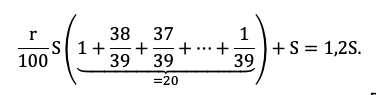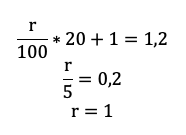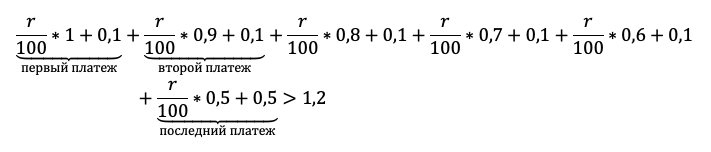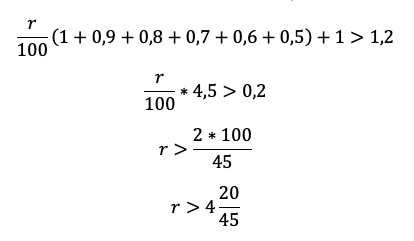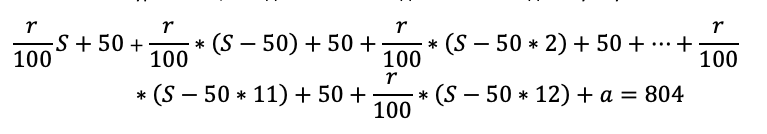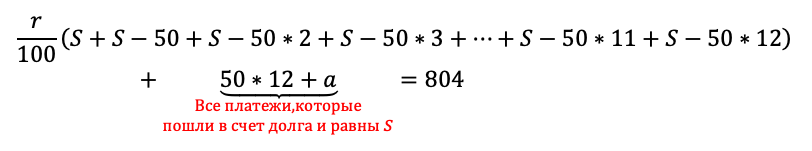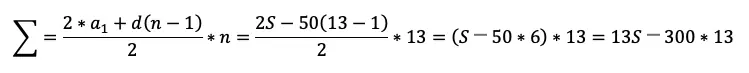Экономические задачи на прогрессию егэ - Помощь в подготовке к экзаменам и поступлению

Задание 15 Профильного ЕГЭ по математике — «экономическая» задача. Как вы уже поняли, речь пойдет о деньгах. О кредитах и вкладах. О ситуациях, где нужно узнать, при каких значениях переменной будет максимальна прибыль или минимальны издержки. С 2022 года задание 15 оценивается на ЕГЭ в 2 первичных балла.

В этой статье:

Как научиться решать «экономические» задачи. С чего начать.

Две схемы решения задач на кредиты и как их распознать.

Комбинированные задачи.

В чем основная сложность «экономической» задачи.

Задания на оптимальный выбор. В том числе — с применением производной.

Если материал покажется вам сложным — вернитесь к теме «Задачи на проценты» из первой части ЕГЭ по математике.

Надеемся, что вы уже сейчас сможете ответить на такие вопросы:

Что принимается за 100%?
Величина х увеличилась на p%. Как это записать?
Величина y дважды уменьшилась на р%. Как это записать?

Ответы на вопросы, а также подготовительные задачи — в статье «Задача 17 Профильного ЕГЭ по математике. Кредиты и вклады. Начисление процентов». Повторите эту тему.

Запомним, что есть всего две схемы решения задач на кредиты

Первая схема: кредит погашается равными платежами. Или известна информация о платежах. Подробно здесь.

Вторая схема: равномерно уменьшается сумма долга. Или дана информация об изменении суммы долга. Подробно здесь.

В задачах первого типа обычно применяется формула для суммы геометрической прогрессии. В задачах второго типа — формула суммы арифметической прогрессии.

Посмотрите, чем эти схемы отличаются друг от друга. На какие ключевые слова в условии надо обратить внимание.

Потому что первое, что надо сделать, когда решаете «экономическую» задачу на кредиты или вклады, — определить, к какому типу она относится.

Давайте потренируемся.

1. 31 декабря 2014 года Аристарх взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Аристарх переводит в банк X рублей. Какой должна быть сумма X, чтобы Аристарх выплатил долг четырьмя равными платежами (то есть за четыре года)?

Конечно, это задача первого типа. Есть информация о платежах. В условии сказано, что Аристарх выплатит долг четырьмя равными платежами.

Введем обозначения:

S=6902 тыс. рублей — сумма долга. Расчеты будем вести в тысячах рублей.

— процент банка,

$k=1+frac{{ p}}{100}=1+frac{125}{1000}=1+frac{1}{8}=frac{9}{8}$ — коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,

— сумма ежегодного платежа.

Составим схему погашения кредита. Заметим, что здесь 4 раза (то есть в течение 4 лет) повторяются одни и те же действия:

— сумма долга увеличивается в раз;

— Аристарх вносит на счет сумму в счет погашения кредита, и сумма долга уменьшается на .

Вот что получается:

Раскроем скобки:

$S{{ k}}^4-{ X}left({{ k}}^3+{{ k}}^2+{ k}+1right)=0.$

Что у нас в скобках? Да, это геометрическая прогрессия, и ее проще записать как

$1+{{ k}+{{ k}}^2+{ k}}^3$ . В этой прогрессии первый член равен 1, а каждый следующий в k раз больше предыдущего, то есть знаменатель прогрессии равен k.

Применим формулу суммы геометрической прогрессии:

${{ Sk}}^4={ X}cdot frac{{{ k}}^4-1}{{ k}-1}=0.$ И выразим из этой формулы .

${ X}=frac{{ S}cdot {{ k}}^4left({ k}-1right)}{{{ k}}^4-1}.$ Что же, можно подставить численные данные. Стараемся, чтобы наши вычисления были максимально простыми. Поменьше столбиков! Например, коэффициент k лучше записать не в виде десятичной дроби 1,125 — а в виде обыкновенной дроби $frac{9}{8}$ , Иначе у вас будет 12 знаков после запятой!

И конечно, не спешить возводить эту дробь в четвертую степень или умножать на S = 6902000 рублей.

${ X}=frac{{ S}cdot {{ k}}^4left({ k}-1right)}{{{ k}}^4-1}=frac{{ S}cdot 9^4left(frac{9}{8}-1right)}{8^4cdot left(frac{9^4}{8^4}-1right)}=frac{{ S}cdot 9^4}{8cdot left(9^4-8^4right)}=frac{{ S}cdot 9^4}{8cdot left(9^2-8^2right)left(9^2+8^2right)}=frac{{ S}cdot 9^4}{8cdot left(9+8right)left(9^2+8^2right)}=$

$=frac{6902cdot {81}^2}{8cdot 17cdot 145}=frac{406cdot {81}^2}{8cdot 145}=frac{203cdot {81}^2}{4cdot 145}=frac{29cdot 7cdot {81}^2}{4cdot 29cdot 5} = 2296,35$ тыс.руб.

Ответ: 2296350 рублей.

Вот следующая задача.

2. Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

В этой задаче сумма долга уменьшается равномерно — задача второго типа.

Пусть S — первоначальная сумма долга, S = 1800 тысяч рублей.

Нарисуем схему начисления процентов и выплат. И заметим некоторые закономерности.

Как обычно, ${ k}=1+frac{{ p}}{100}.$

Сумма долга уменьшается равномерно. Можно сказать — равными ступеньками. И каждая ступенька равна $frac{1}{24}{ S}.$ После первой выплаты сумма долга равна $frac{23}{24}{ S},$ после второй $frac{22}{24}{ S}.$

Тогда первая выплата ${{ X}}_1={ kS}-frac{23}{24}{ S},$ вторая выплата ${{ X}}_2={ k}cdot frac{23}{24}{ S}-frac{22}{24}{ S}$ ,

dots

Последняя в году выплата ${{ X}}_{12}={ k}cdot frac{13}{24}{ S}-frac{12}{24}{ S}.$

Сумма всех выплат в течение первого года:

${ X}={{ X}}_1+{{ X}}_2+dots +{{ X}}_{12}={ kS}left(1+frac{23}{24}+dots frac{13}{24}right)-{ S}left(frac{23}{24}+frac{22}{24}+dots +frac{12}{24}right).$

В первой «скобке» — сумма 12 членов арифметической прогрессии, в которой ${{ a}}_1=frac{13}{24};{{ a}}_{{ n}}=frac{24}{24}=1.$ Обозначим эту сумму ${{ S}}_1.$

${{ S}}_1=frac{{{ a}}_1+{{ a}}_{12}}{2}cdot 12=frac{13+24}{2cdot 24}cdot 12=frac{37}{4}.$

Во второй скобке — также сумма 12 членов арифметической прогрессии, в которой ${{ b}}_1=frac{12}{24};{{ b}}_{{ n}}=frac{23}{24}.$ Эту сумму обозначим ${{ S}}_{2.}$

${{ S}}_2=frac{{{ b}}_1+{{ b}}_{12}}{2}cdot 12=frac{12+23}{2cdot 24}cdot 12=frac{35}{4}.$

Общая сумма выплат за год:

$small X= S left({ kS}_1-{{ S}}_2right)=frac{1800}{4}left({ 1,01}cdot 37-35right)=$
$=frac{1800cdot { 2,37}}{4}={ 2,37}cdot 450= 1066,5$ тыс. рублей.

Ответ: 1066500 рублей.

Еще одна задача — комбинированная. Здесь мы рисуем такую же схему выплаты кредита, как в задачах второго типа.

3. В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:

− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить часть долга;

− в июле 2017, 2018 и 2019 долг остаётся равным S тыс. рублей;

− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;

− к июлю 2021 долг будет выплачен полностью.

Найдите общую сумму выплат за пять лет.

Введем переменные: ${ k}=1+frac{25}{100}=frac{5}{4},Y=625$ тысяч рублей. Рисуем схему погашения кредита:

Общая сумма выплат: Кроме того, долг был полностью погашен последней выплатой .

Это значит, что и тогда

${ S}=frac{left({ k}+1right){ Y}}{{{ k}}^2}{ X}=3cdot frac{left({ k}+1right){ Y}}{{{ k}}^2}left({ k}-1right)+2{ Y}=3{ y}left(frac{{{ k}}^2-1}{{{ k}}^2}right)+2{ Y}=$
$={ Y}left(5-frac{3}{{{ k}}^2}right)=625left(5-frac{3cdot 16}{25}right)=frac{625cdot 77}{25}=77cdot 25=1925$ тысяч рублей.

Ответ: 1925 тыс. рублей.

Но не только задачи на кредиты и вклады могут встретиться в задании 15 Профильного ЕГЭ по математике. Есть еще задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если повезет и функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.

4. Консервный завод выпускает фруктовые компоты в двух видах тары—стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.

Вид тары	Себестоимость, 1 центнера	Отпускная цена, 1 центнера
стеклянная	1500 руб	2100 руб
жестяная	1100 руб	1750 руб

Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).

По условию, завод не может выпускать компот только в стеклянных банках или только в жестяных — должны быть и те, и другие.

Пусть x — доля мощностей завода, занятых под поизводство компотов в стеклянных банках, а y — доля мощностей, занятых под производство компотов в жестяных банках, Тогда x+y=1. (Например, х=0,3 и у = 0,7 — то есть 30% производства — это компот в стеклянных банках, а 70% — компот в жестяных банках).

Если бы завод выпускал только компот в стеклянных банках, их бы получилось 90 центнеров в сутки. Однако выпускаются и те, и другие, и компотов в стеклянных банках производится 90x центнеров, а в жестяных банках — 80y центнеров в сутки.

Составим таблицу.

Вид тары	Доля в общем количестве	Производится в сутки	Прибыль за 1 центнер
стеклянная			2100 — 1500 = 600 руб
жестяная			1750 — 1100 = 650 руб

Общая прибыль завода за сутки равна

По условию, и , то есть $xge frac{2}{9}$ и $yge frac{1}{4}.$

Нужно найти наибольшее значение выражения при выполнении следующих условий:

$left{begin{matrix} x+y=1\ {{2}over{9}}leq x textless 1, \ {1over4}leq y textless 1 end{matrix}right. Leftrightarrow left{begin{matrix} y=1-x\ {2over9}leq x leq {3over4} end{matrix}right. .$

Подставим y=1-x в выражение для прибыли завода за сутки. Получим, что она равна Это линейная функция от x. Она монотонно возрастает и свое наибольшее значение принимает при $x=frac{3}{4}.$ Тогда $y=frac{1}{4}$ и максимально возможная прибыль завода за день равна

$2000cdot left(27cdot frac{3}{4}+26cdot frac{1}{4}right)=2000cdot frac{107}{4}=53500$ руб.

Ответ: 53500 руб.

Больше задач по финансовой математике на нахождение наибольших и наименьших значений функций и применение производной — здесь:

Задача 15 Профильного ЕГЭ по математике. Исследование функций и производная

Вот такая она, задача с экономическим содержанием. Мы рассказали о ней самое главное. Если готов осваивать ее самостоятельно — желаем удачи. А если не все будет сразу получаться — приходи к нам в ЕГЭ-Студию на интенсивы, курсы или Онлайн-курс.

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 15. Финансовая математика u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

ЕГЭ-2017 г.

Составители: 10-а класс.

Филатова Ольга Петровна.

Предисловие.

Для обеспечения достойного проживания в новых для России рыночных условиях каждый человек стремится больше узнать о существующих экономических закономерностях. Новые экономические отношения условно разделили россиян на две группы: одна занимает деньги у финансовых структур, а другая вкладывает деньги в финансовые структуры. С экономической точки знания речь идет о кредитной операции, самом распространенном виде финансовой сделки. Открытие сберегательного счета в банке, выпуск банком депозитных сертификатов, учет векселей, выдача банком кредита, организация паевых инвестиционных фондов— это примеры кредитных операций. Об особенностях финансовых операций взрослые имеют смутное представление, а молодежи эти знания необходимы. Очевидно то, что чем раньше мы, подрастающее поколение, поймём суть и начнём ориентироваться в сложных экономических вопросах, затрагивающих нас в повседневной жизни, тем увереннее мы будем чувствовать себя во взрослой жизни.

Наиболее прочно вошло в жизнь современного человека такая финансовая операция как кредитование физических лиц, или как еще говорят, кредиты частным лицам.

Популярность кредитования в нашей стране растет из года в год.

Огромный интерес физических лиц к разному роду кредитам вполне понятен, люди хотят упростить свою жизнь и жить лучше. И в настоящее время кредиты физическим лицам позволяют достичь желанной цели немедленно, когда нам это необходимо. Благодаря кредитованию любой человек может приобрести машину, бытовую технику, мебель, слетать в отпуск, отдохнуть, сделать ремонт в квартире, получить образование и даже приобрести недвижимость, не дожидаясь полного накопления необходимой для этого суммы. Однако при всей выгодности приобретения любой покупки в кредит перед каждым человеком встает проблема ежемесячной выплаты ощутимой суммы из зарплаты и ожидание того момента, когда наконец-то он освободится от финансовой кабалы.

Сегодня банки и магазины очень умело пользуются создавшимся положением, деньги в кредит предлагаются на каждом шагу и практически любую вещь можно в магазине приобрести в рассрочку. И здесь для каждого из нас встает вопрос: у кого и каким предложением воспользоваться? А чтобы ответить на него, нужны умения производить хотя бы несложные процентные расчеты для сравнения и выбора более выгодных условий. Желание приобрести это умение и определило тему данной работы.

В данном задачнике собраны однотипные задания для ЕГЭ-2017г., которые можно решить с помощью геометрической прогрессией. Тема — банковская система (кредитование), которая играет в нашей жизни особое место.

Составители задачника.

Задачи.

31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.

В одной стране в обращении находилось 1 000 000 долларов, 20% из которых были фальшивыми. Некая криминальная структура стала ввозить в страну по 100000 долларов в месяц, 10% из которых были фальшивыми. В это же время другая структура стала вывозить из страны 50 000 долларов ежемесячно, из которых 30% оказались фальшивыми. Через сколько месяцев содержание фальшивых долларов в стране составит 5%?

Банк планирует вложить на 1 год 30% имеющихся у него средств клиентов в акции золотодобывающего комбината, а остальные 70% — в строительство торгового комплекса. В зависимости от обстоятельств первый проект может принести банку прибыль в размере от 32% до 37% годовых, а второй проект — от 22 до 27% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке, уровень которой должен находиться в пределах от 10% до 20% годовых. Определите, какую наименьшую и наибольшую чистую прибыль в процентах годовых от суммарных вложений в покупку акций и строительство торгового комплекса может при этом получить банк.

В банк был положен вклад под банковский процент 10%. Через год хозяин вклада снял со счета 2000 рублей, а еще через год снова внес 2000 рублей. Однако, вследствие этих действий через три года со времени первоначального вложения вклада он получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы получил в итоге вкладчик?

При рытье колодца глубиной свыше 10 м за первый метр заплатили 1000 руб., а за каждый следующий на 500 руб. больше, чем за предыдущий. Сверх того за весь колодец дополнительно было уплачено 10 000 руб. Средняя стоимость 1 м оказалась равной 6250 руб. Определите глубину колодца.

Семья Ивановых ежемесячно вносит плату за коммунальные услуги, телефон и электричество. Если бы коммунальные услуги подорожали на 50%, то общая сумма платежа увеличилась бы на 35%. Если бы электричество подорожало на 50%, то общая сумма платежа увеличилась бы на 10%. Какой процент от общей суммы платежа приходится на телефон?

Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?

Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей?

В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69690821 рубль.

Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?

Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10% годовых Однако через год и Саша, и Паша сняли со своих счетов соответственно 10% и 20% имеющихся денег. Еще через год каждый из них снял со своего счета соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего года на счету окажется большая сумма денег? На сколько рублей?

Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?

Василий кладет в банк 1 000 000 рублей под 10% годовых на 4 года (проценты начисляются один раз после истечения года) с правом докладывать три раза (в конце каждого года) на счет фиксированную сумму 133 000 рублей. Какая сумма будет на счете у Василия через 4 года?

Анатолий решил взять кредит в банке 331000 рублей на 3 месяца под 10% в месяц. Существуют две схемы выплаты кредита.

По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Анатолий переводит в банк фиксированную сумму и в результате выплачивает весь долг тремя равными платежами (аннуитетные платежи).

По второй схеме тоже сумма долга в конце каждого месяца увеличивается на 10%, а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину (дифференцированные платежи). Какую схему выгоднее выбрать Анатолию? Сколько рублей будет составлять эта выгода?

В начале года 5/6 некоторой суммы денег вложили в банк А, а то, что осталось — в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у. е., к концу следующего — 749 у. е. Если первоначально 5/6 суммы было бы вложено в банк Б, а оставшуюся вложили бы в банк А, то по истечении одного года сумма выросла бы до 710 у. е. Определите сумму вкладов по истечении второго года в этом случае.

В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после начисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу?

Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк 3/4 от всей суммы, которую он должен банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму, на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?

В январе 2000 года ставка по депозитам в банке «Возрождение» составила х % годовых, тогда как в январе 2001 года — у% годовых, причем известно, что x + y = 30%. В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение х при котором сумма на счету вкладчика в январе 2002 года станет максимально возможной.

В конце августа 2001 года администрация Приморского края располагала некой суммой денег, которую предполагалось направить на пополнение нефтяных запасов края. Надеясь на изменение конъюнктуры рынка, руководство края, отсрочив закупку нефти, положила эту сумму 1 сентября 2001 года в банк. Далее известно, что сумма вклада в банке увеличивалась первого числа каждого месяца на 26% по отношению к сумме на первое число предыдущего месяца, а цена барреля сырой нефти убывала на 10% ежемесячно. На сколько процентов больше (от первоначального объема закупок) руководство края смогло пополнить нефтяные запасы края, сняв 1 ноября 2001 года всю сумму, полученную из банка вместе с процентами, и направив ее на закупку нефти?

Транcнациональная компания Amako Inc. решила провести недружественное поглощение компании First Aluminum Company (FAC) путем скупки акций миноритарных акционеров. Известно, что Amako было сделано три предложения владельцам акций FAC, при этом цена покупки одной акции каждый раз повышалась на 1/3. В результате второго предложения Amako сумела увеличить число выкупленных акций на 20% (после второй скупки общее число выкупленных акций увеличилось на 20%), а в результате скупки по третьей цене — еще на 20%. Найдите цену третьего предложения и общее количество скупленных акций FAC, если начальное предложение составляло $27 за одну акцию, а по второй цене Amako скупила 15 тысяч акций.

Два брокера купили акции одного достоинства на сумму 3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?

Баба Валя, накопив часть своей пенсии, решила улучшить свое материальное положение. Она узнала, что в Спёрбанке от пенсионеров принимают вклады под определенный процент годовых и на этих условиях внесла свои сбережения в ближайшее отделение Спёрбанка. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Спёрбанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить свое материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счета в Спёрбанке Баба Валя сняла половину образовавшей суммы от ее вклада, заявив: «Такой навар меня не устраивает!» И открыла счет в том коммерческом банке, о котором говорила ее соседка, не теряя надежды на значительное улучшение своего материального благосостояния.

Надежды оправдались: через год сумма Бабы Вали в коммерческом банке превысила ее первоначальные кровные сбережения на 65%. Сожалела Баба Валя, что год назад в Спёрбанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли?..»Гендиректор коммерческого банка оказался хорошим: не оставил Бабу Валю без навара! А каков в Спёрбанке процент годовых для пенсионеров?

Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Банк увеличил процент годовых на 40 процентных пунктов (то есть увеличил ставку а% до (а + 40)%). К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?

1 января 2015 года Тарас Павлович взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая — 1 числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Тарас Павлович переводит в банк платёж. На какое минимальное количество месяцев Тарас Павлович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?

1 января 2015 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая — 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?

1 января 2015 года Павел Витальевич взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк платёж. На какое минимальное количество месяцев Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не более 125 тыс. рублей?

1 июня 2013 года Всеволод Ярославович взял в банке 900000 рублей в кредит. Схема выплаты кредита следующая — 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300000 рублей?

31 декабря 2014 года Валерий взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на определённое количество процентов), затем Валерий переводит очередной транш. Валерий выплатил кредит за два транша, переводя в первый раз 660 тыс рублей, во второй — 484 тыс. рублей. Под какой процент банк выдал кредит Валерию?

31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк x рублей. Какой должна быть сумма x, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

31 декабря 2014 года Савелий взял в банке 7 378 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Савелий Переводит в банк платёж. Весь долг Савелий выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк X рублей. Какой должна быть сумма X, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?

31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

31 декабря 2014 года Ярослав взял в банке некоторую сумму в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12,5%), затем Ярослав переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?

31 декабря 2014 года Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Пётр переводит очередной транш. Если он будет платить каждый год по 2 592 000 рублей, то выплатит долг за 4 года. Если по 4 392 000 рублей, то за 2 года. Под какой процент Пётр взял деньги в банке?

Гражданин Петров по случаю рождения сына открыл 1 сентября 2008 года в банке счёт, на который он ежегодно кладет 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счёте. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счёт, на который ежегодно кладёт по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?

Оля хочет взять в кредит 100 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 24000 рублей?

Савелий хочет взять в кредит 1,4 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Савелий взять кредит, чтобы ежегодные выплаты были не более 330 тысяч рублей?

Имеется три пакета акций. Общее суммарное количество акций первых двух пакетов совпадает с общим количеством акций в третьем пакете. Первый пакет в 4 раза дешевле второго, а суммарная стоимость первого и второго пакетов совпадает со стоимостью третьего пакета. Одна акция из второго пакета дороже одной акции из первого пакета на величину, заключенную в пределах от 16 тыс. руб. до 20 тыс. руб., а цена акции из третьего пакета не меньше 42 тыс. руб. и не больше 60 тыс. руб. Определите, какой наименьший и наибольший процент от общего количества акций может содержаться в первом пакете.

Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент, свой для каждого банка. В начале года Степан положил 60% некоторой суммы денег в первый банк, а оставшуюся часть суммы во второй банк. К концу года сумма этих вкладов стала равна 590 000 руб., а к концу следующего года 701 000 руб. Если бы Степан первоначально положил 60% своей суммы во второй банк, а оставшуюся часть в первый, то по истечении одного года сумма вкладов стала бы равной 610 000 руб. Какова была бы сумма вкладов в этом случае к концу второго года?

Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.

По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 11 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».

По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 20 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 21 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».

По вкладу «А» банк в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 5% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 2 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 15 млн рублей.

Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 25 млн рублей.

Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 10 млн.

1 января 2015 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая — 1-го числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?

Содержание.

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Источник: Интеллект-центр. Репетиционные варианты ЕГЭ 2015.

Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна вносить в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна выплатит банку в течение первого года кредитования?

Источник: А. Ларин: Тренировочный вариант № 122.

В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69 690 821 рубль.

Источник: А. Ларин: Тренировочный вариант № 131.

Источник: А. Ларин: Тренировочный вариант № 137.

Пройти тестирование по этим заданиям

Источник

В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!

Как научить школьника решать экономическую (банковскую) задачу в ЕГЭ по математике

Прототипы для 17-го номера делятся на три большие группы:

банковские задачи,
на ценные бумаги,
задачи на оптимальный выбор.

В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.

Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.

Как работает процент по кредиту?
На какую сумму начисляется?
Из каких частей состоит платеж?
Как уменьшается долг?

На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!

Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.

С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике

Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:

Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.

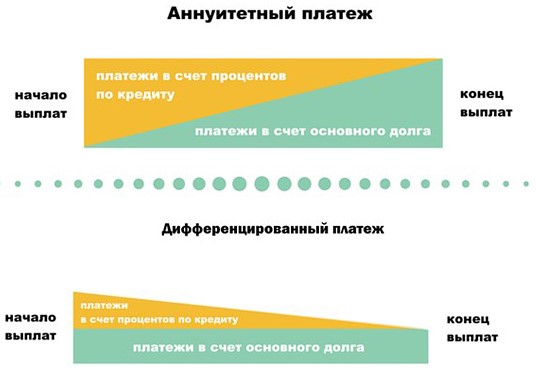
Как научить школьника решать любую банковскую задачу

Экономическая задача ЕГЭ по математике в реальной жизни

Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.

Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.

Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.

Тип 1. Равные платежи

Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!

Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.

Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.

Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!

Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.

Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:

Наше решение не зависит от суммы кредита, S сокращается.

По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:

Пожалуй, все, проще уже некуда. Подставляем значения!

Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.

Вспоминаем, что k=1+r/100, а найти нам надо r.

Ответ: 10%.

Не забудьте после решения расставить акценты в задаче:

Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.

Тип 2. Равномерно убывающий долг

В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.

15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)

Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.

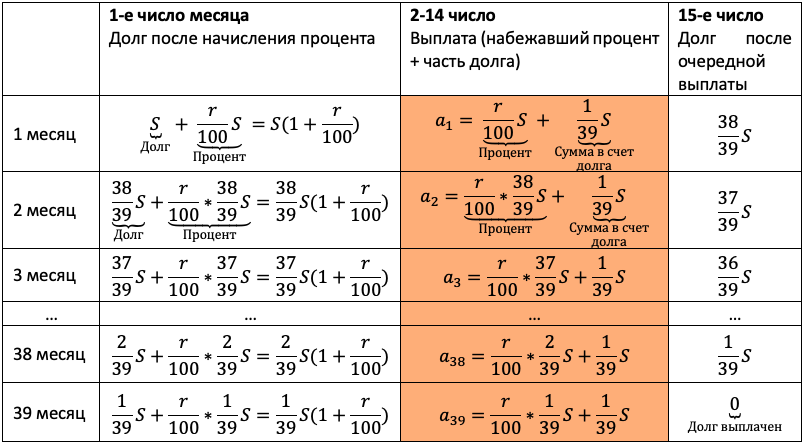
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:

Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:

Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:

Приведем подобные, вынесем общий множитель за скобку:

Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:

Ответ: 1%.

И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.

Тип 3. Долг, убывающий согласно табличке

Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг(в млн рублей)	1	0,9	0,8	0,7	0,6	0,5	0

Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.

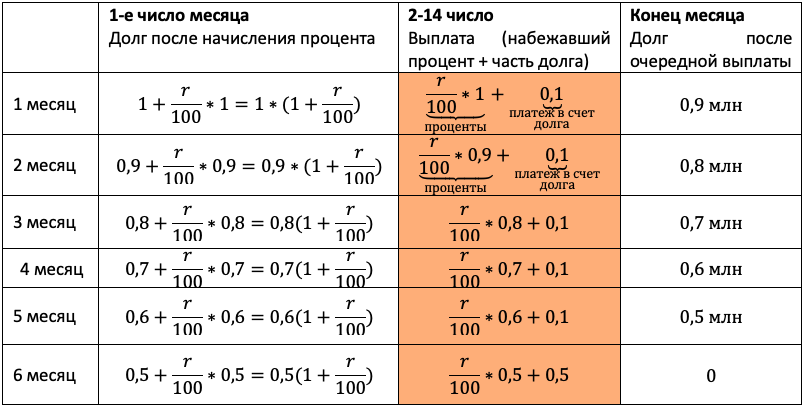
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.

Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:

Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.

Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.

«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:

Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.

Приведем подобные и вынесем общие множители за скобку:

Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.

Ответ: 5%.

Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.

Тип 4. Погашение кредита в два этапа.

По сути, это та же прошлая задача, но месяцев больше

В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!

15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?

И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.

Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.

Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.

Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:

Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:

Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.

Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:

Посчитаем эту сумму:

Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!

Ответ: 700 тысяч.

Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.

Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике

Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:

Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
Повторите типы задач и механизм распределения платежа на проценты и долг;
Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
Проговорите, что математическая модель должна точно отражать условие задачи.

Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.

За что дают баллы?

Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.

17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.

Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.

Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:

А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.

Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.

Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.

Источник