Экстремум функции решу егэ - Помощь в подготовке к экзаменам и поступлению

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 692 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь

На рисунке изображен график производной функции f(x), определенной на интервале (−16; 4). Найдите количество точек экстремума функции f(x) на отрезке [−14; 2].

На рисунке изображен график производной функции f(x), определенной на интервале (−6; 5). Найдите точку экстремума функции f(x) на отрезке [−5; 4].

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].

Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал

На рисунке изображен график функции f(x), определенной на интервале (−7; 4). Найдите сумму точек экстремума функции f(x).

На рисунке изображен график функции y  =  f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).

Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402

На рисунке изображён график функции y  =  f(x), определённой на интервале (−8; 5). Найдите сумму точек экстремума функции f(x).

На рисунке изображён график функции y  =  f(x), определённой на интервале (−4; 8). Найдите сумму точек экстремума функции f(x).

На рисунке изображен график функции y  =  f(x), определенной на интервале (−3; 9) . Найдите количество точек, в которых производная функции f(x) равна 0.

Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 401

На рисунке изображен график функции y  =  f(x),определенной на интервале Найдите количество точек, в которых производная функции f(x) равна 0.

На рисунке изображен график функции y  =  f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых производная функции f(x) равна 0.

На рисунке изображён график функции y  =  F(x)  — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)  =  0 на отрезке [−2; 4].

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.

Всего: 692 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 627 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь

Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал

Найдите точку минимума функции

Найдите точку максимума функции

Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402

Найдите точку максимума функции

Найдите точку максимума функции принадлежащую промежутку

Всего: 627 1–20 | 21–40 | 41–60 | 61–80 …

Источник

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Исследование частных

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 11 № 77467

Найдите точку максимума функции

Аналоги к заданию № 77467: 129843 129871 523993 524020 548510 548529 129845 129847 129849 129851 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на бесконечном промежутке

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 77468

Найдите точку минимума функции

Аналоги к заданию № 77468: 129873 129899 129901 129875 129877 129879 129881 129883 129885 129887 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 11 № 77469

Найдите наименьшее значение функции на отрезке

Аналоги к заданию № 77469: 129903 129931 129905 129907 129909 129911 129913 129915 129917 129919 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 77470

Найдите наибольшее значение функции на отрезке

Аналоги к заданию № 77470: 129933 129961 129935 129937 129939 129941 129943 129945 129947 129949 … Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 11 № 77471

Найдите точку максимума функции

Аналоги к заданию № 77471: 129965 129963 130011 129967 129969 129971 129973 129975 129977 129979 … Все

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Поиск точек экстремума у элементарных функций

(blacktriangleright) Простейшие элементарные функции (ПЭФ) и их производные: [begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]

(blacktriangleright) Элементарные функции (ЭФ) — любые линейные комбинации простейших элементарных функций (то есть их сумма, разность, умножение на число).

Пример: (f(x)=4cos x +dfrac{x^3}2)

(blacktriangleright) Основные формулы поиска производной ((f=f(x), g=g(x)) – функции):

1. Умножение функции на число: [(ccdot f)’=ccdot f’]

2. Сумма или разность двух функций: [(fpm g)’=f’pm
g’]

(blacktriangleright) Хитрости, упрощающие поиск производной:

I. Т.к. (sqrt[n]{x^m}=x^{frac mn}), то производную этой функции можно искать по формуле (2).

Частный случай: (sqrt x =x^{frac12}): [(sqrt x)’=dfrac1{2sqrt x}]

II. Т.к. (dfrac1{x^a}=x^{-a}), то производную этой функции можно также искать по формуле (2): [left(dfrac1{x^a}right)’=-dfrac a{x^{a+1}}]

(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).

Задание
1

#2390

Уровень задания: Легче ЕГЭ

Найдите точку максимума функции (y = -x^2).

ОДЗ: (x) – произвольный.

1) [y’ = -2x]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2x = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, (x = 0) – точка максимума функции (y).

Ответ: 0

Задание
2

#2391

Уровень задания: Легче ЕГЭ

Найдите точку минимума функции (y = x^2 + 2x + 2) на отрезке ([-2; 2]).

ОДЗ: (x) – произвольный.

1) [y’ = 2x + 2]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x + 2 = 0qquadLeftrightarrowqquad x = -1,.] Производная существует при любом (x).

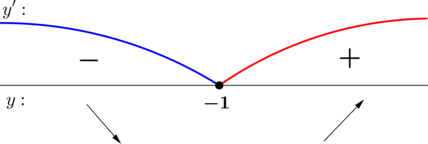
2) Найдём промежутки знакопостоянства (y’):

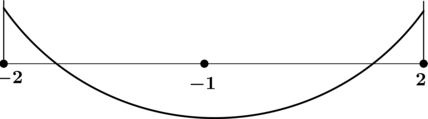
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-2; 2]):

4) Эскиз графика на отрезке ([-2; 2]):

Таким образом, (x = -1) – точка минимума функции (y) на ([-2; 2]).

Ответ: -1

Задание
3

#2392

Уровень задания: Легче ЕГЭ

Найдите точку минимума функции (y = 3x^2 — 6x + pi) на отрезке ([-3; 3]).

ОДЗ: (x) – произвольный.

1) [y’ = 6x — 6]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [6x — 6 = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

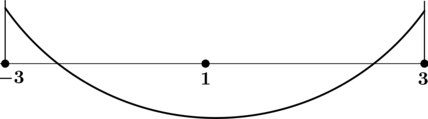
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-3; 3]):

4) Эскиз графика на отрезке ([-3; 3]):

Таким образом, (x = 1) – точка минимума функции (y) на ([-3; 3]).

Ответ: 1

Задание
4

#2691

Уровень задания: Равен ЕГЭ

Найдите точку локального минимума функции (y = x^3 — 3x).

ОДЗ: (x) – произвольный.

1) [y’ = 3x^2 — 3]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3x^2 — 3 = 0qquadLeftrightarrowqquad x = pm 1,.] Производная существует при любом (x).

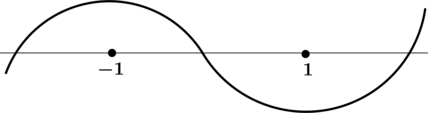
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 1) – точка локального минимума функции (y).

Ответ: 1

Задание
5

#2710

Уровень задания: Равен ЕГЭ

Найдите точку локального максимума функции

(y = x^3 — 15x^2 + 48x + e).

1) (y’ = 3x^2 — 30x + 48 = 3(x^2 — 10x + 16)).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):

[3(x^2 — 10x + 16) = 0qquadLeftrightarrowqquad x^2 — 10x + 16 = 0,] откуда находим (x_1 = 2, x_2 = . Таким образом, [y’ = 3(x — 2)(x — 8).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 2) – точка локального максимума функции (y).

Ответ: 2

Задание
6

#869

Уровень задания: Равен ЕГЭ

Найдите точку локального максимума функции (y = dfrac{1}{3}x^3 — 8x^2 + 55x + 11).

1) (y’ = x^2 — 16x + 55).

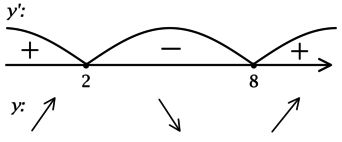
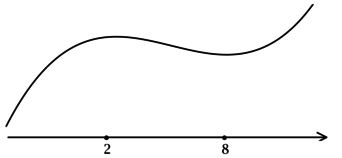
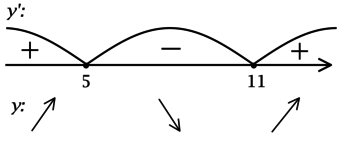
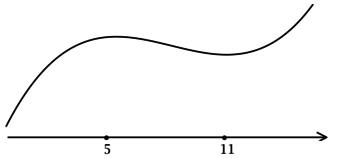
(x^2 — 16x + 55 = 0), откуда находим корни (x_1 = 5, x_2 = 11). Таким образом, [y’ = (x-5)(x-11).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 5) – точка локального максимума функции (y).

Ответ: 5

Задание
7

#868

Уровень задания: Равен ЕГЭ

Найдите точку локального минимума функции (y = dfrac{1}{3}x^3 — 3x^2 + 8x + 2).

1) (y’ = x^2 — 6x + .

(x^2 — 6x + 8 = 0), откуда находим корни (x_1 = 2, x_2 = 4). Таким образом, [y’ = (x-2)(x-4).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 4) – точка локального минимума функции (y).

Ответ: 4

Задачи, при выполнении которых требуется найти точки экстремума у элементарных функций, в ЕГЭ по математике включаются каждый год. Уметь справляться с ними должны школьники, сдающие как базовый уровень экзамена, так и профильный. Научившись безошибочно находить максимум и минимум элементарной функции в задачах ЕГЭ, выпускники смогут выполнить задание и получить конкурентные баллы.

Восполнить пробелы в знаниях и лучше усвоить информацию вам поможет образовательный проект «Школково». Чтобы учащимся было легче справляться с задачами ЕГЭ, в которых необходимо найти минимум и максимум элементарной функции, мы предлагаем прежде всего повторить определения и основные правила. Эту информацию мы разместили в разделе «Теоретическая справка». Здесь собран материал, подготовленный нашими специалистами для выпускников средних школ.

Чтобы закрепить усвоенную информацию и научиться справляться с задачами в ЕГЭ, выполните упражнения, в которых требуется найти точки экстремума у элементарных функций. Богатая подборка задач представлена в разделе «Каталог». Задания здесь регулярно обновляются и дополняются. Выполнить упражнения на нахождение точек экстремума у элементарных функций, которые встречаются в ЕГЭ, можно в режиме онлайн, находясь в Москве или любом другом городе России.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

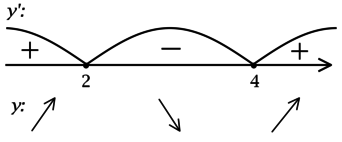
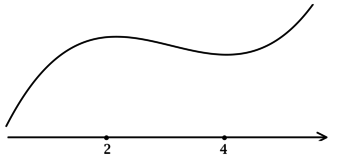
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Точки экстремума функции»

Открытый банк заданий по теме точки экстремума функции. Задания B12 из ЕГЭ по математике (профильный уровень)

Тригонометрические уравнения

Задание №1136

Условие

Найдите наибольшее значение функции y=(7x^2-56x+56)e^x на отрезке [-3; 2].

Показать решение

Решение

Найдём производную исходной функции по формуле производной произведения y’= (7x^2-56x+56)’e^x,+ (7x^2-56x+56)left(e^xright)’= (14x-56)e^x+(7x^2-56x+56)e^x= (7x^2-42x)e^x= 7x(x-6)e^x. Вычислим нули производной: y’=0;

7x(x-6)e^x=0,

x_1=0, x_2=6.

Расставим знаки производной и определим промежутки монотонности исходной функции на заданном отрезке.

Из рисунка видно, что на отрезке [-3; 0] исходная функция возрастает, а на отрезке [0; 2] — убывает. Таким образом, наибольшее значение на отрезке [-3; 2] достигается при x=0 и равно y(0)= 7cdot 0^2-56cdot 0+56=56.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1135

Условие

Найдите наибольшее значение функции y=12x-12tg x-18 на отрезке left[0;,frac{pi}{4}right].

Показать решение

Решение

Найдём производную исходной функции:

y’= (12x)’-12(tg x)’-(18)’= 12-frac{12}{cos ^2x}= frac{12cos ^2x-12}{cos ^2x}leqslant0. Значит, исходная функция является невозрастающей на рассматриваемом промежутке и принимает наибольшее значение на левом конце отрезка, то есть при x=0. Наибольшее значение равно y(0)= 12cdot 0-12 tg (0)-18= -18.

Ответ

-18

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1134

Условие

Найдите точку минимума функции y=(x+8)^2e^{x+52}.

Показать решение

Решение

Будем находить точку минимума функции с помощью производной. Найдём производную заданной функции, пользуясь формулами производной произведения, производной x^alpha и e^x:

y'(x)= left((x+8)^2right)’e^{x+52}+(x+8)^2left(e^{x+52}right)’= 2(x+8)e^{x+52}+(x+8)^2e^{x+52}= (x+8)e^{x+52}(2+x+8)= (x+8)(x+10)e^{x+52}.

Расставим знаки производной и определим промежутки монотонности исходной функции. e^{x+52}>0 при любом x. y’=0 при x=-8, x=-10.

Из рисунка видно, что функция y=(x+8)^2e^{x+52} имеет единственную точку минимума x=-8.

Ответ

-8

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1133

Условие

Найдите точку максимума функции y=8x-frac23x^tfrac32-106.

Показать решение

Решение

ОДЗ: x geqslant 0. Найдём производную исходной функции:

y’=8-frac23cdotfrac32x^tfrac12=8-sqrt x.

Вычислим нули производной:

8-sqrt x=0;

sqrt x=8;

x=64.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что точка x=64 является единственной точкой максимума заданной функции.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1132

Условие

Найдите наименьшее значение функции y=5x^2-12x+2ln x+37 на отрезке left[frac35; frac75right].

Показать решение

Решение

ОДЗ: x>0.

Найдём производную исходной функции:

y'(x)= 10x-12+frac{2}{x}= frac{10x^2-12x+2}{x}.

Определим нули производной: y'(x)=0;

frac{10x^2-12x+2}{x}=0,

5x^2-6x+1=0,

x_{1,2}= frac{3pmsqrt{3^2-5cdot1}}{5}= frac{3pm2}{5},

x_1=frac15notinleft[frac35; frac75right],

x_2=1inleft[frac35; frac75right].

Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом промежутке.

Из рисунка видно, что на отрезке left[frac35; 1right]исходная функция убывает, а на отрезке left[1; frac75right]возрастает. Таким образом, наименьшее значение на отрезке left[frac35; frac75right]достигается при x=1 и равно y(1)= 5cdot 1^2-12cdot 1+2 ln 1+37= 30.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1131

Условие

Найдите наибольшее значение функции y=(x+4)^2(x+1)+19 на отрезке [-5; -3].

Показать решение

Решение

Найдём производную исходной функции, используя формулу производной произведения:

y’= left((x+4)^2right)'(x+1)+(x+4)^2(x+1)’= (19)’= 2(x+ 4)(x+1)+(x+4)^2= (x+4)(2x+2+x+4)= (x+4)(3x+6)= 3(x+4)(x+2).

Отыщем нули производной: y'(x)=0;

(x+4)(x+2)=0;

x_1=-4, x_2=-2.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Из рисунка видно, что на отрезке [-5; -4] исходная функция возрастает, а на отрезке [-4; -3] убывает. Таким образом, наибольшее значение на отрезке [-5; -3] достигается при x=-4 и равно y(-4)= (-4+4)^2(-4+1)+19= 19.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1130

Условие

Найдите точки минимума функции y=sqrt{x^2+60x+1000}.

Показать решение

Решение

Область определения: x^2+60x+1000 geqslant 0;

x^2 +2cdot30x+30^2+(1000-30^2)= (x+30)^2+100>0 для всех вещественных значений x. Заметим, что функция y=sqrt t строго возрастает на множестве tgeqslant0. Отсюда точка минимума исходной функции совпадёт с точкой минимума x_0 функции x^2+60x+1000. Точка минимума квадратичной функции с положительным старшим коэффициентом совпадает с абсциссой вершины соответствующей параболы. Вершина параболы имеет абсциссу x_0=-frac{60}{2cdot1}=-30.

Ответ

-30

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1129

Условие

Найдите наименьшее значение функции y=(5x^2-70x+70)e^{x-12} на отрезке [10; 15].

Показать решение

Решение

Найдём производную исходной функции по формуле производной произведения

y’= (5x^2-70x+70)’e^{x-12},+ (5x^2-70x+70)left(e^{x-12}right)’= (10x-70)e^{x-12},+ (5x^2-70x+70)e^{x-12}= (5x^2-60x)e^{x-12}= 5x(x-12)e^{x-12}.

Вычислим нули производной: y’=0;

5x(x-12)e^{x-12}=0,

x_1=0, x_2=12.

Расставим знаки производной и определим промежутки монотонности исходной функции на заданном отрезке.

Из рисунка видно, что на отрезке [10; 12] исходная функция убывает, а на отрезке [12; 15] — возрастает. Таким образом, наименьшее значение на отрезке [10; 15] достигается при x=12 и равно y(12)= (5cdot 12^2-70cdot 12+70)e^{12-12}= -50.

Ответ

-50

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1128

Условие

Найдите наименьшее значение функции y=32tg x — 32x-8pi+103 на отрезке left[-frac{pi}{4}; frac{pi}{4}right].

Показать решение

Решение

Найдём производную исходной функции:

y’= 32(tg x)’-(32x)’-(8pi )’+(103)’= frac{32}{cos ^2x}-32= frac{32-32cos ^2x}{cos ^2x}geqslant0. Значит, исходная функция является неубывающей на рассматриваемом промежутке и принимает

наименьшее значение на левом конце отрезка, то есть при x=-frac{pi}{4}. Наименьшее значение равно yleft(-frac{pi}{4}right)= 32tgleft(-frac{pi}{4}right)-32cdotleft(-frac{pi}{4}right)-8pi+103= -32+103= 71.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1127

Условие

Найдите точку максимума функции y=(x+3)^2e^{x-2016}.

Показать решение

Решение

Будем находить точку максимума функции с помощью производной. Найдём производную заданной функции, пользуясь формулами производной произведения, производной x^alpha и e^x:

y'(x)= left((x+3)^2right)’e^{x-2016}+(x+3)^2left(e^{x-2016}right)’= 2(x+3)e^{x-2016}+(x+3)^2e^{x-2016}= (x+3)e^{x-2016}(2+x+3)= (x+3)(x+5)e^{x-2016}.

Расставим знаки производной и определим промежутки монотонности исходной функции.

Так как e^{x-2016}>0 для любого x, то y’=0 при x=-3, x=-5.

Из рисунка видно, что функция y=(x+3)^2e^{x-2016} имеет единственную точку максимума x=-5.

Ответ

-5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Задачи по теме
«Исследование функции на экстремум»

1. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

2. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

3. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

4. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

5. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г) множество
значений функции на

6. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

7. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

8. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

9. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

10. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

11. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

12. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

13. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

14. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

15. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

16. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

17. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

18. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г) множество
значений функции на

19. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

20. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

21. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

22. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

23. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

24. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

25. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

26. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

27. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

28. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

29. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

30. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

31. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

32. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

33. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

34. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

35. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

36. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г) множество
значений функции на

37. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

38. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

39. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

40. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

41. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

42. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

43. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

44. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

45. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

46. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

47. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

48. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

49. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г) множество
значений функции на

50. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

51. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

52. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

53. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

54. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

55. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

56. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

57. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

58. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

59. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

60. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

61. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

62. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

63. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

64. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

65. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

66. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

67. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г) множество
значений функции на

68. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

69. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

70. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

71. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

72. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

73. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

74. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

75. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

76. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

77. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

78. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

79. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

80. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

81. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

82. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

83. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

84. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

85. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

86. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

87. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

88. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

89. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

90. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

91. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

92. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

93. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

94. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

95. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

96. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

97. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

98. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г) множество
значений функции на

99. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

100. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

101. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

102. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

103. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

104. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

105. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

106. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

107. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

108. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

109. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

110. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

111. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

112. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

113. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

114. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

115. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

116. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

117. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

118. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

119. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

120. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

121. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

122. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

123. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

124. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

125. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

126. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

127. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

128. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

129. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

130. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

131. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г) множество
значений функции на

132. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

133. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

134. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

135. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

136. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

137. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

138. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

139. Найдите: а) точки экстремума; б) максимумы; в) минимумы; г)
множество значений функции на

№ п/п	Ответ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139

Источник