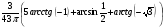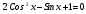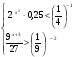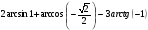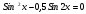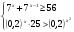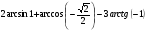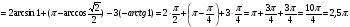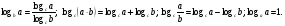Экзамен алгебра 11 класс емн

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

  • Вход / Регистрация

  • Пробный ЕНТ
  • Лента ЕНТ вопросов
  • Тесты по предметам
  • ВОУД
  • Итоговые экзамены 11 класс
  • Новости
  • Подписка
  • Контакты

Алгебра и начала анализа

Выберите направление

Выберите направление

Выберите направление

Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

Источник

Итоговая аттестация по математике ( ЕМН, 2018 год)

Вариант первый

1. Вычислите:

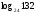
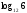
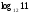
2. Выразите через а и в, если = а, = в

3. Решите уравнение:

4. Решите систему неравенств:

5. Участок в форме прямоугольника площадью 2 га огорожен забором. Найдите стороны участка, имеющего наименьший периметр.

6. Исследуйте функцию и постройте ее график: .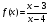

Вариант второй

1. Вычислите:

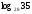
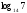
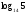
2. Выразите через а и в, если = а , = в

3. Решите уравнение:

4. Решите систему неравенств:

5. Периметр прямоугольника равен 90 метров. Найдите стороны прямоугольника наибольшей площади.

6. Исследуйте функцию и постройте ее график: .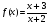

Вариант второй

  1. Вычислите:

Решение. =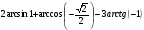

При решении использовались формулы:

arccos(- a)=π – arccosa, arctg(- a)= – arctga.

Ответ:2,5π.

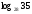
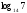
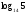
2. Выразите через а и в, если а= , в = .

Решение.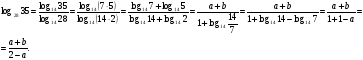

При решении использовались формулы:

Ответ:

  1. Решите уравнение:

Решение.

Формулы: Sin2x=2Sin x Cosx;

Ответ:

  1. Решите систему неравенств:

Решение.

Формулы:

Ответ:

  1. Периметр прямоугольника равен 90 метров. Найдите стороны прямоугольника наибольшей площади.

Решение. Пусть стороны прямоугольника равны а и b ( a0, b0). Тогда:

6. Исследуйте функцию и постройте ее график.

Решение.

  1. Область определения:

  2. Область значений:

  3. Функция ни четная, ни нечетная

  4. Функция не периодическая.

  5. x = — 2 — вертикальная асимптота, у=1 – горизонтальная асимптота.

  7. Функция не имеет точек экстремума.

  8. Строим график функции.

Хафизов Р.З.

Источник

Решения заданий СОР и СОЧ за 11 класс ЕМН

Записаться на онлайн-занятия

2 четверть

СОР 1 по алгебре, объясняет Дария:

СОР 2 по алгебре, объясняет Дария:

СОР 3 по алгебре, объясняет Дария:

СОЧ по алгебре, объясняет Дария:

СОР 1 по геометрии, объясняет Айгерим:

СОР 2 по геометрии, объясняет Айгерим:

СОЧ по геометрии, объясняет Айгерим:

3 четверть

СОР 1 по алгебре, объясняет Айгерим:

СОР 2 по алгебре, объясняет Айгерим:

СОЧ по алгебре, объясняет Айгерим:

СОР по геометрии, объясняет Айгерим:

СОЧ по геометрии, объясняет Айгерим:

Есть ещё физика.

Источник

Годовая контрольная работа по алгебре состоит из 2 вариантов (по 4 задания).

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

Просмотр содержимого документа

«Годовая контрольная работа по алгебре для учащихся 11 классов (ЕМН)»

Источник

С этим файлом связано 1 файл(ов). Среди них: СОЧ Информатика 9-класс 2-четверт. 1-лист.pdf.
Показать все связанные файлы

Подборка по базе: ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА III ЧЕТВЕРТЬ. История Каз , методические рекомендации по курсовым работам (1)-2.doc, КЛИНИЧЕСКИЕ РЕКОМЕНДАЦИИ (ПРОТОКОЛЫ) ПО ОКАЗАНИЮ СКОРОЙ МЕДИЦИНС, Методические рекомендации для проведения стажировки.doc, Теоретические и методические основы организации продуктивных вид, Методические рекомендации Интернет и дети.doc, Метод рекомендации для практ работ по ЦДРиД_2014.pdf, Требования и рекомендации по проектам.docx, Требования к оформлению и общие методические указания по выполне, ТЕМА 1 Теоретический материал, методические указания для обучающ

СОДЕРЖАНИЕ

ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ 4

Суммативное оценивание за раздел «Первообразная и интеграл» 4

Суммативное оценивание за раздел «Элементы математической статистики» 8

ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ 12

Суммативное оценивание за раздел «Степени и корни. Степенная функция» 12

Суммативное оценивание за раздел «Иррациональные уравнения и неравенства» 16

ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ 19

Суммативное оценивание за раздел «Комплексные числа» 19

Суммативное оценивание за раздел «Показательная и логарифмическая функции» 22

Суммативное оценивание за раздел «Показательные и логарифмические уравнения и неравенства» 26

ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ 29

Суммативное оценивание за раздел «Дифференциальные уравнения» 29

Методические рекомендации составлены в помощь учителю при планировании, организации и проведении суммативного оценивания за раздел по предмету «Алгебра и начала анализа» для обучающихся 11 классов естественно-математического направления. Методические рекомендации подготовлены на основе типовой учебной программы и учебного плана.

Задания для суммативного оценивания за раздел/сквозную тему позволят учителю определить уровень достижения обучающимися целей обучения, запланированных на четверть.

Для проведения суммативного оценивания за раздел/сквозную тему в методических рекомендациях предлагаются задания, критерии оценивания с дескрипторами и баллами. Также в сборнике описаны возможные уровни учебных достижений обучающихся (рубрики). Задания с дескрипторами и баллами носят рекомендательный характер.

Методические рекомендации предназначены для учителей, администрации школ, методистов отделов образования, школьных и региональных координаторов по критериальному оцениванию и других заинтересованных лиц.
При подготовке методических рекомендаций использованы ресурсы (рисунки, фотографии, тексты, видео- и аудиоматериалы и др.), находящиеся в открытом доступе на официальных интернет-сайтах.

ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ

Суммативное оценивание за раздел «Первообразная и интеграл»
Тема Первообразная и неопределенный интеграл. Свойства неопределенного интеграла

Методы интегрирования

Криволинейная трапеция и ее площадь. Определенный интеграл

Применение определенного интеграла при решении геометрических и физических задач
Цель обучения 11.4.1.3

11.4.1.5
11.4.1.7
11.4.1.8
11.4.2.1

 Знать основные неопределенные интегралы:

1. kdx kx C

n xn1

2. xdx n 1 C, n 1;

  1. cos xdx sin x C;
  2. sin xdx cos x C;
  3. dx tgx C;

cos2 x

  1. dx ctgx C, и применять их

sin 2 x

при решении задач

Находить интеграл, используя методинтегрирования по частям

Знать понятие определённого интеграла, уметь вычислять определённый интеграл

Вычислять площадь плоской фигуры, ограниченной заданными линиями Применять определённый интеграл для решения физических задач на вычисление работы и расстояния
Критерий оценивания Обучающийся

  • Применяет основные неопределенные интегралы
  • Применяет метод интегрирования по частям для нахождения неопределенного интеграла
  • Использует формулу Ньютона-Лейбница для вычисления определенного интеграла
  • Вычисляет площадь плоской фигуры, ограниченной заданными линиями
  • Использует определенный интеграл для решения физических задач на вычисление расстояния
Уровень мыслительных навыков Применение

Навыки высокого порядка
Время выполнения 30 минут
Задания

  1. Найдите неопределенный интеграл: x2 6 sin 2xdx.

2.

    1. Найдите xexdx.

1

b)Вычислите xexdx.

0

  1. Кривая Сзадана уравнением y

, линия Lзадана уравнением

y x, а линия N-

    1. Изобразите на чертеже область, ограниченную кривыми C,Lи N.
    1. Покажите, что абсциссой точки пересечения линий Cи L, является x 2 . с) Вычислите площадь фигуры, ограниченной кривыми C, Lи N.
  1. Скорость прямолинейного движения тела выражается формулой Найдите путь, пройденный телом за 5 секунд от начала движения.

v 2t 3t2

(м/с).

Критерий оценивания №

задания

 Дескриптор Балл
Обучающийся
Применяет основные неопределенные интегралы

1

 находит интеграл степенной функции; 1
находит интеграл тригонометрической

функции;

 1
находит неопределенный интеграл; 1
Применяет метод интегрирования по частям для нахождения неопределенного интеграла

2a

 вводит соответствующую замену; 1
находит интеграл показательной

функции;

 1
применяет формулу метода

интегрирования по частям;

 1
находит неопределенный интеграл; 1
Использует формулу Ньютона-Лейбница для

вычисления определенного интеграла

2b

 применяет формулу Ньютона –

Лейбница;

 1
вычисляет определенный интеграл; 1
Вычисляет площадь

плоской фигуры, ограниченной заданными линиями

3а

 изображает на координатной плоскости область, ограниченную кривыми C,Lи

N;

1

3b

 составляет уравнение, используя

уравнения линий Cи L;

 1
решает полученное уравнение; 1
находит абсциссу с учётом ОДЗ; 1

3с

 находит площадь фигуры,

ограниченной линией L и прямой х=2;

 1
находит площадь фигуры, ограниченной линией С и прямыми х =

2 и х = 7;

1
вычисляет площадь искомой фигуры; 1
Использует определенный интеграл для решения физических задач на вычисление расстояния

4

 использует формулу для нахождения расстояния через определенный

интеграл;

1
находит первообразную функции; 1
применяет формулу Ньютона –

Лейбница;

 1
вычисляет путь, пройденным телом. 1
Итого: 20

Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Первообразная и интеграл»

Фамилия обучающегося

Критерий оценивания Уровень учебных достижений
Низкий Средний Высокий
Применяет основные неопределенные интегралы Затрудняется основных интегралов в применении неопределенных Допускает ошибки в применении формул основных неопределенных интегралов Вычисляет интеграл неопределенный
Применяет метод интегрирования по частям для нахождения неопределенного интеграла Затрудняется в использовании метода интегрирования по частям для нахождения неопределенного интеграла Допускает ошибки использовании метода интегрирования по частям для нахождения неопределенного интеграла Находит неопределенный интеграл, применяя метод интегрирования по частям
Использует формулу Ньютона-Лейбница для вычисления определенного интеграла Затрудняется в вычислении определенного интеграла Допускает ошибки первообразной, ошибки в нахождении вычислительные Применяет формулу Ньютона- Лейбница для вычисления определенного интеграла
Вычисляет площадь плоской фигуры, ограниченной заданными линиями Затрудняется в вычислении площади плоской фигуры, ограниченной заданными линиями Допускает ошибки при нахождении первообразной, вычислительные ошибки Строит фигуру, ограниченную заданными линиями, и вычисляет площадь фигуры
Использует определенный интеграл для решения физических задач на вычисление расстояния Затрудняется в использовании определенного интеграла для решения физических задач на вычисление расстояния Находит расстояние, используя определенный интеграл; допускает ошибки в нахождении первообразной, вычислительные ошибки Решает физическую задачу на применение определенного интеграла
Источник

Понравилась статья? Поделить с друзьями:
  • Экзамен айлтс что это
  • Экзамен айлтс сдать в москве
  • Экзамен айлтс по английскому цена
  • Экзамен айлтс по английскому задания
  • Экзамен айлтс по английскому в москве