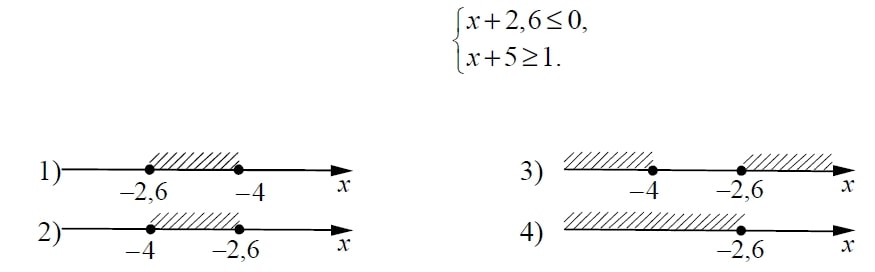Экзамен демо математика 9 класс - Помощь в подготовке к экзаменам и поступлению

Демонстрационная версия ОГЭ 2021−2023 по математике

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

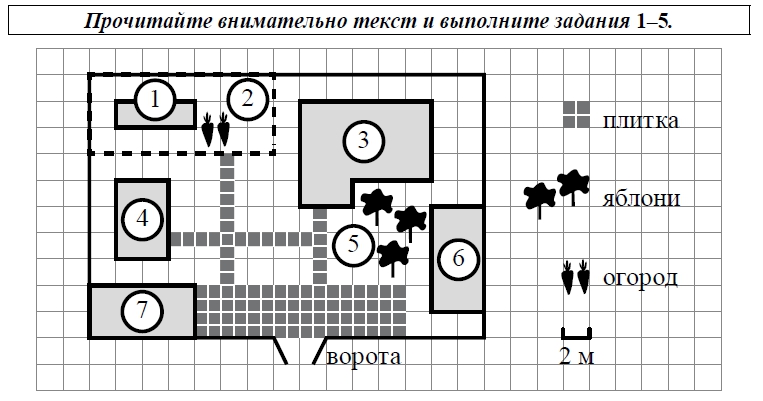
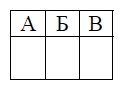
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	жилой дом	сарай	баня	теплица
Цифры

Показать

Ответ:

Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?

Показать

Ответ:

Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.

Показать

Ответ:

Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.

Показать

Ответ:

Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.

	Нагреватель (котел)	Прочее оборудование и монтаж	Сред. расход газа / сред. потребл. мощность	Стоимость газа / электро-энергии
Газовое отопление	24 тыс. руб.	18 280 руб.	1,2 куб. м/ч	5,6 руб./куб. м
Электр. отопление	20 тыс. руб.	15 000 руб.	5,6 кВт	3,8 руб./(кВт · ч )

Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости покупки и установки газового и электрического отопления?

Показать

Ответ:

Найдите значение выражения

Ответ:

На координатной прямой отмечена точка А.

Известно, что она соответствует одному из четырех указанных ниже чисел. Какому из чисел соответствует точка А?

3)  0,6

4)  4

Ответ:

Найдите значение выражения при a  =  5.

Ответ:

Решите уравнение

Если уравнение имеет более одного корня, в ответ запишите больший из корней.

Ответ:

На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.

Ответ:

Установите соответствие между графиками функций и формулами, которые их задают.

Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.

Ответ:

Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой t_F  =  1,8t_C + 32, где t_C  — температура в градусах Цельсия, t_F  — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует −25 градусов по шкале Цельсия?

Ответ:

Решите систему неравенств

На каком рисунке изображено множество её решений?

1)  1

2)  2

3)  3

4)  4

Ответ:

Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика в пятый день?

Ответ:

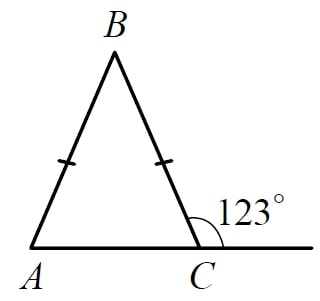
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

Ответ:

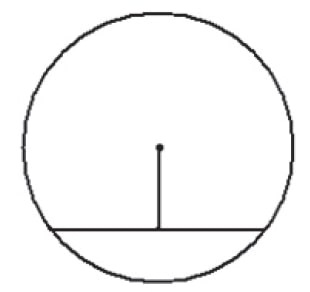
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.

Ответ:

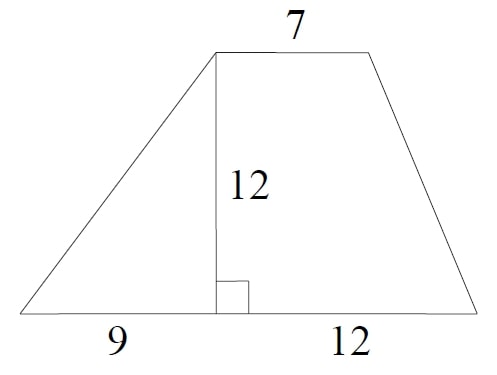
Найдите площадь трапеции, изображённой на рисунке.

Ответ:

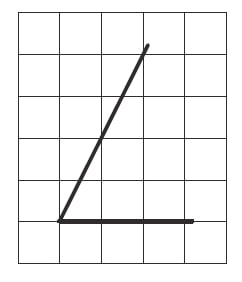
Найдите тангенс острого угла, изображённого на рисунке.

Ответ:

Какие из следующих утверждений верны?

1)  Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2)  Треугольник со сторонами 1, 2, 4 существует.

3)  В любом параллелограмме есть два равных угла.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Ответ:

Решите уравнение

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?

Постройте график функции и определите, при каких значениях параметра с прямая y  =  c имеет с графиком ровно одну общую точку.

В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC  =  6 , BC  =  8 . Найдите медиану CK этого треугольника.

В параллелограмме ABCD точка E  — середина стороны AB. Известно, что EC  =  ED. Докажите, что данный параллелограмм  — прямоугольник.

Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

В данном разделе представлены документы, определяющие структуру и содержание контрольных измерительных материалов основного государственного экзамена 2023 года:

— кодификаторы проверяемых требований к результатам освоения основной образовательной программы основного общего образования и элементов содержания для проведения основного государственного экзамена;

— спецификации контрольных измерительных материалов для проведения основного государственного экзамена по общеобразовательным предметам обучающихся, освоивших основные общеобразовательные программы основного общего образования;

— демонстрационные варианты контрольных измерительных материалов для проведения основного государственного экзамена по общеобразовательным предметам обучающихся, освоивших основные общеобразовательные программы основного общего образования.

Источник

Официальная демоверсия ОГЭ 2023 от ФИПИ.

Изменения структуры и содержания КИМ отсутствуют.

Работа содержит 25 заданий и состоит из двух частей. Часть 1 содержит 19 заданий с кратким ответом; часть 2 – 6 заданий с развёрнутым ответом.

На выполнение экзаменационной работы отводится 3 часа 55 минут.

Участникам экзамена разрешается использовать: линейку, не содержащую справочной информации; выдаваемые вместе с КИМ справочные материалы, содержащие основные формулы курса математики образовательной программы основного общего образования.

Обновлено 10 ноября. Демоверсия утверждена.

→ Демоверсия: ma-9-oge-2023_demo.pdf
→ Спецификация: ma-9-oge-2023_spec.pdf
→ Кодификатор: ma-9-oge-2023_kodif.pdf
→ Скачать одним архивом: ma_9_2023.zip

Обобщённый план варианта КИМ ОГЭ 2023 года по математике

№	Требования к уровню подготовки выпускников, проверяемому на ЕГЭ	Уровень сложности задания	Макс. балл за выполнение задания
Часть 1
1	Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели	Б	1
2	Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели	Б	1
3	Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели	Б	1
4	Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели	Б	1
5	Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели	Б	1
6	Уметь выполнять вычисления и преобразования	Б	1
7	Уметь выполнять вычисления и преобразования	Б	1
8	Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений	Б	1
9	Уметь решать уравнения, неравенства и их системы	Б	1
10	Уметь работать со статистической информацией, находить частоту и вероятность случайного события, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели	Б	1
11	Уметь строить и читать графики функций	Б	1
12	Осуществлять практические расчёты по формулам; составлять несложные формулы, выражающие зависимости между величинами	Б	1
13	Уметь решать уравнения, неравенства и их системы	Б	1
14	Уметь строить и читать графики функций, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели	Б	1
15	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1
`16	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1
17	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1
18	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1
19	Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения	Б	1
Часть 2
20	Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы	П	2
21	Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели	П	2
22	Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели	В	2
23	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	П	2
24	Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения	П	2
25	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	В	2
Всего заданий – 25; из них по типу заданий: заданий с кратким ответом – 19; заданий с развёрнутым ответом – 6; по уровню сложности: Б – 19; П – 4; В – 2. Максимальный первичный балл за работу – 31. Общее время выполнения работы – 3 часа 55 минут.

Источник

Демоверсии и КИМы

Математика — обязательное испытание в списке ОГЭ. Этот предмет является одним из наиболее трудных и требует особенной подготовки. Начать ее следует с изучения официальных документов ФИПИ — кодификатора, спецификации и демоверсий. Эти бумаги определяют состав и содержание госэкзамена.

Все официальные документы для подготовки к ОГЭ по математике в 2023 году вы найдете в данном разделе. С помощью них, вы:

узнаете, какие требования предъявляются к экзаменационным работам;
познакомитесь с перечнем тем, которые могут встретиться на госэкзамене;
узнаете структуру испытания и время его проведения;
сможете испытать свои силы в решении экзаменационных задач;
получите возможность потренироваться.

Скачивайте документы на свой компьютер или знакомьтесь с ними онлайн, тренируйте свои навыки и знания.

Полезная информация

Смотреть все

Источник

25.08.2021

Официальная демоверсия ЕГЭ для 2022 года по математике для 9 классов.

Изменения в КИМ ОГЭ 2022 года относительно КИМ ОГЭ 2021 года отсутствуют.

Автор-составитель: ФИПИ.

Отдельные документы к демоверсии:

Кодификатор ЕГЭ 2022 по математике
Спецификация ЕГЭ 2022 по математике

Дополнительно рекомендуем практику:

Тренировочные варианты ОГЭ по математике
Демоверсии ОГЭ 2022 по другим предметам

Обсудить задания демоверсии и получить ответы на свои вопросы вы можете в комментариях ниже. Пишите!

Подробный видеоразбор демоверсии ОГЭ 2022 по математике

Задания из демоверсии ОГЭ 2022 по химии

ЗАДАНИЕ 2

Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку
перед гаражом?

ЗАДАНИЕ 4

Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.

ЗАДАНИЕ 9

Решите уравнение x² + x −12 = 0.

Если уравнение имеет более одного корня, в ответ запишите больший из корней.

ЗАДАНИЕ 10

На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность
того, что пирожок окажется с яблоками.

ЗАДАНИЕ 14

Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же
количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый
день?

ЗАДАНИЕ 21

Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу
и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки равна 6 км/ч?

Вариант демоверсии в формате PDF

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Источник

Демонстрационные варианты по математике (алгебре) 2010 года представлены в двух видах: демонстрационный вариант 1 и демонстрационный вариант 2. Отличие между ними заключается в том, что первая часть демонстрационного варианта 2 содержит на две задачи больше, чем первая часть демонстрационного варианта 1 (задачи 17 и 18) Эти задачи относятся к теории вероятностей и статистике. Других отличий нет.

Демонстрационный вариант ОГЭ по математике (алгебре) 2011 года почти полностью совпадает с демонстрационным вариантом 2 ОГЭ по математике (алгебре) 2010 года. Отличие заключается лишь в заданиях №10 и №22.

В 2011 году в ряде регионов в порядке эксперимента для проведения ОГЭ-9 по математике была использована перспективная модель КИМов, проект демонстрационного варианта которой мы также размещаем.

В 2012 году в демонстрационный вариант ОГЭ по математике были включены не только задания по алгебре, теории вероятностей и статистике, но также и задания по геометрии.

Демонстрационные варианты ОГЭ по математике 2013-2017 годов отличаются от вариантов предыдущих лет. В них

Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Модули «Алгебра» и «Геометрия» состоят из двух частей: во второй части задачи более сложные по сравнению с первой частью.
За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания расположены по нарастанию сложности и оцениваются в 2 балла (в 2, 3 и 4 балла в демонстрационных вариантах по математике 2013-2015 годов).
Рекомендуемый минимальный порог выполнения экзаменационной работы – 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что по модулю «Алгебра» набрано не менее 3 баллов, по модулю «Геометрия» набрано не менее 2 баллов и по модулю «Реальная математика»набрано не менее 2 баллов.

Демонстрационный вариант ОГЭ по математике 2014 годапрактически полностью совпадает с демонстрационным вариантом ОГЭ по математике 2013 года. Небольшое отличие имеется лишь в задаче №13, где требуется указать номера верных утверждений: в 2013 году условие этой задачи содержало 3 утверждения, а 2014 году к этим трем утверждениям было добавлено еще одно.

В демонстрационном варианте ОГЭ по математике 2015 года по сравнению с демонстрационным вариантом 2014 года были заменены задачи 1, 2, 3, 4, 6, 7, 10 и 17 на другие по той же тематике. Задачи 8 и 12 претерпели лишь косметические изменения. Из чертежа задачи 11 по геометрии удалены лишние данные. Остальные задачи были оставлены без изменений. Кроме того, в 2015 году была изменена форма записи ответа в задачах с выбором ответа: ответ стало нужно записывать цифрой с номером правильного ответа (а не обводить кружком).

В демонстрационных вариантах ОГЭ по математике 2016-2017 годов по сравнению с демонстрационным вариантом 2015 года изменений нет. Снижен максимальный первичный балл за всю работу с 38 до 32 за счет того, что правильное выполнение каждого из заданий части 2 в демонстрационных вариантах ОГЭ по математике 2016-2017 годов оценивается в 2 балла.

В демонстрационный вариант ОГЭ по математике 2018 года по сравнению с демонстрационным вариантом 2017 года были внесены следующие изменения: из демонстрационного варианта был исключен модуль «Реальная математика», а задания, входившие в этот модуль, были распределены по модулям «Алгебра» и «Геометрия». При этом общее количество заданий и максимальный балл за всю работу не изменились.

В демонстрационном варианте ОГЭ по математике 2019 года по сравнению с демонстрационным вариантом 2018 года изменений не было.

В демонстрационном варианте ОГЭ по математике 2020 года по сравнению с демонстрационным вариантом 2019 года были заменены задания 2, 5, 7, 8, 15 на блок практико-ориентированных заданий 1-5, объединенных единым сюжетом.

В демонстрационный вариант ОГЭ по математике 2021 года по сравнению с демонстрационным вариантом 2020 года были внесены следующие изменения:

Были объединены в одно задания 13 и 8 на преобразование выражений
Задание 12 заменено на задание с практическим содержанием, направленное на проверку умения применять знания о последовательностях и прогрессиях в прикладных ситуациях
Изменен порядок заданий в соответствии с тематикой и сложностью
Максимальный балл уменьшен с 32 до 31

В демонстрационных вариантах ОГЭ по математике 2022 и 2023 годов по сравнению с демонстрационным вариантом 2021 года изменений не было.

Источник

Проект ОГЭ 2023. Решение и ответы заданий демонстрационного варианта ОГЭ 2023 по математике. Демоверсия ФИПИ для 9 класса. КИМ.

Изменения в проекте КИМ ОГЭ 2023 года относительно КИМ ОГЭ 2022 года отсутствуют.

ЧАСТЬ 1

Задание 1–5.

На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева – гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м×1м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.

Задание 6.
Найдите значения выражения frac{1}{4}+0,07.

Задание 7.
На координатной прямой отмечена точка А.

Известно, что она соответствует одному из четырёх указанных ниже чисел.
Какому из чисел соответствует точка А?

1) frac{181}{16} 2) sqrt{37} 3) 0,6 4) 4

Задание 8.
Найдите значение выражения а^–7·(a⁵)² при а = 5

Задание 9.
Решите уравнение x² + x −12 = 0.
Если уравнение имеет более одного корня, в ответ запишите больший из корней.

Задание 10.
На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.

Задание 11.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ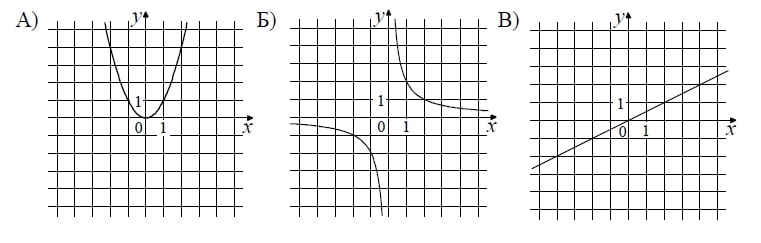
ФОРМУЛЫ

1) y = x²2) y = frac{x}{2} 3) y = frac{2}{x}

В таблице под каждой буквой укажите соответствующий номер.

Задание 12.
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой t_F =1,8t_C + 32 , где t_C – температура в градусах Цельсия, t_F – температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует −25 градусов по шкале Цельсия?

Задание 13.
Укажите решение системы неравенств:

Задание 14.
Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый день?

Задание 15.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

Задание 16.
Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5.

Задание 17.
Найдите площадь трапеции, изображённой на рисунке.

Задание 18.
Найдите тангенс острого угла, изображённого на рисунке.

Задание 19.
Какие из следующих утверждений верны?

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

ЧАСТЬ 2

Задание 20.
Решите уравнение x⁴ = (4x – 5)²

Задание 21.
Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки равна 6 км/ч?

Задание 22.
Постройте график функции y=frac{x^{4}–13x^{2}+36}{(x–3)(x+2)} и определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку.

Задание 23.
В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6 , BC = 8. Найдите медиану CK этого треугольника.

Задание 24.
В параллелограмме ABCD точка E – середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм – прямоугольник.

Задание 25.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.

Источник варианта: fipi.ru

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.9 / 5. Количество оценок: 13

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник