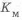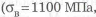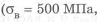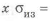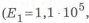Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
Готовые решения задач по деталям машин.
Эта страница подготовлена для студентов любых форм обучения.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Детали машин и основы конструирования
Детали машин и основы конструирования – это научная дисциплина, в которой рассматриваются основы расчета и конструирования деталей и узлов общего назначения, встречающиеся в различных механизмах, установках и машинах
Целью курса ”Детали машин и основы конструирования ” является изучение устройства, принципа работы, расчета и проектирования деталей машин и механизмов общего назначения. Задача курса заключается в том, чтобы, исходя из заданных условий работы деталей и сборочных единиц общего назначения, получить навыки их расчета и конструирования, изучить методы, правила и нормы проектирования, обеспечивающие изготовление надежных и экономичных конструкций.
Тема: Сварные соединения
Расчет ведут в следующем порядке:
1) Выбирают способ сварки (ручная электродуговая, автоматическая и т.д.) или назначают согласно заданию.
2) Принимают (или назначают согласно заданию) тин электрода и материал, свариваемых деталей. Для дуговой сварки применяют электроды с различной обмазкой, или покрытием, обеспечивающим устойчивое горение дуги и защиту материала шва от вредного воздействия окружающей среды. Для сварки конструкционных сталей применяют электроды: Э42, Э42А, Э46, Э46А, Э50, Э50А и др. Число после буквы Э, умноженное на 10, обозначает минимальное значение временного сопротивления металла шва, измеряемого в МПа. Буква А обозначает повышенное качество электрода, обеспечивающее получение более высоких пластических свойств металла шва.
3) Определяют допускаемые напряжения для основного материала и материала сварного шва.
Допускаемые напряжения растяжения основного металла
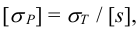
где 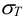
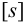
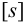
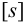
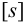
Допускаемые напряжения для сварных швов 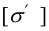
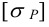
Таблица 3.11

В случае если сваривают детали с различными механическими свойствами, то расчет допускаемых напряжений ведется для материала, обладающего наименьшим значением предела текучести.
4) Составляют расчетную схему соединения, приведя её к схемам, изложенным в конспекте лекций [1, с. 126… 129] или в [2, с. 69… 79].
Внешние силы, действующие на соединение, следует перенести в центр тяжести сварного шва в соответствии с правилами теоретической механики, при этом силы, действующие под углом к плоскости сварных швов, необходимо разложить на перпендикулярные составляющие (рисунок 3.11).
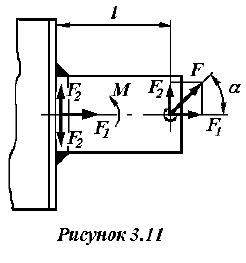
При переносе силы 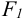
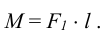
При переносе силы 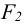
В задаче 8 усилие от каната приложено к барабану несимметрично по отношению к стойкам, поэтому и силы действующие на сварные швы (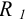
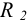
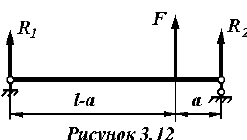
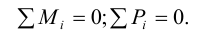
В задаче 10 следует из условия равновесия колеса относительно оси вращения
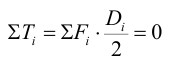
определить усилия 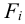
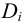
Примеры расчетных схем для задач 1, 2, 3, 4, 6, 7,9 показаны на рисунке 3.13.
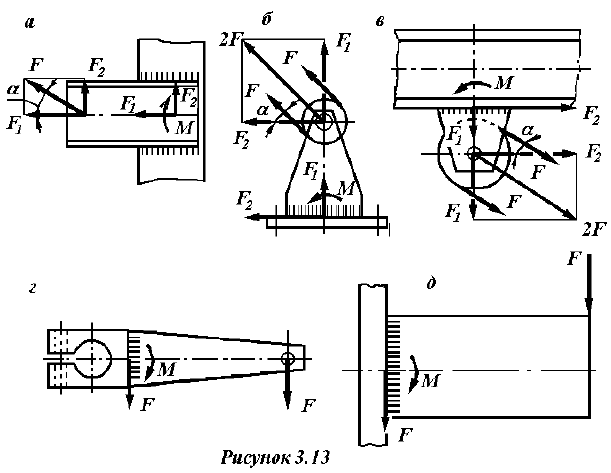
5) Назначают катет шва. В большинстве случаев 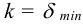
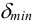
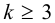
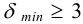
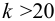
6) Определяют действующие напряжения отдельно для каждого силового фактора (силы, момента). Складывая напряжения, учитывают их направление (если направление векторов совпадает, то их складывают алгебраически, если векторы перпендикулярны, то их складывают геометрически).
7) При проектировании сварных швов обычно из условия прочности определяют их длину. Принимая при этом, что длина фланговых швов обычно не больше 50 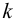
Возможно эта страница вам будет полезна:
Задача №3.3.1
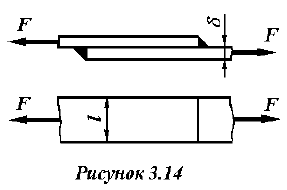
Рассчитать лобовой шов (рисунок 3.14), соединяющий два листа толщиной 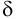
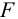
Решение:
1 Определяем допускаемое напряжение растяжения для основного металла, принимая для стали Ст 3 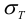
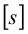
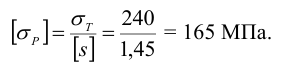
2 В соответствии с таблицей 3.11 вычисляем допускаемое напряжение для сварного шва при срезе
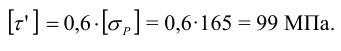
3 Из условия прочности (см. формулу 4.14 [1, с. 128]) определяем длину сварного шва
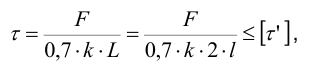
принимая
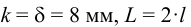
(два шва) получаем
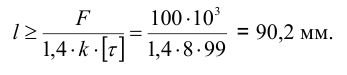
Учитывая возможность технологических дефектов сварки, принимаем
Задача №3.3.2.
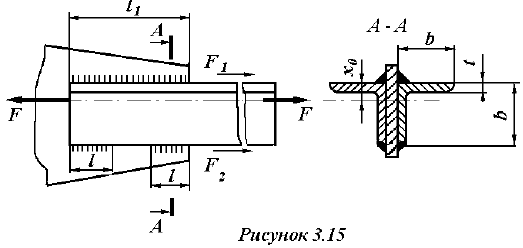
Стержень, состоящий из двух равнополочных уголков, соединенных косынкой, нагружен постоянной растягивающей силой 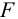
Материал уголков — сталь Ст 3.
Решение:
1 Принимаем, что сварка осуществляется вручную электродами Э42.
2 Определяем допускаемое напряжение растяжения для основного металла, принимая для Ст 3 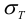
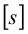
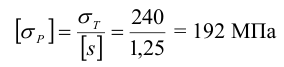
3 Определим допускаемое напряжение на срез для сварного шва, в соответствии с таблицей 3.11
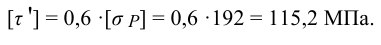
4 Из расчета на растяжение определим площадь сечения уголков
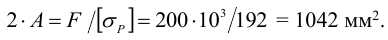
Для одного уголка 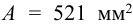
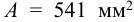
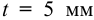
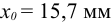
5 Сварные швы располагают так, чтобы напряжения в них были одинаковыми. Поэтому при проектировании соединения уголков с косынками, т.е. при несимметричной конструкции, длину швов делают неодинаковой. Таким образом, каждый шов воспринимает только свою часть нагрузки 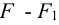
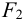
Длину фланговых швов определяют в предположении, что их длина пропорциональна этим частям силы 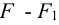
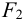
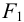
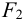
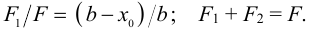
Решая эти уравнения, получим:
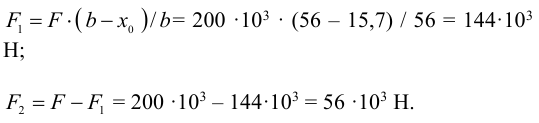
6 Определим длину швов (см. формулу 4.14 [1, с. 128]), приняв катет шва 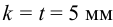
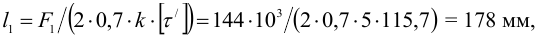
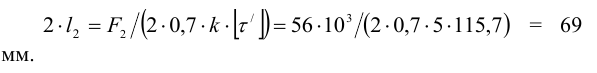
Округляя, принимаем
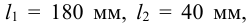
добавив для коротких швов по 5 мм против расчетной длины.
Возможно эта страница вам будет полезна:
Задача №3.3.3
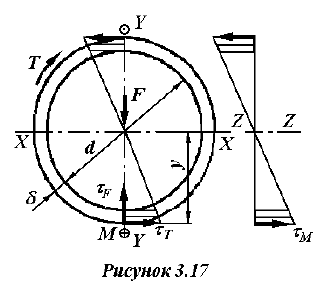
Найти параметры сварных швов кривошипа (рисунок 3.16), нагруженного постоянной силой 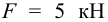
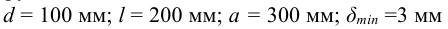
при условии, что прочность основного металла обеспечена.
Решение:
1 Дополнительно принято: основной металл — сталь Ст 4 (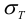
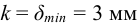
2 Определяем допускаемое напряжение растяжения для основного металла, принимая для стали Ст 4 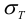
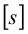
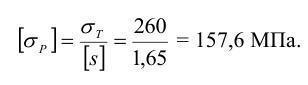
3 Допускаемое касательное напряжение сварного шва (см. таблицу 3.11),
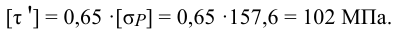
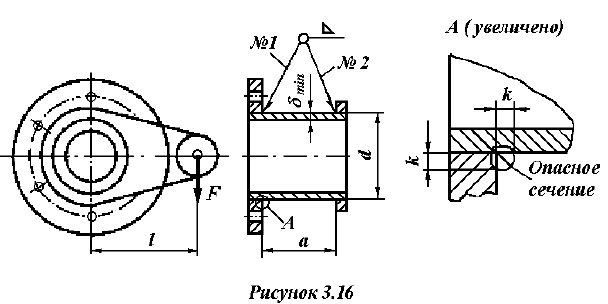
4 Расчету подлежит шов № 1, который по сравнению со швом № 2 дополнительно нагружен изгибающим моментом 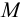
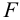
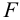
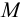
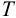
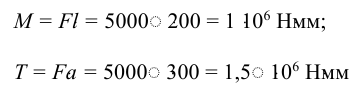
3 В наиболее нагруженных зонах шва, удаленных от оси 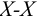
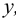
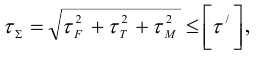
где 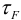
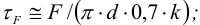
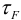
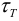
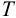
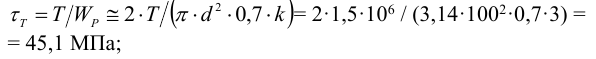
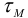
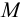
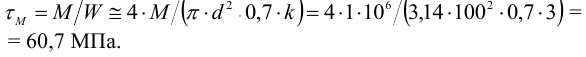
Таким образом,

Статическая прочность угловых швов обеспечена. 6 Определим величину катета 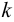
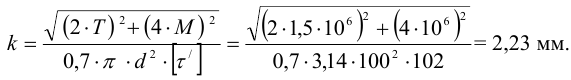
Принято 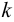
Тема: Соединения с натягом и заклепочные
Теоретический материал по расчету заклепочных соединений изложен в конспекте лекций [1, с. 117… 122] и учебниках [2, с. 61… 67], [3, с. 58… 63], [4, с. 35… 44], а соединений с натягом в источниках [1, с. 122… 124], [2, с. 104… 116], [3, с. 100… 110], [4, с. 57…62].
4.2.1 Подбор посадки с натягом. Исходные данные: 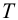
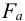
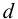
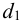
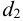
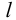
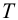
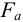
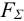
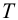
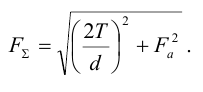
Осевую силу 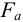
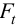
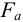
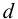
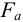
Подбор посадок производят в следующем порядке.
1) Среднее контактное давление (МПа)
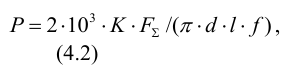
где 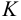
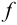
При действии на соединение изгибающего момента 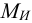
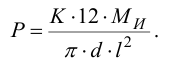
Для предупреждения снижения несущей способности вследствие нестабильности коэффициента трения и контактной коррозии (изнашивания посадочных поверхностей вследствие их микроскольжения при действии переменных напряжений, пиковых нагрузок, особенно в период пуска и останова) или для уменьшения ее влияния в соединениях с натягом следует предусматривать определенный запас сцепления 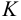
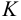
Для определения числовых значений коэффициента трения 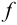
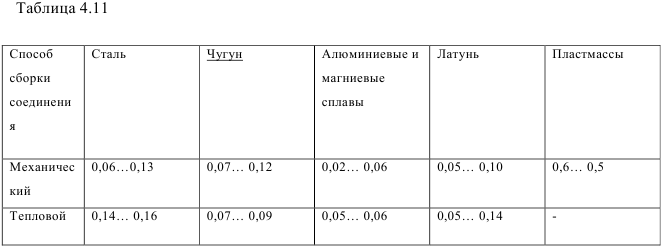
2) Расчетный теоретический натяг (мкм):
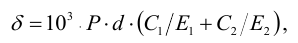
где 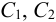
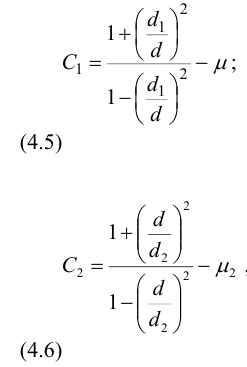
здесь 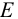
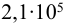
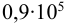
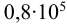
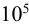
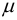
Индекс «1» для охватываемой детали (вала), индекс «2» для охватывающей детали (втулки).
В задачах о посадке подшипника качения (задача 9) диаметры 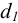
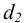
Диаметр по дну желоба (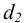
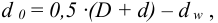
диаметр борта (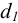
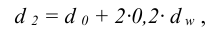
где соответствующие размеры подшипника приведены в таблице Б11.
3) Поправка па обмятые микронеровностей (мкм)
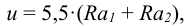
где 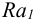
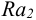
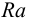
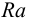
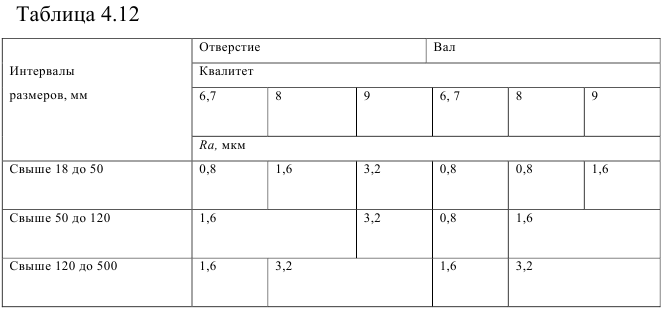
4) Поправка па температурную деформацию (мкм). При подборе посадки зубчатых венцов червячных колес, которые нагреваются при работе передачи до относительно высоких температур, учитывают температурные деформации центра и венца колеса, ослабляющие натяг
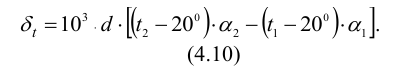
Здесь 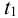
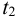
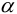
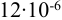
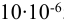
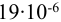
5) Минимальный натяг (мкм), необходимый для передачи вращающего момента,
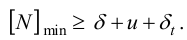
6) Максимальный натяг (мкм), допускаемый прочностью охватывающей детали (ступицы, венца и др.),
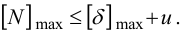
7) Максимальная деформация (мкм), допускаемая прочностью охватывающей детали,
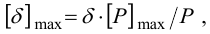
где
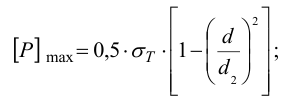
максимальное давление, допускаемое прочностью охватывающей детали (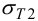

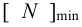
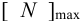
Приводимые в таблице Б10 значения минимального 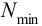
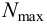
9) Для выбранной посадки определяют силу запрессовки или температуру нагрева детали.
Сила запрессовки,
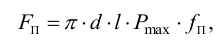
где
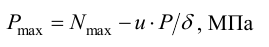
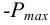
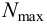
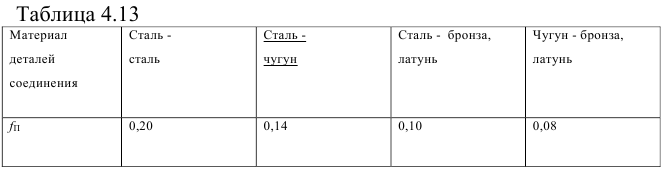
10) Температура нагрева охватывающей детали, °С для обеспечения зазора при сборке
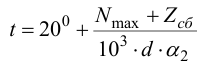
где 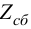
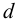

Температура нагрева должна быть такой, чтобы не происходило структурных изменений в материале. Для стали 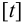
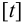
Заклепочные соединения. Последовательность расчета.
Расчет прочных заклепочных швов (задачи 4, 6, 7, 10)
1) Определяют диаметр заклепки 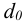
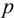
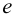
2) Допускаемые напряжения. На практике при расчете прочных заклепочных швов силу трения не учитывают, используя более простой расчет по условным напряжениям среза 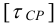
Для заклепок из сталей Ст 0, Ст 2, Ст 3 принимают 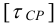
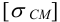
3) Максимальную нагрузку на одну заклепку определяют из условия среза по (см. формулу (4.1) [1, с. 120]).
3) Количество заклепок в шве определяют исходя из приложенной нагрузки. Для исключения возможности поворота соединяемых деталей число заклепок принимают
4) Разрабатывают конструкцию заклепочного шва (при этом уточняют параметры шва
5) Спроектированный заклепочный шов проверяют (см. формулу (4.3) [1, с. 120]) на растяжение деталей (листов) и (см. формулу (4.4) [1,с. 121]) на срез детали.
Расчет прочноплотных заклепочных швов (задача 3) производят в следующем порядке
1) Вычисляют толщину стенки цилиндрического сосуда (котла, автоклава и т, п.):
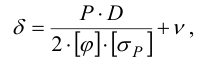
где 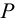
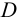
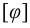
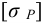
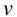
2) Допускаемые напряжения. При расчете прочноплотных заклепочных швов их проверяют на плотность, т.е. на отсутствие относительного скольжения листов. Этому скольжению препятствуют возникающие между листами силы трения. Значение этой силы трения определяют экспериментально и условно относят к поперечному сечению заклепки. Поэтому проверка заклепок по допускаемому условному напряжению 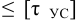
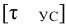
Допускаемые напряжения при растяжении для стенки сосуда определяют в зависимости от температуры нагрева стенки сосуда: при температуре
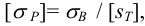
где 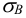
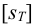
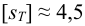
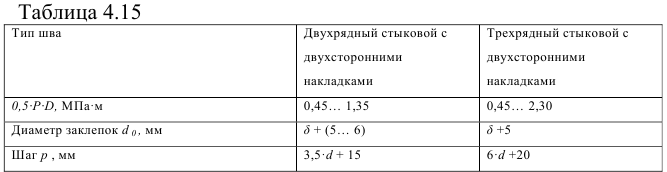

3) Максимальная нагрузка на одну заклепку в продольном шве
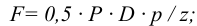
в поперечном шве
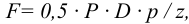
где 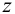
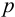
4) Производят проверочный расчет заклепок по допускаемому условному напряжению на срез
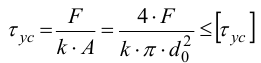
где 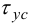
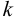
5) После определения 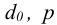
Для прочноплотных швов расстояние заклепки до края листа
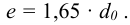
Расстояние между рядами заклепок
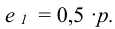
Толщина накладок
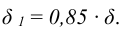
Задача №4.3.1
Косозубое цилиндрическое колесо передает на вал номинальный вращающий момент 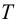
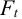
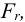
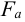
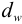
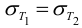
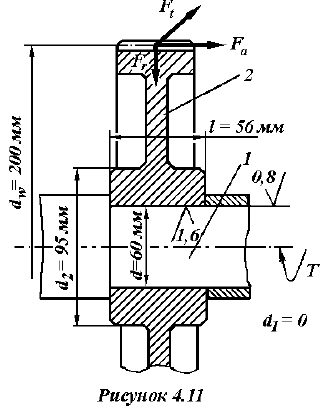
Решение:
1 Коэффициент запаса сцепления принимаем 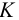
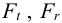
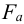
2 Коэффициент трения 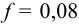
3 Действующий на соединение изгибающий момент от осевой силы 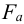
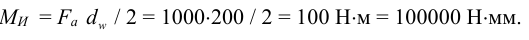
4 Потребное давление для передачи вращающего момента 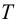
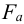
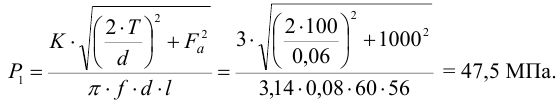
5 Потребное давление для восприятия изгибающего момента 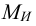

Для дальнейшего расчета в качестве потребного давления 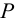
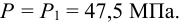
6 Расчетный теоретический натяг определяем по формуле Ляме (4.4)
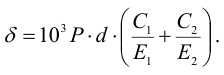
Посадочный диаметр соединения 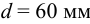
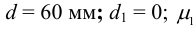
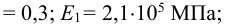
ступица (зубчатое колесо) стальная с параметрами:
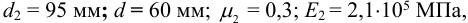
здесь условно принимают наружный диаметр 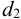
Тогда по формулам (4.5), (4.6) коэффициенты
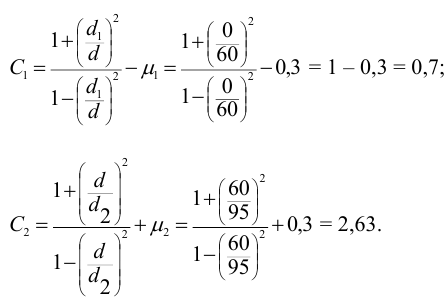
При этих параметрах потребный расчетный теоретический натяг равен (4.4)
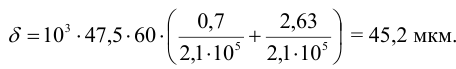
6 Поправка на обмятие микронеровностей (4.9) составляет
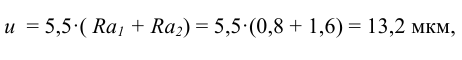
где 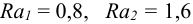
7 Температурную поправку 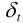
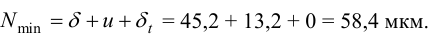
8 Давление на поверхности контакта, при котором эквивалентные напряжения в ступице колеса достигают значения предела текучести материала ступицы 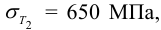
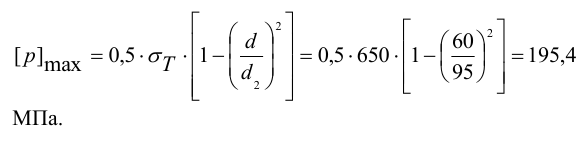
9 Расчетный натяг, соответствующий давлению 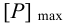
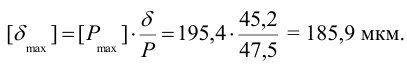
10 Максимально допустимый натяг (4.12) по условию отсутствия зон пластических деформаций у охватывающей детали (ступице зубчатого колеса) равен
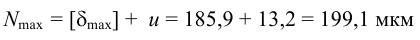
11 Для образования посадок принимаем систему отверстия. Допускаем вероятность появления (риск появления) больших и меньших натягов 0,14%, т.е. принимаем надежность 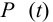
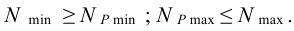
12 В таблице Б10, из числа рекомендуемых стандартных посадок пригодна посадка 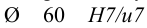
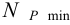
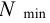
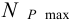
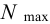
Прочность деталей соединения, в частности ступицы зубчатого колеса, проверять не надо, так как у выбранной посадки максимальный вероятностный натяг 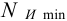
Возможно эта страница вам будет полезна:
Задача №4.3.2
Рассчитать и сконструировать заклепочное соединение внахлестку двух полос с размерами в сечении 
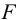
Решение:
1 Расчет ведем для прочного заклепочного соединения [1, с.121].
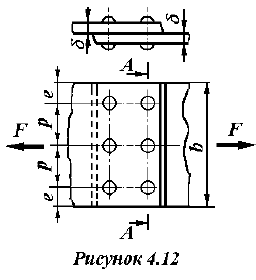
Определим диаметр заклепок
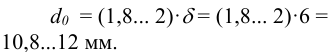
Примем
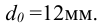
2 Определим максимальную нагрузку на одну заклепку из условия среза (см. формулу (4.1) [ 1, с. 120])
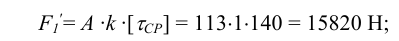
где
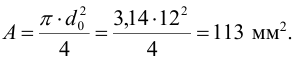
3 Необходимое число заклепок
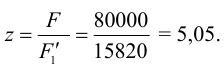
Принимаем число заклепок
Чтобы уменьшить влияние изгиба на прочность соединения, располагаем заклепки в 2 ряда по 3 в каждом (см. рисунок 4.12).
4 Определим расстояние от оси заклепки до края листа — 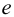
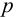
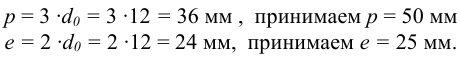
4 Проведем проверку по напряжениям смятия (см. формулу (4.2) [1, с.120])
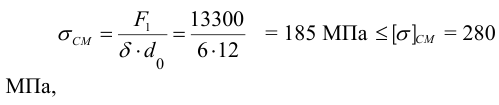
уточнив при этом нагрузку, приходящуюся на одну заклепку
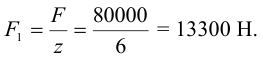
5 Проверим прочность листов по ослабленному заклепками сечению 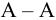
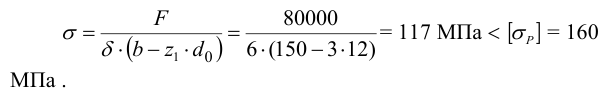
Условие прочности выполнено.
Тема: Резьбовые соединения
Приступая к расчету резьбовых соединений, студенты должны изучить материал, изложенный в конспекте [1, с. 129… 135] и литературе [2, с. 21 …61], [3, с. 21 …78], [4, с. 63… 99].
Решения задач, как правило, ведут в следующем порядке.
1) Составляют расчетную схему соединения и определяют нагрузку, действующую на болт (винт, шпильку).
Внешние нагрузки, действующие на резьбовые соединения, в зависимости от условий нагружения могут быть осевыми, поперечными или комбинированными, по характеру действия -постоянными или циклическими.
При действии поперечной нагрузки применяют соединения двух видов:
болт поставлен в отверстие с зазором; болт поставлен в отверстие без зазора, а) в случае установки болтов с зазором, затяжкой должна создаваться сила трения на поверхности стыка, превышающая внешнюю сдвигающую нагрузку (см. формулы (4.26) [1, с. 134]) и формулу (1.20) [2, с. 37].
При этом сила, растягивающая болт (винт, шпильку), определяется следующим образом
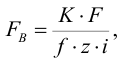
где 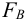
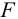
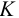
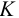
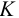
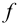
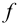
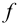
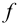
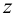
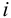
б) при установке болтов без зазора (по переходной или посадке с натягом) силы трения в стыке не учитывают, т.к. затяжка болтов не обязательна. В этом случае стержень болта рассчитывают из условия прочности на срез и смятие, см. формулы (4.27), (4.28) [1, с. 134, 135]; (1.21), (1.22) [2, с. 38]; (6.33), (6.34), (6.35) [4, с. 86].
Приступая к расчету соединений, изображенных на рисунках 5.1, 5.2, 5.5, 5.6, необходимо уяснить, что в этих соединениях действует поперечная сила, стремящаяся сдвинуть соединяемые детали.
Сдвигающую силу определяют из условия равновесия деталей относительно оси вращения:
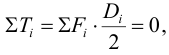
здесь 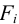
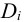
Эту поперечную силу уравновешивает сила трения в стыке соединяемых деталей, которая обеспечивается при затяжке резьбового соединения. При этом болт (винт, шпилька) подвержен растяжению.
В соединении изображенном на рисунке 5.11 для надежной передачи пиле вращения необходимо, чтобы момент сил трения был больше момента резания на 20… 25%, т.е.
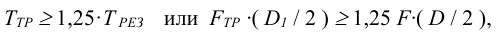
где 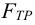
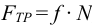
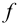
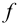
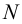
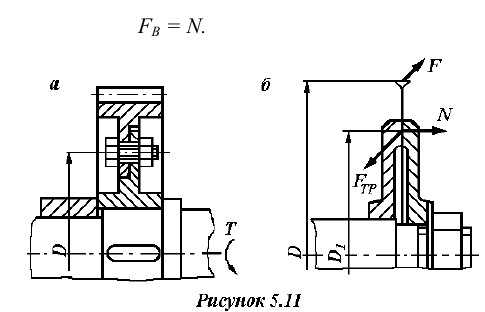
В соединении (рисунок 5.12,а) сила, действующая на винт 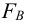
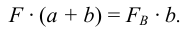
В случае, когда усилие приложено асимметрично, действующую нагрузку раскладывают на составляющие и приводят их к центру тяжести
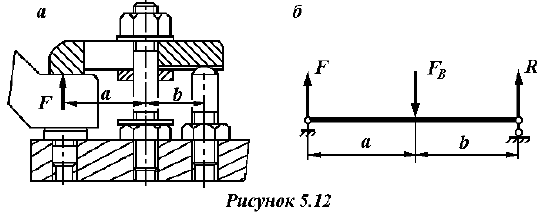
стыка. Если число болтов в задаче не указано, то их количеством задаются.
Рассмотрим соединения в задачах 3, 4, 8, 9 (рисунки 5.13 и 5.14). В этих случаях нагрузка, приложенная асимметрично, раскрывает стык (и вызывает сдвиг деталей). Решение подобных
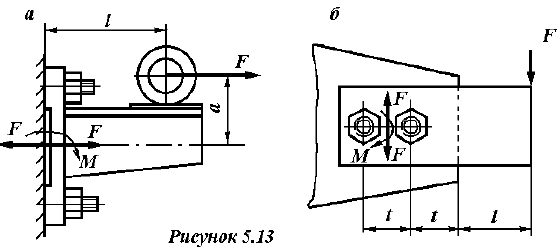
задач является комбинированным. Действующую нагрузку раскладывают на составляющие — осевую и поперечную, а затем приводят их к центру тяжести стыка, см. пример 5.3.2 данных методических указаний и пример 1.4 [2, с. 60] или [4, с. 94]. Также можно воспользоваться рекомендациями, изложенными при решении задач первой группы.
В результате этого к соединению, в общем случае, приложены: осевая и поперечная силы, равномерно воспринимаемые всеми резьбовыми деталями, и опрокидывающий момент, стремящийся раскрыть стык. Из уравнения равновесия — уравнения моментов относительно
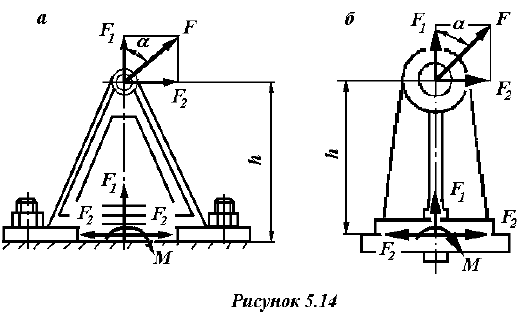
центра тяжести стыка — определяются силы, дополнительно действующие на болты (винты, шпильки) в осевом направлении.
По величине наибольшей осевой (отрывающей) силы из условия прочности стержня болта (винта, шпильки) на растяжение вычисляется внутренний диаметр резьбы.
В соединении (рисунок 5.15) болты поставлены с предварительной затяжкой, обеспечивающей герметичность соединения.
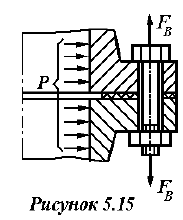
Внешняя сила, действующая на болтовое соединение 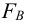
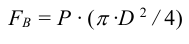
2) Выбирают материал болта (винта, шпильки), а при необходимости и материал соединяемых деталей. Крепежные детали общего назначения изготавливают из низко- и среднеуглеродистых сталей типа Сталь 10… Сталь 35 (таблица А1).
3) Находят допускаемые напряжения растяжения, смятия или среза в зависимости от условий работы резьбовых деталей.
Допускаемое напряжение растяжения 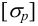
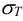
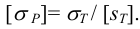
Здесь 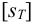
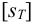
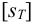
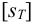
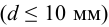
Допускаемое напряжение среза можно определить по зависимости
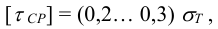
а допускаемое напряжение смятия
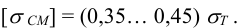
4) Рассчитывают внутренний диаметр резьбы 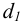
5) Проводят проверочные расчеты.
6) При необходимости можно проверить соединение на отсутствие сдвига по основанию, сравнив сдвигающую составляющую с силой трения, вызванной затяжкой болта (винта, шпильки).
Если материал основания недостаточно прочный по сравнению с материалом болтов, например: чугунный кронштейн крепится к бетонной стене (основанию), то стену проверяют по максимальным напряжениям смятия
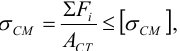
где 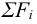
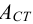
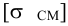
Допускаемое напряжение смятия в стыке для кирпичной кладки на известковом растворе — 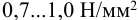
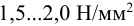
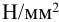
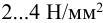
Возможно эта страница вам будет полезна:
Задача №5.3.1
Стальные полосы, растянутые силой 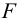
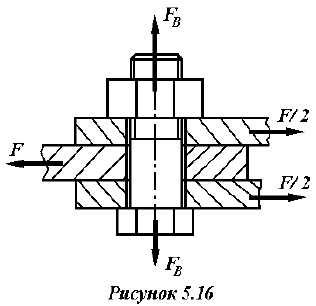
двух болтов, выполненных из стали Сталь 20 (рисунок 5.16). Определить диаметр болтов. Нагрузка постоянная.
Решение:
1 Для болтового соединения с неконтролируемой затяжкой принимаем 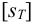
По таблице А1 для Сталь 20 предел текучести материала 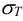
Допускаемое напряжение растяжения по (5.3)
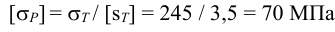
2 Необходимая сила затяжки болта согласно (5.1) Принимаем: коэффициент запаса по сдвигу, листов 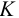
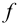
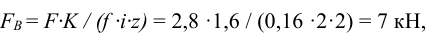
где 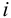
3 С учетом скручивания винта из-за трения в резьбе [1, с. 133] расчетная сила затяжки болта
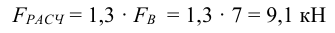
4 Расчетный (внутренний) диаметр резьбы
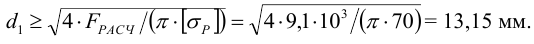
По таблица Б1 принимаем резьбу М 16 с шагом 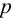
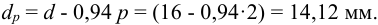
Задача №5.3.2
Приближенно рассчитать (рисунок 5.17): а) болты, крепящие к стене кронштейн, на котором установлен электромотор; б) удельное давление на стену. Данные: 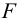
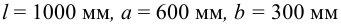
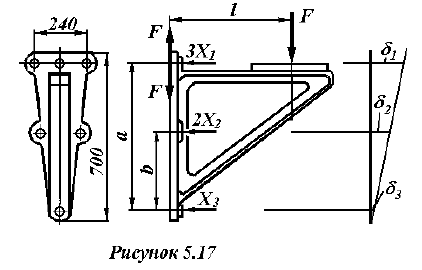
Решение:
1 Нагрузка к соединению приложена асимметрично, поэтому выполним приведение усилия к оси симметрии соединения. Для этого силу 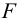
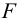
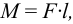
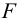
Предполагаем, что кронштейн опрокидывается (поворачивается) вокруг оси, проходящей через центр нижнего болта.
Момент 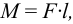
Предполагая, что верхние три болта затянуты каждый с усилием 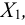
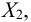
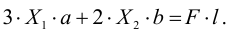
Принимая далее приближенно, что деформации болтов пропорциональны расстояниям 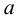
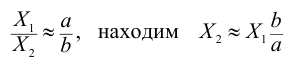
и подставляем это значение в уравнение моментов
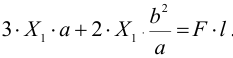
Отсюда усилие затяжки верхнего болта
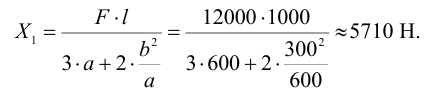
Так как, кроме момента, действует еще усилие 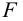
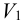
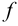
Из условия неподвижности плиты
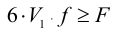
получим
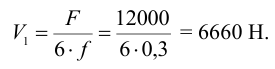
Таким образом, необходимая полная затяжка болта составит
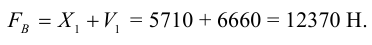
Так как при расчете не учитывалось влияние собственного веса кронштейна и вибрации, имеющей место при работе электромотора, расчетное усилие для болта верхнего ряда необходимо увеличить (обычно достаточно в 1,5 раза)
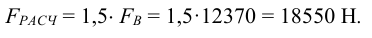
Хотя болты среднего и нижнего рядов несут меньшую нагрузку, чем верхнего ряда, все болты делаем одинаковыми.
2 Принимаем, что материал кронштейна — сталь Ст 5. Крепление кронштейна осуществляется к кирпичной стене, выполненной на цементном растворе.
3 Для болтового соединения с неконтролируемой затяжкой принимаем 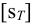
По таблице А1 для стали Ст 5 предел текучести материала
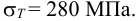
Допускаемое напряжение растяжения по (5.3)
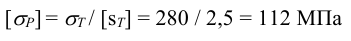
4 Расчетный внутренний диаметр резьбы болта
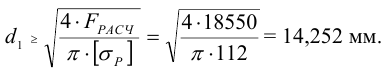
Принимаем болт с метрической резьбой. По таблице Б1 внутренний диаметр резьбы
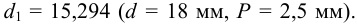
Обозначение резьбы M18x2,5 ГОСТ 9150-81.
5 Общая затяжка шести болтов прижимает плиту кронштейна к стене с усилием
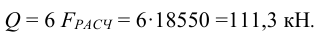
6 Площадь плиты кронштейна составляет примерно (размеры кронштейна см. на рисунке 5.17)
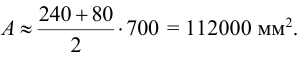
7 Если основание (опорная поверхность) выполнено из материала (бетон, кирпичная кладка, дерево) менее прочного, чем кронштейн, производят проверку прочности основания по напряжениям смятия согласно (5.6)
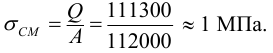
Полученное напряжение смятия равное
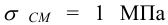
допустимо, если выполнить стену кирпичной на цементном растворе для которой
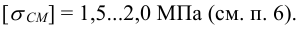
Тема: Шпоночные, шлицевые соединения
Теоретический материал но расчету соединений шпоночных и зубчатых (шлицевых) изложен в [1, с. 136… 141], [2, с. 91… 104], [3, с. 87… 100], [4, с. 101… 111].
Решение задач можно вести в следующем порядке.
1) По диаметру вала 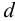
2) Допускаемое напряжение смятия 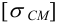
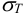
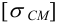
Тогда
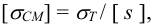
где 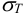
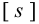
При нереверсивной нагрузке, мало изменяющейся по величине, принимают коэффициент запаса 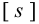
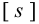
Допускаемые напряжения на срез для шпонок обычно принимают 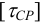
Для шлицевых соединений фактические напряжения сильно зависят от координаты рассматриваемой точки на шлице и поэтому они оказываются значительно больше средних. Это обстоятельство можно учесть, если уменьшать допускаемые напряжения, увеличивая при этом коэффициенты запаса. При статической нагрузке допускаемые напряжения смятия можно принимать 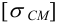
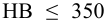
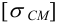
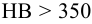
3) Проверить прочность элементов соединения в соответствии с видами разрушения.
а) Призматические шпонки имеют прямоугольное сечение. Стандарт предусматривает для каждого диаметра вала определенные размеры поперечного сечения шпонки. Поэтому при проектных расчетах размеры 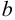
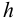
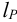
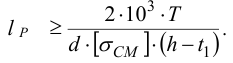
Длину шпонки 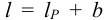
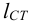
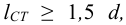
Причиной разрушения шпоночного соединения, помимо нормальных пластических деформаций, может быть пластический сдвиг (срез), вызванный наибольшими касательными напряжениями.
И тогда шпонки проверяют на срез
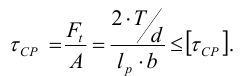
Однако если размеры поперечного сечения шпонки в зависимости от диаметра вала выбираются из нормального ряда, то выполнять такой расчет нет необходимости, так как условие прочности на срез выполняется автоматически.
б) Сегментные шпонки. Размеры сегментных шпонок рекомендуется выбирать в соответствии с данными таблицы Б5 . Расчет сегментных шпонок проводится в форме проверочного и выполняется по той же методике и по тем же формулам, что и расчет на сопротивление смятию для призматических шпоночных соединений. Тогда
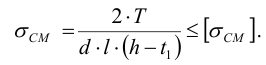
Проверка соединения на срез осуществляется по формуле (6.3), принимая при этом 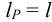
в) Штифтовые соединения.
Диаметр 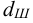
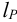
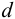
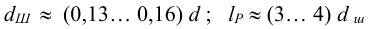
и уточняют по ГОСТ (таблица Б8).
- штифт расположен параллельно оси вращения (рисунок 6.8) соединение при этом обеспечивает передачу момента вращения
.
При нагружении внешним моментом в продольном сечении штифта появляются касательные напряжения, которые не могут превышать предела текучести при сдвиге.
Условие прочности на сопротивление срезу для осевого штифтового соединения можно записать как
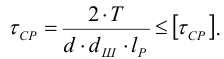
Условие отсутствия на поверхности контакта пластических деформаций (смятия), вызванных нормальными напряжениями, записывается в виде (см. формулу (4.29) [1, с. 137])
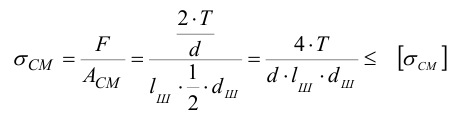
По указанным формулам можно определить длину шпонки, задавшись ее диаметром, или задавшись ее длиной, найти диаметр шпонки.
штифт установлен в радиальном направлении (рисунок 6.2).
Здесь каждая поверхность среза представляет собой круг. Как уже было сказано выше, в момент среза на этих поверхностях действуют касательные напряжения, равные пределу текучести при сдвиге. Тогда условие прочности на сопротивление срезу имеет вид
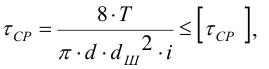
где 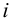
в) Шлицевые соединения.
Смятие и износ рабочих поверхностей зубьев связаны с одним и тем же параметром — напряжением смятия 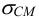
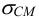
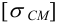
При проектировочном расчете шлицевых соединений после выбора размеров сечения зубьев по стандарту (таблицы Б6 и Б7) определяют длину зубьев 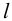
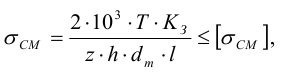
где 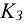
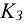
Геометрические размеры шлица вычисляют в зависимости от шлицевого соединения. Так для прямобочных шлицев
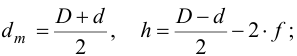
для эвольвентных
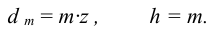
Если получается, что 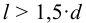
Длину ступицы принимают 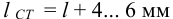
Возможно эта страница вам будет полезна:
Задача №6.3.1
Выбрать по стандарту призматическую шпонку для соединения шестерни с валом 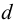
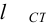
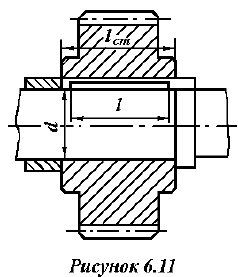
передаваемый момент 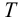
Решение:
1 Согласно стандарту, на призматические шпонки (таблица Б4) выбираем шпонку со следующими размерами: 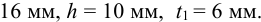
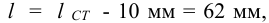
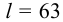
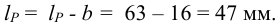
Принята «Шпонка 16 х 10 х 63 ГОСТ 23360 — 78».
2 Находим допускаемое напряжение смятия. Для материала шпонки — Сталь 45 (по заданию) 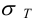
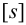
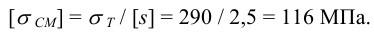
3 Проверяем соединение на смятие (см. формулу (4.29) [1, с. 137])
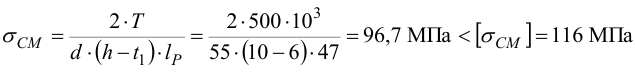
Условие прочности выполнено.
Задача №6.3.2
Подобрать шлицевое соединение для блока шестерен с валом коробки передач (рисунок 6.12). Расчетный диаметр вала 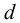
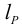
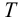
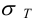
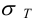
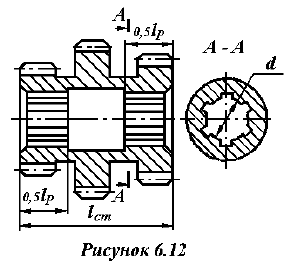
Рабочие поверхности зубьев закалены 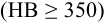
Решение:
1 Выбираем прямобочное шлицевое соединение как наиболее распространенное. Для закаленных зубьев принимаем центрирование по внутреннему диаметру.
2 По таблице Б7 находим размеры соединения по средней серии, которая рекомендуется при перемещении ступиц не под нагрузкой. Для диаметра вала
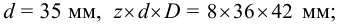
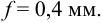
3 Для подвижного соединения при спокойной нагрузке принимаем 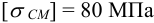
4 Геометрические размеры шлица вычисляют по формуле (6.10)
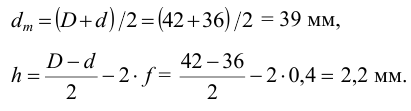
По формуле (6.9) расчетное условное напряжение смятия
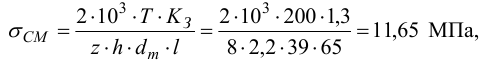
что удовлетворяет условию
Задача №6.3.3
Подобрать и проверить на прочность подвижное шлицевое соединение (шлицы эвольвентные) вала при передаче момента 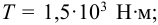
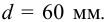
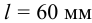
Решение:
1 Для эвольвентных шлицев по таблице Б6 выбираем шлицевое соединение с 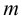
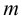
Итак,
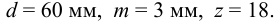
2 Для подвижного соединения при спокойной нагрузке при зубьях подвергнутых специальной термообработке 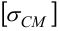
3 Геометрические размеры шлица вычисляют по формуле (6.11)
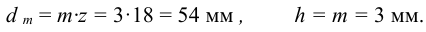
Проверяем соединение на смятие.
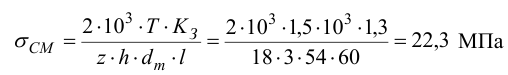
что меньше 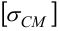
Задача №6.3.4
На консольную часть вала центробежного насоса, выполненного из стали 45, насажено колесо зубчатой передачи (Сталь 35) с помощью штифта (цилиндрической шпонки — см. рисунок 6.8). Штифт (сталь Ст 6) установлен с натягом (напряженное соединение). Определить размеры штифта, если: мощность 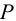
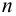
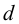
Решение:
1 Определяем момент, передаваемый валом,
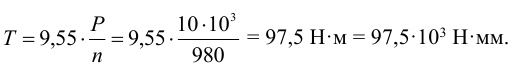
2 Диаметр 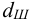
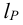
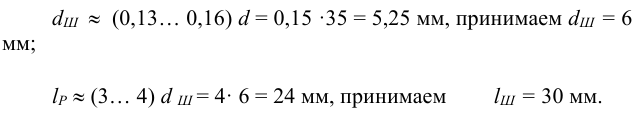
3 Допускаемые напряжения смятия (см. п. 2) для Стали 35, как наименее прочной из материалов соединения, 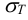
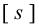
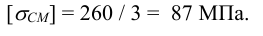
Допускаемые напряжения среза принимаем
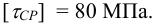
Проверяем соединение на смятие по формуле (6.7)
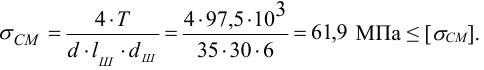
5 Условие прочности на срез по формуле (6.6)
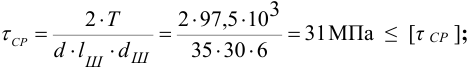
Принимаем штифт по таблице Б8 «Штифт бтб х 30 ГОСТ 3128- 70».
Тема: Передача винт- гайка
Прежде чем приступить к расчету передач винт-гайка следует изучить теоретический материал, изложенный в конспекте [1, с. 76… 78] и литературе [2, с. 310… 313], [3, с. 292… 294]; [4, с.262…268].
Некоторые затруднения вызывает расчет клинчатого домкрата, показанного на рисунке 7.3.
В этом случае необходимо обратить внимание на то, что усилие на винт 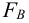
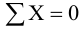
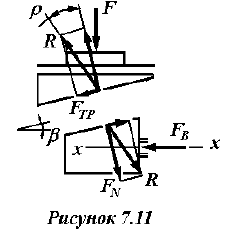
Сила 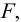
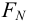
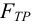
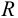
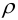
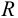
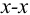
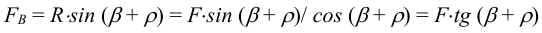
Теперь можно перейти к расчету передачи винт-гайка по стандартной методике, приведенной в литературе, указанной выше.
1) Назначают материалы для изготовления винта и гайки или принимают в соответствие с заданием. Механические характеристики материалов приведены в Приложении А.
2) Определяют допускаемые напряжения 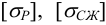
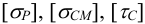
Допускаемое напряжение 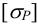
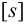
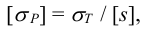
где 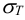
Допускаемые напряжения для материала гайки обычно принимают следующими:
3) Принимают допускаемое давление 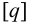
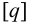
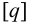
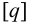
4) Задаемся (или задано в условии задачи) профилем резьбы и относительной рабочей высотой профиля 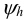
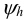
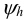
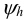
5) Выбираем конструкцию гайки — цельная, разъемная — и принимаем коэффициент высоты гайки: для цельных гаек 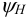
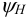
6) Определяем средний диаметр резьбы из условия износостойкости
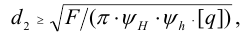
по которому подбирают ближайшие стандартные значения параметров резьбы — диаметры: внутренний 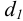
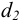
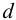
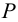
Резьба, параметры которой определены из расчета на износостойкость, обычно имеет избыточный запас прочности на срез, поэтому резьбу винта и гайки на срез обычно не проверяют.
7) Определяется угол подъема винтовой линии 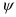
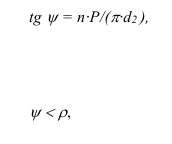
где 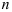
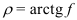
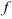


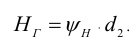
б) Число витков гайки определяют, учитывая неравномерность распределения осевой нагрузки по виткам резьбы, выдерживая условие
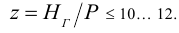
в) Наружный диаметр 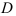
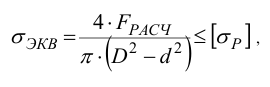
где 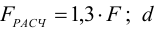
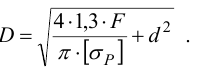
г) Диаметр бурта гайки
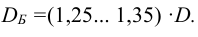
9) Винт проверяется на прочность. Этот расчет выполняется как проверочный. Так как тело винта одновременно подвергается сжатию (или растяжению) и кручению, то, согласно энергетической теории, условие прочности винта записывается так:
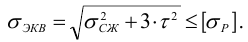
Здесь
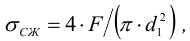
где 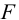
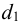
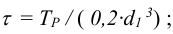
где 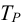
Приближенно можно провести проверочный расчет винта на прочность по расчетной осевой силе 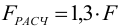
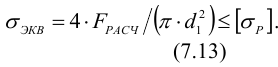
10) Проводится расчет винта па устойчивость. Этот расчет также выполняется как проверочный для работающих на сжатие длинных винтов. Условие устойчивости имеет вид
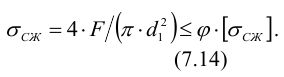
Здесь 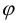
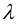
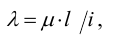
где 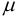
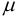
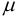
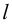
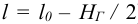
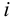
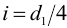
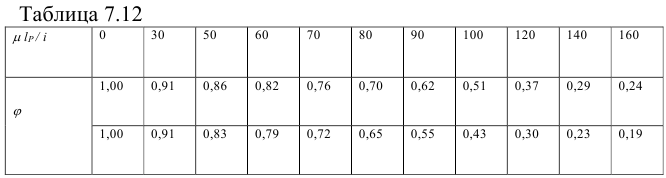
Нижние значения 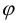
11) Определяется длина рукоятки. Усилие, прикладываемое на рукоятке винтового механизма, должно обеспечивать преодоление момента сил трения в резьбе
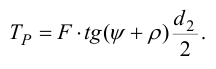
Длину рукоятки определим из равенства моментов силы трения в резьбе и усилия, приложенного к рукоятке, приняв при этом усилие рабочего на рукоятку 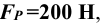
Возможно эта страница вам будет полезна:
Задача №7.3.1
Рассчитать основные параметры ручного домкрата (рисунок 7.12) грузоподъемностью 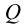
Решение:
1 Расчет винта
1.1 Вес груза 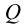
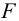
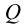
1.2 По условию износостойкости (7.2) резьбы определяем ее средний диаметр 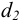
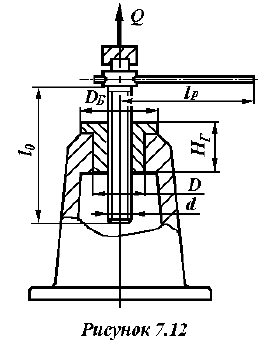
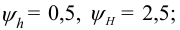
допускаемое давление в резьбе 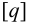
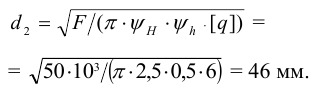
Принимаем стандартную трапецеидальную (по заданию) резьбу винта (таблица Б2) с параметрами: наружный диаметр 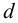
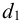
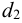
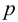
1.3 Определяем угол подъема резьбы 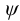
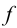
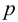
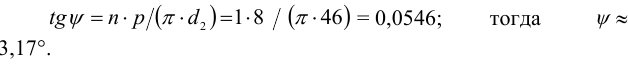
Условие самоторможения соблюдено, так как 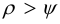
1.4 Проверка винта на прочность. Принимая допускаемое напряжение на растяжение 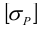
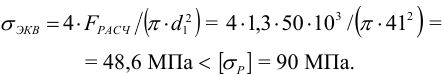
Прочность винта обеспечена.
1.5 Проверка винта на устойчивость. Расчетная длина винта 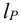
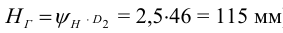
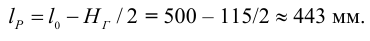
Тогда гибкость винта (при 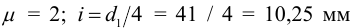
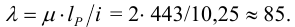
1.6 По таблице 5.11 находим коэффициент продольного изгиба
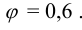
Тогда, приняв по (7.1)
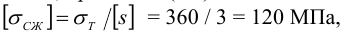
будем иметь по (7.14)
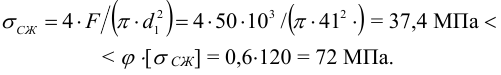
Устойчивость винта обеспечена. 2 Расчет гайки
2.1 Определим ее наружный диаметр 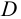
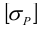
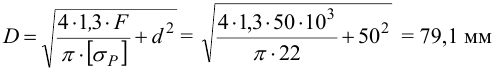
Принимаем 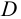
2.2 Диаметр бурта 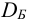
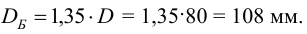
Принимаем 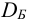
2.3 Выполним проверку бурта на смятие
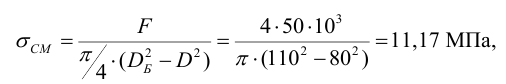
что значительно меньше допускаемого напряжения 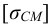
3 Расчет рукоятки
3.1 Момент сил трения в резьбе по формуле (7.16)
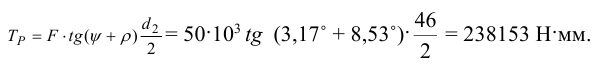
3.2 Длина рукоятки по формуле (7.17)
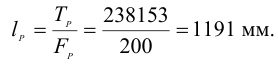
Примем длину рукоятки равной 1190 мм.
Кстати готовые задачи на продажу и теория из учебников по предмету детали машин тут.
Тема: Кинематический и силовой расчет передаточного механизма
Приступая к расчету кинематических и силовых параметров механических передач, студенты должны изучить материал, изложенный в конспекте [1, с.29… 34] или в источниках [2, с.117… 119], [3, с.111…113], [4, с. 114… 115].
Решение задач можно вести в следующем порядке.
1) Определяют передаточные отношения передач; под передаточным отношением и понимается отношение угловых скоростей на ведущем и ведомом колесах (валах) передачи. Помимо этого передаточное отношение передачи можно определить
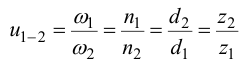
2) Вычисляют частоту вращения и угловую скорость на всех валах привода; зная передаточное отношение и опираясь на (6.1), можно вычислить угловую скорость
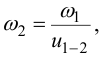
и так далее для каждого вала привода.
Угловую скорость 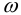
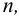
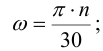
3) Вычисляют мощность на валах привода;
мощность вращательного движения 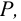
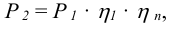
здесь 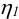
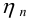
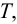
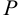
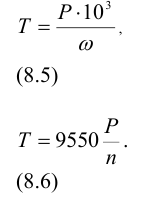
5) Определяют общий к.п.д. и общее передаточное отношение привода.
Как известно, передаточное отношение кинематической цепи, состоящей из 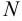
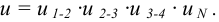
Общий к.п.д. привода при последовательном соединении механизмов и устройств также определяется произведением частных к.п.д.
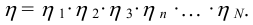
Задача №8.3.1
Определить передаточное отношение между входными и выходными звеньями и каждой передачи в отдельности; угловую скорость, число оборотов, мощность и крутящий момент каждого вала; общий коэффициент полезного действия двухступенчатой передачи, изображенной на рисунке 8.11.
Числа зубьев колес соответствующих передач:
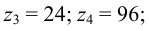
к.п.д. зубчатой цилиндрической передачи 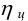
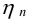
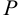
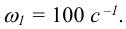
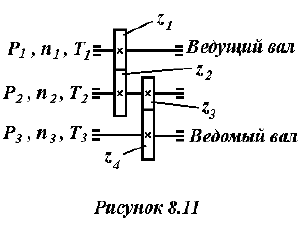
Решение:
1 Передаточные отношения передач по формуле (8.1)
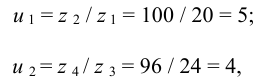
тогда общее передаточное отношение двухступенчатой передачи согласно формуле (8.7)
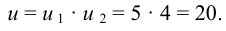
2 Определяем угловые скорости и частоты вращения валов по формулам (8.2) и (8.3)
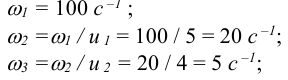
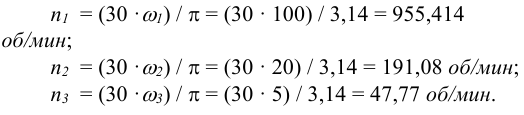
3 Мощности на валах передаточного механизма согласно формуле (8.4)
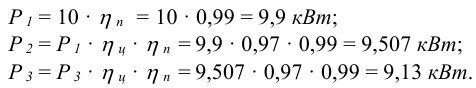
4 Моменты на валах передаточного механизма по (8.5) или (8.6)
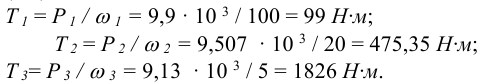
5 Общий к.п.д. передаточного механизма согласно формуле (8.8)
Примеры решения задач по всем темам деталей машин
Детали машин – научная дисциплина по теории расчета и конструированию деталей и узлов машин общемашиностроительного применения. Детали общего назначения применяют в машиностроении в очень больших количествах, поэтому любое усовершенствование расчета и конструкций этих деталей, позволяющее уменьшить затраты материала, снизить стоимость производства, повысить долговечность, приносит большой экономический эффект.
Детали машин и основы конструирования — как наука относится к более общей области науки – машиностроению – и занимается разработкой научных основ расчета и проектирования деталей и узлов общемашиностроительного применения, экспериментальными исследованиями и обобщением инженерного опыта создания машин и механизмов.
Введение в основы конструирования
До изучения типовых узлов и деталей машин необходимо познакомиться с основами конструирования, которые надо использовать при разработке деталей и узлов конструкций. Такой подход позволит в дальнейшем избежать ошибок и создавать не только типовые, а самые разнообразные и совершенные изделия.
При конструировании нужно руководствоваться общими концепциями, в основе которых лежат эксплуатационные, производственно-технологические, экономические и эргономические требования.
Отметим высокую стоимость военной техники 2000 $ за 1 кг (у автомобилей в 200 раз меньше), а у МКС «Спейс Шаттл» — 10000 $ за 1 кг. Такая высокая стоимость связана с большим объемом теоретических и экспериментальных исследований. Это требует тщательного изучения всех элементов создания JIA, включая конструирование.
Конструкция изделия должна максимально удовлетворять потребности пользователя, т. е. при низкой цене должна иметь высокое качество. Технические характеристики должны быть на уровне мировых достижений и иметь резерв развития.
Основные принципы и правила при конструировании механизмов, узлов и деталей с учетом всех изложенных требований реализуют следующие мероприятия:
- Обеспечение показателей, записаппых в техническом задании (ТЗ), определяющих назначение, технические и экономические характеристики объекта: производительность, мощность, скорость движения, стоимость и другие параметры.
- Выбор наиболее рациональной схемы конструкции узлов и их элементов, например, использование вместо развернутой схемы передачи соосной или замена передачи винт — гайка скольжения па роликовинтовую передачу (РВИ). Создание машин нового поколения с использование мехатроники (сочетание механических элементов с электронными устройствами).
- Повышение надежности и ресурса. У детали надежность обеспечивается прочностью, жесткостью и стойкостью к воздействиям: вибрации, износу, температуре, давлению, влажности и др.
- Уменьшение материалоемкости, что выполняется при создании компактных конструкций и изготовлении деталей из материала с высокой удельной прочностью (металлы, биметаллы, неметаллы и композиты), выборе размеров и формы детали, обеспечивающей выравнивание напряжений. Возможно также упрочнение материала различными методами (термическими, химико-термическими, физическим воздействием высоких энергий и др.). Использование заготовок, максимально приближенных к окончательной форме детали, получаемых литьем, штамповкой, сваркой и другими высокопроизводительными способами.
- Малого энергопотребления и высокой износостойкостью при эксплуатации, что реализуется при минимальных потерях на трение и высоком КПД. Например, использование в передачах подшипников качения вместо подшипников скольжения.
- Обоснованному назначению точности и шероховатости деталей и обеспечению их взаимозаменяемости. Использованию стандартизации и унификации деталей и их элементов.
- Исключение попадания грязи, пыли и влаги на подвижные детали изделий, используя герметичные корпуса, кожухи, уплотнения и другие элементы конструкций, а на ряд поверхностей, особенно наружных, нанесение антикоррозионных покрытий. В результате устраняется коррозия, а в узлах трения уменьшается износ.
- Включение элементов (лючков, регулировочных устройств …) для обеспечения технического обслуживания, ремонта и контроля.
- Создание безопасности и комфорта оператору или исключение его присутствия (автоматизировать процесс), устранение вредного зоздействия на человека и окружающую среду.
- Учет производственно-технологических требований (см. гл. 3).
Рассмотрев общие принципы и правила, перейдем к более подробному изучению основ конструирования, иллюстрируя примерами решений и задачами.
Прочность деталей и узлов
Одно из основных эксплуатационных требований — обеспечение надежности конструкций, что особенно важно для узлов ЛЛ. Надежная деталь должна быть прочной, а в ряде случаев и обладать необходимой жесткостью.
Прочная и жесткая деталь при эксплуатации не должна разрушаться и подвергаться недопустимым упругим и пластическим деформациям. Примерами опасных деформаций являются большие прогибы и перекосы валов с зубчатыми колесами при эксплуатации, образование от действия нагрузок ямок на дорожках подшипников качения.
Условия прочности для сечения, в котором под действием внешних силовых факторов возникают лишь нормальные напряжения:
• В расчетах общего машиностроения:
- По допускаемым напряжениям
или
- По запасам прочности
,
где 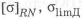
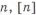
• Расчеты ЛA проводят по разрушающим напряжениям
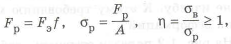
где 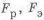
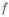
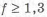
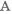
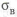
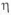
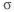
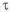
Повышение прочности и жесткости детали наиболее просто можно добиться, увеличивая размеры в опасных сечениях или используя материал лучшего качества. Обычно такое решение приводит к увеличению массы, габаритов и стоимости. Поэтому нужно конструктору использовать способы обеспечения прочности при минимальном увеличении массы. Указанные способы изучаются ниже и позволяют получить деталь с минимальной материалоемкостью.
Конструирование прочных узлов и деталей минимальной массы сводится к выбору рациональной схемы конструкции, формы, размеров и материала деталей. Возможно использование и упрочнения материала.
Минимальная масса конструкции обеспечивается следующими способами:
а) Создание изделия с рациональной конструктивно-силовой схемой:
Пример с решением №1.1.
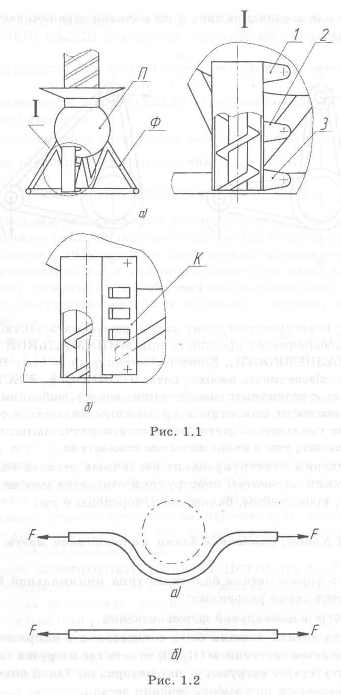
Грунтозаборное устройство корабля, совершающего посадку на Венеру, в исходном вариапте имело трубчатый корпус шнека, который крепился кронштейнами к двум различным элементам конструкции: кронштейны 2,3 — к ферме (Ф), а кронштейн 1 — к приборному отсеку (П) (рис. 1.1,а). При испытаниях было установлено, что в момент посадки при перегрузке 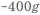
Для получения конструкций минимальной массы необходимо предусмотреть передачу силы но кратчайшему пути. Это осуществляется тогда, когда конструкция подвергается растяжению, сжатию, сдвигу, но не изгибу. К этому требованию можно отнести и метод «блокировка деформаций».
Пример с решением №1.2.
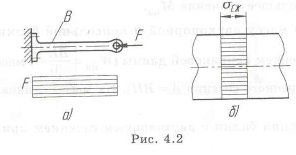
На рис. 1.2 показан стержень, работающий на растяжение от силы 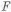
Пример с решением №1.3.
На рис. 1.3,а изображена неудачная конструкция качалки, плечи которой работают на изгиб. В измененной конструкции (рис. 1.3,6) этот недостаток устранен, так как дополнительная полка передает нагрузки по кратчайшему пути, работает на растяжение и напряжения уменьшаются. Последний вариант можно отнести и к использованию метода «блокировка деформаций», так как соединение двух плеч качалки ограничивают их де формацию.
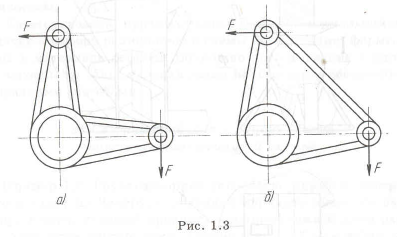
Перед конструктором стоит задача разработать такую деталь, которая обеспечивает прочность при МИНИМАЛЬНОЙ МАССЕ (МАТЕРИАЛОЕМКОСТИ). Конечно, деталь должна быть НАДЕЖНОЙ, т. е. обеспечивать необходимую ПРОЧНОСТЬ, ЖЕСТКОСТЬ и стойкость к различным воздействиям: износу, вибрации, температуре, влажности, давлению и др. Важным является и то, что в результате уменьшения материалоемкости улучшаются как эксплуатационные, так и экономические показатели.
Рассмотрим конструирование различных деталей балочного типа. К таким элементам конструкции относятся многие детали: валы, оси, кронштейны, балки, тяги, торсионы и др.
б) Конструирование балки минимальной массы:
Выбор формы детали балочного типа минимальной МАССЫ определяется двумя условиями:
Выбор рациональной формы сечения.
Форма детали должна быть согласована с напряженно-деформированным состоянием (НДС), то есть где нагрузка там и материал, отсутствует нагрузка — нет материала. Такой подход должен реализоваться при выборе сечения детали.
Создание равпопрочной по длине балки. Для получения РАВНОПРОЧНОЙ БАЛКИ необходимо , чтобы во всех сечениях удовлетворялось равенство
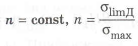
и условие прочности
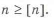
В равнопрочной конструкции вероятность разрушения всех элементов одинакова.
При статическом нагружении можно принимать
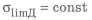
и условие равнонрочности примет вид
Выбор рациональной формы сечения
Рассмотрим ряд примеров конструирования прочных деталей, балочного типа, минимальной массы при статической нагрузке. Эти задачи решаются легко при простом напряженном состоянии. Минимальная масса детали получается при равномерных напряжениях материала в каждом сечении (выравнивание напряжений), что достигается удалением из сечения участков, где напряжения малы.
Пример с решением №1.4.
Рассмотрим кронштейн, нагруженный постоянной силой 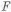
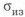

Введем КОФФИЦИЕНТ СОВЕРШЕНСТВА ПО МАССЕ 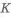
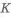
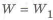

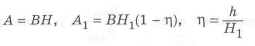
и момента сопротивления
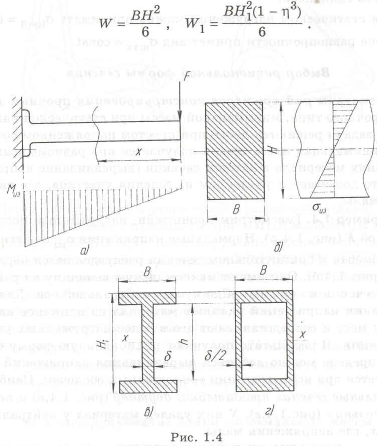
Геометрические характеристики сечений приведены на рис. 1.4. Из формулы (1.2) определяем высоту двутавра равнопрочного прямоугольному сечению, а затем находим
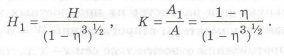
Отметим, что в формулах у двутавра не учитывается стенка, что при 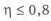
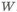
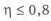
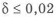
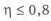
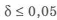
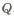
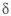
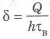
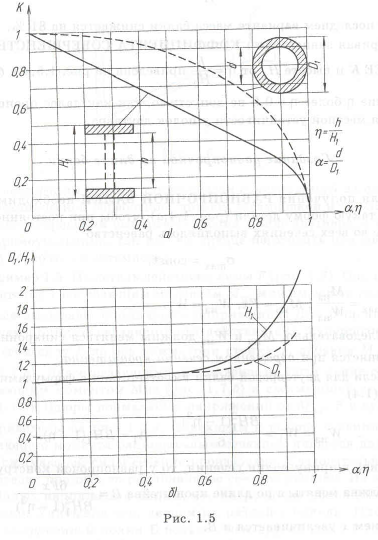
Приведем некоторые результаты:

В последнем варианте масса балки снижается на 81 %. Кривая зависимости КОФФИЦИЕНТА СОВЕРШЕНСТВА ПО МАССЕ 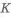
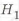
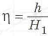
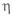
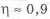
Создание равнопрочной по длине балки
Для получения РАВНОПРОЧНОЙ БАЛКИ необходимо выбрать такую форму детали (рис. 1.4,а), чтобы при постоянной нагрузке во всех сечениях выполнялось равенство
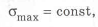
где
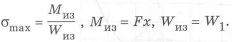
Следовательно, 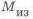
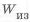
Если для двутавровой балки в соответствии с формулами (1.1), (1.2), (1.4)
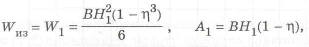
изменить ширину полки сечения, то у равнопрочой конструкции она должна меняться по длине кронштейна
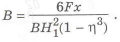
С увеличением 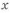
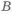
Возможно также изменять и высоту двутавра, тогда
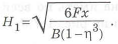
Такая конструкция кронштейна приведена на рис. 1.6, где пунктиром показана расчетная высота 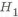
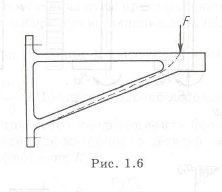
Выбор формы детали также связан с технологией изготовления: механической обработкой, литьем, штамповкой и др. Обычно при конструировании выбирают сечение в виде двутавра, а не полого прямоугольника, так как его проще изготовить при механической обработке и штамповке.
Пример с решением №1.5.
На деталь действуют силы 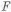
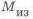
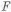
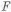
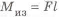

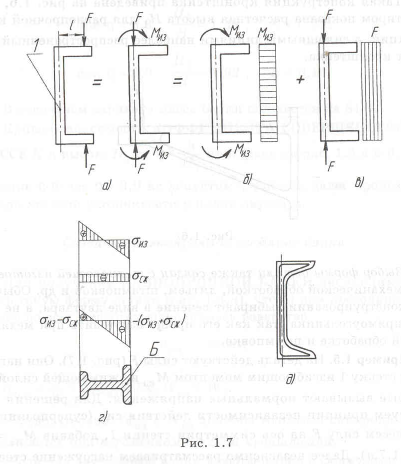
Пример с решением №1.1.1
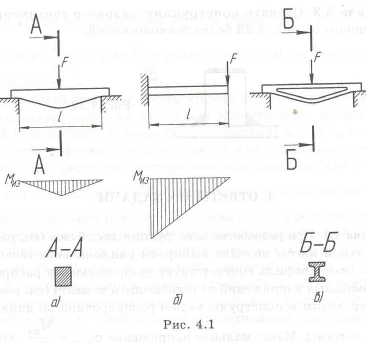
Разработать конструкцию двухопорной балки минимальной массы нагруженной силой 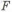
При разработке конструкции двух балок (см. рис. 1.8) минимальной массы вначале выбираем рациональное сечение — двутавр. Этот профиль соответствует рациональному распределению нормальных напряжений от изгибающего момента (см. рис. 1.4). Далее переходим к конструированию равнопрочной по длине балки 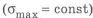
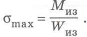
Определим для двух опорной балки максимальный изгибающий момент 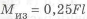
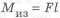
Максимальный изгибающий момент у консольной балки в 4 раза больше, чем у двухопорной.
В качестве примера рассмотрим обеспечение равнопрочности по длине балки прямоугольного сечения. Для выполнения условия 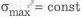
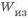
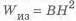
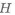
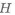
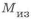
Сравним массу двухопорной и консольной балки с прямоугольным сечением одинаковой длины (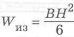
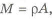
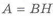
Конструкция балки с двутавровым сечением приведены на рис. 4.1,е.
Пример с решением №1.2.1
Сконструировать кронштейн минимальной массы, нагруженный сжимающей силой 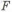
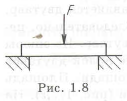

Конструкция кронштейна В минимальной массы, нагруженного сжимающей силой 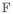
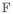
Выбор материала детали
Рассмотрим детали, нагруженные растягивающей силой, из разных материалов (отличаются пределы прочности и плотность материалов). При выборе нужно использовать коэффициент удельной прочности при постоянной нагрузке 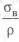
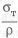
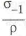
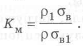
Существенно уменьшается масса равнопрочного стержня при замене стали на легкие сплавы. При переходе от стали ЗОХАГСА 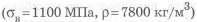
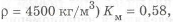
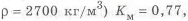

Рассмотрим другой вариант примера 1,5 , когда сравниваются балки из разных материалов, нагруженные изгибающим моментом.
Оценим влияние материалов деталей на массу, вводя коэффициент 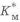
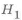
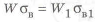
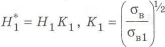
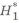
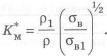
Для получения равнопрочной балки при 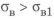
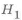
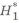
При переходе от прямоугольного сплошного сечения к двутавровому и замене материала детали формула коэффициента совершенства детали по массе запишется в виде 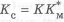
Если при одной и той же конфигурации детали заменить сталь алюминиевым сплавом, то ее масса уменьшится примерно в три раза. Кроме того, у алюминиевых сплавов повышенная теплопроводность, что полезно, например, для теплонагруженных узлов червячных передач. Однако у них модуль упругости в два раза меньше и соответственно меньше жесткость.
В конструкциях, где нужна повышенная податливость и пониженная теплопроводность, нужно использовать композиционные материалы и пластмассы.
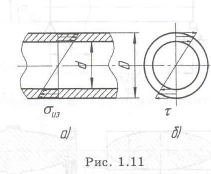
Рассмотрим валы. У вала, нагруженного изгибающим и крутящим моментами, используют сплошное круглое сечение или кольцевое. При увеличении внутреннего диаметра кольцевого сечения возможен переход к равномерному распределению напряжения. Проиллюстрируем это на примере вала, нагруженного изгибающим 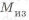
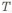
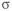
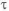
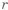
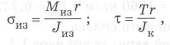
где 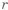
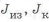
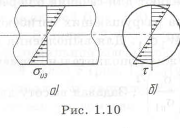
При наличии у вала отверстия напряжения распределяются более равномерно (рис. 1.11,а,б). При
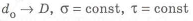
(переход к тонкостенным конструкциям).
Пример с решением №1.6.
Рассмотрим неподвижную ось зубчатого колеса, нагруженную изгибающим моментом от силы 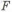
Определим для сплошного круглого и кольцевых сечений площадь
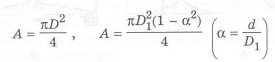
и момент сопротивления
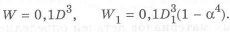
Определим, используя формулы (1.5) и (1.6), наружный диаметр кольцевого сечения равнопрочного сплошному, круглому 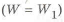
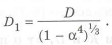
Коэффициент совершенства по массе
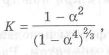
а с учетом разных материалов деталей определяется по формуле
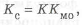
где
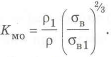
Графики зависимости 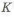
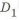
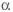
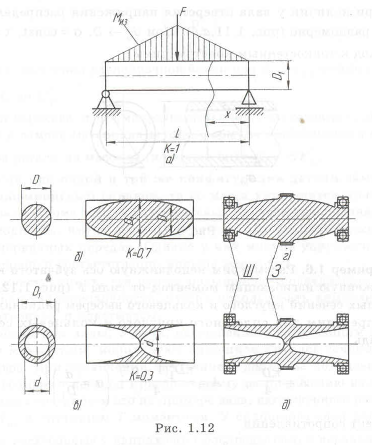
Перейдем к выбору формы неподвижной оси (рис. 1.12), нагруженной изгибающим моментом. Рассмотрим конфигурацию равнопрочной детали для двух случаев:
а) Ось со сплошным, круглым сечением.
В середине оси 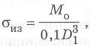
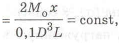
на участке
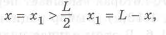
где 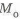
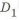
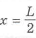
Равнонрочность обеспечиваем путем изменения наружной поверхности. Из выражения (1.8) находим диаметр наружной поверхности по длине оси
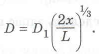
Изменив соответственно наружный диаметра оси 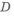
б) Ось с кольцевым сечением и постоянным наружным диаметром сравним со сплошным.
Для сплошного сечения 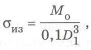
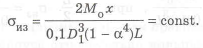
Равнопрочность обеспечиваем путем изменения диаметра отверстия. Из выражения (1.9) находим диаметр отверстия 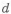
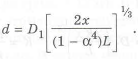
Уменьшение массы у равнопрочной оси с кольцевым сечением (рис. 1.12,в) достигает -70% по сравнению с круглой осью постоянного сечения. На рис. 1.12 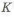
На рис. 1.12,г,д показаны возможные конструкции таких осей, у которых лишь в местах установки подшипников (у шипов (Ш) и кольцевых участков) равнопрочность не обеспечена 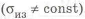
Пример с решением №1.7.
Рассмотрим вращающуюся ось, нагруженную в середине силой 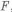
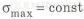
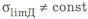
Необходимо отметить, что в этом случае, так как нагрузка переменная, то при определении 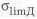
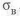
Оценивать равнопрочность нужно но формуле 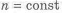
(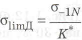
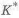
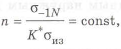
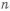
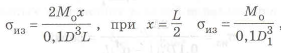
откуда находим
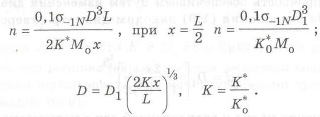
Здесь 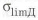
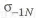
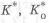
На рис. 1.12,г показана возможная конструкция такой оси. Если у нее в местах установки подшипников и резких переходов у галтелей с малым радиусом и зубьев, не учтен коэффициент 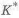
При определении 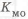
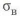
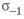
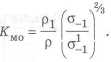
Пример с решением №1.8.
Рассмотрим короткий стержень, нагруженный сжимающей силой. В этом случае прочность определяется из условия
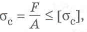
а напряжения распределены равномерно. Поэтому форма сечения не влияет па массу, если сила приложена в центре жесткости сечения. При замене материала коэффициент массового совершенства определяется по формуле
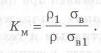
Нужно учитывать, что при растяжении-сжатии балок сечение может быть произвольно, если сила приложена в центре жесткости.
Пример с решением №1.9.
Проанализировать, как правильно выбрать расположения стенки корпуса относительно кольцевых гнезд под подшипники (рис. 1.13). На корпус от подшипника передается сила 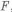
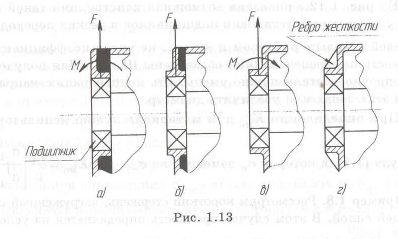
в) Уменьшение концентрации напряжений
Снижение концентрации напряжений важно для увеличения прочности и долговечности деталей при циклическом нагружении.
Уменьшить концентрацию напряжений можно выполнить двумя способами: конструктивным и технологическим. В первом случае не рекомендуется делать резких переходов формы (галтелей с малым радиусом, пазов под шпонки…) и избегать скачков нагрузки от сосредоточенных сил, прессовых посадок и других. При технологическом способе прочность детали увеличивается за счет создания в поверхностном слое остаточных напряжений сжатия и/или повышения прочности поверхностного слоя. Это осуществляется дробеструйной обработкой, обкаткой роликами, химико-термическими способами (цементация, азотирование), методами физического воздействия высокой энергией (лазерная, ионно-плазменная обработка) и др. Особенно опасны участки детали, где имеется двойная концентрация напряжений.
Пример с решением №1.10.
На рис. 1.14,а показан вал с двойной концентрацией напряжений: на наружной поверхности и в отверстии. После устранения резких переходов вала па наружной поверхности или смещения проточки в отверстии или в обоих изменений (1.14,6) его прочность увеличивается.
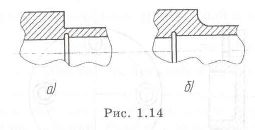
Для уменьшения концентрации напряжений у шипа вала с галтелью (см. рис. 1.15) можно провести следующие изменения: увеличить радиус р, по он не должен быть меньше, чем фаска у устанавливаемого на шип подшипника. Если это не выполняется, то можно взять 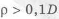
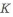
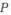
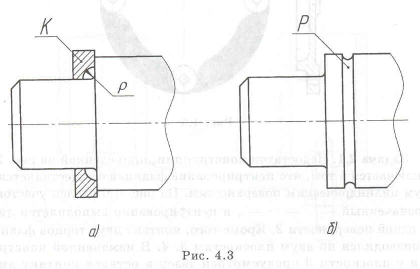
Пример с решением №1.5.1.
У крышки подшипника (рис. риал из малонагруженных участков. Выбрать материал крышки.
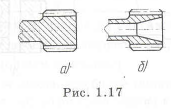
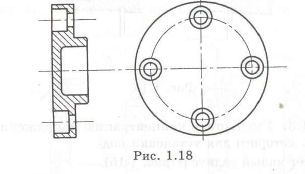
д) Увеличение материала на участках, где нагрузки велики и использование резервирования
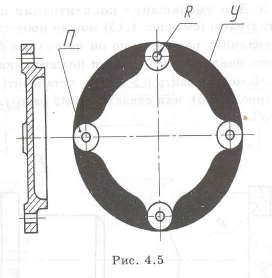
Неудачная крышка подшипника приведена на рис. 1.20. Правильная конструкция литой крышки изображена на рис. 4.5, в которой удален материал из малонагруженных участков, обозначенных У (они зачернены). Материал крышки алюминиевый или магниевый сплавы. Например, у литых изделий AЛ4, MЛ4, а у изготовленных механической обработкой — Д16Т, МА5. У литых деталей делаются приливы П, поверхность которых подвергается обработке.
Жесткость деталей и узлов
Жесткость определяет способность детали сопротивляться деформации при нагружении. Наряду с деталями, где деформация ограничена и жесткость должна быть достаточно высокой (валы, балки), имеются элементы с регламентированной и/или малой жесткостью (пружины, сильфоны, гибкие колеса волновых передач). Целесообразно использовать для обеспечения необходимой жесткости балок рациональные сечения, выбранные из условия прочности. Такие сечения также будут иметь минимальную массу. Однако равнопрочная конструкция имеет минимальную жесткость.
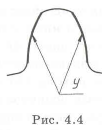
Нельзя допускать потерю общей и местной устойчивости. Общая устойчивость балки, нагруженной сжимающими силами, связана с жесткостью. Действующая сила должна быть меньше критической силы, которую определяют по формуле Эйлера:
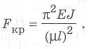
При конструировании длинных стержней, которые могут потерять общую устойчивость, их рациональным сечением, обеспечивающем минимальную массу, будет кольцевое, которое имеет максимальное значение отношения момента инерции сечения к погонной массе. Используются детали, состоящие из труб.
Повышение жесткости возможно путем:
• использования материала с более высоким модулем упругости (например, вместо алюминиевых сплавов 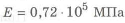
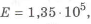
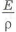
• замена деформации изгиба на растяжение-сжатие;
• использование ребер или перегородок; увеличение площади контакта;
• увеличение жесткости наиболее податливого элемента сжатию (например, упругой прокладки) и др.
Пример 1.15.
Рассмотрим изгиб кронштейна под действием 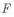
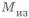
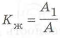
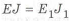
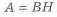
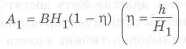
и моментов инерции прямоугольника 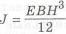
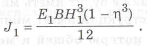
Приравнивая моменты инерции 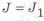
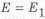
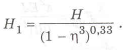
Окончательно получаем коэффициент совершенства по массе
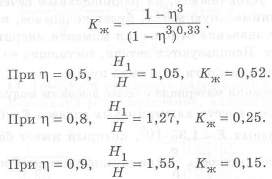
Графики зависимости высоты двутаврого профиля равножесткого прямоугольному и коэффициента совершенства по массе 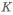
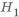
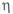
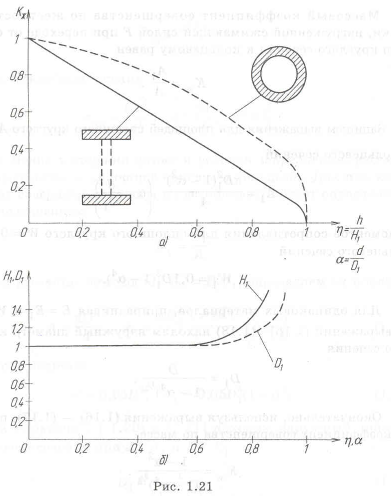
При разных материалах
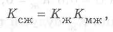
где
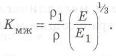
Пример с решением №1.16.
Определить массовый коэффициент совершенства по жесткости для балки, нагруженной изгибающим моментом при замене сплошного круглого сечения на кольцевое у равнопрочных стержней 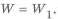
Массовый коэффициент совершенства по жесткости для балки, нагруженной сжимающей силой 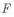
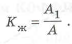
Запишем выражения для площадей сплошного круглого 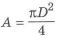
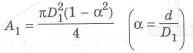
и моментов сопротивления для сплошного круглого 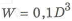
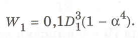
Для одинаковых материалов, приравнивая 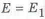
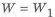
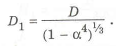
Окончательно, используя выражения (1.16) — (1.17), получаем коэффициент совершенства по массе
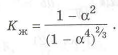
Графики зависимости 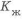
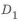
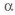
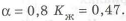
Аналогичные значения 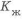
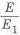
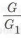
Пример с решением №1.17.
Рассмотрим длинный стержень 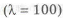
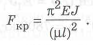
а критические напряжения
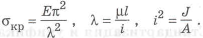
Не меняя у стержня длину и условия закрепления, рассмотрим два сечения — сплошное круглое и кольцевое. Для них коэффициент совершенства массы по устойчивости будет определяться также отношением:

При равенстве жесткостей 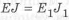
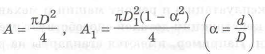
и момент инерции
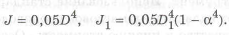
Из выражений ( 1.20) и (1.21) находим наружный диаметр кольцевого сечения при
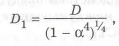
а коэффициент совершенства но массе для устойчивости имеет вид
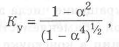
а при
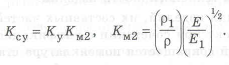
У равножестких стержней 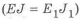
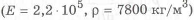
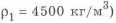
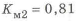
Стандартизация и унификация
Использование стандартизации и унификации деталей и узлов улучшает качество изделий и делает конструкцию более технологичной и экономичной ее производство.
Стандартизация и унификация соответствует, как эксплуатационным, так и производственно-технологическим требованиям.
Стандартизация — это регламентирование конструкции и ти-иоразмеров применяемых машиностроительных деталей, узлов, агрегатов. Стандартизация ускоряет проектирование, облегчает изготовление, эксплуатацию и ремонт машин и механизмов и при целесообразной конструкции деталей способствует увеличению надежности машин. Например, имеются стандарты на резьбу, модули зубчатых колес, что позволяет применять для их изготовления стандартный инструмент. Использование стандартных деталей и изделий позволяет наладить их массовое производство, что обеспечивает высокое качество и низкую стоимость. Особенно это важно для сложных изделий, например, электродвигателей и подшипников.
Л зависимости от сферы действия предусматриваются следующие категории стандартов: международные (ИСО), государственные (ГОСТ) и отраслевые (ОСТ).
Унификация это приведение объектов одинакового, функционального назначения к единообразию но установленному признаку и рациональное сокращение числа этих объектов на основе данных об их эффективной применяемости. Унификация состоит в многократном применении в конструкции одних и тех же элементов и деталей. Это наиболее распространенная и эффективная форма улучшения технологичности изделий.
Стандартизация изделий, их составных частей и деталей дает наибольший эффект при сочетании с унификацией. В результате этих мероприятий сокращается номенклатура стандартного рабочего и мерительного инструмента, что особенно важно при использовании сложного инструмента (фрез, метчикоп, плашек и др.). стоимость которых значительно увеличивается при индивидуальном производстве нестандартных образцов.
Примером унификации может служить использование одинаковых подшипников у вала, хотя действующие на них нагрузки отличаются.
Точность взаимного положения деталей
Точность деталей и их взаимного положения является одной из составляющих эксплуатационных требований к конструкции. Точность самих деталей изучается в курсе метрология, где излагаются основы взаимозаменяемости.
Базирование деталей
Базирование — предание детали требуемого положения, относительно выбранной системы координат. Поверхность, ось, точка, принадлежащие детали и используемые для базирования, называются базами. Погрешностью базирования называют отклонение фактически полученного положения детали от требуемого. Чаще всего базирование деталей производят по плоским, цилиндрическим поверхностям деталей и их комбинациям. При соединении двух деталей вследствие погрешностей формы сопрягаемых поверхностей и некоторых других факторов возможны перекосы деталей. например при установке узких деталей на валах.
Пример с решением №2.1.
Выбрать базу в зависимости от отношения длины сопряженного участка к диаметру 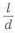
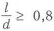
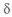
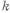
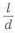
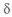
Центрирование деталей. Работоспособность проектируемого изделия во многом определяется необходимой соосностью деталей и узлов, входящих в изделие, то есть требуемой точностью центрирования. Соосность характеризуется величиной смещения номинально совпадающих осей цилиндрических поверхностей. Выбор расположения этих поверхностей определяет допуск соосности. При обеспечении требуемой соосности надо принимать во внимание то, что резьбовые соединения не обеспечивают правильного центрирования из-за биения среднего диаметра и зазоров в резьбе. В качестве центрирующих поверхностей в таких случаях, как правило, используются цилиндрические или соосные с резьбой гладкие цилиндрические пояски.
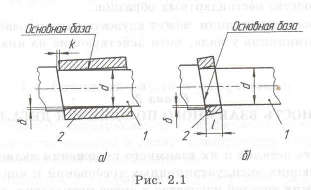
Пример с решением №2.2.
На рис. 2.2,а базой установки пальца водила является резьба, что не обеспечивает необходимой точности положения его оси. Для обеспечения необходимой точности нужно фиксировать палец по цилиндрической поверхности (база). Правиль-
ная конструкция приведена на рис. 2.2,6, в которой палец запрессован в водило и базой является цилиндрическая поверхность.
Необходимо также избегать фиксации детали по нескольким поверхностям, так как это усложняет изготовление и сборку.
Пример с решением №2.3.
Установить призматическую шпонку на валу Неправильная конструкция изображена на рис. 2.3,а где отсутствует зазор 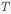
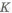
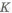
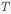
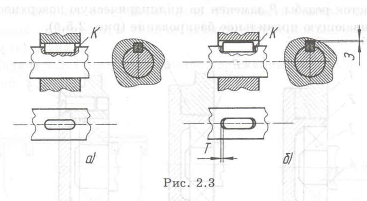
Пример с решением №2.4.
Центрирование втулки в отверстии. На рис. 2.4,а центрирование втулки выполняется по двум цилиндрическим поверхностям 1 и 2. Такое центрирование не оправдано, так как усложняет изготовление и сборку, увеличивает стоимость и не улучшает конструкцию. Правильная конструкция приведена на рис. 2.4,6,
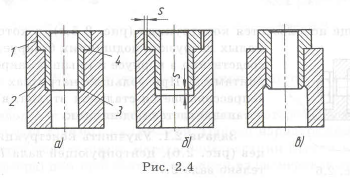
где предусмотрен зазор s, а на рис. 2.4,в верхняя часть (буртик) выступает наружу. На рис. 2А,а также неправильная установка втулки вдоль оси (опора фиксируется по двум поверхностям 3 и 4. Это устранено введением зазора s у торца втулки (рис. 2.4,6) или увеличением диаметра отверстия (рис. 2.4,в).
Пример с решением №2.5.
Изменить конструкцию (рис. 2.5,о) для обеспечения правильного базирования вала в стенке 1 корпуса. Вал 4 в подшипнике 3 и подшипник 3 в крышке 2 базируются по цилиндрическим поверхностям, что обеспечивает точное положение вала относительно крышки. Крышка крепится в корпусе на резьбе Р, которая не обеспечивает необходимой точности. В правильном варианте участок резьбы Р заменен на цилиндрическую поверхность Ц, обеспечивающую правильное базирование (рис. 2.5,(5).
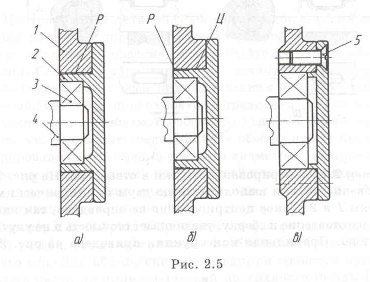
Чаще используется конструкция (рис. 2.5,в), в которой при малых нагрузках подшипник базируется непосредственно в корпусе и крышка закрепляется винтами 5. При больших нагрузках в корпус запрессовывается стальная втулка, в которой устанавливается подшипник.
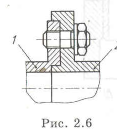
Пример с решением №2.1.1.
Улучшить конструкцию фланцев (рис. 2.6), центрирующей вала 1 относительно вала 2.
Фиксация детали па плоскости
Недостаток конструкции, приведенной на рис. 2.6, заключается в том, что центрирование фланцев осуществляется по двум цилиндрическим поверхностям. На рис. 4.6 удален участок 1, обозначенный — • • — • • — , и центрирование выполняется лишь по одной поверхности 2. Кроме того, контакт двух торцов фланцев производился по двум плоскостям 3,4. В измененной конструкции у плоскости 3 предусмотрен зазор и остался контакт лишь по плоскости 4. Возможен и другой вариант — контакт по плос-
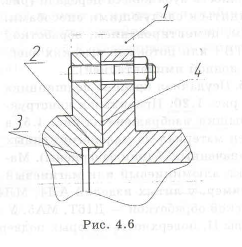
кости .3, а зазор по плоскости 4. Во втором случае нагрузки на фланец больше.
Пример с решением №2.6.
Рассмотрим конструкцию корпуса. Фиксация крышки К на основании О корпуса (рис. 2.7) может осуществляться с помощью двух, а иногда и более штифтов. Более двух штифтов устанавливают, когда оир не только фиксируют деталь, но и передают большие силы, действующие в плоскости стыка. Силы перпендикулярные к плоскости стыка воспринимаются винтами или шпильками с гайками. В местах установки штифтов и крепежных деталей снаружи корпуса делаются приливы. Не рекомендуется плоскость стыка делать ступенчатой, т. к. это усложняет его изготовление и герметизацию. Плоскость стыка основания с крышкой корпуса при окончательной сборке покрывают тонким слоем герметика.
Пример с решением №2.2.1.
Обеспечить точное положение стакана на плоскости (рис. 2.8).
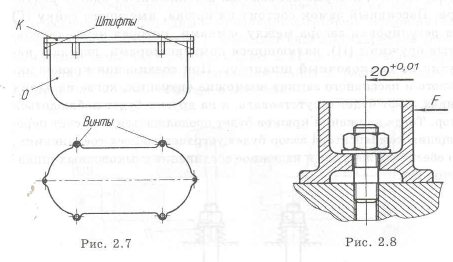
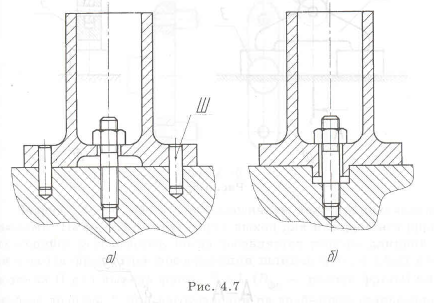
Точное положение стакана на плоскости не обеспечивается его закреплением шпилькой с гайкой (см. рис. 2.8). Точную фиксацию нужно выполнять с помощью двух штифтов (рис. 4.7,а) или цилиндрическим выступом (рис. 4.7,6)- При этом шпилька разгружается от перерезывающих сил, а нагружается лишь растягивающими силами.
Методы взаимозаменяемости
Наиболее технологична конструкция, в которой используется метод полной взаимозаменяемости. Однако наряду с ним иногда приходится использовать методы компенсации (путем введения компенсатора) или пригонки (когда один из размеров подгоняется при сборке). Метод пригонки используется лишь в индивидуальном производстве.
Устранение пригонки (подгонки). Использование пригонки затрудняет изготовление конструкций и его нужно устранять, что особенно важно в круппосерийном и массовом производстве. Точность замыкающего звена вместо пригонки (метод пригонки) может обеспечиваться за счет введения компенсатора (метод регулировки).
Пример с решением №2.7.1.
Использование компенсаторов на КА. На рис. 2.9 показаны активный (ЗА) и пассивный (ЗП) замки, установленные на стыковочных шпангоутах космического аппарата (КА). Крюк активного замка закреплен и перемещается под действием пальца, соединенного с крюком в точке 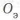
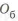
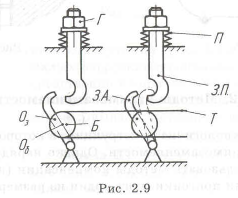
Пример с решением №2.8.
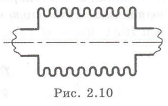
Другие компенсаторы ЛA. В гидравлических системах в качестве компенсаторов используются сильфоны (рис. 2.10), которые имеют меньшую жесткость, чем трубопровод и хорошо деформируются, компенсируя отклонения.
Компенсаторы в виде регулировочных колец используются в схеме установки подшипников враспор, что позволяет установить необходимый зазор для обеспечения удлинения вала при изменении температуры.
Развитием использования компенсаторов можно считать применение метода самоустанавливаемости. Для этого в конструкцию вводят компенсирующие неточности подвижные детали, установленные на цилиндрических или сферических шарнирах или используют телескопические соединения.
Пример с решением №2.9.
Спроектировать устройство, обеспечивающее надежное крепление детали (Д). Узел, приведенный на рис. 2.11,а, не обеспечивает необходимое крепление заготовки. Введение самоустанавливающегося звена I позволяет надежно закрепить деталь, прижимая ее на двух участках (рис. 2.11,6). В этой конструкции под гайку 2 подложена сферическая шайба 3, разгружающая откидной болт 4 от изгибающего момента.
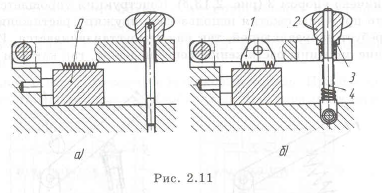
Пример с решением №2.10.
Разработать узел, позволяющий пространственно ориентировать стержень и выполнять осевую регулировку. Для компенсации углового перемещения стержня 1 относительно двух перпендикулярных осей используется шаровая опора III (рис. 2.12, где 1 — стержень; 2 — накидная гайка; 3 — опора; 4 — шпилька; 5 — гайка; 6 — стопорная шайба; 7 — отсек). Осевую регулировку выполняют с помощью винта 8 и гайки 9, которая стопорится шайбой 10.
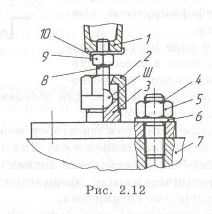
Нример 2.11. На рычаг 1 действует пружина сжатия 4 (рис. 2.13,а). При повороте рычага торцы пружины перекашиваются, и она изгибается, что может привести к потере устойчивости. Это устраняется введением в конструкцию телескопической направляющей 5, которая не дает пружине изгибаться. Длина направляющей, состоящей из двух труб, за счет телескопического соединения меняется. Заделка с двух сторон у труб шарнирная 2. Движение рычага ограничено упором 3 (рис. 2.13,6). Конструкция упрощается, если вместо пружины сжатия использовать пружину растяжения. Она не требует направляющей, так как самоустанавливается. Использование пружины растяжения менее надежно, так как при ее раз-
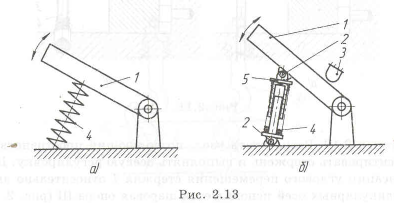
рушении конструкция не работает, а пружина сжатия продолжает функционировать.
Пример с решением №2.3.1.
Внести изменения в конструкцию узла (рис. 2.14) для обеспечения надежного закрепления двух деталей Д1 и Д2 разной высоты.
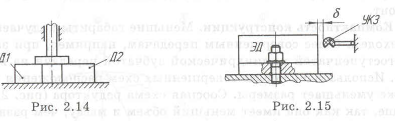
Для обеспечения надежного закрепления двух деталей 3 разной высоты (см. рис. 2.14) внесем изменения в конструкцию узла. Горизонтальную плапку закрепим на штоке, с помощью цилиндрического шарнира 2. Планка самоустанавливается и устраняет зазор между ней и деталью и обе детали надежно закрепляются (рис. 4.8,а). Планку 1 нужно сделать переменной высоты для обеспечения ее равнопрочности. Для цилиндрического шарнира использовано соединение ухо—вилка (рис. 4.8,(5, где 4 — ухо, 5 — вилка планки 1).
Пример с решением №2.4.1.
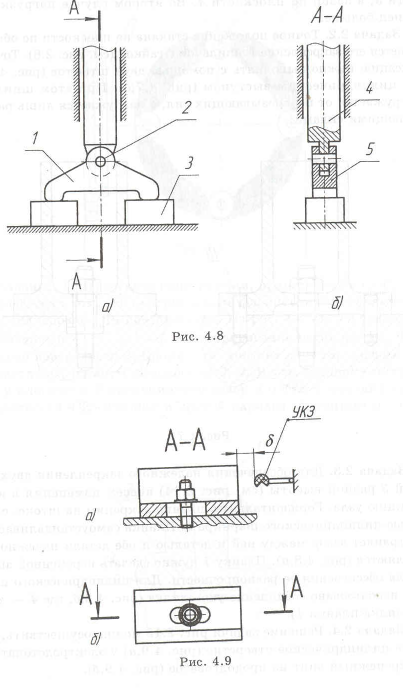
Изменить крепление электродетонатора ЭД для обеспечения точной регулировки зазора 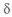
Решение задачи рис. 2.15 можно осуществить, заменив цилиндрическое отверстие (рис. 4.9,а) у электродетонатора под крепежный винт на продолговатое (рис. 4.9,6).
Некоторые методы и принципы конструирования
Рассмотрим их.
Блочный принцип. Использование блочного конструирования позволяет существенно повысить технологичность при сборке и особенно при ремонте изделия.
Пример с решением №2.12.
Сконструировать узел, в котором используется блочный принцип.
На рис. 2.16,а, приведен золотниковый клапан. При износе его требуется сложный ремонт. Необходима пригонка цилиндричес-
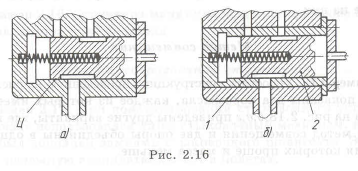
кой поверхности Ц золотника и сопряженного цилиндрического отверстия, выполненного в корпусе. На рис. 2.16,6 изображена более совершенная конструкция, где введен блок, состоящий из золотника 2, заключенного в стакан 1. Наружная поверхность золотника не изнашивается и при ремонте не требуется доработка корпуса, а следует заменить весь блок, что существенно упрощает ремонт.
Компактность конструкции. Меньшие габариты получаем при переходе к более совершенным передачам, например, при замене многоступенчатой цилиндрической зубчатой передачи на волновую. Использование более совершенных схем расположения колес также уменьшает размеры. Соосная схема редуктора (рис. 2.17,6) лучше, так как она имеет меньший объем и массу, чем развернутая (рис. 2.17,а).
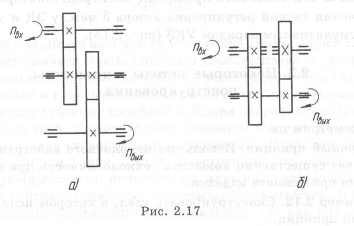
При конструировании для получения более совершенных изделий можно использовать эвристические приемы. Приведем некоторые из них.
Метод совмещения
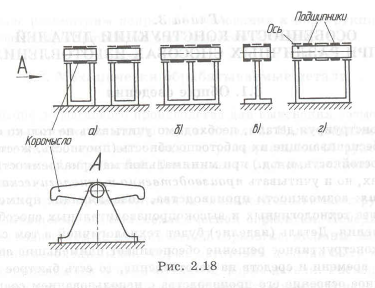
Пример с решением №2.13.
Упростить конструкцию, приведенную на рис. 2.18,а. На ней показаны два коромысла, каждое из которых имеет свою опору, а на рис. 2.18,б,в,г приведены другие варианты, где использовался метод совмещения и две опоры объединены в одну, конструкция которых проще и масса меньше.
Метод «матрешки», когда один элемент конструкции помещается внутри другого.
Пример 2.14. Например, мотор привода лунохода установлен внутри колеса и узел становится более компактным.
Метод наоборот
Пример 2.15. В методе наоборот, например, возможна замена в передаче винт-гайка вращение винта на вращение гайки и др.
Метод применения решений, аналогичных имеющимся в природе
Пример 2.16. Структура манипулятора многоразового КА «Буран» аналогична руке человека.
Метод преобразования структуры
Пример 2.17. При конструировании стыковочного устройства К А вначале использовался лишь стыковочный механизм, который потом был дополнен замками стыковочного шпангоута. Это обеспечило надежную эксплуатацию КА в полетах.
Особенности конструкции деталей при различных способах изготовления
Конструируя детали, необходимо учитывать не только факторы, обеспечивающие их работоспособность (прочность, жесткость, износостойкость, и т.д.) при минимальной материалоемкости и габаритах, но и учитывать производственно-технологические требования: возможности производства, позволяющие применение наиболее технологичных и высокопроизводительных способов изготовления. Деталь (изделие) будет технологичной в том случае, если конструктивное решение обеспечивает наименьшие затраты труда, времени и средств на изготовление, то есть быстрое и экономичное освоение его производства с использованием современных технологических процессов.
Кратко сформулируем общие технологические требования к конструкции деталей и узлов.
- Заготовка должна быть максимально приближена к окончательной форме, а механическая обработка сведена к минимуму.
- Обеспечение использования высокопроизводительных способов механической обработки (обработка напроход, удобные базы, унификация элементов, одновременное изготовление нескольких деталей).
- При изготовлении деталей должна быть предусмотрена возможность использования прогрессивных способов изготовления: прецизионных, лазерных, электронно-ионно-плазменных и других высокопроизводительных технологий, что повышает качество изделий.
- Расчленение сложных деталей на несколько с простыми формами поверхностей и использовать составные конструкции. Обеспечение доступа к составным частям, их установку и съем.
- При изготовлении рядом способов (литье, штамповка, прессование, вытяжка) следует избегать резких переходов и делать плавные очертания.
- Применять стандартизацию и унификацию элементов конструкций.
- Учитывать объем выпуска и возможности производства.
Далее рассмотрим подробнее требования к конструкции для наиболее распространенных способов изготовления
Механически обрабатываемые детали
Обычно до массового производства для выяснения возможностей сбыта выпускают малую серию изделий. Целесообразно изготовление малых серий выполнять на универсальном оборудовании с механической обработкой. Это связано с экономическими требованиями.
Рассмотрим пути обеспечения технологичности конструкции.
Сокращение объема механической обработки. Поверхности детали, подвергаемые механической обработке, должны быть минимально необходимыми. Форма заготовки должна быть максимально приближена к окончательной форме детали. Расход материала при изготовлении детали оценивается коэффициентом использования материала (КИМ)
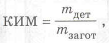
где 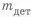
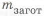
Нужно стремиться к разработке деталей с высоким значением КИМ. При безотходном производстве КИМ = 1.
Пример с решением №3.1.
Сократить объем механической обработки. На рис. 3.1,а представлена неудачная деталь, если она изготавливается из круглого прутка, то отходы в стружку большие. Лучше, когда гайка отдельно от шайбы (рис. 3.1,6) делается из шестигранного прутка, что уменьшает отходы. При большой серии можно изго-
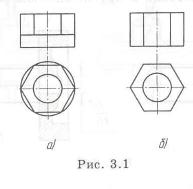
тавливать гайку объемной штамповкой, что приводит также к минимальным отходам и повышается производительность.
Использование составных конструкций. Конструкцию деталей сложной формы целесообразно делать составной, если это не противоречит выполнению других требований.
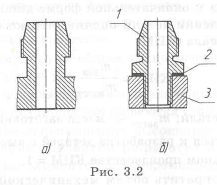
Пример с решением №3.2.
Упростить неудачную конструкцию (рис. 3.2,а), которую сложно изготовить. Переходят к составной конструкции. Отделение штуцера 1 от емкости 3 (рис. 3.2,6) значительно упрощает изготовление каждого элемента сборочной единицы. Возможно присоединение штуцера сваркой, пайкой или с помощью резьбы. В случае использования цилиндрической резьбы для исключения течи среды (газ, жидкость) нужно между кольцевым выступом штуцера 1 и емкостью установить уплотнительную прокладку 2.
Пример с решением №3.3.
Увеличить КИМ у монолитной конструкции (рис. 3.3,а). Переход к составной конструкции, включающей вал и колесо (рис. 3.3,6) существенно сокращает расход металла. Возможны вместо запрессовки и другие способы соединения вала со
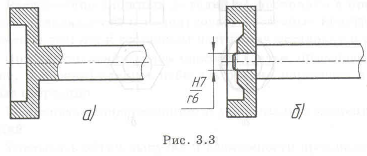
ступицей колеса. Аналогичную составную конструкцию целесообразно использовать и при разработке узла — поршня со штоком.
Пример с решением №3.1.1.
Сделать конструкцию водила, представленную на рис. 3.4, более технологичной.
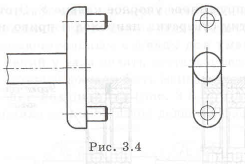
Свободный подход и выход для инструмента повышает качество и производительность.
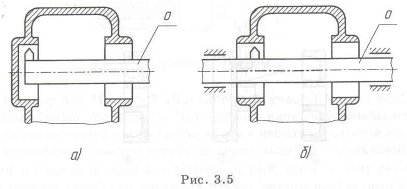
Пример с решением №3.4.
Для обработки отверстий под подшипники в корпусе (рис. 3.5,а) инструмент крепится на оправке О, закрепленной консольно (отсутствует свободный выход). После изменения конструкции (рис. 3.5,6) возможно крепление оправки на двух опорах (имеется свободный подход и выход), что облегчает обработку и повышает точность, необходимую при обработке отверстий под подшипники. Для устранения попадания грязи внутрь корпуса отверстие закрывается крышкой.
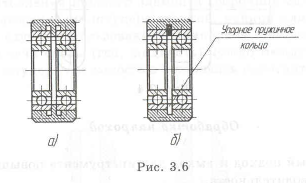
Пример с решением №3.5.
Внести изменения в конструкцию сателлита (рис. 3.6,а) для облегчения изготовления. На рис. показано не технологичное изделие, в котором нельзя изготовить отверстие под подшипники напроход. В измененном варианте (рис. 3.6,0) использована составная конструкция. Кольцевой выступ заменен канавкой, в которую вставлено пружинное упорное кольцо У. Этот вариант обеспечивает обработку отверстия напроход и приводит к увеличению точность.
Обеспечение подхода и выхода инструмента
Размеры и форма элементов детали, назначаемые конструктором, должны учитывать способы механической обработки и необходимых измерений и соответственно размеры и форму режущего и вид измерительного инструментов.
Пример с решением №3.6.
Во втулке (рис. 3.7,а) нужно просверлить отверстие О, что невозможно сделать на обычном оборудовании (свер-
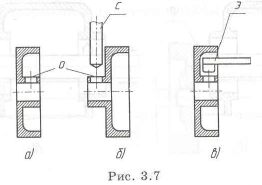
лильном станке…), если нельзя проделать дополнительное отверстие на наружной поверхности детали. В этом случае нужно изменить конструкцию так, чтобы обеспечить подход для инструмента (сверла С рис. 3.7,6) или использовать электроэрозионную обработку (рис. 3.7,в, где Э обозначен электрод).
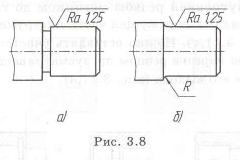
Пример с решением №3.7.
У шлифованных поверхностей шипов для уменьшения износа шлифовального круга нужно делать канавку (рис. 3.8,а). Допускается в исключительных случаях для уменьшения концентрации напряжений у вала делать галтель с регламентированным радиусом R, который должен быть меньше, чем фаска у устанавливаемого на шип подшипника (рис. 3.8,6). Для обеспечения установки подшипника на конце шипа делается фаска.
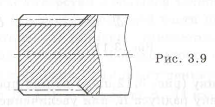
Задача 3.2. Устранить технологические ошибки у вала со шлицами (рис. 3.9).
Пример с решением №3.8.
На рис. 3.10,а приведен участок вала с резьбой, который трудно изготовить. При нарезке наружной резьбы плашкой (из-за режущей части инструмента с неполной высотой профиля) невозможно довести резьбу до торца выступа. Необходимо оставлять участок длиной 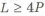
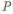
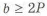
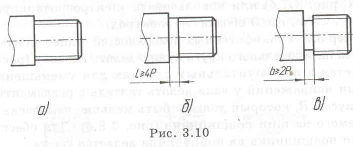
Нарезка внутренней резьбы метчиком до торца отверстия также невозможна (из-за режущей части инструмента с неполным профилем) (рис. 3.11,а). Нужно оставлять участок длиной 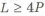
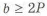
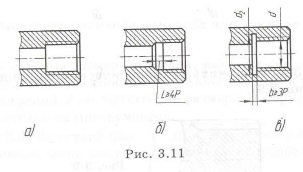
У паза под шпонку (рис. 3.12,аДв) нужно предусмотреть отверстие 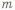
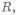
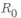
верстия для выхода инструмента (резца) на долбежном станке. В последнем случае можно изготовить паза под шпонку, используя протяжку.
Обработка отверстий
Пример с решением №3.9.
Для упрощения обработки внести изменения в конфигурацию отверстия (рис. 3.13,а), точность диаметра которого определяется 12 квалитетом. На рис. 3.13 изображен неудачный вариант, так как отсутствует конус от сверла, который остается при обработке отверстия. Устранение конуса возможно дополнительной обработкой — расточкой отверстия, но это не целесообразно. Правильный вариант показан на рис. 3.13,б.
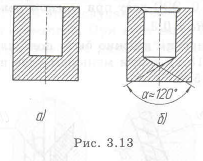
При обработке отверстий с большей точностью остаются переходные участки 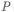
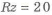
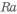
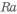
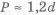
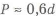
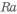
Возможно также изготовление отверстий электроэрозионной обработкой (ЭЭО), но она более энергоемка и менее производительна, чем механическая. Ее использование оправдано для деталей сложной формы с отверстиями и пазами, сплавов высокой твердости, миниатюрных тонкостенных и нежестких изделий. Например, для изготовления отверстия в недоступном для сверления
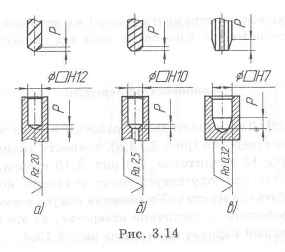
месте в примере 3.6. ЭЭО дает при мягком режиме высокую точность и достигает 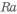
Сверление отверстий должно быть под углом более 70 к поверхности (рис. 3.15,а), а при меньшем угле нужно менять конструкцию (рис. 3.15,6).
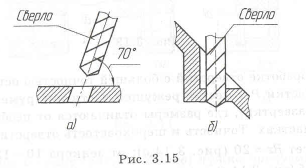
Отделение черновых поверхностей от чистовых и поверхностей с разной точностью.
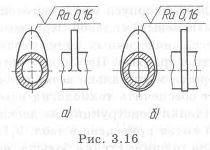
Пример с решением №3.10.
Внести изменения в конструкцию вала (рис. 3.16,а). Ее недостатком является трудность обеспечения качественной обработки поверхности кулачка. На рис. 3.16,6 изображена более технологичная конструкция, где точная поверхность кулачка отделена от грубой поверхности вала и условия шлифования его контура постоянной ширина улучшаются.
Совместную обработку в сборе следует избегать Однако не во всех случаях это возможно.
Пример с решением №3.11.
Единственно возможный вариант изготовления соединения вал-ступица является обработка отверстия под штифт при сборке (рис.3.17). В этом случая делается исключение и детали обрабатываются совместно. При этом легче изготавливать и собирать узел, изображенный на рис. 3.17,6, а не приведенный на рис. 3.17,а.
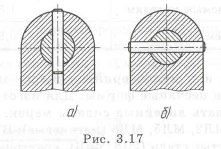
Также наиболее простой вариант изготовления — совместная обработка отверстий под штифты в основании и крышке корпуса редуктора.
Особенности конструкций литых деталей
Литые корпуса мощных редукторов в общем машиностроении обычно изготавливаются из чугуна, а у JIA из легких сплавов. Толщина стенки у таких конструкций находится с учетом обеспечения прочности и жесткости. Если механизм малой мощности (до 100 Вт), то в них литые корпуса всегда изготовляются из легких (алюминиевых и магниевых) сплавов. При замене алюминиевого сплава на сталь масса аналогичных по размерам и форме деталей увеличивается почти в три раза. При малых нагрузках, действующих на корпус, берется минимально возможная толщина стенок, которую позволяет обеспечить технология изготовления. Минимальная толщина стенки конструкций из легких сплавов в зависимости от способа литья приведена в табл. 3.1. При использовании других металлов толщина стенки больше, например, у чугуна не менее б мм, а у стали 4 мм.

В единичном или мелкосерийном производстве обычно используют литье в песчаные формы. Для изготовления деталей можно использовать литейные сплавы марок: AЛ2, AЛ3, AЛ9 (алюминиевые); MЛ2, MЛ5, MЛ6 (магниевые); BT5Л, BT6Л (титановые); углеродистые стали (20Л, 45Л), конструкционные легированные (40ХЛ, 40ХНТЛ, 35ХГСЛ) и высоколегированные (2X1ЗЛ, Х9С2Л, Х18Н24С2Л) стали, чугуны (СЧ10, СЧ20, СЧ40) и др.
Механическую обработку нужно свести к минимуму.
Форма заготовки должна быть максимально приближена к форме детали. Необходимо обратить внимание на приемы, связанные с повышением технологичности, что существенно влияет на себестоимость изделия. Эти приемы заключаются в упрощении формы и конструкции детали, замене механической обработки процессом без снятия стружки, исключения пригоночных работ, унификация конструкции, форм, размеров деталей, использования стандартных элементов.
У литых деталей целесообразно отделять черновые поверхности от чистовых. В местах, где поверхность обрабатывается целесообразно предусмотреть припуск К.
Пример с решением №3.12.
Обеспечить минимальную механическую обработку поверхности литой детали. При конструировании у бобышки нужно предусмотреть, выступающей над поверхностью детали припуск К (рис. 3.18,а). Крышку редуктора на поверхности разъема с основанием лучше также делать с припуском, как показано на рис. 3.18,6.
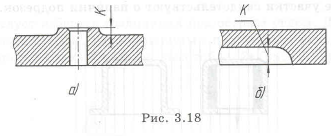
Следует избегать разъема форм по наклонным и ступенчатым поверхностям (рис. 3.19,а), а делать, как показано на рис. 3.19,б. Плоскость разъема основания и крышки корпуса редуктора также должна быть плоской, а не ступенчатой.
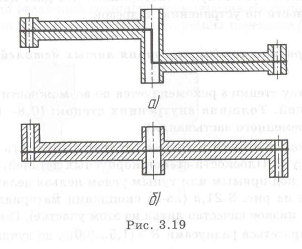
Устранение подрезок
Для беспрепятственного извлечения модели из формы нужно, чтобы на поверхности модели не было подрезок — выступов или углублений, расположенных перпендикулярно или наклонно к направлению выемки, которые при извлечении модели срезают отформованные участки. Модель детали (рис. 3.20,а) нельзя вынуть без подрезки из формы в указанном стрелкой Паправлении при литье в землю (подрезаемые участки зачернены). После изменения конструкции (рис. 3.20,6) подрезка устраняется. Подрезаемые участки можно определить, используя правило теней. При освещении детали лучами перпендикулярными к плоскости разъема затененные участки свидетельствуют о наличии подрезок.
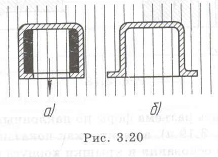
Крупные и сложные литые детали целесообразно разделить на части и делать составную конструкцию, что дает дополнительные возможности по устранению подрезок.
Правила конструирования литых деталей:
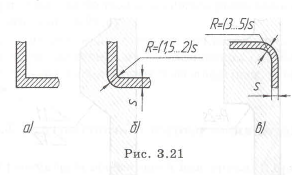
Следует избегать соединения под острым углом. Для сопряжения стенок, расположенных под острым углом, вводят дополнительный участок высотой — 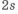
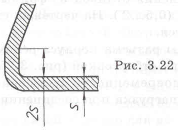
Стенки различной толщины нужно соединять клиновыми переходами (рис. 3.23,6), а не делать резких переходов (рис. 3.23,а).
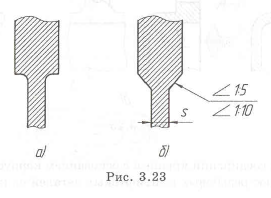
Бобышки соединяют со стенками радиусами 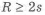
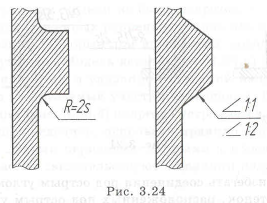
• Поверхности перпендикулярные к плоскости разъема, для облегчения удаления отливок из формы должны иметь литейные уклоны (0,5…2′). На чертежах стандартные уклоны не проставляются.
• Внешние обводы разъема корпуса рекомендуется снабжать но всему контуру отбортовкой (рис. 3.25,а) для увеличения жесткости, одновременности застывания, равномерности распределения нагрузки при соединении и лучшей герметизации стыка.
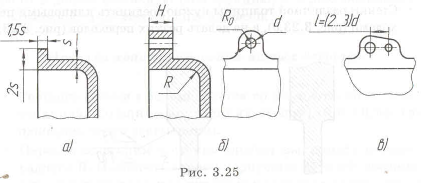
• В местах соединений крышки с основанием корпуса (рис. 3.25,6) с помощью резьбовых и штифтовых деталей на корпусе снаружи делают приливы с радиусом 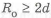
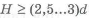
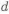
Если приливы для болтов и штифтов расположены близко, то их объединяют (рис. 3.25,в).
Наряду с литыми корпусами из легких сплавов находят применение корпуса, полученные механической обработкой и сваркой. Кроме того, их изготавливают из пластмасс, особенно в бытовой технике.
Другие способы изготовления деталей
Кратко рассмотрим особенности конструкций при других способах изготовления. Ряд правил конструирования существует и для деталей, изготавливаемых штамповкой, прессованием, гибкой, вытяжкой. Например, при штамповке для обеспечения правильного течения металла конфигурацию деталей нужно приближать к простым геометрическим симметричным формам и плавно сопрягать друг с другом. Делать закругления 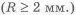
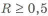
Пример с решением №3.13.
Разработать конструкцию рычага из алюминиевого сплава АК8. Конструкция рычага изготовленного штамповкой приведена на рис. 3.26. Он обладает более высокой прочностью, чем аналогичный литой. Однако для изготовления требуются сложные дорогостоящие штампы, что целесообразно использовать лишь при больших сериях.
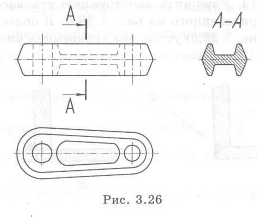
При гибки алюминиевых листов нужно задавать 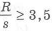
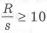
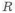
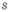
У деталей из пластмасс острые кромки закругляют 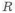
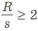
Наиболее простой и надежной является сварка встык. На рис. 3.27 показана сварка встык кожуха. Прочность таких соединений близка к прочности основного металла. Также используются нахлесточные, угловые и тавровые соединения угловыми швами.
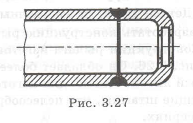
Пример с решением №3.14.
Улучшить конструкцию углового сварного соединения Ш, приведенного на рис. 3.28,а. В более совершенной конструкции (рис. 3.28,6) устранена трудоемкая операция разделки кромки.
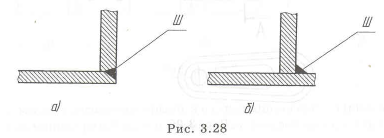
Пример с решением №3.15.
Сделать конструкцию сварного соединения Ш, приведенного на рис. 3.29 более технологичной.
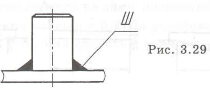
Более качественная конструкция закрепления пальца сваркой приведена на рис. 4.12. В ней палец зафиксирован и сварной шов Ш удален от обрабатываемой поверхности.
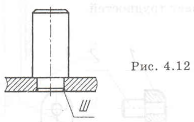

Министерство образования Российской Федерации
_____
САНКТ—ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
В.И. КОРНИЛОВ, А.П. ТЮРИН
ДЕТАЛИ МАШИН И ОСНОВЫ КОНСТРУИРОВАНИЯ
Часть 3
Методические указания по решению задач
Санкт—Петербург Издательство СПбГПУ
2008
УДК 621.81 (075.8)
Корнилов В.И., Тюрин А.П. Детали машин и основы конструирования. Часть 3. Методические указания по решению задач.
СПб.: Изд-во СПбГПУ, 2008.
Пособие соответствует Государственному образовательному стандарту дисциплины «Детали машин и основы конструирования» (ОПД.Ф.02.03), направления бакалаврской подготовки 551800 « Технологические машины и оборудование» и 552900 «Технология оборудования и автоматизация машиностроительных производств»
(ОПД.Ф.05).
Во второй части методических указаний рассматриваются задачи и примеры решения задач по разделам курса: «Подшипниковые опоры» и «Валы, муфты для соединения валов».
Пособие предназначено для подготовки студентов третьего курса механико-машиностроительного факультета к экзамену по дисциплине «Детали машин и основы конструирования».
Ил. 13. Библ.: 3 назв.
СТекст. Корнилов В.И., Тюрин А.П., 2008
СРисунки. Тюрин А.П., 2008
2
|
4. ПОДШИПНИКОВЫЕ ОПОРЫ |
|||||||||||
|
4.1. Подшипник скольжения работает при полужидкостной смазке. |
|||||||||||
|
Радиальная сила, действующая на подшипник, Fr = 27 кН, диаметр цапфы |
|||||||||||
|
d = 40 мм, частота вращения вала n =450 мин-1. |
|||||||||||
|
Fr |
Определить |
минимальную |
длину |
цапфы |
l |
по |
|||||
|
критерию теплостойкости и проверьте подшипник по |
|||||||||||
|
n |
критерию |
износостойкости |
при |
условии, |
что |
||||||
|
допускаемое |
условное |
давление |
[p] |
= |
15 |
МПа, |
|||||
|
d |
допускаемое значение интенсивности работы [p·V] = 12 |
||||||||||
|
МПа·м/с. |
|||||||||||
|
l |
|||||||||||
|
Ответ. l = 53 мм. При этом условное давление p = 12,7 МПа меньше |
|||||||||||
|
допускаемого значения [p] = 15 МПа. |
|
4.2. Радиальный подшипник скольжения (см. рисунок к задаче 4.1) |
||||||||
|
работает при жидкостной смазке с минимальной толщиной масляного слоя |
||||||||
|
hmin = 15 мкм при диаметральном зазоре |
= 150 мкм. |
|||||||
|
Длина цапфы l = 72 мм, диаметр d = 60 мм. |
СF |
|||||||
|
Определить, как изменится минимальная |
8 |
|||||||
|
толщина масляного слоя, если нагрузка на |
7 |
|||||||
|
подшипник уменьшится в два раза. |
l/d=1,2 |
|||||||
|
Используйте |
график |
и |
уравнение |
6 |
||||
|
равновесия Fr = |
μ ×ω |
d × l × CF . |
5 |
0,8 |
||||
|
ψ 2 |
0,4 |
|||||||
|
Примите допущение, что температурный |
4 |
|||||||
|
режим подшипника не изменился. |
3 |
|||||||
|
2 |
||||||||
|
1 |
||||||||
|
0 |
0,5 0,6 0,7 0,8 0,9 |
c |
||||||
|
Ответ. hmin увеличится примерно на 60%. |
3
|
4.3. Радиальный подшипник скольжения (см. рисунок к заданию 4.1) |
||||||
|
работает при жидкостной смазке с коэффициентом запаса по толщине |
||||||
|
масляного слоя sh = 2,5 при диаметральном зазоре |
= 200 мкм |
и |
||||
|
суммарной высоте микронеровностей RZ1 + RZ2 = 10 мкм. |
||||||
|
Длина цапфы l = 48 мм, диаметр d = 60 мм. |
||||||
|
Определить, как изменится коэффициент запаса по толщине |
||||||
|
масляного слоя, если из-за изменения режима охлаждения подшипника его |
||||||
|
температура понизилась, в результате чего динамическая вязкость µ |
||||||
|
увеличилась на 40%. |
||||||
|
Используйте график (см. рисунок к заданию 4.2) и уравнение |
||||||
|
равновесия F |
= μ ×ω d × l × C |
F |
. |
|||
|
r |
ψ 2 |
|||||
|
Ответ. sh увеличится примерно на 30%. |
||||||
|
4.4. Радиальный подшипник скольжения (см. рисунок к задаче 4.1) |
||||||
|
работает при жидкостной смазке с достаточным запасом по толщине |
||||||
|
масляного слоя при угловой скорости вала ω = 50 с-1 и динамической |
||||||
|
вязкости масла µ не менее 0,025 Па·с. |
mt ,ПаÄс |
|||||
|
Подобрать сорт масла в предположении, |
||||||
|
что площадь |
теплоотдающей поверхности |
0,09 |
||||
|
подшипникового узла A = 0,5 м2, температура |
И-45А |
|||||
|
окружающей среды t0 = 20 0C, коэффициент |
0,08 |
И-30А |
||||
|
теплоотдачи kt = 18 Вт/(м2 · 0C). Измеренное |
0,07 |
И-20А |
||||
|
при этих условиях значение момента сил |
0,06 |
И-12А |
||||
|
вязкого трения в подшипнике TТР = 6,4 Н·м. |
0,05 |
|||||
|
0,04 |
||||||
|
0,03 |
||||||
|
0,02 |
||||||
|
0,01 |
||||||
|
30 40 50 60 70 80 90 |
t,Å C |
|||||
|
Ответ. Подходит масло сорта И-45А. |
4

|
4.5. В радиальном роликовом подшипнике качения диаметр ролика d, |
|||||||||||
|
диаметр беговой дорожки внутреннего кольца DВН = 5d, диаметр беговой |
|||||||||||
|
дорожки наружного кольца DН = 7d. |
|||||||||||
|
Определить частоту вращения сепаратора |
d |
||||||||||
|
nС, |
если |
относительно |
корпуса |
||||||||
|
подшипникового |
узла |
наружное |
кольцо |
||||||||
|
подшипника |
неподвижно, |
а |
внутреннее |
n |
D |
В |
Н |
D |
|||
|
-1 |
|||||||||||
|
вращается с частотой n = 1000 мин . |
|||||||||||
|
Н |
|||||||||||
|
А |
Fr |
||||||||||
|
Б |
F |
||||||||||
|
r |
|||||||||||
|
Ответ. nС = 417 мин-1. |
4.6. Радиальный роликовый подшипник нагружен радиальной силой Fr. Размеры роликов и колец подшипника приведены в задании 4.5.
Определить во сколько раз расчетные контактные напряжения σH в контакте по линии A отличаются от напряжений в контакте по линии Б.
|
Ответ. Напряжения (σH)А больше напряжений (σH)Б на 18%. |
||||
|
4.7. Эквивалентная динамическая нагрузка радиально-упорного |
||||
|
шарикового подшипника P = 4000 Н. |
PÄ104, Н |
|||
|
Определить, пользуясь графиком, |
||||
|
базовый |
расчетный |
ресурс |
2,0 |
|
|
подшипника L10h в часах, если |
||||
|
частота вращения вала n = 640 мин-1. |
1,5 |
|||
|
Принять вероятность безотказной |
1,0 |
|||
|
работы |
R(t) = 0,9, коэффициенты |
0,5 |
||
|
Kб = KT = a2 = a3= 1. |
||||
|
0 |
1 2 3 4 5 6 L, млн об. |
|||
|
Ответ. L10h = 3260 ч. |
5
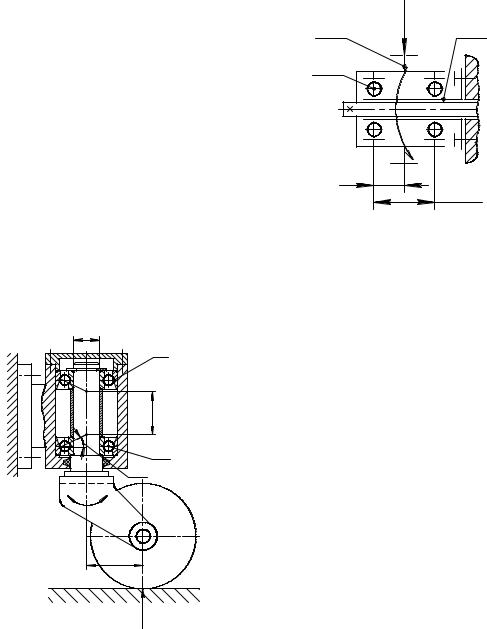
|
4.8. Шкив 1 вращается на двух одинаковых шариковых радиальных |
|||||
|
подшипниках 2 относительно стакана 3 разгрузочного устройства |
|||||
|
ременной передачи. |
|||||
|
Определить |
скорректированный |
1 |
F |
3 |
|
|
расчетный ресурс подшипников L5ah в часах, |
|||||
|
если частота вращения шкива n = 1000 мин-1, |
2 |
||||
|
сила, действующая на |
шкив, F = 2000 Н, |
n |
|||
|
динамическая грузоподъемность каждого из |
|||||
|
подшипников C = 10000 Н. |
|||||
|
Принять вероятность безотказной работы |
|||||
|
R(t) = 0,95, коэффициенты Kб = KT = 1; |
l |
2l |
|||
|
a1 = 0,62; a2 = a3 = 1. |
|||||
|
Ответ. L5ah = 10300 ч. |
|
4.9. Проверить работоспособность подшипников 1 и 2 колесной опоры |
|||||
|
грузовой тележки, в которой использованы шариковые радиально-упорные |
|||||
|
подшипники 46205, если нагрузка на колесо F = 2000 Н и размер b = 0,5·a. |
|||||
|
d |
Принять: вероятность |
||||
|
1 |
безотказной |
работы |
|||
|
Б |
R(t) = 0,9, коэффициенты |
||||
|
Kб = Kt = 1; a2 = a3 |
= 1. |
||||
|
b |
|||||
|
Использовать |
также |
||||
|
А |
|||||
|
данные, |
приведенные |
в |
|||
|
2 |
|||||
|
табл. |
|||||
|
a |
|||||
|
В |
ответе |
указать |
|||
|
серию |
подшипника |
и |
|||
|
значение |
диаметра |
||||
|
a |
посадочной поверхности |
||||
|
внутреннего кольца. |
|||||
|
Угол |
e |
Fa |
£ e |
Fa |
> e |
X0 |
Y0 |
C, |
C0, |
||||
|
контакта |
|||||||||||||
|
Fr |
Fr |
||||||||||||
|
α |
Кн |
Кн |
|||||||||||
|
X |
Y |
X |
Y |
||||||||||
|
26° |
0,68 |
1 |
0 |
0,41 |
0,87 |
0,5 |
0,37 |
12,4 |
8,5 |
Решение следует начать с разработки расчетной схемы оси колесной опоры. Внешнюю нагрузку на консольную часть оси удобно представить в виде осевой силы F и момента пары сил M = F×a. Запишем условие равновесия оси, с учетом того, что при установке радиально-упорных подшипников по схеме “ враспор” расчетное расстояние между ними b.
6

∑M A = F × a — Fr × b = 0 , откуда
|
F |
= F |
= F = F |
a |
. |
|||
|
r1 |
r 2 |
r |
b |
||||
|
Fr2 |
|||||||
|
Fr |
= 2000 × 2 = 4000 Н. |
||||||
Минимальная осевая нагрузка, вызванная действием радиальной силы Fr.
S = e × Fr , где
e – коэффициент осевой нагрузки.
S1 = S2 = S = 0,68 × 4000 = 2720 Н.
|
Fa1 |
Б Fr1 |
|
|
S1 |
b |
|
|
S2 |
||
|
Fa2 |
А |
|
|
a |
F M=Fa
В осевом направлении на вал действуют силы S1, S2 и внешняя нагрузка – сила F. Результирующая сила в рассматриваемом случае равна по величине внешней силе F и направлена верх. Эту дополнительную осевую нагрузку воспринимает подшипник 1. Подшипник, препятствующий перемещению вала под действием осевых сил, определяют как фиксирующий. Тогда для второго нефиксирующего подшипника уравнение равновесия имеет вид
Fa 2 = S2 , где
Fa2 – расчетная осевая нагрузка на подшипник 2.
Fa2 = 2720 Н.
Для подшипника 1 расчетную осевую нагрузку находим из уравнения равновесия
F + Fa 2 — Fa1 = 0 , откуда Fa1 = F + S2 .
Fa1 = 2000 + 2720 = 4720 Н.
Приведенную расчетную динамическую нагрузку на подшипник определяют как радиальную силу P, эквивалентную по разрушающему действию совокупному действию сил Fr и Fa.
P = ( X × Fr + Y × Fa ) × Kб × Kt , где
X и Y – коэффициенты, учитывающие влияние соответственно радиальной и осевой расчетных нагрузок.
Для подшипника 1 Fa1 > e , следовательно X1 = 0,41, Y1 = 0,87.
Fr1
P = (0,41× 4000 + 0,87 × 4720) ×1×1 = 5746 Н.
1
Для подшипника 2 Fa2 = e , тогда X2 = 1, Y2 = 0.
Fr 2
P2 = (1× 4000 + 0 × 2720) ×1×1 = 4000 Н.
7

Расчет по динамической грузоподъемности следует вести по наиболее нагруженному подшипнику, так как расчетная долговечность более нагруженного подшипника 1 будет меньше долговечности подшипника 2. Скорректированный расчетный ресурс подшипника 2
|
3 |
10 |
6 |
|||||||
|
C |
|||||||||
|
Lnah2 |
= a1 × a2 |
× a3 |
× |
, ч. |
|||||
|
P2 |
n × 60 |
Здесь: C – динамическая грузоподъемность, Н;
a1 – коэффициент долговечности, учитывающий заданное значение вероятности безотказной работы (при R(t) = 0,9 a1 = 1);
a2 – коэффициент долговечности, учитывающий особые свойства материала;
a3 – коэффициент долговечности, учитывающий условия эксплуатации;
n – расчетное значение частоты вращения кольца подшипника. Если
частота вращения больше 1 мин-1, но не превышает 10 мин-1, то принимают n = 10 мин-1.
|
12400 |
3 |
106 |
|||||||
|
L10h2 |
=1×1×1× |
=16800 ч. |
|||||||
|
10 × |
60 |
||||||||
|
5746 |
Коэффициент запаса по статической грузоподъемности s0 находят по формуле
s0 = C0 ³ [s0 ], где P0
C0 – статическая грузоподъемность, Н;
P0 – приведенная расчетная статическая нагрузка, Н;
[s0] – допускаемое значение коэффициента запаса. Для большинства конструкций при обычных требованиях к плавности работы принимают
[s0] = 1.
P0 = Max{( X 0 × Fr + Y0 × Fa );(Fr )}.
Для наиболее нагруженной подшипниковой опоры 2
|
P01 = 0,5 × 4000 + 0,37 × 4720 = 3746 или |
P01 = 4000 Н. |
Для расчета коэффициента запаса прочности принимаем большее значение приведенной нагрузки P01 = 4000 Н.
s0 = 8500 = 2,13 . 4000
Ответ. Наименьший расчетный ресурс определен для подшипника 1 Lh102 = 16750 часов. Коэффициент запаса по статической грузоподъемности
8
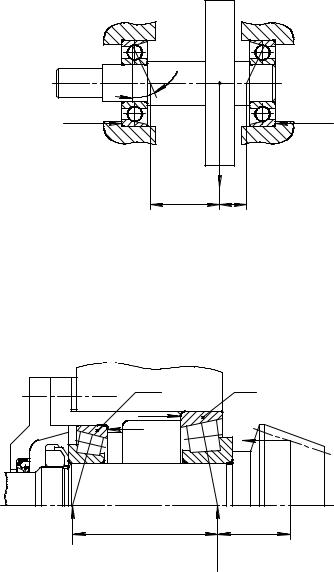
|
подшипника |
1 |
s0 |
= 2,13. |
Работоспособность |
подшипниковых узлов |
||||
|
обеспечена. |
|||||||||
|
4.10. Вал маховика установлен на двух одинаковых шариковых |
|||||||||
|
радиально-упорных |
подшипниках с |
коэффициентом |
осевой |
нагрузки |
|||||
|
e = 0,4. |
1 |
2 |
|||||||
|
Определить |
расчетные |
осевые |
|||||||
|
нагрузки Fa1 и Fa2 , действующие |
|||||||||
|
соответственно на подшипники 1 и 2, |
|||||||||
|
если вес маховика G = 1200 Н. |
a |
||||||||
|
Весом |
вала |
и |
других |
||||||
|
присоединенных деталей допускается |
|||||||||
|
пренебречь. |
Fa1 |
Fa2 |
|||||||
|
2Äl |
G |
l |
|||||||
|
Ответ. Fa1 = |
Fa2 =320 Н. |
|
4.11. Определить расчетные осевые нагрузки Fa1 и Fa2, действующие |
|||
|
на роликовые радиально-упорные подшипники 1 и 2, если радиальные |
|||
|
составляющие реакций в опорах Fr1 и Fr2, равны соответственно 6000 и |
|||
|
10000 Н, а внешняя осевая сила, действующая на вал со стороны |
|||
|
конической шестерни, Fx = 2000 Н. |
|||
|
Принять |
коэффициент |
2 F |
1 |
|
минимальной осевой нагрузки |
|||
|
e = 0,36. |
a1 |
||
|
Fx |
|||
|
Fa2 |
|||
|
l |
a |
||
|
Fr2 |
Fr1 |
||
|
Ответ. Fa1 = 3793 Н, Fa2 = 1793 Н. |
9
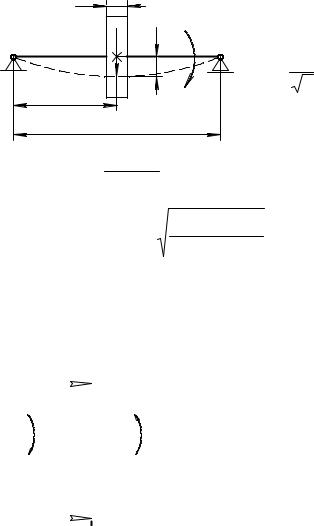
|
5. ВАЛЫ, МУФТЫ ДЛЯ СОЕДИНЕНИЯ ВАЛОВ |
||||||
|
5.1. Вал с установленным на нем диском массой m вращается с |
||||||
|
угловой скоростью ω. Расчетная схема вала показана на рисунке. |
||||||
|
b |
Определить |
выражение |
для |
|||
|
определения минимального диаметра вала |
||||||
|
F |
y |
d, при котором обеспечивается условие |
||||
|
w |
ω £ 1 ω0 |
(безопасная |
работа |
в |
||
|
l/2 |
2 |
|||||
|
дорезонансной зоне), где ω0 – |
собственная |
|||||
|
l |
||||||
|
частота поперечных колебаний вала. |
||||||
|
y = |
F × l |
3 |
Принять диаметр постоянным по всей |
|||
|
длине вала, а толщину b диска – малой по |
||||||
|
48E × J |
сравнению с длиной пролета l. |
|||||
Ответ. d ³ 4 8 × m × l 3 ×ω 2 . 3 ×π × E
5.2.Привод, состоящий из двигателя, жесткой соединительной муфты
иисполнительного механизма, может быть представлен динамической моделью, схема которой представлена на рисунке.
|
À |
Определить максимальный крутящий момент в |
||||||||||||||
|
сечении |
вала |
А-А, |
если моменты инерции |
||||||||||||
|
T2 |
двигателя |
J1 |
= 30 |
Нм·с, исполнительного |
|||||||||||
|
устройства J2 = |
60 Нм·с, муфты J3 = 10 Нм·с, |
||||||||||||||
|
T1 |
движущий вращающий момент T1 = 600 Нм, |
||||||||||||||
|
вращающий момент сил полезного сопротивления |
|||||||||||||||
|
J |
J |
J |
T2 = 600 + 300sinωt. |
||||||||||||
|
1 |
3 |
2 |
|||||||||||||
À
Решение. Для определения крутящего момента T(t) в сечении вала А- А мысленно рассечем привод на две части, после чего для каждой из частей запишем дифференциальное уравнение движения, принимая во внимание жесткую связь между массами J1 и J3:
|
(J1 + J3 )ϕ1 = T1 (t ) — T (t ) |
|||
|
&& |
, где |
||
|
= T (t ) — T2 (t ) |
|||
|
J 2ϕ2 |
|||
|
&& |
T1(t) = Tm – движущий вращающий момент двигателя;
10
Тест (Экзамен)
Дисциплина «Детали машин» ГР213
1.На сколько оборотов необходимо закрутить гайку, чтобы стянуть металлические листы?
A. 8 оборотов B. 10 оборотов
C. 16 оборотов D. 20 оборотов
2. Сталь болта имеет предел прочности на растяжение 1000 МПа.
Прочность болта при испытании 830 МПа.
При преднатяге болта напряжение в стержне достигло 700 МПа.
Находится ли напряжение в рекомендуемых пределах?
-
Да
-
Нет. Преднатяг слишком большой.
-
Нет. Преднатяг слишком маленький
3.Редуктор жестко соединен с электрическим мотором.
Что не является причиной углового смещения валов?
-
Износ зубчатых передач.
-
Чрезмерные радиальные и осевые вибрации.
-
Разлом в вале.
-
Незатянутые болты в основаниях.
-
Чрезмерная утечка масла из подшипников
4.Какая функция смазки не является основной?
-
Снижение трения.
-
Уменьшение нагревания.
-
Снижение изнашивания.
-
Предотвращение коррозии металла подшипника
5. Винтовые зубчатые передачи (II) имеют наклонные зубья.
Какое преимущество использования винтовых передач (II) по сравнению с прямозубыми передачами (I)?
-
.Имеется осевой компонент силы.
-
Тихий и плавный ход.
-
У винтовых передач стоимость изготовления меньше.
6. Какая форма зубьев у колеса?
A В
C D
7.Как влияет увеличение расстояния между центрами колес на передаточное отношение?
-
Передаточное отношение уменьшается
-
Передаточное отношение не изменяется
-
Передаточное отношение увеличивается
8. Входное колесо имеет 9 зубьев.
Какое возможное количество зубьев у выходного колеса?
-
16 — 18 зубьев
-
18 — 20 зубьев
-
16 — 20 зубьев
-
только 18 зубьев
9. Вам необходима зубчатая передача с передаточным отношением 4:1 и выходным колесом вращающимся в том же направлении, что и входное. Выберите подходящую передачу.
A В
C D
10.Каково главное преимущество у составных зубчатых передач (I) по сравнению с одинарными передачами (II)?
-
.Выше передаточное отношение.
-
Корпус с составными передачами имеет меньший размер (высоту) с тем же передаточным отношением.
-
Меньше размер зубьев
11. Тепловой расчет необходим для…
-
фрикционной передачи;
-
коническо-цилиндрического редуктора
-
червячного редуктора.
-
Поясните, за счет чего осуществляется искусственное охлаждение редуктора (см. рис).
-
установка вентилятора на валу червяка
-
установка масляного радиатора;
-
установка в масляную ванну змеевика, по которому пропускают проточную воду.
-
Какой вид ременных передач получил наибольшее распространение в современных машинах?
-
Плоскоременные
-
Клиноременные
-
С плоским ремнем и натяжным роликом
-
Основным недостатком ременных передач является…
-
Непостоянство передаточного отношения
-
Шум при работе
-
Высокая стоимость
-
Низкий кпд
-
Сепаратор в подшипнике……
-
Разделяет и направляет тела качения
-
Увеличивает нагрузочную способность
-
Уменьшает трение
-
Направляет тела качения
-
Общий КПД многоступенчатого последовательного привода равен…
-
произведению КПД всех ступеней;
-
сумме КПД всех ступеней;
-
среднему значению КПД всех ступеней.
-
Назначение вала в машине
-
передача вращения
-
пердача усилия
-
передача крутящего момента
-
фиксация вращающейся детали
-
Что характеризует данное определение: «Деталь предназначена для поддержания установленных на ней шкивов, зубчатых колёс для передачи вращающего момента?»
-
Ось;
-
Вал;
-
Балка.
-
Как называется деталь, показанная на рисунке?
-
Болт;
-
Винт;
-
Шпилька;
-
Винт с потайной головкой
-
Как называется соединение, показанное на рисунке?
-
Клеевое;
-
Сварное;
-
Разъемное;
-
Неразъемное.
-
Как называется деталь 1, изображенная на рисунке?
-
Червяк
-
Шестерня
-
Колесо зубчатое
-
Звездочка
-
Шкив
-
Как называется окружность диаметр которой D 140 мм?
-
Начальная окружность;
-
Окружность вершин зубьев;
-
Делительная окружность;
-
Окружность впадин.
-
Как называется окружность диаметр которой D 130 мм?
-
Окружность ступицы колеса;
-
Окружность впадин;
-
Окружность вершин зубьев;
-
Делительная окружность.
-
Напишите формулу для определения модуля зубчатого зацепления
-
.
;
-
;
-
.
-
Определите, передаточное число червячной передачи, если число зубьев колеса равно
= 30, число витков червяка
= 2
-
60;
-
15;
-
1/15;
-
Определить нельзя.
-
Почему подшипники скольжения состоят из двух или более частей?
-
Для снижения трения;
-
Для снижения термических напряжений;
-
Для облегчения установки и снятия.
-
На какой детали обозначение соответствует дюймовой резьбе?
-
1;
-
2.
-
Какой внутренний диаметр (мм) имеет подшипник 302?
-
0,2;
-
10;
-
15.
-
Резьба М16. Что обозначает цифра 16?
-
Наружный диаметр резьбы;
-
Средний диаметр резьбы;
-
Внутренний диаметр резьбы;
-
Шаг резьбы.
-
Как называется деталь поз.4?
-
Корпус;
-
Кольцо;
-
Радиальный роликоподшипник;
-
Штифт конический.
7
Методические указания по лабораторным работам БНТУ,ч.1 и ч.2
Здесь размещены методические указания БНТУ по проведению лабораторных работ и оформлению отчетов. Данные работы проводятся на базе кафедры ”Детали машин и ПТМ ” БНТУ , часть 1 и часть 2.
Также здесь, вы найдете методические указаний и формуляры для оформления отчетов по лабораторным работам, выполненным на ОАО ”МЗКТ” на базе филиала кафедры.
Прочитать больше
Задача 28
Условие задачи : Определить основные геометрические размеры открытой конической нереверсивной зубчатой передачи привода шнека, если известно: передаваемая мощность N=1,7 кВт; угловая скорость шнека – ω3=6,27 рад/с; угловая скорость входного вала – ω1=148,7 рад/с; передаточное число цилиндрического редуктора – uр=6,3. Срок службы передачи не ограничен. Принять коэффициент неравномерности распределения нагрузки – КНβ=1,5; допускаемое контактное напряжение – [σH]=70 Н/мм2; число зубьев шестерни – z1=20.
Прочитать больше
Задачи 27
Условие задачи : Определить долговечность плоского ремня без прослоек, сечение 125х5мм, передаваемая мощность N=10 кВт. Скорость ремня v=10м/с, диаметры шкивов D1=200мм, D2=450мм. Ремень прорезиненный (модуль продольной упругости – Е=80 Н/мм2, плотность – ρ=1,1 кг/дм3, напряжение от предварительного натяжения – σ0=1,8 Н/мм2, предел выносливости – σу=6 Н/мм2). Межосевое расстояние А=1м. Коэффициент, учитывающий передаточное число принять из таблицы, коэффициент, учитывающий непостоянство нагрузки – Сн=1.
Прочитать больше
Задача 26
Условие задача: Определить натяжение ведущей ветви плоского ремня сечением 125х5мм, если передаваемая мощность N=10 кВт, скорость ремня v=10м/с, диаметры шкивов D1=200мм, D2=450мм. Ремень прорезиненный (модуль продольной упругости – Е=80 Н/мм2, плотность – ρ=1100 кг/м3, напряжение от предварительного натяжения – σ0=1,8 Н/мм2). Вычислить максимальное напряжение в опасном сечении ведущей ветви ремня с учетом действия центробежных сил.
Прочитать больше
Экзаменационные вопросы (примерный перечень) по курсу «Детали машин и основы конструирования» с ответами для студентов очной, заочной и дистанционной форм обучения
Заказать курсовой проект >
Помощь на экзамене по ДМ >
Сохранить и поделиться с друзьями
Вводные понятия в курсе ДМ и ОК
- Вводные понятия в курсе ДМ и ОК. Классификация типовых деталей машин. Требования, предъявляемые к современным машинам. Этапы проектирования ДМ и стадии разработки конструкторской документации.
- Виды нагрузок, действующих на ДМ. Типовые циклы изменения напряжений в сечениях ДМ.
- Основные критерии работоспособности ДМ.
Соединения
- Классификация резьб. Геометрические параметры резьб. Основные типы резьб.
- Момент сопротивления завинчиванию гаек и винтов: момент сопротивления в резьбе и момент сопротивления на опорной поверхности гаек и винтов.
- КПД винтовой пары. Условие самоторможения винтовой пары. Понятие о приведенном коэффициенте трения.
- Расчет витков крепежных и ходовых резьб.
- Расчет на прочность стержня незатянутого болта, нагружаемого только внешней осевой силой (схема 1).
- Расчет на прочность стержня болта (призонного или обычного), нагружаемого поперечной силой (схема 2).
- Расчет группы болтов. Допущения при расчете группы болтов. Порядок расчета группы болтов. Расчет группы болтов (призонных или обычных), нагружаемых усилием и моментом, действующими в плоскости cтыка (1 случай).
- Расчет группы предварительно затягиваемых болтов, нагружаемых внешней продольной силой, с учетом податливостей деталей соединения (2 случай).
- Расчет группы болтов, нагружаемых усилием, действующим в плоскости перпендикулярной стыку и проходящим через одну из осей симметрии стыка (3 случай).
- Соединения призматической, цилиндрической, сегментной, клиновой, тангенциальной шпонками: особенности конструкций, достоинства и недостатки, расчеты на прочность.
- Зубчатые (шлицевые) соединения: достоинства и недостатки, классификация, расчет.
- Расчет соединения с гарантированным натягом (прессового).
- Виды сварных соединений и расчеты их на прочность.
Передаточные механизмы
- Назначение и разновидности механических передач. Основные силовые, энергетические и кинематические соотношения для механических передач вращательного движения.
- Виды повреждений зубьев зубчатых колес.
- Усилия в зацеплении цилиндрических прямозубых колес и расчетная нагрузка.
- Вывод формулы для определения расчетного контактного напряжения в полюсе зацепления зубьев цилиндрической прямозубой передачи.
- Вывод формулы для определения напряжения изгиба в опасном сечении на переходной поверхности зуба колеса цилиндрической прямозубой передачи.
- Выбор допускаемых напряжений при расчете цилиндрических передач на контактную и изгибную выносливость зубьев.
- Достоинства и недостатки косозубых передач и шевронных. Геометрия косозубых колёс. Коэффициент перекрытия зубьев в косозубых передачах.
- Усилия в зацеплении цилиндрических косозубых колес. Особенности расчета косозубых передач на контактную и изгибную выносливость.
- Конические передачи: достоинства и недостатки, классификация, геометрия конических колёс. Усилия в зацеплении конических колес. Особенности расчета конических передач на контактную и изгибную выносливость.
- Червячные передачи: достоинства, недостатки, классификация. Геометрия колес и кинематика червячной передачи. Усилия в зацеплении колес. Особенности расчета червячных передач по контактным и изгибным напряжениям.
- Цепные передачи: достоинства, недостатки, классификация. Конструкции приводных цепей. Расчет роликовых цепей на износостойкость шарнира. Проверка прочности цепи на разрыв. Оценка долговечности цепи. Нагрузка на вал от звездочки цепной передачи.
- Ременные передачи: достоинства, недостатки, классификация. Материалы и конструкции плоских и клиновых приводных ремней. Усилия и напряжения в ветвях ремня. Картина распределения напряжений по длине ремня.
- Расчёт ремней на сопротивление изгибной усталости. Расчёт на тяговую способность по кривым скольжения. Нагрузки на вал от шкива ремённой передачи.
Валы и оси
- Проектировочные расчеты валов на прочность (ориентировочный и приближенный).
- Проверочный (уточненный) расчет вала на сопротивление усталости.
Подшипники
- Подшипники скольжения. Приближенный расчет подшипников скольжения на износостойкость и отсутствие перегрева.
- Подшипники качения: достоинства, недостатки, классификация, условное обозначение. Схемы установки подшипников качения на валах.
- Подбор подшипников качения по статической грузоподъемности.
- Подбор подшипников качения по динамической грузоподъемности.
- Частные случаи определения эквивалентной динамической нагрузки на подшипники (для 5 расчетных схем).
Лекции по деталям машин >
Помощь на экзамене и защите курсовых >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее




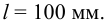
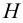
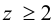
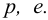
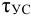
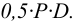
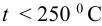
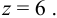
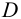
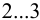
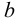
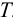 .
.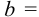
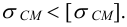
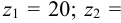
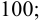
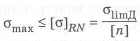 или
или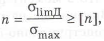 ,
,